Introduction

Concrete, as the primary material supporting construction production, has been widely used in China’s urban infrastructure. The overuse of concrete necessitates the production of large quantities of cement and extensive mining of natural sand and gravel, inevitably leading to severe carbon emission problems that impact the human living environment. Concurrently, a significant amount of waste glass is generated annually in China, yet efficient recycling methods remain scarce1. Against this backdrop, researchers, from the perspective of green energy conservation, have proposed crushing and processing waste glass to replace cement or aggregates in the production of waste glass concrete, thereby integrating solid waste utilization with energy saving and emission reduction, and offering a new avenue for waste glass recycling2,3.

Existing research indicates a strong correlation between the particle size of waste glass and its reactivity. After crushing and grinding, waste glass powder with a particle size below 75 μm exhibits pozzolanic characteristics and can replace cement in concrete4, whereas waste glass particles larger than 800 μm possess high hardness, high compressive strength, and high chemical stability, making them suitable for replacing sand or crushed stone in concrete5. Addressing this characteristic, scholars have conducted numerous studies on various applications of waste glass in concrete, which can be primarily categorized into five types: partial replacement of cement6; partial or complete replacement of fine aggregate7; partial or complete replacement of coarse aggregate8; partial mixed replacement of cement and fine aggregate9; and partial mixed replacement of fine and coarse aggregates10. Research has found that replacing coarse aggregate, fine aggregate, or cement with waste glass at different rates invariably leads to varying degrees of alkali-silica reaction (ASR) issues in the prepared waste glass concrete, causing it to be prone to expansion and cracking. Especially when waste glass is used as coarse aggregate, the workability and mechanical performance of waste glass concrete are unstable with poor regularity, and the risk of ASR is significantly increased11,12,13. These problems restrict the further promotion and application of waste glass concrete, severely impeding the development of solid waste utilization and energy conservation and emission reduction.

To advance the research and application of waste glass concrete, some scholars have proposed filling steel tubes with waste glass concrete to form waste glass concrete-filled steel tubes. This approach utilizes the confining effect of the steel tube on the core concrete to enhance the mechanical properties of the core waste glass concrete and mitigate the alkali-silica expansion defects associated with the incorporation of waste glass14,15,16. However, a literature review indicates that current research on waste glass concrete-filled steel tubes primarily focuses on waste glass as coarse aggregate14, with relatively few studies on replacing river sand or cement in concrete-filled steel tubes with micron-sized waste glass. Although the replacement of sand and cement in concrete with micron-sized waste glass still poses ASR issues, this problem can be somewhat suppressed as the particle size of the waste glass decreases13. Simultaneously, research has found that concrete-filled steel tubes with waste glass coarse aggregate still exhibit certain deficiencies: (1) The bond strength of the interfacial transition zone (ITZ) between the surface of waste glass coarse aggregate and the cement paste is weak, leading to increased brittleness of the core concrete and consequently, poor stability in the mechanical performance of the members; (2) The multi-angular shape and larger aspect ratio of waste glass coarse aggregate surfaces tend to reduce concrete flowability and decrease workability; (3) The risk of ASR remains high, and the internal concrete is prone to expansion and cracking.

In response to the existing research gaps, and to further enhance the mechanical and workability performance of waste glass concrete-filled steel tubes, investigating the mechanical properties of micron-sized waste glass when applied in concrete-filled steel tubes holds significant practical importance. This paper considers replacing sand and cement in concrete-filled steel tubes with micron-sized waste glass sand (median particle size 1072 μm) at four replacement rates of 5%, 15%, 30%, and 60% by equal mass. Four steel tube waste glass sand concrete short columns were cast, along with one ordinary concrete-filled steel tube short column as a reference. Through axial compression tests, numerical simulations, and bearing capacity calculation analysis of these five specimens, the study investigated the influence of different glass sand replacement rates on the axial bearing capacity, failure modes, ductility, energy dissipation, and confinement effect of the steel tube glass sand concrete short columns. This research aims to provide a theoretical reference for the future promotion and application of waste glass concrete-filled steel tubes and to offer an efficient and green pathway for processing waste glass.

Experimental overview

Experimental materials

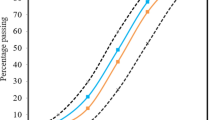
The waste glass used in this experiment to prepare glass sand was sourced from commonly recycled waste glass bottles, flat glass, and other products. Its main chemical composition is shown in Table 1. The technical route for processing waste glass to produce glass sand is shown in Fig. 1, and the particle size distribution of the prepared glass sand (median particle size 1072 μm) is shown in Fig. 2. Ordinary Portland cement was used as the main cementitious material, with a specific surface area of 375 m2/kg and a bulk density of 3.08 g/cm3. River sand with a fineness modulus of 2.9, an apparent density of 2550 kg/m3, and a bulk density of 1.470 g/cm3 was selected. Crushed stone with a particle size range of 5 mm ~ 20 mm was used as coarse aggregate, and tap water was used for mixing.

Table 1 Main chemical composition of waste glass.
Full size table
Fig. 1
figure 1

Technical route for waste glass processing.

Full size image
Fig. 2
figure 2

Particle size distribution curve of glass sand.

Full size image
Table 2 Mix proportion design and basic mechanical indicators of glass sand concrete.
Full size table

Referring to the “Specification for Mix Proportion Design of Ordinary Concrete” (JGJ55-2011)17, glass sand was used to replace river sand and cement in ordinary C30 concrete by equal mass at replacement rates of 5%, 15%, 30%, and 60%, respectively. The mix proportions of the prepared glass sand concrete are shown in Table 2, which also lists its cubic compressive strength fcu, prismatic compressive strength fck, elastic modulus Ec, and peak strain εck.

The steel tube material was Q235 carbon structural steel. According to “Metallic materials - Tensile testing - Part 1: Method of test at room temperature” (GB/T50081-2021)18, reserved steel tubes were cut and processed, and a set of curved cross-section specimens were designed for tensile tests. The measured average thickness t, yield strength fy, ultimate tensile strength fu, elastic modulus Es, and Poisson’s ratio µs of the steel tubes are shown in Table 3.

Table 3 Material properties of steel.
Full size table

Specimen design and fabrication

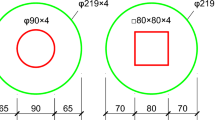
The glass sand concrete prepared as shown in Table 2 was poured into pre-designed steel tubes. A total of 4 steel tube glass sand concrete short columns were designed and fabricated, along with 1 ordinary concrete-filled steel tube short column as a reference, to investigate the effect of glass sand replacement rate on the axial compression performance of concrete-filled steel tube short columns. The slenderness ratio of the short columns was taken as 3.16 according to Zhong Shantong’s recommendation19, with an outer diameter of 114 mm, a tube length of 360 mm, and a measured steel tube wall thickness of 4.03 mm. The circular steel tubes were fabricated using a straight seam welded pipe process, and end plates were welded to the top and bottom. For ease of pouring, a filling hole was reserved in the top end plate. The concrete was poured in three layers, with each layer vibrated once after pouring to ensure compaction. After 28 days of natural curing, the cement laitance on the specimen surface was removed, and mortar was used to smooth the surface at the opening on the upper end of the specimen, ensuring close contact between the end plate, steel tube, and concrete. The geometric dimensions of the steel tubes and site photos are shown in Fig. 3, and the design parameters of each specimen are shown in Table 4.

Fig. 3
figure 3

Geometric dimensions and fabrication photos of steel tube model (unit: mm).

Full size image
Table 4 Design parameters of steel tube glass sand concrete short columns.
Full size table

Measurement point layout and loading scheme

The arrangement of measuring points and the on-site loading device are shown in Fig. 4. Four 120-3AA type resistance strain gauges were evenly pasted around the circumference at the middle of the specimen, including one pair of longitudinal strain gauges and one pair of transverse strain gauges, arranged alternately at 90° intervals, to measure the longitudinal and hoop strains at the middle of the steel tube. One pair of transverse strain gauges was evenly pasted around the circumference at both the top and bottom of the steel tube to measure the hoop strains at the top and bottom of the steel tube. In addition, displacement gauges with a range of 50 mm were arranged at the top and bottom ends of the specimen to measure the axial deformation of the short column.

A 500 t electro-hydraulic servo press was used for loading. To ensure that the specimen was under axial compression, geometric centering was performed to ensure that the geometric centers of the specimen end plate, hydraulic jack, and base remained on the same axis. First, pre-loading was carried out at 5% of the estimated bearing capacity to check whether the data acquisition system, displacement gauges, strain gauges, and the press were functioning normally. Afterward, formal loading was conducted using displacement control at a loading rate of 1 mm/min. Loading was stopped when the load dropped to 70% of the peak load or when the axial compression deformation reached approximately 5 cm, at which point the test was concluded.

Fig. 4
figure 4

The arrangement of measuring points and loading device.

Full size image

Experimental results and analysis

Failure mode

As shown in Fig. 5, the failure modes of all steel tube glass sand concrete short columns were generally similar to that of the reference specimen, all exhibiting a bulging shape failure, characterized by severe bulging in the middle of the short column. Taking specimen GSCFST-30 as an example to illustrate its experimental phenomena and failure mode, in the initial stage of loading, the load was small, and the short column was in an elastic working state, with no obvious deformation observed on the specimen surface. When loaded to about 70% of the peak load, slight buckling began to appear in the upper part of the steel tube. With continued loading, bulging started to occur in the middle of the steel tube, accompanied by cracking sounds from within the specimen. When loaded to the peak load, the core concrete was crushed due to severe bulging in the middle of the steel tube. After the peak load, the axial deformation of the specimen developed rapidly, while the bearing capacity did not decrease significantly, showing good ductility. Most tests were terminated due to excessive axial deformation. Experimental research found that as the glass sand replacement rate increased, the crushed area of the core concrete at the mid-height bulge expanded, and the bulging failure mode changed from a single layer to a double layer.

Fig. 5
figure 5

Bulging axial compression failure mode of steel tube glass sand concrete short columns.

Full size image

Load–displacement curves

As can be seen from Fig. 6, the load-displacement (P-Δ) curves of each specimen are mainly divided into three parts: elastic stage, elasto-plastic stage, and hardening stage. For the steel tube glass sand concrete short columns, in the elastic stage, as the glass sand replacement rate increased, the slope of the P-Δ curve increased. The analysis suggests that this is because the hardness of glass sand itself is greater than that of river sand, and its appropriate addition, under the filling effect, increases the elastic modulus of the concrete, thereby enhancing its resistance to deformation. When the displacement loading reached about 3 mm, the elasto-plastic stage began, and after reaching the peak load, the P-Δ curve showed a slight decrease. When the displacement loading reached about 15 mm, it entered the hardening stage. The loading was eventually terminated due to excessive axial deformation, and no significant descending branch appeared throughout, with even a slight upward trend. Among them, specimen GSCFST-15 had the best bearing capacity. The analysis suggests that the appropriate replacement of river sand with glass sand can improve the aggregate gradation, and coupled with the fact that glass sand itself has higher hardness than river sand, its bearing capacity was significantly improved compared to the reference specimen, while the other specimens were generally close to the reference specimen.

Fig. 6
figure 6

Load-displacement curves of steel tube glass sand concrete short columns.

Full size image

The characteristic values of load and displacement for each specimen are shown in Table 5. Among them, the peak load is the maximum load when the trend of the specimen’s load-displacement curve first changes from rising to falling, and the corresponding displacement is the peak displacement. The definition of ultimate load satisfies the following sufficient conditions20: (1) After the specimen’s bearing capacity reaches the peak load and remains stable or slowly increases, the minimum load in this stage is selected; (2) Obvious deformation appears on the specimen surface, making further loading impossible. The displacement corresponding to the ultimate load is the ultimate displacement. The yield load is taken as the smaller value between the load calculated by the equivalent energy method and 70% of the peak load21, and the corresponding displacement is the yield displacement; (3) All glass sand specimens (µ = 4.7 ~ 5.38) were higher than those of ordinary concrete specimens (µ = 3.94), indicating that the addition of glass sand significantly improves the plastic deformation capacity of the components. Among them, GSCFST-15 performed the best (µ = 5.38), indicating that 15% glass sand replacement rate can form the best particle gradation and optimize the elastic-plastic response of concrete; (4) The energy dissipation value of GSCFST-15 reaches 39,690 J, which is 15% higher than that of the reference specimen (34535 J), which confirms the mechanism that glass sand enhances energy absorption through interface friction during microcrack development. However, when the substitution rate exceeds 30% (such as GSCFST-60), the energy dissipation capacity shows a downward trend.

Table 5 Characteristic values of load and displacement, strength indices, ductility, and energy dissipation of each specimen.
Full size table

Load–strain curves

The load-strain (P-ε) curves at the mid-height of the steel tube are taken for detailed analysis, as shown in Fig. 7, where longitudinal strain is positive and transverse strain is negative. For the steel tube glass sand concrete short columns, when the load was less than 400 kN, the transverse strain was very small, and the longitudinal strain also developed slowly. With continued loading, the growth rate of both transverse and longitudinal strains accelerated, and the strain increased sharply after the steel tube bulged. Overall, as the glass sand replacement rate increased, the stiffness of the specimens improved. When loaded to about 600 kN, the longitudinal strains of specimens GSCFST-60 and GSCFST-30 were not large, while the longitudinal strain of the reference specimen had already reached 0.00925.

Fig. 7
figure 7

Load-strain curves of steel tube glass sand concrete short columns.

Full size image

Ductility and energy dissipation

Referring to literature22, the ductility coefficient of steel tube glass sand concrete short columns is defined as:

$$\mu ={\Delta _{\text{u}}}/{\Delta _{\text{y}}}$$
(1)

Where Δu is the ultimate displacement and Δy is the yield displacement.

The ductility coefficients of each specimen are shown in the preceding Table 5. It can be seen that the ductility coefficients of the steel tube glass sand concrete short columns are relatively high, higher than that of ordinary concrete-filled steel tube short columns. As the glass sand replacement rate increases, its ductility coefficient generally improves, with specimen GSCFST-15 exhibiting the best ductility, an increase of 36.5% compared to the reference specimen. The index E is selected to evaluate the energy dissipation capacity of the steel tube glass sand concrete short columns. E represents the energy absorbed by the specimen when its own materials undergo bending, fracture, stacking, and other states. The calculation formula is as follows21:

$$E{\text{=}}\int_{0}^{d} {P{\text{d}}\delta }$$
(2)

In the above formula, d is the compressive displacement of the specimen; P is the compressive force. As can be seen from Table 5, when the glass sand replacement rate does not exceed 30%, the energy dissipation capacity of the steel tube glass sand concrete short columns is superior to that of the reference specimen, with specimen GSCFST-15 having the strongest energy dissipation capacity, which is 14.9% higher than that of the reference specimen. It is worth noting that the energy dissipation capacity of specimen GSCFST-60 is only 2.5% lower than that of the reference specimen.

Confinement effect

The strength index SI is used to evaluate the enhancement effect of the actual bearing capacity of steel tube glass sand concrete short columns under axial compression compared to the nominal bearing capacity. The calculation formula is as follows23:

$$SI=\frac{{{N_{\text{u}}}}}{{{A_{\text{s}}}{f_{\text{y}}}+{A_{\text{c}}}{f_{\text{c}}}}}$$
(3)

Where Nu is the measured peak load of each specimen; As is the cross-sectional area of the steel tube (mm2); fy is the yield strength of the steel (MPa); Ac is the cross-sectional area of the concrete (mm2); fc is the axial compressive strength of the concrete (MPa).

From the preceding Table 5, it can be seen that the SI values of all specimens are greater than 1, which fully demonstrates the significant confinement effect of the steel tube on the core concrete. The combination of steel tube and concrete achieves an enhancement effect greater than “1 + 1”. For the steel tube glass sand concrete short columns, the steel tube has the best enhancement effect on specimen GSCFST-15, with its SI value increasing by 13.8% compared to the reference specimen. The differences between the other specimens and the reference specimen are relatively small.

Figure 8 shows the change curves of the ratio of transverse strain to longitudinal strain of the steel tube (εsh/εsv) with the longitudinal strain εsv for each specimen, where µs is the Poisson’s ratio of steel. It can be seen that as εsv increases, εsh/εsv of each specimen continuously increases. In the initial stage of loading, the value of εsh/εsv is between 0.2 and 0.3, both of which are less than µs, indicating that the steel tube has not yet exerted its confinement effect at this stage. As the load increases, the value of εsh/εsv becomes higher than µs, indicating that the confinement effect of the steel tube on the core concrete begins to manifest.

Fig. 8
figure 8

Change curves of the ratio of transverse strain to longitudinal strain εh/εv with longitudinal strain εv for steel tube glass sand concrete short columns.

Full size image

Finite element analysis

Model establishment

Both the core concrete and the steel tube were modeled using C3D8R solid elements. The constitutive relationship for steel adopted the secondary plastic flow model24, as shown in Fig. 9a. For the compressive constitutive relationship of the core glass sand concrete, the enhancement coefficient method proposed by Liu Changtian25 was adopted, and it was obtained by modifying the E. Hognestad compressive concrete constitutive model (Fig. 9b). Let T = fck*/fck, where T is the enhancement coefficient for the prismatic compressive strength of concrete, fck* is the equivalent prismatic compressive strength of concrete, and fck is the measured axial prismatic compressive strength of concrete. For circular concrete-filled steel tube short columns, based on the unified theory design method19, fck* is taken as(1.212 + Bξck + Cξck2)fck; this can be determined by substituting the measured axial bearing capacity of each specimen into the calculation formula Nu=Asc༈1.212 + Bξck + Cξck2༉fck and then performing a conversion. Let I = ε0*/ε0, where ε0 is the peak strain of ordinary concrete, ε0* is the peak strain of glass sand concrete (see Table 2), and I is the peak strain enhancement coefficient for concrete. The calculation results for the strength enhancement coefficient T and the strain enhancement coefficient I are shown in Table 6.

Fig. 9
figure 9

Material constitutive relationships.

Full size image
Table 6 Calculation results for strength enhancement coefficient T and strain enhancement coefficient I.
Full size table

The tensile constitutive model for the core concrete was defined using the concrete fracture energy criterion recommended by Tao26, where GFI was selected for tensile behavior, and the fracture energy GF and the concrete cracking stress σt0 were calculated according to Eqs. (4) and (5), respectively. In the equations, fc’ is the standard value of the cylindrical compressive strength of concrete (MPa); dmax is the maximum size of coarse aggregate, taken as 25 mm.

$${\sigma _{{\text{t0}}}}=0.1{f_{\text{c}}}^{\prime }$$
(4)
$${G_{\text{F}}}=(0.0469d_{{{\text{max}}}}^{{^{2}}} - 0.5{d_{\hbox{max} }}+26){(\frac{{{f_{\text{c}}}^{\prime }}}{{10}})^{0.7}}$$
(5)

The contact surface between the concrete and the steel tube was modeled using surface-to-surface contact, with hard contact in the normal direction and frictional contact in the tangential direction, with a friction coefficient of 0.3. The boundary conditions of the model were set according to the loading scheme of the axial compression test.

Simulation result analysis

The numerical simulations were performed using Abaqus27, a finite element simulation method based software. The model incorporates contact interactions in the normal direction and bond-slip behavior in the tangential direction. Coupling reference points were established at the geometric centers of both the top and bottom surfaces of each axially compressed short column model to apply boundary conditions. Surface-to-surface contact interactions were implemented between the end plates, steel tube, and concrete core. Considering the dimensions of the specimens, finite element models with mesh sizes ranging from 2 mm to 20 mm were established successively for trial calculations to evaluate the influence of mesh size on the simulation results, based on this assessment, an optimized mesh size of 8 mm was selected. The degrees of freedom in 6 directions of the bottom reference points of both models were constrained, and loading was performed by applying longitudinal displacement on the reference points.

Figure 10 shows the Mises stress contours for the steel tube and core concrete of each specimen, as well as the compressive and tensile damage contours for the two-dimensional elements of the core concrete. Comparing the actual failure modes of each specimen with their stress distribution contours, it can be seen that the simulation results are in good agreement with the experimental results. From the damage contours, it is evident that under the ultimate state, the compressive damage of the core concrete is mainly located in the middle and upper parts of the specimen. The compressive damage contours show clear stratification, indicating that during the loading process, under the combined action of the steel tube confinement effect and the glass sand filling effect, the internal concrete gradually densified, and compressive stress could be transmitted relatively uniformly and continuously. For the tensile damage of the core concrete, the distribution range is larger and more dispersed, the tensile damage contours are less distinct, and the damaged area expands as the replacement rate increases. Figure 11 shows a comparison of the load-displacement curves obtained from finite element calculations with the experimental data. It can be seen that the two are in good agreement, and the established finite element model can effectively simulate the entire axial loading behavior of each specimen.

Fig. 10
figure 10

The Mises stress distribution for the steel tube and core concrete.

Full size image
Fig. 11
figure 11

Comparison of numerical simulation results and experimental results of load-displacement curves.

Full size image

Axial bearing capacity calculation

Calculation formula based on unified theory

The unified theory treats concrete-filled steel tubes as a unified whole, considering them as a new type of composite material composed of steel tubes and concrete. Among these, the calculation formula (6) proposed by Han Linhai28 and the calculation formula (7) proposed by Zhong Shantong19 are relatively representative.

$${N_{\text{u}}}={A_{{\text{sc}}}}(1.28+1.15{\xi _{{\text{ck}}}}){f_{{\text{ck}}}}$$
(6)
$${N_{\text{u}}}={A_{{\text{sc}}}}(1.212+B{\xi _{{\text{ck}}}}+C{\xi _{{\text{ck}}}}^{2}){f_{{\text{ck}}}}$$
(7)

Where Asc is the cross-sectional area of the member (mm2); fck is the measured compressive strength of the core concrete (MPa); ξck is the confinement coefficient, ξck = Asfy/(Acfck), Ac is the cross-sectional area of concrete (mm2), As is the cross-sectional area of the steel tube (mm2), fy is the yield strength of steel (MPa); B, C are control coefficients, B = 0.1759fy/235 + 0.974, C = 0.1038fck/20 + 0.0309.

Calculation formula based on limit equilibrium theory

The limit equilibrium theory considers the confinement effect of the steel tube on the core concrete, improving the effective utilization rate of steel and concrete. The formula for calculating the axial bearing capacity of concrete-filled steel tube short columns specified in China’s “Technical Specification for Concrete-Filled Steel Tubular Structures” (CECS28-2012)29 is based on the limit equilibrium theory, as follows:

$${N_{\text{u}}}=\left\{ \begin{gathered} 0.9{A_{\text{c}}}{f_{{\text{ck}}}}(1+{\alpha _0}{\xi _{{\text{ck}}}}){\text{ 0}}{\text{.5<}}{\xi _{{\text{ck}}}} \leqslant {\text{[}}{\xi _{{\text{ck}}}}{\text{]}} \hfill \\ 0.9{A_{\text{c}}}{f_{{\text{ck}}}}(1+\sqrt {{\xi _{{\text{ck}}}}} +{\xi _{{\text{ck}}}}){\text{ }}\left[ {{\xi _{{\text{ck}}}}} \right]<{\xi _{{\text{ck}}}} \leqslant 2.5 \hfill \\ \end{gathered} \right.$$
(8)

Where α0 is a control coefficient, with a recommended value of 2 in the specification; [ξck] is the limit value of the confinement effect coefficient, with a recommended value of 1 in the specification; Ac is the cross-sectional area of concrete (mm2), fck is the measured compressive strength of core concrete (MPa).

Discussion of bearing capacity calculation formulas

Formulas (6), (7), and (8) were used to calculate the axial bearing capacity of the steel tube glass sand concrete short columns, and the calculated values were compared with the experimental values (see Table 7). It can be seen that the calculation accuracy of all three bearing capacity calculation formulas is relatively high. Among them, the calculated values from Han Linhai’s formula are generally slightly larger than the experimental values, with a maximum error of 6% for the steel tube glass sand concrete short columns. The calculated values from Zhong Shantong’s formula are generally conservative, mostly slightly smaller than the experimental values, with a maximum error of 9% for the steel tube glass sand concrete short columns. For the steel tube glass sand concrete short columns, the CECS28-2012 formula has the highest calculation accuracy, with a maximum error of 4%.

In summary, if calculating the axial bearing capacity of steel tube glass sand concrete short columns, this paper recommends using the CECS28-2012 specification formula. It should be noted that for the axial bearing capacity of steel tube glass sand concrete short columns, Zhong Shantong’s formula can be used for a conservative calculation, and its calculation results are relatively accurate and on the safe side.

Table 7 Comparison of calculated and experimental bearing capacity values for each specimen (Unit: kN).
Full size table

Conclusions

This study focuses on the goals of resource utilisation of construction solid waste and energy conservation and emission reduction. Through experiments, finite element simulations, and theoretical calculations, it systematically investigates the influence of waste glass sand replacement rates (0%, 5%, 15%, 30%, and 60%) on the axial compressive behaviour of glass sand concrete-filled steel tubular short columns. The aim is to provide theoretical support for the efficient utilisation of waste glass and the engineering application of glass sand concrete-filled steel tubes. Based on the ordinary C30 concrete-filled steel tubular stub columns, this study designed four groups of glass sand concrete-filled steel tubular short columns with different glass sand replacement rates (5%, 15%, 30%, and 60%). Axial compression tests were conducted to analyse their failure modes, load-displacement curves, ductility, energy dissipation capacity, and confinement effect. A finite element model was established to verify the reliability of the experimental results. Meanwhile, the calculation accuracy of formulas such as CECS28-2012, Zhong Shantong’s, and Han Linhai’s for axial bearing capacity was compared.

The results show that all specimens exhibit buckling failure, and the central buckling is obvious. With the increase of glass sand replacement rate, the crushing area of core concrete expands, and the failure mode changes from single-layer buckling to double-layer buckling. The ductility of specimens with glass sand replacement is higher than that of ordinary concrete-filled steel tube, and the ductility of specimens with 15% replacement rate is the best (increased by 36.5%). When the replacement rate is less than 30%, the energy dissipation capacity is better than that of the reference specimen, and the strongest energy dissipation capacity was achieved at a 15% replacement rate (increased by 14.9%). The calculation error of CECS28-2012 formula is less than 4%, and the accuracy is the highest. The results of Zhong Shantong’s formula are conservative and suitable for scenarios with high safety reserve requirements. Finally, the finite element model can effectively simulate the whole process of axial compression, and the load-displacement curve and stress distribution are in good agreement with the experimental results.

This study confirms the feasibility of replacing fine aggregates and cement with waste glass sand in concrete-filled steel tubes. It not only provides a new path for the resource utilisation of waste glass but also offers references for the mechanical property optimisation and bearing capacity design of glass sand concrete-filled steel tubes, thus possessing both environmental protection value and engineering significance.