Void discovery inside Esztramos Hill using muographic methods

Abstract

Muography is a novel geophysical method that allows the determination of density distribution inside large objects by measuring the flux of cosmic muons that travel through them. By comparing the measured data with atmospheric muon flux models and conducting 3-D muographic inversion on multiple datasets it is possible to accurately locate density anomalies that might indicate cavities. The Esztramos Hill, located in northeastern Hungary, was subject to decades of iron ore and limestone mining, which led to the discovery of multiple caves ranging from a few to a few hundred meters in length. A muographic detector system was installed in four positions inside one of the abandoned drifts to explore the surrounding area over several months. The evaluated data confirm the location of partially collapsed, inaccessible mined-out stopes and indicate the existence of a possible cave nearby.

Introduction

The underground mining of iron ore in the Esztramos Hill began in 1893 and lasted until 1960, producing over 160,000 tons of ore during its time span¹. Also, between 1948 and 1997 the top of the hill was subject to large scale limestone quarrying, which reduced the maximum height of it by 60 meters. The resulting, roughly flat surface can be observed on the satellite image of the site on Fig. 1. During these mining operations dozens of natural caves, ranging greatly in size, were discovered on various levels of the hill^2,3, but unfortunately many of them were destroyed or filled up with debris. However those that survived were placed under the protection of the Aggtelek National Park of Hungary, with the most exceptional ones being added to the UNESCO World Heritage list in 1995⁴.

Fig. 1

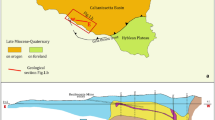
Google satellite image⁵ and position of the Esztramos Hill inside Hungary, located between the villages of Bódvarákó and Tornaszentandrás. The surface mining left the limestone on the top of the hill flat and exposed, both of which are ideal for muography. The location of the conducted measurements is marked with purple. (Imagery date: 2018-Apr-18).

Most of the caves in Esztramos Hill were formed in the triassic crystalline limestone² of the Steinalm Formation (marked with ’3’ on Fig. 2A). The ones on lower levels, located at roughly 170 meters above sea level (masl) formed around fractures and structural lines of approximately northwest-southeast direction² and the ones near the surface, around 300 masl, developed in the phreatic zone under the karstic water table in Middle Pliocene and Early Pleistocene times⁶. Muography is a radiographic imaging technology based on the measurement of cosmic muon particles passing through the observed body. The well known properties of this cosmic muon radiation and its absorption process⁷ allow the exploration of large objects, such as volcanoes^8,9 and pyramids^10,11. The method is sensitive to the inner density distribution of the observed body and it has been proven as suitable tool for cavity research in several projects^{11,12,13,14,15,16}. It is a non-invasive, inexpensive technology that can be safely deployed in such harsh environments as mines and caves^17,18,19,20. The abundance and wide distribution of caves provided the motivation for our team to conduct a muographic measurement campaign by installing an MWPC-based detector system in the lower levels of the abandoned iron mine. Esztramos is an ideal area for muographic research because the limestone quarrying removed most of the sediment from the top of the hill, making the explored rock volume fairly homogeneous in density, while also flattened it, making it easy to create a digital model of the surface. Underground muographic measurements explore a roughly cone shaped segment of the rock above their position (marked by a semi-transparent green cone on Fig. 2B). An extensive muographic survey has been continuously going on since 2019, with the four measurements published in this paper taking place between March and December of 2020.

Fig. 2

(A) Geological profile of the Esztramos Hill^21,22. 1: Edelényi Variegated Clay Formation—Pannonian, 2: Gutenstein Formation (dolomite)—Middle Triassic, 3: Steinalm Formation (crystalline limestone)—Middle Triassic, 4: Szentjánoshegy Limestone Formation (cherty limestone)—Middle Triassic, 5: Tornaszentandrás Shale Formation (shale)—Upper Triassic. (B) The laser scanned cavities and surface from the viewpoint of the geological profile. The positions of the detector system are marked with purple spheres, while the explored volume by one of the measurements is marked with a green cone with the half angle of $50^{\circ }$ as an example.

Results

Experimental setup and study area

Since the end of iron ore mining in the Esztramos Hill, the structure of the tunnels inside have greatly degraded, and large parts were left inaccessible by partial collapses. As a result of these conditions, it is incredibly dangerous to explore these areas in person, which is the main reason why muographic techniques were required. Thankfully in 2009 the 7th level of the mine (at 180 masl) was partially renovated, which provided the right conditions for a muograph to be safely installed therein. New maps of the mine were also created based on the original archive data^23,24. The experimental setup that is deployed in the Esztramos Hill is a gaseous, MWPC-based muographic detector system that is capable of detecting the 3-D trajectories of muon particles that pass through it by utilizing their ionizing effect¹⁸. The detector system, called ’MTL-1’ can operate in the harsh environment of the mines, running on the local electric grid and a portable gas cylinder for months before needing to be resupplied. The explored area is located near a raise, at the end of one of the mine’s main drifts, which itself was dug through an existing, vertical cave. The raise is too dangerous to climb and the top of it cannot be connected to any of the currently accessible parts of the mine. To explore the surrounding area, four measurement positions were chosen which are indicated on both parts of Fig. 3 and their details, such as position, time of operation and number of detected muons are listed in Table 1.

Table 1 Details of the four measurements. Coordinates are provided in the EOV/HD72 coordinate system.

Fig. 3

(A) The currently accessible parts of the abandoned iron mine, colored by elevation. (B) White bodies indicate the largest extent of the currently inaccessible old mining operations based on contemporary maps^23,24.

Table 2 Details of the digitally reconstructed, inaccessible mine segments shown on Fig. 3B.

As it is shown on Fig. 3B, there are several parts of multiple levels of the mine that could not be scanned due to their poor condition. Their names and approximate elevation are shown in Table 2. These cavities take up a large portion of the explored rock volume and yield considerable effects on the resulting muograms.

Muographic images and 3-D inversion

By evaluating the measured flux data a muogram was created for each of the measurement runs, shown on Fig. 4. The number of absorbed muons along a trajectory is a monotonically decreasing function of its length and the average density along it. The product of these two values is called opacity, and it can be derived from the measured muon flux²⁵. This grants the opportunity to measure the length of rock in each direction if an average density is assumed. These muographic images depict the difference of this measured rock length and detector-to-surface distance, calculated from the scanned digital models. The largest and most coherent shapes are caused by the inaccessible parts of the mine, depicted on Fig. 3B and listed in Table 2. These are the combined effect of segments I, II, III, IV and V in the northeastern direction on Run142, IV in the northern and I, II, III, V in the northeastern direction on Run143, III and IV in the southwestern and I, II and V in the northeastern direction on Run144 and Run145. The outlines of the areas where these known cavities are located are marked with white dotted lines on the muograms. On each of the images, areas with apparent excess of rock appear in the northeastern direction, highlighted by dashed blue lines. This is caused by the proximity of a geological boundary, shown on Fig. 2A. The slightly higher average density of dolomite compared to limestone causes the measured rock length to increase in the areas affected by it.

Fig. 4

Missing rock values of the four measurements. Azimuth angle is depicted on the edge of the muograms, zenith angle increases outwards from the central direction. Cardinal directions are indicated on the edges. An average density of 2.71 $\mathrm {g/cm^3}$ was used to convert opacity to rock length. White dotted lines mark the outlines of areas affected by known cavities, continuous green ones mark those affected by the void identified by inversion and dashed blue lines mark the effect of the nearby dolomite.

Muographic inversion is an underdetermined mathematical problem, due to the small number of measurement positions compared to the large number of voxels. The explored area is only accessible from underneath, which also limits the vertical resolution of the method. This effect causes the density anomalies of large cavities, such as the stopes of the 2nd and 4th level to be smoothed vertically, and also causes small artifacts of low density to appear closely over each detectors position, concentrated into the volume that is not yet intersected by the area of view of other measurement positions. In this paper we calculated the density distribution of the study area based on opacity results from the four measurements, using a voxel size of $1.8\times 2.1\times 2.7$ m. Relevant slices of the inverted density distribution are shown on Fig. 5. From these results a previously unknown low density anomaly was identified, marked by a continuous brown line, located in close proximity of the raise. The anomaly was also projected to the muograms and its position and extent are marked by green lines on Fig. 4.

Fig. 5

Slices of the 3-D inversion results. White dotted lines outline the effects of known cavities and continuous brown ones mark the newly identified void. At the lowest elevation, areas with low inverted density can be seen in the location of the raise and above the positions of Run144 and Run145. As elevation increases, an elongated anomaly in the north direction from the raise starts to appear with low density, separating from it at 228 masl. The anomaly retains its shape and intensity for roughly ten meters upwards, beginning to lose integrity above 240 masl.

Discussion

The results of the muographic measurements conducted in the abandoned iron ore mine of Esztramos Hill suggest the existence of a previously unknown void in the mine’s southwestern wing. The results show the existence and extent of several density anomalies and cavities inside the hill, both on 2-D muographic images (Fig. 4) and on 3-D muographic inversion data (Fig. 5). The large density inhomogeneities detected correspond well with our knowledge of the hill’s inner structure (Fig. 3B). We were successfully able to measure both the change in average rock density caused by a geological boundary (shown on Fig. 2A) and the effect of man-made cavities that are known, but have been inaccessible for over 60 years. The results of the 3-D muograpic inversion indicate the existence of a previously unknown density anomaly (shown on Fig. 6A) in the northern direction from the nearby raise. Its shape suggests, that the raise itself was originally dug through a cave with large vertical extent. The narrow, but tall southern parts of this cave provided the location for the measurement ’Run143’, and can be seen on Fig. 6B. We conclude that the discovered density anomaly is most probably caused by a void, which is likely a part of this cave system, based on its shape, size, orientation and location.

Fig. 6

(A) Voxels of the low density anomaly (inverted density is in the $2.5-2.6 \ \mathrm {g/cm^3}$ range) colored by elevation. (B) The continuation of the raise’s cave in the southern direction with the person holding the flashlight standing in the position of Run143.

Fig. 7

Pictures of the accessible bottom of the raise, that has an approximate diameter of 3.5 m. The point where its straight shape breaks can be observed on the original (A) and the zoomed photo (B).

Due to the restrictions of the measurement area we have not yet been able to confirm the existence of the void by other methods, such as drilling. Climbing the raise is prohibited and only the bottom part of it can be observed, as at one point its straightness is broken, blocking further view upwards. This can be seen on Fig. 7 and it is represented in the inversion results by the corresponding low density region’s slight shift to the northeastern direction, depicted on slices A–D of Fig. 5. The shape of this proposed cave limits its detectability from the sides, as its narrowness results only in small anomalies when observed from those directions. Positioning the detector in line with the cave’s main axis yields considerably higher missing rock values, as it can be seen on the muograms of Fig. 4, however in the case of ’Run143’ this is disturbed by the effect of the raise. This is the reason why our conclusions are mainly based on the less ambiguous results of the 3-D inversion.

Methods

Detector system and data acqusition

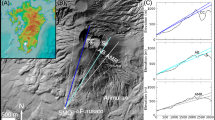
During the campaign all measurements were conducted by the ’MTL-1’ muograph detector (depicted Fig. 8B), designed and built at HUN-REN Wigner RCP. The muograph uses eight layers of position sensitive MWPC²⁶ based gaseous particle detectors, optimized for high efficiency and large area operation in challenging environmental conditions¹⁸. The individual muons leave hits on some or all of the eight layers, and with a straight line fit the direction of the individual tracks can be reconstructed. After correction for detection efficiencies and acceptance the angle dependent differential muon flux is determined²⁷. The intrinsic angular resolution is about 0.7 degrees. The detection (tracking) efficiency, defined by the probability of a valid hit in a specific detector layer in case hits in all but that layer form a good quality track, was typically 96–98%. The condition for accepting a track for flux calculation required at least 7 valid hits in such geometrical configurations where 8 hits are expected. This condition ensures a very high ( > 99%) global track finding probability²⁸, as it is shown on figure 8/A.

Fig. 8

Tracking efficiency time evolution during the measurement campaign, with labels marking the start of each run on (A), and a picture of the ’Mtl-1’ detector system inside the Esztramos-Hill on (B). The high and stable efficiencies of all the layers of the muograph during the data taking period ensured the good quality of the used raw data.

Data evaluation

The campaign ran for a total of 9 months and 6 days, during that time over 10,300,000 events were recorded, roughly 4,200,000 of which were classified as muon tracks. The first step in creating a muogram is to divide the area of view into bins and determine the number of muon tracks (N) they contain. During our calculations we used a bin size of 2 degrees. From this information, the muon flux can be calculated²⁷ and its uncertainty can be derived from $\sqrt{1/N}$. In this paper we only used bins with a flux uncertainty no higher than 10%. By comparing the measured flux to atmospheric flux models the measured opacity can be calculated, which is equal to the length of the rock along the muon trajectory, multiplied by its average density. There are several available atmospheric muon flux models, during this campaign we used Reyna’s parametrization²⁹ for the opacity conversions. We created 3-D models of the hill’s surface and its accessible cavities and tunnels using a portable laser scanner. These digital models were used to calculate the distance between the detector positions and the surface. By dividing the opacity with the local limestone’s average density (which we assumed to be $2.71 \ \mathrm {g/cm^3}$ based on archive reports from the mine²³) we also measured the length of rock to the surface. By taking the difference of the real rock length and the detector-to-surface distance we were able to calculate the amount of missing rock in each direction. The quality of the resulting images was increased by subtracting the distance measured from the detector to the roof of the drift from the missing rock values. The main steps of this process are depicted on figure 9.

Fig. 9

An example of the steps in the process of creating a muogram. The number of recorded muon tracks during the measurement ’Run143’ are shown on (A), the muon flux on (B), the measured opacity on (C) and the opacity calculated from the digital models on (D).

3-D muographic inversion

The classical method of muographic imaging produces 2 dimensional results in the form of flux maps and muograms. Cavity research often requires more precise datasets due to the complexity of geological structures. A mathematical method of solving the 3-D muographic inversion problem was developed and validated on high precision underground muographic measurements conducted by the HUN-REN Wigner RCP³⁰. The problem is largely underdetermined and ill-posed, due to the low number of measurements compared to the high number of voxels and narrow angle mapping, but by introducing geologically relevant Bayesian constraints, such as the characteristic density of the surrounding rock as a prior assumption, the inversion can be stabilised. In this paper a linearized, opacity based inversion was conducted on the datasets recorded from the four measurement positions in the campaign. The a priori assumption for the density distribution is the solid limestone model, which is based on the presumption that the fraction of fracture cavities in the whole rock volume under investigation is assumed to be small. Accordingly, the expected value of the a priori densities was $2.7 \ \mathrm {g/cm^3}$ for all voxels. The prior distribution of voxel densities is assumed to be multivariate Gaussian with a diagonal covariance matrix with 0.2 $\mathrm {g^2 \, cm^{-6}}$ uniform variances. This characterizes the reliability of the a priori information about the voxels, which determines the weight factor of this information in the estimates. Adding non-diagonal elements to the covariance matrix was investigated and resulted in reduced noise, but the inversion became less sensitive to sudden changes and small details, so the current one was chosen for inclusion in this paper. The cavities appearing in the results are the results of inversion, as the a priori model did not include known cavities, so their appearance provides an opportunity for verification. The structures in the results appear somewhat blurred, however this effect is natural, in single muograms they are partly caused by the limited angular resolution of the detector system and mostly by spatial discretization (binning) and the multiple-scattering of muons on the material of the mountain rocks³¹. Blurriness in the inversion results is mostly caused by the the effects inherited from the muograms, and the voxelization process, as real objects are usually not contained in a single voxel but influence multiple nearby ones.