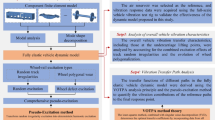
Abstract
This study examines the natural frequency and frame vibration pattern of the tractor vibration system, with an agricultural wheeled tractor serving as the research object. Theoretical natural frequencies of vertical and pitching vibrations for a planar vibration model of a tractor with two-degree-of-freedom biaxial rigid suspension were derived, and experiments were conducted to test the vibration characteristics and natural frequency of a tractor traveling at moderate speeds on a Class D road surface. Modal analysis of the structure of the tractor frame was then carried out using ANSYS Workbench software. The findings indicate that the vertical and pitching vibrations of the fuselage are interrelated, with the natural frequency being contingent upon the mass of the tractor, the rotational inertia, the stiffness coefficients of the front and rear tires, and the axle spacing of the front and rear axles. The vertical vibration intrinsic frequency is mainly affected by the “mass + front and rear tire stiffness”, the pitch vibration intrinsic frequency is determined by the “moment of inertia + front and rear wheel stiffness + wheelbase” together. The natural frequency of the tractor fuselage resulting from engine operation is predominantly concentrated within the 0–40 Hz range. The natural frequency of the tractor vibration system is primarily concentrated within the range of 3 to 5 Hz. The peak natural frequency of the front axle is markedly higher than that of the rear axle, and the peak natural frequency in the pitch direction at the center of mass of the fuselage is higher than the natural frequency of the vertical vibration. The vibration amplitude in this frequency range can be reduced through frame optimization (e.g. optimizing the front and rear axle wheelbase and damping matching for the coupling characteristics of pitching vibration), which can directly improve comfort. The intrinsic vibration pattern of the tractor frame is predominantly a modal vibration pattern, characterised by overall vibration. The first, second and third orders represent first-order bending vibration patterns, while the fourth order indicates localised vibration. The fifth and sixth orders correspond to second-order bending vibration patterns. There is a “directional weak zone” in the overall stiffness distribution of the tractor frame, and the bending stiffness along the length direction of the frame presents “multi-region synergistic insufficiency”. It is necessary to eliminate the multi-order coupling basis of the first-order bending vibration through the “whole-area stiffness balanced design”, such as optimizing the spacing of the cross beams and adjusting the gradient distribution of the cross-section moment of inertia along the length direction. The intrinsic frequency of second-order bending vibration can be enhanced through “end stiffness enhancement design”, such as adding variable cross-section longitudinal beams at the rear of the frame and adopting bionic bending-resistant structures, to avoid the attenuation of dynamic performance under high-frequency working conditions.
Similar content being viewed by others
Introduction
The advancement of vibration theory and associated fields has prompted a shift in the conventional approach to structural design, which previously relied solely on static strength theory. In practice, a considerable number of structures are in motion as a result of external excitation or their intrinsic dynamics, thereby displaying characteristics associated with vibration. It is therefore evident that the design and evaluation of these machines must necessarily take into account their dynamic characteristics1,2. The rapid development of agricultural mechanization has led to the emergence of high-power tractors as a crucial power machine in agricultural operations3,4. The use of rigid suspension between the tractor’s components is typical, as it allows for greater stability when traversing uneven terrain. However, this also results in increased vibration levels. The tractor’s vibration system, in particular, is a crucial aspect to consider, as it influences the transmission of vibrations. When the excitation frequency and the tractor’s natural frequency are closely aligned, resonance can occur, leading to reduced operational efficiency, amplified vibration, and potential damage to the mechanical structure. Concurrently, when the tractor’s excitation frequency coincides with the driver’s body parts’ natural frequency range, it is simple to induce driver fatigue, which may result in damage to driver body parts5,6,7,8. It is therefore of great importance to study the natural frequency of the vibration system of the tractor, as well as to perform modal analysis of important mechanical structures.
The natural frequency of the tractor system has also been the subject of extensive research by scholars from both domestic and foreign academic institutions. Gang Xu et al. employed theoretical calculations and experimental tests to investigate the natural frequency of vertical, pitch, and side tilt vibration in a domestic tractor vibration system. Their findings indicate that the natural frequency of the tractor vibration system is primarily influenced by the stiffness of the tires, the quality attributes of the tractor, and the structural parameters. The installation position of the tractor components exerts a certain influence on the natural frequency of the tractor vibration system. The findings indicate that the natural frequency of the tractor vibration is at its maximum, followed by the pitch vibration natural frequency, with the natural frequency of the vibration being at its minimum. The results demonstrate that the natural frequency of tractor vertical vibration is the largest, the natural frequency of lateral tilt vibration is the second largest, and the natural frequency of pitching vibration is the smallest9. Jinlin Xue et al. studied the transverse natural frequency of the tractor vibration system and showed that the transverse natural frequency decreases with an increase in driving speed and is associated with the stiffness coefficient of the tire10. Jiaqi Yuan et al. studied the vibration characteristics of the tractor under different driving conditions, the results show that the peak frequency of the acceleration power spectrum is is primarily concentrated between 1 and 5 Hz. They also noted that the peak frequencies of the front and rear axles are higher than those of the cab and seat position, which generally exhibit lower longitudinal and transverse peak frequencies. Additionally, the vertical direction showed a higher peak value of the acceleration power spectrum, which tended to increase with increasing driving speed11. Yong Chen et al. evaluated the tractor vibration using the power spectral density (PSD) curve and the “fatigue-reduced ergonomics limit” curve, and the results showed that the peak frequency of the horizontal and vertical spectra in the low-frequency range is concentrated in the 10 Hz or less range, with a pronounced impact on driver comfort. The impact on driver comfort is more pronounced12. Greneker et al. measured the natural frequency of a high-speed tractor using X-band radar and concluded that the lowest natural frequency of the tractor is 1 Hz, while the highest natural frequency reaches 5 Hz. Additionally, they observed that the magnitude of the natural frequency is contingent upon the loaded mass of the tractor and the parameters of the vibration damping device13. In their investigation, Do Minh Cuong et al. examined the impact of varying ground contact and inflation pressure on the vertical natural frequency of tractor tires. They employed the free decay method to analyze the data, and their findings revealed that when the tire was subjected to free decay vibration on a rigid ground, The increase in inflation pressure did not result in a notable change in the natural frequency of the tire. Conversely, when the tire was subjected to free decay vibration on a soft soil, the natural frequency of the tractor exhibited a significant increase with the rise in inflation pressure of the tire. The natural frequency of the tire increases significantly, while the vertical acceleration decreases slightly. The natural frequency of the tire and tire-soil system falls within the range of 3 to 10 Hz, which is within the most critical natural frequency range for the human body14. Jinming Zhang et al. investigated the vibration characteristics of wheeled tractor suspension farm implement system under plowing conditions, and obtained the natural frequencies of vertical vibration of the front axle, cab, driver’s seat, and implement of the tractor system. Their findings revealed that the unevenness of the farmland road surface and the resistance to plowing can markedly diminish the vibration response of the front axle suspension wheeled tractor suspension farm implement system15.
This study establishes a biaxial rigid suspension plane model for the tractor vibration system, analyzes the natural frequency of vertical vibration and pitching vibration of the tractor system, and conducts a real vehicle test of the tractor to obtain the natural frequency of the vibration system. Finally, a modal analysis of the structure of the tractor frame is performed, which provides theoretical support for the design of the tractor system.
Theoretical derivation of natural frequency of tractor vibration
During the operation of the tractor, a multitude of factors contribute to the occurrence of vibration. These include the unevenness of the road surface, the suspension of agricultural tools, engine vibration, and the transmission system, which is subjected to mechanical vibration and other sources of vibration. Consequently, the vibration is subjected to spatial multi-dimensional vibration. As illustrated in Fig. 1, the six degrees of freedom vibration system of the tractor exhibits vibration along the X, Y, and Z directions, representing longitudinal, lateral, and vertical displacement, respectively. Additionally, the system demonstrates vibration around the X, Y, and Z directions, representing roll, pitch, and yaw displacement, respectively.
Establishment of vibration model equations of motion
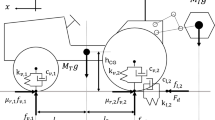
The coupling of the six directions of vibration of the tractor system makes it challenging to accurately calculate the natural frequency of vibration in each direction. Among these, the vertical vibration, pitching vibration, and yaw vibration are particularly intense16,17. In consideration of the tractor’s symmetrical structural configuration, the tractor is reduced to a biaxial rigid suspension planar model, as illustrated in Fig. 2. This model is limited to the analysis of droop and pitch vibrations.
kf, cf: stiffness and damping coefficients of front tires;kr, cr: stiffness and damping coefficients of rear tires; mc: mass of the tractor body; Jc: rotational inertia of the tractor body around the center of mass; lf, lr: horizontal distance from the front and rear axles to the center of mass of the body; hf, hr: road excitation of the front and rear wheel.
The differential equations of motion for the vibration system of a tractor with two-axis rigid suspension can be established:
The aforementioned differential equations of motion should be written in matrix form:
Or written as:
Where:
\({\mathbf{q}}=\left( {\begin{array}{*{20}{c}} {{z_c}} \\ {{\phi _c}} \end{array}} \right)\;{\mathbf{M}}=\left( {\begin{array}{*{20}{c}} {{m_c}}&0 \\ 0&{{J_c}} \end{array}} \right)\)
\({\mathbf{C}}=\left( {\begin{array}{*{20}{c}} {{c_f}+{c_r}}&{{c_r}{l_r} - {c_r}{l_r}} \\ {{c_r}{l_r} - {c_f}{l_f}}&{{c_f}{l_f}^{2}+{c_r}{l_r}^{2}} \end{array}} \right)\;\;{\mathbf{K}}=\left( {\begin{array}{*{20}{c}} {{k_f}+{k_r}}&{{k_r}{l_r} - {k_f}{l_f}} \\ {{k_r}{l_r} - {k_f}{l_f}}&{{k_f}{l_f}^{2}+{k_r}{l_r}^{2}} \end{array}} \right)\)
\({\mathbf{F}}=\left( {\begin{array}{*{20}{c}} {{c_f}{h_f}+{k_f}{{\dot {h}}_f}+{c_r}{h_r}+{k_r}{{\dot {h}}_r}} \\ {{c_r}{l_r}{{\dot {h}}_r} - {c_f}{l_f}{{\dot {h}}_f}+{k_r}{l_r}{h_r} - {k_f}{l_f}{h_f}} \end{array}} \right)\)
Vibration frequency analysis
In the above equation of motion, if \({\mathbf{C}}=0\),\({\mathbf{F}}=0\), then the undamped free vibration equations of motion for a vehicle with biaxial rigid suspension are obtained:
From the equations of motion, it can be observed that the vertical vibration of the fuselage and the pitch direction vibration are mutually coupled. That is to say, the excitation of the vertical vibration of the fuselage causes the pitch direction vibration, and vice versa. Furthermore, the pitch direction vibration of the fuselage also excites the vertical vibration in the reverse direction.
If the vertical and pitch direction vibrations of the fuselage are considered separately, the respective equations of motion are as follows:
The corresponding undamped natural circular frequency is given by:
The solution of the equations of motion provides the two principal frequencies at which the system vibrates:
In the equation: \({\eta _1}=\frac{{{k_f}{l_f} - {k_r}{l_r}}}{{{m_c}}}\), \({\eta _2}=\frac{{{k_f}{l_f} - {k_r}{l_r}}}{{{J_c}}}\).
From the above equation, it can be seen that \({k_f}{l_f} - {k_r}{l_r}=0\), then\({\eta _1}=0\), \({\eta _2}=0\), and so there is:
.
In other words, the vertical vibration of the fuselage and the pitch direction vibration are not coupled. The main frequency of the system is equal to the natural circular frequency of the vertical vibration and the pitch direction vibration, respectively. Furthermore, the main vibration mode is equal to the vibration mode of the vertical vibration and the pitch angle vibration, respectively.
When \({k_f}{l_f} - {k_r}{l_r} \ne 0\), \({\omega _1}\) with \({\omega _{0z}}\) close, \({\omega _2}\) with \({\omega _{0\phi }}\) close.If the vibration system parameters are properly matched, such that \({\omega _{0\phi }}<{\omega _{0z}}\), then \({\omega _1}<{\omega _2}\), this results in a reduction in vibration in the pitch direction and a reduction in longitudinal horizontal vibration in the fuselage, which may contribute to an improvement in smoothness.
The extant research has primarily centered on the ride comfort and safety of the tractor, i.e., the vibration acceleration values and tire dynamic load parameters of the tractor. The present study concentrates on the intrinsic frequency of the unsuspended tractor in the vertical and pitch directions. The theoretical analysis and computation are relatively straightforward due to the establishment of a simple two-degree-of-freedom vibration model. This model is verified by means of a vibration test, and then the modal analysis and design of the frame are carried out.
Testing of the natural frequency of the tractor vibration system
Test methods
The objective of this test is to ascertain the natural frequency of vibration of the tractor. Figure 3 depicts the schematic diagram of the tractor vibration test and analysis system. The acceleration sensor configuration, situated within the front and rear axles of the tractor, can be evaluated to obtain the vertical acceleration data for the front and rear axles. The test was conducted using a CA-YD-185TNC piezoelectric unidirectional acceleration sensor, which had been recalibrated by the manufacturer’s technicians prior to the test in order to ensure the accuracy of the test results(FIG S3). In accordance with the positional relationship between the test point and the center of mass of the tractor, the data obtained from the test are processed to yield the vertical acceleration data and pitch angle acceleration data at the center of mass of the tractor. The acceleration time-domain signals can then be obtained through the Fourier transform of the frequency-domain signals, which can be utilized to ascertain the natural frequency of the tractor body.
A schematic diagram of the tractor’s front and rear axle acceleration sensor mounting locations is shown in Fig. 4.
The main technical parameters of the tractor were measured on a self-developed test rig (FIG S1). The principal technical specifications of the tractor can be quantified and calculated in accordance with the data presented in Table 118,19.
Engine running vibration test
The operation of the engine gives rise to a number of factors that contribute to the generation of vibration. Of these, the reciprocating inertia force of the engine is identified as the principal source of exciting force20,21,22. The vibration of the tractor system, caused by the operation of the tractor engine, is tested in a parked state. The frequency domain signals of the tractor can be obtained by Fourier transforming the acceleration time-domain signals, as illustrated in Figs. 5, 6 and 7. The test results indicate that the vibration frequency caused by engine operation on the front and rear axle of the tractor and the cab floor is predominantly concentrated at 40 Hz, with notable peak values observed near 0 to 10 Hz, 20 Hz, 30 Hz, 50 Hz, 60 Hz, 80 Hz, and other frequencies.
Vibration test under tractor driving condition
Vibration tests were conducted on the tractor in accordance with Class D road excitation parameters(FIG S2). The tractor was operated at a medium speed (approximately 6 km/h) throughout the course of the tests. Each experimental group was tested three times, and the resulting mean value was recorded.
The construction of the simulation model for theoretical analysis was performed using Matlab/Simulink simulation software. The comparison between the theoretical analysis results of the vibration of the tractor without suspension and the test results under the same conditions is shown in Table 2. Given the consideration of the tractor engine vibration, transverse vibration, tire pressure changes, and other practical factors, the discrepancy between the theoretical analysis results and the vibration test results of the tractor is within the acceptable range. This suggests that the theoretical analysis possesses a certain degree of reliability.
The Fourier variation of the measured front-axis and rear-axis acceleration data yielded the acceleration power spectral densities in each direction, as illustrated in Figs. 8, 9 and 10. As illustrated in the power spectral density plot, the natural frequency of the tractor system is predominantly concentrated within the 3 ~ 5 Hz range. Additionally, the peak natural frequency of the front axle is notably higher than that of the rear axle. The peak natural frequency in the pitch direction at the center of mass of the fuselage is higher than that in the droop direction. Additionally, the natural frequency in the droop direction exhibits multiple peaks across a wide range of frequencies. The theoretical undamped natural frequencies for the center of mass of the fuselage in the vertical vibration and pitch direction are 3.67 Hz and 3.58 Hz, respectively. The experimental values are in close agreement with the theoretical values.
According to the international standard ISO 2631 “Evaluation of Whole Body Vibration on the Human Body”, 3–5 Hz is the sensitive interval between vertical vibration and pitching vibration of the human body, and the vibration in this frequency range is prone to cause resonance of the driver’s internal organs, muscle fatigue, and blurring of vision (e.g., it is difficult to align with the rows when planting seeds). Research has pointed out that the peak intrinsic frequency in the pitching direction is higher than that in the vertical direction, and pitching vibration (body tilting forward and backward) has a more significant impact on the human body: the driver’s torso will repeatedly flex and extend with the body tilting, and the lumbar vertebrae will be concentrated, which may lead to lumbar muscle strain in the long term. Reducing the vibration amplitude in this frequency range through frame optimization (e.g. optimizing the front and rear axle distance and damping matching for the coupling characteristics of pitching vibration) can directly improve comfort.
The intrinsic frequency of the front axle of the tractor is higher than that of the rear axle, if the damping design of the front axle suspension is unreasonable, the vibration of the front axle is easy to be transferred to the driver’s cab through the frame, resulting in fatigue of the parts (such as steering mechanism) accelerated. Viscoelastic damping pads can be added to the connection parts of the frame and the front axle, or high-damping alloy materials can be selected to utilize the damping to consume the resonance energy, and the amplitude can be controlled within the safety range. The study found that there is coupling between vertical vibration and pitching vibration, and damping can break the “coupled vibration vicious cycle”. For example, when vertical vibration is coupled with pitching vibration, if the vertical vibration frequency is reduced only by stiffness adjustment (e.g., increasing tire stiffness), the pitching vibration amplitude may rise due to the coupling; however, if the damping is optimized synchronously (e.g., adjustable dampers are added to the front suspension), the coupling energy can be attenuated in the vibration transmission path. When vertical vibration triggers pitching vibration, the dampers consume part of the energy in real time, avoiding the two vibrations from “superimposing and amplifying” each other. This means that the damping design needs to be synergistic with the intrinsic frequency and vibration mode: for the first-order bending vibration of the frame (first to third-order vibration mode), a local damping structure (e.g., a chamber with a built-in damping fluid) can be added in the area with the largest bending deformation (e.g., the middle of the frame) to give priority to attenuating the overall vibration energy.
Modal analysis of tractor frame structure
The tractor frame serves as the primary support structure for the entire tractor, providing stability for both the body and other essential components. Additionally, the frame is mounted on wheels through a suspension system, which enables the tractor to withstand various road surface excitations through the wheels23. When a tractor is traversing a challenging road surface, the fluctuations in speed and the inherent variability of the driving environment can bring the frequency of the dynamic loads it encounters to a point that is close to the natural frequency of certain structural components. This can result in the generation of significant vibration, which in turn gives rise to considerable dynamic stress. This, in turn, can lead to premature fatigue damage or the onset of unacceptable deformation. In order to circumvent resonance, mitigate noise, guarantee the reliability and safety of tractor operation, it is imperative to ascertain the natural frequency of structural vibration and its associated vibration pattern.
The ANSYS Workbench software was employed to conduct a modal analysis of the tractor frame structure in accordance with the geometric parameters of the frame. Three-dimensional modeling software was utilized to design and establish a three-dimensional geometric model of the frame. During the modeling process, considerations were made to ensure that the cover, minor components, and other frame elements would not unduly impact the frame’s structural integrity. Some features were excluded, and certain chamfers and transition fillets were simplified into right angles. Based on the aforementioned methodology, the finite element model and boundary conditions were established using Workbeach. To simplify the problem, the frame is constrained here to move only in the vertical direction, without considering translations and rotations in the other five directions(FIG S4), and the entire frame is made of structural stee(FIG S5). Considering the actual working conditions of the tractor, the upper surface A of the frame is subjected to a uniformly distributed load of 0.1 MPa, and the upper surface B is subjected to a uniformly distributed load of 0.15 MPa(FIG S6).
The model was then imported into Workbeach, where the unit and mesh were set. The division of grids with varying densities is primarily employed for stress analysis, encompassing both static and dynamic stress conditions. Conversely, a more uniform grid configuration is typically preferred when calculating inherent dynamic characteristics. This phenomenon can be attributed to the fact that natural frequencies and mode shapes are predominantly influenced by the mass and stiffness distributions of the structure, in the absence of stress concentration phenomena. The utilization of a uniform grid is instrumental in preventing substantial discrepancies among the elements of the structural stiffness and mass matrices, thereby minimizing numerical computation errors. Following a thorough evaluation, it was determined that a baseline element length of 40 millimeters would be optimal. Consequently, the frame was discretized into 23,891 elements, comprising a total of 86,840 nodes. The resulting effect is illustrated in Fig. 11.
In order to facilitate the mathematical analysis, only the vertical vibration of the frame is considered in this study, and the motion of the frame is constrained to occur exclusively along the vertical direction. For a large system with multiple degrees of freedom, such as the body frame, it is a challenging endeavor to ascertain all the natural frequencies and mode vectors. The lower orders of natural frequencies and their corresponding mode vectors contribute the most to the dynamic response; thus, only a few natural frequencies and mode vectors are required to study the response of the system. The initial six orders of natural frequencies and shapes of the rack are calculated and illustrated in Fig. 12.
Figure 13 illustrates the modal vibration patterns of the tractor frame at the first six orders of natural frequency. From an analysis of the modal vibration patterns of the frame depicted in the figure, it can be discerned that the inherent vibration patterns of the designed tractor frame can be classified into two categories: one is the overall vibration of the frame, and the other is the local vibration, which is dominated by the vibration of one or a few parts of the frame. It can be observed that the modal vibration patterns dominated by the overall vibration are more prevalent. The first, second, and third orders are all first-order bending vibration patterns. The fourth order vibration patterns manifest as localized vibration, while the fifth and sixth orders are second-order bending vibration patterns.
The external source of vibration affects the tractor in two primary ways. The first is due to the unevenness of the road surface, which causes excitation through wheel imbalance. The second is the result of engine operation, including the working stroke, combustion burst pressure, and piston reciprocating inertia force. This excitation is characterized by a very wide range of frequencies and is known as simple harmonic excitation24,25,26. In the actual work process, it is essential to ensure that the tractor frame low-order frequency response is higher than the natural frequency of the suspension structure and lower than the engine idling frequency. This is necessary to prevent the occurrence of overall resonance. Additionally, the elastic modal frequency of the frame should be positioned as far as possible outside of the frequency range typically utilized by the engine. This helps to avoid sudden changes in vibration pattern.
The uneven road surface on the tractor results in driving that is characterized by excitation vibrations with a frequency that is 20 Hz below the vertical vibration. Additionally, the excitation frequency of the engine idling is observed to be 35 Hz; The intrinsic rate of unsprung masses is typically observed to be within the range of 10 to 18 Hz27,28. From an analysis of the natural frequency of the frame, it can be observed that the structural design of the frame is capable of effectively mitigating the excitation frequency of the excitation force within the operational environment, thereby preventing the occurrence of the vibration phenomenon across the entire vehicle. The frame’s center exhibits a lack of stiffness, rendering it susceptible to fatigue damage. It may be advisable to consider implementing measures to enhance the stiffness of the specified region, such as incorporating additional welding points or other techniques, with the aim of improving its vibration characteristics.
There is a “directional weak zone” in the overall stiffness distribution of the tractor frame - the bending stiffness along the length of the frame shows “multi-region synergistic insufficiency”. Frame optimization needs to break through the limitations of “local strengthening”, if only for a certain order of bending vibration to enhance the stiffness (such as increasing the thickness of the longitudinal beam), may not be resolved due to the uneven distribution of the overall stiffness, resulting in the transfer of vibration energy to other orders of the same cluster. Therefore, it is necessary to eliminate the multi-order coupling basis of the first-order bending vibration through the “whole-domain stiffness equalization design” (e.g., optimizing the spacing of the cross beams and adjusting the gradient distribution of the cross-section moment of inertia along the length direction). Second-order bending vibration (fifth and sixth order) as a higher-order mode, its vibration frequency is usually higher than the tractor’s common operating frequency, but combined with the tractor operating scenarios (such as high-speed transfer in the field, driving on rugged surfaces) it can be seen that the hysteresis of the second-order bending vibration occurs, in essence, the frame of the high-frequency excitation of the “dynamic response threshold “: when the tractor traveling speed exceeds a certain threshold, the high-frequency excitation of the road surface (close to the fifth- and sixth-order frequencies) triggers the second-order bending vibration, leading to the intensification of vibration at the end of the frame (e.g., rear suspension, power output shaft), which directly affects the operational accuracy (e.g., row spacing deviation of the planter) and the life of the components (e.g., fatigue fracture of the drive shaft). The intrinsic frequency of second-order bending vibration can be enhanced through “end stiffness enhancement design” (e.g., adding variable cross-section longitudinal beams at the rear of the frame and adopting bionic bending-resistant structures) to be higher than the highest road excitation frequency (e.g., more than 40 Hz) that may be encountered by the tractor, so as to fundamentally avoid the attenuation of the dynamic performance under high-frequency working conditions.
Conclusion
This study employs a multi-methodological approach to analyze the natural frequency of the tractor vibration system. This includes a theoretical derivation, real vehicle testing, and modal simulation. The findings of this analysis yield the following conclusions:
-
(1)
The mathematical model of the tractor and the differential equations of motion of the biaxial rigid suspension system of the tractor vibration system have been established. It has been demonstrated that the vertical vibration and the pitch direction vibration of the fuselage are coupled with each other. The natural frequency of the vertical vibration is primarily influenced by the mass of the tractor and the stiffness coefficients of the front and rear tires. Conversely, the natural frequency of the pitch direction vibration is contingent upon the rotational moment of inertia of the tractor, the stiffness coefficients of the front and rear wheels, and the axle distance of the front and rear axles. The intrinsic frequency of the front axle of the tractor is higher than that of the rear axle, if the damping design of the front axle suspension is unreasonable, the vibration of the front axle is easy to be transferred to the driver’s cab through the frame, resulting in fatigue of the parts (such as steering mechanism) accelerated. Viscoelastic damping pads can be added to the connection between the frame and the front axle, or the use of high damping alloy materials, the use of damping to consume the resonance energy, the amplitude will be controlled within the safety range.
-
(2)
The tractor vibration test system has been constructed and the requisite tractor vibration data has been obtained. The natural frequency of the tractor fuselage, which is caused by engine operation, is primarily concentrated in the range of 0 to 40 Hz, with a particularly pronounced effect observed in integer multiples. In the context of driving, the natural frequency of the tractor vibration system is predominantly concentrated within the 3–5 Hz range. Additionally, the peak natural frequency of the axle is notably higher than that of the rear axle. The peak natural frequency in the pitch direction is higher than that in the vertical vibration. The natural frequency of vertical vibration exhibits a multitude of peaks, with a considerable range of frequencies occurring within the peak range. The unevenness of the road surface in the tractor operation scenario (field, mountain road, etc.) is random, and the excitation frequency range is wide (may cover the intrinsic frequency interval of 0–40 Hz). For example, when passing the bumpy road surface at low speed, the excitation is mainly low frequency (1–3 Hz), which is easy to cause the body pitching vibration; when driving at high speed on the continuous bumpy road surface, the excitation frequency may rise to 5–10 Hz, which is close to the local vibration frequency of the frame. If the frame design is only based on static modal analysis, unpredicted resonance may occur under dynamic excitation. Through real-time vibration diagnostics (e.g., installing accelerometers in key parts of the frame to collect vibration data in real time), it is possible to identify the excitation characteristics of different road surfaces and thus optimize the “dynamic stiffness” of the frame structure.
-
(3)
By conducting a modal analysis of the tractor frame structure, the first six orders of the frame’s natural frequency and vibration pattern were calculated, and the natural vibration pattern of the tractor frame was obtained. This resulted in the identification of two distinct categories of vibration: overall vibration and local vibration. The overall vibration category was found to be predominantly modal vibration, while the local vibration category was found to be predominantly first-order bending vibration. The first, second, and third orders represent first-order bending vibration patterns, while the fourth order vibration patterns indicate local vibration. The fifth and sixth orders correspond to second-order bending vibration patterns. The results of the modal simulation analysis provide a theoretical basis for the optimal design of the frame, through the optimization of the structure of the frame, which in turn improves the frame’s dynamic performance and enhances its contribution to the overall vehicle performance. The modal analysis identifies two types of vibration in the frame (global and localized) and the first six orders of vibration: first- to third-order for first-order bending vibration, fourth-order for localized vibration, and fifth- to sixth-order for second-order bending vibration. This means that the weak parts of the frame can be pinpointed - for example, localized vibration (fourth order) may correspond to the lack of stiffness in a specific area of the frame (e.g., connection points, cantilever structure), and long-term vibration will easily lead to stress concentration and cracks in that area; while overall bending vibration (first and second order) may affect the overall load-bearing capacity of the frame The overall bending vibration (first and second order) may affect the overall load carrying capacity of the frame, and even cause body deformation. Structural optimization based on vibration analysis (e.g., adding reinforcement to local vibration areas and adjusting cross-section stiffness for bending vibration modes) can enhance the vibration-resistant performance of the frame, reduce vibration-induced failures such as bolt loosening and structural cracking, significantly extend the service life of the frame and related parts (e.g., engine, transmission system), and reduce maintenance costs and safety hazards.
Data availability
All data generated or analysed during this study are included in this published article and its supplementary information files.
References
Li, Y. Mechanical Vibration Theory and Application[M] (China Science Publishing & Media Ltd.(CSPM), 2020).
Cao, S. Zhang Wen-de, Xiao Long-xiang. Modal Analysis of Vibrating Structures - Theoretical Experiments and Applications (2nd ed.)[M]. (Tianjing: Tianjin University, 2014).
Tian, X. et al. Kong De-gang, Su Jin-tao,. Analysis of Research Status on Vibration Comfort of Tractor Driver-seat. Journal of Agricultural Mechanization Research, 32(9): 249–252. (2010).
Tae-Hwan Kang and Yutaka Kaizu. Vibration analysis during grass harvesting according to ISO vibration standards. Comput. Electron. Agric. 79 (2), 226–235 (2011).
Stephan et al. All-terrain vehicle use in agriculture: exposure to whole body vibration and mechanic all shock. Appl. Ergon. 41 (4), 530–535 (2010).
Hostens, I. Descriptive analysis of combine cabin vibration and their effect on the human body. J. Sound Vib. 266 (3), 453–464 (2003).
Scarlett, A. J., Price, J. S. & Stayner, R. M. Whole-body vibration: evaluation of emission and exposure levels arising from agricultural tractors. J. Terrramech. 44 (1), 65–73 (2007).
Maleki, A. M. & Sayyed Saeid Mohtasebi. Natural frequency analysis of tractor operators body parts, J. Res. Rehabil. Sci. 10(2), 250–268. (2014).
Xu & Gang Zhu Si-hong, Nie Xin-tian, he liang, Li ke. Natural frequencies calculation for vibrating systems of tractors made in China. J. Vib. Shock. 33 (15), 157–161 (2014).
Jinlin, X., Zhenzhen, W., Yilidaer·Yiliyasi, N., Xintian, Z. & Sihong Lateral natural frequency modeling and verification for vibration systems of wheeled tractors. Trans. Chin. Soc. Agricultural Eng. (Transactions CSAE). 32 (19), 51–56 (2016).
Yu, J. & Jun, Z. Y. F. Lu Zhi-xiong. Research on vibration characteristics of tractor driving on the farmland. J. Chin. Agricultural Mechanization. 41 (2), 127–134 (2020).
Chen & Yong Zhu Si-hong, Ma ran. Test research on influence of tractor vibration on driver comfort. Tract. Farm. Transporter. 40 (5), 13–15 (2013).
Eugene, F., Greneker, I. I. I. & Jonathan, L. Geisheimer, and David Asbell Extraction of micro-Doppler data from vehicle targets at x-band frequencies, Proc. SPIE 4374, Radar Sensor Technology VI22 (2001).
Cuong, D. M. & Zhu, S. Natural frequency analysis of tractor tire with different ground contacts and inflation pressures. COUPLED Syst. Mech. Volume. 9, Issue 5., 455–471 (2020).
Zhang, J. Yao Hao-ping, Chen Li-zhong, Zheng En-lai, Zhu yue, Xue Jin-lin. Vibration characteristics analysis and suspension parameter optimization of tractor/implement system with front axle suspension under ploughing operation condition. J. Terramechanics . 102, 49–64 (2022).
Wang, X. Yu Qing-quan, Hu Wen-yi, Xu Yao-hui. The establishment of traveling vibration mechanics model and equation of vibration of wheeled tractors. J.Of Heilongjiang August first land reclamation university, 10(1), 45–48 (1998).
Chen Zhun. Research on System Dynamics Analysis and Continuously Variable Speed of Tractor[D] (Nanjing Agricultural University, 2022).
Nie, X., Li-xin, S. & Hao, G. Zhu Si-hong.Research on the radial stiffness and damping of tractor coefficient tires through test. J. Nanjing Agricultural Univ. 34 (5), 139–143 (2011).
Nie, X., Li-xin, S. & Hao, G. Zhu Si-hong.Method of measuring the moment of inertia of tractors and the error analysis. Mech. Sci. Technol. Aerosp. Eng. 31(8), 1325–1328 (2012).
Wang Bao-an. Study on Shafting Shock Excitation of Engine of Automabile Based on MATLAB[D] (Shandong University of Traditional Chinese Medicine, 2015).
Xie, Z. Xu Quan-yong,Guan Nan-xiang, Zhou Ming. A new closed-form method for inertia force and moment calculation in reciprocating piston engine design. Science China(Technological Sciences) 61(06), 879–885. (2018).
Zuo, S. et al. Zhou Modeling and analysis on the vibration excitation of three-cylinder engine considering the inertia parameters of connecting rod. J. Vib. Shock 38(02), 247–252. (2019).
Mao, Z. Jiang Jian-dong, Zhang Shen-qiang, Yang Zhen-xing, Zhang Fen-fei, Yang Jin-zhang. Design and optimization of the frame of a full frame crawler tractor. J. Chin. Agricultural Mechanization. 42 (7), 122–129 (2021).
Chen, H. Huang Da-xing, Li Li-qun. Study on vibration performance testing system of engine for Tractor. J. Agricultural Mechanization Res. 32 (05), 156–158 (2010).
Feng, D., Gang, L. J. W. & Zhang Jian. Fast modeling and dynamic analysis method for vehicle-bridge interaction system considering road roughness[J]. J. Southeast. University(Natural Sci. Edition). 52 (06), 1088–1094 (2022).
Song Bao-weu. Calculation of the frame of A mobile lifting Platform. Constr. Mach. Technol. Manage. 35 (01), 69–71 (2022).
Si, J. & Lu, H. Ren Qing-shuang. Modal analysis of structure of the Sub-frame of dump truck based on ANSYS. J. Inner Mongolia Univ. Technology(Natural Sci. Edition). 30 (03), 328–333 (2011).
Zhao Hui-hui. Finite Element Analysis and Lightweight Design for Heavy Vehicle Frame[D] (Nanjing University of Aeronautics and Astronautics, 2009).
Author information
Authors and Affiliations
Contributions
J.Y wrote the main manuscript text and L.Z. prepared Figs. 1, 2, 3 and 4 and Wrote some content. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Yuan, Jq., Zhang, L. Natural frequency and modal analysis of tractor vibration system. Sci Rep 15, 33259 (2025). https://doi.org/10.1038/s41598-025-18736-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-18736-x