Introduction of FixFRM package for gene-based association test and its innovative application to mixture exposure analysis

Abstract

Functional regression-based method (FRM) is an efficient and powerful tool for identifying genetic variants associated with complex traits and diseases by jointly considering the effects of multiple variants within a gene, however, no accessible software has been developed to realize the methods in practice. In this paper, we introduce the FixFRM R package that implements FRMs for gene-based tests. It provides a unified framework for quantitative and dichotomous trait analysis with various options for genetic variant and effect estimation. We use the package to identify gene that significantly associated withasthma using data from SNPassoc R package and compare to SKAT and SKAT-O. We further showcase an innovative application of FRMs to mixture exposure analysis using National Health and Nutrition Examination Survey data, modeling the joint effects of multiple environmental exposures by treating exposure levels as “genetic variants”. FRM achieves acceptable performance in the simulation study and obtains similar p-value as weighted quantile sum regression does in real application. The FixFRM package bridges the gap between the theoretical advantages and practical implementation for gene-based tests and mixture exposure analysis. Its user-friendly interface and comprehensive options facilitate powerful screening of genetic and environmental effects on complex traits.

Introduction

Gene-based association tests have gained popularity in recent years as a powerful approach identifying genetic variants associated with complex traits and diseases. Unlike single-variant association tests, gene-based tests consider the joint effects of multiple genetic variants within a gene, which can increase statistical power and reduce multiple testing burden¹. Several methods have been proposed for gene-based association tests, including burden tests², variance-component tests such as the sequence kernel association test (SKAT)¹, and combined tests like SKAT-O³. Burden tests are powerful when the genetic variants within a gene have similar effects on the phenotype, but they lose power when the effects are in opposite directions or the majority of the variants are non-causal¹. In contrast, variance-component tests like SKAT are more robust to the presence of both risk and protective variants and can maintain power when a large proportion of the variants are non-causal¹. However, these methods often assume that the genetic effects are constant across the gene region, which may not be realistic in practice⁴.

Functional regression-based methods (FRM) have emerged as a promising alternative to traditional gene-based association tests. These methods model the genetic effects as smooth functions of the physical positions of the variants within the gene, allowing for more flexible and biologically plausible assumptions about the genetic architecture^5,6. By incorporating functional data analysis techniques, such as basis function expansions and functional principal component analysis⁷, FRMs can effectively capture the spatial patterns and correlations among the genetic variants.

In this paper, we introduce the FixFRM package, an R package we develop to implements FRM for gene-based association tests. The package provides a unified framework for fitting fixed-effect FRMs with various options for modeling the genetic variant functions (GVFs) and the genetic effect functions (GEFs). Users can choose from different basis function systems, such as B-splines and Fourier basis⁸, and different estimation methods, such as ordinary linear squares and functional principal component analysis⁹. The package also supports different types of phenotypes, including quantitative and dichotomous traits, and allows for covariate adjustment and gene-environment interaction testing.

To demonstrate the utility and flexibility of the FixFRM package, we present an example of real data analysis. Mixture exposure analysis aims to assess the joint effects of multiple environmental exposures on health outcomes, which shares some similarities with gene-based association tests in terms of modeling the collective effects of multiple variables¹⁰. We apply the FRM to analyze the association between a mixture of seven xenobiotics and obesity using data from the National Health and Nutrition Examination Survey (NHANES)¹¹. By treating the exposure levels of the xenobiotics as “genetic variants” and the physical locations as the order of the exposures, we demonstrate how the functional regression framework can be adapted to model the mixture effects of environmental exposures. We compare the results from the functional regression-based methods with those from generalized linear models and weighted quantile sum regression¹² and show that proposed methods can provide more powerful and robust tests for the overall mixture effects.

In summary, this paper introduces the FixFRM package as a comprehensive and user-friendly tool for conducting gene-based association tests using functional regression-based methods. The package offers a range of options for modeling the genetic effects and accommodates different types of phenotypes and study designs. Through a real data analysis example, we demonstrate the benefits and potential of applying these methods to mixture exposure analysis. The FixFRM package is freely available on GitHub and can be easily installed and used by researchers interested in gene-based association tests and related applications.

Methods

Fixed effect generalized linear functional regression models (FRM)

Consider $\:n$ individuals with sequenced data of a genomic region of $\:m$ variants. We assume that the $\:m$ variants are located in a region with ordered physical locations $\:0\le\:{t}_{1}<\cdots\:<{t}_{m}=T$. We assume that each variant’s physical location $\:{t}_{j}$ is known. For simplicity, we normalized the region $\:[{t}_{1},\:T]$ to be $\:[0,\:1]$. For the $\:i$th individual, let $\:{y}_{i}$ denote the trait, which can be either quantitative or dichotomous, $\:{\varvec{G}}_{i}={\left({g}_{i}\left({t}_{1}\right),\:\cdots\:,\:{g}_{i}\left({t}_{m}\right)\right)}^{T}$ denote the genotype of the $\:m$ variants in which $\:{g}_{i}\left({t}_{j}\right)\left(=0,\:1,\:2\right)$ is the number of minor alleles of the individual at $\:j$th variant located at the position $\:{t}_{j}$, and $\:{\varvec{Z}}_{i}={\left({z}_{i1},\:\cdots\:,\:{z}_{ic}\right)}^{T}$ denote the covariates.

Under the functional regression framework, we denote $\:{X}_{i}\left(t\right),\:t\in\:[0,\:1]$ as the genetic variant function (GVF) for $\:i$th individual, which is estimated by the $\:n$ discrete realizations $\:{\varvec{G}}_{i}$ of the observed sample. To relate the genetic variant function to the phenotype while adjusting for covariates, we construct the following functional linear model for quantitative trait,

$$\:\begin{array}{c}{y}_{i}={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t+{ \varepsilon }_{i}. \end{array}$$

(1)

The model for dichotomous trait is,

$$\:\begin{array}{c}\text{logit}\left(\text{P}\left({y}_{i}=1\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t. \end{array}$$

(2)

For simplicity, we use Eq. (3) afterward unless otherwise stated for specific purpose,

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t, \end{array}$$

(3)

in which $\:g\left(\cdot\:\right)$ is identical link for quantitative traits and logit link for dichotomous traits, $\:{\alpha\:}_{0}$ is the overall mean, $\:\alpha\:$ is a $\:c\times\:1$ vector of regression coefficients for covariates, and $\:\beta\:\left(t\right)$ is genetic effect of genetic variant $\:{X}_{i}\left(t\right)$ at location $\:t$.

Estimation of genetic variant function

To estimate GVF $\:{X}_{i}\left(t\right)$ from observed genotype data $\:{G}_{i}$, we can use either ordinary linear square (OLS) smoother⁷ or functional principal component analysis (FPCA)^13,14,15, depending on the necessity of smoothness assumption.

Under OLS framework, we consider three commonly used assumptions for minor allele effect in gene-based association studies, which are all discrete realizations of $\:{G}_{i}$: (1) define $\:{X}_{i}\left(t\right)={g}_{i}\left({t}_{j}\right)$ for additive effect, (2) define $\:{X}_{i}\left(t\right)=1$ when $\:{g}_{i}\left({t}_{j}\right)=1,\:2$, and $\:{X}_{i}\left(t\right)=0$ when $\:{g}_{i}\left({t}_{j}\right)=0$ for dominant effect, (3) define $\:{X}_{i}\left(t\right)=1$ when $\:{g}_{i}\left({t}_{j}\right)=2$, and $\:{X}_{i}\left(t\right)=0$ when $\:{g}_{i}\left({t}_{j}\right)=0,\:1$ for recessive effect. Let $\:{\varphi\:}_{k}\left(t\right),\:k=1,\:\ldots\:,\:K$, be a series of basis functions, $\:{\Phi\:}$ denote $\:m\times\:K$ matrix containing the values $\:{\varphi\:}_{k}\left({t}_{j}\right)$ where $\:{t}_{j}$ is the variant location. Then GVF $\:{X}_{i}\left(t\right)$ can be estimated by

$$\:\begin{array}{c}{\widehat{X}}_{i}\left(t\right)=\left({g}_{i}\left({t}_{1}\right),\:\ldots\:,\:{g}_{i}\left({t}_{m}\right)\right)\varPhi\:{\left[{{\Phi\:}}^{T}{\Phi\:}\right]}^{-1}\varphi\:\left(t\right),\end{array}$$

(4)

where $\:\varvec{\varphi\:}\left(t\right)={\left({\varphi\:}_{1}\left(t\right),\:\ldots\:,\:{\varphi\:}_{K}\left(t\right)\right)}^{T}$ is a column vector of basis functions. Corresponding to the three discrete realizations of minor allele effect, Eq. (4) is called additive, dominant, and recessive, respectively. In this paper, we consider two types of basis functions: (1) the B-spline basis $\:{B}_{k}\left(t\right),\:k=1,\:\ldots\:,\:K$, and (2) the Fourier basis $\:{F}_{0}\left(t\right)=1,\:{F}_{2r-1}\left(t\right)=\text{sin}\left(2\pi\:rt\right),$ and $\:{F}_{2r}\left(t\right)=\text{cos}\left(2\pi\:rt\right),\:r=1,\:\ldots\:,\:\left(K-1\right)/2$. For the Fourier basis, $\:K$ is a positive odd integer^8,16.

The GVF $\:{X}_{i}\left(t\right)$ can also be estimated by FPCA techniques. Let $\:{{\Sigma\:}}_{X}\left(s,\:t\right)$ be the covariance function of GVF, which can be estimated from observed genotype data $\:{\varvec{G}}_{i}={\left({g}_{i}\left({t}_{1}\right),\:\ldots\:,\:{g}_{i}\left({t}_{m}\right)\right)}^{T},\:i=1,\:2,\:\ldots\:,\:n$ as $\:{\widehat{{\Sigma\:}}}_{X}\left(s,\:t\right)=\frac{1}{n+1}{\sum\:}_{i=1}^{n}\left[{g}_{i}\left(s\right)-\stackrel{-}{g}\left(s\right)\right]\left[{g}_{i}\left(t\right)-\stackrel{-}{g}\left(t\right)\right]$, where $\:\stackrel{-}{g}\left(s\right)=\frac{1}{n}{\sum\:}_{i=1}^{n}{g}_{i}\left(s\right)$ is the sample mean at position $\:s$. Denote the spectral decomposition of $\:{{\Sigma\:}}_{X}\left(s,\:t\right)$ by $\:{\sum\:}_{k=1}^{\infty\:}{\lambda\:}_{k}{\varphi\:}_{k}\left(s\right){\varphi\:}_{k}\left(t\right)$, where $\:{\lambda\:}_{1}\ge\:{\lambda\:}_{2}\ge\:\ldots\:$ are the nondecreasing eigenvalues and $\:{\varphi\:}_{k}\left(t\right),\:k=1,\:2,\:\ldots\:$ are the corresponding orthonormal eigenfunctions. By truncated Karhunen–Loève expansion, the approximation of $\:{X}_{i}\left(t\right)$ is

$$\:\begin{array}{c}{\widehat{X}}_{i}\left(t\right)=\left({c}_{i1},\:\ldots\:,\:{c}_{iK}\right)\varphi\:\left(t\right), \end{array}$$

(5)

where $\:K$ is the truncation lag, $\:\varvec{\varphi\:}\left(t\right)={\left({\varphi\:}_{1}\left(t\right),\:\ldots\:,\:{\varphi\:}_{K}\left(t\right)\right)}^{T}$, and $\:{c}_{ik}={\int\:}_{0}^{1}{X}_{i}\left(t\right){\varphi\:}_{k}\left(t\right)dt$, which can be estimated using observed genotype data.

Revised functional regression model

In model (3), $\:\beta\:\left(t\right)$ is defined as the genetic effect function (GEF) of genetic variant $\:{g}_{i}\left(t\right)$ at position $\:t$, or the effect of $\:{X}_{i}\left(t\right)$ if $\:{g}_{i}\left(t\right)$ is substituted by GVF realization at the position. Followed OLS framework, we expand $\:\beta\:\left(t\right)$ by a series of basis functions $\:{\psi\:}_{k}\left(t\right),\:k=1,\:\ldots\:,\:{K}_{\beta\:}$ as $\:\beta\:\left(t\right)=\left({\psi\:}_{1}\left(t\right),\:\cdots\:,\:{\psi\:}_{{K}_{\beta\:}}\left(t\right)\right){\left({\beta\:}_{1},\:\ldots\:,\:{\beta\:}_{{K}_{\beta\:}}\right)}^{T}$ where $\:\mathbf{{\rm\:B}}={\left({\beta\:}_{1},\:\ldots\:,\:{\beta\:}_{{K}_{\beta\:}}\right)}^{T}$ is a vector of coefficients. Note that the basis functions to expand $\:\beta\:\left(t\right)$ can be different from the one for GVF. Let $\:\varvec{\psi\:}\left(t\right)={\left({\psi\:}_{1}\left(t\right),\:\ldots\:,\:{\psi\:}_{{K}_{\beta\:}}\left(t\right)\right)}^{T}$, by replacing $\:{X}_{i}\left(t\right)$ and $\:\beta\:\left(t\right)$ by corresponding OLS expansion we can rewrite Eq. (3) as

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{\widehat{X}}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t\\\:={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}\left({g}_{i}\left({t}_{1}\right),\:\cdots\:,\:{g}_{i}\left({t}_{m}\right)\right){\Phi\:}{\left[{{\Phi\:}}^{T}{\Phi\:}\right]}^{-1}\varvec{\varphi\:}\left(t\right){\varvec{\psi\:}}^{\text{T}}\left(\text{t}\right)\mathbf{{\rm\:B}}\text{d}t\\\:={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+\left[\left({g}_{i}\left({t}_{1}\right),\:\cdots\:,\:{g}_{i}\left({t}_{m}\right)\right){\Phi\:}{\left[{{\Phi\:}}^{T}{\Phi\:}\right]}^{-1}{\int\:}_{0}^{1}\varvec{\varphi\:}\left(t\right){\varvec{\psi\:}}^{\text{T}}\left(\text{t}\right)\text{d}t\right]{\rm\:B}\\\:={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\varvec{W}}_{i}^{T}{\rm\:B}. \end{array}$$

(6)

.

In Eq. (6), $\:{\varvec{W}}_{i}^{T}=\left({g}_{i}\left({t}_{1}\right),\:\ldots\:,\:{g}_{i}\left({t}_{m}\right)\right){\Phi\:}{\left[{{\Phi\:}}^{T}{\Phi\:}\right]}^{-1}{\int\:}_{0}^{1}\varvec{\varphi\:}\left(t\right){\varvec{\psi\:}}^{\text{T}}\left(\text{t}\right)\text{d}t$ is readily available in existed R packages¹⁵. For computation efficiency, $\:{\int\:}_{0}^{1}\varvec{\varphi\:}\left(t\right){\varvec{\psi\:}}^{\text{T}}\left(\text{t}\right)\text{d}t=1$ when $\:\varvec{\varphi\:}\left(t\right)=\varvec{\psi\:}\left(t\right)$, that is we use the same set of basis function to expand GVF and GEF.

In the case of FPCA, the GEF $\:\beta\:\left(t\right)$ is expanded by linear spline basis for accessible computation purpose, which is

$$\:\begin{array}{c}\beta\:\left(t\right)={\beta\:}_{1}+{\beta\:}_{2}t+\sum\:_{k=3}^{{K}_{\beta\:}}{\beta\:}_{k}{\left(t-{\kappa\:}_{k}\right)}_{+}, \end{array}$$

(7)

where $\:{\kappa\:}_{k}$ are knots in the interval $\:\left[0,\:1\right]$, $\:{\left(t-{\kappa\:}_{k}\right)}_{+}$ is the indication function, i.e., $\:{\left(t-{\kappa\:}_{k}\right)}_{+}=0$ if $\:t\le\:{\kappa\:}_{k}$ and 1 if $\:t>{\kappa\:}_{k}$. In this case, we rewrite $\:\beta\:\left(t\right)=\left(1,\:t,\:{\left(t-{\kappa\:}_{k}\right)}_{3},\:\ldots\:,\:{\left(t-{\kappa\:}_{{K}_{\beta\:}}\right)}_{+}\right){\left({\beta\:}_{1},\:\ldots\:,\:{\beta\:}_{{K}_{\beta\:}}\right)}^{T}:={\varvec{\theta\:}}^{T}\left(t\right)\mathbf{{\rm\:B}}$ and Eq. (3) can be simplified as

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\varvec{W}}_{i}^{T}{\rm\:B}, \end{array}$$

(8)

where $\:{\varvec{W}}_{i}^{T}=\left({c}_{i1},\:\cdots\:,\:{c}_{iK}\right){\int\:}_{0}^{1}\varvec{\varphi\:}\left(t\right){\varvec{\theta\:}}^{\text{T}}\left(\text{t}\right)\text{d}t$.

In the beta-smooth only case, Eq. (3) is revised as

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\sum\:}_{j=1}^{m}{g}_{i}\left({t}_{j}\right)\beta\:\left({t}_{j}\right). \end{array}$$

(9)

The difference between Eqs. (3) and (9) is that the integration term $\:{\int\:}_{0}^{1}{X}_{i}\left(t\right)\beta\:\left(t\right)\text{d}t$ is substituted by summation term $\:{\sum\:}_{j=1}^{m}{g}_{i}\left({t}_{j}\right)\beta\:\left({t}_{j}\right)$, in which no smooth assumption is made for genetic variants. Note that in both cases the GEFs $\:\beta\:\left(t\right)$ are assumed to be smooth and estimated by OLS or linear spline. Expanding $\:\beta\:\left(t\right)=\left({\psi\:}_{1}\left(t\right),\:\ldots\:,\:{\psi\:}_{{K}_{\beta\:}}\left(t\right)\right){\left({\beta\:}_{1},\:\ldots\:,\:{\beta\:}_{{K}_{\beta\:}}\right)}^{T}$then Eq. (9) can be revised as

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\sum\:}_{j=1}^{m}{g}_{i}\left({t}_{j}\right)\beta\:\left({t}_{j}\right)\\\:={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+\left(\sum\:_{j=1}^{m}{g}_{i}\left({t}_{j}\right){\psi\:}_{1}\left({t}_{j}\right),\:\cdots\:,\:\sum\:_{j=1}^{m}{g}_{i}\left({t}_{j}\right){\psi\:}_{{K}_{\beta\:}}\left({t}_{j}\right)\right){\rm\:B}\\\:={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\varvec{W}}_{i}^{T}{\rm\:B}. \end{array}$$

(10)

By using observed genotype rather than estimating smooth genetic variant function, Eq. (10) is intuitive and straightforward. Additionally, it is computationally efficient and performs similarly compared to Eq. (6) in terms of type I error and power^17,18.

In summary, the FRMs consist of two types based on the realization of genetic variant function. Regardless of GVF, genetic effect function $\:\beta\:\left(t\right)$ is always assumed to be smooth which can be expanded by either OLS smoother or linear spline basis. A detailed comparison of the aforementioned models is shown in Table 1.

Table 1 Summary of available models based on functional regression framework.

Gene–environment interaction model

Gene-environment interaction term can be added to the functional regression association test model. Based on revised Model (6), the interaction model is

$$\:\begin{array}{c}g\left(\text{E}\left({y}_{i}\right)\right)={\alpha\:}_{0}+{\varvec{Z}}_{i}^{T}\alpha\:+{\varvec{W}}_{i}^{T}{\rm\:B}+{\mathbf{Z}}_{\text{i}} \otimes {\varvec{W}}_{i}b, \end{array}$$

(11)

where $\:{\mathbf{Z}}_{\text{i}} \otimes {\varvec{W}}_{i}$ is the outer product and $\:b$ is the coefficient of interaction term. Notice that Model (11) assume one general interaction coefficient for computation simplicity.

Statistical test

The goal of gene-based association test is to identify the relationship between genotype and phenotype, typically genetic variant with traits. In Model (3), testing genetic effect is to test the hypothesis $\:{H}_{0}:\beta\:\left(u\right)=0$ versus $\:{H}_{1}:\beta\:\left(u\right)\ne\:0$. By expanding $\:\beta\:\left(u\right)$, Model (3) is revised to (6), then the original hypothesis is equivalent to test: $\:{H}_{0}:\mathbf{{\rm\:B}}={\left({\beta\:}_{1},\:\ldots\:,\:{\beta\:}_{{K}_{\beta\:}}\right)}^{T}=0$ versus $\:{H}_{1}:\mathbf{{\rm\:B}}\ne\:0$. In Model (6), $\:\mathbf{{\rm\:B}}$ can be estimated by maximizing likelihood function and its variance-covariance matrix is estimated by Fisher information as standard multivariate linear regression does. Therefore, we can test he null hypothesis $\:{H}_{0}:\mathbf{{\rm\:B}}=0$ by a $\:F$-distributed statistic with degree of freedom $\:\left({K}_{\beta\:},\:n-{K}_{\beta\:}-1\right)$¹⁷. General score test statistic which follows $\:{\chi\:}^{2}$ distribution with degree of freedom $\:{K}_{\beta\:}$ is accessible, but we use Rao’s efficient score statistics for computation efficiency purpose in this study. Additionally, likelihood ratio test (LRT) statistics with degree of freedom $\:{K}_{\beta\:}$ is also available since testing $\:\mathbf{{\rm\:B}}$ of Model (6) is under nested model framework.

Besides traditional testing statistics, we treat the regression coefficients $\:\mathbf{{\rm\:B}}$ as a random vector in genetic and genomic statistics. Assume $\:{\beta\:}_{k}$’s are identically, and independently distributed variables follows normal distribution with a mean of zero and variance $\:\tau\:$. Denote $\:\varvec{W}={\left({W}_{1},\ldots\:,\:{W}_{n}\right)}^{T}$ the revised genotype data matrix of coefficient $\:\mathbf{{\rm\:B}}$. Then, Models (6) and (10) can be viewed as linear-square kernel machine regression with a kernel $\:\mathcal{K}=\varvec{W}{\varvec{W}}^{T}$ proposed by Liu et al.¹⁸. Under these assumptions, testing genetic effect is equivalent to test the hypothesis $\:{H}_{0}:\tau\:=0$ versus $\:{H}_{1}:\tau\:\ne\:0$. A variance-component functional kernel score test below can be used

$$\:\begin{array}{c}S\left(\widehat{\mu\:},\:{\widehat{\sigma\:}}_{e}^{2}\right)=\frac{{\left(Y-\widehat{\mu\:}\right)}^{T}\mathcal{K}\left(Y-\widehat{\mu\:}\right)}{{\widehat{\sigma\:}}_{e}^{2}}, \end{array}$$

(12)

where $\:Y={\left({y}_{1},\:\ldots\:,\:{y}_{n}\right)}^{T}$ is a vector of trait values, $\:\widehat{\mu\:}$ and $\:{\widehat{\sigma\:}}_{e}^{2}$ are the prediction mean and variance of $\:Y$ under the null hypothesis, respectively^{1,3,21,22,23,24}. The test statistic $\:S\left(\widehat{\mu\:},\:{\widehat{\sigma\:}}_{e}^{2}\right)$ follows a mixture $\:{\chi\:}^{2}$ distribution which is approximated by a scaled $\:{\chi\:}^{2}$ distributed statistics $\:\delta\:{\chi\:}_{v}^{2}$, where $\:\delta\:$ is scale parameter and $\:v$ is the degree of freedom^23,24,25,26.

FixFRM package

functional regression models were extensively validated in prior work through comprehensive simulation studies using COSI coalescent model data across multiple scenarios including rare-only and mixed rare/common causal variants, various effect directions, and sample sizes ranging from 250 to 2000 individuals^4,27. In summary, FRMs control type I error rates at preferred levels, $\:F$-distributed test statistics are more powerful than SKAT-based tests for quantitative traits, while Rao’s efficient score test statistics performs robustly for dichotomous traits. In this section, we will introduce the usage of FixFRM package to conduct functional regression gene-based association test.

The FixFRM package is designed to fit Model (3) to test genetic effect in gene-based studies. Depending on the smoothness assumption of GVF, there are two sets of functions in the package: fixed effect model and beta-smooth only model, corresponding to revised Model (6) and (10), respectively. The typical usage of fixed effect model is.

FLM_fixed_model(pheno, mode = “Additive”, geno, pos, order, bbasis, fbasis, gbasis, covariate, base, interaction = FALSE).

Here pheno, geno, covariate, and pos are arguments for trait information, genotype data, covariates, and physical position of variants, respectively. Detailed explanation and entry requirements are shown in Table 2. The mode argument accepts discrete realization of minor allele effect as mentioned in the Method section, with options including additive, dominant, and recessive. The bbasis, fbasis, gbasis, order, and base arguments specify expansion methods for GVF and GEF (as shown in Table 1). In detail, base is a character value to specify the basis function system to expand both GVF and GEF. When specifying B-spline basis function, the order, bbasis, gbasis arguments are needed to decide the order and number of basis functions in the expansion of GVF and GEF, while only fbasis is needed for Fourier spline expansion cases. The last argument, interaction, is a logical value indicating whether an interaction term is included in the model.

Table 2 Entries of data structures.

The beta-smooth model (10) assumes no functional expansion for genetic variants, and therefore only arguments of genetic effect function are needed, as shown below:

FLM_beta_smooth_only(pheno, mode = “Additive”, geno, pos, order, bbasis, covariate, base, interaction = FALSE).

The package has been uploaded to GitHub community, in which there are also functions to fit FPCA functional regression models and generalized functional linear models, example datasets to test the functions, and instructions. The installation process is similar to others general packages uploaded to GitHub, readers who are interested can go to: https://github.com/Peng247/FixFRM.

Application

To demonstrate the practical utility of the FixFRM package for gene-based association testing, we applied our method to analyze genetic variants associated with asthma using data from the SNPassoc R package. This dataset contains genotype information for 1578 individuals across 50 SNPs, with asthma case-control status and covariates including gender, age, and BMI. From the available SNPs, we identified 6 gene regions with sufficient variant coverage and compared the performance of traditional burden tests, SKAT, and the proposed FRM approach using beta-smooth only implementation with B-spline basis functions.

The analysis revealed distinct performance patterns across different genes, with FRM demonstrating higher detection capability in several cases (Table 3). Most notably, FRM identified a significant association between PHF11 and asthma (p = 0.0031), while both burden tests (p = 0.649) and SKAT (p = 0.648) failed to detect this association. This finding is consistent with previous research that identified PHF11 through positional cloning as a quantitative trait locus on chromosome 13q14 influencing immunoglobulin E levels and asthma susceptibility^28,29, and subsequent studies linking PHF11 polymorphisms to childhood atopic dermatitis³⁰ and asthma-related traits in Chinese populations³¹. For NPSR1-AS1, FRM also showed enhanced sensitivity (p = 0.099) compared to burden tests (p = 0.478) and SKAT (p = 0.615). The analysis also illustrated a key limitation of FRM: for SPINK5, which contained only one informative variant among four SNPs (three were monomorphic), FRM could not perform the analysis as the functional regression framework requires multiple variants to estimate smooth effect functions.

Table 3 Comparison of p-values from gene-based association tests for asthma.

Application to mixture exposure analysis

Model formulation

The application of FRM to mixture exposure analysis represents an innovative extension of gene-based association testing methodology. In mixture exposure studies, we aim to test the joint effects of multiple environmental exposures on health outcomes, which shares conceptual similarities with gene-based association tests in modeling the collective effects of multiple variables.

Model construction

Consider $\:n$ individuals with measured data of a mixture of $\:m$ exposure substances. For the $\:i$-th individual, let $\:{y}_{i}$ denote the health outcome of interest (quantitative or dichotomous), $\:{E}_{i}=\left({e}_{i1},\:\ldots\:,\:{e}_{im}\right)$ denote the measured levels of $\:m$ exposures, and $\:{Z}_{i}=\left({z}_{i1},\:\ldots\:,\:{z}_{im}\right)$denote the covariates. For mixture exposure analysis, we adapt the functional regression framework by treating exposure levels as analogous to “genetic variants” at fixed positions. The exposures are assigned sequential positions $\:{t}_{1},\:{t}_{2},\:\:\ldots\:,\:{t}_{m}$ in their natural order as they appear in the dataset, and we normalize the interval to $\:[0,\:1]\:$for computational convenience. The model is constructed as Model 9 and parameter estimation is following Model 10. In this study, we apply FRM for continuous outcomes in mixture exposure research.

Hypothesis test

The primary objective in mixture exposure analysis is to test whether the exposure mixture has any effect on the health outcome. This is to test the hypothesis $\:{H}_{0}:\beta\:\left(t\right)=0$ for all $\:t\in\:\left[0,\:1\right]$ versus $\:{H}_{1}:\beta\:\left(t\right)\ne\:0$ for some $\:t\in\:\left[0,\:1\right]$. Equivalently, using the basis expansion, this becomes $\:{H}_{0}:\:{\rm\:B}=0$ versus $\:{H}_{1}:{\rm\:B}\ne\:0$. If $\:{H}_{0}$ is not rejected, it suggests that $\:\beta\:\left(t\right)=0$, indicating no mixture exposure effect on the outcome. Conversely, rejecting $\:{H}_{0}$ provides evidence for a significant mixture effect. We employ permutation tests to evaluate statistical significance. The permutation testing procedure begins with fitting Model (3) to the original data and calculating the likelihood ratio test statistic $\:{T}_{obs}$. For each permutation $\:b=1,\:2,\:\ldots\:,\:B$, we randomly permute the outcome vector $\:\varvec{y}$ while keeping the exposure matrix $\:\varvec{E}$ and covariate matrix $\:\varvec{Z}$ fixed. This preserves the correlation structure among exposures while breaking any association between exposures and outcomes under the null hypothesis. We then fit Model (3) to the permuted data and calculate the test statistic $\:{T}_{b}$. The permutation p-value is calculated as $\:{p}_{perm}=\frac{{\sum\:}_{b=1}^{B}I\left({T}_{b}\ge\:{T}_{obs}\right)+1}{B+1}$, where $\:I(\cdot\:)$is the indicator function. We typically use $\:B=99$ permutations to achieve precise p-value estimation with sufficient resolution for standard significance levels.

Simulation study

To evaluate the performance of FRM with permutation testing in mixture exposure analysis, we designed a comprehensive simulation study using realistic exposure correlation structures derived from environmental health data. We utilized the NHANES 2011–2016 dataset as a data pool, which contains measurements of 37 nutrients with complex correlation patterns among 5,960 participants aged 20–60 years. Details about sample selection and summary statistics can be found in Renzetti et al.³².

Type I error rate

For Type I error assessment under the permutation framework, we employed a simulation design that maintains the complex exposure correlation structure while ensuring no true association between exposures and outcomes. We used the original NHANES exposure data with randomly permuted outcomes, ensuring that the null hypothesis of no association is strictly true while preserving the realistic correlation patterns among exposures that could potentially challenge the method’s performance.

We drew random samples of 1000 or 2000 participants from the data pool. For each sample, we applied FRM using age and sex as covariates and all 37 nutrients as mixture exposures. For each dataset, we performed 99 permutations to calculate permutation p-values, balancing computational efficiency with adequate precision. We repeated this entire process 1000 times to obtain robust estimates of empirical Type I error rates. It was calculated as $\:\widehat{\alpha\:}=\frac{{\sum\:}_{r=1}^{1000}I\left({p}_{\left\{perm,\:r\right\}}<\alpha\:{\prime\:}\right)}{1000}$, where $\:{p}_{\left\{perm,\:r\right\}}$ is the permutation p-value from the $\:r$-th replication and $\:\alpha\:{\prime\:}$ is the nominal significance level.

Power

For power evaluation, we generated synthetic outcomes with known mixture effects while preserving the realistic NHANES exposure correlation structure. This approach ensures that power estimates reflect performance under realistic exposure patterns rather than idealized scenarios. The outcome generation model was

$$\:E\left({y}_{i}\right)={\alpha\:}_{0}+{w}_{1}{Z}_{1i}+{w}_{2}{Z}_{2i}+\sum\:_{j\in\:S}{w}_{j}{e}_{ij}+{ \varepsilon }_{i},$$

where $\:{Z}_{1i}\sim N \left(0,\:1\right)$ and $\:{Z}_{2i}\sim Bernoulli \left(0.5\right)$ are continuous and binary covariates, $\:S\subset\:\left\{1,\:2,\:\ldots\:,\:m\right\}$ is the set of causal exposures, $\:{w}_{j}$ are exposure effect sizes, and $\:{\varepsilon}_{i}\sim\:N\left(0,\:1\right)$ are random errors. Effect patterns included random selection of causal exposures representing 1/2, 1/8, and 1/16 of total exposures, reflecting varying degrees of mixture complexity from sparse effects (where only a few exposures contribute) to dense effects (where most exposures contribute). Effect sizes were calibrated to produce small (R² = 1/10), medium (R² = 1/5), and large (R² = 1/3) mixture effects. Each parameter combination was replicated 1000 times to ensure robust power estimates, resulting in a comprehensive evaluation covering 18 distinct scenarios.

Simulation results

The permutation-based FRM demonstrated conservative and robust Type I error control across all tested scenarios as showed in Table 4. All observed rates remained close to or below the nominal significance level of α = 0.05, with no systematic relationship to sample size or number of basis functions. These results indicate that the permutation-based approach provides reliable and conservative statistical inference, making it a robust choice for mixture exposure analysis.

Table 4 Simulation results of type I error rate of permutation-based FRM for mixture exposure studies.

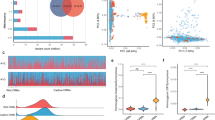
The power simulation results revealed patterns that demonstrate the method’s ability to detect mixture effects under realistic scenarios, which are showed in Fig. 1. For large effects (R² = 1/3), the method achieved high power across all tested scenarios. Medium effect sizes (R² = 1/5) demonstrated good to excellent power, with values ranging from 0.612 to 0.925 across different scenarios. The method consistently exceeded the conventional power threshold of 0.80 for medium effects when sample sizes reached 2000 participants and achieved respectable power even with smaller samples of 1000 participants. The increased power observed with lower proportions of causal exposures (moving from 1/16 to 1/2 causal exposures) suggests that the FRM performs better at identifying mixture effects where only a subset of measured exposures contribute meaningfully to the health outcome.

Fig. 1

Statistical power by effect size and proportion of causal exposure for different sample size.

Application

To evaluate the impact of mixture exposure of seven xenobiotics (three phthalate metabolites, two phenols, and two pesticides) on obesity, Zhang et al.³³ applied generalized linear regression, weighted quantile sum (WQS) regression, and Bayesian kernel machine regression (BKMR) models to analyze the U.S.-based National Health and Nutrition Examination Survey (NHANES) from 2013 to 2014 data. In their study, generalized linear regression was established for single chemical analysis and three chemical substances were found significantly associated with obesity. In WQS regression analysis, the WQS index indicated that the mixture exposure was significantly associated with obesity. In BKMR analysis, the overall effect of mixture was significantly associated with general obesity when all the chemicals were at their 60th percentile or above it, compared to all of them at their 50th percentile.

We follow the same workflow to extract subjects from NHANES 2013–2014 cycle and reanalyze them by using FRM. We treat age, sex (female, male), ethnicity (Hispanic, non-Hispanic white, non-Hispanic black, and others), education levels (lower than high school, high school, some college or AA degree, college graduation, or above), family income-to-poverty ratio ($\:\le\:1.30,\:1.31-3.50,\:>3.50)$, smoking status (never smoker: < 100 cigarettes in life; former smoker: > 100 cigarettes in life and did not smoke at the time of survey; current smoker: > 100 cigarettes in life and smoked every day or some days at the time of survey), physical activity (< 600, 600–1199, $\:\ge\:$1200 Met min per week), total energy intake (males: < 2000, 2000–3000, >3000 kcal/day; females: < 1600, 1600–2400, >2400 kcal/day), and log-transformed creatinine as covariates, the original value or quartile of the urinary levels of seven chemical substances as “genotype data” by fitting Model (9). The p-values shows significance of the association between the overall exposure effect and obesity.

Table 5 shows that all three methods detected significant associations between the xenobiotic mixture and obesity. GLM yielded a p-value of 0.0078, while WQS regression provided stronger evidence with a p-value of 2.1 × 10^− 6. FRM demonstrated the strongest statistical evidence, though we report the p-value as < 10^− 6 rather than an exact value. This is because FRM uses permutation testing for statistical inference - even after conducting 10⁶ permutations, we did not observe any permuted likelihood ratio test statistics that exceeded the value calculated from the observed data. This indicates extremely strong evidence against the null hypothesis of no mixture effect, but the permutation-based approach cannot provide a more precise p-value estimate without conducting an impractically large number of additional permutations.

To investigate the impact of exposure ordering, we examined all 5,040 possible orderings of the seven xenobiotics. The minimum F statistic across all orderings was 6.12, while the maximum F statistic under the null distribution (10⁶ permutations) was 1.3. This demonstrates that every possible ordering yields p-values < 10^− 6, providing strong evidence that our significant mixture effect finding is robust to exposure arrangement and validating the FRM approach for mixture exposure analysis.

Table 5 Analysis result of testing the mixture exposure effect on obesity, NHANES, 2013–2014.

Discussion

In this paper, we introduced the FixFRM package, an R package that implements FRM for gene-based association tests, providing a unified framework for analyzing quantitative and dichotomous traits with various options for modeling genetic variants and effects. The package addresses a critical gap between the theoretical advantages of FRMs and their practical implementation, as no accessible software had been previously developed for these methods despite their demonstrated superior performance over traditional approaches like SKAT and burden tests. Most notably, we present an innovative application of FRMs to mixture exposure analysis, representing the first adaptation of gene-based functional regression methodology to environmental health research. By treating exposure levels as “genetic variants” and applying permutation-based hypothesis testing, we demonstrate how established genetic analysis methods can be extended to address complex environmental health questions involving multiple correlated exposures.

Based on the simulation study results, we provide practical recommendations for implementing FRM in mixture exposure analysis. For study design, we recommend sample sizes of at least 1500 participants for detecting moderate mixture effects, with 2,000 or more participants preferred for optimal statistical power across various scenarios. Regarding methodological specifications, our results demonstrate robust performance with 5 to 9 basis functions, as this provides an appropriate balance between model flexibility and computational efficiency. The method shows conservative Type I error control regardless of sample size or basis function choice, making it a reliable approach for mixture exposure screening in environmental health research.

Despite these promising results, our study has several important limitations. First, the current FRM implementation focuses on hypothesis testing to detect mixture effects rather than quantifying effect sizes or individual exposure contributions, requiring complementary methods for detailed effect estimation. Second, the permutation-based approach can lead to imprecise p-value estimation for very small ones, as demonstrated by our inability to provide exact values beyond p < 10^− 6 even after millions of permutations. Additionally, the method assumes mixture effects can be captured through smooth functions, which may not hold for all exposure patterns, and computational requirements increase substantially with high-dimensional exposure data. Another limitation is that the FRM framework cannot be applied to single-variant analysis. Unlike SKAT, which reduces to standard single-variant association tests when only one variant is present, our method fundamentally requires multiple variants to estimate the smooth genetic effect function β(t). The functional regression approach depends on fitting smooth curves across variant positions, which is impossible with a single data point. Finally, the method’s performance with missing data or measurement error also requires further evaluation.

In conclusion, the FixFRM package provides a valuable and accessible implementation of functional regression methods for both gene-based association testing and mixture exposure analysis. The innovative application of FRM to environmental health research demonstrates the potential for cross-disciplinary methodological adaptation, offering researchers a computationally efficient and statistically robust tool for detecting complex mixture effects. While the method has limitations in effect size estimation and p-value precision, it serves as an alternative screening tool for identifying significant mixture associations in environmental epidemiology. The package bridges an important gap between advanced statistical methodology and practical application, facilitating broader adoption of functional regression approaches in genetic and environmental health research.