4E analysis of supercritical carbon dioxide (sCO₂) cycles: evaluating energy, exergy, environmental sustainability, and economic impacts in combined systems

Abstract

Supercritical carbon dioxide (sCO₂) emerges as an effective working fluid in closed-loop energy conversion cycles, offering significant advantages over traditional steam-based Rankine cycles. This research focuses on optimizing combined cycle systems utilizing sCO₂ to enhance energy efficiency, improve exergy performance, increase stability, reduce emissions, and lower costs. Various configurations of the sCO₂ cycle are analyzed, with an emphasis on their impact on efficiency as dictated by the first and second laws of thermodynamics. Key parameters include a gas turbine outlet temperature of 489 °C, a smoke flow rate of 89 kg/s, and a maximum cycle pressure of 230 bar, alongside turbine pinch temperatures of 30 °C and condenser pinch temperatures of 20 °C. The study evaluates three configurations: simple cycle, recuperator cycle, and split cycle, achieving first law efficiencies of 17.73%, 19.26%, and 23.56%, respectively. By minimizing exergy losses, this research enhances environmental sustainability and system stability, leading to reduced pollutant emissions. Economic analyses further compare the electricity generation costs of sCO₂ cycles to those of steam cycles, revealing cost ratios of 0.80, 0.92, and 0.98 for the simple, recuperator, and split cycles, respectively. Additionally, sustainability indices for the simple, recuperator, and split cycles are calculated at 1.92, 2.09, and 2.76, respectively. The findings underscore that advancements in sCO₂ cycles not only improve power output, energy efficiency, and environmental sustainability but also reduce cycle costs and environmental pollution.

Introduction

Sustainable energy production is a significant challenge in modern industrial systems. Gas turbine combined cycle power plants are highly efficient for electricity generation, integrating gas turbines with steam cycles. Incorporating supercritical carbon dioxide (sCO2) into energy production and heat recovery offers advantages over traditional steam systems, including smaller turbine sizes, simpler heat recovery exchangers, and reduced water treatment needs, leading to lower capital and installation costs. This study explores replacing the steam cycle in gas turbine combined cycles with an sCO2 system to enhance environmental sustainability and stability. The use of sCO2 improves efficiency and cost-effectiveness compared to conventional Rankine cycles, and the research also examines optimization techniques to maximize performance while minimizing environmental impact.

Literature review

The supercritical carbon dioxide (sCO₂) cycle has evolved over the past fifty years, starting with Fehr’s 1967 comparison of critical conditions among various fluids in supercritical cycles¹. Angelino later demonstrated the advantages of sCO₂ cycles over traditional Brayton and Rankine cycles, emphasizing their simplicity and higher efficiency². One notable finding was the reduction in specific volume, which decreases compressor work, and the importance of minimizing heat capacity differences to enhance efficiency. The smaller diameter of the sCO₂ turbine rotor allows for a volumetric flow per unit of power that is 30 to 50 times smaller than conventional heating cycles³. In 1971, Chermanne examined cycles with three compressors and two intercoolers, highlighting their compactness and efficiency for the shipping industry, ultimately leading to reduced fuel consumption⁴. Petr’s 1997 research focused on the applications of sCO₂ cycles in new power plants, particularly regarding the Brayton cycle and the effects of reheating on the efficiency of recompression cycles⁵. Dostal’s 2006 study analyzed the impact of pressure drops in components on cycle efficiency and concluded that utilizing multiple reheating stages is not cost-effective⁶. In 2007, Zhang explored solar heating cycles and their effects on the performance of sCO₂ power generation⁷. Ishiyama’s 2008 research compared various power generation systems, including the sCO₂ turbine cycle⁸. Moisseytsev’s 2009 work examined the advantages of sCO₂ Brayton cycles for sodium-cooled reactors, noting increased efficiency and simpler designs compared to traditional steam Rankine cycles⁹. Sarkar’s 2009 analysis focused on exergy optimization within the sCO₂ cycle, evaluating the effects of exergy and irreversibility on efficiency¹⁰. Yari’s 2010 research investigated the efficiency of combined cycles, finding that their performance was 5–26% superior to that of the sCO₂ cycle¹¹. Jiangfeng et al. also studied the thermodynamic performance of sCO₂ components for waste heat recovery¹². In 2012, Halimi and Kune performed a numerical analysis of the sCO₂ Brayton cycle as a means of energy production¹³. Pichel et al. examined various configurations of the sCO₂ power cycle, achieving a maximum efficiency of 43.31%, comparable to that of the Rankine cycle¹⁴. Kim et al. (2016) studied sCO₂ Rankine cycles for recovering waste heat from turbine exhaust, evaluating multiple cycle configurations¹⁵. In 2019, Dhinest et al. analyzed the thermal performance and economics of sCO₂ cycles in combined power plants, while Jinliang et al. explored system design challenges and energy conversion mechanisms^16,17. More recently, Ahmadi and Zirak (2022) focused on improving the efficiency of the sCO₂ cycle through energy analysis¹⁸, and Galledari and Ahmadi (2023) contributed to the thermal design of a recuperator within the sCO₂ cycle¹⁹. Ahmadi and Zirak investigated the integration of supercritical carbon dioxide (sCO2) cycles with multi-effect desalination (MED) and organic Rankine cycles (ORC), highlighting its potential to improve environmental sustainability. By employing the 3E analysis framework—encompassing energy, exergy, and environmental impacts—they provided a thorough assessment of the efficiency of these systems and their roles in managing water and energy resources effectively²⁰. Yilmaz et al. (2024) present a biomass-based multigeneration plant utilizing a supercritical CO₂ Brayton cycle, achieving an energy efficiency of 44.50% and generating 2674 kW of power, hydrogen, and fresh water²¹. Bakırcıoğlu et al. (2025) introduce a solar-powered multigeneration system that combines supercritical CO₂ and transcritical CO₂ cycles, achieving a net power capacity of 1052 kW and an energy efficiency of 50.28% through multi-objective optimization²². Both studies highlight innovative approaches to sustainable energy production and zero-emission goals.

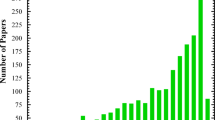
Overall, these studies highlight innovative strategies to enhance the efficiency and applicability of sCO₂ technologies in energy production and water desalination. Figure 1 illustrates the rising trend in publications related to “sCO₂” from 2000 to 2025.

Fig. 1

The growth of articles related to the sCO₂ cycle between 2000 and 2025.

In conclusion, the optimization of supercritical carbon dioxide combined cycle systems represents a significant step towards achieving environmental sustainability and stability in energy production. By addressing key challenges such as increasing energy efficiency, improving exergy performance, and reducing cycle costs, these systems have the potential to play a vital role in the transition towards sustainable energy practices on a global scale.

Research gaps

While previous studies have thoroughly examined supercritical carbon dioxide (sCO₂) cycles and explored various analytical frameworks and their applications across different industrial sectors, a significant gap remains in the comprehensive assessment that combines energy, exergy, economic, and environmental sustainability analyses for different configurations. This paper aims to address this gap by providing an in-depth and holistic analysis of these essential elements, thereby enhancing our understanding of the potential synergies and efficiencies that can be achieved through integrated systems.

Innovations

This research introduces an innovative approach to integrating environmental sustainability into supercritical carbon dioxide (sCO₂) combined cycle systems. The primary goal is to mitigate environmental impacts by employing sustainable practices. A noteworthy aspect of this study is its comprehensive optimization strategy, which not only enhances energy efficiency but also improves exergy performance, leading to an overall enhancement of the system. The focus is on maximizing exergy efficiency while minimizing energy losses to optimize energy utilization. The originality of this work lies in its integrated methodology, which concurrently advances environmental sustainability and energy efficiency in sCO₂ combined cycle systems, making a significant contribution to sustainable energy practices and the optimization of system performance.

Research methodology

This study uses a structured methodological framework to address gaps in supercritical carbon dioxide (sCO₂) cycles. It starts with a comprehensive literature review to identify shortcomings in integrating energy, exergy, economics, and environmental sustainability within sCO₂ systems. Following this, the research conducts a comparative analysis of various sCO₂ cycle configurations, focusing on innovative strategies to enhance energy efficiency and exergy performance by reducing energy losses. A thorough sustainability assessment evaluates the environmental impacts of the proposed systems, ensuring they align with sustainable energy practices. Economic considerations are also included for a holistic perspective. The findings will be presented through infographics and charts for clarity, with Fig. 2 illustrating the sustainability analysis method used in the project.

Fig. 2

Infographic diagram of the research method.

This methodological approach aims to enhance understanding of supercritical carbon dioxide (sCO₂) cycles, advance sustainable energy practices, and optimize system performance. The research emphasizes that achieving environmental sustainability involves optimizing fossil fuel use, minimizing waste, promoting recycling, recovering energy, saving time, and reducing pollution, in accordance with the principles of economic, social, and environmental development.

System description

Supercritical carbon dioxide power generation cycles possess distinct characteristics that significantly influence their design and application. A key feature of this cycle is that the discharge pressure from the pump and the inlet pressure to the turbine are substantially higher than the critical pressure of 7.38 MPa. Under these conditions, the fluid transitions into a supercritical state, where it no longer exhibits distinct liquid and vapor phases. Figure 3 presents the phase transition diagram for carbon dioxide. Moreover, according to thermodynamic principles, when heat is added to the supercritical fluid, its temperature increases continuously. This contrasts with subcritical fluids, which maintain a constant temperature during the phase transition from liquid to vapor.

Figure 4 compares the temperature changes based on the relative percentage of heat power for the combined steam cycle, the combined supercritical carbon dioxide cycle, and the organic Rankine cycle. In these cycles, heat transfer occurs in the gas turbine exhaust between gas (flue gas) and steam, toluene (an organic fluid), and supercritical carbon dioxide, respectively. This figure illustrates the advantages of supercritical carbon dioxide over other fluids under specific conditions. The superiority of supercritical carbon dioxide is evident, as steam and toluene undergo a phase change between 150 and 200 degrees Celsius, resulting in a portion of the heat power being utilized at a constant temperature for this phase transition. In contrast, supercritical carbon dioxide achieves the highest efficiency in heat transfer with flue gas, as indicated by the two parallel lines in the graph.

Fig. 3

The phase transition diagram of carbon dioxide.

Fig. 4

Thermal efficiency Comparison of CO₂ with other fluids.

One of the key advantages of supercritical carbon dioxide (sCO₂) power cycles is the compact physical size of the turbomachines, which is attributable to the high density of the working fluid and the low-pressure ratio of the cycle. This reduced size leads to lower costs, simpler turbomachine designs, and decreased installation expenses.

Advantages of carbon dioxide over other fluids

The use of supercritical carbon dioxide (sCO₂) is significant for several reasons. It operates effectively within a suitable temperature range in its supercritical phase and is cost-efficient due to its high density, which reduces the size of cycle equipment, thereby lowering construction costs and fuel needs. This high density also allows for smaller turbines and compressors, optimizing equipment layout and saving space. Additionally, sCO₂ possesses favorable physical properties, including non-toxicity, thermal stability, and non-flammability. Environmentally, the sCO₂ cycle is eco-friendly, avoiding water and thermal pollution and greenhouse gas emissions. It also achieves high efficiency at elevated operating temperatures due to its high specific heat capacity near the critical point²³.

Different cycle configurations and design inputs

The sCO₂ cycle operates alongside an industrial gas turbine, using the turbine’s hot exhaust gas as a heat recovery steam generator (HRSG) for the sCO₂ cycle boiler. In a warm climate with an average annual temperature of 23 °C, the CO₂ pressure at the pump is approximately 69 bar, matching the turbine outlet pressure with no circuit losses. This results in a turbine exit temperature of 326.8 °C, which must be cooled in a condenser. To enhance energy efficiency, a recuperator is incorporated to reduce the condenser load. Additionally, some CO₂ mass flow is bypassed from the recuperator, leading to a division of the HRSG into high and low-temperature boilers. The cycle configurations include the integration of either a multi-effect desalination (MED) cycle or an organic Rankine cycle (ORC).

Cycle specification

The gas turbine exhaust, at 489 °C and a mass flow rate of 89 kg/s, serves as the primary heat input for the sCO₂ cycle. With a pinch of 30 °C, the carbon dioxide turbine inlet temperature is 459 °C. An air-cooled condenser, using surrounding air at 23 °C, cools the CO₂ to 28 °C before it enters the pump, accounting for a 5 °C pinch to the atmosphere. This air temperature represents average seasonal conditions. The turbine and pump have isentropic efficiencies of 90% and 80%, respectively, with the pump raising CO₂ pressure to 230 bar, chosen for pipeline safety. The CO₂ enters the pump as a saturated liquid, and the minimum temperature from the HRSG is 90 °C, limited by dew point considerations. All pressure losses in the pipelines are ignored.

Cycle design procedure

The method of designing supercritical carbon dioxide cycles for increased stability and reduced pollution is described as follows:

sCO₂ simple cycle

Figure 5 illustrates the first configuration of the simple supercritical carbon dioxide (sCO₂) cycle, with thermodynamic properties provided for different nodes in Table 1, based on the isentropic efficiencies of the pump and turbine. All calculations were conducted using EES software. The cycle has a mass flow rate of 67.44 kg/s, with a condenser cooling air mass flow rate of 1666 kg/s and a turbine exhaust smoke mass flow rate of 89 kg/s. This simple cycle configuration exhibits an efficiency of 17.73%, indicating low overall cycle efficiency. Energy modeling was performed separately for each component.

Fig. 5

Schematic of sCO₂ simple cycle

Table 1 Thermodynamic properties for sCO₂ simple cycle.

The governing energy equations are²⁴:

Turbine power and efficiency:

$$\:{\dot{W}}_{T}=\dot{m}\left({h}_{in}-{h}_{out}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{1}-{h}_{2}\right)$$

(1)

$$\:{\text{Ƞ}}_{I,T}=\frac{\left({h}_{in}-{h}_{out}\right)}{\left({h}_{in}-{h}_{outs}\right)}=\frac{\left({h}_{1}-{h}_{2}\right)}{\left({h}_{1}-{h}_{2s}\right)}$$

(2)

Pump power and efficiency:

$$\:{\dot{W}}_{P}=\dot{m}\left({h}_{out}-{h}_{in}\right)=\dot{{\dot{m}}_{{CO}_{2}}}\left({h}_{5}-{h}_{4}\right)$$

(3)

$$\:{\text{Ƞ}}_{I,P}=\frac{\left({h}_{outs}-{h}_{in}\right)}{\left({h}_{out}-{h}_{in}\right)}=\frac{\left({h}_{5s}-{h}_{4}\right)}{\left({h}_{5}-{h}_{4}\right)}$$

(4)

Condenser cold and hot sides:

$$\:{Q}_{C,h}={\dot{m}}_{C,h}\times\:\left({h}_{C,h.in}-{h}_{C,h.out}\right)={\dot{m}}_{{co}_{2}}\times\:\left({h}_{3}-{h}_{4}\right)$$

(5)

$$\:{Q}_{C,c}={\dot{m}}_{C,c}\times\:\left({h}_{C,c.out}-{h}_{C,c.in}\right)={\dot{m}}_{Air}\times\:\left({h}_{12}-{h}_{11}\right)$$

(6)

Heat Recovery Steam Generator (HRSG)

In this study, the value specific heat capacity at constant pressure is 1.148 kJ/kg K. below Equations represents the heat transfer for the hot and cold sides of HRSGs²⁴:

$$\:{Q}_{H1,h}={\dot{m}}_{H1,h}\left({h}_{H1,h.in}-{h}_{H1,h.out}\right)={\dot{m}}_{smoke}\:{{c}_{p}}_{g}\left({T}_{13}-{T}_{14}\right)$$

(7)

$$\:{Q}_{H1,c}={\dot{m}}_{H1,c}\left({h}_{H1,c.out}-{h}_{H1,c.in}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{1}-{h}_{8}\right)$$

(8)

$$\:{Q}_{H2,h}={\dot{m}}_{H2,h}\left({h}_{H2,h.in}-{h}_{H2,h.out}\right)={\dot{m}}_{smoke}\:{{c}_{p}}_{g}\left({T}_{14}-{T}_{15}\right)$$

(9)

$$\:{Q}_{H2,c}={\dot{m}}_{H2,c}\left({h}_{H2,c.out}-{h}_{H2,c.in}\right)=x\:{\dot{m}}_{{CO}_{2}}\left({h}_{10}-{h}_{9}\right)$$

(10)

First law cycle efficiency.

The cycle efficiency of the first law of thermodynamics is:

$$\:\eta _{I} = \frac{{\dot{W}_{{Net}} \:}}{{\dot{Q}_{{in}} \:}} = \frac{{\dot{W}_{T} - \dot{W}_{P} }}{{\sum {\:_{i} } \dot{Q}_{{Hi}} }}$$

(11)

For the thermal efficiency of the cycle:

$$\:\eta _{{CYC}} = \frac{{\dot{W}_{T} - \dot{W}_{P} }}{{\sum {\:_{i} } \dot{Q}_{{Hi}} }}$$

(12)

The heat recovery efficiency of waste heat recovery (WHR) from a waste heat source can be defined as follows²⁴:

$$\:\eta _{{HR}} = \frac{{\sum {\:_{i} } \dot{Q}_{{Hi}} }}{{\sum {\:_{i} } \dot{Q}_{{Hi_{{Max}} }} }} = \frac{{\sum {\:_{i} } \dot{m}_{{smoke}} \left( {h_{{in}} - h_{{out}} } \right)_{i} }}{{\sum {\:_{i} } \dot{m}_{{smoke}} \left( {h_{{in}} - h_{0} } \right)_{i} }} = \frac{{\sum {\:_{i} } \left( {h_{{in}} - h_{{out}} } \right)_{i} }}{{\sum {\:_{i} } \left( {h_{{in}} - h_{{surr}} } \right)_{i} }}$$

(13)

where Q_{H, max} is the maximum allowable heat rate from the waste heat source; h_in and h_out are the inlet and outlet specific enthalpies of the waste heat source, respectively; and the subscript 0 indicates that the properties are taken at the reference temperature and pressure (T₀, P₀) representing the dead state. The system thermal efficiency of the sCO₂ cycle for the waste heat recovery can be defined as the ratio of the net power to the maximum allowable heat rate from the waste heat source. This is expressed as follows²⁴:

$$\:\eta _{{SYS}} = \frac{{\dot{W}_{T} - \dot{W}_{P} }}{{\sum {\:_{i} } \dot{Q}_{{Hi_{{\max }} }} }}$$

(14)

sCO₂ recuperator cycle

In the second configuration, depicted in Fig. 6, a recuperator is added after the turbine. Table 2 details the thermodynamic properties of this recuperator configuration. The cycle mass flow rate increases to 73.45 kg/s, while the condenser cooling air mass flow rate decreases to 1635 kg/s. The recuperator facilitates heat savings, raising the cycle efficiency to 19.26%. This improvement is attributed to a temperature increase at Point 8, which boosts the cycle mass flow rate and reduces the cooling air mass flow rate in the condenser.

Fig. 6

Schematic of sCO₂ recuperator cycle.

Table 2 Thermodynamic properties for sCO₂ recuperator cycle.

Recuperator

Equations (15) and (16) represent the heat transfer for the hot and cold sides in the Recuperator²⁴:

$$\:{Q}_{R,h}={\dot{m}}_{R,h}\left({h}_{R,h.in}-{h}_{R,h.out}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{2}-{h}_{3}\right)$$

(15)

$$\:{Q}_{R,c}={\dot{m}}_{R,c}\left({h}_{R,c.out}-{h}_{R,c.in}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{8}-{h}_{5}\right)$$

(16)

sCO₂ split cycle

In the split cycle, at the pump exit and before the recuperator, a portion of the mass flow (X) is bypassed from the main cycle and enters to the second HRSG, therefore, the rest of (1-X) enters to the recuperator. Figure 7 illustrates the arrangement of the supercritical carbon dioxide split cycle.

Fig. 7

Schematic of sCO₂ split cycle.

For split cycle, Equations (17) and (18) represent the heat transfer for the hot and cold sides in the Recuperator²⁴:

$$\:{Q}_{R,h}={\dot{m}}_{R,h}\left({h}_{R,h.in}-{h}_{R,h.out}\right)={\dot{m}}_{{CO}_{2}}\left({h}_{2}-{h}_{3}\right)$$

(17)

$$\:{Q}_{R,c}={\dot{m}}_{R,c}\left({h}_{R,c.out}-{h}_{R,c.in}\right)=\left(1-x\right)\:{\dot{m}}_{{CO}_{2}}\left({h}_{7}-{h}_{6}\right)$$

(18)

The thermodynamic properties of different cycle nodes are given in Table 3.

Table 3 Thermodynamic properties for sCO₂ split cycle.

As it is observed, the mass flow rate of carbon dioxide in the main cycle is 89.86 kg/s while that is 31.45 kg/s at Point 6, giving the split ratio of X = 0.65. The cooling air mass flow rate of condenser is 1548 kg/s. It is clearly observed an increase in cycle flow rate and the cycle efficiency increases to 23.56%. Heat recovery, cycle and system efficiency of sCO₂ cycles shown in Fig. 8 are as follows:

Fig. 8

Heat recovery, cycle and system efficiency of sCO₂ cycles based on T1: (a) simple cycle, (b) recuperator cycle, (c) split cycle

T-S diagrams of sCO₂ cycles shown in Fig. 9 are as follows:

Fig. 9

T-S diagram of sCO₂ cycles: (a) simple sCO2 cycle, (b) recuperator sCO2 cycle, (c) split sCO2 cycle.

As can be seen in Fig. 9, the positions of all points related to supercritical carbon dioxide cycles on the constant pressure curves are known and the enthalpy value of each point is comparable to other points.

Environmental sustainability analysis modelling

All power plants, including nuclear, thermal, hydropower, and solar, have environmental impacts that cause pollution and ecological disruption. While electricity is essential, its production can degrade the environment, necessitating efforts for mitigation. Efficient resource use and sustainable energy sources are vital for development. Exergy methods improve efficiency by optimizing resource use and reducing environmental harm. Cornelissen highlights that exergy analysis is crucial for sustainability, as it identifies energy losses and assesses emissions impacts. By minimizing exergy destruction, power plants can enhance sustainability, with analyses conducted at temperatures of 25 °C to 45 °C²⁶.

Exergy efficiency calculations

The general equation of Exergy Balance for a Steady-Flow System is²⁴:

$$\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}-\dot{W}+\sum\:_{in}\dot{m}ᴪ-\sum\:_{out}\dot{m}ᴪ-{\dot{X}}_{des}=0$$

(19)

$$\psi = \left( {h - h_{0} } \right) - T_{0} \left( {s - s_{0} } \right)$$

(20)

Turbine and pump

The exergy Balance for the turbine and pump:

$$\:\dot{X}_{{des,T}} = \dot{m}_{{CO_{2} }} \left( {\psi _{1} - \psi _{2} } \right) - \dot{W}_{T}$$

(21)

$$\:\dot{X}_{{des,P}} = \dot{m}_{{CO_{2} }} \left( {\psi _{4} - \psi _{5} } \right) + \dot{W}_{P}$$

(22)

Second law efficiency is calculated as shown:

$$\psi _{{II,T}} = \frac{{\dot{W}_{{out}} }}{{\dot{W}_{{rev,out}} }} = \frac{{\left( {h_{1} - h_{2} } \right)}}{{\left( {\psi _{1} - \psi _{2} } \right)}} = \frac{{\left( {h_{1} - h_{2} } \right)}}{{\left( {h_{1} - h_{2} } \right) - T_{0} \left( {s_{1} - s_{2} } \right)}}$$

(23)

$$\psi _{{II,P}} = \frac{{\dot{W}_{{rev,in}} }}{{\dot{W}_{{in}} }} = \frac{{\left( {\psi _{5} - \psi _{4} } \right)}}{{\left( {h_{5} - h_{4} } \right)}} = \frac{{\left( {h_{5} - h_{4} } \right) - T_{0} \left( {s_{5} - s_{4} } \right)}}{{\left( {h_{5} - h_{4} } \right)}}$$

(24)

Condenser

In the condenser, temperature $\:{T}_{k}\:\:\:$that gives $\:{\dot{Q}}_{k}\:\:$is equal to the ambient temperature. Therefore, the value of $\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}$ is equal to zero. The exergy Balance for the condenser as shown:

$$\:\dot{X}_{{des,C}} = \dot{m}_{{CO_{2} }} \left( {\psi _{3} - \psi _{4} } \right)$$

(25)

The efficiency of the second law of thermodynamics for the condenser as shown:

$$\:\eta _{{II,C}} = \frac{{\dot{m}_{{cold}} \:\Delta \psi _{{cold}} }}{{\dot{m}_{{hot}} \:\Delta \psi _{{hot}} }} = \frac{{\dot{m}_{{air}} \left( {\psi _{{12}} - \psi _{{11}} } \right)}}{{\dot{m}_{{CO_{2} }} \left( {\psi _{3} - \psi _{4} } \right)}} = 1 - \frac{{\dot{X}_{{des,C}} }}{{\dot{m}_{{CO_{2} }} \left( {\psi _{3} - \psi _{4} } \right)}}$$

(26)

Recuperator

In the recuperator, because both sides are in the cycle. Therefore, the value of $\:\sum\:\left(1-\frac{{T}_{0}}{{T}_{k}}\right){\dot{Q}}_{k}$ is zero. The exergy Balance for the recuperator and efficiency of the second law of thermodynamics for recuperator cycle as shown:

$$\:\dot{X}_{{des,R}} = \dot{m}_{{CO_{2} }} \left( {\psi _{2} - \psi _{3} } \right) + \dot{m}_{{CO_{2} }} \left( {\psi _{5} - \psi _{8} } \right)$$

(27)

$$\eta _{{II,R}} = \frac{{\dot{m}_{{cold}} {\mkern 1mu} \Delta \psi _{{cold}} }}{{\dot{m}_{{hot}} \:\Delta \psi _{{hot}} }} = \frac{{\left( {\psi _{8} - \psi _{5} } \right)}}{{\left( {\psi _{2} - \psi _{3} } \right)}} = 1 - \frac{{\dot{X}_{{des,R}} }}{{\dot{m}_{{CO_{2} }} \:\left( {\psi _{2} - \psi _{3} } \right)}}$$

(28)

The exergy Balance for the recuperator and efficiency of the second law of thermodynamics for split cycle as shown:

$$\:\dot{X}_{{des,R}} = \dot{m}_{{CO_{2} }} \left( {\psi _{2} - \psi _{3} } \right) + (1 - x)\dot{m}_{{CO_{2} }} \left( {\psi _{6} - \psi _{7} } \right)$$

(29)

$$\:\eta _{{II,R}} = \frac{{\dot{m}_{{cold}} \:\Delta \psi _{{cold}} }}{{\dot{m}_{{hot}} \:\Delta \psi _{{hot}} }} = \frac{{\left( {1 - x} \right)\left( {\psi _{7} - \psi _{6} } \right)}}{{\left( {\psi _{2} - \psi _{3} } \right)}} = 1 - \frac{{\dot{X}_{{des,R}} }}{{\dot{m}_{{CO_{2} }} \:\left( {\psi _{2} - \psi _{3} } \right)}}$$

(30)

Heat recovery steam generator (HRSG)

The exergy Balance for the HRSGs as shown:

$$\:\dot{X}_{{des,H1}} = \left( {1 - \frac{{T_{0} }}{{T_{{13}} }}} \right)Q_{{H1\:\left( {air} \right)}} + \dot{m}_{{co_{2} }} \left( {\psi _{8} - \psi _{1} } \right)$$

(31)

$$\:\dot{X}_{{des,H2}} = \left( {1 - \frac{{T_{0} }}{{T_{{14}} }}} \right)Q_{{H2\:\left( {air} \right)}} + \dot{m}_{{co_{2} }} \left( {\psi _{9} - \psi _{{10}} } \right)$$

(32)

The efficiency of the second law of thermodynamics for the HRSGs as shown:

$$\:\eta _{{II,H1}} = \frac{{\dot{m}_{{cold}} \:\Delta \psi _{{cold}} }}{{\dot{m}_{{hot}} \:\Delta \psi _{{hot}} }} = \frac{{\dot{m}_{{CO_{2} }} \left( {\psi _{1} - \psi _{8} } \right)}}{{\dot{m}_{{air}} \left( {\psi _{{13}} - \psi _{{14}} } \right)}} = 1 - \frac{{\dot{X}_{{des,H1}} }}{{\dot{m}_{{air}} \left( {\psi _{{13}} - \psi _{{14}} } \right)}}$$

(33)

$$\:\eta _{{II,H2}} = \frac{{\dot{m}_{{cold}} \,\Delta \psi _{{cold}} }}{{\dot{m}_{{hot}} \:\Delta \psi _{{hot}} }} = \frac{{\mathop {xm}\limits^{.} _{{CO_{2} }} \left( {\psi _{{10}} - \psi _{9} } \right)}}{{\dot{m}_{{air}} \left( {\psi _{{14}} - \psi _{{15}} } \right)}} = 1 - \frac{{\dot{X}_{{des,H2}} }}{{\dot{m}_{{air}} \left( {\psi _{{14}} - \psi _{{15}} } \right)}}$$

(34)

Second law cycle efficiency

The cycle efficiency of the second law of thermodynamics as shown:

$$\:\eta _{{II}} = \frac{{\dot{\psi }_{{wanted}} \:}}{{\dot{\psi }_{{source}} \:}} = \frac{{\dot{\psi }_{T} - \dot{\psi }_{P} }}{{\dot{\psi }_{{H1}} + \dot{\psi }_{{H2}} }}$$

(35)

Sustainability calculations

Connelly and Koshland propose using a depletion number (DP) to assess the efficiency of fossil fuel consumption, aiming to explore the relationship between sustainability, environmental impact, and exergy efficiency²⁸:

$$\:D_{P} = \frac{{\dot{X}_{d} }}{{\psi _{{in}} }}$$

(36)

where $\:{\dot{X}}_{d}$ = exergy destruction and $\:\psi _{{in}} \:$= exergy input. The relationship between exergy efficiency and the depletion number is as follows:

$$\:\eta _{{II}} = 1 - D_{P}$$

(37)

Now, the relationship between the sustainability index (SI) and the depletion number is:

$$\:SI=\frac{1}{{D}_{P}}$$

(38)

Economic analysis modelling for cycle components

Economic evaluations are crucial for designing cost-effective systems. Cost accounting involves determining actual costs, establishing pricing, managing expenditures, and informing operational decisions. The unit cost of electricity from a power plant, expressed as cost per kilowatt-hour, includes three main components: equipment purchases costs, operating and maintenance costs, and fuel costs. The primary aim of economic modeling is to calculate this cost per kilowatt-hour, based on initial investment, operating expenses, and fuel costs²⁹.

$${{\text{Z}}_{\text{E}}}={\text{ }}{{\text{Z}}_{\text{C}}}+{\text{ }}{{\text{Z}}_{{\text{OM}}}}+{\text{ }}{{\text{Z}}_{\text{F}}}$$

(39)

The cost of initial investment in equipment purchases (Z_C)

Following equations determine the purchase costs of the cogeneration system components as function of thermodynamic parameters. Some equations are based on input parameters such as temperature, pressure, etc., and some equations are based on output parameters such as net power, etc. These equations are presented below for different components of the cycle²⁹:

Turbine

The turbine purchase cost in the cogeneration systems is stated in:

$$PEC_{T} = \left( {\frac{{479.34 - \dot{m}_{{co_{2} }} }}{{0.92 - \eta _{T} }}} \right)\ln \left( {\frac{{P_{{Turbin~inlet}} }}{{P_{{Turbin~outlet}} }}} \right)\left( {1 + e^{{0.036T_{{Turbin~inlet}} - 54.4}} } \right)~~\left[ T \right]~:^\circ C$$

(40)

Pump

The purchase costs of the pump are calculated based on:

$$\ \:PEC_{P} = \left( {\frac{{71.1 - \dot{m}_{{co_{2} }} }}{{0.9 - \psi _{P} }}} \right)\left( {\frac{{P_{{Pump\:outlet}} }}{{P_{{Pump\:inlet}} }}} \right)\:{\text{ln}}\left( {\frac{{P_{{Pump\:outlet}} }}{{P_{{Pump\:inlet}} }}} \right)$$

(41)

Condenser and recuperator

Following Equation show the purchase costs of the condenser and recuperator for the cogeneration system based on:

$$\:{PEC}_{C\:or\:R}=4122{\left\{\frac{{\dot{m}}_{{co}_{2}}\:\left({h}_{in}-{h}_{out}\right)}{18\:{\varDelta\:T}_{LMTD}}\right\}}^{0.6}$$

(42)

Heat recovery steam generator (HRSG)

Following Equations show the purchase costs of the HRSG for the cogeneration system based on:

$$\:{PEC}_{HRSG}=6570{\left(\frac{{\dot{Q}}_{HRSG}}{{\varDelta\:T}_{LMTD}}\right)}^{0.8}+21276\:{\dot{m}}_{{co}_{2}}+1184.4\:{{\dot{m}}_{smoke}}^{1.2}\:\:\:\:\:\:\:\:\left[{\dot{Q}}_{HRSG}\right]\::Mw$$

(43)

The cost of purchasing equipment for the cycle components for the three stated cycles is presented. The purchasing equipment cost (PEC) of different cycle are given in Table 4.

Table 4 Purchasing equipment cost (PEC) of sCO₂ cycles (M$).

Total cost.

The total cost of the initial investment of a sCO₂ power plant per kilowatt-hour of electricity generated is obtained by²⁹:

$$\:{Z}_{C}=\frac{TCI\:\times\:\:\:CRF}{\dot{W}\:H}[\$/kWh]$$

(44)

where, TCI is the total investment cost depends on:

$$\:TCI=6.32\:{(1+{r}_{n})}^{n}\:PEC\:\:\left[\$\right]$$

(45)

r_n is the annual interest rate which is considered as 5%. The coefficients of these relationships are not related to the present time, so the expression provided in the parentheses is an approximation for updating this relation, in which n is the number of years since the introduction of this formula. Also, the PEC statement provided in the above formula is the price of the purchased equipment, which is calculated using the following equation:

$$\:PEC={Z}_{Turbine}+{Z}_{Pump}+{Z}_{Condenser}+{Z}_{Recouprator}+{Z}_{HRSG}\:\:\left[\$\right]$$

(46)

To determine the capital recovery factor, below equation has been used²⁷:

$$\:CRF=\frac{i{(i+1)}^{n}}{{(i+1)}^{n}-1}$$

(47)

In the above relation, i is the amount of interest rate and n is capital return span, which are considered equal to 12% and 30 years, respectively. H, which is the duration of the annual operation of the new power plant, with an availability rate of 91%, is considered as 8000 h.

Operating and maintenance cost (Z_OM)

Operating and maintenance costs (fixed or variable) in general and assuming the power plant’s operation under nominal load conditions, can be written in a relation in terms of the total cost of the initial investment²⁹:

$$\:{Z}_{OM}=\left(\phi\:-1\right)\:{Z}_{C}[\$/kWh]$$

(48)

φ is the operating and maintenance factor and its value is determined according to the type of the power plant. But with a good approximation, we can use a value of 1.06²⁹.

Fuel cost (Z_F)

The annual fuel consumption cost is calculated by:

$$\:M={C}_{F}\:.\:{\dot{m}}_{F}\:.\:{LHV}_{F}\:.\:{t}_{s}\:\:[\$/Annum]$$

(49)

Where $\:{C}_{F}$, $\:{\dot{m}}_{F}\:\:$and $\:{LHV}_{F}$respectively are the cost of preparation, mass flow rate and lower heating value of the fuel consumed, and $\:{t}_{s}$ is the nominal time of the plant’s operating in seconds. Therefore, the fuel cost per kilowatt-hour is calculated according to the net power of the power plant and the annual operating hours of the power plant, as follows:

$$\:{Z}_{F}=\frac{{C}_{F}\:.\:{\dot{m}}_{F}\:.\:{LHV}_{F}}{\dot{W}\:H}\:\:{t}_{s}\:[\$/kWh]$$

(50)

On the other hand, the following equation is used to calculate the heat rate of the power plant:

$$\:{Z}_{F}=\frac{{C}_{F}\:.\:{\dot{m}}_{F}\:.\:{LHV}_{F}}{\dot{W}\:H}\:\:{t}_{s}\:[\$/kWh]$$

(51)

Thus, from the combination of relations (42) and (43), we obtain (44), which indicates the cost of fuel based on the heat rate of the power plant²⁹:

$$\:{Z}_{F}={C}_{F}\:\:{HR}_{PP}\:[\$/kWh]$$

(52)

In the supercritical carbon dioxide cycle, fuel is not used independently. Therefore, we do not include the cost of fuel in the calculations. So, we have:

$$\:{Z}_{F}=0$$

(53)

The price of each kilowatt-hour of electricity produced will eventually be calculated by combining above relations. The cost per kilowatt-hour of electricity generated is calculated as follows²⁹:

$$\:{Z}_{E}=\left(\frac{TCI\:\times\:\:CRF}{\dot{W}\:H}\right)\phi\:\:\:\:\:[\$/kWh]$$

(54)

Energy, exergy and environmental sustainability analysis

The energy and exergy analysis results for simple, recuperator, and split cycles are presented in Tables 5, 6 and 7. The turbine has an isentropic efficiency of 90%, and the pump’s efficiency is 80%. The cycle efficiencies are 17.73% for the simple cycle, 19.26% for the recuperator cycle, and 23.57% for the split cycle. The CO₂ mass flow rates for the three cycles are 67.44 kg/s, 73.45 kg/s, and 89.86 kg/s, respectively, with the mass fraction of the split cycle (X) at 0.65. The second law efficiencies for the cycles are 48.01%, 52.14%, and 63.79%. Despite high turbine and pump efficiencies, exergy destruction in the condenser and HRSGs significantly impacts overall cycle efficiencies.

Table 5 Energy and Exergy analysis of supercritical carbon dioxide simple cycle.

Table 6 Energy and Exergy analysis of supercritical carbon dioxide recuperator cycle.

Table 7 Energy and Exergy analysis of supercritical carbon dioxide split cycle.

Table 8 presents the results of sustainability and environmental analysis, showing that the development of the supercritical carbon dioxide cycle from the simple to the split cycle enhances stability and reduces environmental pollution. The stability numbers are 1.920 for the simple cycle, 2.090 for the recuperator cycle, and 2.760 for the split cycle, indicating that higher stability numbers correlate with greater stability and lower pollution levels.

Table 8 Energy and exergy analysis of supercritical carbon dioxide split cycle.

Economic analysis

Cost estimation can be conducted using two methods: the first method is based on the inlet properties of the components, while the second method relies on the duties of the components for cost estimation. Both methods are compared using previously introduced correlations to estimate the cycle cost, with the results presented in Table 9. The cycle cost includes initial investment, equipment purchases, and maintenance. Table 10 calculates and compares the cost of electricity generation for three configurations of the supercritical carbon dioxide cycle (simple, recuperative, and split) against the steam cycle. The split cycle has the highest cost at $0.122 per kWh, while the conventional steam cycle costs $0.138 per kWh.

Table 9 Purchasing equipment cost of supercritical carbon dioxide cycles.

Table 10 Electricity generation cost of supercritical carbon dioxide cycles.

Sensitivity analysis

To analyze sensitivity, the parameters considered are controllable factors: the cycle’s upper pressure (P1 or Pmax), the HRSG intermediate temperature (T8), and the split mass fraction (X). The cycle’s lower pressure (P2) is set to ensure that the pump inlet is a saturated liquid at the surrounding temperature. Flow splitting defines the mass flow fraction directed to the bypass line of the recuperator.

Cycle upper pressure (P₁)

Figures 10 depict the effect of maximum cycle pressure on cycle parameters.

Fig. 10

The effect of cycle upper pressure (P₁) on: (a) energy efficiency, (b) exergy efficiency, (c) net power, (d) exergy destruction, (e) condenser air mass flow, (f) CO₂ air mass flow, (g) cycle cost, (h)sustainability.

Figure 10a illustrates that the efficiencies of all three cycles are significantly lower than that of the Carnot cycle, with the split cycle being the most efficient due to better heat recovery. Figure 10b shows that the second law efficiency surpasses the first law efficiency. The highest exergy losses occur in the HRSG and condenser, with losses of 17,702 kW for the simple cycle, 17,081 kW for the recuperator cycle, and 12,532 kW for the split cycle, indicating improved efficiency as the cycles develop. Figure 10c reveals that increasing maximum cycle pressure boosts turbine power more than pump power, raising net output power from about 4 MW to 10 MW. Figure 10d indicates that the simple cycle has the highest exergy loss, which decreases in the recuperator and split cycles. The split cycle achieves a reduction in exergy loss of 4,549 kW compared to the recuperator cycle. Figure 10e shows that higher maximum pressure reduces the condenser’s air flow rate, while Fig. 10f indicates varying carbon dioxide mass flow rates with increasing maximum pressure across the cycles. Figure 10 g highlights that equipment costs rise with maximum pressure, with the simple cycle facing higher costs when adding a recuperator. Lastly, Fig. 10h demonstrates that the split cycle significantly improves stability and reduces environmental pollution compared to the others. Further analysis will focus on additional parameters related to the optimal split cycle³⁰.

HRSG intermediate temperature (T₈)

Figures 11 depict the effect of HRSG intermediate temperature on split cycle parameters. In this analysis, the mass fraction of the split is considered to be 0.65.

Fig. 11

The effect of HRSG intermediate temperature (T₈) on: (a) energy efficiency, (b) exergy efficiency, (c) net power, (d) exergy destruction, (e) condenser air mass flow, (f) CO₂ air mass flow, (g) cycle cost, (h)sustainability.

The temperature T8, defined as the difference between T14 and the recuperator’s pinch point, becomes more constrained as T15 decreases. For example, when the exhaust outlet temperature is 90 °C, T14 is lower, limiting the permissible range for T8. Figure 11a shows that in the split cycle, energy efficiency remains constant across all exhaust outlet temperatures, as output power is dependent on the mass flow rate of carbon dioxide influenced by T8. In contrast, Fig. 11b indicates that second law efficiency is higher than first law efficiency and improves with lower exhaust outlet temperatures, maximizing input heat utilization. Figure 11c highlights that output power sharply declines for temperatures above 150 °C due to reduced mass flow rates of carbon dioxide. Figure 11d reveals that exergy loss is greater at lower exhaust temperatures, with maximum loss at 90 °C and minimum loss at 300 °C, reinforcing the benefits of integrating ORC and MED cycles with supercritical carbon dioxide cycles. Figure 11e shows that higher exhaust temperatures increase condenser load and air flow rate, while Fig. 11f confirms that mass flow rates of carbon dioxide decrease with rising exhaust temperatures³¹. Figure 11 g illustrates that higher exhaust temperatures lead to reduced equipment costs, particularly for HRSGs, though costs rise significantly when HRSG inlet temperatures approach exhaust temperatures. Optimal conditions for economic efficiency occur with T8 around 150 °C. Figure 11 h indicates that lower exhaust temperatures improve stability and reduce environmental pollution in the split cycle, though the range of stability is limited. Overall, the figures demonstrate the relationships between energy efficiency, exergy efficiency, and net power concerning recuperator outlet temperatures across various exhaust outlet temperatures. The optimal exhaust outlet temperature for effective heat exchange in the cycle is calculated to be approximately 150–200 °C, utilizing energy from the exhaust for the supercritical carbon dioxide cycle and the remainder for desalination or organic fluid cycles. Additionally, the effects of mass fraction on energy efficiency and flow rates in the split cycle are also noted³².

Therefore, the idea of utilizing a desalination cycle or an organic fluid cycle is raised. The fresh water cycle will be employed to produce fresh water without altering energy efficiency, while the organic fluid cycle will be used to enhance the cycle’s efficiency. An overview of these two cycles is presented in Figs. 12 and 13.

Fig. 12

Schematic of sCO₂ with ORC cycle.

Fig. 13

Schematic of sCO₂ with MED cycle.

The Organic Rankine Cycle (ORC) converts low-temperature heat into mechanical energy for electricity, using organic fluids to efficiently harness sources like industrial waste heat and solar energy. Multi-Effect Distillation (MED) uses heat to produce fresh water from seawater. Integrating ORC and MED with the supercritical CO₂ (sCO₂) cycle offers benefits such as:

Cost-Effective energy for desalination

ORC provides low-cost thermal energy for desalination using waste heat or renewables.

Improved efficiency

Waste heat from the sCO₂ cycle enhances overall system efficiency.

Sustainability

Supercritical CO₂ reduces greenhouse gas emissions.

Optimized resource use

The system maximizes thermal energy usage, reducing reliance on conventional sources.

Overall, this integration enhances energy efficiency and sustainability in producing fresh water and electricity, especially in arid regions³³.

Split mass fraction (X)

Figures 14 depict the effect of split mass fraction on cycle parameters. This parameter is limited by the logarithmic mean temperature difference (LMTD) of the heat exchangers in the cycle, which include HRSG1, HRSG2, condenser and recuperator, and it must be positive. The acceptable range for the mass fraction of the split is between 0.65 and 0.85.

Fig. 14

the effect of the split mass fraction (X) on: (a) energy efficiency, (b) exergy efficiency, (c) net power, (d) exergy destruction, (e) condenser air mass flow, (f) CO₂ air mass flow, (g) cycle cost, (h)sustainability.

Figure 14a demonstrates an inverse relationship between the mass fraction of the split and the energy efficiency of the split cycle. As the mass fraction (X) increases, the upper section’s flow rate rises while the lower section’s flow rate through the recuperator decreases, leading to reduced output power and overall efficiency. Figure 14b shows that higher mass fractions diminish the thermal recovery capability of the recuperator, raising its output temperature and increasing the load on the condenser, which in turn elevates exergy losses and reduces exergy efficiency. Figure 14c further illustrates that increased mass fraction negatively impacts output power due to decreased flow in the lower section, affecting pump and turbine performance. Figure 14d indicates that this reduction in flow raises the input temperature to the condenser, increasing exergy losses. In Fig. 14e, the correlation between mass fraction and condenser airflow is evident; higher mass fractions increase the condenser load and air mass flow rate. Figure 14f reveals that as mass fraction increases, flow in the lower section decreases, requiring a reduction in input temperature to HRSG1, which leads to a greater enthalpy difference and reduced carbon dioxide mass flow rate. Economically, Fig. 14g shows that increasing mass fraction reduces the size of equipment in the lower section while increasing the size of HRSG2, ultimately lowering overall equipment costs. Figure 14h indicates that optimal stability and minimal pollution occur at a mass fraction of 0.65; beyond this point, stability decreases and pollution rises. The analysis will continue by examining economic variables, particularly the cost of electricity production and the purchase cost of primary equipment (PEC). Figure 15a indicates that while increasing turbine inlet temperature (TIT) does not significantly change mass flow rates, it has notable economic implications. Figure 15b illustrates how rising TIT affects the costs of cycle components, while Fig. 15c shows the impact of both TIT and mass fraction on electricity production costs, highlighting the relationship between increased mass fraction and higher electricity costs.

Fig. 15

the effect of sCO₂ Turbine Inlet Temperature (TIT) on: (a) air and CO₂ mass flow rate (kg/s) & electricity generate cost ($/kWh), (b) equipment cost (M$) and electricity generate cost($/kW), (c) electricity generate cost ($/kWh) and ($/kW).

Presented below are three Pareto charts corresponding to three objective functions. Figure 16a illustrates the impact of the mass fraction on the reduction of exergy. Figure 16b demonstrates how the mass fraction affects the cost of electricity generation, while Fig. 16c depicts the influence of the mass fraction on exergy efficiency.

Fig. 16

Pareto chart for the effect of mass fraction on: (a) exergy destroyed, (b) electricity generate cost, (c) exergy efficiency.

As evident from the above Pareto diagrams, in the supercritical carbon dioxide split cycle; exergy loss, electricity generation cost, and energy efficiency occur at a mass fraction of 0.65.

Conclusions

The supercritical carbon dioxide (sCO₂) power cycle presents a compact and highly efficient solution for recovering waste heat from gas turbines, offering significant advantages over traditional steam cycles. The energy efficiency of the simple sCO₂ cycle stands at 17.73%, with the highest exergy losses occurring in the heat recovery steam generator (HRSG) at 52.27% and the condenser at 43%. The integration of a recuperator improves the efficiency to 19.26%, while exergy losses are reduced to 49.09% for the HRSG and 38.38% for the condenser. The split cycle configuration further enhances energy efficiency to 23.56%, with a mass fraction of 0.65. Exergy efficiencies for the simple, recuperator, and split cycles are measured at 48.01%, 52.14%, and 63.79%, respectively. Sensitivity analysis reveals that maximum cycle pressure significantly influences efficiency more than turbine inlet temperature, while increasing the mass fraction negatively affects first law efficiency. It was also found that enhancing the mass fraction in the split cycle adversely impacts energy efficiency, exergy, and net power output, although it reduces cycle costs and improves environmental stability. Moreover, sCO₂ cycles are shown to be more cost-effective for electricity generation compared to steam cycles, with cost ratios of 0.71, 0.79, and 0.86 for the simple, recuperator, and split cycles, respectively.

In conclusion, optimizing cycle configurations significantly improves both first and second law efficiencies, contributing to greater environmental sustainability and reduced pollution, as evidenced by sustainability indices of 1.92, 2.09, and 2.76 for the simple, recuperator, and split cycles, respectively.

For future studies, the following recommendations are proposed:

• Conducting a project involving the construction and laboratory analysis of the supercritical carbon dioxide cycle.

• Undertaking a numerical analysis project on the supercritical carbon dioxide cycle.

• Comparing the results of this study with laboratory and numerical analyses.

• Investigating existing economic relationships and developing unique correlations specifically for the supercritical carbon dioxide cycle.