A GIS-based fermatean fuzzy MCDM approach for identifying the optimal sites for solar power plant installation in Kermanshah Province

Abstract

Transitioning to renewable energy sources is crucial for sustainable, cost-effective, and clean electricity generation in Iran. While Iran’s location within the global solar belt makes it ideal for solar power plant (SPP) development, determining optimal locations is essential. This study identifies suitable areas for SPP establishment in Kermanshah Province using a GIS-based Fermatean Fuzzy MCDM approach. Fermatean Fuzzy Step-wise Weight Assessment Ratio Analysis (FFSWARA) was employed to model experts’ opinions uncertainties and determine reliable criteria weights, identifying solar radiation as the most important criterion (weight: 0.12). Spatial criteria were aggregated using Root Assessment Method (RAM) and Compromise Ranking of Alternatives from Distance to Ideal Solution (CRADIS) to generate suitability maps, with RAM proving more reliable and stable through sensitivity analysis. The RAM-derived suitability map indicates that 10% of the study area is highly suitable for SPP construction. Developing SPPs across 153 square kilometers of these areas could meet the province’s electricity demands and prevent 2.84 million metric tons of CO₂ emissions. These findings can aid decision-makers in planning and managing sustainable electricity production in Kermanshah Province.

Introduction

Energy is a fundamental pillar of economic growth in today’s world, playing a crucial role across all sectors. It enables the production of goods and services, making modern life and industry possible. From transportation and mobility to food preparation, water purification, and communication, countless essential activities rely on a steady energy supply^1,2,3,4. The rising global population and economic growth have led to a relentless increase in energy consumption⁵. Despite advancements in alternative sources, fossil fuels remain the dominant energy supply worldwide. However, their continued use raises significant environmental concerns, especially as fossil fuel reserves are being depleted at an accelerating rate⁶. The shift in the global energy mix will reshape trade dynamics, international dependencies, and geopolitical relations. Many nations heavily rely on fossil fuel imports, making them strategically vulnerable. While fossil fuels have driven economic growth for over 150 years, their environmental impact and geopolitical risks highlight the urgent need for transition, as reinforced by COP28. Renewable energy, with its abundance and broad availability, offers greater stability and resilience, reducing dependency on volatile fossil fuel markets. However, challenges remain in the global distribution of low-carbon technologies. The 2022 fossil fuel crisis underscored renewables’ economic benefits, with global deployment since 2000 saving an estimated USD 521 billion in fuel costs that year⁷. The use of fossil fuels negatively impacts the environment by contributing to CO₂ emissions. At the same time, modern energy alternatives, such as liquefied petroleum gas (LPG) and renewable, eco-friendly sources, remain largely inaccessible in many developing nations. Growing concerns over fossil fuel consumption and the reduction of fuel subsidies have shifted focus away from critical challenges faced by low-income countries, where the abrupt removal of such subsidies could lead to severe political and social consequences^8,9.

The Middle East is a major player in global energy production, hosting five of the top oil producers, Saudi Arabia, Iraq, the UAE, Iran, and Kuwait as well as key natural gas suppliers like Iran, Qatar, and the UAE. However, fossil fuel investment far outweighs clean energy spending, with only 20 cents allocated to renewables for every dollar spent on fossil fuels, well below the global average¹⁰. The region also experiences significant disparities in income and energy consumption, with Saudi Arabia, the UAE, and Kuwait at the higher end, while Yemen and Syria lag behind. Sovereign credit ratings vary widely, with Persian Gulf nations generally rated higher, whereas Iraq and Lebanon hold some of the lowest ratings¹⁰.

Some resource-rich nations have yet to acknowledge renewable energy investment as a key factor in sustainable development. This is especially evident in Iran, where plentiful oil and natural gas continue to dominate the energy sector. Iran possesses vast hydrocarbon reserves and abundant renewable energy potential but has yet to make significant investments in developing renewables. Expanding renewable energy for domestic use could free up more fossil fuels for export, boosting national income. Additionally, the energy and industrial sectors stand to benefit from renewable expansion. However, to achieve sustainable economic growth, Iran must adopt new policies and strategies to effectively harness its energy resources¹¹. By 2030, wind power is projected to generate approximately 22 TWh of electricity annually in Iran, aligning with international estimates. Biomass is expected to contribute around 0.018 TWh/year, while geothermal sources could produce 5.25 TWh/year. Concentrated solar power (CSP) is estimated to generate 94 TWh/year, with photovoltaic systems adding 0.007 TWh/year. Additionally, large hydropower sources are anticipated to supply 17.3 TWh/year to overall electricity production¹¹.

The government has been heavily subsidizing the electricity sector, with state-owned companies primarily managing power generation, distribution, and transmission¹². As part of the government’s 20-year plan focuses on expanding the role of the private sector in renewable energy (RE) production, advancing competitive technologies through academic research, improving RE accessibility in remote and rural areas, and boosting its industrial contribution for short-term competitiveness^13,14. Consequently, fossil fuel prices are expected to rise, leading to increased subsidies for RE generation¹². Integrating RE sources like solar power into electric distribution networks has gained traction due to its economic and environmental advantages, contributions to energy sustainability and security, and role in mitigating climate change and CO₂ emissions^15,16.

Recently, Iran has faced a significant shortage of electricity supply due to declining fuel reserves for power plants, resulting in prevalent blackouts across all sectors. This situation has caused to growing dissatisfaction among both the public and businesses. Corresponding to statistics from the Ministry of Energy in Iran, the fuel reserves of natural gas available for power plants decreased by approximately 560 million cubic meters between August and November 2024. To tackle this issue and ensure a stable electricity supply, it is fundamental to shift towards renewable energy sources, particularly solar power. Investing in solar energy not only offers a sustainable alternative but also helps reduce reliance on fossil fuels, thereby enhancing energy security and promoting long-term economic stability. Emphasizing the development of renewable energy infrastructure will be crucial in easing the current electricity crisis and meeting the growing demands of the population and economy.

Regard as the Kermanshah province, it is vital to address the high overall energy demand, remarkably the significant consumption of electricity, natural gas, and petroleum products. The household sector accounts for a major share of this demand, especially in electricity and light gas consumption, while petroleum products such as kerosene and diesel fuel are widely used in the commercial, public, and agricultural sectors. The top priority should be reducing household electricity consumption, followed by household natural gas usage. Improving efficiency in these sectors will have the greatest impact on lowering the province’s overall energy demand and enhancing energy sustainability¹⁷. Figure 1 point out the average electricity demand across different sectors in Kermanshah province, with the residential, industrial, and agricultural sectors exhibiting the highest electricity consumption.

Fig. 1

The average electricity consumption in different sectors in Kermanshah Province¹⁸.

The transition to renewable energy is fundamental in Kermanshah province due to the rising electricity demand across various sectors. The residential sector is experiencing increased consumption driven by the growing use of electrical appliances and heating and cooling systems. In agricultural, the number of electrified wells is rising, while the industrial sector requires significant amounts of electricity for production. Given the recent power shortages and frequent outages, expanding renewable energy projects, specifically solar energy, is critical to ensuring a stable and sustainable electricity supply.

This study employs a GIS-based Fermatean Fuzzy MCDM approach to identify suitable locations for establishing Solar Power Plants (SPPs) in Kermanshah Province, Iran. The objectives of the present study are as follows:

• Identifying the appropriate criteria to determine optimal areas for Solar Power Plant installation and computing reliable decision-making criteria weights using an effective weighting method.

• Determining the optimal areas for Solar Power Plant installation in the study area using a robust MCDM method which that method is identified based on a set of reliable evaluation measures.

• Evaluating the potential for solar electricity generation, surveying necessary infrastructure, and assessing the economic, social, and environmental benefits of transitioning from fossil fuels.

The methodology used to achieve the stated objectives consists of four main steps: First, a review of prior studies is conducted to identify relevant criteria for SPP siting. Second, spatial data is gathered, and spatial layers for the criteria are created through spatial analyses. Third, the criteria weights are determined using the Fermatean Fuzzy Step-wise Weight Assessment Ratio Analysis (SWARA). Finally, the spatial criteria are aggregated using three MCDM methods—Root Assessment Method (RAM), Compromise Ranking of Alternatives from Distance to Ideal Solution (CRADIS), and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)—and evaluated through comprehensive correlation and sensitivity analyses, and rank reversal evaluation to identify the most reliable model and the most critical criteria for SPP siting. Additionally, the research investigates strategies to enhance electricity supply, reduce shortages, and prevent future power disruptions, contributing to the province’s long-term energy security and sustainability.

This study introduces several key innovations. The first is the application of Fermatean Fuzzy SWARA to calculate reliable criteria weights and account for uncertainties in expert opinions, a method not previously utilized in SPP siting research. Another significant contribution is the incorporation of two advanced MCDM methods—RAM and CRADIS—for aggregating criteria and identifying suitable locations for SPPs, both of which have not been explored in prior studies within the field. Furthermore, the study includes a comprehensive correlation and sensitivity analysis, and rank reversal evaluation to compare these new methods with the established TOPSIS method, helping to identify the most reliable and stable approach for SPP siting. In addition, the research assesses the solar energy potential in the province, predicts the required infrastructure, and evaluates the economic, social, and environmental benefits of transitioning from fossil fuel-based electricity to solar power.

The subsequent sections of the article are organized as follows: the literature review and identification of research gaps are presented. In the second section, the materials and methods are outlined. In the third section, the results are discussed. In the fourth section, the outcomes are analyzed. In the fifth section, and the study concludes in the sixth section with recommendations for future work.

Literature review and research gaps

The most used weighing technique in SPP siting has been the Analytical Hierarchy Process (AHP)^19,20,21. Nevertheless, AHP has significant drawbacks, including inconsistent expert evaluations, a large number of pairwise comparisons, and an inability to account for correlations between criteria. A few studies like Uyan and Dogmus²²employed the Analytical Network Process (ANP), which takes into account correlations between criteria and produces weights that are more dependable; yet, concerns regarding the quantity of paired comparisons and inconsistencies persist. The Best-Worst Method (BWM), utilized by the studies^23,24,25addresses both the number of pairwise comparisons and inconsistencies. It should be noted that Cavallo and Ishizaka’s elaborated that the BWM method does not differ significantly from the AHP method. Additionally, SWARA, employed by the studies^26,27further reduces the number of pairwise comparisons and improves handling of inconsistencies compared to previous methods. SWARA employs a straightforward procedure for criteria evaluation by experts: experts first rank the criteria and then assess their relative importance²⁸. Zandi et al.²⁹ (2024) compared three weighting methods, AHP, BWM, and SWARA, based on a sensitivity analysis process for hospital location selection, and the results revealed that the SWARA method outperformed the other two methods. However, the ambiguity and uncertainty of expert opinions present a major obstacle to weighting systems³⁰. Integrating Fuzzy Sets (FSs) with the SWARA approach successfully simulates ambiguity in expert opinions to handle this problem³¹.

In addition, compared to fuzzy AHP, fuzzy ANP, and fuzzy BWM, fuzzy SWARA is simpler and takes less time^32,33. Fermatean fuzzy sets (FFSs), Pythagorean fuzzy sets (PFSs), Hesitant fuzzy sets (HFSs), and Intuitionistic fuzzy sets (IFSs) are some of the advancements in FSs. FFSs provide more versatility and realism than PFSs and IFSs³⁴. They are able to control a wider range of uncertainty, which makes more thorough assessments possible^35,36. In field of SPP siting integration of FFSs and MCDM methods could provide an effective and practical procedure³⁷. Aydoğan and Ozkir³⁵ proved that Fermatean Fuzzy SWARA (FFSWARA) performed better than Intuitionistic Fuzzy SWARA and Fuzzy SWARA. Based on the literature review, the FFSWARA weighting method has not been used in the field of SPP site selection so far. Therefore, in the present study, in order to achieve more accurate and trustworthy criteria weights, this study uses FFSWARA. The most common criteria aggregation technique used in earlier studies^20,38,39,40 is the Weighted Linear Combination (WLC). Other MCDM methods utilized include TOPSIS^{37,41,42,43,44,45}Multi-Attributive Border Approximation area Comparison (MABAC)²⁵and Order Weighted Average (OWA)⁴⁶. Other aggregation techniques mentioned in earlier research include WASPAS, COPRAS, AROMAN, and VIKOR. Known for its dependability and ease of use, TOPSIS has demonstrated superior performance when compared to alternative approaches⁴⁴. However, there is a lack of research on new MCDM techniques that enhance current methods or offer simpler and more reliable processes. Each research field needs to validate and compare new methods with traditional approaches to determine the most effective solutions. However, a key challenge is the lack of focus on new MCDM methods for combining criteria, as well as the difficulty of comparing different MCDM techniques³⁰. New methods are usually compared to well-established methods and have been able to provide similar or better results than previously established methods. Methods such as TOPSIS, VIKOR, MABAC, MOORA, COPRAS, ARAS, WASPAS and WLC are among the best-known MCDM methods, with which new methods are mainly compared. The present study in order to criteria aggregation uses two novel MCDM method which mainly those outperformed the mentioned well-known MCDM methods —RAM and CRADIS. The decision maker needs to fully understand the decision-making process in order to avoid computational complexities. The RAM method has been developed accordingly and provides a straightforward process that is easy to understand. In addition, this method is able to avoid the reverse rank phenomenon that is common in MCDM methods. These two new methods have not been used in the field of SPP site selection so far. CRADIS ensures that evaluation results remain unaffected by changes in alternatives or criteria⁴⁷. CRADIS is developed based on the fundamental of the well-known previous MCDM methods —TOPSIS, MARCOS and ARAS—while avoids from their disadvantages include computational complexity, processing time and exposure to extreme values⁴⁸.

Sensitivity analysis, though crucial for evaluating MCDM methods, is often overlooked in MCDM research, including SPP site selection^49,50. While Shorabeh et al.⁴⁶ implemented a thorough sensitivity analysis comparing TOPSIS, WASPAS, COPRAS, and AROMAN for SPP site selection, they did not address the comparison of land suitability maps across different methods (as in Nafi’Shehab et al.⁵¹ or the rank reversal phenomenon, both important considerations for decision-makers. To address this gap, this study evaluates the methods using four approaches: comparison with the established TOPSIS method, correlation of suitability maps using Pearson’s correlation coefficient and Percent Change, robustness evaluation via comprehensive sensitivity analysis, and resistance evaluation against rank reversal.

Prior studies^44,46 on SPP siting in Kermanshah Province, has not addressed the potential of solar energy to meet existing energy demands in Kermanshah Province. This study investigates that potential, examining the economic, environmental, and social benefits of solar electricity generation, including job creation, reduced reliance on fossil fuels, and CO₂ emission prevention.

Materials and methods

Study area

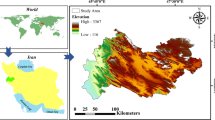
Kermanshah province in western Iran spans longitude 45°24’ to 48°7’ east and latitude 33°40’ to 35°18’ north (Fig. 2), covering an area of 25,045 km², which is 1.5% of the country’s total land area⁵². Kermanshah Province comprises 14 counties, with Kermanshah County being the largest and the provincial capital. The average entire Kermanshah province is 1200 m above sea level, with elevations ranging from 116 to 3367 m in different places. The province as a whole receives an average of 466 mm of precipitation annually, with regional variations ranging from 300 to 800 mm. The province of Kermanshah has more than 2,800 h of sunshine annually^53,54with values for photovoltaic power output (PVOUT) of 1890 kWh/kWp (maximum), 1150 kWh/kWp (minimum), and an average of 1764 kWh/kWp. This province is among Iran’s most promising areas for producing electricity from solar power because of these characteristics.

Fig. 2

Study area. The map is prepared by the authors using ArcGIS 10.8.1 software (https://support.esri.com/en-us/) .

Methodology

In order to determine the best locations for SPP establishment in Kermanshah Province, Iran, this paper proposes a Fermatean Fuzzy MCDM approach based on GIS. To produce more trustworthy criteria weights and model experts’ opinions uncertainty, this method combines Fermatean Fuzzy Sets with the SWARA weighting method. Using a sensitivity analysis process and a rank reversal evaluation procedure, the new efficient MCDM approaches for criteria aggregation were thoroughly contrasted with a proven MCDM method from earlier research. As illustrated in Fig. 3, the proposed methodology consists of four steps. In Step 1, a survey of previous studies on SPP siting and experts’ opinions was conducted to identify the most relevant criteria. In Step 2, relevant spatial data was collected to prepare the spatial layer for each criterion using appropriate analyses in a GIS environment. In Step 3, we assembled a team of experts to establish the criteria weights for SPP siting. They defined the importance of each criterion using linguistic terms, which were then converted into FFSs. The aggregated Fermatean Fuzzy decision matrix of all experts was created and utilized to calculate the criteria weights using the SWARA method. In Step 4, we aggregated the spatial layers of the criteria from Step 2 based on the weights calculated in Step 3, employing two new MCDM methods alongside a well-established one. To compare these three methods, a comprehensive correlation and sensitivity analysis, and a rank reversal evaluation were conducted to identify the most stable model for SPP siting, and the Percent Change indicators among the results of the three models were assessed. Ultimately, the most suitable areas for SPP establishment in Kermanshah Province were identified and verified based on the ground surveys, and the counties were prioritized.

Fig. 3

Overall structure of the proposed methodology.

Identifying influential criteria and Preparing Spatial layers

The effectiveness of an MCDM solution relies entirely on the chosen criteria; therefore, selecting the appropriate criteria is essential for ensuring robust and accurate results. This study identified the most influential criteria in SPP siting by reviewing scientific literature and utilizing the experts’ opinions. We aimed to select the effective criteria based on the literature, experts’ opinions, and available spatial data, ensuring that all important factors were included. It is worth noting that RE experts recommended using criteria such as distance from power transmission lines and energy demand in different parts of the study area, and GIS experts also suggested using criteria such as land price and ownership, but due to the unavailability of the spatial layer, these criteria were not used in the research. The following criteria include distance to cities (C₁), distance to faults (C₂), distance to roads (C₃), distance to subsidence areas (C₄), elevation (C₅), precipitation (C₆), average annual relative humidity (C₇), slope (C₈), average annual solar radiation (C₉), annual summation sunshine (C₁₀), average annual air temperature (C₁₁) and average annual wind speed (C₁₂). Table 1 presents the spatial analysis and the data used to create the criteria layers, while Fig. 4 visually represents these spatial criteria layers.

In order to provide energy to the urban population and nearby industries, an SPP for Cost-effectiveness should be situated close to human habitats and cities^55,56. In urban and suburban areas, electrical grids are also accessible for the transfer of electricity⁵⁷. The urban area boundaries shapefile from openstreetmap.org and the Euclidean distance tool in ArcGIS 10.8 are used in this study to compute the spatial layer for the distance to cities criterion. An SPP should be situated far from faults as this renders it more susceptible to earthquakes, which can cause more damage or destruction^44,58. A Cost-effectiveness SPP should be located near major roads to reduce transmission costs and facilitate access^55,59. Additionally, building new roads for SPP access adds extra expenses⁵⁷. A SPP should be located away from subsidence areas to reduce vulnerability⁴⁴ and protect infrastructure, such as transmission networks and roads.

The amount of solar energy generated in an area is influenced by elevation; higher elevations receive more sunlight⁴⁵. Additionally, the atmosphere in highlands is narrower than in lowlands, leading to reduced atmospheric absorption⁶⁰. Therefore, higher elevations yield more solar energy potential⁶¹. Solar radiation is absorbed more effectively in regions with high precipitation, resulting in reduced energy output from SPP^45,46,62. Conversely, areas with low precipitation are more fitting for establishing SPP. Air humidity directly impacts solar radiation and could reduce SPP’s energy production⁶³. While regions with low relative humidity are more suited for the development of SPP, high humidity lowers the efficiency of solar cells⁶².

Flat areas absorb more solar energy⁵⁷. The slope of the terrain should be taken into account while creating an SPP because it has an impact on energy production and installation costs^64,65. Low-sloped areas have greater potential for SPP deployments. The main determinant of SPP siting is solar radiation, which also determines the amount of energy SPP generates^65,66. The solar energy acquired at a particular location on the surface of the Earth is referred to as solar radiation⁵⁷. High solar radiation locations have a greater potential for the development of SPP. Sunshine affects the amount of solar energy available for SPP by indicating the periods of the year when a given area receives direct sunshine⁴⁵. High levels of sunshine are superior for the development of SPP⁴⁶. The solar modules in SPP are impacted by air temperature, and high temperatures can lower SPP performance and energy production^57,60,63. SPP development should not be carried out in areas where air temperatures rise above 28°C⁶⁷. SPP installations could collapse due to high wind speeds, causing damage and malfunctions^68,69. High wind regions are undesirable for SPP development thanks to these factors, which lower performance and energy production⁴⁵.

Table 1 Spatial analyses and data for Preparation criteria Spatial layers.

Fig. 4

Criteria. The map is prepared by the authors using ArcGIS 10.8.1 software (https://support.esri.com/en-us/).

Fermatean fuzzy SWARA

SWARA, presented by Keršuliene et al.⁷¹is a subjective weighing technique that is effective in minimizing the inconsistency of expert opinions by minimizing the number of pairwise comparisons; nonetheless, it is unable to address the subjectivity and uncertainty of expert assessments. To model this uncertainty effectively, the earlier studies^34,35 utilized FFSs to refine SWARA’s computational procedures. Their results, termed FFSWARA, demonstrated greater consistency with experts’ opinions in scenarios involving a larger number of judgments and attributes compared to traditional FSs and IFSs³⁵. The steps for FFSWARA are detailed as follows:

Step 1. In order to form the linguistic decision matrix, after identifying the set of influential criteria in MCDM problem, each decision-maker based on her/his expertise assigns a linguistic term to each criterion (Eq. (1), here m and k represent the number of criteria and decision-makers). Table 2 demonstrates the linguistic terms and their corresponding Fermatean Fuzzy numbers. In Table 2, $\:\mu\:$ and $\:\vartheta\:$ denote the membership and non-membership degrees (the element of a Fermatean Fuzzy number).

$$\:{C}_{m\times\:k}=\left[\begin{array}{cc}\begin{array}{cc}[{\mu\:}_{\text{1,1}},{v}_{\text{1,1}}]&\:[{\mu\:}_{\text{1,2}},{v}_{\text{1,2}}]\\\:[{\mu\:}_{\text{2,1}},{v}_{\text{2,1}}]\:&\:[{\mu\:}_{\text{2,2}},{v}_{\text{2,2}}]\end{array}&\:\begin{array}{cc}\cdots\:&\:[{\mu\:}_{1,k},{v}_{1,k}]\\\:\cdots\:&\:[{\mu\:}_{2,k},{v}_{2,k}]\end{array}\\\:\begin{array}{cc}\vdots&\:\vdots\\\:[{\mu\:}_{m,1},{v}_{m,1}]&\:[{\mu\:}_{m,2},{v}_{m,2}]\end{array}&\:\begin{array}{cc}\ddots\:&\:\vdots\\\:\cdots\:&\:[{\mu\:}_{m,k},{v}_{m,k}]\end{array}\end{array}\right]$$

(1)

Table 2 The linguistic terms and their corresponding fermatean fuzzy numbers.

Step 2. The linguistic decision matrices are aggregated using Eq. (2). Here, $\:{\psi\:}_{k}$ represents the weight of the k^th decision-maker, with all decision-makers assumed to have equal weight in this study.

$$\:{\text{{\rm\:Z}}}_{j}=\left({\mu\:}_{j},{\vartheta\:}_{j}\right)=\left(\prod\:_{d=1}^{k}{{(\mu\:}_{jd})}^{{\psi\:}_{k}},\sqrt[3]{1-\prod\:_{d=1}^{k}{{{(1-(v}_{jd})}^{3})}^{{\psi\:}_{k}}}\right),\:\text{{\rm\:Z}}={\left[{\text{{\rm\:Z}}}_{j}\right]}_{1\times\:m}$$

(2)

Step 3. Each criterion’s positive score is calculated using Eq. (3), after which the criteria are ranked, with the highest positive score receiving the top rank.

$$\:{\text{P}\text{S}}_{j}=1+{{\mu\:}_{j}}^{3}-{{\vartheta\:}_{j}}^{3}$$

(3)

Step 4. Each criterion’s comparative significance of positive score is calculated using Eq. (4), with comparative significance of positive score of the top criterion set to 0.

$$\:{CPS}_{j}={PS}_{j}-{PS}_{j-1},\:j\ne\:1$$

(4)

Step 5. Each criterion’s comparative coefficient is calculated using Eq. (5), with comparative coefficient of the top criterion set to 1.

$$\:{CC}_{j}=1+{CPS}_{j},\:j\ne\:1$$

(5)

Step 6. Each criterion’s initial weight is calculated using Eq. (6), with initial weight of the top criterion set to 1.

$$\:{q}_{j}=\frac{{q}_{j-1}}{{CC}_{j}},\:j\ne\:1$$

(6)

Step 7. Each criterion’s final weight is calculated using Eq. (7).

$$\:{w}_{j}=\frac{{q}_{j}}{\sum\:_{j=1}^{m}{q}_{j}}$$

(7)

CRADIS

CRADIS is a novel distance-based MCDM method introduced by Puška et al.⁷². It evaluates alternatives by measuring their distance from both ideal and anti-ideal solutions. This method integrates procedures from three existing MCDM methods: ARAS (Additive Ratio Assessment), MARCOS (Measurement of Alternatives and Ranking according to Compromise Solution), and TOPSIS. The steps of CRADIS are detailed below:

Step 1. The decision matrix is formed using Eq. (8), where n represents the number of alternatives, m denotes the number of criteria, and x_ij indicates the performance of the j^th criterion for the i^th alternative.

$$\:{X}_{n\times\:m}=\left[\begin{array}{cc}\begin{array}{cc}{x}_{11}&\:{x}_{12}\\\:{x}_{21}&\:{x}_{22}\end{array}&\:\begin{array}{cc}\cdots\:&\:{x}_{1m}\\\:\cdots\:&\:{x}_{2m}\end{array}\\\:\begin{array}{cc}\vdots&\:\vdots\\\:{x}_{n1}&\:{x}_{n2}\end{array}&\:\begin{array}{cc}\ddots\:&\:\vdots\\\:\cdots\:&\:{x}_{nm}\end{array}\end{array}\right]$$

(8)

Step 2. The decision matrix is normalized using Eqs. (9) and (10), with Eq. (9) applied to beneficial criteria and Eq. (10) to cost criteria. Here, n_ij represents the normalized value of x_ij in the decision matrix.

$$\:{n}_{ij}=\frac{{x}_{ij}}{\underset{i}{\text{max}}{(x}_{ij})}$$

(9)

$$\:{n}_{ij}=\frac{\underset{i}{\text{min}}\left({x}_{ij}\right)}{{x}_{ij}}$$

(10)

Step 3. The normalized decision matrix is aggravated using Equations (11). Here, w_j represents the weight of the j^th criterion.

$$\:{v}_{ij}={n}_{ij}\times\:{w}_{j}\:,\:V={\left[{v}_{ij}\right]}_{n\times\:m}$$

(11)

Step 4. The ideal and anti-ideal solution are identified using Eqs. (12) and (13), with Eq. (12) applied to ideal solution and Eq. (13) to anti-ideal solution.

$$\:{t}_{j}=\underset{i}{\text{max}}{(v}_{ij})\:,\:T={\left[{t}_{j}\right]}_{1\times\:m}$$

(12)

$$\:{at}_{j}=\underset{i}{\text{min}}\left({v}_{ij}\right)\:,\:AT={\left[{at}_{j}\right]}_{1\times\:m}$$

(13)

Step 5. For each criterion of each alternative, distances to the ideal and anti-ideal solutions are calculated using Eqs. (14) and (15), with Eq. (14) for the ideal solution and Eq. (15) for the anti-ideal solution. Here, $\:{d}_{ij}^{+}$ denotes the distance between the j^th criterion of the ith alternative and the ideal solution, while $\:{d}_{ij}^{-}$ indicates the distance to the anti-ideal solution for the same criterion.

$$\:{d}_{ij}^{+}={t}_{j}-{v}_{ij}$$

(14)

$$\:{d}_{ij}^{-}={{v}_{ij}-at}_{j}\:$$

(15)

Step 6. For each alternative, the overall distances to the ideal and anti-ideal solutions are calculated using Eqs. (16) and (17), with Eq. (16) for the ideal solution and Eq. (17) for the anti-ideal solution.

$$\:{{S}_{i}}^{+}=\sum\:_{j=1}^{m}{d}_{ij}^{+}$$

(16)

$$\:{{S}_{i}}^{-}=\sum\:_{j=1}^{m}{d}_{ij}^{-}$$

(17)

Step 7. For each alternative, the two utility functions are calculated using Eqs. (18) and (19). Here, $\:{{S}_{0}}^{+}$equal to the optimal value of the all $\:{{S}_{i}}^{+}$(the minimum of the all $\:{{S}_{i}}^{+}$), and $\:{{S}_{0}}^{-}$equal to the optimal value of the all $\:{{S}_{i}}^{-}$(the maximum of the all $\:{{S}_{i}}^{-}$),

$$\:{K}_{i}^{+}=\frac{{{S}_{0}}^{+}}{{{S}_{i}}^{+}}$$

(18)

$$\:{K}_{i}^{-}=\frac{{{S}_{i}}^{-}}{{{S}_{0}}^{-}}$$

(19)

Step 7. For each alternative, the final score is calculated using Eq. (20). The best alternative has the largest $\:{Q}_{i}$.

$$\:{Q}_{i}=\frac{{K}_{i}^{+}+\:{K}_{i}^{-}}{2}$$

(20)

RAM

RAM is a straightforward MCDM method introduced by Sotoudeh-Anvari⁷³. Its motivation lies in providing decision-makers with a deep understanding of the entire decision-making process while avoiding potential computational pitfalls. RAM utilizes a radical aggregation function, allowing for a broad range of compensation between cost and benefit criteria. Additionally, it considers cost and benefit criteria simultaneously without requiring any transformations. The steps of RAM are detailed below:

Step 1. The decision matrix is formed using Eq. (8).

Step 2. The decision matrix is normalized using Eq. (21).

$$\:{r}_{ij}=\frac{{x}_{ij}}{\sqrt{\sum\:_{i=1}^{n}{x}_{ij}}}$$

(21)

Step 3. The weighted normalized decision matrix is computed using Eq. (22). Here, w_j represents the weight of the j^th criterion.

$$\:{y}_{ij}={r}_{ij}\times\:{w}_{j}\:,\:V={\left[{y}_{ij}\right]}_{n\times\:m}$$

(22)

Step 4. The summations of the weighted normalized decision matrix for beneficial and cost criteria are computed using Eqs. (23) and (24), with Eq. (23) applied to beneficial criteria and Eq. (24) to cost criteria. Here, $\:{J}^{+}$represents the set of beneficial criteria and, $\:{J}^{-}$represents the set of cost criteria.

$$\:{{S}_{i}}^{+}=\sum\:_{j\in\:{J}^{+}}{y}_{ij}$$

(23)

$$\:{{S}_{i}}^{-}=\sum\:_{j\in\:{J}^{-}}{y}_{ij}$$

(24)

Step 5. For each alternative, the final score is calculated using Eq. (25). The best alternative has the largest $\:{RI}_{i}$.

$$\:{RI}_{i}=\sqrt[2+{{S}_{i}}^{-}]{2+{{S}_{i}}^{+}}$$

(25)

Correlation and sensitivity analysis

A key component of MCDM techniques is the validation of methods and their outcomes, which evaluates the methods’ confidence and the dependability of the results⁵¹. To validate the suggested methodology, this study uses sensitivity analysis, comparisons with accepted MCDM techniques, and the Suitability Change Rate and Percent Change indicators. To assess how modifications to the weights vector impact the results of each MCDM technique, a One-At-a-Time (OAT) sensitivity analysis is carried out. In this procedure, the weight of one criterion is set to zero, and the weights of the other criteria are changed so that their sum equals one. The Suitability Change Rate indicator is derived from the percentage of pixels in the study region that undergo changes in suitability classes. Additionally, the Percent Change indicator is computed by comparing the suitability map derived from the original weights and updated weights. The criterion whose removal results in the most significant Suitability Change Rate and Percent Change is determined to be the most essential criterion in SPPSS, while the MCDM approach with the least Suitability Change Rate and Percent Change is considered the most stable and dependable for SPPSS. The results are validated by contrasting the novel MCDM techniques with well-established ones from earlier research. In the MCDM and SPP siting domains, this study compares the suggested methodology with the proven TOPSIS method^44,74,75. For an instructive comparison, we compute Pearson’s correlations between TOPSIS and the suggested methods along with a sensitivity analysis. To improve the comparison, we may use the Percent Change indicator. As a sensitivity analysis indicator, the Percent Change is computed for pairs of MCDM models (CRADIS-RAM, CRADIS-TOPSIS, and RAM-TOPSIS). This indicator evaluates the degree of agreement between the two models’ outputs and draws attention to their differences. Equation (26) is employed to calculate the Percent Change between each pair of MCDM models within specific suitability classes, where N and M represent the number of pixels in a class across each model, and n_share denotes the number of shared pixels in that class.

$$\:Pc=\frac{N+M-{2*n}_{share}}{N+M}\times\:100$$

(26)

Results

Criteria weights determination using FFSWARA

To calculate the criteria weights using FFSWARA, a group of five experts was formed, including two GIS specialists, one RE engineer, and two RE managers. Experts were selected by first consulting with colleagues at their workplaces to identify a pool of candidates twice the required capacity for each specialty. Resumes were then reviewed, and the 50% of candidates with the most relevant experience were chosen for the study (demographic characteristics are presented in Table 3). To ensure a diverse range of expertise, the selected community comprised three industry experts (M.Sc.) and two university professors (Ph.D.) with experience in solar power plant location, design, development, and renewable energy planning. To avoid expert confusion and improve pairwise comparison matrix accuracy, experts received detailed explanations of the research purpose, outcome, and criteria. They were also trained on completing the matrices and interpreting linguistic terms (Fermatean Fuzzy numbers).

Table 3 Demographic characteristics of experts.

The experts then assessed the importance of each criterion using linguistic terms, as shown in Table 4. Using Eq. (2), the linguistic decision matrices were aggregated to compute the final Fermatean Fuzzy number for each criterion. Steps 3–7 of FFSWARA were then executed to determine the criteria weights. Table 5 presents the final Fermatean Fuzzy number, positive score, comparative significance of the positive score, comparative coefficient, initial weight, and final weight for each criterion. As seen in Table 5, average annual solar radiation (C9) is the most important criterion in SPP siting with a weight of 0.119, while average annual wind speed (C12) is the least important with a weight of 0.049.

Table 4 The linguistic decision matrices of experts.

Table 5 The results of FFSWARA weighting method.

Criteria aggregation using RAM, CRADIS and TOPSIS

To prepare the suitability map for SPP establishment, spatial layers of criteria based on calculated weights were aggregated using three MCDM methods: RAM, CRADIS and TOPSIS in Matlab 2018. The resulting suitability maps are shown in Fig. 5, indicating a general similarity across the three methods, particularly between RAM and TOPSIS. As illustrated in Fig. 6, the suitability maps reveal that most of the study area is classified as having moderate suitability. According to CRADIS, the percentages of very low, low, moderate, high, and very high suitability categories in the study area are 15%, 30%, 32%, 20%, and 3%, respectively. According to RAM, the percentages of very low, low, moderate, high, and very high suitability categories in the study area are 12%, 27%, 28%, 23%, and10%, respectively. According to TOPSIS, the percentages of very low, low, moderate, high, and very high suitability categories in the study area are 8%, 22%, 32%, 26%, and12%, respectively.

Fig. 5

the prepared suitability maps using CRADIS, RAM and TOPSIS MCDM methods. The map is prepared by the authors using ArcGIS 10.8.1 software (https://support.esri.com/en-us/) .

Fig. 6

The percentage of suitability categories of CRADIS, RAM and TOPSIS MCDM methods.

Models’ correlation and sensitivity analysis

A method for evaluating a new model within a specific application is to assess its correlation with established models. In this study, we evaluated two new MCDM methods—CRADIS and RAM—by comparing their suitability maps with those produced by the well-known TOPSIS method. Figure 7 illustrates the correlation heatmap for the three MCDM methods. The correlation between the suitability maps generated by RAM and TOPSIS is very high (0.96), while the correlation between CRADIS and TOPSIS is moderate (0.65). Additionally, the correlation between CRADIS and RAM is also moderate (0.51).

Fig. 7

The heatmap of three considered MCDM methods.

To understand the agreement and differences among the MCDM models, we calculated the number of pixels in each suitability class for each model and assessed the variation between them. Table 6 shows that the CRADIS and RAM models classified 121,518 pixels in the VL class, 287,010 in L, 288,090 in M, 217,924 in H, and 39,347 in VH. The Percent Change for each class is listed in the last row of Table 6, with the VH class showing the highest change, followed by VL, M, H, and L. On average, 63.67% of the suitability classes assigned by CRADIS differ from those assigned by RAM.

Table 7 presents the agreement between CRADIS and TOPSIS, with classifying 59,005 pixels in VL, 211,509 in L, 254,577 in M, 195,935 in H, and 29,014 in VH. The last row of Table 7 details the Percent Changes, where L shows the highest change, followed by H, M, VH, and VL. On average, 84.26% of the suitability classes assigned by CRADIS differ from those assigned by TOPSIS.

Table 8 illustrates the agreement between RAM and TOPSIS, showing that RAM and TOPSIS classified 175,657 pixels in VL, 378,940 in L, 494,311 in M, 446,795 in H, and 207,059 in VH. The last row of Table 8 provides the Percent Changes, with VL showing the highest change, followed by M, H, L, and VH. On average, 23.07% of the suitability classes assigned by RAM differ from those assigned by TOPSIS.

Table 6 The agreement between CRADIS and RAM results.

Table 7 The agreement between CRADIS and TOPSIS results.

Table 8 The agreement between RAM and TOPSIS results.

We conducted a sensitivity analysis involving 12 scenarios alongside correlation analysis to identify the most stable model for SPP siting application. In each scenario, one criterion was assigned a weight of 0, effectively removing it, while the weights of the remaining criteria were adjusted to total 1. We then calculated the number of pixels whose suitability classes changed in each scenario. The model with the least Suitability Change Rate was deemed the most stable, while the criterion whose removal led to the greatest Suitability Change Rate was recognized as the most influential in SPP siting.

Figure 8 shows the Suitability Change Rate across the study area for each scenario. The CRADIS and TOPSIS models demonstrated the most significant changes in pixel suitability across 10 and 2 scenarios, respectively. In contrast, the RAM model exhibited the least Suitability Change Rate in 4 scenarios, with an average change of 27.59% over all 12 scenarios, while CRADIS and TOPSIS had average changes of 62.06% and 32.31%, respectively. Consequently, RAM was identified as the most stable model, followed by TOPSIS and CRADIS.

Fig. 8

The Suitability Change Rates of sensitivity analysis scenarios.

In the CRADIS model, the most influential criteria were distance to cities, distance to roads, and average annual solar radiation, with changes of 97%, 96%, and 82%, respectively. In contrast, the least influential criteria were average annual wind speed, average annual air temperature, and average annual relative humidity, with changes of 10%, 29%, and 44%. In the RAM model, the most influential criteria included slope, distance to faults, and annual summation sunshine, with changes of 70%, 55%, and 48%. The least influential criteria were average annual relative humidity, average annual wind speed, and average annual precipitation, with changes of 2%, 4%, and 5%. In the TOPSIS model, the most influential criteria were slope, distance to faults, and distance to roads, with changes of 92%, 87%, and 72%. The least influential criteria here were average annual wind speed, average annual relative humidity, and average annual solar radiation, with changes of 1%, 1%, and 3%.

Figure 9 displays the Percent Change for each scenario across the study area, highlighting the differences from the original model results. The CRADIS and TOPSIS models showed the largest discrepancies, while the RAM model had an average difference of 4.40% across all 12 scenarios. In comparison, CRADIS and TOPSIS had average differences of 8.75% and 5.80%, respectively. Thus, RAM is the most stable model, followed by TOPSIS and CRADIS.

Fig. 9

The Percent Changes of sensitivity analysis scenarios.

As illustrated in Fig. 9, in the CRADIS model, the most influential criteria were distance to cities, distance to roads, and slope, with Percent Changes of 18%, 17%, and 11%, respectively. In contrast, the least influential criteria were average annual wind speed, average annual relative humidity and average annual air temperature with Percent Changes of 3%, 4%, and 5%. In the RAM model, the most influential criteria included distance to faults, annual summation sunshine and slope with Percent Changes of 12%, 9%, and 8%. The least influential criteria were average annual relative humidity, average annual wind speed, and average annual precipitation, with Percent Changes of 1%, 1%, and 1%. In the TOPSIS model, the most influential criteria were slope, distance to faults, and distance to roads, with Percent Changes of 20%, 15%, and 11%. The least influential criteria here were average annual wind speed, average annual relative humidity, and average annual solar radiation, with Percent Changes of 0%, 0%, and 0%.

This study considers the resistance of MCDM methods to rank reversal, a key evaluation parameter. To examine rank reversal, a five-step process removes pixels of specific fitness classes, re-ranks the remaining pixels using the MCDM method, and classifies them into suitability classes. MCDM methods exhibiting fewer changes in pixel suitability class throughout this process demonstrate greater resistance to rank reversal and are thus considered superior. Figure 10 points out the generated suitability maps by RAM, CRADIS and TOPSIS MCDM methods during the rank reversal evaluation process. Figure 11 illustrates the rank reversal rate for each step across the study area, highlighting the differences from the original model results (Fig. 5). The CRADIS and TOPSIS models showed the smallest rank reversal, while the RAM model had an average difference of 19.62% across all 5 evaluation steps. In comparison, CRADIS and TOPSIS had average rank reversal of 4.99% and 13.19%, respectively. Thus, CRADIS is the most resilient model against rank reversal phenomenon, followed by TOPSIS and RAM.

Fig. 10

The prepared suitability maps using CRADIS, RAM and TOPSIS MCDM methods during the rank reversal evaluation process. The map is prepared by the authors using ArcGIS 10.8.1 software (https://support.esri.com/en-us/).

Fig. 11

The rank reversal rate evaluation results.

Most capable counties for SPP establishment

This section prioritizes the counties of Kermanshah Province based on their capabilities. To achieve this, the average suitability for each county is calculated using suitability maps created from three MCDM models and the Zonal Statistics tool in ArcGIS 10.8. As shown in Figs. 12 and 13, the CRADIS model indicates that the top counties for SPP establishment are Dalahu, Sarpol-e Zahab, and Kangavar, while the least capable counties are Harsin, Sahneh, and Javanrud. According to the RAM model, Qasr-e Shirin, Dalahu, and Sarpol-e Zahab are the most suitable, with Harsin, Javanrud, and Sahneh being the least. In the TOPSIS model, the leading counties are Qasr-e Shirin, Dalahu, and Salas-e Babajani, while Javanrud, Harsin, and Paveh rank the lowest.

Fig. 12

The prioritization of the counties of Kermanshah Province based on the created suitability maps using the three considered MCDM models. The map is prepared by the authors using ArcGIS 10.8.1 software (https://support.esri.com/en-us/) .

Fig. 13

The ranking of the counties of Kermanshah Province based on the created suitability maps using the three considered MCDM models.

Electricity generation potential of photovoltaic farms in Kermanshah province, considering electricity demand and fossil fuel-based pricing

The findings indicate that solar energy has the potential to completely transform the electricity landscape of Kermanshah Province by addressing supply shortages, reducing dependency on fossil fuels, and generating economic benefits. The estimated solar generation potential according Table 9 is 370,458 GWh per year is nearly 94 times the total electricity demand of 3,940 GWh in 2021, meaning that a fully utilized solar infrastructure could not only meet local energy needs but also provide a massive surplus for export or storage. This surplus could help stabilize electricity supply, eliminate blackouts and rationing, and reduce reliance on imported electricity during peak seasons.

Economically, transitioning to solar energy could lead to substantial cost savings and revenue generation. Given that the government supports solar electricity purchases at rates ranging from 2,271 to 9,086 Rials/kWh, the province could generate significant revenue from surplus electricity, potentially amounting to trillions of Rials annually. This shift would also benefit various sectors by providing stable and affordable energy, particularly for industries and agriculture, where electricity costs significantly impact production expenses. Additionally, the large-scale adoption of solar power would reduce power generation costs, lowering the financial burden on both the government and consumers.

From an environmental perspective, solar energy adoption could result in a significant reduction in greenhouse gas emissions. Currently, the province’s power plants consume 31.6 million liters of oil, 550.6 million liters of fuel oil, and 506.8 million cubic meters of natural gas annually, leading to high CO₂ emissions. Replacing fossil-fuel-based electricity generation with solar energy would prevent 2.84 million metric tons of CO₂ emissions per year, which is equivalent to removing 600,000 gasoline-powered vehicles from the roads. This reduction in emissions would contribute to improved air quality, public health, and compliance with global climate commitments.

Additionally, solar energy investments would boost local economic growth by generating a significant number of jobs. Over 406,000 temporary jobs might be created during the installation and building phase alone, and 14,387 permanent positions would be created throughout the operation and maintenance of solar plants, creating long-term work prospects. These employment numbers demonstrate the possibility of economic diversification, especially in areas that depend on conventional energy sources, and may open up a new, long-term job market for the local labor population. Ultimately, utilizing Kermanshah Province’s solar energy potential could promote economic expansion, job creation, and environmental sustainability in addition to ensuring energy security and affordability. Solar energy has the potential to become the region’s primary energy source with the proper infrastructure, investments, and government regulations, rendering Kermanshah a pioneer in Iran’s shift to renewable energy. To fully meet Kermanshah Province’s total electricity demand of 3,940 GWh/year using solar energy, an installed capacity of 765 MW would be required. Given the region’s high solar potential (PVOUT: 5,150 MWh/MW/year), this capacity could be achieved using just 153 km² of land equivalent to 0.4% of the province’s area. This transition would eliminate the need for 31.6 million liters of oil, 550.6 million liters of fuel oil, and 506.8 million cubic meters of natural gas annually, preventing 2.84 million metric tons of CO₂ emissions each year. Economically, the cost of continuing fossil fuel-based power generation is ~$345 million per year, while the one-time investment in a 765 MW solar farm would be around $612 million, making solar at least 7 times cheaper over a 25-year period. However, rather than relying solely on large-scale solar farms, a decentralized approach involving private households, agricultural landowners, and small businesses installing solar panels could accelerate the transition and reduce infrastructure burdens. With government incentives, net metering policies, and feed-in tariffs, local households and farmers could generate their own electricity, sell excess power to the grid, and significantly reduce upfront investment costs for the province. This distributed model would not only speed up solar deployment but also create additional income opportunities for residents while ensuring energy security and decentralizing electricity production, making Kermanshah a leader in renewable energy adoption in Iran.

Table 9 The economic and social advantages of solar generation.

The installation of solar panels in Kermanshah Province offers numerous advantages, as illustrated in Fig. 14. One of the most significant benefits is CO₂ reduction, which supports the province’s transition toward green and sustainable energy. Economically, solar adoption would stimulate job creation, increase employment rates, and provide a new source of green income for households. Farmers, in particular, would benefit from switching to solar energy, ensuring a reliable and sustainable power source for electrified wells while reducing network costs, especially for greenhouses across the province. Additionally, solar energy could play a crucial role in compensating for peak demand, preventing power outages in households and businesses, and mitigating financial losses. Given the increasing frequency of extreme weather events, integrating solar energy would also enhance energy resilience, ensuring a stable and secure power supply in Kermanshah.

Fig. 14

Solar potentials benefit in Kermanshah province.

Discussion

Sustainable, reliable, and cost-efficient energy production is vital due to energy’s critical role in human life. A viable substitute for fossil fuels is solar energy, which is a plentiful and clean resource. In light of these considerations, this work presents a Fermatean Fuzzy MCDM strategy for optimal solar power plant (SPP) siting that is based on Geographic Information System (GIS). GIS makes it possible to prepare criteria through spatial analysis and to thoroughly evaluate a large number of potential locations⁴⁵. By aggregating criteria data, MCDM techniques improve decision-making through presenting trustworthy scores for site comparison. For SPP siting, combining GIS with scientifically valid MCDM techniques provides a dependable and efficient strategy.

Criteria identification, spatial layer preparation, criteria weighting, and suitability map construction are the four elements that constitute up this study’s approach. First, a review of past studies and experts’ consultation determined important factors for SPP siting. The distance to subsidence zones was one of these criteria since it is crucial for plant safety, a criterion that was only used by Zandi and Lotfata⁴⁴. The criteria values were then computed throughout the research region using the proper GIS spatial analysis tools. Finally, the SWARA weighting method was selected since it is comparatively underutilized in SPP siting studies and is more efficient than AHP, ANP, and BWM, requiring fewer pairwise comparisons and producing weights that are more consistent and dependable. SWARA depends on the opinions of frequently ambiguous specialists. To overcome these uncertainties, this study uses the Fermatean Fuzzy SWARA technique, a framework developed by Aydoğan and Ozkir³⁵ in order to overcome the drawbacks of intuitionistic fuzzy sets. As shown by Aydoğan and Ozkir³⁵Fermatean fuzzy sets outperform Intuitionistic fuzzy sets and fuzzy triangular numbers. Thus, Weights for the criterion are determined here using Fermatean Fuzzy SWARA. According to the data, the key factor in SPP siting is average yearly solar radiation, which aligns with earlier studies^{44,46,51,58,66,76,77,78,79,80}. The criteria in order of weight are: average annual solar radiation (0.119), annual summation sunshine (0.109), average annual air temperature (0.102), distance to cities (0.091), distance to faults (0.087), distance to roads (0.087), distance to subsidence areas (0.087), elevation (0.072), slope (0.070), average annual precipitation (0.065), average annual relative humidity (0.063), and average annual wind speed (0.049). While this study modeled experts’ opinions’ uncertainties to weight criteria, analyzing the relationships between decision-making criteria in studies Choukolaei et al.⁸¹Kanani-Sadat et al.⁸² and Sahraei et al.⁸³using methods like DEMATEL and fuzzy cognitive mapping, could offer decision-makers better insight into relationships among the criteria and results interpretation.

This study employed two effective MCDM methods, CRADIS and RAM, to aggregate criteria and create suitability maps for SPP establishment. CRADIS, introduced by Puška et al.⁷²is a flexible MCDM method known for effectively addressing the rank reversal problem. RAM, introduced by Sotoudeh-Anvari⁷³is a simple and efficient MCDM method that provides complete rankings through a straightforward procedure and handles both beneficial and cost criteria without transformation. These methods were compared to the well-known TOPSIS method. The normalization methods used are linear for CRADIS, linear sum for RAM, and vector normalization for TOPSIS. While CRADIS and TOPSIS utilize two sets of ideal solutions, RAM does not. Additionally, the aggregation functions differ among the three methods. While all three methods are straightforward, the RAM method offers simpler computation and is easier for decision-makers to understand compared to the more computationally intensive CRADIS and TOPSIS methods. CARDIS and TOPSIS both require calculating ideal solution sets, and options are evaluated based on their distance from these sets. While MCDM methods use ideal and anti-ideal solution sets, minimizing distance to the ideal and maximizing distance to the anti-ideal solution doesn’t always guarantee the optimal solution in real-world decision-making⁸⁴. Besides the computational cost, this can lead to rank reversal because removing alternatives can alter the ideal solution sets, thus changing the ranking of remaining alternatives.

Suitability maps for SPP establishment were created using CRADIS, RAM, and TOPSIS. The majority of the study area was classified as moderately suitable: 32% by CRADIS, 28% by RAM, and 32% by TOPSIS. CRADIS identified 3% of the area as very highly suitable and 15% as very lowly suitable. RAM indicated 10% as very highly suitable and 12% as very lowly suitable, while TOPSIS showed 12% as very highly suitable and 8% as very lowly suitable. These results correspond with Zandi and Lotfata⁴⁴. Correlation analysis of three MCDM methods—CRADIS, RAM, and TOPSIS—showed a strong similarity between RAM and TOPSIS (0.96), while the correlation between CRADIS and TOPSIS was weak (0.51). CRADIS and RAM classified 39% of the study area in same suitability classes, CRADIS and TOPSIS classified 30% of the study area in same suitability classes, and RAM and TOPSIS classified 69% of the study area in same suitability classes. Although CRADIS and TOPSIS follow similar procedures, which involve calculating scores based on distances from ideal solutions, their results did not align significantly. In contrast, RAM employs a straightforward process with simpler calculations that differ from TOPSIS, yet its results were notably correlated with those of TOPSIS. Notably, the RAM method is more straightforward than CRADIS and TOPSIS, yet demonstrates greater reliability and stability. The differences in the results of CRADIS and TOPSIS correspond with Puška et al.⁷²while the similarities between RAM and TOPSIS are consistent with Sotoudeh-Anvari⁷³.

The appropriateness map generated by RAM was very different from the ones made by earlier studies^44,46. Unlike prior studies, we used average yearly wind speed and average annual relative humidity as criteria in this analysis. Furthermore, Shorabeh et al.⁴⁶ used the Normalized Difference Vegetation Index (NDVI), which we did not consider, and they excluded distance to subsidence areas, a criterion we employed. The gap in suitability maps between our study and theirs is probably explained by these criteria differences. This study’s weights vector was different from those employed by earlier studies^44,46. For example, our study’s weight for average yearly solar radiation was 0.12, but earlier studies^44,46 had weights of 0.18 and 0.46, respectively. The weight ranges for the criterion were 0.05 to 0.12 in the current study, 0.01 to 0.46 in Zandi and Lotfata⁴⁴and 0.03 to 0.18 inShorabeh⁴⁶. This suggests that the weight vector’s dispersion was smaller in our investigation. We carried a sensitivity study across 12 scenarios, determining the Suitability Change Rate and Percent Change indicators for each model in order to determine which was the most stable and dependable. The Suitability Change Rate indicates the overall changes in the suitability map compared to the original, while the Percent Change reflects the differences per scenario. Results indicated RAM as the most trustworthy and stable model, followed by TOPSIS and CRADIS. In the RAM model, slope was the key criterion, with average annual relative humidity being less significant. In the TOPSIS model, slope was also crucial, while average annual wind speed received less importance. In the CRADIS model, distance to cities was the main criterion, with average annual wind speed as a lesser factor. In the RAM model, removing the slope affected 70% of the study area’s suitability classes, while removing average annual relative humidity impacted only 2%. In the TOPSIS model, the removal of the slope changed 92% of the suitability classes, but removing average annual wind speed affected just 1%. In the CRADIS model, the removal of distance to cities changed 97% of the suitability classes, whereas removing average annual wind speed influenced only 10%.

This study evaluates rank reversal in MCDM methods to better understand their performance. Unlike previous studies with fewer alternatives, spatial problems involve a large number of alternatives, making simple elimination ineffective. Therefore, we employ a five-step process, eliminating alternatives from a specific suitability class in each step and re-ranking the remaining alternatives. The percentage of alternatives changing suitability class serves as the rank reversal criterion. This approach increases the diversity of alternative elimination, assessing the methods’ resilience against removing alternatives with varying suitability levels. Evaluation of rank reversal showed RAM experiencing the most rank reversal upon alternatives removal, contradicting Sotoudeh-Anvari⁷³’s finding of RAM’s high resistance. This discrepancy likely stems from the smaller number of alternatives in Sotoudeh-Anvari⁷³’s study. Conversely, CRADIS exhibited higher-than-expected resistance, with only 5% of alternatives experiencing rank reversal on average. In the RAM method, removing moderate-suitability alternatives caused the greatest rank reversal. In contrast, the CRADIS method saw the highest rank reversal when very low-suitability alternatives were removed, while the TOPSIS method experienced it when very high-suitability alternatives were removed. Unlike Research Zandi and Lotfata⁴⁴ and Zandi et al.⁸⁵which only used sensitivity analysis, this study examines various criteria to compare criteria aggregation MCDM methods and their results. In addition, the used approach for evaluation of the impact of each criterion and the relationships between criteria on location selection results, which conducted by research A, can provide invaluable information for results interpreting and analysis.

To identify the most suitable counties in Kermanshah Province for SPP establishment, we ranked all counties. According to the most reliable model, RAM, the counties of Qasr-e Shirin, Dalahu, and Sarpol-e Zahab emerged as the best areas for SPP construction. In Zandi and Lotfata⁴⁴Eslamabad-e Gharb, Kangavar, and Gilan-e Gharb counties and in Shorabe et al.⁴⁶the west and southwest parts of Kermanshah Province identified as the most suitable counties for solar power plant installation. The reasons for the variation in our suitability maps also apply here. Field surveys by the Western Regional Electricity Company of Iran⁸⁶ identified 84 of 300 sites in Kermanshah Province as suitable for solar power plants. the largest number of these 84 sites were located in counties of Qasr-e Shirin, Sarpol-e Zahab and Gilan-e Gharb. The results of the present study determined Qasr-e Shirin and Sarpol-e Zahab as highly suitable for solar power plants instalation, while Gilan-e Gharb was identified as moderate suitable. Generally, the findings from RAM and CRADIS are consistent with the field surveys. Overall, considering similarity to established methods, stability, rank reversal resistance, and alignment with field surveys, RAM identified as the mor suitable method for SPP siting rather than CRADIS. Furthermore, RAM offers advantages in calculation speed, processing time, and ease of understanding for decision-makers, making it preferable for real-world applications. This study identified potential sites for solar power plants. However, final site selection requires a supply chain analysis, considering both the forward supply of solar cells and the reverse supply chain for recycling used cells. This analysis should aim to maximize profits and customer satisfaction while minimizing costs, particularly transportation, as demonstrated in Ghasemi et al.⁸⁷ conducted on Iran.

In 2021, Kermanshah province’s 3940 GWh electricity demand could be met by deploying solar power plants across 153 square kilometers, eliminating the annual consumption of 31.6 million liters of oil, 550.6 million liters of fuel oil, and 506.8 million cubic meters of natural gas, thereby preventing 2.84 million metric tons of CO₂ emissions. This solar energy investment would also stimulate local economic development, generating over 406,000 temporary construction jobs and 14,387 permanent operation and maintenance positions.

Spatial resolution directly affects the quality of spatial analyses as well as the accuracy of spatial modeling. Various studies like Dai et al.⁸⁸ have investigated the impact of different spatial resolutions on spatial modeling, although not specifically SPP siting. Spatial resolution is significantly impacted by the size of the study area; larger areas necessitate lower resolutions due to computational demands and required detail⁸⁹. For instance, national-level studies typically begin with a 1 km resolution, improving to a maximum of 250 m. Available data resolution and the minimum area needed (e.g., for a power plant) also influence this choice. Prior national-level studies commonly used 1 km resolution⁹⁰while provincial studies employed 100 m resolution (need reference). A hierarchical resolution approach, tailored to the decision-making level, offers a logical and cost-effective solution. At the macro level (country-wide), a 1000-meter resolution identifies provinces suitable for SPP deployment. The medium level refines this by using a 100-meter resolution to pinpoint optimal areas within selected provinces. Finally, at the micro level, resolutions of 30 and 10 m are used to locate specific deployment sites. For limited solar panel deployments, a very fine resolution of 1 to 5 m can be employed. Considering that most Iranian power plants exceed 1 MW (requiring roughly 1.7 hectares), this study utilizes a 100-meter spatial resolution, where each pixel represents 1 hectare, effectively meeting decision-making requirements.

A significant limitation of this study is that it did not account for land cost, ownership, distance from transition networks, and spatial demand distribution due to the unavailability of relevant data.

Conclusion

This study presents a GIS-based Fermatean Fuzzy MCDM approach for selecting Solar Power Plant sites in Kermanshah Province. To model uncertainties in experts’ opinions regarding criteria weights, we utilize Fermatean Fuzzy Sets integrated with the SWARA weighting method. Additionally, we employ two innovative MCDM models, RAM and CRADIS, for criteria aggregation and suitability maps generation, comparing their performance with the established TOPSIS model through ground-truth evaluations, comprehensive correlation and sensitivity analysis, and rank reversal evaluation. The results indicate that RAM outperformed the other models in terms of reliability and stability based on the most evaluation criteria. Slope and average annual relative humidity were identified as the most and least important criteria for site selection, respectively. The suitability map generated showed that 33% of the study area is highly or very highly suitable for solar power plant establishment, with Qasr-e Shirin, Dalahu, and Sarpol-e Zahab identified as the top areas for construction. This study’s analyses demonstrate that deploying solar infrastructure across 153 square kilometers of the province could satisfy its total electricity demand, reduce CO₂ emissions by more than 2.8 million tons, and generate over 420,000 temporary and permanent jobs, significantly boosting the provincial economy.

Integrating D-numbers into the weighting method and comparing them to those used in this study could enhance the quality and rationality of the weighting process. Including critical criteria such as proximity to electric transition lines, land cost, energy consumption, and households with limited access to sustainable energy would strengthen the validity of the results. Additionally, applying the proposed methodology for selecting multi-renewable power plant sites can identify the most efficient renewable power plant type for each area of the study.