Introduction

Food security is closely related to the sustained and healthy development of the economy and society, and is an important component of national security, as well as the cornerstone supporting national security. In 1974, the Food and Agriculture Organization of the United Nations (FAO) first proposed the concept of ‘food security’, which has since been used by countries around the world(FAO, 1974). In the post pandemic era, multiple factors have combined to pose significant challenges to international food security1,2, such as slowing global economic growth, imbalanced food supply and distribution3, geopolitical conflicts4,5, and climate change6,7. As a major grain producing country, China is making efforts to promote the development strategy of food security and incorporate it into the text of the rural revitalization strategy plan. As of 2022, China’s total grain output has achieved ‘nineteen consecutive harvests’, making significant progress in grain production and supply. However, in the current complex international environment, China continues to face instability risks, such as widening food supply and demand gaps, prominent structural contradictions in food, and increasingly severe resource constraints for a long period of time in the future8. Therefore, it is urgent to scientifically and reasonably construct a food security assessment system and objectively measure the actual development level of China’s food security. This is an important topic for clarifying China’s food security development goals, resolving risks, and enhancing the modernization level of China’s food security governance system and governance capacity.

Over the past decade, researchers have endeavoured to study the food security topic. The researchers mainly focused on three aspects: firstly, elaborating on the current situation of food security in different regions at the national or regional level. For example, some studies explained the dynamics of food security in the Asia Pacific region from a political economy perspective and propose policy methods to address the regional food security paradox9. Some studies conducted research on food security, economic and social factors in Europe10. Some studies analyzed the global level of food security based on textual materials, with a particular focus on the food security and nutritional status of affected individuals in low-and middle-income countries11. Some studies explored the food security situation in South Asia, such as systematically mapping the levels, methods, and dimensions of food security research conducted in academic literature from Pakistan, Bangladesh, and India12. Some studies explored the household food security situation of impoverished and extremely poor families in vulnerable rural areas of Bangladesh13, and they generally believed that the level of food security in the region was not high. Some studies explored the current situation of China’s food security and generally believed that the development level of China’s food security was on the rising, but the evolution process was slow14,15,16. Scholars have also discussed the level of food security in a certain region of China, including Henan Province17, Sichuan Province18, Shaanxi Province19 and Shandong Province20, among others.

Secondly, researchers have discussed the construction of food security indicators. The evaluation of food security level is a dynamic and constantly adjusting process, and currently there is still no unified evaluation standard in the academic community. In terms of indicator construction, the Economist Intelligence Unit (EIU) proposed the Global Food Security Index (GFSI) in 2012, which used a total of 30 indicators in the areas of food security, affordability, availability, and quality and safety, providing a standard for measuring national level food security. Some scholars constructed a food security evaluation system based on four dimensions: supply, stability, acquisition capacity, and utilization level, and evaluated the food security situation of some countries or regions21,22. Some scholars used the Core Food Security Module (CFSM) to measure the fit of Hawaii data, including behavior, aid, income, diet, and other aspects23. In terms of evaluation methods, there were a wide variety of options available for food security, mainly based on quantitative research, including RANCOM24, SPOTIS24, principal component analysis25, emerging ESP-COMET methods26, etc.

In addition, researchers have explored and studied the factors affecting food security. The existing literature on food security research are mainly divided into four schools: sustainability and environmental, socio-economic, cultural, and political factors27. A large number of researchers studied the impact of factors such as population growth, land degradation, water scarcity, and climate change on global food production and security28,29,30. Some scholars analyzed the impact of factors such as the overall level of economic development, agricultural investment, and foreign trade of agricultural products on the food security level of countries in the former Yugoslavia31.

To summarize, researchers have achieved fruitful results in the study of food security development. However, there still exists certain expandable space. First, the determination of the weights of food security evaluation indicators is subjective, such as the AHP method and the fuzzy comprehensive evaluation method, which may lead to the weights of the evaluation indicators not being objective, and the importance of the food security evaluation indicators cannot be accurately assessed. Secondly, existing research on food security mainly focuses on the national or regional level, often ignoring regional differences within countries. Although this research method can provide macro level insights, it cannot reveal the specific problems and needs of different regions in terms of food security. At the same time, there is relatively little research on regional differences in China’s three major regions (grain producing areas, main sales areas, and production sales balance areas), and research methods mainly include Theil index method, coefficient of variation method, etc.32. Thirdly, existing studies mainly focus on a single aspect of food security level, and seldom explore the spatial and temporal evolution characteristics of food security level, regional differences and other issues at the same time.

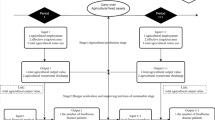
In this study, related existing researches were referenced, the entropy weight TOPSIS model and the panel data of 30 provinces (and cities) in China from 2011–2021 were used to evaluate their food security levels. We used the standard deviation ellipse technique, Moran’s index, and Dagum Gini coefficient to analyze the spatial characteristics and regional differences of China’s food security. Meanwhile, we analyzed the dynamic evolution process of food security level development based on Markov chain model. The results of this study can help us to further understand the China’s food security, propose basic strategies for ensuring food security and provide theoretical support for narrowing the development imbalance between regions. The research objectives of this study are twofold. Firstly, theoretical objective is to construct evaluation indicators for food security from a theoretical perspective, and analyze the temporal and spatial characteristics of China’s food security, thus expanding the theoretical perspective of food security research. Secondly, application goal, this study is to provide ideas for the construction and improvement of a long-term mechanism for ensuring food security in China, and also to provide scientific references for global food security.

The marginal contributions of this article are as follows. Firstly, this paper is focusing on regional differences to fill the research gap. A systematic study was conducted on the differences in food security among the three major regions of China (the main grain producing areas, the main sales areas, and the production sales balance areas) for the first time, filling the gap of insufficient attention to regional heterogeneity within countries in existing literature and provides a theoretical basis for regional coordinated development. Secondly, this paper adoptd the cutting-edge dynamic evolution analysis methods. Markov Chain model was introduced to reveal the spatiotemporal evolution law of food security level, breaking through the limitations of traditional static analysis, clarifying the path dependence and spatial spillover effects of regional development, and providing dynamic reference for policy-making. Thirdly, the evaluation results were more objective compared to traditional researches. Dagum Gini coefficient was used to overcome the shortcomings of traditional methods such as Theil index(which ignored sample cross overlap). And Entropy Weight TOPSIS model was combined to avoid subjective weighting bias, achieving dual objectivity in regional difference measurement and safety assessment.

Materials and methods

Variable selection and data sources

Food security evaluation indicators

In order to accurately understand the development status of various aspects of food security, a new food security evaluation system has been established, which is based on the existing food security evaluation system33,34 (Table 1). Due to the numerous indicators related to food security, this study considers the four dimensions of agricultural production safety level, agricultural environmental safety level, agricultural infrastructure level, and agricultural risk management level based on the availability, stability, and sustainability of data. Thirteen secondary indicators with strong complementarity, low repetition rate, and the most representative are retained. Each dimension covers different aspects of food security to ensure the comprehensiveness and scientificalness of the evaluation system. Datas in Table 1 are all original values.

Table 1 Food security evaluation indicators.
Full size table

Data sources

The sample examined in this study is the panel data of 30 provinces and cities (autonomous regions and municipalities directly under the central government) in China from 2011 to 2021. There are several important reasons for this paper to choose data from 2011–2021 for research. Firstly, 2011 was the beginning year of China’s 12th Five Year Plan, which marked a new stage in China’s economic and social development. Food security, as an important component of national strategy, had received special attention and policy support during this period. Therefore, data from 2011 onwards could reflect the level and changes of food security under this policy background. Secondly, after 2021, the global epidemic had a profound impact on the economic and social activities of countries, resulting in the loss or incompleteness of many data. Choosing 2021 as the endpoint of the study could avoid the impact of missing data on the accuracy and reliability of the research results. Thirdly, selecting data from 2011–2021 could ensure the continuity and integrity of data. The data from the past decade was relatively complete, providing a long-term perspective that helped researchers better analyzing the spatial–temporal changes and dynamic evolution of food security levels.

Due to the fact that part of the data of Tibet is missing, the study area of this paper excludes Tibet. The data for the study mainly come from China Statistical Yearbook, China Rural Statistical Yearbook, China Financial Statistical Yearbook, China Grain and Material Reserve Yearbook. The values of some indexes are missing, which are supplemented by checking the data published by China’s Ministry of Agriculture, State Forestry Administration, and China’s National Bureau of Statistics, etc., and the individual missing data have been made up by linear interpolation method.

Research methodology

Entropy weight TOPSIS method

We use Entropy weight method as the core weighting method, mainly based on the balance between its unique data-driven characteristics and comprehensive evaluation ability. Taking the RANCOM method as an example, the Entropy weight method calculates weights based on the degree of dispersion of the data itself, completely relying on objective data, and avoiding the bias introduced by expert preferences or artificial ranking in subjective weighting methods such as RANCOM24. Compared to the emerging ESP-COMET method, the Entropy weight method only requires data standardization and entropy calculation, with simpler steps and is suitable for quickly generating weights. ESP-COMET needs to define “expected solution points” to reflect personalized preferences and construct complex decision matrices, which involve multi-stage modeling26. In comparison with methods such as SPOTIS, the sensitivity of entropy weight method to extreme values can be alleviated through data standardization,If the ideal solution of SPOTIS contains extreme values, it may lead to sorting distortion. In summary, the entropy weight method is suitable for large-scale datasets without human intervention, especially for scenarios such as China’s food security that require processing massive statistical data35.

The fusion innovation of entropy weight method and TOPSIS further amplifies its methodological advantages. In thus, this paper constructs the Entropy weight TOPSIS model, and evaluates the food security of 30 provinces and cities in China in 2011–2021.The specific steps are as follows:

Firstly, data normalization.

Due to the different scales of each indicator, the data are first standardized, and the initial evaluation matrix of China’s food security is set as follows:

$$X=\left[\begin{array}{ccc}{a}_{11}& \cdots & {a}_{1n}\\ \vdots & \ddots & \vdots \\ {a}_{m1}& \cdots & {a}_{mn}\end{array}\right]$$
(1)

For data processing, the standardized matrix was obtained using the extreme value method, as detailed in Eqs. (2) and (3):

$$\text{positive indicator}:{p}_{ij}=\frac{{x}_{ij}-\text{min}\left({x}_{ij}\right)}{\text{max}\left({x}_{ij}\right)-\text{min}\left({x}_{ij}\right)}$$
(2)
$$\text{negative indicator}:{p}_{ij}=\frac{\text{max}\left({x}_{ij}\right){-x}_{ij}}{\text{max}\left({x}_{ij}\right)-\text{min}\left({x}_{ij}\right)}$$
(3)

Get the normalization matrix: \(P={\left[{p}_{ij}\right]}_{m\times n}\)

Secondly, establishment of a weighted decision evaluation matrix.

The weight vector \(\text{W}\) consists of indicator weights \({\upomega }_{\text{i}}\), based on normalization \(\text{P}\), to obtain a normalized weighting matrix \(\text{V}\), as detailed in Eq. (4):

$$V=P\times W={\left[{v}_{ij}\right]}_{m\times n}$$
(4)

Thirdly, determine positive and negative ideal solutions, \({\text{V}}^{+}\) 和 \({\text{V}}^{-}\):

$${V}^{+}=\left\{\mathit{max}{V}_{\mathit{ij}}\left|i=\text{1,2},\cdots \right.,m\right\}=\left\{{V}_{1}^{+},{V}_{2}^{+},\cdots ,{V}_{m}^{+}\right\}$$
(5)
$${V}^{-}=\left\{\mathit{min}{V}_{\mathit{ij}}\left|i=\text{1,2},\cdots \right.,m\right\}=\left\{{V}_{1}^{-},{V}_{2}^{-},\cdots ,{V}_{m}^{-}\right\}$$
(6)

Fourthly, calculating Distance.

The distances \({D}_{j}^{+}\) and \({D}_{j}^{-}\) from the food security assessment vector to the best security state \({V}^{+}\) and the worst security state \({V}^{-}\) were calculated for each year, respectively, as detailed in Eqs. (7) and (8):

$${D}_{j}^{+}=\sqrt{\sum_{i=1}^{m}{\left({V}_{i}^{+}-{V}_{ij}\right)}^{2}}$$
(7)
$${D}_{j}^{-}=\sqrt{\sum_{i=1}^{m}{\left({V}_{i}^{-}-{V}_{ij}\right)}^{2}}$$
(8)

Fifthly, calculating posting progress.

Calculating the proximity of the assessment goal to the optimal program in each year, expressed as \({T}_{J}\), taking a value between 0 and 1. The larger the value, the closer the country’s food security is to the optimal level, and the formula is shown in Eq. (9):

$${T}_{J}=\frac{{D}_{j}^{-}}{{D}_{j}^{+}+{D}_{j}^{-}}$$
(9)

Standard deviation ellipse technique

The standard deviation ellipse technique is a method used to analyze the directionality of spatial distribution, and the main parameters include ellipse perimeter and area, centroid coordinates, and directional angle, etc. This method can clearly show the spatial location characteristics of the configuration level of geographic elements36,37. In this study, the standard deviation ellipse technique is used to analyze the spatial characteristics of food security development in Chinese provinces and cities, and its calculation formula is as follows.

Center point coordinates:

$${SDE}_{X}=\sqrt{\frac{\sum_{i=1}^{n}{{(x}_{i}-\overline{X })}^{2}}{n}},{SDE}_{y}=\sqrt{\frac{\sum_{i=1}^{n}{{(y}_{i}-\overline{Y })}^{2}}{n}}$$
(10)

where \({\text{x}}_{\text{i}}\) and \({\text{y}}_{\text{i}}\) are the spatial location coordinates of each element, \(\widetilde{\text{X}}\) and \(\widetilde{\text{Y}}\) are the arithmetic mean centers.

Azimuth:

$$tan\theta =\frac{\left(\sum_{i=1}^{n}{\widetilde{x}}_{i}^{2}-\sum_{i=1}^{n}{\widetilde{y}}_{i}^{2}\right)\sqrt{{\left(\sum_{i=1}^{n}{\widetilde{x}}_{i}^{2}-\sum_{i=1}^{n}{\widetilde{y}}_{i}^{2}\right)}^{2}+4{\left(\sum_{i=1}^{n}{\widetilde{x}}_{i}{\widetilde{y}}_{i}\right)}^{2}}}{2\sum_{i=1}^{n}{\widetilde{x}}_{i}{\widetilde{y}}_{i}}$$
(11)

where \(\widetilde{{\text{x}}_{\text{i}}}\) and \(\widetilde{{\text{y}}_{\text{i}}}\) are the difference between the mean center and xy coordinates.

Moran’s index

In this study, the Moran’s index is applied to test whether there is spatial correlation in the food security level of 30 provinces and cities in China, including global correlation and local correlation, with the following formulas38,39,40.

Global Moran’s index:

$${Moran^{\prime}s}\;I = \frac{{n\sum\limits_{i = 1}^{n} {} \sum\limits_{j = 1}^{n} {\omega_{ij} } \left( {x_{i} - \overline{x} } \right)\left( {x_{j} - \overline{x} } \right)}}{{\left( {\sum\limits_{i = 1}^{n} {} \sum\limits_{j = 1}^{n} {\omega_{ij} } } \right)\sum\limits_{i = 1}^{n} {\left( {x_{i} - \overline{x} } \right)^{2} } }}$$
(12)

where \({\text{x}}_{\text{i}}\) and \({\text{x}}_{\text{j}}\) are the indicator values of variable \(\text{x}\) in cities \(\text{i}\) and \(\text{j}\), respectively; \(\overline{\text{x} }\) is the mean value of \(\text{x}\); and \({\upomega }_{\text{ij}}\) is the matrix of economic spatial weights.

Localized Moran’s index:

$$\rm{Moran^{\prime}s}\;\rm{I}_{\rm{i}} = \frac{{\left( {\rm{x}_{\rm{i}} - \overline{\rm{x}} } \right)}}{{\rm{S}^{2} }}\sum\limits_{{\rm{i} = 1}}^{\rm{n}} {\upomega _{{\rm{ij}}} \left( {\rm{x}_{\rm{i}} - \overline{\rm{x}} } \right)}$$
(13)

where, \({\text{s}}^{2}=\frac{\sum_{\text{i}=1}^{\text{n}}{\left({\text{x}}_{\text{i}}-\overline{\text{x} }\right)}^{2}}{\text{n}}\)

Dagum Gini coefficient and decomposition methods

The Dagum Gini coefficient has been widely used in studies measuring regional differences. The specific calculations are as follows41,42:

$$G=\sum_{j=1}^{k}\sum_{h=1}^{k}\sum_{i=1}^{k}\sum_{r=1}^{k}\left|{y}_{ji}-{y}_{hr}\right|)/2{n}^{2}\overline{y }$$
(14)
$${G}_{jj}=\frac{\frac{1}{2\overline{{Y }_{j}}}\sum_{i=1}^{{n}_{j}}\sum_{r=1}^{{n}_{j}}\left|{y}_{ji}-{y}_{jr}\right|}{{n}_{j}^{2}}$$
(15)
$${G}_{\omega }=\sum_{j=1}^{k}{G}_{jj}{P}_{j}{S}_{j}$$
(16)
$${G}_{jh}=\frac{\sum_{i=1}^{{n}_{j}}\sum_{r=1}^{{n}_{k}}\left|{y}_{ji}-{y}_{hr}\right|}{{n}_{j}{n}_{h}\left(\overline{{Y }_{j}}+\overline{{Y }_{j}}\right)}$$
(17)
$${G}_{nb}=\sum_{j=2}^{k}\sum_{h=1}^{j-1}{G}_{jh}\left({P}_{j}{S}_{h}+{P}_{h}{S}_{j}\right){D}_{jh}$$
(18)
$${G}_{t}=\sum_{j=1}^{k}\sum_{h=1}^{j-1}{G}_{jh}\left({P}_{j}{S}_{h}+{P}_{h}{S}_{j}\right){(1-D}_{jh})$$
(19)
$${D}_{jh}=\frac{{d}_{jh}-{p}_{jh}}{{d}_{jh}-{p}_{jh}}$$
(20)
$${d}_{jh}={\int }_{0}^{\infty }d{F}_{i}\left(y\right){\int }_{0}^{y}\left(y-x\right)d{F}_{h}\left(x\right)$$
(21)
$${p}_{jh}={\int }_{0}^{\infty }d{F}_{h}\left(y\right){\int }_{0}^{y}\left(y-x\right)d{F}_{j}\left(x\right)$$
(22)

\({\text{G}}_{\text{jj}}\) and \({\text{G}}_{\text{jh}}\) denote intra-regional and inter-regional Gini coefficients, respectively, \({\text{y}}_{\text{ji}}\left({\text{y}}_{\text{hr}}\right)\) denotes the level of food security in provinces and municipalities in region \(\text{j}\left(\text{h}\right)\), \(\overline{\text{y} }\) denotes the average value of food security level, \(\text{k}\) denotes the number of sample regions, \({\text{D}}_{\text{jh}}\) denotes the relative impact of food security level between regions \(\text{j}\) and \(\text{h}\), \({\text{d}}_{\text{jh}}\) denotes the difference in the level of food security between regions, and \({\text{p}}_{\text{jh}}\) denotes the hypervariable first-order moment. The Gini coefficient mainly consists of intra-regional differences \({\text{G}}_{\upomega }\), inter-regional differences \({\text{G}}_{\text{nb}}\) and hypervariable density \({\text{G}}_{\text{t}}\), i.e., \({\text{G}}_{\upomega }+{\text{G}}_{\text{nb}}+{\text{G}}_{\text{t}}\).

Markov chain models

Markov chain can accurately analyze the state of regional things occurring and its trend of upward or downward transfer, so as to reveal the dynamic development characteristics of regional things. The traditional Markov chain model constructs the order \(N\times N\) Markov probability transfer matrix to determine the dynamic evolution characteristics of China’s food security level32,43. Assuming that \({P}_{ij}\) is the transfer probability of cropland utilization eco-efficiency in a major grain producing area to transfer from state \({E}_{i}\) in year \(t\) to state \({E}_{j}\) in year \(t+1\), the transfer probability of cropland utilization eco-efficiency can be estimated by using the frequency approximation of the transfer, which is calculated as follows:

$${P}_{IJ}\left({E}_{i}\to {E}_{j}\right)=\frac{{n}_{ij}}{{n}_{i}}$$
(23)

\({\text{n}}_{\text{ij}}\) in Eq. (23) represents the total number of districts that shifted from level \(\text{i}\) to level \(\text{j}\) when the level of food security shifted from state \({\text{E}}_{\text{i}}\) to state \({\text{E}}_{\text{j}}\); \({\text{n}}_{\text{i}}\) represents the number of districts where \({\text{E}}_{\text{i}}\) is at level \(\text{i}\).

Spatial Markov chain analysis, on the other hand, is based on the traditional Markov chain analysis, which further considers that the values of the same attribute of neighboring things interact with each other in geospatial space, and incorporates the spatial lag into the Markov probability transfer matrix. Under the condition of spatial lag \({\text{N}}_{\text{i}}\), the traditional \(\text{N}\times \text{N}\) order Markov probability transfer matrix is decomposed into a \(\text{N}\times \text{N}\times \text{N}\) order probability transfer matrix, with \({\text{P}}_{\text{ij}}(\text{N})\) denoting the probability that the food security level transfer from type \({\text{E}}_{\text{i}}\) to type \({\text{E}}_{\text{j}}\) occurs under the condition of spatial lag \({\text{N}}_{\text{i}}\). The probability of the food security level transferring from type F to type G is also expressed in terms of the probability of the food security level transferring from type F to type G. By comparing the traditional Markov probability transfer matrix and the spatial Markov probability transfer matrix, the mechanism of the spatial spillover effect in the dynamic evolution of food security level development can be revealed.

Results

Determination of indicator weights

The weights of the evaluation indicators are calculated according to Eqs. (1) ~ (9) as shown in Table 2. As can be seen from Table 2, in the food security system quantity security and quality security have the highest weights, respectively 0.415, 0.307, followed by environmental security with a weight of 0.176, and economic security and ecological security with lower weights, respectively 0.09, 0.012, indicating that our country attaches great importance to the food production capacity, and the development of the economy and ecology is still at a relatively low level.

Table 2 Weight of evaluation indicators.
Full size table

Food security results in China

According to the above method, the raw data are first substituted into formula (6) to obtain the weights of each indicator, after which the raw data are substituted into formula (7) to standardize the data, and finally the results obtained from formula (6) and formula (7) are substituted into formula (8) to obtain the food security scores of China’s regions, with the trend of change shown in Fig. 1.

Fig. 1
figure 1

Trend chart of food security scores in various regions of China.

Full size image

Taken as a whole, trends in food security changes can be categorized into three phases: the fluctuation phase (2011–2014), the equilibrium phase (2015–2018) and the growth phase (2019–2021). During these three phases, the food security scores of the three regions show different trends as follows:

Fluctuation stage: the food security score of the main production area showed fluctuation during 2011–2014, decreasing from 0.4430 to 0.4340 and then increasing to 0.4468. the food security score of the main distribution area showed an increasing and then decreasing trend during the period of 2011–2014, increasing from 0.1508 to 0.1540, and then decreasing to 0.1529, during which time the main distribution area The grain consumption and import and export of provinces and cities were affected by some unstable factors, such as population growth, income level, international trade, etc., which led to the imbalance of grain supply and demand and market volatility. The food security scores of the provinces and cities in the production and marketing balance area changed more gently, with the average value rising from 0.2311 to 0.2377, which maintained a certain amount of growth in general, reflecting the relative balance of grain supply and demand and the relative stability of the market in the production and marketing balance area. The food security score of China as a whole, on the other hand, rose from 0.2749 to 0.2792. China’s food supply and demand fluctuated under the influence of various factors such as the economy and nature, but generally maintained some growth, reflecting the relative stability of China’s food security.

Equilibrium stage: The food security score of the main production area increased slightly during this stage, from 0.4439 to 0.4455, with a rate of change of 0.36%, reflecting the fact that the region’s food production and reserves have maintained a high level, and food supply and demand are basically balanced. The food security score of the main marketing zone increased significantly during 2015–2018, from 0.1584 to 0.1656, with a change rate of 4.55%, reflecting the region’s increased food consumption and imports and exports, as well as the improvement in food supply and demand and the development of the market. The food security score of the production and marketing balance region increased significantly during 2015–2018, from 0.2403 to 0.2498, with a rate of change of 3.95%, reflecting an increase in food production, consumption, and imports/exports in the region, improvement in food supply and demand, and market development. The overall food security score increased steadily between 2015–2018, from 0.2809 to 0.2870, with a rate of change of 2.17%, indicating that China’s food supply and demand maintained a better balance and growth during this period.

Growth phase: During this phase, the food security scores of all regions increased to varying degrees. Among them, the main production areas and the balance of production and marketing areas showed faster growth, from 0.4396 and 0.2600 to 0.4481 and 0.2671, respectively. the main marketing areas showed slower growth, from 0.1651 to 0.1672. the overall food security score also showed a faster growth trend, from 0.2882 to 0.2927. this indicates that food security situation in this phase had significant improvement.

Results of spatial characterization

Standard deviation ellipse technique

This study uses the standard deviation ellipse technique to examine the spatial pattern of the development of China’s food security level, thus revealing the spatial characteristics of its development (Table 3). As shown in Table 3, China’s food security level develops from the northeast to the southwest distribution from 2011 to 2021. From the point of view of changes in the perimeter and area of the ellipse, there is an overall fluctuating upward trend, and the area of the ellipse increases year by year from 383.8580 in 2011 to 406.4405 in 2021, showing a stable upward trend, indicating that the development of food security in China is a diffusion phenomenon. From the perspective of azimuthal rotation, the azimuthal angle increases from 65.32 degrees to 69.30 degrees, with a rotation of about 4 degrees, which indicates that the development pattern of China’s food security is shifting to the southwest. Specifically, with the help of Arcgis 10.2 analysis, it can be seen that the central city where the center of the standard deviation ellipse is located from 2011 to 2021 is Henan Province.

Table 3 The standard deviation ellipse parameter of China’s food security level.
Full size table

Moran’s index

On the basis of the above analysis, the spatial autocorrelation and dependence of China’s food security level are further tested by the Moran’s index (usually including the global Moran’s index and local Moran’s index). Using Stata to measure the Moran’s index in different years, if the P-value is less than 0.1 and the Moran’s index is positive, it means that there is spatial correlation in China’s food security level; conversely, if the P-value is greater than 0.1 or the Moran’s index is negative, it means that there is no spatial correlation in China’s food security level. Table 4 shows the results of the global Moran’s index measurements of China’s food security development level from 2011 to 2021.

Table 4 Overall Moran’s index of China’s food security development level.
Full size table

As can be seen from Table 4, China’s food security level passed the significance test at the 1% level from 2011 to 2021, and the Moran’s indexes are all positive, indicating that there is spatial autocorrelation in China’s food security level in recent years. From the trend of global Moran’s index, China’s food security level in 2011–2021 shows an overall fluctuating upward development, from 0.533 in 2011 to 0.597 in 2021, indicating that the trend of spatial agglomeration has been increasing on the whole.

In order to further analyze the local spatial autocorrelation of China’s food security level, based on Eq. (13), the local Moran’s index was used to examine the local correlation, and the scatterplot (Fig. 2) was plotted and the results of 2011, 2015, 2018 and 2021 were compared and analyzed. According to the four quadrants of the scatterplot, China’s food security level is categorized into ‘high – high’, ‘low – high’, ‘low – low’ and ‘high—low’ and ‘high-low’ agglomeration states, and correspond to the first, second, third and fourth quadrants in turn. Figure 2 shows that most cities are distributed in the first and third quadrants, i.e., most cities have ‘high-high’ and ‘low-low’ agglomeration effects, indicating that the level of food security in China is dominated by the same kind of agglomeration. The level of food security is dominated by similar types of agglomeration. Specifically, in 2021, the cities located in the first quadrant are Anhui, Shandong, Henan and other cities, which have a higher level of food security and can better drive the development of the surrounding cities, and can give full play to its positive spatial spillover effect; while Shanghai, Sichuan, Tianjin and other cities are located in the third quadrant, which have a low level of food security and do not have a driving effect on the surrounding cities, and the capitals of the various provinces have not been able to play a good role in radiating and driving the development. The provincial capitals of each province also fail to play a good role in radiation driving.

Fig. 2
figure 2

Scatter plot of the local Moran’s index of China’s food security level.

Full size image

Discussion

Discussion of regional variances

On the basis of measuring China’s food security level, the Dagum Gini coefficient method was applied to measure the overall differences in China’s food security level, inter-regional differences, intra-regional differences, and their contribution rates from 2011 to 2021, and the specific results are shown in Tables 5 ~ Table8.

Table 5 Gini coefficient of China’s overall and three regional food security levels.
Full size table

Overall regional differences.

Table 5 reflects the regional differences in China’s food security level and its evolutionary characteristics from 2011 to 2021. In general, the Gini coefficient as a whole shows a fluctuating downward trend, from 0.281 in 2011 to 0.264 in 2021. It can be seen that the overall difference in the level of food security in China shows a trend of narrowing, and this trend of narrowing mainly arises after 2014, and the main reasons for this phenomenon may be: firstly, the government’s implementation of the policy of poverty alleviation and assistance to farmers, which has effectively increased the incentive of farmers to grow grain Secondly, the optimization of the regional layout of grain production and the adjustment of crop structures, with an emphasis on varieties and regional balance, have improved the productivity and stability of the main grain-producing areas.

Variations within regions

As can be seen from Table 5, the overall trend of internal differences in China’s food security level is narrowing, and from the mean value, the mean values of the food security level in the three major regions of the main grain-producing areas, the main grain-selling areas, and the balance of grain production and marketing areas in the period of 2011–2021 are 0.140, 0.182, and 0.165, respectively, which can be seen from the fact that the intra-regional differences in the level of China’s food security show the characteristics of ‘main grain-selling areas > balance of production and marketing areas > main production areas’. It can be seen that the intra-regional difference in China’s food security level is characterized by ‘main marketing area > main production and marketing balance area > main production area’. From the perspective of the trend of change, the average annual growth rate of the Gini coefficient of food security level in the three major regions of the main grain-producing area, the main grain-marketing area, and the balance of grain production and marketing area is −0.83%, 0.52% and 2.26%, respectively, which indicates that only the main producing area has a trend of narrowing the imbalance of the development of food security, while the main marketing area and the balance of production and marketing area have a tendency to expand; and the Gini coefficient of the balance of production and marketing area has the largest change, and the change of the main production and marketing area has a smaller change. The Gini coefficient of balanced production and marketing areas has changed the most, while the main production areas and main marketing areas have changed less. In summary, intraregional differences in the level of food security are smallest in the main production areas and least volatile in the main marketing areas.

Interregional differences

Table 6 shows the characteristics of changes in the interregional Gini coefficients of food security levels in China’s three major regions. From the mean value, the mean values of Gini coefficients of main production-main sales, main production-balance, and main sales-balance are 0.275, 0.217, and 0.210 respectively, which shows that the inter-regional differences in the level of food security in China are characterized by the following features: ‘main production-main sales > main production-balance > main sales-balance’. It can be seen that the inter-regional differences in China’s food security level are characterized by ‘main production—main marketing > main production—balance > main marketing – balance’. In terms of the trend of change, the overall interregional differences between the main production-main marketing and main production-balance areas show a small reduction in trend, while the interregional differences between the main marketing-balance areas show a small increase in trend, which is relatively stable on the whole.

Table 6 Inter regional Gini coefficient of food security level in three major regions of China.
Full size table

As can be seen from Table 7, in terms of the contribution rate of gap sources, the average value of the contribution rate of inter-regional differences, hypervariable density, and intra-regional differences are 76.04%, 2.78%, and 21.19%, respectively, which shows that the contribution rate of inter-regional differences accounts for the largest proportion and that of hypervariable density accounts for the smallest proportion; in terms of the increase of the contribution rate, the contribution rate of inter-regional differences decreases from 77.72% in 2011 to 74.39% in 2011 to 3.68% in 2021, a decrease of 3.33 percentage points; the contribution rate of hypervariable density increases from 1.55% in 2011 to 3.68% in 2021, an increase of 2.13%; the contribution rate of intra-regional differences increases from 20.73% in 2011 to 21.93% in 2021, an increase of 1.20%. It can be seen that the contribution rate of intra-regional variance and hypervariable density shows a fluctuating upward trend, while the contribution rate of inter-regional variance shows a downward trend; the main source of regional variance is inter-regional variance. Therefore, only by narrowing the differences within the three regions can the problem of regional differences in the level of food security in China be effectively resolved, thereby promoting the coordinated development of food security among regions.

Table 7 Sources and contribution rates of regional differences in food security levels among the three major regions of China.
Full size table

Discussion of time evolution

Traditional Markov chain

Based on the quartile division method, the 30 provinces and cities from 2011 to 2021 are divided into three different types of state spaces according to the differences in the level of food security development with 1/3 and 2/3 quartiles as the boundaries, which are represented by Roman numerals I, II and III, and the larger the value, the higher the level of food security in the region, and the probability transfer matrices obtained based on the traditional Markov chain analysis are shown in Table 8.

Table 8 Traditional Markov chain probability transfer Matrix of China’s food security level.
Full size table

The values on the diagonal line in Table 8 indicate the probability that the food security level has not shifted, and the values on the off-diagonal line indicate the probability that the food security level status has shifted in each interval, which gives an idea of the evolutionary characteristics of China’s food security level without considering the spatial spillover effect:

  1. (1)

    The development of food security level in each region is highly stable. The probability on the diagonal is significantly larger than that on the non-diagonal, with the minimum value of 0.929 and the maximum value of 0.980, which indicates that the probability that the food security level of a certain region will maintain the stability of the original state in the process of the future development is at least 92.90%; in the past ten years, the food security level states were able to maintain the original state in most cases, especially Type III states, whose probability of maintaining stability is as high as 98%. The probability of maintaining stability is as high as 98%.

  2. (2)

    The developmental transfer of food security level shows a stable and continuous process, and it is difficult to realize leapfrog transfer in the short term. The non-diagonal probability of state transfer is significantly lower than the diagonal probability, with the maximum value of 0.051 and the minimum value of 0. The overall probability of leapfrog state transfer is low, indicating that it takes time for China’s food security level to be accumulated and gradually realized.

Spatial Markov chain

In order to further reflect the impact of the spillover effect of the development of food security level in neighboring regions on its own region, the economic distance matrix is accessed, and the spatial Markov probability transfer matrix is constructed based on the spatial lag type of each region in the initial year. It is also divided into three different types of state spaces based on the quantile division method, and the running results are shown in Table 9.

Table 9 Spatial Markov chain probability transfer matrix of China’s food security level.
Full size table

Overall, after the introduction of geographic elements, the probability on the diagonal is still significantly greater than that on the non-diagonal, and the level of food security in each region still has a stable tendency to maintain its original state, and it is difficult to realize a leapfrog transfer. However, by comparing Tables 8 and 9, the following spatial evolution characteristics can be derived:

Firstly, the spatial dependence is significantly enhanced, and the spillover effect exhibits asymmetry. After incorporating geographic spatial elements, the level of food security in adjacent regions has a significant impact on the local state transition. When the region is at a low level (Type I) and neighboring areas are also at a low level (Spatial Lag Type I), the local state is completely solidified, and the probability of upward transition is 0, reflecting the poverty trap effect, such as a 100% probability of maintaining the Type I region. When the intermediate level region (type II) is surrounded by high-level adjacent regions (spatially lagged type III), its upward transition probability increases from the traditional analysis of 0.051 to 0.069, indicating that high-value regions have a positive spillover effect on adjacent intermediate level regions, but the strength of the effect is limited.

Secondly, Further solidification of regional differentiation pattern. High level regions (type III) maintain a probability of up to 100% when adjacent to regions of the same type, forming a self reinforcing“club convergence”. For example, when the main production areas (such as Henan and Heilongjiang) are adjacent to high-value provinces, the probability of maintaining a high-yield state is close to absolute stability, while the probability of low-level areas (such as Shanghai) being radiated by neighboring high-value areas is 0, revealing the intensification of the “center edge” structure and the absence of regional coordination mechanisms.

Thirdly, Space constraints hinder gradient transitions. Despite the existence of spatial correlation, leapfrog transfer is still strictly limited. Low level areas (Type I) cannot break through the “zero upgrade” dilemma regardless of the surrounding environment (with a transition probability of 0), while medium level areas (Type II) have an increased risk of downward transfer when adjacent to low-level areas (spatially lagged Type I), their degradation probability increases from the traditional analysis of 0.020 to 0.028, indicating that negative spatial spillover may weaken the stability of medium level areas.

Fourthly, the polarization effect of high-level regions is prominent. The spatial Markov chain reveals the existence of a “siphon lock” dual mechanism in high-level regions (type III): On the one hand, its maintenance probability reaches 100% under spatial correlation, forming an irreversible absolute advantage; On the other hand, adjacent high-level regions suppress the possibility of intermediate regions transitioning to higher levels (such as the transition probability from type II to III being only 0.069 under spatial correlation), reflecting the development ceiling caused by resource aggregation and technological barriers.

Conclusions and recommendations

Conclusions

This paper applies the entropy weight TOPSIS model to measure the food security level of 30 provinces and municipalities in China from 2011 to 2021; combines the standard deviation ellipse technique, Moran’s index and Dagum’s Gini coefficient to analyze the spatial characteristics of China’s food security and regional differences; and analyzes the process of state transfer in the development of food security level based on the Markov chain model. The following conclusions are drawn:

Firstly, the spatial pattern of food security is expanding along the “Northeast Southwest” axis. Based on the Standard Deviation Ellipse analysis, the standard deviation ellipse area of grain production center of gravity expanded from 3.838 million square kilometers to 4.064 million square kilometers in 2011–2021, the azimuth rotated 4 degrees to the southwest, and the geographical center of gravity continued to stabilize in Henan Province, further consolidating its strategic position of “Central Plains Grain Storehouse”. At the same time, the risk of concentration in the main production areas has intensified, and it is necessary to disperse the pressure through regional collaborative optimization.

Secondly, spatial autocorrelation and the “club convergence” effect strengthen regional differentiation, hindering the transformation of intermediate level regions. The spatial differentiation of food security is showing a strengthening trend, and the regional coordination mechanism urgently needs to be improved. The global Moran’s index increased from 0.533 to 0.597, significantly enhancing spatial agglomeration and forming a polarized pattern of “high high” and “low low” agglomeration areas. Anhui, Shandong, Henan and other major provinces constitute contiguous high-value areas, while Shanghai, Sichuan and other major sales areas have a self-sufficiency rate of less than 30%, with regional differences contributing 76.04%. The transformation of intermediate level regions is hindered, for example, the probability of Hubei and Hunan being affected by technology spillover effects from neighboring high-value areas is less than 5%. Markov chain analysis shows that the probability of maintaining the status quo in high-level regions is as high as 98%, forming a solidified“club convergence”structure.

Thirdly, the root cause of regional differences is the imbalance between main production and main sales areas, with a dual absence of policy compensation and market mechanisms. The distribution of benefits between major production areas is unbalanced, for example, in Heilongjiang Province, the annual export volume accounts for 20%, but agricultural subsidies only account for 3.2% of the output value. The main sales area relies on cross provincial procurement but lacks ecological compensation. For example, Guangdong Province obtains grain sources from outside the province through market mechanisms, but has not established a horizontal fiscal transfer payment system. In thus, this “responsibility-benefit” mismatch has led to intensified regional conflicts, and it is necessary to reconstruct the mechanism of interest distribution through institutional innovation.

Recommendations

Based on the above conclusions, this paper draws the following recommendations:

Firstly, differentiatal regional governance framework: categorized policies to resolve structural contradictions. In the main production areas of Northeast China, a linkage mechanism of “black soil protection capacity compensation” can be implemented, providing financial subsidies based on the amount of grain exported per 10,000 tons, and incorporating the annual increase in soil organic matter content into the performance evaluation system. Establish a dual constraint of “balanced occupation and compensation of arable land-technological substitution” for the main sales areas with self-sufficiency rates below 30%, such as the Yangtze River Delta and Pearl River Delta, and promote urban vertical farm technology to increase production capacity per unit area. Build high standard emergency production capacity reserve warehouses for farmland in balanced areas such as the Huang Huai Hai region, and lock in supply agreements through the “abundant and scarce adjustment” mechanism to ensure emergency food sources in southern China.

Secondly, creating a three-dimensional collaborative network to activate spatial spillover effects. For the logistics dimension, constructing an intelligent corridor for the transportation of grain from the north to the south, and laying out blockchain traceability hubs in Zhengzhou and Wuhan to reduce circulation loss rates. For the data dimension, integrating remote sensing monitoring of county-level farmland and inventory warning system for main sales areas, achieving dynamic interconnection between quarterly updates of farmland quality in Henan and monthly inventory forecasting in Guangdong. For the ecological dimension, the food security tax collected from the main sales area will be directed towards the water-saving irrigation project in the Hetao Irrigation Area of Inner Mongolia.

Thirdly, creating ladder style policy tools to break down barriers to “club convergence”. In high-level production areas, carbon market can be piloted, where the carbon sequestration capacity of conservation tillage in Heilongjiang can be converted into carbon quotas and sold to high energy consuming enterprises in the main sales areas. In medium-level areas, the “contract agriculture-technology package” model can be promoted, and build a full industry chain by combining Henan japonica rice varieties with Zhejiang market demand in Anhui, to increase farmers’ income. In low-level areas, the “Enclave Agriculture” plan can be launched, with Shanghai and Heilongjiang jointly building production bases and adopting a mechanism of yield sharing and risk sharing to ensure the supply of grain sources for mega cities.