Introduction

The movement patterns and mechanical characteristics of overlying strata structures constitute one of the critical factors constraining safe extraction in deep coal mining. Overlying strata serve as stress-transfer media, regulating energy distribution within mining-affected zones. Their inherent structural stiffness directly governs the failure threshold of the coal-rock system1,2. The synergistic bearing mechanism between overlying strata and coal pillars profoundly influences the elastoplastic deformation of surrounding rocks and fracture network propagation patterns in mining faces by dynamically adjusting roof load transfer pathways3.

From the perspective of rock mechanics, mining-induced effects essentially represent a nonlinear reconstruction process of the stress field in the roadway surrounding rocks caused by large-scale coal extraction4,5. Stress redistribution leads to the formation of high-stress concentration zones in unmined zones6,7,8. The response of surrounding rocks under mining-induced stresses exhibits typical nonlinear characteristics9. Subjected to 3D stresses, surrounding rocks demonstrate time-dependent volumetric expansion behavior with complex deformation trajectories10,11. The mining-induced stress gradient field drives fracture evolution in surrounding rocks, which results in progressive deterioration of rock mass integrity and load-bearing capacity. Ref12. reveals the evolution mechanism of the unloading arch structure in the roadway surrounding rocks and the migration pattern of low-stress zones. This research identifies sensitive zones for fault instability slip under mining influence and establishes critical conditions for fault slip initiation.

Researchers have studied the stability of overlying strata and roadway surrounding rocks to ensure mining safety under coal extraction disturbances13. A representative contribution is Qian’s voussoir beam theory14, which marks a transition from empirical models to quantitative mechanics. This theory reveals the spatiotemporal evolution characteristics of strata pressure in mining faces, providing a theoretical foundation for developing green mining technologies15,16,17. Building upon the voussoir beam theory, Qian further proposed the key stratum theory in the 1990s. Mining pressure, strata movement, and surface subsidence are investigated by establishing mechanical connections between the entire overlying strata movement process (from the mining face to the surface). Yang et al.18 proposed that the overlying strata form spatially superimposed structures. High-position key strata exhibit typical voussoir beam configurations; however, low-position key strata develop cantilever beam structures. Pang et al.19 developed a stability analysis method for mine pillars based on triaxial mining stress evolution patterns to investigate the relationship between fracture structures in overlying strata and pillar stability. Lyu et al.20 proposed a finite difference method-based solution for the deflection function of main roof under irregular loads on elastic foundations to analyze the fracture locations, types, and patterns of main roof under different loadings.

Borehole pressure relief technology is a critical regional measure for preventing rockburst in coal mine safety operations. By constructing pressure-relief boreholes in deep surrounding rock masses, stress concentration can be effectively reduced. This optimization of the stress state minimizes rock deformation21. Borehole pressure-relief technology offers distinct advantages: high process feasibility and strong operational adaptability, while avoiding vibration disturbances and environmental contamination associated with blasting methods. Crucially, it preserves structural integrity of rock masses and optimizes project scale22,23,24. It significantly reduces stress concentration in the surrounding rocks and support pressure, with improved working conditions. Laboratory experimental studies25 serve as essential means for understanding, mastering, and applying this technology. These controlled experiments enable systematic observation and analysis of the pressure relief process, revealing the mechanical behavior of rocks, fracture propagation patterns, and their impact on surrounding rocks. Sophisticated simulation systems are established to precisely control in-situ stress, temperature, as well as borehole location, depth, diameter, and spacing. Thus, pressure relief processes are reproduced under different geological conditions. Advanced monitoring equipment and sophisticated data processing techniques are applied for the real-time observation of rock mass deformation, stress evolution, and seepage characteristics. This capability provides deeper insights into the physical mechanisms and mechanical effects associated with borehole pressure relief26. The results can evaluate the influences of factors (e.g., in-situ stresses, coal seam thickness, and borehole parameters) on pressure relief, providing a reliable scientific basis for optimized design.

Construction of the mechanical model and experimental scheme

Construction of the mechanical model

Borehole pressure relief is an effective engineering measure to regulate the stress state of the roof surrounding rocks, reduce localized stress concentration, and mitigate the risk of surrounding rock failure. Roof surrounding rocks are simplified as a true triaxial stress field under the 3D stress. True triaxial testing with different borehole parameters can realistically simulate the borehole pressure relief process in mining area roof to analyze the influence of parameters (e.g., borehole quantity, spacing, and arrangement) on stress field distribution and surrounding rock failure. Figure 1 shows the mechanical model.

Fig. 1
figure 1

Mechanical model of the surrounding rocks with roof boreholes.

Full size image

Experimental scheme

The experiment was conducted using a true triaxial electro-hydraulic servo-controlled testing system for rocks (Fig. 2(a)). This system enables precise control of the three principal stresses, allowing for independent or combined loading and unloading of the sample (Fig. 2 (b)).

Fig. 2
figure 2

True Triaxial testing system for rocks.

Full size image

The test samples are taken from the roof sandstone stratum. In-situ sandstone appears gray, composed of mineral particles such as quartz, feldspar, and mica. Rock samples used in the experiment are cuboid with dimensions of 50 × 50 × 100 mm (Fig. 3).

Pre-prepared intact cuboid samples are drilled with a borehole diameter of 6 mm for the mechanical property tests of the surrounding rocks with boreholes. The borehole configurations include three types: single-hole, double-hole, and triple-hole.

Fig. 3
figure 3

Sandstone samples with boreholes.

Full size image

The borehole spacings are set at 15, 25, and 35 mm, respectively, in the double-hole and triple-hole samples to investigate the influence of borehole spacing on the mechanical properties of the surrounding rocks. Figure 4 presents borehole characteristics in the samples. The influence of roof boreholes on surrounding rock stability across diverse engineering conditions is assessed through analyzing borehole arrangement patterns. Consequently, the mechanisms by which variations in borehole quantity and arrangement affect the mechanical response of the surrounding rock mass can be examined.

Fig. 4
figure 4

Characteristics of samples with different borehole configurations.

Full size image

Figure 5 shows the loading process of the experiment. A triaxial load is gradually applied under force-controlled loading until sample failure occurs (at time tn).

Fig. 5
figure 5

True triaxial testing procedure for rocks.

Full size image

Table 1 Lists the experimental scheme, where each sample follows a specific numbering convention for identification. \(\sigma_{3}\) (minimum principal stress) is uniformly set to 15 mpa during testing. The numbering rules are as follows.

WZ-20 represents the intact rock sample. WZ denotes intact (hole-free) rock; 20 denotes initial stress \(\sigma_{2}\) of 20 MPa.

C1 represents the sample with a single borehole. C denotes a single hole; 1 denotes one hole.

Z2-15 represents the sample with two vertically aligned boreholes. Z denotes vertical arrangement; 2 denotes two holes; 15 denotes the spacing (15 mm).

X3-15 represents the sample with three diagonally arranged boreholes. X denotes diagonal arrangement; 3 denotes three holes; 15 denotes the spacing (15 mm).

Table 1 Characteristics of different sample groups.
Full size table

Deformation and strength characteristics of holed rocks

Figure 6 (a) displays the stress-strain curve of intact rocks under true triaxial conditions. The σ1-direction stress-strain curve exhibits a distinct concave-downward characteristic, with pronounced strain hardening behavior. The sample enters the failure stage upon reaching the peak strength of 123 MPa. As shown by the green curve. Its load-bearing capacity rapidly declines, and residual strength stabilizes at approximately 30% of peak strength.

Fig. 6
figure 6

Stress-strain curves of holed rocks under true triaxial conditions.

Full size image

Figure 6 (b) shows the stress-strain evolution law of rock samples containing a single hole under true triaxial stress. Compared with intact rock samples, the elastic deformation interval is significantly shortened during the elastic stage, with strain relatively smaller than that of intact samples. The expansion deformation in the σ2 and σ3 directions intensifies. Peak strength drops to approximately 110 MPa, about 10.6% lower than that of intact rock samples.

Figure 6 (c) presents the stress-strain curve of a rock specimen containing two holes (vertically arranged with a hole spacing of 15 mm). The stress-strain curve in the σ1 direction exhibits a prolonged, slightly concave trend during this stage, reflecting the gradual closure of internal pores in rocks. When σ1 reaches 100 MPa, the sample enters the failure stage. The sample also exhibits ductile failure characteristics in the post-peak failure stage.

Figure 6 (d) displays the stress-strain curve of a rock sample containing three holes (arranged diagonally with a hole spacing of 15 mm). The compaction process is quite evident. The stress-strain curve shows a concave downward trend in the σ1 direction, while strain is relatively small in the σ2 and σ3 directions. When σ1 reaches its peak of 85 MPa, the sample enters the failure stage. Compared to the intact rock sample, the overall deformation of the sample with three holes is smaller. The failure process of the sample is relatively gradual due to the hole structure.

Figure 7 illustrates the relationship between the number and arrangement of holes and the peak strength of rocks. The axial stress of intact rocks is significantly higher than that of the holed samples. The peak strength of the samples declines as the number of holes increases. The axial stress at failure for vertically arranged samples is higher than that for diagonally arranged ones. Diagonal hole arrangements promote stress concentration between holes, which makes it easier for fractures to interconnect and reduces overall strength. Holes weaken the overall load-bearing capacity of the rock samples, with both the number of holes and their arrangement significantly affecting the structural strength of rocks.

Fig. 7
figure 7

Strength variation of rocks under different hole characteristics.

Full size image

Figure 8 illustrates the strength variation of rocks under different hole spacings (three holes). Vertical and diagonal alignments are compared, with hole spacings of 15, 25, and 35 mm. The average peak stress of vertically aligned three-hole samples changes sequentially to 98, 110, and 113 MPa as the hole spacing increases from 15 to 35 mm. For diagonally aligned three-hole samples, the average peak stress changes sequentially to 91, 101, and 104 MPa.

Peak strength exhibits significant growth at the spacing of 15–25 mm but stabilizes at 25–35 mm. The vertical arrangement generally demonstrates higher peak strength, with this advantage being most pronounced at a small hole spacing (15 mm). The strength difference between the two configurations gradually diminishes as the hole spacing increases.

Fig. 8
figure 8

Strength variation of rocks under different hole spacings (three holes).

Full size image

Fracture characteristics of holed rocks

Figure 9 illustrates the true triaxial fracture characteristics of intact and single-holed rocks. The samples expand along the σ3 direction under the true triaxial stress (σ1 > σ2 > σ3) due to constrained lateral deformation and the stress state (σ2 > σ3). Macroscopically, both types of samples develop intersecting double-fracture surfaces inside, exhibiting a typical Y-shaped through-going failure pattern. However, the single-holed rock sample displays significantly different fracture behavior. Holes alter internal stress distribution, which causes fractures to initiate predominantly from the hole edge and propagate outward.

Fig. 9
figure 9

True triaxial fracture characteristics of intact and single-holed rocks.

Full size image

Figure 10 shows the true triaxial fracture characteristics of double-holed rocks, with vertically arranged holes spaced at 15 mm. Two dominant macroscopic fracture surfaces develop during failure, exhibiting a Y-shaped failure pattern penetrating the entire sample. A connecting fracture forms between the two holes, accompanied by hole collapse. When the hole spacing increases to 25 mm, the sample undergoes shear slip along the hole edges. A macroscopic fracture surface forms at a spacing of 35 mm through the lower hole, which results in hole collapse. In the figure, 15, 25, and 35 represent the spacing between holes.

The work analyzes the true triaxial fracture characteristics of rocks containing diagonally arranged double holes. Rock samples with hole spacings of 15, 25, and 35 mm all exhibit failure in the σ1-σ3 planes due to the constraint of lateral deformation under true triaxial stress. When the hole spacing is 15 mm, the proximity of double holes during loading results in larger fracture widths on the sample surface. The stresses around the holes produce a superimposed effect, which leads to noticeable shear fractures and hole collapse on the sample surface.

Fig. 10
figure 10

True triaxial fracture characteristics of rocks containing double holes.

Full size image

Figure 11 shows the true triaxial fracture characteristics of rocks containing three holes. When the hole spacing is 15 mm, the main fracture surface has fewer fractures, and the circular holes appear elliptical. When the hole spacing is 25 mm, the number of fractures significantly increases, accompanied by hole collapse and greater fracture severity. When the hole spacing is 35 mm, the main fracture surface becomes more pronounced, with longer fracture propagation paths. As the hole spacing increases, the stress concentration zones also expand, which interconnects fractures. Fracture propagation occurs along the paths between the holes, which induces larger fractures and accelerates the failure process of rock mass.

Fig. 11
figure 11

True triaxial fracture characteristics of rocks containing triple holes.

Full size image

The true triaxial fracture characteristics of rocks with diagonally arranged triple holes reveal that the main fractures propagate along the diagonal direction. Fracture paths along the diagonal become more pronounced as the hole spacing increases, with intensified fracture strength. Multiple holes induce greater stress concentration and fracture propagation. The stress concentration effect around each hole results in the overlap of these stress fields, expanding the stress superposition zone. Consequently, this compromises the integrity of the overall rock structure and diminishes its load-bearing capacity.

In summary, the development of internal fractures in rocks exhibits significant directionality. Pre-existing holes induce shear slip along the hole boundaries. Rocks containing pre-existing holes predominantly undergo shear failure under true triaxial stress. For vertically arranged holes, the constraint of lateral deformation under true triaxial stress leads to widespread failure in rock samples. Pre-existing holes significantly alter rocks’ fracture patterns, with the orientation and number of holes playing a crucial role in the failure process. These findings hold substantial academic value for understanding the directional fracture mechanisms of rocks under complex stress states, providing a theoretical basis for stability analysis in rock engineering applications.

REV model for rocks

Heterogeneity of rocks

Natural rocks contain numerous micro-defects such as microscopic fractures and fine joints27. Traditional rock mechanics research primarily relies on macroscopic constitutive models, determining apparent mechanical parameters (e.g., elastic modulus and compressive strength) through uniaxial/triaxial compression tests. Modern rock mechanics is transitioning toward a multi-scale coupled analysis, in which meso-mechanical characterization techniques play a pivotal role.

A 3D digital model of the mineral grain-microfracture-pore system is established by integrating scanning electron microscopy (SEM) and focused ion beam (FIB). However, this approach faces dual challenges. At the experimental level, it is necessary to resolve the compatibility between sub-micron visualization accuracy and millimeter-scale view field of view. At the theoretical level, cross-scale constitutive models shall be developed to bridge crystal plasticity mechanics and macroscopic continuum mechanics.

Based on the statistical damage mechanics, the REV can achieve cross-scale mapping from microscopic damage evolution to macroscopic mechanical responses by introducing probability distribution functions of microstructural characteristic parameters28. It enables the analysis of mechanical response characteristics incorporating microstructural features29. Two essential attributes define the REV30,31. (1) The REV serves as the fundamental building block of rocks, representing the macroscopic properties of entire rock mass. (2) The REV can reflect the microscopic structure and properties of rocks, e.g., micro-fractures and small joints (Fig. 12).

Fig. 12
figure 12

REV model for rocks.

Full size image

Statistical distribution of mesoscopic element mechanical properties

The fundamental mechanical properties of mesoscopic elements are assumed to follow Weibull statistical distribution in material space29. The probability density function is defined by.

$$f(x,m,n) = \left\{ \begin{gathered} \frac{m}{n}\left( \frac{x}{n} \right)^{m - 1} \exp \left[ { - \left( \frac{x}{n} \right)^{m} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \ge 0 \hfill \\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x < 0{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.$$
(1)

where x is the basic variable; m is the shape parameter; n is the mean parameter. m represents the heterogeneity, reflecting the uniformity of rocks’ mechanical properties. When m approaches infinity, rocks become homogeneous.

Figure 13 illustrates the probability density distribution of the rocks’ elastic modulus under different m. As m increases, the mechanical properties of the mesoscopic elements become concentrated within a narrower range, indicating that rocks exhibit more uniform mechanical behavior.

Fig. 13
figure 13

Probability density distribution of elastic modulus under different m (n = 10 GPa).

Full size image

Failure criteria for rock mesoscopic elements

A macro-meso dual-scale model is established32. The maximum tensile stress criterion and the Mogi-Coulomb failure criterion are employed to characterize the tensile and shear failure mechanisms of rock elements, respectively. Specifically, when the stress state of a given rock element satisfies either failure criterion threshold, the element is considered to have failed. The specific criteria are as follows.

  1. (1)

    Maximum tensile stress criterion: When the element stress in rocks or rock mass reaches its tensile strength, tensile fracture occurs. Since the tensile strength of rocks is significantly lower than their compressive strength, tensile failure occurs preferentially.

  2. (2)

    Mogi-coulomb criterion33: This criterion provides a more accurate description of rock strength by incorporating the intermediate principal stress. It accounts for the effects of all three principal stresses (\(\sigma_{2}\), \(\sigma_{2}\), and \(\sigma_{3}\)) on material strength. \(\sigma_{1}\) is the maximum principal stress; \(\sigma_{3}\) is the minimum principal stress; \(\sigma_{2}\) is the intermediate principal stress.

$$\tau_{oct} = a + b\sigma_{m,2}$$
(2)
$$\tau_{oct} = \frac{1}{3}\sqrt {(\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} + (\sigma_{1} - \sigma_{3} )^{2} }$$
(3)
$$\sigma_{m,2} = \frac{{\sigma_{1} + \sigma_{3} }}{2}$$
(4)
$$\left\{ \begin{gathered} a = \frac{2\sqrt 2 }{3}c\cos \varphi \hfill \\ b = \frac{2\sqrt 2 }{3}\sin \varphi \hfill \\ \end{gathered} \right.$$
(5)

where \(c\) and \(\varphi\) represent the cohesion and internal friction angle of rocks, respectively.

The two failure criteria can be expressed uniformly by.

$$F_{1} = \sigma_{1} - f_{t} = 0$$
(6)
$$F_{2} = \frac{1}{3}\sqrt {(\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} + (\sigma_{1} - \sigma_{3} )^{2} } - a - b\frac{{\sigma_{1} + \sigma_{3} }}{2}$$
(7)

where \(F_{1}\) and \(F_{2}\) are the threshold functions for the tensile and shear criteria, respectively; \(f_{t}\) is the uniaxial tensile strength of rocks.

Figure 14 demonstrates the application of the Mogi-Coulomb criterion in fitting triaxial test results of coal-rock samples, showing excellent agreement. Given the shear-dominated failure characteristics of rocks, the Mogi-Coulomb criterion is adopted to determine shear failure in elements.

Fig. 14
figure 14

Fitting of the Mogi-Coulomb criterion based on true triaxial test results of rocks.

Full size image

Figure 15 illustrates the fracture behavior of mesoscopic elements. An element will fracture when its stress satisfies either the maximum tensile stress criterion or the Mogi-Coulomb criterion. When the stress of an element reaches the preset failure criterion, the element is considered fully fractured in the study of rock fracture mechanics. Besides, its load-bearing capacity significantly decreases. Stiffness degradation is applied to the fractured elements to address physically nonlinear media problems using continuum mechanics. Specifically, the stiffness of a fractured element is defined as 1/10 of its initial stiffness, representing the weakened medium characteristics of rocks after fracture. These weakened medium characteristics exhibit a residual threshold feature, meaning that fractured rocks retain a certain load-bearing capacity, albeit limited.

Fig. 15
figure 15

Simplified tensile and compressive curves of rock mesoscopic elements after fracture.

Full size image

Establishment of a true triaxial multi-scale numerical calculation model for rocks

Finite element software ABAQUS is employed for secondary development. The USDFLD subroutine is used to visualize the rock mesoscopic fracture evolution process. A detailed simulation framework is constructed through Fortran, which simulates the fracture evolution process of coal-rock mass under triaxial stress.

The USDFLD subroutine (User-Defined FIELD subroutine) embedded in ABAQUS provides users with the capability to define custom field variables. This subroutine allows users to redefine field variables at specific material points. These field variables can be used to describe material nonlinear behavior, damage evolution, or any other material-related state.

Embedding Weibull distribution for rock elements

First, the random distribution of rock mechanical parameters is configured to ensure they conform to the Weibull probability density function. Using Fortran, random numbers following Weibull distribution are generated and assigned to each element in the model. Thus, rock elements with varying elastic moduli exhibit spatial randomness. Figure 16 (a) illustrates the specific procedure.

Fig. 16
figure 16

Flowchart of mechanical parameter assignment for rock elements.

Full size image

Figure 16 (b) shows the Weibull distribution of rock elastic modulus when shape parameter m = 5. The probability distribution method quantifies the variability of elastic modulus within a specified range, providing a statistical description of the mechanical behavior of rocks. When the mean elastic modulus is 9.0 GPa, the contour plot illustrates the probability distribution characteristics of elastic modulus at 1.0 to 20.0 GPa. This approach offers an intuitive understanding of heterogeneity in rock elastic modulus.

Construction of numerical model logic flow

Figure 17 presents the specific numerical calculation process. Secondary development is conducted using the USDFLD subroutine in ABAQUS to achieve numerical solutions for the model. The steps for determining element failure are as follows.

  1. (1)

    A numerical geometric model is established based on the actual geometric dimensions and shape, which are then discretized into a series of RVEs.

  2. (2)

    Random number x conforming to the Weibull probability density function is generated using Fortran to simulate the spatial variability of material parameters. These parameters are then assigned to different elements to reflect the mechanical properties of materials at various locations.

  3. (3)

    Boundary conditions are applied to the model, with initial loading implemented. The boundary conditions mainly include displacement constraints and stress boundary conditions, while the loading primarily consists of static and dynamic loads.

  4. (4)

    The numerical simulation is performed using ABAQUS, employing an incremental iterative method for computation. Element failure is determined based on the maximum tensile stress criterion and the Mogi-Coulomb failure criterion.

  5. (5)

    For failed solid elements, stiffness degradation is implemented to characterize the damage evolution process.

  6. (6)

    The load is increased for the next loading stage. Iterative computations continue to simulate the progressive stress experienced by rocks under realistic scenarios until macroscopic failure occurs.

Fig. 17
figure 17

Numerical calculation flowchart.

Full size image

Numerical calculation

A true triaxial compression numerical simulation test was conducted to verify the effectiveness of the macro- and micro-scale fracture evolution model of rocks. The lower surfaces of rocks were assigned a fixed boundary constraint condition in the experimental design. Meanwhile, stress loads were applied to the surrounding boundaries, with confining pressures of 20 and 15 MPa, respectively. Displacement loading was applied at the top at 0.002 mm/step. The deformation behavior, mechanical response, and the entire process of fracture development in rocks were monitored and recorded during true triaxial compression. This allowed for a deeper understanding of the progressive fracture evolution mechanism of rocks and validated the correctness of the model. Table 2 lists the basic physical and mechanical parameters of rocks used in the test.

Table 2 Numerical mechanical parameters of rocks.
Full size table

A comparative analysis was performed comparing stress-strain curves from numerical simulations of intact rock samples against true triaxial test results (Fig. 18) to validate the rock parameters (Table 2). Mechanical responses from the numerical simulation and the true triaxial test results exhibited high consistency. This confirmed that the basic physical and mechanical parameters of rocks are suitable for numerical simulation calculations.

Fig. 18
figure 18

Numerical calculation parameters for true triaxial compression of rocks.

Full size image

Figure 19 (a) illustrates the progressive tensile fracturing process of rocks. X-shaped tensile fracture zones appear around the holes, with fewer tensile fractures surrounding the X-shaped zones in rocks containing three holes. Rocks fracture outward along the X-shaped pattern as stress increases. However, the fracture zone forms an asymmetric X shape in the case of three holes arranged diagonally. Fracturing gradually intensifies with continued expansion. The fractured zone progressively enlarges and eventually penetrates entire rock mass.

Fig. 19
figure 19

Fracture characteristics of holed rocks under true triaxial compression.

Full size image

Figure 19 (b) depicts the progressive shear failure process of rocks. X-shaped shear fracture zones develop around the holes and continuously extend outward, with fractures propagating throughout entire rock mass. When three holes are arranged diagonally, the progressive shear failure process becomes evident. Stress interference between the holes intensifies due to the increased number of holes and altered distribution patterns, which forms more fractures. These fractures are more prone to propagate along shear planes under true triaxial loading, which enhances shear stress near the holes. Shear failure occurs along the hole edges, indicating that the failure mechanism is primarily shear-driven rather than purely tensile.

Fig. 20
figure 20

Evolution of equivalent stress during true triaxial fracturing of holed rocks.

Full size image

Figure 20 illustrates the variation pattern of equivalent stress during the true triaxial fracturing process of holed rocks. An X-shaped stress concentration zone forms around each hole. The stress radiates outward along the X pattern, gradually attenuating as the stress extends away from the holes. Stress redistribution occurs around the holes with an increase in the number of holes and changes in their arrangement, which forms additional high-stress concentration zones. This phenomenon accelerates rock failure and compromises the overall stability of rocks.

Borehole pressure relief and roof weakening mechanism

Directional fracture zone formation in pressure relief boreholes

The mining-induced stress redistributes during coal mining, and the resulting stress disturbances intensify the mechanical response of surrounding rocks. The borehole pressure relief technique is applied to roadway roof to mitigate this effect. The overall stress level of the rock mass is reduced by artificially inducing partial release of the in-situ stress within the surrounding rocks. Figure 21 illustrates how pre-drilled boreholes interact with surrounding rocks.

Fig. 21
figure 21

Mechanism of pre-drilled boreholes on surrounding rocks.

Full size image

A series of pre-designed fracture zones is created by arranging borehole clusters at different locations within the roadway. These fracture zones serve as barriers to mitigate mining-induced stress disturbances on the surrounding rock. Furthermore, based on engineering requirements, the propagation direction and spatial distribution of fractures are precisely controlled to manage rock fracturing behavior.

Influence of pressure-relief borehole layout on fracturing

Pre-drilled boreholes significantly alter the stress distribution characteristics within rock mass, which affects its fracturing behavior. Numerical simulation techniques are employed to reconstruct and extract schematic diagrams of fracture zones induced by roof boreholes (Fig. 22).

Fig. 22
figure 22

Fracture zones induced by roof boreholes.

Full size image

Figure 23 (a) presents the influence of borehole spacing on the formation effectiveness of directional fracture surfaces, where the pressure-relief boreholes have a diameter of 0.1 m. When the borehole spacing exceeds 0.5 m, the fracture zones fail to fully connect, which results in localized fragmented zones with Limited pressure-relief effectiveness. However, when the spacing is reduced below 0.5 m, the fracture zones of adjacent boreholes interconnect to form continuous directional fracture surfaces. This guides stress release and significantly enhances pressure-relief performance. Furthermore, dynamically adjusting borehole parameters based on the in-situ stress field and rock mass properties ensures that the pressure-relief design matches the geological conditions.

Fig. 23
figure 23

Characteristics of fracture zones under different borehole spacings.

Full size image

Figure 23 (b) illustrates fracture zone formation in a row of pressure-relief boreholes under external loading. When confining pressure is applied at the boundary and the local stress intensity exceeds the ultimate compressive strength of rock mass, radial fracture zones and plastic zones develop around the boreholes. The propagation pattern of these zones is governed by the interaction between the in-situ stress state of rock mass and the geometric parameters of boreholes. As the borehole spacing gradually decreases (e.g., to 0.4 m), the stress disturbance fields of adjacent boreholes exhibit significant nonlinear superposition effects (Fig. 23 (c)). The superposition effect manifests as the interconnection of fracture zones around the boreholes. Thus, a continuous fracture band forms, achieving the intended engineering outcome.

Based on the foregoing analysis, rock specimens with prefabricated boreholes exhibit significant directional control in internal fracture development. These boreholes induce shear slip along their boundaries, and under true triaxial stress conditions, rocks containing such boreholes predominantly fail in shear due to stress concentration gradients. The presence of prefabricated boreholes fundamentally alters fracture propagation patterns, where borehole orientation and density critically influence failure mechanisms.Strategically arranged borehole clusters within roadways establish engineered fracture zones that function as stress barriers, effectively mitigating mining-induced disturbances to surrounding rock masses. Furthermore, fracture propagation direction and spatial distribution are precisely controlled according to engineering requirements, enabling targeted management of rock fracturing behavior. These findings establish a theoretical framework for stability analysis in rock engineering applications.

Engineering applications

Borehole pressure relief technology

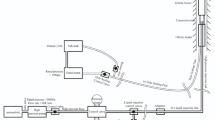
The borehole implementation site was located in the roof of the 13# coal seam in the 131,304 and 131,306 working faces of the East Mining Area of Liuzhuang Mine. The suspended roof strata in the goaf resulted in significant abutment pressure in the working faces after mining. Therefore, deep boreholes were selected to be drilled from the roadway side into goaf roof to achieve pressure relief and mitigate the abutment pressure. Boreholes were drilled from the side of the 131,304 belt conveyor roadway into 131,304 goaf roof, and from the 131,306 belt conveyor roadway into 131,306 goaf roof. The borehole locations were within 200 m ahead of the working faces (Fig. 24).

Fig. 24
figure 24

Slotting boreholes in the 131,304 belt conveyor roadway.

Full size image

Considering the geological conditions at the engineering site and comprehensive cost, the borehole inclination angle was set at 60°. The boreholes were drilled at 60° toward the working face, positioned 2,300 mm from the sides of the 131,304 and 131,306 working faces. The spacing between adjacent boreholes was 0.5 m, with a borehole diameter of 113 mm and the drilling depth of 11.56 m (Table 3).

Table 3 Borehole Information.
Full size table

Bolt (cable) force

A bolt (cable) stress observation station is established in the 131,306 track roadway to track and monitor the stress state of bolts (cables) in real time. Pressure cell sensors are installed at the anchoring ends of the bolts. MCS-400 mining intrinsically safe bolt dynamometers are employed, along with FCH2G/1 intrinsically safe handheld data collectors, to enable continuous data acquisition (Fig. 25).

Fig. 25
figure 25

Observation patterns of force measurement instruments for bolts (cables) in the 131,306 track roadway.

Full size image

Figure 25 presents the statistical data of force measurement instruments placed at four different locations—left-side bolts, right-side bolts, roof bolts, and roof cables—over a period. Approximately 140 m ahead of the working face, maximum measured force on the roof cable is about 128 kN, while at other times it remains stable at around 124 kN. Maximum force measured on the roof bolt is approximately 45 kN, and the left-side bolt reaches a maximum of about 91 kN. Overall, force data for the left-side bolts are slightly lower than those for the right-side bolts, though the difference between the two is minimal. Since the roof cables extend into the deep strata where stress is most concentrated, force transmitted to the cable measurement instruments is the greatest. The small difference in force data between the left and right sides reflects minimal variation in surrounding rock stress.

Deformation rate of roadway surrounding rocks

A displacement velocity variation curve (Fig. 26) is generated by analyzing the maximum observed values. These values are recorded at various displacement points and different time, all located at a consistent distance ahead of the advancing working face.

Fig. 26
figure 26

Deformation rate of roadway surrounding rocks.

Full size image

The closer displacement point to the face represents the faster deformation rate within 100 m ahead of the working face; the change is negligible beyond 100 m. The displacement velocity fluctuates most drastically within 70 m of the working face. The roadway deformation rate gradually decreases and stabilizes beyond 130 m, indicating minimal mining-induced influence.

The immediate collapse of the rock strata demonstrates effective pressure relief after drilling operations. This contrasts sharply with roof without drilling. Roof drilling pressure-relief technology severs the stress transmission path in the overlying strata, which reduces the transfer of roof pressure. Consequently, the stress environment of surrounding rocks is altered, mitigating the pressure exerted on the narrow coal pillar. The application of this drilling-based pressure-relief technique has yielded positive results.

Conclusion

  1. (1)

    Experimental studies on holed rock samples were conducted under true triaxial conditions to analyze the mechanical response and failure characteristics under different hole parameters. Holes induced stress concentration effects, which served as primary driving force for fracture initiation and propagation during true triaxial fracturing. As the number of holes increases and the spacing between holes decreases, stress concentration effects superimpose. This phenomenon significantly reduced the overall structural stability of rock mass. Vertical and diagonal alignments are compared, with hole spacings of 15, 25, and 35 mm. The average peak stress of vertically aligned three-hole samples changes sequentially to 98, 110, and 113 MPa as the hole spacing increases from 15 to 35 mm. For diagonally aligned three-hole samples, the average peak stress changes sequentially to 91, 101, and 104 MPa.

  2. (2)

    A REV model of rocks was established, employing the Weibull distribution function to quantify and characterize the heterogeneity of rocks. The Mogi-Coulomb criterion was adopted to describe the damage evolution process of rock meso-elements.

  3. (3)

    A macro-meso dual-scale fracture evolution model was developed to characterize rock Heterogeneity, along with a specialized numerical simulation program for rock macro-meso analysis. The investigation focused on the fracture evolution mechanisms in holed rocks across multiple scales. Stress concentration zones in holed rocks expanded outward in an X pattern, exhibiting nonlinear superposition effects. Fracture zones were interconnected around holes, which formed continuous fracture bands. When the borehole spacing exceeds 0.5 m, the fracture zones fail to fully connect, which results in localized fragmented zones with Limited pressure-relief effectiveness. However, when the spacing is reduced below 0.5 m, the fracture zones of adjacent boreholes interconnect to form continuous directional fracture surfaces.