Introduction

Tunnel Boring Machine (TBM) exhibits excellent adaptability in the construction of hard rock tunnels, boasting advantages such as rapid excavation speed and a high degree of automation. Consequently, it has been widely employed in highway tunnels, railway tunnels, and diversion tunnels1,2,3,4,5. However, due to limited preliminary geological survey information, tunnel construction is fraught with potential accidents, including collapses6,7,8, water and mud inrushes9,10, rockbursts11,12, and large deformation of the surrounding rock13,14. Especially when the tunnel is under complex geological conditions such as large burial depth, fractured rock, and high geostress, the surrounding rock develops significant squeezing deformation. This leads to increased frictional resistance between the surrounding rock and the shield. When the thrust force of the TBM becomes insufficient to overcome this resistance, machine jamming occurs. In addition, the strength and geological characteristics of different rock strata significantly influence the risk of TBM jamming, softer and fractured formations are particularly prone to triggering such incidents. Consequently, variations in TBM operational parameters, including cutterhead torque, thrust force, and penetration rate, serve as critical indicators by reflecting the dynamic interaction between the machine and surrounding rock mass15,16,17.

Many scholars have conducted research on the causes of TBM jamming through approaches such as in-situ monitoring and numerical simulation. Liu et al.18,19 found that with the release of geostress, the deformation of surrounding rock becomes more severe, eventually pressing against the TBM shield and increasing frictional resistance. When the machine’s thrust is unable to counteract this resistance, jamming occurs. They developed a model to perceive the jamming state based on theoretical formulas and finite element simulations. Zhang et al.20 analyzed the time-varying interactions between the TBM and surrounding rock, including contact, compression, and friction, using a theoretical model. The results showed that the main reasons for jamming are the increase in shield pressure and the expansion of the compression contact area. Huang et al.21 achieved real-time monitoring of shield pressure by installing strain gauges, sensors, and pressure cells on the surface of the TBM shield, and combined this with computer programs to realize real-time warning of jamming. Xu et al.22 and Lin et al.23 summarized and analyzed 121 cases of TBM jamming and identified fault fracture zones as one of the most common unfavorable geological conditions when jamming happens. They then proposed a method to identify fault fracture zones by integrating the microstructure, geochemistry, and mineralogy of rocks.

In the realm of TBM jamming warning research, Hasanpour et al.24 employed FLAC3D to simulate to simulate TBM excavation processes, accurately estimated tunnel squeezing and shield pressure, and thereby determined the risks associated with TBM jamming. Liu et al.25 conducted numerical simulations of jamming accidents, proposing comprehensive TBM jamming criteria that take into account rock strength, geostress, and surrounding rock deformation, effectively enabling the assessment of jamming risks. Yu et al.26 developed a dynamic TBM performance evaluation model that incorporates both translational and angular velocity characteristics, utilizing the fuzzy analytic hierarchy process (FAHP) to assign weights within the model. Furthermore, Hasanpour et al.27 leveraged artificial neural networks and Bayesian networks to analyze jamming risks, achieving notable success in predicting TBM jamming induced by soft rock squeezing.

However, these prior works have certain limitations. Some studies only qualitatively predict the risk of TBM jamming, lacking the quantitative probability of risk occurrence. Other studies rely heavily on single-parameter models or have limited interpretability. For example, certain machine learning methods, while effective in prediction, are often criticized as “black boxes” due to their complex structures and numerous parameters, making it difficult to explain the decision-making process and the contribution of each factor to the results. This limits the practical application of these models in actual TBM excavation scenarios where engineers need clear and transparent risk assessment information.

To address these research gaps, this paper proposes a Bayesian statistics framework for TBM jamming risk assessment. Unlike previous models, this framework offers high interpretability, providing a clear explanation of the underlying decision-making process and the contribution of each factor to the risk results. It can not only qualitatively determine whether there is a risk but also quantitatively provide the probability of risk occurrence. This enables engineers to make more informed decisions and take appropriate actions based on the risk probability. In addition, this framework fully utilizes the rich information from multi-source monitoring data, effectively capturing the complex relationships between various factors during the excavation process. It is expected to provide strong support for safe TBM excavation, improving excavation efficiency and reliability, and has significant theoretical and practical value for TBM excavation in complex geological conditions.

Project brief

Geological and TBM machine

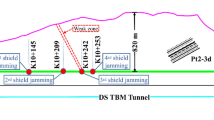
The subway project is located in Shenzhen, Guangdong Province, China. The total length of the tunnel is 4546.72 m, and 1781.85 m has been excavated, with a total of 992 rings in the excavated section. The tunnel is buried at a depth of 15–525 m. The crossing strata are mainly composed of gravelly sand, clay, and weathered granite, with slightly weathered granite accounting for 65% of the total. The longitudinal profile of the excavated section is shown in Fig. 1. The strength of the strata varies significantly, with the uniaxial compressive strength (UCS) of weathered granite in the tunnel area ranging from 27 to 67 MPa, while the maximum strength of slightly weathered granite reaches approximately 106 MPa.

Fig. 1
figure 1

Geological profile of the excavated area. Note: The rock is classified into Classes II, III, IV, and V according to the Chinese rock classification system, Similar to the RMR system28,29, the rock mass classification standard is based on rock strength, joints, water conditions, and field stress conditions30.

Full size image

To overcome the limitations of low excavation efficiency in composite strata when using a single-mode shield machine, an EPB/TBM dual-mode shield machine is employed. The EPB (Earth Pressure Balance) mode is utilized for excavation in weak strata to ensure tunnel face stability and minimize ground settlement. Conversely, the TBM (Tunnel Boring Machine) mode is adopted for excavation in hard rock strata, avoiding issues such as slow excavation speed and severe secondary wear of the disc cutter that may occur in EPB mode. The main specifications of the shield machine are detailed in Table 1.

Table 1 Main specification of EPB /TBM dual-mode shield machine.
Full size table

Dataset

Prior to March 11, 2023, the TBM recorded boring data at a frequency of 1 time per second. Starting from March 12, 2023, the recording frequency was adjusted to 1 time per 10 s. Over the course of 478 days, a total of raw data was generated, with each sample comprising 843 parameters. The raw data was organized by ring number, excluding data collected during non-boring states. Subsequently, abnormal data was cleaned using the Pauta criterion31, ensuring the integrity and reliability of the dataset for further analysis.

To more accurately analyze the interrelationship between geological conditions and tunneling parameter, seven parameters were preliminarily selected as the analysis objects based on existing research32,33,34,3536. These parameters include: (1) Total torque of the cutterhead T, (2) Total thrust of the cutterhead F, (3) Penetration of the cutterhead p, (4) Cutterhead rotation speed n, (5) Penetration rate v, (6) Field penetration index FPI, (7) Torque penetration index TPI.

Due to the significant difference in data between TBM mode and EPB mode, as well as the occurrence of jamming events in TBM mode, subsequent analysis focuses exclusively on data from TBM mode. Based on the actual excavation situation, the dataset is divided into two categories: jamming samples and normal excavation samples. The jamming section dataset contains 743 sets of samples, while the normal excavation section dataset includes 79,531 sets of samples.

Taking some typical parameters as examples, the statistical characteristics of the two types of samples are shown in Fig. 2. The figure reveals that the statistical indicators (mean, median, and range of values) for jamming and normal excavation samples exhibit significant different. Table 2 further details the geological conditions and excavation modes corresponding to different categories of samples, providing a clear basis for comparative analysis.

Fig. 2
figure 2

Statistical characteristics of typical parameters in two types of samples.

Full size image
Table 2 Geological condition and excavation mode along chainage.
Full size table

Bayesian statistical method for jamming perception

To address the limitations of existing methods, we propose a comprehensive Bayesian statistical framework for TBM jamming risk assessment. This framework integrates multiple parameters to provide a more accurate and interpretable risk assessment. Specifically, we introduce a comprehensive jamming perception index η that synthesizes multiple parameters to accurately identify jamming states. Additionally, we develop a quantitative model for calculating jamming probability, accounting for differences in sample size between jamming and normal excavation sections. These innovations enable more accurate and reliable risk assessment.

The distribution dissimilarity between different categories of samples

To quantitatively analyze the difference in feature distribution between machine jamming samples (jam) and normal excavation samples (non-jam), we denote the values of feature variables \(X_{i}\) in non-jam and jam samples as \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\), respectively. Figure 3 illustrates the distribution of these feature variables \(X_{i}\) in both categories of samples, where \(x_{i}^{c}\) serving as the threshold for distinguishing between the two classes.

Fig. 3
figure 3

Distribution of feature Xi in both datasets.

Full size image

In the samples located to the left side of \(x_{i}^{c}\) in the figure, not only are the correctly identified jam category samples included, but also the non-jam samples that were mistakenly classified as jam. Within the non-jam category, the proportion of samples misclassified as jam is referred to as the false positive rate (FPR), which can be estimated by the cumulative probability density of \(x_{i}^{{\text{non - jam}}} < x_{i}^{c}\), as shown in the grey shaded area in Fig. 3, corresponding to Eq. 1.

Similarly, on the right side of \(x_{i}^{c}\) in the figure, there are samples that include correctly classified non-jam category samples and jam samples that were mistakenly classified as non-jam. Among these, the proportion of jam samples misclassified as non-jam is known as the false negative rate (FNR), which can be estimated by the cumulative probability density of \(x_{i}^{{{\text{jam}}}} > x_{i}^{c}\), as shown in the red shaded area in the Fig. 3, corresponding to Eq. 2.

$$FPR = \user1{\Phi }_{i}^{{\text{non - jam}}} (x_{i}^{{\text{non - jam}}} ) = \int_{{\min (x_{i}^{{\text{non - jam}}} )}}^{{x_{i}^{c} }} {\varphi_{i}^{{\text{non - jam}}} (x_{i}^{{\text{non - jam}}} )} dx$$
(1)
$$FNR = 1 - \user1{\Phi }_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} ) = \int_{{x_{i}^{c} }}^{{{\max (x_{i}{{\text{jam}}}} )}} {\varphi_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} )} dx$$
(2)

Here \(\user1{\Phi }_{i}^{{{\text{jam}}}}\) and \(\varphi_{i}^{{{\text{jam}}}}\) respectively represent the cumulative probability density function (CDF) and probability density function (PDF) of feature Xi in the jam category samples; \(\user1{\Phi }_{i}^{{\text{non - jam}}}\) and \(\varphi_{i}^{{\text{non - jam}}}\) respectively represent the CDF and PDF of feature Xi in the non-jam category samples.

As can be seen from Fig. 3, as \(x_{i}^{c}\) increases, the FPR will also increase, while the FNR will decrease. To minimize the sum of FPR and FNR, the following relationship should be satisfied:

$$\left\{ {\begin{array}{*{20}l} {\min (FPR + FNR) = \min (\user1{\Phi }_{i}^{{\text{non - jam}}} (x_{i}^{{\text{non - jam}}} ) - \user1{\Phi }_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} ) + 1)} \hfill \\ {x_{i}^{c} \in [\min (x_{i}^{{\text{non - jam}}} ), \, \max (x_{i}^{{{\text{jam}}}} )]} \hfill \\ \end{array} } \right.$$
(3)
$$\left\{ \begin{gathered} (\user1{\Phi }_{i}^{{\text{non - jam}}} (x_{i}^{{\text{non - jam}}} ) - \user1{\Phi }_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} ) + 1)^{\prime} = 0 \, \hfill \\ x_{i}^{c} \in [\min (x_{i}^{{\text{non - jam}}} ), \, \max (x_{i}^{{{\text{jam}}}} )] \hfill \\ \end{gathered} \right.$$
(4)
$$\left\{ \begin{gathered} \varphi_{i}^{{\text{non - jam }}} (x_{i}^{{\text{non - jam}}} ) - \varphi_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} ) = 0 \hfill \\ x_{\user1{i}}^{\user1{c}} \in [\min (x_{i}^{{\text{non - jam}}} ), \, \max (x_{i}^{{{\text{jam}}}} )] \hfill \\ \end{gathered} \right.$$
(5)

When the two distributions overlap within the range [min(\(x_{i}^{{\text{non - jam}}}\)), max(\(x_{i}^{{{\text{jam}}}}\))], the threshold \(x_{i}^{\user1{c}}\) must fall within this interval. When \(x_{i}^{\user1{c}}\) is positioned at the intersection point of the two distribution curves, the sum of FPR and FNR can be minimized.

When the sample size is sufficiently large, it can be assumed that \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\) are approximately normally distributed, and the following relationship holds:

$$\beta_{i} = \frac{{\mu_{i}^{{\text{non - jam}}} - x_{i}^{c} }}{{\sigma_{i}^{{\text{non - jam}}} }} = \frac{{x_{i}^{c} - \mu_{i}^{{{\text{jam}}}} }}{{\sigma_{i}^{{{\text{jam}}}} }}$$
(6)

Here βi represents the distribution dissimilarity of the feature Xi between the two categories samples. \(\mu_{i}^{{\text{non - jam}}}\) and \(\sigma_{i}^{{\text{non - jam}}}\) are the mean and standard deviation of \(x_{i}^{{\text{non - jam}}}\), respectively, while \(\mu_{i}^{{{\text{jam}}}}\) and \(\sigma_{i}^{{{\text{jam}}}}\) are the mean and standard deviation of \(x_{i}^{{{\text{jam}}}}\), respectively. By rearranging Eq. 6, the following relationship can be obtained:

$$x_{i}^{c} = \mu_{i}^{{{\text{jam}}}} + \beta_{i} \sigma_{i}^{{{\text{jam}}}} = \mu_{i}^{{\text{non - jam}}} - \beta_{i} \sigma_{i}^{{\text{non - jam}}}$$
(7)
$$\beta_{i} = \frac{{\mu_{i}^{{\text{non - jam}}} - \mu_{i}^{{{\text{jam}}}} }}{{\sigma_{i}^{{\text{non - jam}}} + \sigma_{i}^{{{\text{jam}}}} }}$$
(8)

Here the larger the value of βi, the more pronounced the statistical difference between \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\). As shown in Table 3, when the βi value is 0, it indicates that the two distributions have the same mean, and at this point, \(x_{i}^{c}\) cannot effectively distinguish between the two categories. In this situation, both FPR and FNR are 50.0%. When the βi value is 1, and both \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\) strictly follow a normal distribution, the FPR and FNR are approximately 16.0%. When the βi value is 2, and both \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\) strictly follow a normal distribution, the FPR and FNR are approximately 2.0%. When the βi value is 3, and both \(x_{i}^{{\text{non - jam}}}\) and \(x_{i}^{{{\text{jam}}}}\) strictly follow a normal distribution, the FPR and FNR are approximately 0.15%.

Table 3 Relationship between βi-values and FPR and FNR in normal distribution.
Full size table

Qualitative model for jamming risk

Through the above process, we can establish a qualitative discrimination model based on the feature Xi to identify the risk of jamming machines. This model employs a binary classification method by setting a decision threshold \(x_{i}^{c}\) to distinguish whether a sample poses a jamming risk or not.

Specifically, if the value \(x_{i}\) of the sample’s feature \(X_{i}\) is lower than the corresponding decision threshold \(x_{i}^{c}\), the sample is judged as “jam”; conversely, if \(x_{i}\) exceeds the threshold \(x_{i}^{c}\), the sample is judged as "non-jam". The mathematical expression of this model is as follows:

$$IFJ = \left\{ {\begin{array}{*{20}c} 1 & {if \, x_{i} < x_{i}^{c} } \\ 0 & {if \, x_{i} > x_{i}^{c} } \\ \end{array} } \right.$$
(9)

Here IFJ represents the model’s identification result, with a value of 1 indicating a positive identification result (in this case, “jam”), and a value of 0 indicating a negative identification result (here, "non-jam"). Additionally, this model contains another layer of meaning: the closer the value of \(x_{i}\) is to the threshold \(x_{i}^{c}\), the higher the credibility of the identification result. This implies that samples near the threshold are more uncertain in their classification compared to those further away from \(x_{i}^{c}\).

Comprehensive evaluation index for jamming risk

Using Eq. 7 and 8, we can calculate the \(x_{i}^{c}\) and βi values for classification using each individual indicator. Clearly, the βi values for each indicator differ, indicating varying abilities of these indicators to distinguish between jam and non-jam conditions. A larger βi value signifies a stronger overall recognition effect, but this does not necessarily translate to better recognition for every specific sample. For instance, when β1 > β2, feature X1 outperforms feature X2 in overall recognition effectiveness, yet for certain specific samples, feature X2 may provide better discrimination than feature X1. This indicates that a single feature can only reflect a limited aspect of the rock mass conditions, highlighting the importance of considering multiple features for robust classification.

To address this issue, we attempt to integrate all individual features for jamming risk warning to enhance overall accuracy. The specific steps are as follows:

  1. (1)

    Calculation of the weight of each individual feature.

Based on the distribution dissimilarity index βi, the weight \(w_{i}\) of each single feature is calculated using Eq. 10:

$$w_{i} = \frac{{\beta_{i} }}{{\sum\nolimits_{1}^{N} {\beta_{i} } }}$$
(10)

Here \(w_{i}\) represents the weight of feature Xi, βi is the distribution dissimilarity of feature Xi, and N is the total number of features. A smaller distribution dissimilarity implies a lower weight, indicating that this feature carries less significance in the comprehensive evaluation.

  1. (2)

    Calculation of the comprehensive evaluation feature.

The comprehensive evaluation feature η, based on the weighted approach, can be calculated using Eq. 11:

$$\eta = \sum {[1 - \user1{\Phi }_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} )]} w_{i}$$
(11)

Here η is the comprehensive feature used to evaluate jamming risk, with a value range of [0, 1]. \(x_{i}^{{{\text{jam}}}}\) represents the value of feature Xi in the jam category. \(\user1{\Phi }_{i}^{{{\text{jam}}}}\) denotes the CDF of feature Xi in the jam category, calculated as follows:

$$\user1{\Phi }_{i}^{{{\text{jam}}}} (x_{i}^{{{\text{jam}}}} ) = \Psi (\frac{{x_{i}^{{{\text{jam}}}} - \mu_{i}^{{{\text{jam}}}} }}{{\sigma_{i}^{{{\text{jam}}}} }})$$
(12)

Here Ψ represents the CDF of the standard normal distribution.

Probability model for jamming risk

This section focuses on constructing a quantitative probability model based on Bayesian conditional probability theory to assess the risk of machine jamming during TBM excavation processes. By collecting real-time data, we calculate the comprehensive feature η of the current sample. Using the qualitative identification model, we make a preliminary judgment to determine whether the sample belongs to a “jam” situation. However, while the qualitative model identifies “jam” states, it cannot quantify the probability of jamming. To address this limitation, we establish a quantitative probability model for jamming risk warming, leveraging the comprehensive feature η and Bayesian theory. The derivation process is as follows:

Assuming the comprehensive feature of the current sample is \(\eta ^{\prime}\), and the recognition result of the qualitative model is \(IFJ(\eta ^{\prime})\) (where IFJ = 1 for “positive” and IFJ = 0 for “negative”), we use the posterior conditional probability \(P({\text{jam}}\left| {IFJ(\eta ^{\prime})} \right.)\) to evaluate the reliability or accuracy of the qualitative model. For instance, \(P({\text{jam}}\left| {{\text{positive}}} \right.) = 0.9\) indicates that the credibility of the qualitative model judging the current rock mass as “positive” (jam) aligns with the actual situation (jam) at a 90.0% confidence level.

From previous analysis, we know that the comprehensive feature η, similar to indicators such as TPI and FPI, reflects the quality of the rock mass through its value. Therefore, we use the posterior conditional probability to estimate the probability \(R(\eta ^{\prime})\) of a jamming occurring in the current rock mass. This includes two events: the conditional event is the recognition result \(IFJ(\eta ^{\prime})\) (where IFJ = 1 for “positive” and IFJ = 0 for “negative”) of the qualitative model for the current sample, and the outcome event is that the real label of the sample is “jam”. According to Bayes’ theorem, \(P({\text{jam}}\left| {IFJ(\eta ^{\prime})} \right.)\) can be expressed as:

$$R(\eta ^{\prime}) = P({\text{jam}}\left| {IFJ(\eta ^{\prime})} \right.){ = }\frac{{P({\text{jam}}) \times P(IFJ(\eta ^{\prime})\left| {{\text{jam}}} \right.)}}{P(IFJ(\eta ^{\prime}))}$$
(13)

This contains three terms, which we will introduce one by one.

  1. (1)

    (1) \(P(IFJ(\eta ^{\prime}))\) represents the ability of the qualitative model to recognize samples as “positive” or “negative”. Taking \(IFJ(\eta ^{\prime}) = 1\) (positive) as an example, this includes two scenarios:

Correct identification: The real label of the sample is “jam”, and the identification result is also positive.

False alarm: The real label of the sample is “non-jam”, but the identification result is positive.

Similarly, \(IFJ(\eta ^{\prime}) = 0\) (negative), it also includes two scenarios:

Correct identification: The real label of the sample is “non-jam”, and the identification result is also negative.

Missing: The real label of the sample is “jam”, but the identification result is negative.

We can express this using the following formula:

$$P(IFJ(\eta ^{\prime})) = P(IFJ(\eta ^{\prime}) \cap {\text{jam}}){ + }P(IFJ(\eta ^{\prime}) \cap {\text{non - jam}})$$
(14)

According to the method of calculating joint probability, the two terms on the right side of Eq. 14 can be expressed in the following forms:

$$P(IFJ(\eta ^{\prime}) \cap {\text{jam}}) = P(IFJ(\eta ^{\prime})\left| {{\text{jam}}} \right.) \times P({\text{jam}})$$
(15)
$$P(IFJ(\eta ^{\prime}) \cap {\text{non - jam}}) = P(IFJ(\eta ^{\prime})\left| {\text{non - jam}} \right.) \times P({\text{non - jam}})$$
(16)
  1. (2)

    \(P({\text{jam}})\) and \(P({\text{non - jam}})\) represent the probabilities of a sample belonging to “jam” or “non-jam” categories. These probabilities can be determined in two ways:

First approach: Using prior probabilities. The prior probabilities are derived from the proportions of samples belonging to the “jam” and "non-jam" categories within the entire dataset. This can be formulated as follows:

$$\left\{ {\begin{array}{*{20}l} {P({\text{jam}}) = \frac{{N_{2} }}{{N_{1} + N_{2} }}} \hfill \\ {P({\text{non - jam}}) = \frac{{N_{1} }}{{N_{1} + N_{2} }}} \hfill \\ \end{array} } \right.$$
(17)

Here N1 and N2 represent the number of "non-jam" samples and “jam” samples, respectively, in the original dataset.

Second approach: Treating both categories as equally likely. This approach disregards the prior probabilities and assumes that both categories have an equal probability of appearing. This can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {P({\text{jam}}) = 0.5} \hfill \\ {P({\text{non - jam}}) = 0.5} \hfill \\ \end{array} } \right.$$
(18)

In this case, the occurrence of both categories is treated as a random event with no bias toward either category.

  1. (3)

    \(P(IFJ(\eta ^{\prime})\left| {{\text{jam}}} \right.)\) represents the likelihood of the model’s prediction given the true label. These terms represent the probability that a qualitative model predicts the sample as \(IFJ(\eta ^{\prime})\), given the true label of the sample. Specifically:

\(P(IFJ(\eta ^{\prime})\left| {{\text{jam}}} \right.)\) is the likelihood that when the sample belongs to the “jam” category, it falls near a specific value \(\eta ^{\prime}\).

\(P(IFJ(\eta ^{\prime})\left| {\text{non - jam}} \right.)\) is the likelihood that when the sample belongs to the "non-jam" category, it falls near a specific value \(\eta ^{\prime}\).

This can be expressed using the following formula:

$$\left\{ {\begin{array}{*{20}l} {P(IFJ(\eta ^{\prime})\left| {{\text{jam}}} \right.) = \varphi^{{{\text{jam}}}} (\eta ^{\prime})} \hfill \\ {P(IFJ(\eta ^{\prime})\left| {\text{non - jam}} \right.) = \varphi^{{\text{non - jam}}} (\eta ^{\prime})} \hfill \\ \end{array} } \right.$$
(19)

Here, φjam and φnon-jam represent the prior distribution functions for samples belonging to the “jam” and “non-jam” categories, respectively. These distributions reflect the inherent characteristics of the rock mass quality indicators (e.g., TPI, FPI) under each category, providing a basis for calculating the likelihood of the model’s predictions.

  1. (4)

    Calculating the probability of jamming risk using substituted terms: By substituting these terms into Eq. 13, can calculate the probability of the current tunnel face rock mass experiencing jamming risk. The final expression is as follows:

    $$\left\{ {\begin{array}{*{20}l} {R_{1} (\eta ^{\prime}) = \frac{{N_{2} \cdot \varphi^{{{\text{jam}}}} (\eta ^{\prime})}}{{N_{2} \cdot \varphi^{{{\text{jam}}}} (\eta ^{\prime}) + N_{1} \cdot \varphi^{{\text{non - jam}}} (\eta ^{\prime})}}} \hfill & {\text{Using prior probabilities}} \hfill \\ {R_{2} (\eta ^{\prime}) = \frac{{\varphi^{{{\text{jam}}}} (\eta ^{\prime})}}{{\varphi^{{{\text{jam}}}} (\eta ^{\prime}) + \varphi^{{\text{non - jam}}} (\eta ^{\prime})}}} \hfill & {\text{Not using prior probabilities}} \hfill \\ \end{array} } \right.$$
    (20)

Here R1 represents the quantitative probability model that considers the influence of the category proportions in the prior distribution, while R2 represents the quantitative probability model that does not consider the influence of the category proportions in the prior distribution.

Results and discussion

Performance of qualitative model

Through Equations 7 and 8, Table 4 summarizes the statistical outcomes of key tunneling parameters across two sub datasets and the calculated distribution dissimilarity β for each parameter. The analysis reveals the following insights: The βp is relatively small, indicating minimal variability. This makes it unsuitable for identifying jamming states, as there is insufficient distinction between “jam” and “non-jam” conditions. The parameter n is primarily influenced by the driver’s subjective judgment and operational habits, leading to high variability. Due to its dependence on human factors, it is also unsuitable for jamming state identification. Other five tunneling parameters (T, F, v, TPI, FPI) exhibit significant distribution dissimilarity β in both “jam” and “non-jam” samples. This large variability makes them effective indicators for identifying jamming states. Figure 4 illustrates the distribution results of the five selected tunneling parameters (T, F, v, TPI, FPI) in both jammed and normal excavation sections. The key observations are that the distributions of these parameters show considerable overlap between jammed and normal conditions, suggesting that they alone may not provide a clear distinction.

Table 4 Statistical analysis results of the key tunneling parameters in two datasets.
Full size table
Fig. 4
figure 4

Probability density distribution of tunneling parameters.

Full size image

Figure 5 illustrates the identification performance of jamming states using the selected tunneling parameters T, F, v, TPI, and FPI along with their corresponding thresholds. The samples within a 300 m interval near the jamming section are analyzed to distinguish between normal excavation and jammed conditions. Notably, significant mutations in the samples are observed in the jamming section, and the thresholds effectively separate most non-jamming state samples from jamming state samples.

Fig. 5
figure 5

Identification performance of the threshold.

Full size image

For example, in Fig. 5a, the red dashed line represents the threshold for T, defined as \({T}^{c}\) = 1090. Black sample points correspond to data from the normal excavation section, while purple points represent data from the jamming section. Visually, it is evident that using \({T}^{c}\) = 1090 as the threshold successfully identifies most jamming samples. However, some non-jamming samples are incorrectly classified as jamming. Similarly, the identification results using F, v, TPI, and FPI as indicators are presented in Figs. 5b–e, demonstrating consistent performance with varying degrees of accuracy and misclassification.

To comprehensively account for the influence of various parameters and further enhance identification performance, the weights of each parameter were calculated using Eq. 10, and a comprehensive perception index η for each sample group was derived via Eq. 11. The identification rate of the qualitative model IFJ in the jamming section dataset was computed using Eq. 9, while the false positive rate (FPR) and false negative rate (FNR) for each parameter’s threshold and the comprehensive perception index were determined through Eqs. 1 and 2. The parameter weights and identification rates are summarized in Table 5, and the distribution of the comprehensive perception index along with a comparison of parameter identification performance is illustrated in Fig. 6.

Table 5 Average calculation result of risk probability.
Full size table
Fig. 6
figure 6

Display of the identification performance of various parameters.

Full size image

From Table 4 and Fig. 6, it is evident that the distribution dissimilarity of the comprehensive perception index η is significant between the jamming and normal excavation sections, demonstrating its strong ability to identify jamming states. As shown in Table 4, η achieves the highest IFJ identification rate among all six parameters (T, F, v, TPI, FPI, and η), successfully identifying 97.8% of jamming data in the jamming section dataset with only a 2.2% false negative rate. This indicates that η, which integrates multiple parameters, is highly effective in distinguishing whether a given excavation data sample is in a jamming state.

Figure 6a illustrates the distribution of η across both datasets, revealing that nearly all samples in the jamming section dataset exceed the threshold line (Fig. 6b). A more detailed analysis in Fig. 6c shows that the qualitative model using η also maintains a high identification rate for normal excavation states, achieving 96.1% accuracy with a 3.9% false positive rate. Furthermore, Fig. 6d compares the FPR and FNR of each parameter’s threshold, highlighting η as the optimal indicator with the lowest FPR and FNR among all six parameters.

Performance of quantitative model

In the case studied in this article, the sample size of the jamming section is 743, while the sample size of the normal excavation section is 79,531. Following Eq. 17, the proportion of jamming samples P(Jam) = 0.009 and the proportion of normal excavation samples P(Non-jam) = 0.991. By inputting the statistical results of η into Eq. 20, the probability of jamming corresponding to each group of samples can be calculated. Figure 7 illustrates the trend of jamming risk near 100 m in the area where the accident occurred, and Table 5 presents the jamming probabilities for all data samples.

Fig. 7
figure 7

Probability calculation results of jamming risk: a R1 model; b R2 model.

Full size image

As shown in Table 5, without considering the influence of sample size, the average probability of jamming in the jamming section is 77%, while in the normal excavation section it is 2%. However, after accounting for the significant difference in sample size, the average probability of jamming in the jamming section increases to 94%, and in the normal excavation section it rises to 7%. This indicates that the disparity in sample size between the jamming and normal excavation sections leads to an underestimation of jamming risk when sample size is not considered. In reality, jamming accidents are not sudden but develop over time22. As depicted in Fig. 7a, the jamming probability appears relatively stable with minimal fluctuations due to the imbalanced dataset, resulting in a lack of sensitivity in the calculated risk R. When a jamming accident occurs, the probability abruptly increases to a very high value. However, after incorporating the influence of sample size, the jamming probability dynamically reflects real-time changes in the data, as shown in Fig. 7b. Thus, the calculated results of R2, which account for sample size, align more closely with actual conditions.

Performance of quantitative model in different rock mass

As shown in Fig. 1, the TBM mode is applied in hard rock strata, including classes II, III, and IV, with the jamming accident occurring in class II surrounding rock. The jamming probability varies during excavation in different classes of surrounding rock, as illustrated in Fig. 8. Rock class is directly related to its strength, with the following hierarchy: Class Ⅱ > Class Ⅲ > Class Ⅳ in terms of strength. The wear rate of disc cutters increases with rock strength37, and excessive wear can lead to abnormal conditions or even jamming accidents.

Fig. 8
figure 8

Average calculated jamming probability under different rock class via model.

Full size image

From Fig. 8, it is evident that the average jamming probability in class II surrounding rock is approximately 3% higher than in classes III and IV. Even after excluding data from the jamming section, the average jamming probability in class II remains about 0.5% higher than in classes III and IV. Additionally, the average probability in class IV is 0.02% higher than in class III, likely due to the higher prevalence of weak and fractured rock masses in lower-strength rocks, which increase the likelihood of jamming accidents. Thus, class III rock is identified as the most suitable stratum for excavation. It effectively reduces jamming probability and minimizes disc cutter wear rates, thereby enhancing overall excavation efficiency.

Practical application in TBM operations

Our comprehensive Bayesian statistical framework demonstrates significant improvements in jamming risk assessment. The comprehensive jamming perception index η achieves a 95% recognition rate, significantly higher than single-parameter models. The refined jamming probability model, which accounts for sample size differences, provides more accurate estimates of jamming probability, with an average of 94% in jamming sections and 7% in normal excavation sections. These results highlight the effectiveness of our proposed framework. In practical TBM operations, our model can be used in real-time to assist engineers in risk assessment and decision-making:

  1. (1)

    Real-time Data Monitoring The model calculates the comprehensive jamming perception index η and jamming probability R2 in real-time based on monitoring data. Engineers can obtain these indicators through the TBM control system to promptly understand the current jamming risk.

  2. (2)

    Early Warning System Integration: The model can be integrated into the TBM’s early warning system. When the jamming probability exceeds a preset threshold, the system can automatically trigger an alarm to alert engineers to take appropriate measures.

  3. (3)

    Decision Support: The quantitative risk assessment provided by the model helps engineers make more informed decisions. For example, if the jamming probability is high, engineers can adjust the TBM operating parameters or take preventive measures.

  4. (4)

    Construction Plan Optimization: By analyzing the jamming risk under different geological conditions, engineers can optimize the construction plan and choose safer construction routes and methods.

Conclusions

This study presents a comprehensive Bayesian statistical framework for TBM jamming risk assessment, which effectively enhances the accuracy and reliability of jamming risk assessment through a comprehensive multi-parameter jamming perception index η and a jamming probability model that accounts for sample size differences. The main conclusions are as follows:

  1. (1)

    By introducing the comprehensive jamming perception index η, we overcame the limitations of single-parameter analysis and significantly improved the recognition rate of jamming states. The experimental results show that the recognition rate of η reaches 95%, which is much higher than that of single-parameter models. This demonstrates the significant advantages of multi-parameter integrated assessment in jamming risk assessment.

  2. (2)

    By developing a new jamming probability model R2 that accounts for the differences in sample sizes between jamming and normal excavation samples, we made the model more practical and accurate in real applications. In actual jamming accidents, the average jamming probability in jamming sections is 94%, and in normal excavation sections, it is 7%. This indicates that considering sample size differences is crucial for improving model performance.

  3. (3)

    Through geological analysis, we found that Class III surrounding rock is the most suitable stratum for excavation, with the lowest jamming probability. This finding highlights the importance of considering geological conditions in excavation planning to effectively reduce jamming risks and improve construction efficiency.

  4. (4)

    Our Bayesian statistical method not only provides a clear decision-making process and the contribution of each factor to the risk results but also quantitatively offers the probability of jamming events. This quantitative assessment capability is crucial for site managers, as it can provide them with more specific and reliable references for their decision-making.

Although this study has yielded valuable findings regarding the TBM jamming risk assessment, several aspects still warrant further investigation. Future work will focus on the following priorities: First, we will collect additional independent datasets to verify the model’s applicability and generalizability across diverse geological conditions and engineering scenarios. Second, we will conduct further optimization of the model to enhance its performance in addressing imbalanced data and adapting to complex geological environments.