Machine learning-assisted thermal analysis of propylene glycol nanofluid with dual flux and bioconvection over a Riga plate

Abstract

The current study investigates the behavior of non-Newtonian nanofluids with Cattaneo-Christov dual flux by using various effects of different physical parameters over a Riga plate. Nanoparticles significantly increase the heat transfer rate and serve as powerful tools for improving energy storage devices and solar thermal systems. The novelty of the current research study is the mixing of copper nanoparticles (Cu) in the propylene glycol. (C₃H₈O₂) has highly thermodynamic properties. The main objective of the present analysis is to enhance the rate of heat and mass transfer in the nanofluid. Therefore, the Cattaneo-Christov model was used in the heat and mass equations to increase the heat transfer rate of the fluid model. The PDE system of the problem is converted into an ODE system using suitable transformations. The solution to the mathematical problem was obtained by applying the bvp4c technique of MATLAB. The graphical results represent the physical properties of the nanofluid, including the bioconvection, concentration, temperature, and velocity profiles. Furthermore, tables were used to compute the numerical values of motile microorganisms, Sherwood number, Nusselt number, and skin friction coefficient. Boosting the parameters, such as the modified Hartmann number, buoyancy ratio, and Rayleigh number, of bio-convection increases the velocity profile. The temperature profile increased as the thermophoresis parameter, heat relaxation time parameter, and Eckert number increased. Additionally, this study uses an intelligent numerical computing method known as MLFF, which is based on ANN. These artificial neural networks are used to optimize physical quantities and verify the accuracy of data by training, validation, and testing.

Introduction

Nanofluids utilize the specific properties of nanoparticles to improve the thermal properties of the fluids. Magnetohydrodynamics influences fluid flow in many industries and engineering sectors, including power sources, cooling liquid sheets for nuclear reactors, flow gauges, and oilfield technology. Electromagnetic body forces can impact fluid flow, which conducts electricity, and control the motion of the fluid at the boundary layer. The magnetic field of outer space, approximately 1 Tesla, can alter fluids with high electrical conductivity. The electrical current produced by an external magnetic field is insufficient for fluids with weak conductivity. An external electric field must exist to produce a wall-parallel Lorentz force, which enables efficient flow regulation.

Jawad et al.¹ evaluated the numerical solutions of the heat radiative flow of tangent hyperbolic nanofluid across a Riga plate. The behavior of the flow under the parameters of Brownian motion and chemical reaction was observed for the current physical problem. Furthermore, the ND solver tool in Wolfram Mathematica 11 was used to solve the highly nonlinear ODEs and compare the results with those in the existing literature. This study suggested that when the power-law index m and magnetic parameter M increased, the fluid velocity decreased. Abbas et al.² observed the behavior of a nanofluid having time-dependent viscosity across the Riga plate. This investigation aims to identify heat transfer enhancements that exceed those of hybrid nanofluids as compared to nanofluids. In addition, the heat transfer properties and modified nanofluids exhibited dynamic behavior that deserves further research. It is feasible to produce more energy in the form of heat by dispersing it with heat rather than using a mixture of nanoparticles. Rafique et al.³ investigated dynamic laminar flow for micropolar nanofluid across a Riga plate. This study analyzed the physical flow behavior of micro-rotational flow using various parameters. Additionally, it is crucial to examine how double stratification affects the flow in energy and mass transfer phenomena. Mixed convection in a double-stratified medium is a major area of research because of its importance in solar ponds, nuclear power, geophysical flows, and other applications. The current study overcomes these constraints and improves the scientific knowledge of non-Newtonian fluids for real-world applications. Khan et al.⁴ explored the dynamic outcomes for thermal flow with radiation parameters for a micropolar nanofluid. The modified micropolar fluids preserved the viscosity properties and produced results similar to those of second-grade fluids. Furthermore, the solutal concentration of the nanoparticles was predicted using double-diffusive thermal expressions, and convective heat transport constraints were applied to examine the heat transfer analysis. Ouyang et al.⁵ examined the effects of discharge concentration and convective boundary conditions on unsteady hybrid nanofluid flow in a porous medium. The main goal of this study is to improve the existing literature by describing the complex behavior of fluctuating boundary-layer motions above a flow that is close to the stagnation area on a stretched or contracted surface. The current research has practical applications in biomedical engineering, industrial processes such as heat exchangers, filtration systems, catalytic reactors, and environmental engineering. Gupta et al.⁶ analyzed the MHD flow of a rotating micropolar fluid between two plates by using DTM. A porous plate absorbs fluid at a constant suction velocity when subjected to a uniform magnetic field applied perpendicularly to it. The numerical solution of the flow problem was obtained using a semi-analytical technique. The impact of different flow parameters on the flow field was investigated and illustrated using graphs. Gupta⁷ examined the application of DTM to a heat source/sink in the squeezing flow of iron oxide polymer nanofluid between electromagnetic surfaces. Additionally, this study examined the mass and heat transfer problems for Riga plates, which incorporate chemical reactions, heat sources, and sinks. In this study, iron oxide nanoparticles suspended in a fluid made of polymers were used to prepare the nanofluid. This study incorporates tables and graphs that show how different physical characteristics affect the temperature, concentration, and velocity.

Khan et al.⁸ determined the thermal nature of the bioconvection for Eyring Powell nanofluid via a Riga plate. The various parameters of thermal flow, along with boundary conditions, have been employed to compute the energy as well as the mass of the nanofluid. Furthermore, the tabular comparison between the current results and the results from the literature is used in the specific case to show the accuracy of the current numerical scheme. Ultimately, the results of this investigation indicate that the relevant parameters produced a major impact on the boundary layer profiles. Ramasekhar et al.⁹ inspected the thermal behavior of nanofluid with the bioconvected tangent hyperbolic nanofluid flow having activation energy through a Riga plate. This analysis explores the effects of joule heating with activation energy for nanofluids under the motile microorganisms. Furthermore, in specific cases, streamlines are plotted to provide motivation and innovation for the flow problems. The validity of the obtained results has been checked by comparing them with previously published research, and observed a significant level of compatibility has been observed. Khan et al.¹⁰ analyzed the Cattaneo-Christov models along with bio-convection effects over nanofluid flow to boost the diffusion rate of particles. The parameters of heat radiation, as well as activation energy, are taken into account for the present physical problem. Moreover, the novel aspect of the present analysis is the examination of the bio-convective, cross-diffusion flow of a viscous nanofluid with multiple geometries (plate, wedge, and cone) under Cattaneo-Christov heat and mass flux, and the outstanding consistency has been established while the results have been verified. Waqas et al.¹¹ provided the numerical inspection based on the bio-convection flow of tangential hyperbole geometrical structure for nanofluid across a Riga plate. The process of heat convection, along with zero nanoparticle conditions, was utilized to explore the nature of physical quantities. In addition, the bvp4c technique is used to solve the dimensionless equations and compute the numerical solution within the framework of the methodology. The impact of several significant parameters on the profiles of concentration, velocity, temperature, and motile microorganisms are shown graphically. Awan et al.¹² analyzed the bio-convection implications for Williamson nanofluid flowing by exponential radiation as well as motile microorganisms on the stretching surface. This work explores that nanomaterials with outstanding thermal properties have numerous applications in the industrial field. Additionally, the physical characteristics of nanofluids, including temperature, volumetric concentration, fluid velocity, and motile organism profiles, are investigated along with various parameters. The effects of magnetic forces and activation energy are also examined.

Ragupathi et al.¹³ studied the heat source effects on a nanofluid of Fe3O4 /Al2O3 over a Riga plate. The graphs and tables illustrate the effects of different parameters on three-dimensional flow in this study. Furthermore, the physical quantities of interest were calculated in this study. There is good quantitative consistency between the numerical results and the data that have already been collected. Anjum et al.¹⁴ analyzed the effects of heat stratification and slippery conditions on the flow towards a thicker Riga plate. Solar thermal radiation phenomena are used to study the features of thermal flow. Furthermore, this study provides a comprehensive examination of graphical representations of temperature and velocity distributions corresponding to several relevant parameters. Das et al.¹⁵ calculated the behavior for the nuclear rGO-magnetite flow employing a Riga plate. The flow model considers various physical variables to increase the thermal flow of nanofluids. Moreover, the main findings of this study show that the velocity distribution increases with a higher modified Hartmann number and decreases with an increase in the electrode width. The observation that a hybrid nanofluid with fewer graphene nanoparticles transfers more heat in the flow regime is also encouraging. Khashi et al.¹⁶ investigated stagnation point flow with convection towards the vertical Riga plate utilizing a double nanofluid. In addition, the solution was confirmed to be a physical solution by analyzing its flow stability. This study demonstrates that a temporal stability study is necessary to verify the validity of the similarity solutions. Mishra and Kumar¹⁷ studied how the heat generation and absorption, along with viscosity dissipation, affected to Ag-water nanofluid flowing over a Riga plate. Furthermore, the effects of different parameters on the nondimensional temperature, velocity, and concentration profiles are illustrated using tables and graphs. The results of the present study show that as the Prandtl number and suction parameter increase, the modulus of the Nusselt number decreases.

Gupta and Wakif¹⁸ are using the neural network to investigate heat and mass transfer in the flow of nanofluid between two disks. Furthermore, the Dufour and Soret (DS) effects were examined in the energy and concentration equations when a magnetic field was applied vertically over the nanofluid flow. A visual representation and explanation of the impact of the different parameters on each profile are provided. The analysis of the training, testing, and validation processes using the Levenberg–Marquardt artificial neural network (ANN) is a novel aspect of this study. The accuracy of the developed ANN model during the training, validation, and testing phases demonstrated its validity. Gupta¹⁹ utilized an artificial neural network to analyze the heat and mass transfer of a ternary hybrid nanofluid between two parallel plates with an inclined magnetic field. A graphical representation and discussion of the effects of various physical parameters on the temperature, concentration, and velocity are provided. Moreover, the Levenberg–Marquardt algorithm is used in the model to train the neural network, which is innovative in the current study.

The combination of copper (Cu) nanoparticles with the base fluid propylene glycol (C₃H₈O₂) yields superior thermophysical properties, making it suitable for a wide range of industrial applications, particularly in the automobile and pharmaceutical industries. The stability of Cu nanoparticles in propylene glycol ensures long-term usability without significant sedimentation, making the (Cu-C₃H₈O₂) nanofluid an effective medium for advanced fluid dynamics and heat transfer applications.

The novelty of this study lies in incorporating a Riga plate and Cattaneo-Christov dual flux into the analysis of (Cu-C₃H₈O₂) nanofluid flow, an approach that has not been previously explored in the literature. The Riga plate enhances fluid dynamics by coupling electric and magnetic fields, whereas the Cattaneo–Christov model refines the heat transfer representation. Using similarity transformations, the governing PDEs were reduced to ODEs and solved numerically using the MATLAB bvp4c solver.

Traditionally, researchers have faced significant computational challenges and numerical errors in complex flow problems. To address this gap, the present study integrated artificial neural networks (ANNs) for optimization, ensuring data accuracy through training, testing, and validation. This approach enhances the reliability and provides a strong foundation for future experimental investigations. The insight research questions that are addressed in this work are:

• How do (Ha, $N_{r}$, $N_{c}$) influence velocity and skin friction in (Cu-C₃H₈O₂ nanofluid flow?

• Which parameters most significantly enhance heat and mass transfer?

• What is the effect of Copper nanoparticles in propylene glycol?

• Can ANN accurately predict physical quantities with minimal error compared to bvp4c?

Problem formulation

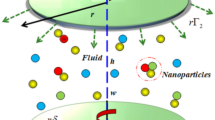
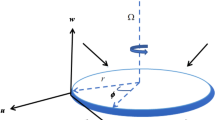
Assume a viscoelastic, incompressible, and two-dimensional (Cu-C₃H₈O₂) nanofluid that flows through a Riga plate. Here, (u, v) indicate velocity components in the x and y directions, while the x-axis represents the surface of the sheet and the y-axis is perpendicular to it. The Riga plate stimulates a magnetic field that generates a parallel Lorentz force. The nanofluid that flows above the plate is taken linearly if b > 0 is constant. Let $T_{m}$ and $C_{m}$ represent the ambient temperature and concentration of the nanofluid. Figure 1 shows the geometrical structure of the Riga plate. The Riga plate utilizes a combination of magnetic and electric fields to govern the boundary layer flow on a surface. The velocity vector u indicates that the nanofluid flows along the x-direction, and the plate lies in the x–z plane. The direction of the boundary layer growth is indicated along the y-direction, which is perpendicular to the plate. The north (N) and south (S) poles of the magnets were arranged alternately in the z-direction. The interaction between the electric and magnetic fields in this arrangement produces a Lorentz force (F), given by Fig. (1) represents an efficient flow for the current nanofluid model. Table 1 lists the thermophysical properties of the nanoparticles and base fluid, and Table 2 presents the thermophysical characteristics of the nanofluids. The governing equations are given as^12,17

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$

(1)

$$\begin{gathered} u\frac{\partial u}{{\partial x}} + v\frac{\partial v}{{\partial y}} = b^{2} x + \frac{1}{{\rho_{bf} }}\left[ {((1 - C_{\infty } )\rho_{bf\infty } } \right.\beta (T - T_{\infty } )g) - ((\rho_{sf} - \rho_{nf\infty } )(C - C_{\infty } )g \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left. {((\rho_{m} - \rho_{p} )(N_{\infty } - N)g\gamma^{ * } )} \right] + \frac{{\mu_{nf} }}{{\rho_{nf} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\pi J_{0} M_{0} }}{{8\rho_{nf} }}e^{{ - \left( {\frac{\pi }{\rho }} \right)y}} , \hfill \\ \end{gathered}$$

(2)

$$\begin{gathered} u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} + \lambda_{T} \Omega_{T} = \, \alpha_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \, \tau \left[ {D_{B} \frac{\partial T}{{\partial y}}\frac{\partial C}{{\partial y}} + \, \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right] + \, \frac{{Q_{ \circ } \left( {T - T_{\infty } } \right)}}{{\left( {\rho C_{p} } \right)_{nf} }} \hfill \\ + \, \frac{{\mu_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \, \frac{{Q_{ \circ } }}{{\rho C_{p} }}\lambda_{T} \left( {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right), \hfill \\ \end{gathered}$$

(3)

$$u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} + \lambda_{C} \Omega_{C} = {\text{ D}}_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \, \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \, \lambda_{C} \left( {u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}}} \right),$$

(4)

$$v\frac{\partial N}{{\partial y}} + u\frac{\partial N}{{\partial x}} = D_{m} \frac{{\partial^{2} N}}{{\partial y^{2} }} + \frac{{bw_{c} }}{{\left( {C_{\infty } - C_{w} } \right)}}\frac{\partial }{\partial y}\left( {N\frac{\partial C}{{\partial y}}} \right),$$

(5)

where

$$\begin{gathered} \left\{ \begin{gathered} \Omega_{T} = u\frac{\partial u}{{\partial x}}\frac{\partial T}{{\partial x}} + v\frac{\partial v}{{\partial y}}\frac{\partial T}{{\partial y}} + u^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} T}}{\partial x\partial y} + u\frac{\partial v}{{\partial x}}\frac{\partial T}{{\partial y}} + v\frac{\partial u}{{\partial y}}\frac{\partial T}{{\partial x}}, \hfill \\ \Omega_{C} = u\frac{\partial u}{{\partial x}}\frac{\partial C}{{\partial x}} + v\frac{\partial v}{{\partial y}}\frac{\partial C}{{\partial y}} + u^{2} \frac{{\partial^{2} C}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} C}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} C}}{\partial x\partial y} + u\frac{\partial v}{{\partial x}}\frac{\partial C}{{\partial y}} + v\frac{\partial u}{{\partial y}}\frac{\partial C}{{\partial x}}. \hfill \\ \end{gathered} \right\}. \hfill \\ \hfill \\ \end{gathered}$$

Fig. 1

Geometrical representation of the problem¹⁷.

Table 1 Thermophysical properties for propylene glycol and solid particles.

Table 2 Thermophysical properties for nanofluid.

Here, T and C represent the temperature and concentration of the nanofluid, $D_{T}$ and $D_{B}$ are the coefficients of thermophoresis and Brownian motion parameter, $M_{0}$ represents the magnetization of the magnet, $J_{0}$ is the current density, $\beta$ used as the thermal expansion constant, $Q_{0}$ the coefficient of heat generation/absorption parameter, $D_{m}$ is the bio-convection coefficient, N denotes the motile microorganisms, $\Omega_{T}$ and $\Omega_{C}$ represents the Cattaneo-Christov heat and mass flux.

Boundary conditions and similarity transformations are given as^12,17.

$$\left\{ \begin{gathered} u = 0,{\text{ v = v}}_{w} , \, - \frac{\partial T}{{\partial y}} = \, \frac{{h_{bf} }}{{k_{bf} }}\left( {T_{bf} - T} \right),{\text{ D}}_{B} \frac{\partial C}{{\partial y}} + \, \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{{\partial y}} = {\text{ 0, N}}_{W} {\text{ = N at y = 0}} \hfill \\ {\text{u}} \to {\text{u}}_{\infty } \left( x \right) = {\text{ bx, T}} \to {\text{T}}_{\infty ,} {\text{ C}} \to {\text{C}}_{\infty } {\text{, N}} \to {\text{N}}_{\infty } {\text{ at y}} \to \infty \hfill \\ \end{gathered} \right\},$$

(6)

$$\left\{ \begin{gathered} u = bxf{\prime} \left( \eta \right),{\text{ v = }} - \sqrt {b\nu_{bf} } f\left( \eta \right), \, \eta = {\text{ y}}\sqrt {\frac{b}{{\nu_{bf} }}} , \, \hfill \\ \chi \left( \eta \right) = \, \frac{{N_{\infty } - N}}{{N_{\infty } - N_{w} }}, \, \theta \left( \eta \right) = \, \frac{{T - T_{\infty } }}{{T_{bf} - T_{\infty } }}, \, \varphi \left( \eta \right) = \, \frac{{C - C_{\infty } }}{{C_{\infty } }} \hfill \\ \hfill \\ \end{gathered} \right\}.$$

(7)

Using Eqs. (6) and (7) into Eqs. (2–5), we get

$$\frac{1}{{A_{2} \left( {1 - \phi } \right)^{2.5} }}f^{{\prime\prime\prime}} - ff{\prime} - f^{{{{\prime}{2}} }} + \left( { \, \frac{\theta }{{A_{2} }} - \, \frac{{N_{r} \varphi }}{{A_{2} }} + N_{c} \chi } \right)\lambda + \, \frac{{{\text{Hae}}^{ - d\eta } }}{{A_{2} }} + {1 = 0},$$

(8)

$$\theta^{^{\prime\prime}} + \left[ {1 - \phi + \phi \frac{{\left( {\rho C_{p} } \right)_{sp} }}{{\left( {\rho C_{p} } \right)_{nf} }}} \right]\left( {N_{b} \theta{\prime} + {\text{ N}}_{t} \theta^{{^{{\prime}{2}} }} - \Gamma_{1} \theta \theta{\prime} - f\theta{\prime} - \Gamma_{1} ff{\prime} \theta{\prime} + Q\theta + Ecf^{{^{{\prime\prime}{2}} }} } \right)\frac{\Pr }{{A_{4} }} = 0,$$

(9)

$$\varphi^{^{\prime\prime}} - \left( {f\varphi{\prime} + \Gamma_{2} ff{\prime} \varphi{\prime} + \Gamma_{2} f\varphi{\prime} } \right)Sc + \frac{{N_{t} }}{{N_{b} }}\theta^{^{\prime\prime}} = 0,$$

(10)

$$\chi^{\prime} + Lbf\chi^{\prime} - \left[ {\left( {\varpi + \chi } \right)\phi^{\prime} + \phi^{\prime}\chi^{\prime}} \right]pe = 0,$$

(11)

where, (Ha) represents the modified Hartmann number, ($N_{r}$) is the buoyancy ratio parameter, ($N_{c}$) is used as the Rayleigh number of bio convection, ($\lambda$) as mixed convection parameter, ($A_{2}$) denotes the thermophysical property, and (d) is the thickness of electrodes and magnets, ($N_{b}$) represents the Brownian motion parameter, ($N_{t}$) denotes the thermophoresis parameter, ($\Gamma_{1}$) is used as a heat relaxation parameter, (Q) is the heat generation/absorption parameter, (Ec) represents the Eckert number, and ($\Pr$) denotes the Prandtl number, ($\Gamma_{2}$) represents the mass relaxation parameter, and (Sc) denotes the Schmidt number, (Lb) represents the Lewis number, ($\varpi$) is the bio-convection constant, and (Pe) denotes the Peclet number.

Converted boundary conditions are provided as

$$\left\{ \begin{gathered} f\left( \eta \right) = S, \, f{\prime} \left( \eta \right) = 0, \, \theta{\prime} \left( \eta \right) = - Bi\left[ {1 - \theta \left( \eta \right)} \right], \, \hfill \\ \varphi{\prime} \left( \eta \right) + \frac{{N_{t} }}{{N_{b} }}\theta{\prime} = 0, \, \chi {\text{ = 1 at }}\eta { = 0} \hfill \\ \end{gathered} \right\},$$

(12)

$$f^{\prime}\left( \eta \right) = 1,\,\,\,\theta \left( \eta \right) = 0,\,\,\,\phi \left( \eta \right) = 0,\,\,\,\chi = 0\,\,\,{\text{at }}\eta \to \infty ,$$

(13)

where

$$\left[ \begin{gathered} A_{1} = \, \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}, \hfill \\ \, A_{2} { = }\left( {1 - \phi + \phi \frac{{\rho_{sp} }}{{\rho_{bf} }}} \right), \, \hfill \\ A_{3} { = }\left\{ {1 - \phi + \phi \frac{{\left( {\rho C_{p} } \right)_{sp} }}{{\left( {\rho C_{p} } \right)_{bf} }}} \right\}, \, \hfill \\ A_{4} { = }\frac{{k_{nf} }}{{k_{bf} }}. \hfill \\ \end{gathered} \right].$$

Various physical quantities as skin friction, Nusselt number, Sherwood number, and motile micro-organism, are given below

$$\left[ \begin{gathered} {\text{Re}}_{x}^{0.5} C_{f} = \, \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}f^{^{\prime\prime}} \left( 0 \right), \hfill \\ {\text{Re}}_{x}^{ - 0.5} Nu_{x} = - \frac{{k_{nf} }}{{k_{bf} }}\theta{\prime} \left( 0 \right), \hfill \\ Sh_{x} = - {\text{Re}}_{x}^{0.5} \varphi{\prime} \left( 0 \right), \hfill \\ Nh_{x} = - {\text{Re}}_{x}^{0.5} \chi{\prime} \left( 0 \right). \hfill \\ \end{gathered} \right].$$

(14)

Physical parameters

The above dimensionless ODEs, with the boundary conditions, are derived by employing different parameters such as $\lambda = \, \frac{{g{\prime} \beta{\prime} \left( {1 - C_{\infty } } \right)\left( {T_{bf} - T_{\infty } } \right)}}{{ab^{2} x^{2} }}$ used as a mixed convection parameter, $N_{r} = \, \frac{{\left( {\rho_{p} - \rho_{bf\infty } } \right)\left( {C_{\omega } - C_{\infty } } \right)C_{\infty } }}{{\rho_{bf} \beta \left( {1 - C_{\infty } } \right)\left( {T_{bf} - T_{\infty } } \right)}}$ as buoyancy ratio parameter, $Ha = \, \frac{{\pi M_{ \circ } J_{ \circ } }}{{8\rho_{bf} b^{2} x}}$ as modified Hartmann number, $d = \frac{\pi }{p}\sqrt {\frac{{\nu_{bf} }}{b}}$ as the thickness of the electrodes and magnets, $N_{t} = \, \frac{{\tau D_{T} \left( {T_{bf} - T_{\infty } } \right)}}{{\nu_{bf} T_{\infty } }}$ as a thermophoresis parameter, $Q = \, \frac{{Q_{ \circ } x}}{{u_{\infty } \left( {\rho C_{p} } \right)_{bf} }}$ as a heat generation/absorption parameter, $N_{b} = \, \frac{{\tau D_{B} C_{\infty } }}{{\nu_{bf} }}$ as Brownian motion parameter, ${\text{Ec = }}\frac{{\left( {bx} \right)^{2} }}{{\left( {C_{p} } \right)_{bf} \left( {T_{bf} - T_{\infty } } \right)}}$ as the Eckert number, $S = \, \frac{{ - v_{w} }}{{x\sqrt {b\nu_{bf} } }}$ as a suction parameter, $Bi = \, \sqrt {\frac{{\nu_{bf} }}{b}} \frac{{h_{bf} }}{{k_{bf} }}$ as Biot number, $\Gamma_{1} = \lambda_{T} a$ as a heat relaxation time parameter, $\Pr = \, \frac{{\nu_{bf} }}{{\alpha_{bf} }}$ as Prandtl number, ${\text{Sc = }}\frac{{\nu_{bf} }}{{D_{B} }}$ as Schmit number, $\Gamma_{2} = \lambda_{c} a$ as a mass relaxation time parameter, $Lb = \frac{v}{{D_{m} }}$ as the bio-convection Lewis number, $Pe = \frac{{bw_{c} }}{{D_{B} }}$ as Peclet number, $\varpi { = }\frac{{N_{\infty } }}{{N_{\omega } - N_{\infty } }}$ as a non-dimensional bioconvection parameter.

Solution for the flow problem

BVP4C technique

In this section, the MATLAB bvp4c technique is employed to numerically solve the dimensionless momentum Eq. (8), the energy Eq. (9), the concentration Eq. (10), and the bioconvection Eq. (11), along with the transformed boundary conditions (12, 13). Now, a new variable ($Y_{i = 1 - 9}$) taking into account, and replace with the derivatives of different functions such as ($f,\theta ,\phi ,\chi$). Here $(Y_{i} = Y_{1} ,Y_{2} ,...,Y_{9} )$ given as

$$\left[ \begin{gathered} Y_{1} = f, \, \hfill \\ Y_{2} = f^{\prime} , \, \hfill \\ Y_{3} = f^{{\prime\prime}} , \, \hfill \\ Y_{3}^{\prime} = f^{{\prime\prime\prime}} , \hfill \\ Y_{4} = \theta , \, \hfill \\ Y_{5} = \theta^{\prime} , \, \hfill \\ Y_{5}^{\prime} = \theta^{{\prime\prime}} , \hfill \\ Y_{6} = \varphi , \, \hfill \\ Y_{7} = \varphi^{\prime} , \, \hfill \\ Y_{7}^{\prime} = \varphi^{{\prime\prime}} , \hfill \\ Y_{8} = \chi , \, \hfill \\ Y_{9} = \chi^{\prime} , \, \hfill \\ Y_{9}^{\prime} = \chi^{{\prime\prime}} . \hfill \\ \end{gathered} \right].$$

(15)

By introducing a new variable $Y_{i = 1 - 9}$ to represent each derivative, the entire system of higher-order differential equations is transformed into a system of first-order ordinary differential equations, which simplifies the numerical solution process. The resulting first-order ODE system is given below. This system describes the fluid flow model, heat transfer process, nanoparticles concentration, and bio-convection phenomena.

$$\left[ \begin{gathered} Y_{3}{\prime} = {\text{ A}}_{2} \left( {1 - \phi } \right)^{2.5} \left\{ {y_{1} y_{2} + y_{2}^{2} - \frac{\lambda \theta }{{{\text{A}}_{2} }} + \frac{{N_{r} \lambda \varphi }}{{{\text{A}}_{2} }} - N_{c} \lambda \chi - \frac{{Hae^{ - d\eta } }}{{{\text{A}}_{2} }} - 1} \right\}, \hfill \\ Y_{5}{\prime} = \, - \left\{ {1 - \phi + \phi \frac{{\left( {\rho C_{p} } \right)_{sp} }}{{\left( {\rho C_{p} } \right)_{nf} }}} \right\}\left( {N_{b} y_{5} + N_{t} y_{5}^{2} - \Gamma_{1} y_{1} y_{4} y_{5} - fy_{5} - \Gamma_{1} y_{1} y_{2} y_{5} + Qy_{4} + Ecy_{3}^{2} } \right)\frac{\Pr }{{{\text{A}}_{4} }}, \hfill \\ Y_{7}{\prime} = \, \left( {y_{7} + \, \Gamma_{2} y_{1} y_{2} y_{7} { + }\Gamma_{2} y_{1} y_{7} } \right)Sc - \frac{{N_{t} }}{{N_{b} }}y_{1} y_{2} , \hfill \\ Y_{9}{\prime} = \, \left\{ {\left( {\omega + \chi } \right)y_{1} y_{3} + y_{7} y_{9} } \right\}Pe - Lbfy_{9} , \hfill \\ \end{gathered} \right]$$

(16)

The first-order boundary conditions for numerically solving the aforementioned ODE system are as follows:

$$\left[ \begin{gathered} Y_{1} \left( \eta \right) = S, \, Y_{2} \left( \eta \right) = 0, \, Y_{5} \left( \eta \right) = - Bi\left\{ {1 - Y_{4} \left( \eta \right)} \right\}, \, \hfill \\ \, Y_{7} \left( \eta \right) + \frac{{N_{t} }}{{N_{b} }}Y_{5} = 0, \, Y_{8} {\text{ = 1 at }}\eta { = 0}{\text{.}} \hfill \\ \end{gathered} \right],$$

(17)

$$\left[ {Y_{2} \left( \eta \right) = 1, \, Y_{4} \left( \eta \right) = 0, \, Y_{6} \left( \eta \right) = 0, \, Y_{8} { = 0 }at \, \eta \to \infty } \right].$$

(18)

Now, we apply the MATLAB bvp4c technique for producing graphical representations of the different physical parameters from the first-order ODE system, along with the boundary conditions.

Comparative analysis

Figure 2 compares the Sherwood number predicted in the present study with those from three previously published studies. The trends show that increasing Sc raises the Sherwood number owing to decreased mass diffusivity, which aligns well with the findings of Gupta and Wakif¹⁸, Mishra and Kumar¹⁷, and Anjum et al.¹⁴. The close match between our numerical results and these benchmark studies confirms the accuracy of our bvp4c computations and validates the ANN-based predictions. The minor deviations at higher Sc values can be attributed to the wider parameter range in the present analysis, which offers a broader understanding of the mass transfer behavior of nanofluids.

Fig. 2

Comparison of Sherwood number with previous studies.

Results and discussion

This section provides velocity, temperature, concentration, and bio-convection profiles for various parameter values named as modified Hartmann number (Ha), buoyancy ratio ($N_{r}$), Rayleigh number of bio convections ($N_{c}$), thickness effects of electrodes and magnets (d), Prandtl number (Pr), thermophoresis parameter ($N_{t}$), heat relaxation time parameter ($\Gamma_{1}$), Eckert number (Ec), heat generation/absorption (Q), Brownian motion ($N_{b}$), mass relaxation time ($\Gamma_{2}$), Schmidt number (Sc), Peclet number (Pe), and Lewis number (Lb).

Velocity profile

Figure 3 shows the effect of the modified Hartmann number (Ha) on the fluid velocity profile. The graph indicates clearly that increasing (Ha) increases fluid velocity. The fluid velocity increased when the modified Hartmann number increased because of the effect of the magnetic field on the electrically conducting fluid. An increase in the modified Hartmann number corresponds to a decrease in the boundary layer resistance, causing the fluid to flow more rapidly. Furthermore, an increase in (Ha) indicates a decrease in the opposing Lorentz force in certain regions, causing the fluid velocity profile to increase. Figure 4 shows the effect of the parameter of the buoyancy ratio ($N_{r}$) on the fluid velocity profile. It can be observed that the fluid velocity is enhanced when ($N_{r}$) increases. The increased buoyancy ratio parameter indicates a more efficient heat transfer due to greater convective currents. This enhanced heat transfer may cause stronger fluid movements, which increases the velocity profile. Additionally, as increases, the contribution of the solutal buoyancy force becomes more significant, leading to a stronger overall buoyancy-driven flow. This additional buoyancy force acts in the direction of thermal buoyancy, thereby accelerating the fluid motion. Consequently, the convective motion within the boundary layer became more perceptible, enhancing the fluid velocity.

Fig. 3

Change in velocity profile over Ha.

Fig. 4

Change in velocity profile over $N_{r}$.

Figure 5 shows the effect of the Rayleigh number ($N_{c}$) on the fluid velocity profile. It can be observed that as ($N_{c}$) increases, the fluid velocity increases. As the Rayleigh number increases, the buoyancy forces take precedence over the viscous and diffusive effects, forcing the fluid to move faster and resulting in a more distinct velocity distribution. Moreover, as the Rayleigh number increases, the temperature gradient of the fluid becomes more significant, causing the colder, denser fluid to fall and the hotter, lighter fluid to rise rapidly. As a consequence of this improved transportation, convective currents have become stronger and fluid velocities have increased.

Fig. 5

Change in velocity profile over $N_{c}$.

Figure 6 represents the thickness effects of electrodes and magnets (d) over the velocity profile. The graphical representation shows that the velocity of the fluid decreased when (d) increased. Increasing the thickness of the electrodes and magnets often decreases the velocity profile in the fluid because of the higher magnetic field intensity and Lorentz forces opposing the fluid motion. In addition, the magnetic field intensity inside the flow region becomes stronger and more consistent as the electrode and magnet thicknesses increase. When the electrically conducting fluid interacts with this stronger magnetic field, a stronger Lorentz force is created, which acts against the fluid’s velocity. Consequently, the fluid flow decreased owing to this electromagnetic restraining effect.

Fig. 6

Change in velocity profile over d.

Temperature profile

Figure 7 illustrates the effect of the Prandtl number (Pr) on the nanofluid temperature profile. As Pr increases, the fluid temperature decreases. This occurs because higher Prandtl numbers (Pr) reduce thermal diffusivity relative to momentum diffusivity, causing the thermal boundary layer to thin and creating a sharper temperature gradient near the surface. Consequently, fluids with high Prandtl numbers (Pr) transfer momentum more effectively than heat, resulting in a thicker velocity boundary layer compared to the thermal boundary layer. Reduced thermal diffusion also slows heat penetration into the fluid, causing temperature to drop rapidly away from the heated surface.

Fig. 7

Change in temperature profile over Pr.

Figure 8 presents the influence of the thermophoresis parameter ($N_{t}$) on fluid temperature. The results indicate that as the parameter increases, fluid temperature rises. Larger thermophoresis ($N_{t}$) values enhance particle movement due to temperature gradients, increasing thermal energy transport and raising fluid temperature. More particles migrate from the heated surface into the cooler fluid, thickening the thermal boundary layer and reducing local cooling. This leads to an overall rise in temperature distribution and an increased temperature profile within the fluid.

Fig. 8

Change in temperature profile over $N_{t}$.

Figure 9 represents the impacts of heat relaxation ($\Gamma_{1}$) in the temperature profile. The graph clearly shows that when ($\Gamma_{1}$) enhances, then the temperature goes up. When the heat relaxation time parameter increases, the heat flux’s reaction to a temperature gradient slows down.

Fig. 9

Change in temperature profile over $\Gamma_{1}$.

Moreover, the surrounding temperature of the fluid rises as a result of this accumulation. In consequence of this, a greater heat relaxation value indicates more thermal resistance, which causes the fluid to preserve heat for a longer period of time and raises the temperature in the flow field. Instead of heat being quickly transported away (as in Fourier’s law), there is a delay. This delay causes heat to accumulate locally in specific regions and as a result, temperature increases.

Figure 10 exhibits the impacts of the Eckert number (Ec) for temperature. The graph shows that as (Ec) increases, the fluid temperature rises. As the Eckert number goes up, more kinetic energy of particles is converted to heat energy through viscous dissipation, causing the fluid temperature to rise. Further, this process occurs when some of the mechanical energy is transformed into heat by the friction between fluid layers, raising the temperature. Figure 11 indicates the impacts of heat generation and absorption parameter (Q) on the temperature profile of the fluid. The graph indicates that when (Q) goes up, the temperature profile shows a decline. When (Q) increases, the temperature gradients become slow, which produces a uniform temperature distribution, and reduces the heat flow. This can cause the temperature of initially hot regions to drop as the system distributes the heat more uniformly over time, resulting in an overall reduction in fluid temperature. In addition, in a fluid flow system, heat absorption has a greater influence than generation. Therefore, when the parameters for heat generation and absorption rise, the fluid temperature falls.

Fig. 10

Change in temperature profile over Ec.

Fig. 11

Change in temperature profile over Q.

Concentration profile

Figure 12 depicts the variation in concentration due to the thermophoresis parameter ($N_{t}$) of the fluid. According to the graph, the fluid concentration rises as ($N_{t}$) goes up. The greater values of ($N_{t}$) enhance particle movement to cooler regions, causing the fluid concentration to increase where the particles assemble. Moreover, when $N_{t}$ increases, it produces a stronger thermophoretic force acting on the particles of fluid. This force causes more particles to be moved toward the cooler area from the hot area, accumulating particles and raising the concentration in the fluid’s cooler areas.

Fig. 12

Change in concentration profile over $N_{t}$.

Figure 13 indicates that the Brownian motion ($N_{b}$) affects the concentration of fluid. The graph shows that when ($N_{b}$) increases, the fluid concentration declines. A higher value of ($N_{b}$) generates more random dispersion of particles throughout the fluid, reducing the possibility of particle accumulation in any particular region and hence diminishing the concentration. Consequently, local concentration gradients are reduced as nanoparticles disperse more rapidly and uniformly throughout the fluid. The overall concentration at certain locations within the domain decreases as a result of this greater dispersion, which reduces the accumulation of particles in any particular region.

Fig. 13

Change in concentration profile over $N_{b}$.

Figure 14 visualizes the effects of the parameter of mass relaxation ($\Gamma_{2}$) in the concentration profile of the fluid. The graph demonstrates that when ($\Gamma_{2}$) increases, the fluid is more concentrated. An increase in mass relaxation time indicates that the diffusion process, which spreads particles out and reduces concentration gradients, is slower. As a result, particles are unable to disperse rapidly resulting in larger concentrations in specific regions of fluid. In addition, the fluid concentration tends to rise as the mass relaxation parameter rises because it relates to how long it takes the mass diffusion process to react to variations in the concentration gradient.

Fig. 14

Change in concentration profile over $\Gamma_{2}$.

Figure 15 demonstrates how the Schmit number (Sc) affects the concentration profile of the fluid. The graph shows that as (Sc) increases, the fluid’s concentration goes up. When (Sc) goes up, the mass diffusivity (D) falls as compared to the momentum diffusivity. Lower mass diffusivity shows that particles of the fluid are less likely to spread or diffuse through it, causing the fluid concentration to rise. Furthermore, the greater Schmidt number indicates that momentum diffuses more efficiently than mass, indicating that the fluid’s viscosity is dominant over its mass diffusivity. As a result, solute particle dispersion is decreased and mass transfer slows down, and the overall fluid concentration increases.

Fig. 15

Change in concentration profile over Sc.

Bioconvection profile

Figure 16 shows the influence of Lewis number (Lb) on the bioconvection profile of the fluid. The graphical structure represents that when (Lb) increases, the bioconvection profile declines, and the greater (Lb) decreases the bioconvection because it improves chemical species diffusion compared to momentum diffusion, decreasing the concentration gradients and density differences that cause bioconvection. Additionally, the higher Lewis number implies that heat diffuses more rapidly than the solute particles or motile microorganisms for bioconvection. Consequently, the fluid motion caused by the collective movement of microorganisms becomes less turbulent, leading to a decrease in the overall bioconvection profile. Figure 17 represents how the Peclet number (Pe) affects the bioconvection profile of the fluid. The graph shows that when (Pe) goes up, the bioconvection profile of fluid decreases. Greater values of (Pe) result in lower concentration gradients and diminish the convection currents that promote bioconversion. As a result, the microorganisms tend to accumulate in certain regions rather than forming strong, uniform upward movement patterns that contribute to bioconvection. This reduces the overall bioconvection profile because the fluid becomes more homogenized and less susceptible to the density-driven fluxes that characterize bioconvection.

Fig. 16

Change in bio-convection profile over Lb.

Fig. 17

Change in bio-convection profile over Pe.

Results and discussion of physical quantities with bvp4c

Skin friction

Figure 18 visualizes the effects of Hartmann number (Ha) on skin friction ($Cf_{x}$). The graph indicates that when (Ha) enhances, then the $Cf_{x}$ rises. The higher quantities of (Ha) will increase the $Cf_{x}$ because the magnetic field raises the velocity of fluid on the boundary of the surface, resulting in a higher shear stress and, hence, increased skin friction. In addition, the Lorentz force acting on the fluid is increased when the modified Hartmann number rises, indicating a larger magnetic field. This force tends to reduce the velocity near the boundary by preventing the fluid from moving perpendicular to the magnetic field lines. Consequently, a more precise velocity gradient forms around the wall, which raises skin friction. Figure 19 represents the impacts of the buoyancy ratio ($N_{r}$) parameter on skin friction $Cf_{x}$. The graph illustrates that when ($N_{r}$) goes up, the skin friction also rises. Further, when ($N_{r}$) rises, the stronger buoyancy flow changes the velocity pattern along the boundary, increasing the velocity gradient and thus increasing shear stress and skin friction on the surface. Furthermore, the higher buoyancy ratio raises the fluid skin friction coefficient by causing stronger wall interactions and more intense convection currents.

Fig. 18

Change in skin friction over Ha.

Fig. 19

Change in skin friction over $N_{r}$.

Nusselt number

Figure 20 shows how the Eckerut number (Ec) affects the Nusselt number ($Nu_{x}$). The graph shows that as (Ec) increases, the Nusselt number declines. The Nusselt number decreases as the (Ec) increases because the greater fluid heating caused by viscous dissipation reduces the temperature differential at the boundary, reducing convective heat transfer. Moreover, an increase in the Eckert number indicates that more mechanical energy is being transformed into internal energy by viscous forces, which raises the temperature of the fluid. This additional internal heating decreases the temperature gradient between the surface and the fluid. Therefore, the efficiency of heat transfer by convection goes down, causing the Nusselt number to decrease. Figure 21 indicates the impacts of the heat relaxation time parameter ($\Gamma_{1}$) for the Nusselt number ($Nu_{x}$). The graph reveals that when ($\Gamma_{1}$) increases, then the Nusselt number declines. The physical reasoning behind this behavior of fluid is that the interruption in heat propagation reduces heat flux and diminishes the temperature on the boundary, reducing the efficiency of convective thermal flow relative to conduction. Additionally, as heat relaxation time increases, the thermal inertia of the fluid becomes more significant, slowing down the heat transfer process. This delay reduces convective heat transfer and lowers the Nusselt number by decreasing the temperature gradient near the heated surface.

Fig. 20

Change in Nusselt number over Ec.

Fig. 21

Change in Nusselt number over $\Gamma_{1}$.

Sherwood number

Figure 22 depicts the variation in the Sherwood number ($Sh_{x}$) by the influence of the Schmit number (Sc). The graph shows that when (Sc) increases, the Sherwood number increases. Higher values of (Sc) demonstrate that the convection property is compulsory for the mass transfer of fluid, causing the Sherwood number to increase. Moreover, the greater Schmidt number indicates that the particles diffuse more slowly because the mass diffusivity is lower than the momentum diffusivity. Consequently, a more precise concentration gradient at the surface occurs due to the concentration boundary layer become thinner, cause the Sherwood number to increases. Figure 23 represents how the mass relaxation time parameter ($\Gamma_{2}$) affects the Sherwood number ($Sh_{x}$). The graph reveals that when ($\Gamma_{2}$) goes up, the Sherwood number increases, which means that greater relaxation time shows slower diffusion. This increases convective transport, increasing Sherwood’s number. Furthermore, an increase in the mass relaxation value indicates that the system is able to deal with rapid fluctuations in mass concentration gradients, resulting in a more stable and steady diffusion process. This stabilization increases the mass transfer efficiency close to the surface and increases the concentration boundary layer overall, and consequently Sherwood number increases.

Fig. 22

Change in Sherwood number over Sc.

Fig. 23

Change in Sherwood number over $\Gamma_{2}$.

Motile number

Figure 24 shows the variation in the motile number ($Nh_{x}$) due to the Peclet number (Pe). The graph indicates that when (Pe) increases, the motile number falls. The motile number rises corresponding to the Peclet number because, as convective transport becomes more significant, the relative influence of motility on overall transport improves. This results in an increased Motile number, indicating that motility is more important when convective effects are substantial. In addition, the relative contribution of microorganism movement to total transport is decreased as (Pe) rises because the effects of motility-driven dispersion are often overshadowed by the strong flow. As a result, the motile number decreases.

Fig. 24

Change in motile organism number over Pe.

Figure 25 indicates the influence of the Lewis number (Lb) on the motile number ($Nh_{x}$). The graph demonstrates that when the (Lb) rises, the motile number goes up, because a greater bioconvection Lewis number enhances the influence of heat diffusivity in comparison to motile organism diffusivity. This increases the convective flows caused by bioconvection, making the organisms’ motility more significant in the overall transport dynamics. Moreover, due to the greater influence of mass transport mechanisms under high Lewis number conditions, the motile number, which measures the contribution of mass diffusion about thermal effects increases.

Fig. 25

Change in motile organism number over Lb.

Artificial neural network (ANN)

Primary information

ANN refers to a mathematical human/animal brain model. The brain of a human is made up of cells that are called neurons. The connection between these neurons generates a neural network. ANN is the recreation of the natural neural network, in which artificial neurons are linked exactly in the pattern of a genuine brain network. Furthermore, a neural network has produced significant developments in various areas of science, including recognizing images, natural language analysis, and automobiles.

Model for flow problem (ANN)

This mathematical model of an ANN receives one or more inputs and sums them to generate a single output. The sum is passed across a non-linear function, named an activation function. Figure 26 represents an artificial neural networking model with input values ${(x}_{1}, {x}_{2}, {x}_{3},\dots , {x}_{n}$) and weights (${w}_{1}, {w}_{2}, {x}_{1}, {w}_{3},\dots , {w}_{n})$. The total weight of the system is multiplied by all input values to obtain the input signal magnitude. A neuron receives numerous signals from its outer area and generates one output.

$$\left[ \begin{gathered} \sum\limits_{i = 1}^{n} {x_{i} } w_{i} = x_{1} w_{1} + x_{2} w_{2} + x_{3} w_{3} + ....x_{n} w_{n} , \hfill \\ y_{output} = f\left( {\sum\limits_{i = 1}^{n} {x_{i} } w_{i} } \right). \hfill \\ \end{gathered} \right].$$

(19)

Fig. 26

ANN model.

Figure 27 illustrates the overall workflow of the proposed methodology. Initially, parameter ranges are selected based on physical relevance and sensitivity analysis. The governing boundary value problem is solved using MATLAB bvp4c to generate velocity, temperature, concentration, and bioconvection profiles. These outputs, along with corresponding physical quantities (skin friction, Nusselt, Sherwood, and motile microorganism numbers), form the dataset for ANN training and testing. The multi-layer feed-forward ANN then predicts the physical responses for various parameter scenarios with high accuracy (R > 0.95), enabling efficient analysis and optimization without repeatedly solving the numerical model.

Fig. 27

Workflow diagram of this study.

ANN multi-layer feed forward method

In ANN, the technique of MLFF represents several hidden layers and different inputs with a single output. The connecting weights of the system give important network information. This network operates similarly in the human brain to enhance the quality of optimization and learning. The complete input equation for the jth hidden neuron’s layer is expressed as

$$y_{j} \left( x \right) = \sum\limits_{i = 1}^{l} {W1_{ji} x_{i} + a_{j} ,}$$

(20)

where, $\left( {x_{i} ,a_{j} } \right)$ symbolize hidden layers, and $x_{i}$ connected to $a_{j}$ through $W1_{ji}$. The network activation function is given as

$$z_{j} \left( x \right) = \frac{1}{{1 + e^{{ - y_{j} \left( x \right)}} }},$$

(21)

The formulation for the output equation is given as

$$O_{k} \left( x \right) = \sum\limits_{j = 1}^{m} {W2_{kj} z_{j} + b_{k} .}$$

(22)

The kth node is linked with the jth node through $W2_{kj}$ and $b_{k}$ used for the output layer. Errors with trials are being implemented to ensure stable learning convergence, hidden layer strength, along with input variables the present study, an Artificial Neural Network based on a multi-layer feed-forward structure was employed to predict the physical quantities obtained from the bvp4c numerical solution. The network consists of one input layer with 3 neurons (corresponding to the selected physical parameters), two hidden layers with 10 and 8 neurons, and one output layer for each target variable (skin friction, Nusselt number, Sherwood number, or motile microorganism density). Sigmoid activation functions were applied in the hidden layers, and a linear activation function was used in the output layer. Training was performed using the Levenberg–Marquardt (LM) backpropagation algorithm, which is widely used in engineering problems due to its fast convergence and low mean square error (MSE). With this architecture, the network achieved a correlation coefficient R > 0.95 and a minimum (MSE) of $10^{ - 5}$ demonstrating high prediction accuracy.

Physical significance of tabular results

Table 3 presents the variation in different physical quantities, such as skin friction, Nusselt number, Sherwood number, and motile number, due to various physical parameters. Table 3 shows that skin friction decreases with increasing buoyancy ratio, modified Hartmann number, and Rayleigh number. This indicates that stronger buoyancy forces, enhanced magnetic effects, and intensified convection promote fluid flow along the surface, thereby reducing resistive shear stress at the wall. The results also reveal that higher Eckert numbers and heat relaxation parameters lower the Nusselt number, signifying reduced heat transfer. Larger Eckert numbers intensify viscous dissipation, increasing fluid temperature and weakening the wall temperature gradient, while higher heat relaxation slows the thermal response, further decreasing heat flux. Conversely, greater heat generation/absorption enhances the Nusselt number by strengthening the thermal gradient near the surface.

Table 3 Variation in various physical quantities.

For mass transfer, the Sherwood number increases with higher Schmidt and mass relaxation parameters due to reduced mass diffusivity and faster concentration response, respectively. However, stronger Brownian motion reduces Sherwood numbers by weakening concentration gradients. Regarding bioconvection, the motile density number decreases with higher Peclet and bioconvection parameters but increases with larger Lewis numbers, as stronger solute diffusivity relative to microorganism diffusivity enhances microorganism concentration near the wall.

Table 4 presents the coded and actual levels of the buoyancy ratio parameter $N_{r}$, modified Hartmann number (Ha), and modified Rayleigh number $N_{c}$, considered in the skin friction analysis. The three coded levels (− 1, 0, 1) represent the minimum, middle, and maximum values of each parameter, defining the parametric range for numerical investigation. This tabulation reflects the systematic variation of thermal buoyancy, magnetic field strength, and solutal convection to evaluate their influence on skin friction, serving as the input framework for subsequent analysis.

Table 4 Variation in skin friction with parameters.

Table 5 provides the coded and actual levels of the Eckert number (Ec), heat relaxation parameter, and heat generation parameter (Q) for the Nusselt number analysis. The coded levels (− 1, 0, 1) denote the minimum, middle, and maximum values of each parameter. Physically, Ec quantifies viscous dissipation effects, the heat relaxation parameter ($\Gamma_{1}$) accounts for thermal relaxation time, and Q represents internal heat generation. These values establish the input range for systematically examining their impact on heat transfer.

Table 5 Variation in Nusselt number with parameters.

Table 6 shows the coded and actual levels of the Schmidt number (Sc), mass relaxation parameter ($\Gamma_{2}$), and Brownian motion parameter ($N_{b}$), used in the Sherwood number analysis. Again, the coded levels (− 1, 0, 1) indicate the minimum, middle, and maximum values for each parameter. Here, Schmidt number Sc represents the ratio of momentum to mass diffusivity, $\Gamma_{2}$ the mass relaxation parameter accounts for relaxation effects in mass transfer, and the Brownian motion parameter $N_{b}$ characterizes the influence of nanoparticle movement. These ranges from the framework for analyzing concentration transport and overall mass transfer behavior.

Table 6 Variation in Sherwood number with parameters.

Table 7 presents the coded levels (− 1, 0, 1), which correspond to the minimum, middle, and maximum values assigned to each parameter. The Peclet number (Pe) reflects the relative significance of convection to diffusion, while the bioconvection Lewis number (Lb) describes the relationship between nanoparticle diffusion and microorganism movement. The non-dimensional bioconvection parameter represents the combined influence of motile microorganisms on the flow field. These ranges provide the basis for analyzing transport and flow behavior. Collectively, Tables 4–7 summarize the coded levels of various parameters, denoted by the symbols X, Y, and Z. The combined variations of these parameters are summarized in Table 8. The findings derived from the variations of three types of parameters and their respective effects as shown in Table 8. Here, the dataset for ANN training and testing was prepared by the authors from the numerical solutions obtained using MATLAB bvp4c solver for 21 parameter combinations. These combinations correspond to low, medium, and high levels coded as ( –1, 0, 1) of three parameters for each scenario: (Ha, $N_{r}$, $N_{c}$) for velocity, (Ec, $\Gamma_{1}$, Q) for temperature, (Sc, $\Gamma_{2}$, $N_{b}$) for concentration, and (Pe, Lb, $\varpi$) for bioconvection. Each run produced outputs of skin friction, Nusselt number, Sherwood number, and motile number, which formed the ANN training dataset with 70% training, 15% validation, and 15% testing.

Table 7 Variation of motile number with parameters.

Table 8 Responses of physical quantities with 21 runs.

Heatmap analysis of parameters sensitivity

Figure 28 presents a sensitivity heat map to identify the impact of each physical parameter on the system’s outputs. It is evident that magnetic parameter Ha, the buoyancy ratio $N_{r}$, and solutal parameters (Sc and $\Gamma_{2}$) have the most significant influence on velocity and mass transfer. Thermal parameters, including (Ec, Q, $\Gamma_{1}$) and predominantly control the Nusselt number. The bioconvection-related parameters Pe, Lb, and ω show a notable effect on the motile microorganism density number. This sensitivity analysis justifies the selection of parameter ranges for the ANN dataset, ensuring that all dominant physical effects are captured within the chosen variation limits.

Fig. 28

Sensitivity heatmap generated using Python 3.13 with Matplotlib 3.9.2 and Seaborn 0.13.2 (https://www.python.org/, https://matplotlib.org/; https://seaborn.pydata.org/).

The sensitivity heatmap in Fig. 28 was generated using Python (version 3.13) with the Matplotlib (version 3.9.2) and Seaborne (version 0.13.2) libraries. The heatmap was constructed by computing the parameter–quantity correlations from the trained PINN outputs and visualized with Seaborn’s heatmap function.

Results of physical quantities with ANN

Skin friction

Skin friction optimization is performed by using artificial neural networks (ANN). Figure 29 indicates that the best validation performance for skin friction is $10^{ - 6}$ with 4 epochs. The best validation performance graph shows the mean squared error (MSE) or another loss function against the number of epochs for the training set, validation set, and the test set. Figure 30 presents the variation in the error histogram for 20 bins. This error has been generated by employing training, validation, and testing. Each bin represents an arrangement of errors, while the height of all the bars shows the number of inspections falling within the range. The visualization of the graph demonstrates that zero error accuracy has been obtained up to $10^{ - 5}$. Figure 31 displays the regression graphs of regression for testing, validation, training, and all. The Fit method is applied to the given data to create regression graphs. The visualization of the graph reveals that training accuracy is 1. The validation and test accuracy is $10^{ - 5}$. The calculated results of the regression graph overall are R = 0.95779. So, the accuracy of all data is $10^{ - 5}$. Table 9 exhibits the numerical computation for skin friction through the MATLAB-bvp4c technique and ANN. Further, the X, Y, and Z represent the coded quantities used in the neural approach and the bvp4c technique for evaluating the $Cf_{x}$ over 21 runs. The findings derived by the MATLAB-bvp4c, along with the ANN represent the error accuracy. The uncertainty in error for the flow problem has been calculated.

Fig. 29

Best validation performance of skin friction.

Fig. 30

Error histogram for skin friction.

Fig. 31

Regression graphs for skin friction.

Table 9 Comparing numerical techniques with ANN.

Nusselt number

Artificial neural networks (ANN) are used to optimize the Nusselt number. Figure 32 shows the best validation performance for the Nusselt number is $10^{ - 6}$ with 8 epochs. Figure 33 displays the variation in the error histogram by utilizing 20 bins over testing, training, and validation as well as zero error and the error accuracy is $10^{ - 5}$. The error histogram in an ANN is a graphical representation that shows the distribution of errors between the predicted and actual outputs. Figure 34 provides the graphs of regression over validation, training, and testing, along with all data, and the performance of accuracy is observed by applying the fit method. The visualization of regression graphs over training is 1, and $10^{ - 5}$ is calculated for validation, test, and all data. So, based on accuracy, the computed result for all data is $10^{ - 5}$. Moreover, Table 10 compares the MATLAB-bvp4c technique and ANN for the Nusselt number. Coded quantities are represented as X, Y, and Z which are utilized in the bvp4c as well as ANN technique methods to analyze the Nusselt number. Here, 21 runs are considered for error percentage. The given data is investigated, as well as the percentage of error for approximate values is calculated.

Fig. 32

Best validation performance of Nusselt number.

Fig. 33

Error histogram for Nusselt number.

Fig. 34

Regression graphs for Nusselt number.

Table 10 Comparing numerical techniques with ANN.

Sherwood number

The Sherwood number was optimized using an ANN. Figure 35 indicates that the best validation performance for the Sherwood number was $10^{ - 7}$ with 3 epochs. The data for the analysis were obtained using the MATLAB-bvp4c technique. The variation in the error histogram is demonstrated in Fig. 36, with 20 bins. This error was used to explore the components of the ANN, such as training, validation, testing, and zero error. Then, the error accuracy is inspected up to $10^{ - 5}$. Figure 37 depicts the regression graphs formed over the training, validation, testing, and all data using the fit method. The regression graph in an ANN provides a graphical representation that shows a comparative analysis between the predicted values from the model and the actual target values. The graph reveals that the accuracy of training, validation, and testing is. Furthermore, the obtained values for all data are R = 0.90693, which indicates that the total inspection for accuracy is $10^{ - 5}$. Table 11 displays the data for MATLAB-bvp4c and the ANN technique, along with the percentage error for the predicted values. To examine the variance produced for the Sherwood number, the bvp4c and ANN strategies were applied, and X, Y, and Z were used as coded quantities in the given table.

Fig. 35

Best validation performance of Sherwood number.

Fig. 36

Error histogram for Sherwood number.

Fig. 37

Regression graphs for Sherwood number.

Table 11 Comparing numerical techniques with ANN.

Motile number

The artificial neural network method optimizes the motile number. Figure 38 indicates that the best validation performance for the Sherwood number is $10^{ - 7}$ with 7 epochs. The error histogram for 20 bins has been illustrated in Fig. 39. This error is being utilized for training, validation, and testing, along with the zero error. The accuracy level is observed at $10^{ - 5}$. The regression graph is a useful diagnostic tool during the training, validation, and testing phases of ANN development because it provides an effective technique for analyzing the model’s performance over various data ranges. Figure 40 demonstrates regression graphs of regression for training, validation, testing, and all data through the fit method. According to this graph, the training accuracy is 1, accuracy of validation and testing is $10^{ - 5}$. The determined value of this graph based on all data is R = 0.94943. It shows that the observation of accuracy is $10^{ - 5}$. The data for the analysis is collected by applying the MATLAB-bvp4c technique. Table 12 provides the data on motile number by utilizing the MATLAB-bvp4c and artificial neural network methods, and it also shows the percentage of error of predicted values. In this table, to observe the variation of error produced in the motile number, the method of ANN as well as bvp4c are employed, and coded quantities represented through X, Y, and Z.

Fig. 38

Best validation performance of motile organism number.

Fig. 39

Error histogram for motile organism number.

Fig. 40

Regression graphs for motile organism number.

Table 12 Comparing numerical techniques with ANN.

Computational efficiency of ANN

Artificial Neural Networks (ANNs) have emerged as powerful tools for reducing computational costs in scientific and engineering applications. After the training phase, an ANN can approximate complex nonlinear relationships and provide rapid predictions without the need for repeated numerical simulations or extensive experimental procedures. This feature makes ANN a cost-effective solution for both real-time and large-scale applications.

Training requirements of ANN

The present study demonstrates that the ANN-based approach is highly effective in reducing computational costs during prediction compared with conventional numerical methods. However, it is important to note that the initial training phase requires additional time and hardware resources. In particular, generating a sufficiently large and representative dataset requires considerable computational time, ranging from several hours to weeks, depending on the complexity of the underlying models and the data source. Furthermore, efficient training of ANN models generally requires hardware resources such as multi-core Central Processing Units (CPUs) and Graphics Processing Units (GPUs) with sufficient memory, whereas large-scale applications may necessitate access to high-performance computing systems.

Conclusion

This study examines the behavior of nanofluid, including nanoparticles of copper (Cu) nanoparticles, Propylene glycol (C₃H₈O₂), with bio-convection effects. The physical and geometrical model is the Riga plate. The Cattaneo-Christov dual flow model is employed to improve thermal flow. The PDEs are converted into ODEs using suitable symmetry variables. Then bvp4c approach is applied to obtain the numerical results. Furthermore, a neural network is employed, which optimizes the data accuracy of the flow problem.

Significant findings

The significant findings of the physical quantities are given as

• When the buoyancy ratio parameter and modified Hartmann number are enhanced, the velocity profile of the nanofluid rises.

• The temperature profile of nanofluid decreases with the higher values of the heat generation/absorption parameter and Prandtl number increase.

• Greater values of the Brownian motion parameter decrease the concentration profile of the nanofluid.

• It has been observed that the profile of bioconvection for the nanofluid flow declines with the greater Lewis number and the Peclet number.

• The skin friction profile increases for the higher modified Hartmann number and buoyancy ratio parameter.

• The profile of the Nusselt number goes down for the greater heat relaxation parameter and the Eckert number.

• When the Schmidt number and mass relaxation parameters are enhanced, the profiles of the Sherwood number increase.

• The profile of motile organisms increases with the greater bioconvection Lewis number and declines as the Peclet number enhance.

Novelty

The novelty of the current research is the production of better approximations and reduction of the error by applying the ANN technique. The novel findings of the present analysis for the various physical quantities are given as

• The best validation performance for skin friction is $10^{ - 6}$ with 4 epochs.

• The error histogram shows that the error accuracy of testing, training, and validation with 20 bins is $10^{ - 5}$ for the Nusselt number.

• The error accuracy of the Sherwood number is $10^{ - 5}$ by using the fit method for validation, training, and testing.

• The overall accuracy level of the ANN for all the data has been observed up to $10^{ - 5}$.

Limitations of the study

The present study is limited to analyzing the behavior of propylene glycol (C₃H₈O₂) nanofluid flow with Cattaneo-Christov dual flux and bioconvection effects over a Riga plate. The numerical investigations were conducted by assuming copper (Cu) nanoparticles in the propylene glycol base fluid. Artificial neural networks were employed for the thermal analysis of the flow problem.

Future scope

The current flow problem deals with the thermal analysis of the propylene glycol fluid flow containing copper nanoparticles through a Riga plate. In the future, the current flow model can be used to investigate various nanoparticles, and by altering the base fluid, as taken in a scenario similar to blood flow, for directing the medicine product in the blood. This study utilized the bvp4c technique to obtain numerical solutions for the flow problem. In the future, different numerical methods, such as the homotopy analysis method, Runge–Kutta method, and finite difference method, can also be applied to obtain numerical solutions for flow problems.