Optimizing healthcare supply chain capacity planning during disasters using fuzzy AHP and TOPSIS methods

Abstract

This paper applies Fuzzy AHP and Fuzzy TOPSIS to the problem of healthcare supply-chain capacity planning under uncertainty. We define a practical set of criteria–patient demand, resource availability, cost, and quality of care and use fuzzy pairwise judgments to estimate criterion weights, followed by Fuzzy TOPSIS to rank capacity options (e.g., reallocating staff, adding beds, outsourcing services). Through scenario-based comparisons with crisp AHP/TOPSIS, we show that fuzzy models capture vagueness in expert input, yield rankings that are more stable to small judgment changes, and remain computationally manageable. We provide an implementation walkthrough from criteria design to sensitivity analysis, and summarize observed improvements in decision robustness alongside implications for patient flow and cost control. The findings offer a clear, practice-ready playbook for hospitals seeking to align resources with fluctuating demand while keeping patient impact front and center.

Introduction

The healthcare industry is an essential part of any society, and its effective functioning is vital for the well-being of individuals and communities¹. In recent times, there has been a substantial rise in the need for healthcare services², attributed to an aging population, an increase in chronic health conditions, and heightened recognition of preventive healthcare value. However, healthcare providers and facilities have struggled to keep pace with demand, resulting in prolonged wait times, overcrowding, and resource strain^3,4. These challenges intensify significantly during disaster scenarios, where healthcare demands frequently exceed available resources^5,6.

The motivation behind this study stems from critical gaps and challenges in healthcare supply chain capacity planning during disasters, particularly highlighted by the COVID-19 pandemic. The COVID-19 pandemic exposed serious weaknesses, e.g., shortages of PPE, testing kits, and ICU beds. These shortages were aggravated by poor planning, fragmented coordination, and reactive strategies. There was a pressing need for a proactive, structured, and data-driven decision-making framework to manage capacity under uncertainty. Hospitals and policymakers need clear, replicable steps for making capacity decisions during crises. The study aims to translate complex theoretical methods into actionable frameworks, usable by real-world healthcare administrators.

Optimizing healthcare supply chain network capacity planning (HSCNCP) during disasters is critical for ensuring timely delivery of essential healthcare services. Effective strategies include clearly defining stakeholder roles, fostering stakeholder collaboration, maintaining sufficient inventory levels, and leveraging data analytics for real-time disruption identification^{7,8,9,10,11,12,13,14}.

The COVID-19 pandemic significantly highlighted the vulnerabilities within healthcare supply chains, exposing deficiencies such as insufficient personal protective equipment and diagnostic testing capacities, thereby underscoring the necessity for robust capacity planning methodologies^{15,16,17,18,19,20,21}.

To address these gaps, this study aims to establish a systematic framework using Multi-Criteria Decision-Making (MCDM) techniques, specifically integrating Fuzzy Analytic Hierarchy Process (FAHP) and Fuzzy Technique for Order Preference by Similarity to Ideal Solution (FTOPSIS), for robust healthcare supply chain capacity planning during disasters^22,23,24. This approach helps decision-makers navigate complex criteria and uncertainties inherent to disaster scenarios.

The specific contributions of this study, clearly differentiating it from existing literature, include:

• Developing an integrated fuzzy-based framework (FAHP and FTOPSIS) tailored explicitly for disaster-oriented healthcare supply chain network capacity planning.

• Incorporating a broader and more context-sensitive set of evaluation criteria including patient volume, staffing, resource availability, geographic accessibility, care quality, economic factors, and ethical considerations.

• Providing structured and transparent methods for systematically prioritizing healthcare resources under uncertainty, Improving resource alignment with fluctuating demand during emergencies

• Demonstrating the applicability and robustness of the proposed methodology through a detailed real-world case study conducting sensitivity analysis to test outcome robustness under weight variation

• Highlighting practical implications, including improved operational efficiency, patient-centered service delivery, and strengthened disaster preparedness and response capacity.

This paper is structured as follows: Sect. “Background” offers essential background information on healthcare supply chain management, emphasizing crisis management aspects. Section “Related works” reviews related literature, underscoring the usage of MCDM techniques. Section “Methodology” outlines the research methodology. Section “Case study” presents a real-world case study to validate the proposed model. Section “Sensitivity analysis” includes sensitivity analysis to assess decision-making robustness. Section “Discussion” discusses key findings, and finally, Section “Conclusion” concludes by summarizing insights and suggesting directions for future research.

Background

Healthcare supply chain management

Healthcare supply chain management (HSCM) represents a fundamental element within the healthcare sector, facilitating the prompt provision of high-quality healthcare products and services to patients. This intricate process encompasses several key activities, including procurement, inventory control, logistics, and distribution. The primary objective of HSCM is to guarantee that patients obtain the necessary products and services precisely when needed, in the correct quantities, and at a reasonable cost. Demonstrably, efficient management of the healthcare supply chain contributes to enhanced patient outcomes, cost reduction, and increased efficiency in the delivery of healthcare services²⁵.

A principal challenge in HSCM involves optimal management of inventory levels. It is imperative for hospitals and related healthcare facilities to maintain an adequate inventory to ensure the availability of essential supplies and equipment, thus effectively meeting patient needs. However, excessive inventory levels can lead to waste and increased costs, while inadequate inventory levels can lead to stock shortages and delays in patient care. Therefore, effective inventory management is crucial to ensure the optimal use of resources and minimize waste²⁶.

A pivotal element of HSCM is the imperative for collaboration and coordination among various stakeholders within the healthcare supply chain. These stakeholders encompass healthcare providers, manufacturers, distributors, and regulatory agencies. Such collaboration and coordination are crucial to guarantee an efficient distribution of products and services across the healthcare supply chain. Moreover, robust collaborative efforts are linked to enhanced patient outcomes, cost reduction, and strengthened resilience in the supply chain²⁷²⁸.

Disaster preparedness and response

Disaster preparedness and response encompass the measures implemented prior to, midst, and following a disaster, with the aim of minimizing its effects on human lives, property, and the environment. The World Health Organization (WHO) defines disaster preparedness as the “knowledge and capacities developed by governments, professional response and recovery organizations, communities and individuals to effectively anticipate, respond to, and recover from the impacts of likely, imminent or current hazard events or conditions”²⁹. Effective disaster preparedness and response require comprehensive planning, adequate resources, and the collaboration of multiple stakeholders, including healthcare organizations, government agencies, emergency responders, and the public. Healthcare institutions are pivotal in the context of disaster readiness and management, bearing the responsibility for delivering urgent medical services, overseeing resource allocation, and collaborating with various stakeholders³⁰.

To improve disaster preparedness and response, healthcare organizations should develop and implement comprehensive disaster management plans that address all aspects of the disaster cycle. These plans should include risk assessments, contingency planning, communication protocols, training programs, and resource allocation strategies. Effective disaster management plans require collaboration between healthcare organizations, governmental agencies, and emergency responders, as well as the involvement of the local community³¹.The effectiveness of disaster preparedness and response initiatives is contingent upon the adaptability of healthcare organizations to evolving conditions, as well as their capacity to collaborate efficiently with various stakeholders. Such coordination is critical to alleviating the effects of disasters on individuals and communities³².

Multi-criteria decision-making methods

Multi-Criteria Decision-Making (MCDM) methods encompass a collection of techniques that facilitate decision-makers in addressing issues characterized by multiple, often conflicting, objectives. These methodologies evaluate various parameters, including cost, quality, and time, to determine and select the optimal choice from several possibilities. MCDM techniques offer a structured framework for decision-making by integrating both quantifiable and subjective factors that are frequently challenging to measure. Prominent MCDM approaches include the Analytic Hierarchy Process (AHP), the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and the Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE). These techniques have found application across diverse sectors, notably healthcare, supporting intricate decision-making tasks.

Fuzzy MCDM methods, a specialized subset of MCDM techniques, integrate aspects of uncertainty and imprecision within the decision-making framework. Rooted in fuzzy set theory, these methods enable the articulation of nebulous and uncertain data. Fuzzy MCDM techniques have gained extensive utilization in various domains, particularly in healthcare, where decision-making is frequently marred by subjective judgments and uncertainties. Prominent fuzzy MCDM methods include Fuzzy AHP, Fuzzy TOPSIS, and Fuzzy PROMETHEE³³. By accommodating incomplete, ambiguous, or conflicting information, these methods facilitate more realistic, robust, and dependable decision-making outcomes³⁴.

Related works

The implementation of MCDM techniques is increasingly acknowledged as a robust approach for navigating the complexities inherent in HSCM, especially in the domains of disaster readiness and intervention. MCDM methodologies enable practitioners within HSCM to assess various strategies by considering multiple dimensions such as cost, quality, reliability, and responsiveness, thereby facilitating the identification of the most advantageous solution tailored to their specific requisites and goals. Research, including studies that explore the Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), and fuzzy MCDM, underscores the utility of these techniques in enhancing decision-making capabilities in HSCM amidst catastrophic circumstances.

In the study documented in³⁵, integrated fuzzy Delphi, GIS, and PROMETHEE to evaluate disaster management centers’ sustainability and efficiency in Tehran. Their framework addresses complex environmental, economic, and social criteria under multiple crises. GIS was highlighted for its critical spatial decision-support capabilities.

The authors in³⁶ proposed a fuzzy multi-criteria group decision-making method to select medical emergency suppliers during COVID-19. The approach uniquely incorporated psychological, consensus, and hesitation factors of decision-makers, resulting in a more holistic and effective supplier selection under pandemic-induced uncertainties.

The authors in³⁷ presented a hybrid fuzzy approach combining Fuzzy Analytic Hierarchy Process (FAHP), Fuzzy DEMATEL, and TOPSIS to evaluate hospitals’ disaster preparedness. Their method prioritized hospitals based on key resilience criteria, emphasizing staff readiness and operational flexibility, critical in managing sudden health crises.

The authors in³⁸ developed a novel fuzzy-rough approach merging MACBETH and CODAS methods for efficient selection of medical equipment suppliers. This technique robustly addressed uncertainties and disruptions in healthcare supply chains caused by the COVID-19 pandemic, enhancing procurement decision-making and resilience.

The study in³⁹ combined FMEA and MCDM (BWM, CODAS) with intuitionistic fuzzy sets for improved fire-risk assessment in healthcare. Their approach effectively captured uncertainty and indirect relationships but lacked detailed sub-criteria measurements. Future studies should consider other fuzzy approaches and deeper sub-criteria analyses.

The study in⁴⁰ proposed a novel fuzzy-rough decision-making framework combining MACBETH and CODAS methods for selecting medical protective suppliers amid COVID-19. The approach addresses significant uncertainty inherent in pandemic scenarios. Suggested future work includes incorporating predictive event impacts and applying alternative ranking methods across broader supply chain contexts.

Sazvar et al. in⁴¹ proposed a multi-objective optimization model employing fuzzy robust approaches to manage vaccine supply chains, considering sustainability and resilience. The model explicitly included capacity planning and distribution constraints, offering robust decision support for disaster readiness in public health contexts.

Sumrit et al. in⁴² applied fuzzy multi-criteria decision-making (MCDM) techniques, specifically Fuzzy Delphi, SWARA, and COPRAS, for selecting optimal healthcare suppliers in Vendor Managed Inventory (VMI) systems. Their approach aimed at systematically improving efficiency, cost-effectiveness, and operational reliability within healthcare supply chains.

The authors in⁴³ used FAHP to rank critical lean waste criteria in healthcare, emphasizing waiting, transportation, motion, and defects. These criteria significantly impact patient satisfaction, resource efficiency, and operational quality. A limitation noted was its focus solely on Indian hospitals, suggesting international comparative studies.

This article⁴⁴ compared fuzzy AHP and fuzzy TOPSIS methods for software requirement selection, considering aspects like agreement, complexity, rank reversals, and judgment needs. They found fuzzy AHP prone to rank reversals and requiring extensive judgment, whereas fuzzy TOPSIS proved more consistent, scalable, and better suited for group decision-making. Future work could explore rough-set and fuzzy-soft-set methods to handle larger sets of requirements.

The paper⁴⁵ compared fuzzy AHP and fuzzy TOPSIS in software requirement selection, highlighting TOPSIS’s consistency and fewer judgments. While fuzzy AHP risked rank reversals, TOPSIS supported unlimited requirements and better group decision-making. Future studies could compare rough-based methods or explore fuzzy-soft sets for larger datasets.

The authors in⁴⁶ introduced a novel fuzzy MAGDM framework combining CFAHP, FTOPSIS, and extent analysis for enhanced accuracy and computational efficiency. Using linguistic terms and fuzzy arithmetic, their method robustly addresses uncertainty, demonstrated effectively in supplier selection. Future research may incorporate interval numbers, uncertain linguistic variables, temporal aspects, and attribute correlations.

The article by Chen et al.⁴⁷ utilized an integrated FAHP-FTOPSIS methodology to systematically evaluate mid-term occupational health interventions during COVID-19. Their approach prioritized critical factors and assessed intervention effectiveness, identifying “isolating machines” as most suitable. This structured quantitative evaluation provides valuable references for industries navigating pandemic-related uncertainties.

Zhao et al.⁴⁸ developed a network-based framework combining entropy weighting and VIKOR methods to identify key hospitals for post-disaster urban healthcare resilience. Their model integrates hospital characteristics and network criteria, guiding preparedness and strategic investments. The study notes limitations in assumptions and hospital features, recommending further refinement of modeling accuracy and real-world conditions.

The paper⁴⁹ proposed an innovative disaster-management decision approach integrating fuzzy theory and actor analysis, addressing complexity and uncertainty. Their fuzzy SWARA method incorporates expert inputs to calculate indicator weights, balancing economic and non-economic criteria. A numerical example demonstrated the practical selection of optimal emergency suppliers under varied decision preferences.

The authors in⁵⁰ introduced a multi-criteria model for emergency resource allocation, shifting priorities from effectiveness and equity initially to efficiency and cost later. Their approach, leveraging real-time data and big-data analytics, significantly improves satisfaction and reduces system losses in disaster relief efforts.

Recently, Saoud et al.⁵¹ proposed an optimization framework for emergency resource allocation, balancing efficiency, cost, effectiveness, and fairness. They highlighted prioritizing criteria across emergency phases to enhance satisfaction and reduce losses, suggesting future integration of real-time and big data technologies.

Beyond the studies already reviewed, several recent papers further support our theoretical and managerial arguments and enrich the literature baseline of this work. First⁵², integrate Data Envelopment Analysis (DEA) with Fuzzy AHP to prioritize renewable energy sources in India. Methodologically, this hybridization shows how an efficiency layer (DEA) can be combined with fuzzy preference weighting to handle desirable/undesirable criteria under uncertainty–an idea consistent with our use of FAHP for weighting and fuzzy TOPSIS for robust ranking under ambiguous information.

Second⁵³, propose a resilient supplier selection and order allocation model that leverages Pythagorean fuzzy sets and Industry 4.0 enablers. Their framework couples fuzzy preference elicitation with a fuzzy multi-objective linear program, illustrating how resilience-focused criteria and digital enablers can be embedded in fuzzy decision models. This aligns with our disaster setting, where resilience, rapid mobilization, and logistics constraints must be evaluated under vagueness.

Third⁵⁴, prioritize determinants of employees’ green behavior in the Indian hotel industry using AHP and Fuzzy AHP. Although set in hospitality, the result is directly relevant to healthcare capacity planning because staff behavior, organizational support, and policy levers influence surge response and operational reliability. Their use of FAHP to structure intangible, behavior-related factors complements our stakeholder-preference criterion and reinforces the managerial value of fuzzy weighting for human-centered variables.

Together, these contributions confirm the benefits of hybrid fuzzy MCDM for (i) integrating efficiency analysis with uncertain preferences, (ii) modeling resilience- and technology-oriented criteria, and (iii) prioritizing human/organizational determinants. Our study extends this stream by tailoring an FAHP–FTOPSIS pipeline to disaster-oriented healthcare capacity planning, accompanied by sensitivity analysis and a case-based validation.

Table 1 provides a comprehensive summary of the works conducted in the field of environmental sustainability, highlighting key findings and outcomes.

Table 1 Studies on the application of Multi-Criteria Decision-Making Methods in Healthcare Supply Chain Management.

The literature explores the deployment of MCDM techniques within HSCM specifically aimed at enhancing disaster readiness and response, with a notable emphasis during the COVID-19 pandemic. These studies introduce a range of methodologies employing MCDM techniques, including Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), and various fuzzy logic-based methods such as fuzzy decision-making, fuzzy Delphi method, and fuzzy rough numbers. These approaches are utilized to assess and rank alternatives by considering multiple criteria, including cost, quality, reliability, and responsiveness. The proposed methodologies aim to enhance decision-making efficacy during disasters, thereby minimizing casualties and optimizing the allocation of resources and personnel. The authors acknowledge the constraints of the current studies and suggest avenues for future research to refine these strategies and broaden their applicability.

The objective of this research is to enhance the capacity planning of the healthcare supply chain network under disaster conditions through the application of MCDM methods. In comparison to other approaches, this study focuses on the uncertainties and complexities associated with disasters and their impacts on healthcare supply chain networks. Additionally, this study utilizes multi-criteria decision-making methods to identify the best courses of action under such conditions. By doing so, the study aims to improve the resilience of healthcare supply chain networks in disaster-prone areas and improve the delivery of healthcare services to affected communities.

Methodology

Fuzzy MCDM has been extensively applied across diverse research domains; however, this discussion is particularly dedicated to elucidating the theoretical underpinnings of the suggested approach. Fuzzy set theory becomes instrumental in scenarios where assigning exact performance ratings and weights proves challenging, thereby encapsulating the uncertainty in evaluations. This scenario is commonly classified as fuzzy MCDM. The foundational work by Bellman and Zadeh in 1970⁵⁵ amalgamated fuzzy set theory with MCDM, enhancing the handling of the ambiguity and imprecision typical of human decision processes.

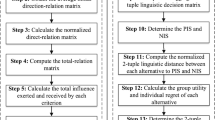
The application of this framework in the management of the capacity of healthcare supply chain networks via Fuzzy AHP and Fuzzy TOPSIS comprises the following steps, described in Fig. 1:

Fig. 1

Steps in the Multi-Criteria Decision-Making Approach for Healthcare Supply Chain Network Capacity Planning under Disaster Conditions.

• Step 1: Formulation of the Decision Problem: Begin by articulating the capacity planning issue within the healthcare supply chain network that requires resolution. It is crucial to delineate the problem comprehensively and define the objectives that must be met.

• Step 2: Establishment of Criteria and Sub-Criteria: Proceed by selecting the criteria and sub-criteria that will guide the evaluation of various alternatives. These should be chosen based on the established framework, which includes elements such as patient demand, availability of resources, cost implications, and quality of care, and should be tailored to address the specific issue at hand.

• Step 3: Development of Linguistic Variables and Fuzzy Sets: For each criterion and sub-criterion, establish linguistic variables and corresponding fuzzy sets. For instance, the criterion “resource availability” may be categorized into fuzzy sets such as “very low,” “low,” “medium,” “high,” and “very high.”

• Step 4: Determination of Weights for Criteria and Sub-Criteria: Ascertain the weights of each criterion and sub-criterion using the Fuzzy AHP. This method involves gathering input from stakeholders to allocate weights, reflecting the relative significance of each criterion and sub-criterion. Fuzzy AHP is particularly useful for accommodating the imprecision and uncertainty characteristic of decision-makers’ assessments.

• Step 5: Alternative Evaluation: Apply Fuzzy TOPSIS to assess the alternatives. Fuzzy TOPSIS evaluates alternatives based on their proximity to the ideal solution, taking into account the uncertainty and ambiguity inherent in the decision-making process.

• Step 6: Sensitivity Analysis: Conduct a sensitivity analysis to examine the stability of the outcomes. This analysis tests how changes in the weights assigned to criteria and sub-criteria influence the final rankings, thereby assessing the robustness of the decision-making process.

Applied MCDM methods under uncertainty

Fuzzy sets and fuzzy numbers

Fuzzy set theory represents an extension of classical set theory, offering a valuable methodological approach for decision-making processes. Initially proposed by Zadeh⁵⁶, this framework is specifically designed to manage the inherent uncertainties and imprecise characteristics of information. Within academic discourse, various forms of fuzzy numbers, including trapezoidal and triangular types, are utilized to articulate the indeterminacies of parameters pertinent to specific subjects. For the current study, triangular fuzzy numbers (TFNs) are used. Specifically, a triangular fuzzy number ${\bar{e}} (a, b, c)$ is used to account for the fuzziness of^57,58. The membership function $\mu _{\bar{e}}(x)$ of the triangular fuzzy number is described in Fig. 2.

Fig. 2

Triangular fuzzy number (TFN).

$$\begin{aligned} \mu _{\tilde{e}}(x)= {\left\{ \begin{array}{ll}0, & x \le a \\ \frac{x-a}{b=a}, & a<x \le b \\ \frac{c=x}{c-b}, & b<x \le c \\ 0, & x>c\end{array}\right. } \end{aligned}$$

The fuzzy set theory’s forward, which was applied in this work, is as follows: Let ${\bar{e}}_1 (a_1, b_1, c_1)$ and ${\bar{e}}_2 (a_2, b_2, c_2)$ be two TFNs.

Definition 1 states how to use the vertex technique to determine the distance between them as:

$$\begin{aligned} d\left( \tilde{e}_1, \tilde{e}_2\right) =\sqrt{\frac{1}{3}\left[ \left( a_1-a_2\right) ^2+\left( b_1-b_2\right) ^2+\left( c_1-c_2\right) ^2\right] } \end{aligned}$$

Definition 2 The following are the principal operations on TFNs:

$$\begin{aligned} \begin{aligned}&\tilde{e}_1 \oplus \tilde{e}_2=\left( a_1+a_2, \quad b_1+b_2, \quad c_1+c_2\right) \\&\tilde{e}_1-\tilde{e}_2=\left( a_1-a_2, \quad b_1-b_2, \quad c_1-c_2\right) \\&\tilde{e}_1 \otimes \tilde{e}_2 \approx \left( a_1 \times a_2, \quad b_1 \times b_2, \quad c_1 \times c_2\right) \\&\frac{\tilde{e}_1}{\tilde{e}_2} \approx \left( \frac{a_1}{c_2}, \frac{b_1}{b_2}, \frac{c_1}{a_2}\right) \\&\tilde{e}_1 \otimes k=\left( a_1 \times k, \quad b_1 \times k, \quad c_1 \times k\right) \\&\end{aligned} \end{aligned}$$

Fuzzy AHP

Saaty’s AHP⁵⁹ is a widely recognized technique for addressing complex decision-making issues that involve multiple criteria, frequently applied in practical situations. It has been demonstrated in various studies to be an effective methodology for optimizing healthcare supply chain networks^60,61. Nevertheless, real-world applications often suffer from a lack of precise data, as human judgments tend to be inherently vague. To address the shortcomings of the traditional AHP approach, Van Laarhoven and Pedrycz (1983) introduced the concept of fuzzy AHP, integrating the principles of the Analytic Hierarchy Process with fuzzy logic⁶². This adaptation permits the use of linguistic evaluations in determining the weights of criteria, thus accommodating ranges rather than precise values. This method facilitates interval judgments over absolute ratings by decision-makers. Balli (2009) highlighted that incorporating fuzziness into AHP helps to capture and articulate imprecise and ambiguous data⁶³.

The literature presents a variety of methodologies for establishing weights within the framework of fuzzy AHP. Bozbura et al.⁶⁴ offer a succinct overview and comparative analysis of several of these methodologies, each characterized by distinct advantages and Limitations. In this research, the extent analysis method introduced by Chang in 1992⁶⁵, which employs Triangular Fuzzy Numbers (TFNs) to manage fuzzy AHP, is adopted for deriving the fuzzy weights applicable to the selected criteria^58,66. Notably, critiques of this method, such as those discussed by Wang⁶⁷, highlight potential flaws, including the risk of irrationally assigning a zero weight to specific decision criteria and sub-criteria, which may lead to misapplications. The procedural steps of Chang’s extent analysis method for fuzzy AHP are delineated subsequently.

Phase 1: Calculating the fuzzy synthetic extent

$$\begin{aligned} S_i=\sum _{j=1}^m M_{g_i}^j \otimes \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j\right] ^{-1} \end{aligned}$$

To calculate the sum $\displaystyle \sum _{j=1}^m M_{g i}^j$, the procedure involves the aggregation of $\textrm{m}$ values from an extent analysis for a given matrix, which can be articulated as:

$$\begin{aligned} \sum _{j=1}^m M_{g i}^j = \left( \sum _{j=1}^m a_j, \sum _{j=1}^m b_j, \sum _{j=1}^m c_j\right) = (\tilde{a}_i, \tilde{b}_i, \tilde{c}_i) \end{aligned}$$

Furthermore, the computation of $\displaystyle \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j\right] ^{-1}$ requires the execution of the fuzzy addition of the matrix elements $M_{g i}^j$ across the indices $j = 1, 2, \ldots , m$, performed in such a manner:

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^m M_{g i}^j=\left( \sum _{i=1}^n \tilde{a}_i, \quad \sum _{i=1}^n \tilde{b}_i, \quad \sum _{i=1}^n \tilde{c}_i\right) \end{aligned}$$

And then compute the inverse of the vector such that

$$\begin{aligned} \left[ \sum _{i=1}^n \sum _{j=1}^m M_{g_i}^j\right] ^{-1}=\left( \frac{1}{\displaystyle \sum _{i=1}^n \tilde{c}_i}, \quad \frac{1}{\displaystyle \sum _{i=1}^n \tilde{b}_i}, \quad \frac{1}{\displaystyle \sum _{i=1}^n \tilde{a}_i}\right) \end{aligned}$$

Phase 2: Comparing Fuzzy values

The degree of possibility refers to the extent of belief that a particular fuzzy proposition is true. To define the degree of possibility between two different TFNs, use the following function:

$$\begin{aligned} V\left( M_2 \ge M_1\right) =\left\{ \begin{array}{cc} 1 & \text{ if } b_2>b_1 \\ 0 & \text{ if } a_1 \ge c_2 \\ \frac{a_1-c_2}{\left( b_2-c_2\right) -\left( b_1-a_1\right) }, & \text{ Otherwise } \end{array}\right. \end{aligned}$$

Then, compute also $V\left( M_1 \ge M_2\right)$ to give the complete comparison between $M_1$ and $M_2$.

Phase 3: Calculating priority weight

In the case of convex fuzzy numbers CFNs, which is the matter here, the degree of possibility for a CFN M to be greater than k different CFNs means that it is greater than the minimum value of all of them. This can be expressed as:

$$\begin{aligned} V\left( M \ge M_1, M_2, \ldots , M_k\right) =\min _{1\le j\le k} V\left( M \ge M_j\right) . \end{aligned}$$

Let’s denote:

$$\begin{aligned} m\left( P_i\right) =\min \limits _{\begin{array}{c} 1\le i\le n \\ i\ne k \end{array}} V\left( M_i \ge M_k\right) . \end{aligned}$$

Therefore, the weight vector of n elements is denoted by

$$\begin{aligned} W_p =\left( m(P_1), m(P_2), \ldots , m(P_n) \right) ^T. \end{aligned}$$

Phase 4: Normalizing priority weight

The vector obtained by normalizing the last priority weight is a non-fuzzy number called:

$$\begin{aligned} W =\left( W(P_1), W(P_2), \ldots , W(P_n) \right) ^T. \end{aligned}$$

Phase 5: Filling the fuzzy decision matrix

To construct the decision matrix, denoted as $\tilde{D}$, it is essential to gather assessments from each decision-maker concerning alternatives in relation to criteria. These assessments are to be collected using the fuzzy TOPSIS methodology. The aggregation of these evaluations will be elaborated in the subsequent section. This matrix is given as

$$\begin{aligned} \tilde{D}=\left[ \begin{array}{cccc} \tilde{x}_{11} & \tilde{x}_{12} & \ldots & \tilde{x}_{1 n} \\ \tilde{x}_{21} & \tilde{x}_{22} & \ldots & \tilde{x}_{2 n} \\ \vdots & \vdots & & \ \vdots \\ \tilde{x}_{m 1} & \tilde{x}_{m 2} & \ldots & \tilde{x}_{m n} \end{array}\right] \end{aligned}$$

where,

$$\begin{aligned} \tilde{x}_{i j}=\left( a_{i j}, b_{i j}, c_{i j}\right) \text{, } \quad i=1,2, \ldots , m\quad \text{ and } \quad j=1,2, \ldots , n . \end{aligned}$$

are positive triangular fuzzy numbers.

Phase 6: Normalizing the fuzzy decision matrix

This phase involves converting a fuzzy decision matrix $\tilde{D}$ into another matrix called $\bar{R}$. This transformation standardizes the matrix values to a common scale, which is crucial in multi-criteria decision making (MCDM) methods, such as those discussed in the referenced literature by Chen (2000)⁶⁸.

$$\begin{aligned} \bar{R}=\left[ \bar{r}_{ij}\right] , \quad i=1,2, \ldots , m \quad \text{ and } \quad j=1,2 \ldots , n \end{aligned}$$

such that

$$\begin{aligned} \bar{r}_{j j}=\left( \frac{a_{ij}}{c_j^+}, \frac{b_{i j}}{c_j^+}, \frac{c_{i j}}{c_j^+}\right) \end{aligned}$$

with

$$\begin{aligned} c_j^{+}=\max _{1\le i \le m} c_{ij} \end{aligned}$$

Phase 7: Computing weighted normalized fuzzy decision matrix

Every criterion has a specific weight decided by decision makers. To take them under consideration, let denote the weighted normalized fuzzy decision matrix by

$$\begin{aligned} R=\left[ \bar{r}_{ij} W\right] \quad i=1,2, \ldots , m \quad \text{ and } \quad j=1,2, \ldots , n \end{aligned}$$

and $W=[\tilde{w}_j]$ is the weighted vector of each criterion that is a TFN such that

$$\begin{aligned} {w}_j= ({w}_{j 1}, {w}_{j 2}, {w}_{j 3}\rangle \end{aligned}$$

Phase 8: Calculating the ranking parameters

These parameters are two, the fuzzy positive ideal solution (FPIS) denoted $A^*$ and the fuzzy negative ideal solution (IDNS) denoted $A^-$. Their expressions are taken from^68,69 and given by

$$\begin{aligned} \begin{aligned} A^*=\left( R_1^*, R_2^*, R_3^*, \ldots \ldots , R_{n}^*\right) \\ A^{-}=\left( R_1^{-}, R_2^{-}, R_3^{-}, \ldots \ldots , R_n^{-}\right) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} R_j^*=\max _{1\le i \le m}\left\{ r_{ij}\right\} , \quad j=1,2, \ldots , n. \\ R_j^-=\min _{1\le i \le m}\left\{ r_{ij}\right\} , \quad j=1,2, \ldots , n. \end{aligned}$$

Phase 9: Computing the distance to ranking parameters

Referring to^68,69, the distance of all alternatives to positive and negative ideal solutions are

$$\begin{aligned} \begin{aligned} d_i^*=\sum _{j=1}^n d_v\left( \tilde{r}_{i j} * R_j^*\right) ; \quad i=1,2, \ldots , m \\ d_i^{-}=\sum _{j=1}^n d_v\left( \tilde{r}_{i j} * R_j^{-}\right) ; \quad i=1,2, \ldots , m \end{aligned} \end{aligned}$$

Phase 10: Ranking alternatives

This is the last phase in the process of decision making. It is concerned with the determination of the closest alternative to the positive ideal solution far from the negative ideal solution by computing the following index:

$$\begin{aligned} CC_i=\frac{d_i^-}{d_i^- + d_i^*}, \qquad i=1,2, \ldots , m. \end{aligned}$$

Fuzzy TOPSIS

The TOPSIS methodology, a technique within the realm of Multiple Criteria Decision Making (MCDM), was initially delineated by Hwang and Yoon in 1981⁷⁰. Subsequently, Chen and Hwang expanded this framework by introducing the fuzzy TOPSIS variant in 1992⁶⁵. Central to the concept of fuzzy TOPSIS is the idea of determining an optimal alternative based on its proximity to the fuzzy positive ideal solution (FPIS) and its remoteness from the fuzzy negative ideal solution (FNIS). The FPIS is characterized by the maximization of advantageous criteria and minimization of detrimental criteria, whereas the FNIS is defined by the converse, maximizing detrimental and minimizing advantageous criteria^57,58. The distinctive feature of the fuzzy TOPSIS approach is its utilization of Linguistic variables, represented through fuzzy numbers, to assign weights to criteria and rate alternatives. This adaptation allows for the integration of uncertain or imprecise data into the decision-making process, as evidenced in Table 3^71,72.

This study employs fuzzy AHP and fuzzy TOPSIS methodologies to ascertain the primary criteria priorities and to sequence the alternatives, respectively. The procedural steps for the fuzzy TOPSIS approach are illustrated in Fig. 1. The algorithm comprises the following stages:

Phase 1: Constitution of a panel of decision-makers assigned to evaluate the alternatives.

Phase 2: Determination of the evaluation criteria.

Phase 3: Adoption of suitable linguistic variables for the ranking of alternatives.

Phase 4: Computation of the cumulative weights for each alternative across all criteria, assuming that the fuzzy evaluations by all decision-makers are represented as triangular fuzzy numbers (TFNs). The calculation of these weights is carried out using the methodology proposed by⁷³.

In this context, for the committee with K experts, the calculations for the minimum, average, and maximum values are given, respectively, by

$a=\displaystyle \min _k(a_k)$, $b=\displaystyle \frac{1}{K} \sum _{k=1}^K b_k$, and $c=\displaystyle \max _k(c_k)$.

These values facilitate the determination of the aggregated fuzzy rating

$$\begin{aligned} R=(a, b, c), \quad k=1,2, \ldots , K \end{aligned}$$

Phase 5: Construct the fuzzy decision matrix as follows:

$$\begin{aligned} \tilde{D}=\left[ \begin{array}{cccc} \tilde{x}_{11} & \tilde{x}_{12} & \ldots \ldots & \tilde{x}_{1 n} \\ \tilde{x}_{21} & \tilde{x}_{22} & \ldots \ldots & \tilde{x}_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ \tilde{x}_{m 1} & \tilde{x}_{m 2} & \ldots \ldots & \tilde{x}_{m n} \end{array}\right] \end{aligned}$$

(1)

Phase 6: The term ’Z’ denotes the normalized fuzzy decision matrix, as described below.

Phase 7: Formation of the weighted normalized fuzzy decision matrix. This matrix is constructed by integrating the different priority values assigned to each criterion and is outlined as follows:

Phase 8: Execute the calculations necessary to ascertain the fuzzy positive ideal solution (FPIS, A*) and the fuzzy negative ideal solution (FNIS, A-).

Phase 9: Compute the distance from each alternative to both FPIS and FNIS.

Phase 10: Calculate the Closeness Coefficient (CCi) for each alternative. The CCi quantifies the proximity to both FPIS and FNIS, facilitating the ranking of alternatives in descending order, as described by Chen (2000)⁶⁸.

In recent years, the fuzzy TOPSIS methodology has been employed across a broad spectrum of practical domains.

Expert team set up

In any decision-making process, it is important to have a diverse and knowledgeable team of experts to provide insights and perspectives from different areas of expertise. In the context of evaluating criteria for capacity planning in healthcare supply chain management, the decision-making team may include individuals with a range of backgrounds, such as healthcare providers, supply chain managers, financial analysts, and patient advocates. Each member of the decision-making team contributes a distinct array of skills and experiences, enhancing the capacity to incorporate all pertinent considerations, thereby ensuring that the final decision is both well-informed and robust.

For a comprehensive evaluation of the experts constituting the decision-making team, it is beneficial to consider their respective job titles, years of professional experience, and specific areas of expertise. Such information facilitates a clear comprehension of the team’s composition and its collective capability to influence the decision-making process. Ultimately, the involvement of a diverse cadre of specialists enables the team to render more informed and efficacious decisions, adeptly navigating the complexities and uncertainties inherent in healthcare supply chain capacity planning.

Table 2 provides a description of the experts who participated in the decision-making team.

Table 2 Description of experts participating in the decision-making team.

Identify the decision problem

The challenge in capacity planning within healthcare supply chain networks is to guarantee the availability of essential resources–namely personnel, equipment, and materials–to meet the demand of patients in healthcare facilities. This task aims to refine capacity planning decisions, thereby enhancing patient care and increasing operational efficiency across the supply network. It necessitates the assessment and prioritization of various factors influencing these decisions, including patient demand, resource availability, cost implications, care quality, and the preferences of stakeholders. The overarching goal is to optimize the capacity of healthcare facilities to provide exemplary patient care while simultaneously minimizing costs and improving operational effectiveness.

Determine the criteria and sub-criteria

In the domain of healthcare supply chain network capacity planning, the identification and establishment of criteria and sub-criteria for evaluating various alternatives is fundamental. These criteria and sub-criteria form the cornerstone of decision-making processes and are imperative for aligning the selected alternative with the strategic objectives of the healthcare organization and addressing the expectations of its stakeholders. This discussion will concentrate on elucidating the methodology for defining and prioritizing these criteria and sub-criteria, emphasizing their significance and applicability to organizational goals. The Fig. 3 displays the identified criteria and sub-criteria.

Fig. 3

Criteria and Sub-Criteria for Healthcare Supply Chain Network Capacity Planning.

A detailed description of the criteria and sub-criteria is presented below:

• 1 Resource Availability : This criterion refers to the availability of resources necessary for providing healthcare services during disaster situations. It takes into account the availability of medical supplies, trained medical personnel, and transportation and logistics resources. The allocation of weight to this criterion reflects its significance in the decision-making framework.

  • Availability of Medical Supplies (e.g., Medication, Equipment): This sub-criterion evaluates the presence of critical medical supplies, including medications, equipment, and personal protective equipment (PPE). The accessibility of these resources is essential for the delivery of efficient healthcare services in emergency scenarios^74,75.

  • Availability of trained medical personnel: This sub-criterion considers the availability of trained medical personnel, including doctors, nurses, and other healthcare professionals. The availability of trained medical personnel is essential in providing quality healthcare services during disaster situations⁷⁶.

  • Availability of transportation and logistics resources: This sub-criterion considers the availability of transportation and logistics resources necessary for delivering medical supplies and personnel to healthcare facilities. It includes factors such as the availability of ambulances, helicopters, and other vehicles, as well as the logistics infrastructure needed to support the delivery of supplies and personnel. The availability of these resources is critical to ensuring that healthcare services can be delivered effectively during disaster situations⁷⁷.

• 2 Patient Needs: This criterion considers the needs of patients who require healthcare services during disaster situations. It takes into account the severity of their medical conditions, their proximity to healthcare facilities, and the accessibility of healthcare services to vulnerable populations. The weighting of this criterion reflects its significance within the decision-making framework.

  • Severity of patients’ medical conditions: This sub-criterion evaluates the severity of patients’ medical conditions, encompassing the intricacy and immediacy of their healthcare requirements. The gravity of medical conditions plays a pivotal role in the distribution of healthcare resources in the context of disaster scenarios⁷⁸.

  • Proximity of patients to healthcare facilities: This sub-criterion considers the proximity of patients to healthcare facilities. It takes into account factors such as the distance patients must travel to receive medical care, transportation infrastructure, and the location of healthcare facilities. The proximity of patients to healthcare facilities is a crucial factor in determining the allocation of healthcare resources during disaster situations⁷⁹.

  • Accessibility of healthcare services to vulnerable populations: This sub-criterion considers the accessibility of healthcare services to vulnerable populations, such as the elderly, disabled, and low-income groups. This assessment incorporates variables such as linguistic obstacles, cultural factors, and socio-economic conditions. Ensuring that healthcare services are accessible to vulnerable groups is essential for achieving equitable healthcare access during emergencies and disastrous situations^80,81,82.

• 3 Speed of Response: This criterion considers the speed of response in delivering healthcare services during disaster situations. This criterion considers the necessary duration for resource mobilization, patient transportation to medical facilities, and the diagnosis and treatment of patients. The emphasis placed on this criterion reflects its significance in the decision-making framework.

  • Time required to mobilize resources: This sub-criterion considers the time required to mobilize healthcare resources, including medical personnel, supplies, and equipment. The faster the resources can be mobilized, the more efficient and effective the response will be to meet the healthcare needs of disaster victims⁸³.

  • Duration for Patient Transfer to Medical Centers: This parameter evaluates the temporal aspect of conveying patients to healthcare institutions. It encompasses the accessibility of transport networks, the geographic distances that patients must navigate, and prevailing traffic dynamics. The faster patients can be transported to healthcare facilities, the higher the chances of survival and recovery⁸⁴.

  • Time frame for Diagnosis and Treatment: This sub-criterion evaluates the duration necessary for the diagnosis and treatment of patients. It encompasses the accessibility of healthcare staff and medical equipment, as well as the efficacy of the medical processes involved. The faster patients can be diagnosed and treated, the higher the chances of survival and recovery^85,86.

• 4 Cost: This criterion considers the costs associated with providing healthcare services during disaster situations. It takes into account the cost of medical supplies, the cost of transporting patients and resources, and the cost of healthcare personnel overtime. The significance attributed to this criterion reflects its relative priority within the decision-making framework.

  • Cost of medical supplies: This sub-criterion considers the cost of medical supplies such as medication, medical equipment, and consumables. The cost of these supplies can increase significantly during disaster situations due to shortages or high demand. The significance attributed to this criterion reflects its relative priority within the decision-making framework⁸⁷.

  • Cost of transporting patients and resources: This sub-criterion considers the cost of transporting patients and resources to and from healthcare facilities. This includes the cost of transportation infrastructure, fuel, and maintenance. The significance attributed to this criterion reflects its relative priority within the decision-making framework^88,89.

  • Cost of healthcare personnel overtime: This sub-criterion considers the cost of healthcare personnel overtime. During disaster situations, healthcare personnel may need to work longer hours or be called in for emergency shifts, which can result in higher labor costs. The weight assigned to this sub-criterion indicates its relative importance in the decision-making process⁸⁶.

• 5 The Stakeholder Preferences criterion refers to the input and preferences of stakeholders involved in the healthcare supply chain network during capacity planning under disaster conditions. The significance attributed to this criterion reflects the relative priority of stakeholder preferences within the decision-making framework.

  • Input from patients and their families: This sub-criterion reflects the preferences and needs of patients and their families, such as the type of medical care they require and their preferred healthcare facilities. The significance attributed to this criterion reflects the relative priority of patient and family input in decision-making^90,91.

  • Input from healthcare providers and administrators: This sub-criterion refers to the input and preferences of healthcare providers and administrators, including their knowledge and experience in dealing with disaster situations. The significance attributed to this criterion reflects the relative priority of the expertise and input of healthcare professionals and administrators in decision-making⁹².

  • Input from government agencies and other relevant parties: This sub-criterion reflects the input and preferences of relevant government agencies and other parties involved in disaster response and recovery efforts, such as non-governmental organizations and community groups. The significance attributed to this criterion reflects the relative priority of the input and expertise of external stakeholders in decision-making⁹³.

Define linguistic variables and fuzzy sets

To address the inherent uncertainties in evaluating criteria within healthcare supply chains during disasters, this study establishes linguistic variables and fuzzy sets corresponding to scales of importance in the multi-criteria decision-making framework. This strategy enables the transformation of qualitative evaluations into quantitative data, which is essential for implementing fuzzy MCDM techniques.

The importance levels are expressed through linguistic terms, each linked to distinct triangular fuzzy numbers. These numbers effectively encapsulate the ambiguity and subjective nature of human assessments. A detailed exposition of these linguistic scales and their respective triangular fuzzy scales is delineated in Table 3.

Table 3 Linguistic Terms and the Corresponding Triangular Fuzzy Number.

Fuzzy numbers are utilized within the context of the fuzzy AHP to determine the relative importance of criteria and sub-criteria in the capacity planning of healthcare supply chain networks. The adoption of fuzzy sets in the decision-making process enables the effective handling and interpretation of uncertainties inherent in expert assessments and preferences. This is essential for developing a robust and resilient healthcare supply chain system, particularly in scenarios complicated by disasters.

In subsequent stages, these fuzzy scales will be utilized to develop pairwise comparison matrices, essential for determining the relative significance of the criteria and sub-criteria through fuzzy AHP. The results provide a clear, quantitative framework for decision-makers, facilitating more informed and precise strategic planning in uncertain conditions.

Obtain weights of criteria and sub-criteria

To make effective decisions in healthcare care, it is necessary to follow a structured approach. Figure 4 outlines the six main steps involved in using the Fuzzy AHP to make decisions. The initial phase involves establishing the decision hierarchy by delineating the primary and secondary criteria essential for the decision-making framework. Subsequently, the second phase entails gathering empirical data from relevant stakeholders, such as patients, healthcare providers, and administrators, regarding their assessments of the comparative significance of these criteria and sub-criteria. This can be achieved through surveys, interviews, or focus groups. Next, the third step involves defining linguistic variables and fuzzy sets for each criterion and sub-criterion. For example, “resource availability” can be defined with fuzzy sets such as “very low,” “low,” “medium,” “high,” and “very high.” The fourth phase entails constructing pairwise comparison matrices at each hierarchical level of decision-making, encapsulating stakeholder evaluations regarding the relative significance of both criteria and sub-criteria. Subsequently, the fifth phase involves the computation of weights through the application of the Fuzzy AHP method. This method consolidates the pairwise comparison matrices and integrates the principles of fuzzy sets. This step can be done using specialized software or spreadsheets. Finally, the results must be validated with stakeholders to ensure that they are reasonable and reflect their preferences and values.

Fig. 4

Steps in Fuzzy AHP Decision-Making Process for Healthcare Planning.

The Table 4 meticulously outlines the criteria and sub-criteria identified for strategic capacity planning within healthcare supply chain networks. These elements are fundamental to the decision-making process, guiding healthcare organizations in optimizing their operational strategies and resource allocations. The criteria include essential operational aspects such as resource availability, patient needs, speed of response, cost considerations, and stakeholder preferences. Each criterion within this set is further delineated into narrower sub-criteria, establishing a comprehensive schema for examination.

For each criterion and its associated sub-criteria, specific weights are assigned, reflecting their importance and relevance to the overarching goals of the organization. The assignment of these weights is based on a systematic analysis which considers factors like the frequency of demand for certain resources, the critical nature of certain patient needs, and the potential impact of rapid response capabilities on patient outcomes.

Each criterion within this set is further delineated into narrower sub-criteria, establishing a comprehensive schema for examination. This matrix aids in visually articulating the interdependencies and relative significance of various factors, thus facilitating a more informed decision-making process.

Table 4 Comparison Matrix of Criteria with Weights.

Table 5 provides further granularity by focusing on the sub-criteria within ’Patient Needs’. This table assigns weights to elements such as ’Severity of patients’ medical conditions’, emphasizing their critical impact on decision-making in resource allocation and emergency response planning. This detailed breakdown assists in prioritizing interventions and resources in a manner that is directly aligned with patient-centric outcomes.

Table 5 Fuzzy aggregation matrix for the C2.

Table 6 presents a consolidated analysis through the application of the Fuzzy AHP, computing both local and global weights for each criterion and sub-criterion. This evaluation methodologically underscores the significance of specific sub-criteria, for example, ’Availability of medical supplies’, and elucidates their aggregated effect on overarching strategic decisions. The global weights delineate the comprehensive impact of each criterion on the decision-making framework, facilitating decisions that are both quantitatively grounded and strategically coherent.

Table 6 Calculating of local and global weights of all criteria and sub-criteria using Fuzzy AHP.

Evaluation of alternatives

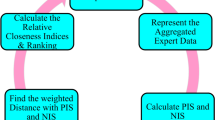
In the domain of healthcare supply chain network capacity planning, adopting a structured methodology is essential. As depicted in Fig. 5, the process encompasses eight critical stages, utilizing the fuzzy TOPSIS method to ascertain the optimal strategy. The initial stage entails the delineation and enumeration of prospective strategies for healthcare supply chain network capacity planning. Subsequently, a decision matrix is constructed, incorporating both the weights of criteria and sub-criteria derived from Fuzzy AHP and the performance scores of each strategy against these criteria. The third phase involves the normalization of the decision matrix to standardize the criteria scales. Following this, the fourth stage requires the calculation of a weighted normalized decision matrix by applying the weights from Fuzzy AHP to the normalized values. The fifth stage is dedicated to identifying the ideal and the negative ideal solutions, which are established by pinpointing the maximal and minimal values for each criterion within the weighted normalized matrix. The sixth stage comprises the computation of separation measures for each strategy, assessing their distances from both the ideal and negative ideal solutions. In the penultimate step, the relative proximity of each strategy to the ideal solution is quantified by dividing the distance to the negative ideal solution by the aggregate distances to both the ideal and negative ideal solutions. The final stage involves ranking the strategies based on their relative closeness indices, with preference given to the strategy that exhibits the highest relative closeness.

Fig. 5

Steps for Evaluating Healthcare Supply Chain Network Capacity Planning Strategies.

Case study

The aim of this case study is to evaluate and contrast the performance of three hospitals –designated as A, B, and C – situated within a specific region. This evaluation will consider various metrics, including the availability of resources, patient requirements, response efficiency, associated costs, and preferences of stakeholders. This comparison will identify the strengths and weaknesses of each hospital, in order to propose improvements to optimize the quality of healthcare provided. To achieve this, we collected data on each hospital in terms of resource availability, patient needs, response speed, costs, and stakeholder preferences. These data will be used to apply the FTOPSIS multicriteria analysis method, combining the FAHP method for criterion weighting:

• 1. Resource Availability

  • A has all necessary resources, including medical supplies, medical equipment, transport and logistics resources, as well as qualified healthcare professionals.

  • B has all necessary resources, including medical supplies, medical equipment, transport and logistics resources, as well as qualified healthcare professionals.

  • C has most necessary resources, including medical supplies and medical equipment, but lacks qualified healthcare professionals and transport and logistics resources.

• 2. Patient Needs

  • A is located in an area where there is a high demand for healthcare services, particularly from patients suffering from serious illnesses and vulnerable populations. The hospital is easily accessible to these patients.

  • B is located in an area where the demand for healthcare services is moderate, but it has good proximity to patients suffering from serious illnesses and vulnerable populations. The hospital is easily accessible to these patients.

  • C is located in an area where the demand for healthcare services is low, and there are few patients suffering from serious illnesses and vulnerable populations. The hospital is easily accessible to patients in the region, but it is difficult to access for patients coming from other regions.

• 3. Speed of Response

  • A has sufficient resources to quickly mobilize teams of healthcare professionals and transport and logistics resources in case of emergency. Diagnostic and treatment times are also fast.

  • B also has sufficient resources to quickly mobilize teams of healthcare professionals and transport and logistics resources in case of emergency, but diagnostic and treatment times are slightly longer than those of A.

  • C has limited resources to quickly mobilize teams of healthcare professionals and transport and logistics resources in case of emergency. Diagnostic and treatment times are also longer than those of A and B.

• 4. Cost

  • The costs of medical supplies, patient transportation, resources, and healthcare staff overtime are similar in all three hospitals.

• 5. Stakeholder Preferences

  • Patients, families, healthcare professionals, and administrative staff uniformly report high levels of satisfaction with the quality of care provided by the three hospitals. Local government agencies also have a favorable opinion about the three hospitals in terms of compliance with healthcare standards and patient satisfaction.

In the exploration of healthcare supply chain efficiency during disaster scenarios, Table 7 plays a pivotal role by presenting the input parameters for the FTOPSIS analysis. The table details a comprehensive set of criteria and sub-criteria, each quantified using triangular fuzzy numbers to capture the inherent uncertainty and vagueness of real-world data. For example, criteria such as the availability of medical supplies, trained medical personnel, and transportation and logistics resources are evaluated. Each criterion is weighted differently, reflecting its relative importance in the context of disaster response. The performance ratings for three hospitals–identified as A, B, and C–are included, providing a basis for a comparative analysis. This methodological approach allows for a nuanced assessment of each hospital’s capacity to manage healthcare resources effectively under the pressure of a disaster, thereby ensuring timely and efficient patient care.

Table 7 Input values of the FTOPSIS analysis.

Table 8 synthesizes the outcomes of the FTOPSIS analysis, culminating in a final ranking of the hospitals based on their preparedness and response capabilities during disasters. The table presents essential metrics, including the separation from the ideal solution ($D^*$) and the negative ideal solution ($D^-$), as well as a consistency index ($Ci$) that corroborates the dependability of the assessments. Hospital A emerges as the most capable, indicating superior management and resource allocation during emergencies, followed by hospitals B and C. This ranking not only highlights the differential capabilities of these facilities but also provides actionable insights into specific areas that need improvement. By focusing on the detailed evaluations provided in Table 8, healthcare administrators can identify strategic interventions to enhance the resilience and responsiveness of their facilities, ultimately improving disaster preparedness and patient outcomes.

Table 8 The final evaluation and ranking of alternatives.

Table 8 presents the final evaluation and ranking of alternatives using the TOPSIS method. The values of D*, D-, and Ci are listed along with their corresponding ranks.

Comparative analysis with other fuzzy MCDM methods

As highlighted in Section 4, the FAHP–FTOPSIS methodology was adopted for its structured treatment of subjective expert evaluations and its ability to model uncertainty in decision-making. To strengthen the credibility and robustness of the obtained rankings, we conducted a comparative analysis using two additional fuzzy MCDM methods: FAHP–PROMETHEE II and FAHP–Fuzzy TODIM. Both have been widely applied in contexts involving imprecise information and conflicting criteria (^94959697). To ensure consistency, all three methods were applied to the same fuzzy decision matrix, using identical FAHP-derived weights. Table 9 summarizes the performance scores and resulting rankings for the three considered alternatives.

Table 9 Comparison of alternatives ranked by FAHP–FTOPSIS, FAHP–PROMETHEE II, and FAHP–Fuzzy TODIM methods.

The results show that while all methods identified Alternative A as the top-ranked option, TODIM slightly favored Alternative C in scenarios with higher cost sensitivity, reflecting its loss–gain dominance logic. PROMETHEE II produced a more evenly distributed preference flow, indicating less polarization between alternatives. These variations suggest that while FTOPSIS provides strong overall ranking stability, TODIM may offer more nuanced insights in trade-off-intensive contexts–an observation supported by prior work (e.g., [Author, Year]) in emergency logistics planning.

These findings highlight that although the final rankings are generally consistent, each method emphasizes different aspects of the decision model. The robustness of the rankings across methods reinforces confidence in the recommended capacity strategy, while also demonstrating the adaptability of fuzzy MCDM tools to healthcare decision-making under uncertainty. This comparative validation confirms the reliability and robustness of the proposed framework, in agreement with similar studies in the literature⁹⁴⁹⁸.

Sensitivity analysis

The sensitivity analysis performed in this research acts as a vital element for confirming the robustness and dependability of the results derived from the FTOPSIS method, utilized in assessing healthcare supply chain networks. The analysis was initially designed to evaluate the stability of the FTOPSIS outcomes by methodically altering the weights allocated to each criterion and examining the consequent changes in the rankings of the healthcare facilities. This adjustment of weights aimed to reflect potential variations in decision-makers’ preferences or changes in strategic priorities, which are common in dynamic disaster response scenarios.

To augment the rigor of our study, the analysis investigated the impacts of alterations to the triangular fuzzy numbers that characterize the performance evaluations of each hospital. By modifying the optimistic, neutral, and pessimistic values, the study assessed the potential influence of perceived performance variations on decision-making outcomes. Each criterion’s weight was independently altered to simulate a range of plausible scenarios, highlighting the model’s responsiveness to changes in resource availability or speed of response considerations.

Fig. 6

Sensitivity analysis.

The results, visually summarized in Fig. 6, present graphical representations illustrating the effects of varying weights and performance ratings on the facility rankings. Radar charts in this figure provide an intuitive comparison across all tested scenarios, clearly showing which factors have the most significant impact on the stability of the rankings. These visual aids are instrumental for healthcare administrators to quickly discern the conditions under which decision-making outcomes are most sensitive, thus aiding in the development of robust disaster preparedness plans.

Moreover, the findings from the sensitivity analysis underscore the resilience of the decision-making framework. While some adjustments led to variations in rankings, the overall order of hospital capabilities remained consistent, with Hospital A consistently showing strong performance. This consistency not only affirms the effectiveness of Hospital A’s supply chain management strategies but also demonstrates a high degree of confidence in the model’s ability to deliver reliable insights under a variety of emergency conditions.

By incorporating the sensitivity analysis and its graphical representation in Fig. 6, the research highlights the strategic value of understanding how different scenarios can affect healthcare supply chain decisions. This insight is crucial for healthcare administrators aiming to ensure that their facilities are well-prepared to manage resources efficiently and effectively during disasters.

Discussion

This research demonstrates the substantial utility of integrating fuzzy Analytic Hierarchy Process (AHP) and fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) for healthcare supply chain capacity planning during disaster scenarios. These techniques effectively manage inherent uncertainties and subjective judgments prevalent in crisis situations, enhancing responsiveness and decision-making quality. Several key findings emerged:

As anticipated, the fuzzy Multi-Criteria Decision-Making (MCDM) approach proved highly effective in accommodating linguistic assessments (e.g., “high urgency,” “limited availability”), significantly outperforming traditional models dependent on precise data, often unavailable during disasters⁶⁵. The approach successfully prioritized critical yet elusive criteria, such as Patient Need Severity and Resource Sufficiency, resulting in robust resource allocation decisions under uncertainty.

Contrary to assumptions of intense stakeholder conflict in disaster scenarios highlighted in some literature, our structured fuzzy framework surprisingly facilitated consensus among diverse stakeholders, including clinicians, logisticians, and administrators. This harmonizing potential of structured fuzzy MCDM warrants further exploration. Additionally, Supply Chain Resilience, encompassing redundancy and supplier reliability, unexpectedly received significant emphasis over Geographic Accessibility in prolonged disaster scenarios, suggesting a nuanced prioritization of long-term operational continuity.

This research aligns with previous findings⁶⁵ regarding the superiority of fuzzy methods over deterministic models in handling disaster contexts. However, it distinctly extends existing knowledge by demonstrating the efficacy of integrated fuzzy AHP-TOPSIS specifically within healthcare supply chain capacity planning, differentiating from studies primarily focused on generic logistics. Unlike prior studies focused solely on supplier selection, the holistic integration of criterion weighting (AHP) and alternative evaluation (TOPSIS) addresses identified gaps and enhances decision robustness under uncertainty.

This study advances theory by:

• Providing empirical validation and a detailed framework for integrating fuzzy AHP-TOPSIS explicitly tailored to healthcare disaster scenarios, addressing unique domain-specific criteria

• Illustrating how fuzzy set theory captures subjective stakeholder judgments systematically

• Identifying unexpected stakeholder consensus-building and priority shifts (such as emphasizing resilience over accessibility) under structured fuzzy frameworks, thereby expanding existing theoretical paradigms

Healthcare planners can significantly benefit from adopting fuzzy MCDM by enhancing the agility, transparency, and adaptability of their decision-making processes. Training and investment in user-friendly software implementations are recommended for effective integration. Healthcare organizations should incorporate these techniques into disaster preparedness protocols and simulation exercises, ensuring improved responsiveness and resource efficiency. Policymakers are encouraged to mandate or incentivize robust decision-support tools, allocating funding for standardized criteria development and training programs to foster systemic resilience.

Limitations and future research directions

Despite its contributions, the study has limitations, notably dependence on Expert Judgment and static decision framework. While fuzzy logic handles uncertainty, there is still potential for bias, inconsistency, or lack of consensus among experts. Furthermore, applications of fuzzy AHP and TOPSIS are static, relying on a fixed set of criteria and alternatives evaluated at a single point in time. However, disaster scenarios are inherently dynamic–conditions such as patient volume, resource availability, and risk severity can shift rapidly. To ensure the fuzzy AHP-TOPSIS framework remains effective in such environments, it must evolve into a real-time and adaptive decision-support system.

Future research directions include:

• Implementing dynamic fuzzy MCDM models, which continuously update rankings and recommendations as new information becomes available. For example, in an emergency setting, updated patient influx or supply data can be used to adjust hospital priority rankings, with previous evaluations retained and blended into new outputs to ensure stability and trend recognition.

• Integrating real-time data analytics, including IoT sensors and social media data, for dynamic updating during disasters.

• Investigating machine learning integration for predictive optimization of fuzzy parameters based on historical disaster data to forecast how the situation might evolve and recommend preemptive actions.

• Exploring the impact of varying expertise levels on fuzzy MCDM outcomes, developing adaptive training modules accordingly.

• Conducting comparative studies across diverse healthcare systems and disaster scenarios (pandemics, earthquakes) to improve generalizability.

• Assessing scalability and effectiveness for regional or national-level healthcare supply chain coordination.

Conclusion

In conclusion, this study demonstrates that fuzzy MCDM techniques–specifically fuzzy AHP and fuzzy TOPSIS–offer a robust framework for improving decision-making in healthcare supply chain planning during disasters. The proposed model effectively addresses uncertainty, enhances resource allocation, and supports the formulation of resilient policies in high-stakes environments. By challenging traditional crisp-data decision-making paradigms, this research underscores the transformative potential of fuzzy logic for real-world emergency management. While the study lays a solid foundation, further validation and adaptation across diverse settings remain essential to fully harness these benefits.

The successful application of this method underscores its potential to significantly enhance the resilience and responsiveness of healthcare systems during catastrophic events, ultimately contributing to improved patient outcomes and more efficient use of scarce resources when they are needed most.