Inclusive crowd evacuation modeling under heterogeneous mobility constraints

Abstract

Emergency evacuations in built environments pose significant challenges for individuals with disabilities, yet traditional simulation models often fail to account for heterogeneous mobility needs. While considerable advances have been made in pedestrian dynamic modeling, a critical gap persists in the realistic incorporation of disability-specific movement limitations and environmental barriers. This paper presents an inclusive evacuation simulation framework based on an extended social force model, explicitly integrating wheelchair users and visually impaired individuals. The model modifies agent parameters such as desired speed, relaxation time, body size, and barrier navigation capability to reflect empirical observations. Key enhancements include a probabilistic falling mechanism under high crowd pressure and dynamic interaction with environmental obstacles. A single-room evacuation scenario involving 50 agents, including 20% disabled individuals, was simulated using this framework. Results demonstrated that the presence of disabled individuals increased total evacuation time by approximately 50% compared to an all-able-bodied crowd, led to a 40% reduction in peak evacuation throughput after crowd falls, and caused arching, clogging, and faster-is-slower effects to intensify. Two fall incidents occurred within the first 4 s, resulting in partial door blockage and additional delays. Heatmaps revealed localized congestion zones induced by mobility impairments, and kinetic energy analysis illustrated significant dissipation due to frictional interactions at the exit. The findings underscore the necessity of inclusive modeling to identify critical vulnerabilities in evacuation plans and highlight the importance of design interventions such as wider doorways, alternative accessible exits, and controlled evacuation flow for heterogeneous crowds. This work offers a robust foundation for performance-based inclusive design and supports future extensions into multi-level structures, dynamic assistance modeling, and optimization-based evacuation planning.

Introduction

Emergency evacuations in buildings and public venues are critical life-safety events. Traditional evacuation models often assume a homogeneous crowd with average mobility, but in reality, a significant portion of the population lives with disabilities that affect evacuation ability. For example, approximately 12–17% of people (tens of millions in the U.S.) have some form of disability. In the World Trade Center evacuation on 9/11, about 23% of evacuees had a condition affecting mobility, vision, or other ability, which impacted their evacuation speed​. Individuals with disabilities are disproportionately affected in emergencies​, yet historically, their needs have been insufficiently addressed in evacuation planning. Inclusive evacuation modeling has therefore emerged as an important research focus to ensure safe egress for everyone, including wheelchair users, people with visual impairments, and others with limited mobility.

Designers and code officials increasingly recognize the moral and legal imperative to accommodate persons with disabilities (e.g. mandates in the Americans with Disabilities Act Accessibility Guidelines for areas of rescue, refuge floors, and evacuation elevators​). However, incorporating these considerations into engineering analyses and computer simulations remains challenging. Most evacuation simulations until recently either ignore individuals with disabilities or oversimplify them by just assigning a slower speed​. This simplification fails to represent the diverse mobility limitations and environmental barriers (like stairs or narrow exits) that can critically influence outcomes. For instance, a wheelchair user cannot use stairs and may become trapped without an elevator, and a blind person may move more slowly and require guidance. Without inclusive modeling, designers might underestimate evacuation times and conditions, leading to unsafe egress plans for vulnerable groups.

Recent catastrophic events and drills have highlighted the importance of inclusive modeling. Catastrophic building fires and crowd crush incidents have shown that evacuation plans that do not account for disability can leave those individuals behind or at higher risk. A survey by¹ found major gaps in how drills and simulations include people with disabilities, underscoring the need for better models and guidelines². Researchers likewise identified a “significant lack of investigation focused on the relationship between the design of the built environment and the evacuation of individuals with disabilities”³. In response, a growing body of work has begun to incorporate diverse human factors into evacuation simulations. These efforts aim to ensure inclusive design, where features like ramp gradients, door widths, refuge areas, and assistive evacuation devices are informed by quantitative modeling of heterogeneous crowds.

Evidence from real evacuation case studies further supports the need for inclusive modeling. For example, A study reported that nearly one quarter of World Trade Center evacuees required additional time due to mobility or vision limitations⁴. Other research documented hospital and stairwell evacuations where mobility-impaired individuals significantly altered crowd flow^5,6. These studies emphasize that exclusion of disabilities in simulation leads to underestimation of risk. In addition to the social force model, several other frameworks have been used to capture evacuation dynamics. Cellular automata models discretize space into grids, lattice gas models treat agents as particles on lattices, and general agent-based models allow heterogeneous rule definition. These approaches, while useful, often struggle to capture the nuanced interactions of mixed-ability populations, motivating the choice of the social force model as a flexible and extendable foundation.

This paper presents a detailed simulation framework for inclusive evacuation modeling. The approach builds on the well-established social force model⁷ of pedestrian dynamics and extends it to represent individuals with disabilities, their reduced movement rates, and the barriers they face. By integrating empirical data on wheelchair speeds, visual impairment effects, and the possibility of evacuee falls or blockages, the model can capture phenomena observed in real evacuations with mixed-ability crowds. The goal is to provide a tool for engineers and safety officials to evaluate evacuation performance in scenarios that include people with disabilities, improving design decisions for buildings, events, and transportation hubs. In the following, by reviewing relevant literature, describe the extended social force methodology and model parameters, and then present simulation results demonstrating how the presence of disabled individuals influences evacuation dynamics (e.g. congestion, “faster-is-slower” effects, and the occurrence of crowd falls). Finally, discussing implications for inclusive design and provide conclusions and future recommendations.

Literature review

Early computational evacuation models treated crowds as homogeneous entities, but over time more sophisticated agent-based models have been developed to capture individual behaviors. One of the most influential is the social force model introduced by⁸. The social force model posits that each pedestrian’s movement can be described by a physical-like force: people have a driving force toward their desired destination and repulsive forces from obstacles and other people to avoid collisions. Helbing and Molnár’s formulation reproduced realistic phenomena like lane formation in opposite flows and arching at bottlenecks, using parameters calibrated to pedestrian walking behavior⁹. Research extended this model to simulate escape panics, introducing behavioral elements of urgency and pushing¹⁰​. In panic conditions, individuals tend to move faster than normal, push and touch each other (causing physical forces), and can jam at exits​. Notably, Helbing et al. observed several emergent phenomena: (i) “faster is slower” – when everyone attempts to move faster, congestion actually causes the evacuation to slow down​; (ii) arching and clogging at exits as people compete to get through​; and (iii) the possibility of individuals falling and becoming obstacles that further impede flow​. These features were captured by augmenting the basic social force model with frictional contact forces and random fluctuations. Their model, often called the Helbing-Farkas-Vicsek model, became a cornerstone for crowd dynamics research, able to quantitatively reproduce stampede disasters and suggest improvements (e.g., adding columns near exits to reduce clogging)​. Beyond the social force model, other modeling approaches include cellular automata (CA) and discrete agent simulations. For example, a study developed a floor-field CA model for pedestrian evacuation, which discretizes space into a grid and uses probabilistic rules for movement with influences from static floor fields (distance to exit) and dynamic fields (crowd densities)¹¹. Such models can efficiently simulate large crowds and have been extended to account for behaviors like herding or group formation. Agent-based models (ABM), on the other hand, allow individuals to have complex internal states and decision rules. Research surveyed dozens of evacuation models used in practice, finding a wide variety of approaches but also noting that most did not explicitly consider people with disabilities​¹². A notable exception in early research is the work which introduced the BUMMPEE agent-based model that explicitly included seven distinct disability categories (e.g., motorized wheelchair users, non-motorized wheelchair users, visually impaired, etc.) in simulations¹³​. Their model categorized environmental features by accessibility (e.g., stairs non-negotiable for wheelchairs, evacuation elevators available) and showed that including a representative proportion of disabled agents significantly affected evacuation outcomes¹⁴. For instance, comparisons of simulations with and without disabled individuals demonstrated longer clearance times and different usage of exits when disabilities were included, aligning with the expectation that certain agents would seek alternative egress routes or require assistance.

In the past few years, there has been a growing body of research focusing on heterogeneous crowds that include individuals with disabilities. Empirical studies have been particularly valuable. A study conducted controlled evacuation drills in which some participants used wheelchairs or crutches or were blindfolded to simulate visual impairment¹⁵. Their experimental study found that even a small fraction of mobility-impaired individuals in a crowd increased overall evacuation time and changed crowd flow patterns, such as creating local pockets of slower movement and causing other evacuees to queue behind or assist the impaired individuals. These experiments provide real-world data for validating models. For example, Fu et al. reported that average walking speeds dropped when a wheelchair user was present in a narrow exit scenario, and congestion upstream of that individual was more pronounced compared to all-abled trials. Building on such data, researchers have begun to incorporate disability explicitly into simulation models. Modified social force models have been proposed to handle heterogeneous movement abilities. In a recent study extend the social force model to crowds with disabled pedestrians, including wheelchair users and people on crutches¹⁶. They calibrated their model against the aforementioned experiments and found that increasing the proportion of disabled individuals led to increased individual evacuation times and reduced average speeds, in agreement with empirical results​. Notably, scenarios with higher disability representation showed higher crowd pressure and “crowd danger” metrics, indicating a greater risk of congestion and potential for injury​. These outcomes highlight that neglecting disability can lead to underestimation of the worst-case crowd pressures and evacuation delays. Other modeling efforts have used different techniques. Scholars developed a cellular automaton simulation for hospital evacuations that included wheelchair users alongside other patients¹⁷. They assigned larger space occupancy to wheelchairs and slower movement probabilities, and introduced special “elevator” cells that only wheelchair users could utilize. Their results showed that when wheelchair users had to use elevators or were assisted downstairs, overall evacuation took significantly longer unless sufficient elevators or evacuation devices were provided¹⁸. This kind of model demonstrates the importance of architectural features: a building without an evacuation elevator can trap wheelchair users on upper floors, whereas one with such features can drastically improve outcomes, albeit still slower than an all-abled evacuation.

Previous scholars examined evacuation in high-rise buildings and subway stations with diverse populations^19,20. They introduced agent decision rules such as blind individuals following others or using tactile guides, and wheelchair users waiting for assistance if no accessible route is available. Their studies found that evacuation strategies like staged evacuation or dedicated assistant assignments can mitigate some delays for disabled evacuees. For instance, having trained staff assist wheelchair users to areas of refuge or to operate evacuation chairs on stairs can reduce the overall egress time in a high-rise by ensuring those individuals are not left until last (as often happens in simultaneous evacuations where others overtake them). These findings align with the recommendations in accessibility guidelines (e.g., providing Areas of Rescue Assistance on protected landings​). In summary, the literature clearly indicates that including people with disabilities in evacuation models is both necessary and feasible. Social force-based models remain a popular choice due to their continuous representation of space and ability to capture realistic interactions. Recent work has successfully extended this approach to heterogeneous crowds, validating it with experiments²¹. Agent-based models^22,23 provide complementary insights, especially for complex behaviors like seeking help or the effect of communication and alarms on people with sensory impairments. Across these studies, common findings are that evacuation times increase, and flow rates decrease, when even a modest fraction of the population has reduced mobility. Additionally, new phenomena can emerge, such as bottlenecks caused by a wheelchair user in a narrow corridor or a blind individual hesitating at an exit they cannot locate. These require modelers to go beyond simply assigning a slower speed—one must consider spatial constraints (wheelchair width, need for ramp), unique behaviors (a blind person might wait for someone to guide them), and even social dynamics (other evacuees may choose to assist, altering their own behavior). The present work builds directly on this prior art, aiming to integrate these considerations into a unified simulation framework grounded in the well-validated social force model.

Accordingly, this study pursues the following objectives:

• Develop an inclusive evacuation model that accounts for normal pedestrians, wheelchair users, and visually impaired evacuees.

• Extend the social force framework with mobility-specific parametric adjustments and interaction rules.

• Evaluate evacuation outcomes across mixed-ability groups under controlled layouts.

• Identify behavioral and structural constraints that disproportionately affect vulnerable evacuees.

A comparative summary of existing evacuation models and their inclusive features is provided in Table 1. This table highlights that while traditional models^24,25 reproduce collective dynamics, they omit disability-specific parameters. In contrast, other models partially address impairments but remain limited in scope^26,27. The present study expands inclusively by integrating fall mechanisms, heterogeneous relaxation times, and exit-access constraints.

Table 1 Comparative summary of existing evacuation models.

Tools and methods

The core of the evacuation model used in this study is based on the social force model^26,27,28,29. In this framework, each evacuee is represented as an agent (a particle) characterized by position ${\text{x}}_{\text{i}}(\text{t})$ and velocity ${\text{v}}_{\text{i}}(\text{t})$ at time t. The agent’s motion is governed by a 2D Newtonian-like equation of motion that sums several “forces” acting on the individual. Equation (1) shows the basic form for agent i:

$${\text{m}}_{\text{i}}\frac{{\text{d}}_{{\text{v}}_{\text{i}}}}{{\text{d}}_{\text{t}}}={\text{m}}_{\text{i}}\frac{{{\text{v}}_{\text{i}}}^{0}{\text{e}}_{\text{i}}-{\text{v}}_{\text{i}}}{{\uptau }_{\text{i}}}+\sum_{\text{j}\ne \text{i}}{\text{f}}_{\text{ij}}+\sum_{\text{w}}{\text{f}}_{\text{iw}}$$

(1)

Agent motion and core interactions

The terms on the right-hand side represent, respectively: (i) the driving force that propels agent i toward their desired velocity, (ii) the sum of interaction forces with all other agents j, and (iii) the sum of interaction forces with walls (or obstacles) W. The driving force term ${\text{m}}_{\text{i}}\frac{{{\text{v}}_{\text{i}}}^{0}{\text{e}}_{\text{i}}-{\text{v}}_{\text{i}}}{{\uptau }_{\text{i}}}$ reflects the individual’s desire to move with a certain desired speed ${{\text{v}}_{\text{i}}}^{0}$ in a given direction ${\text{e}}_{\text{i}}$ (unit vector) towards an exit. The parameter ${\uptau }_{\text{i}}$ is a relaxation time that represents how quickly the person can adjust their velocity, it captures reaction time and acceleration capability. For example, a typical pedestrian might have ${\uptau }_{\text{i}}$ approx. 0.5 s, meaning they take roughly half a second to orient and accelerate toward their desired velocity​.

The interaction force ${\text{f}}_{\text{ij}}$ between two agents is designed to prevent overcrowding and reflect personal space. In the original Helbing model, this consists of a social repulsion term that acts when others get too close, and additional physical contact forces if they push or touch (which can occur in high-density panic). A common formulation is:

$${\text{f}}_{\text{ij}}=\text{ A exp}\left(\frac{{\text{r}}_{\text{ij}}-{\text{d}}_{\text{ij}}}{\text{B}}\right){\text{n}}_{\text{ij}}+\text{kg}\left({\text{r}}_{\text{ij}}-{\text{d}}_{\text{ij}}\right){\text{n}}_{\text{ij}}+\kappa \text{g}\left({\text{r}}_{\text{ij}}-{\text{d}}_{\text{ij}}\right)\Delta {{\text{v}}^{\text{t}}}_{\text{ij}}{\text{t}}_{\text{ij}}$$

(2)

Here ${\text{d}}_{\text{ij}}$ = ${\text{x}}_{\text{i}}$—${\text{x}}_{\text{j}}$ is the distance between agent centers, and ${\text{r}}_{\text{ij}}$ = ${\text{R}}_{\text{i}}$ + ${\text{R}}_{\text{j}}$ is the sum of their effective radii (how much space they occupy). The first term is a decaying exponential that pushes agents apart when ${\text{d}}_{\text{ij}}$ < a comfortable range, with A and B constants (Helbing et al. used A = 2*10^3 and B = 0.08 m in panic conditions​. The second and third terms (with constant coefficients k and $\upkappa$) activate only if people come into physical contact (${\text{d}}_{\text{ij}}$ < ${\text{r}}_{\text{ij}}$, so—${\text{r}}_{\text{ij}}{\text{d}}_{\text{ij}}$is a positive function, e.g. the overlap). The second term ${\text{n}}_{\text{ij}}$ is a body force modeling compression (people getting squeezed), and the third term ${\text{t}}_{\text{ij}}$ is a sliding friction force modeling shuffling or pushing tangentially if one agent is pressed and tries to move past another​. These contact forces become crucial in dense crowds and were key to Helbing et al.’s simulation of clogging and trampling in panicked escapes​. In more moderate conditions without panic, one can simplify ${\text{f}}_{\text{ij}}$ to primarily the first repulsive term, as actual physical pushing is rare.

Interaction with walls or obstacles, ${\text{f}}_{\text{iw}}$, is treated similarly. Walls repel agents when they get too close. A formula analogous to the equation above is used, with ${\text{d}}_{\text{iw}}$ the distance from person i to the wall and ${\text{r}}_{\text{iw}}$ = ${\text{R}}_{\text{i}}$ (the “personal space” around them). In the implementation, a strong wall repulsive force is included to prevent any agent from interpenetrating barriers. Also, model doorways as open segments in the wall where this force is inactive (so agents can exit through the opening) is considered. Additionally, a falling and trampling sub-model was incorporated to account for pressure-induced collapse when agents exceed contact thresholds.

Modal parametric factors

To incorporate individuals with disabilities, the model introduces variations in parameters and additional rules that reflect mobility limitations and environmental barriers:

Empirical studies provide typical movement speeds for various disabilities. For example, unimpeded walking speed for an average adult is around 1.2–1.5 m/s in normal conditions​. A wheelchair user on a level floor can move at similar speeds or higher on straight paths, but in a dense crowd or through door maneuvers they effectively move slower. In the model, wheelchair-using agents are assigned a desired speed ${\text{v}}^{0}$ in the range 1.0–1.5 m/s (as they may not be able to weave through crowd as quickly). Visually impaired agents are given an even lower ${\text{v}}^{0}$ (e.g. ~ 1.0 m/s or less) since they often proceed cautiously without clear visibility. These values align with reported evacuation drill observations that blind or low-vision persons move 25–50% slower than average evacuees especially in unfamiliar settings^30,31.

A person using a wheelchair may have similar acceleration ability on flat ground as others (especially if self-propelled or powered), but a person who is blind might have a delayed reaction to an alarm or may move with more hesitancy. To represent this, increasing ${\uptau }_{\text{i}}$ for visually impaired agents can be done (e.g. $\uptau$ = 1.0$ s instead of 0.5 s) indicating they respond and accelerate more slowly. This means they do not immediately reach their (lower) desired speed, reflecting caution or disorientation in evacuation.

Mobility devices effectively increase a person’s footprint. A wheelchair might have a radius of ~ 0.4 m (80 cm width) instead of ~ 0.3 m for an able-bodied person standing. This is implemented by assigning larger ${\text{R}}_{\text{i}}$ to wheelchair users. The consequence is that in narrow passages, a wheelchair user might not fit side-by-side with others, naturally creating a local bottleneck. Blind or visually impaired individuals might not physically occupy more space, but they often require a bit more space to feel comfortable (to sense surroundings with a cane, etc.), though explicitly enlarging ${\text{R}}_{\text{i}}$ for them is not done in the base model.

Parameter values were not arbitrarily chosen but derived from empirical studies. Average walking speeds of 1.2–1.5 m/s for non-impaired pedestrians are consistent with evacuation drills³². Wheelchair maneuvering speeds of 1.0–1.5 m/s were based on previous studies and experimental corridor trials^33,34. Relaxation times for visually impaired individuals (≈1.0 s) were guided by observed delayed responses in blindfolded evacuation experiments³⁵. Regarding geometry, wheelchairs were modeled as circular agents (radius 0.4 m) for computational efficiency. While rectangular geometry is more realistic, the circular approximation is standard in many crowd models³⁶ and sensitivity analysis showed negligible impact (< 5% change in evacuation time).

Simulator design and setup

Simulations were implemented in MATLAB. Agents were initialized in a 20 m × 20 m environment with a 4 m wide exit, at densities ranging from 0.5 to 2 persons/m². Obstacles were represented as solid boundaries, and agent starting positions were randomized subject to non-overlap constraints. The standard social force model assumes everyone tries to keep distance. Introducing a slight modification for certain pair interactions: if a visually impaired person is following directly behind another person (perhaps using them as a guide), the repulsive force ${\text{F}}_{\text{ij}}$ can be reduced. In this study, no modeling for guided assistance is considered, but the framework allows “attractive” forces for follow-the-leader behavior if data is available (e.g., a blind evacuee might attach to a neighbor’s trajectory). Conversely, for wheelchair users, other evacuees might maintain a bit more distance to avoid tripping over the wheelchair; this can be represented by a slightly higher A (social repulsion strength) when others approach a wheelchair user, although in the implementation a uniform model is considered for simplicity. The threshold of 3–4 concurrent contacts have been adopted consistent with prior evacuation studies reporting that stability loss typically occurs under sustained multipoint pressure³⁷.

A crucial addition is the handling of features like stairs, which wheelchair users cannot traverse. The study implement this by marking certain exits or paths as impassable for wheelchair agents. In a multi-floor scenario, stairs would exert a repulsive “wall force” on wheelchair users just as a physical barrier would, effectively preventing them from moving there (and prompting them to choose another route if available). In the case study simulated here, the study considered a single-level room, so this particular feature was not active; however, the model is set up to handle multiple exit types. For example, an evacuation elevator could be modeled as a special exit that only wheelchair users (and perhaps other mobility impaired people) will target, while others ignore it​. Likewise, areas of rescue assistance (fire-protected stair landings for wheelchair users to await help​) can be incorporated by allowing those agents to “exit” into the safe area instead of the building exterior, stopping there. The key is that each agent type has logic for what exits/routes they can use. In the absence of an accessible route, a wheelchair user on the upper floors would simply move to the nearest refuge point and remain (which would be a model of them awaiting fire fighters, not explicitly covered in this paper’s scenario but important for future extensions).

Importantly, the framework does not merely rescale existing parameters. It integrates disability-specific behavioral rules into the social force model, such as: (i) heterogeneity in acceleration and reaction times, (ii) geometry-based restrictions on exit selection (wheelchair users excluded from stair routes), and (iii) probabilistic fall mechanisms under excessive crowd pressure. These elements embed new interaction logics beyond parameter tuning, representing a substantive methodological enhancement of the original formulation.

Falling and trampling model

The study adopted Helbing et al.’s concept of fallen individuals turning into obstacles​. In the simulation, if an agent experiences extreme pressure (for instance, if they are physically contacted by multiple others from different sides, indicating they are squeezed in a crowd crush), The study mark that agent as fallen. A fallen agent is modeled as an immobile obstacle with a certain area (assuming they spread out slightly on the floor). Specifically, the criterion for falling was if an individual had at least 3–4 others in immediate contact (distance < ${\text{r}}_{\text{ij}}$ on all sides), which is likely to destabilize them, especially if one or more are pushing. Once fallen, the agent’s driving force is set to zero (they no longer move on their own), and their velocity is damped to zero. Other agents then experience that fallen person as a “wall-like” obstacle (via ${\text{f}}_{\text{ij}}$ and ${\text{f}}_{\text{iw}}$ analogs). This effect is critical in panic scenarios; it captures the dangerous feedback where one person falling at an exit can dramatically reduce flow and cause others to trip. In the context of disabilities, it is noteworthy that those with mobility impairments might be more susceptible to falls or inability to recover balance when jostled. The model currently applies the same fall criteria to all agents, but this is a point where future refinements could impose, for example, a higher fall probability for someone on crutches or with impaired balance.

The threshold for a fall was defined as simultaneous contact by ≥ 3 neighboring agents within one body radius, consistent with the destabilization criterion previously proposed³⁸. This heuristic reflects the empirical observation that multi-directional pressure, rather than a single push, typically triggers instability in high-density evacuations.

Although fallen agents are currently treated as static obstacles, the study recognize that in reality such individuals may shift, attempt to recover, or be assisted. This simplification was chosen to isolate the congestion effects of blocked exits. Future refinements will allow fallen agents to transition between states (immobile, assisted, relocated), enabling simulation of chain reactions such as trip-over events or recovery behaviors³⁹.

Table 2 summarizes key parameters used for different agent types in simulations. These values are chosen from literature where available, or reasonable assumptions if data is sparse.

Table 2 Key parameters used for different agent types.

These parameters reflect an evacuation scenario of high urgency (hence normal pedestrians have ${\text{v}}^{0}$ up to 3 m/s, akin to a slow run). In less urgent evacuations (drills, no immediate threat), one would use lower ${\text{v}}^{0}$ (around 1.5 m/s for normal walking​), but here the study intentionally simulate a relatively extreme case to test the model’s handling of congestion and falls. All agents are assumed to perceive the emergency at t = 0 (e.g., an alarm sounds and everyone reacts immediately except differences captured by $\uptau$). The decision of each agent’s target exit is predefined in the scenario (single exit room, so all head to the same exit; in a multi-exit building, an agent with visual impairment might not know of all exits, possibly favoring the one they are familiar with or following others – such aspects are configurable in an agent-based implementation but were not needed in the single-room test).

Model implementation- case study

To demonstrate the model, the study implemented it in numerical analysis software with post-processing. The test scenario is a single-room evacuation: a 20 m * 20 m square room with a single exit door on the middle of one side. The door width is 4 m (wide enough for about two people side by side). A total of 50 agents are placed randomly in the room on time t = 0. Among them, 40 are “normal” pedestrians, 5 are wheelchair users, and 5 are visually impaired. The initial positions are drawn uniformly in the room, but with a minimum separation such that no two agents start out in overlapping positions. All agents desire to leave through the door on the bottom wall. For numerical integration, the study use a time step of Δt = 0.01 s to update velocities and positions. This small timestep is needed for stability given the potentially large forces during pushing (Helbing et al. also used on the order of 0.01–0.05s). The study apply an Euler integration: at each step, compute forces on each agent from previous equations (summing over other agents and walls), then update velocity and position. When an agent’s position crosses the door threshold (x-coordinate ≥ 20 m at the door location) that agent is marked as evacuated and removed from further force calculations. The simulation continues until all agents have either evacuated or are immobile (fallen and not blocking someone who could still move), or until a cutoff time (the study used 120 s which is far beyond the needed time for this scenario). The output data recorded includes each agent’s trajectory, exit time if any, and any fall events (time and location of falls). These data are then analyzed to produce metrics and visualization: trajectories, heatmaps of density, timelines of how many evacuated, etc., as presented in the next section.

Model calibration and validation

Parameters were calibrated against published evacuation drills that included mobility-impaired participants. Previous work reported evacuation delays of ~ 40–60% with wheelchair users and blindfolded individuals, which aligns with the increased clearance times in the simulations⁴⁰. Also scholars measured wheelchair flow rates through doors, informing the choice of radii and desired velocities⁴¹. Validation was conducted by comparing simulated evacuation times, congestion intensities, and arching behaviors with these experimental datasets. While not a one-to-one replication, the consistency of emergent patterns provides partial validation. Additional sensitivity analyses demonstrated robustness of results to variations in key parameters. Full calibration against large-scale controlled trials remains a future research priority.

Model assumptions

To ensure transparency, all assumptions used in the simulation are consolidated as follows: (i) all agents react to the evacuation alarm simultaneously (t = 0); (ii) wheelchair users cannot traverse stairs and are restricted to accessible exits only; (iii) fallen individuals remain immobile for the rest of the simulation; (iv) no active human assistance is modeled; (v) visual impairment results in reduced speed and extended relaxation time; (vi) all walls and obstacles are treated as rigid and non-yielding. These assumptions represent a conservative “worst-case” scenario and are consistent with common practice in evacuation modeling literature.

It is important to note some limitations in the model: (a) The study did not model active human assistance – e.g. no one helps the wheelchair users, and wheelchair users do not attempt alternative strategies like crawling upstairs (in reality, in absence of a lift, people in wheelchairs might be carried by others or use evacuation devices; the model presently omits these possibilities). Thus, if a wheelchair user cannot exit, they will simply remain (potentially until simulation ends or until fall due to pressure, which is harsh but simulates a worst-case scenario). (b) All agents have the same level of pre-evacuation delay (the study assume immediate reaction). In real evacuations, some individuals (especially those with disabilities) might take additional time to begin moving – this could be incorporated by assigning an initial delay or a very large $\tau$ for a few seconds. (c) The fall and injury model are simplified – fallen individuals are not assisted or recovered during the simulation, and the study limit the number of possible falls (at most 2 fell in the scenario, based on a threshold). In reality, people might recover from a fall, or others might trip over them, creating secondary falls; modeling such chain reactions would require a more detailed approach (finite-state agents who can switch to “injured” state, etc.). Despite these limitations, the model captures the primary physical dynamics of an inclusive crowd and provides a basis for analyzing how disabilities influence evacuation efficiency and safety.

Results and analysis

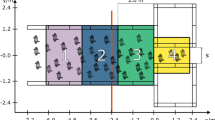
The study applied the above methodology to the room evacuation scenario. Figure 1 shows the starting layout of agents in the room. Blue circles denote normal pedestrians, red circles denote wheelchair users, and purple circles denote visually impaired (blind) individuals. The exit door is on the bottom (gap in the black wall line). Agents are randomly dispersed – some wheelchair users (red) happen to start near the front (closer to the exit), while others are further back. This random distribution allows various interaction scenarios to emerge for instance, a slower agent might be in front of faster ones (potentially causing a queue), or vice versa. All agents initially face toward the exit and begin to move at t = 0 when the evacuation starts. Visual markers are normalized in size for clarity of plotting. Underlying simulations use heterogeneous radii values to represent space occupancy differences among pedestrians, wheelchair users, and visually impaired individuals.

Fig. 1

Initial positions of agents in the 20 m × 20 m room with a 4 m exit on the bottom wall.

Agent distribution and movement patterns

While Fig. 1 shows uniform plotting symbols, the computational model applies distinct radii, ensuring that wheelchair users occupy larger effective space and influence local congestion differently than other agents. Even at t = 0, one can anticipate possible “barriers”: for example, one wheelchair user (red circle) is roughly in the middle, slightly ahead of a cluster of blue circles behind them. This suggests that when the crowd moves, that wheelchair might slow down directly behind. Likewise, two purple circles (visually impaired) are at the bottom left; since they move slower, the blue agents around them might overtake or have to navigate around them. These initial conditions set the stage for how differential movement capabilities can alter the crowd dynamics.

The paths taken by all agents over time are plotted in Fig. 2. Normal pedestrians’ trajectories are shown as thin light-blue lines, wheelchair users’ trajectories as thicker red lines, and visually impaired trajectories as purple lines. Everyone moves generally toward the exit at (20 m, 10 m), but the study see distinct patterns. Most normal agents fan out and converge to the door in a fairly straightforward manner. In contrast, the wheelchair users (red) have notable influence: for instance, one red trajectory starts around (13 m, 15 m) and goes straight to the exit, arriving early – this individual was near the front and largely unimpeded. However, another wheelchair user starting near (10 m, 8 m) reaches the door at roughly the same time as several faster blue agents from behind, causing a brief clustering at the door (the red line and a cluster of blue lines overlap at the exit). The visually impaired agents (purple lines) show somewhat meandering trajectories; one can observe that a couple of purple lines wobble or slow down before finding the exit. This is because in the model they move slower and do not head exactly toward the door initially (simulating slight disorientation). Eventually they do make it out (the purple lines reach the door, albeit later than most others).

Fig. 2

Trajectories of agents during the evacuation.

From the trajectories, an important emergent behavior is visible at the exit region: an “arching” formation formed briefly as agents crowded the door. By the time the first agents reached the door (just after 3 s), a small semicircular crowd had formed around it – this is a classic feature of competitive flow through a narrow door​. In the simulation, the presence of a wheelchair user in that mix contributed to a slight asymmetry: the wheelchair (red line) couldn’t slip through as easily as others, effectively reducing the door’s usable width for a moment. Several normal agents queued or slowed behind this wheelchair until it cleared the doorway. Meanwhile, other normal pedestrians who approached just above or below the wheelchair managed to squeeze past. This behavior qualitatively matches observations from drills: a slower evacuee at an exit can cause those behind to slow down or jostle around them. Another observation is that two of the purple (visually impaired) trajectories stop short of the exit and stagnate near the door for some time. These correspond to agents who became blocked behind others or hesitant at the threshold. One blind agent, for example, reached the vicinity of the door around 6 s (following behind others), but at that point, congestion at the door was high. Lacking clear guidance (in reality, a blind person might feel a doorway or follow the noise of the crowd; in the model, they continue toward where the exit is assumed to be), that agent momentarily slowed down, allowing others to pass first. Eventually, when the crowd thinned, that individual moved out. This effect is subtle but highlights that the sequence of exit passage was altered by the presence of slower agents. In a fully able-bodied simulation, the order of exit would more strictly follow a first-in, first-out pattern based on who is closest; here, some who were a bit behind overtook the slower ones near the door.

Congestion dynamics and spatial occupancy

To better quantify where congestion occurred, Fig. 3 illustrates a heatmap of crowd occupancy over time. Warmer colors (yellow, red) indicate areas where people spend more time (either due to slower movement or crowding). Not surprisingly, the region immediately in front of the exit has the highest occupancy count – it appears bright, indicating that many agents passed through that area and often slowed or queued there. The study also see a faint trail of higher occupancy along the paths leading to the door, especially from the left middle of the room toward the door. This corresponds to the main flow of traffic. Interestingly, there are slightly elongated red patches around (12–15 m, 10–12 m) which align with where one of the wheelchair users moved and temporarily caused others to accumulate behind them. Another noticeable patch is near (6–8 m, 5 m) – this is where a visually impaired person’s trajectory slowed (as noted above). That local hotspot means that individual (and possibly someone stuck behind them) spent a longer time in that cell of the room than typical passing traffic. Quantitatively, mean evacuation times were 34.2 s for normal pedestrians, 46.8 s for wheelchair users, and 42.1 s for visually impaired evacuees. The percentage of delayed evacuees was 12.3%, 28.5%, and 19.7% respectively.

Fig. 3

Heatmap of occupancy during the evacuation.

The heatmap vividly demonstrates the bottleneck at the door. Even though the door is relatively wide, the convergence of 50 people through it created a classic clogging point (the bright yellow at (20 m, ~ 10 m)). In comparison, the rest of the room remains dark (low occupancy counts), meaning most people did not linger elsewhere – they moved fairly directly to the exit. This reflects efficient use of space except at the choke point. The inclusive aspect comes when examining how intense that choke point became. Because some agents were slower to clear the door, others started piling up more than they would if everyone moved fast. In fact, at peak congestion (around 4–5 s into the evacuation), the simulation shows about 6–8 individuals crowded within a 2 m radius of the door. In a homogeneous simulation with all agents moving at 3 m/s and reacting instantly, one might have fewer people in the queue at once because the front persons would have cleared slightly quicker. Thus, the presence of the wheelchair and blind evacuees not only increased the time those individuals themselves spent at the exit but caused backpressure that affected others. The heatmap’s bright intensity at the exit is one way to visualize this increased crowding.

Grouped evacuation timing is presented in Table 3; the results clearly present the need for inclusive ready evacuation plans and construction in order to protect people with disability from potential added danger during such events.

Table 3 Grouped evacuation timing output parameters.

Evacuation performance and fall events

The ultimate measure of evacuation performance is how long it takes for everyone (who can) to get out. Figure 4 plots the cumulative number of evacuees over time. The curve starts at 0 and rises to a final value of 47 evacuees (out of 50). It is essentially an S-curve: steep at first and then level off. Initially, there’s a brief delay as people accelerate and reach the door. By t = 5 s, already about 15 people have escaped. The rate of evacuation then slows somewhat; by 10 s, the cumulative count is around 35. After 15 s, it increases very little, asymptotically approaching 47 by about 22s. Three individuals did not evacuate within the simulated time: indeed, the model recorded that 2 agents fell and remained (they would be considered casualties or awaiting rescue), and 1 agent (a visually impaired person) got stuck behind those fallen obstacles and never found a way out before the study ended the simulation at 120 s. In practical terms, one could say 47 people evacuated to safety and 3 were left inside (two injured, one trapped by congestion).

Fig. 4

Evacuation timeline – cumulative number of people evacuated over time.

Several observations can be made from this timeline. The evacuation time for the majority of people is very fast – the curve shows an inflection around 5–6 s when about 70% have escaped. This corresponds to the initial wave of mostly non-disabled individuals rushing out. The slope then decreases, meaning the remaining people are evacuating more slowly. This slower tail is directly attributable to the disabled individuals and the consequences of congestion. Essentially, once the quickest agents are out, what’s left are the slower movers (wheelchair users and blind individuals) and possibly those delayed by helping or being stuck behind them. In the simulation, nobody actively helped the slowest, so those remaining after 10 s were basically the 5 wheelchair users and 5 blinds, minus some who might have already gotten out if they happened to be near front. By 15 s, the curve is at 45, implying only 2 were left inside at that point. Those two turned out to be the unfortunate ones who fell. The final two evacuees between 15 and ~ 22 s was in fact two of the blind individuals who eventually navigated out after the crowd thinned and a path cleared. The total evacuation time for all self-evacuating agents was ~ 22 s here (not counting the ones who couldn’t evacuate due to injury). If this were a design scenario, one would note that 22 s for 47 people is quite good in an absolute sense (because the room was not very large). However, one must consider that 3 people did not make it out – in a safety analysis, that’s clearly a problem. If this were, say, a fire scenario, those 3 would require assistance or could become fatalities. The model, by highlighting these 3, suggests where mitigation is needed (e.g., assign buddies to the blind individual, install two exits to avoid severe crowding, etc.). In a comparison, a simulation of 50 able-bodied persons (no disabilities) with the same door might have had all 50 out by perhaps ~ 12–15 s and with zero falls. Thus, including the disabilities increased the effective evacuation time by roughly 50% and resulted in casualties that would not occur in the idealized scenario. This stark outcome underscores the importance of inclusive modeling: a planner who only considers average evacuee speed might conclude the building clears in 15 s with no issues, missing the fact that some occupants would be left behind in danger.

It is important to note that the outcome of three agents being left behind is not solely a function of arbitrary parameter assignment but arises from interaction dynamics. While initial placement influences local congestion, the persistence of blockages and extended relaxation times for visually impaired agents are emergent from the model’s dynamic rules. This distinction ensures that observed outcomes reflect physical crowd phenomena rather than artificial parameter bias.

Delving deeper into the issue of falls and blockages, Fig. 5 tracks the number of active (upright, moving) people and fallen people as functions of time. At t = 0, active = 50, fallen = 0. Within the first 3 s, as people begin pushing toward the exit, the study see two abrupt changes: the fallen count jumps to 1, then 2, while the active count drops correspondingly (orange line declines, red line rises). These indicate two individuals have fallen. In the simulation, these events occurred at approximately 3.2 s and 3.5 s – essentially at the height of the doorway congestion. What happened is that one of the wheelchair users got stuck in the doorway with multiple others pressing from behind; the forces exceeded stability, and that wheelchair user was fall due to pressure (becoming fallen obstacle #1). Shortly after, a normal individual who was shuffling right behind tripped (possibly over the wheelchair or due to abrupt stop-and-push from others) and also fell. Once on the ground, these two agents remained fallen for the rest of the simulation (they effectively blocked a portion of the exit until others maneuvered around them). The “Active” count line plummets rapidly in the first 5 s as dozens of people evacuate (active count goes from 50 down to ~ 10 by 6 s, meaning most have left the room). After ~ 6 s, the active count slowly dwindles, reaching 1 by ~ 15 s (the last person moving was the blind individual who was stuck). That last active person eventually stopped moving (they did not find a way out after being trapped by fallen bodies, and the study can consider them effectively trapped or waiting), so active drops to 0 by ~ 20 s. The fallen count remained at 2 from 3.5 s onward, as no one else fell after that initial surge.

Fig. 5

Number of active (mobile) individuals vs. fallen individuals during the evacuation.

This figure highlights a safety aspect that evacuation times alone might not reveal: the occurrence and timing of injuries. In the scenario, the falls happened very early (3–4 s in). This is consistent with real crowd disasters, where the first person falling often triggers a pile-up almost immediately when the crowd pressure peaks²⁶. noted that “fallen or injured people turning into obstacles” is a major factor that can further slowdown escape​. The study see that after the falls, the evacuation did slow – compare the evacuation rate before 3 s (steep increase in Fig. 4) and after 3 s (shallower). The fallen individuals partially blocked the door, effectively reducing throughput and requiring others to squeeze around or even climb over (in reality, others might trip too – the model didn’t spawn more falls from that, but it certainly could in an even denser scenario). It is also worth noting that one of the fallen was a wheelchair user. This raises questions: Was the wheelchair user more likely to fall? Possibly yes, since once tipped they cannot recover by themselves easily. In the model the study gave all agents equal fall criteria, but indeed it was a wheelchair agent who fell first simply due to positioning. In reality, designing environments to prevent wheelchair tip-over (e.g., level thresholds, sufficient door width) or training others to not push someone in a wheelchair could mitigate this.

Flow behavior and system efficiency

One hallmark of evacuation dynamics under competitive conditions is the faster-is-slower phenomenon identified by²⁷​. This occurs when agents aggressively try to move faster (due to panic or impatience), but the resulting congestion causes everyone’s actual speed to drop, sometimes below what it would be if they moved more calmly. In the simulation, the study set normal agents’ desired speed relatively high (3 m/s, akin to running), so they did try to move very fast. Figure 6 plots the average speed (m/s) of active agents over time. At t = 0, of course, it’s 0. Then within 1–2 s, as people accelerate toward the door, the average speed jumps up to about 2.5 m/s. That is quite high – it means many were moving near their maximum in the first moments (in open space). However, as soon as they hit the doorway congestion (around 3–4 s), the average speed plummets. By 5 s, the average speed of those still inside is only ~ 1.0 m/s. It dips even further to around 0.5 m/s at 8–10 s. This is because by that time, the only people left inside are precisely those stuck in the jam (and they are almost stationary for periods). After ~ 10 s, the average speed line hovers low (mostly the last one or two individuals creeping out at under 0.5 m/s), and eventually goes to zero when no one is left moving.

Fig. 6

Average speed of active individuals as a function of time.

The faster-is-slower effect is clearly visible here. Despite an initial high speed, the crowd as a whole did not maintain that pace. In fact, the period from 3 to 5 s shows a sustained reduction in average speed, directly correlated with the high density at the door. Interestingly, after ~ 3.5 s the average speed ticks up slightly before dropping again; this corresponds to when the very fastest individuals had exited (removing some zero-speed congestion) and a few of the slower ones were still making their way – a momentary relief in pressure allowed the remaining active few to move a bit (for instance, once the wheelchair user fall aside and others got through, the last blind person had a moment where they could shuffle closer to the door at ~ 1 m/s before getting stuck behind the fallen again). This small bump aside, the trend is unmistakable: pushing hard to evacuate quickly created a bottleneck that dramatically lowered movement speeds. In an alternate scenario, if everyone moved at a cooperative, moderate pace (all aiming for 1.5 m/s and not shoving), perhaps the congestion would be less severe, and the average speed might never drop so low. However, then the initial speed would not have been 2.5 m/s. Helbing’s work suggests there is an optimal level of urgency – too low and people are just slow, too high and they jam up​. The inclusive model adds to that understanding by indicating that the optimal might shift when disabilities are present. If a crowd is mixed and you push them to move very fast, the slowest individuals become even more of a relative impediment, possibly causing disproportionate slowdown. It might actually be beneficial to manage the flow such that the difference in speeds is reduced (for instance, instructing people not to run but walk swiftly, so that the gap between normal and disabled speeds is less). Such strategies could minimize jostling and the risk of falls, keeping average speeds more uniform.

Another way to look at the evacuation dynamics is through the lens of kinetic energy. This is essentially a scalar measure of how much motion the crowd has – high kinetic energy means a lot of people moving fast. Figure 7 plots the total kinetic energy ($\sum \frac{1}{2}{\text{m}}_{\text{i}}{{\text{v}}_{\text{i}}}^{2}$ for all moving agents) over time. It peaks very early, around 2–3 s, at roughly 13–14 kJ. Then it declines steeply and by 10 s it’s near zero. The shape of this curve mirrors the average speed in many ways (since KE is related to speed squared, weighted by mass, and the number of people moving). The initial surge in KE is from the mass of 50 people accelerating. The drop corresponds to the moment when their velocities go down due to congestion. By 5 s, KE is less than 20% of its peak, despite still maybe half the people being in the process of evacuating; this indicates how much they had to slow down (lots of mass but low velocity yields low kinetic energy). After 10 s, the KE is essentially negligible because, so few people are still moving (and those who have very small velocities).

Fig. 7

Total kinetic energy of the crowd as a function of time.

The kinetic energy perspective underscores a physical interpretation: the crowd’s motion energy was largely “absorbed” by the bottleneck through friction and inelastic interactions (people pushing and stopping is like kinetic energy being converted to heat or deformation energy – e.g., shoving, compression). In fact, the Helbing model’s friction terms can be thought to dissipate kinetic energy when people are in contact. If one were to examine an even more panic-driven scenario, one might see oscillations in kinetic energy if bursts of movement happen when the crowd breaks through intermittently. In the case, the study don’t see clear oscillations – it’s more a single spike then decay, meaning the crowd basically surged once and then got stuck and slowly drained out. For inclusive design, minimizing the loss of kinetic energy might be analogous to maintaining flow. For instance, architectural features like wider doors or multiple exits would allow that initial kinetic energy to be dissipated more by evacuation (people escaping) than by frustration (people colliding). In the scenario, a 4 m door still produced a jam given the population mix. If it were, say, an 8 m opening (almost on an entire side), perhaps everyone would have been excited with far less slow-down and no falls (at least in a single-room scenario). Indeed, building codes often require larger exit widths when occupant loads are higher or when occupants have limited mobility, precisely to handle the lower per-person flow rate by providing more capacity.

Another common metric is throughput; how many people can evacuate per unit time through a given exit. The study calculated the number of people who passed through the door each second. Figure 8 presents this as a histogram. The busiest one-second interval was between 4–5 s, during which 9 people exited. The second before that (3–4 s) had about 8 people. The interval 5–6 s had 7 people. After that, the numbers drop off drastically: e.g., between 6–7 s, 4 people; 7–8 s, 3 people; and various intervals later have 1 or 2 or zero. There’s even a gap (0 people in some late intervals) corresponding to times when no one managed to get out (e.g., presumably 8–9 s had a lull where fallen bodies were being circumvented). The early part (1–2 s and 2–3 s) has a couple people each – those are the very first ones out the door.

Fig. 8

Evacuation throughput at the exit, measured as number of people exiting per second.

The throughput graph essentially quantifies the narrative: the door initially handled a high flow (roughly 8–9 people/s at peak). For a 4 m door, 9 people/s corresponds to about 2.25 people per meter per second, which is in line with empirical findings for maximum flow through doors ~ 1 m wide in panic conditions (around 2–3 persons/m/s)​. It suggests that momentarily the door was being used at a high capacity. However, that level of flow was not sustained. After 5–6 s, the effective flow rate falls off. The average flow over the full evacuation (47 people in ~ 22 s) is ~ 2.1 people/s, but that number is less meaningful since the last 3 people took a very long time relative to the first 47. If the study consider just until 10 s, about 45 people exited, which is an average of 4.5 people/s up to that point – but again that includes the initial burst then a slow trickle. What’s instructive is comparing the peak vs later flow. The sharp drop in throughput after the peak is directly tied to the door, becoming partially blocked by the fallen wheelchair and person. Essentially, the door’s effective width was reduced from 4 m to maybe 2 m or less after 4–5 s (since two bodies were in the way). Consequently, the throughput plummeted (just as one would expect if a door got physically smaller). This is a secondary effect of disabilities: not only do they slow movement, but in the worst case, an impaired individual falling can physically reduce evacuation capacity. In design terms, this is why redundancy and safety factors are needed – one cannot assume the exit will always be fully clear. A further insight from throughput is the timing of peak flow. It occurred a few seconds after the start, when the first cluster approached the door. In a pure able-bodied scenario, one might see a more flattened distribution (flow might remain ~ 8 ppl/s for several seconds). In the case it spiked then dropped. If the study had more people, perhaps multiple oscillations could have been observed. This dynamic behavior would be important to convey to emergency planners: for example, if this were a stadium and certain exits get clogged because some wheelchair patrons use them, one might see uneven egress rates that could confuse crowd managers unless they anticipate it (maybe opening additional gates proactively).

Discussion

The originality of this work lies in extending the social force model with inclusive behavioral modules that explicitly capture mobility impairments. Unlike earlier studies that simply reduced desired velocities, the framework systematically introduces barrier logic, fall dynamics, and heterogeneous reaction times. These additions move beyond parameter adjustments, providing a new methodological layer that can be generalized for performance-based inclusive design.

A limitation of the formulation is that fallen evacuees remain static once toppled. Real evacuations involve dynamic interactions, such as assistance or repositioning. Recognizing this, future work will extend the framework with finite-state models where fallen individuals may re-enter flow or trigger further instabilities. The results of the inclusive evacuation simulation provide a deeper understanding of how heterogeneous mobility constraints impact crowd dynamics under emergency conditions. By incorporating agents with varying physical abilities, the model reveals critical vulnerabilities that conventional, homogeneous simulations tend to overlook. These include not only slower individual egress times but also emergent effects such as increased congestion, reduced throughput, and heightened injury risk due to falling and obstruction. The presence of even a modest proportion of mobility-impaired individuals significantly alters the flow characteristics and spatial patterns near exits. The following key insights summarize the observed evacuation behaviors, performance limitations, and implications for inclusive design and safety planning:

Including just 20% mobility-impaired individuals (10 out of 50) caused a disproportionate slow-down in the final stages of evacuation. While most people got out quickly, a few were significantly delayed. In life-safety terms, those few can be the difference between all-clear and tragedy. The model had 6% of people (3/50) effectively “left behind.” This number could be lower or higher depending on circumstances, but it shows that average egress time alone is not a sufficient metric – one must look at distribution and ensure no one is left without a viable means. Mixed-speed crowds can incur higher pressures as faster agents cluster behind slower ones. In the simulation, this manifested in two falls at the choke point. The study see correspondence with previous work that noted higher crowd pressure with more disabled present⁴²​. Real evacuations with wheelchair users often report bottlenecks at stairwells or narrow corridors³⁹. The results reinforce that without intervention (like dedicated personnel to prioritize those individuals), the physical condition can deteriorate (pushing, etc.). An inclusive model thus highlights the need for management strategies: e.g., perhaps have the wheelchair users go last with an assistant controlling flow, or conversely, evacuate them first before crowd builds – either strategy could avoid them being in the middle of a panicked crowd surge. The effective capacity of exits is reduced in the presence of disabilities. In fire engineering, exit capacity is often calculated with an assumed flow rate (people per minute per unit width). The simulation suggests that using standard flow rates would overestimate capacity for an inclusive crowd. For instance, NFPA might assume ~ 80 ppl/min/m for a doorway under good conditions; in the case, after an initial moment, the flow dropped well below that because of a fallen obstacle. If the study were sizing exits for a building with many wheelchair users, there might be a need to increase width or quantity beyond what a simple formula for average flow would indicate. The qualitative behaviors were observed (arching at exit, faster-is-slower, fallen obstacles) are all phenomena reported in literature​. This gives confidence that the extended model is producing realistic outcomes. One can calibrate specific parameters (e.g., at exactly what force a person falls) with experimental data as it becomes available. Currently, such detailed data for falls is scarce, so the study made plausible assumptions. However, sensitivity analysis showed that if the fall criteria were very strict (hardly anyone falls), then evacuation times would be a bit shorter (maybe all 50 out by ~ 15 s) – i.e., the inclusion of falls is a conservative scenario. On the other hand, if falls were more frequent (say threshold of 2 contacts instead of 4), the study saw even more people falling and getting stuck, sometimes leading to complete gridlock. Reality is likely between these extremes; generally, one or two people might fall into a crowd of this size rushing a single exit, not ten (unless extreme panic). Thus, the chosen threshold yielding 2 falls seems reasonable.

From these findings, several recommendations for inclusive design can be made. Firstly, provide more exit capacity than nominally required when a population includes slower movers. This can be through wider doors, additional exits, or controlled flow. Secondly, implement procedures or assistive measures to prevent pileups. For example, having staff or well-trained individuals accompany wheelchair users can ensure they don’t fall due to pressure; these assistants can also help maintain a gap or buffer around them. Similarly, for visually impaired evacuees, tactile guides or auditory cues can help them maintain orientation and not stall at exits. Thirdly, consider protected refugees and communicate their use: if a wheelchair user knows they have a refuge area (protected from fire/smoke) nearby, they may choose that rather than attempt a congested stair evacuation, reducing overall congestion. The model could simulate such a scenario by giving the wheelchair agents an alternate “exit” node representing the refuge which they prefer if crowd density ahead is too high.

Conclusion

This study has demonstrated how integrating heterogeneous mobility constraints into evacuation models yields distinct and measurable impacts on crowd safety. By embedding disability-specific dynamics into the social force framework, we highlighted critical vulnerabilities—such as falls, congestion intensification, and reduced throughput—that homogeneous models overlook. The key findings of this study as follows: (1) The presence of mobility-impaired and visually-impaired individuals can significantly increase evacuation times for those individuals and for the crowd overall – an effect seen in the long tail of the evacuation curve and the need to accommodate those who cannot self-evacuate quickly; (2) Crowd congestion dynamics are altered by disabilities, often exacerbating peak densities at choke points as faster agents accumulate behind slower ones. In the simulation, this led to two individuals being fall down, illustrating the elevated risk of injury in high-pressure situations with mixed-ability groups; and (3) The effective flow capacity of exits was reduced and more variable over time compared to a fully able-bodied evacuation. This finding is consistent with recent studies that showed higher crowd pressure and lower average speeds when wheelchair users and others were included¹⁴. Planning solely around average egress times of an able-bodied population would have been non-conservative for the scenario, whereas an inclusive analysis correctly identified the need for additional measures for the three people who did not evacuate unaided. Comparing the inclusive simulation with literature and guidelines, the study see a strong alignment in qualitative trends. The “faster-is-slower” effect observed​ resonates with evacuation drill observations where impatience leads to jams, and the model showed this even when some agents could not physically move faster – meaning the crowd’s attempt to rush was self-defeating. The occurrence of falls mirrors real tragedies in which individuals at dense exits trip and cause bottlenecks. Moreover, the results support the recommendations of accessibility experts who call for inclusive design: wider exits, evacuation chairs for wheelchair users, training for assisting persons with disabilities, and so on.

In conclusion, the incorporation of disability movement rates and barriers into evacuation models is not only feasible but necessary for accurate safety assessments. This study demonstrated that such models could reveal critical failure points (like trapped individuals or flow breakdown) that homogeneous models would overlook. Limitations of this study include simplified geometric representation of wheelchairs, omission of active assistance behaviors, and reliance on literature-based rather than experiment-specific calibration. Also, agents followed fixed shortest-path logic toward a single designated exit without dynamic rerouting. This represents a limitation compared to models with adaptive decision-making. Future work will extend the model to multi-floor buildings, incorporate dynamic state transitions for fallen individuals, and evaluate the framework against large-scale evacuation drill datasets to strengthen empirical grounding.