Introduction

Machine vision inspection and measurement technology has become a key tool in advancing the intelligent development of industrial production. Vision-based measurement technologies, particularly those utilizing line-structured light active imaging, offer benefits such as speed, non-contact operation, high flexibility, and strong anti-interference capabilities. As a result, these technologies find widespread use in fields such as non-destructive testing of industrial products, visual navigation, 3D modeling, and military applications1,2,3. For example, in line laser 3D scanning reconstruction, challenges arise due to uneven illumination and noise, which can interfere with the stripe extraction process. These disturbances affect the accuracy of stripe detection, making it a significant area of research4,5,6,7. In industrial environments, efficiently segmenting stripes and accurately extracting their centers are crucial for achieving precise line laser measurements and ensuring reliable detection results.

With the progress in line laser detection technology, researchers worldwide have been exploring methods for accurately segmenting line lasers and quickly extracting the centerline of light stripes. Hu et al.8 proposed a technique for extracting structured light stripe centerlines using templates in horizontal, vertical, 45°, and 135° directions. However, this template-based method is susceptible to interference from environmental factors. Song et al.9 proposed using the geometric features and correlation of laser stripes to create convolution templates, enhancing the method’s adaptability for extracting line laser centerlines in diverse conditions. Wang et al.10 employed deep learning models for laser stripe segmentation and used the centroid method to locate the stripe center, which improved accuracy but added computational complexity. Liu et al.11 segmented stripes by applying a gradient threshold, selecting the maximum cross-correlation value as an initial center, then refined it through curve fitting. He et al.12 utilized an extreme value approach combined with connected component analysis for laser stripe extraction, which, while improving accuracy, was time-intensive. Steger13 applied the Hessian matrix to determine stripe direction, achieving high precision but raising concerns regarding real-time performance.

Although extensive research has been conducted on laser stripe center extraction algorithms, most applications assume a uniform lighting environment. This paper presents a method for accurately extracting the center of structured light stripes under conditions of background noise and uneven illumination. The approach enhances the contrast between the laser stripes and the background while suppressing background noise. It uses wavelet transform for feature fusion, segments the stripes using the maximum entropy model, and applies piecewise polynomial fitting to extract the stripe center. Experimental results demonstrate that the algorithm effectively handles uneven illumination and noise interference, providing practical support for the industrial application of structured light-based vision inspection.

Basic principles and methodological design

Saliency feature fusion laser stripe detection model

In industrial measurement environments, structured light 3D measurements are prone to interference from uneven illumination and noise, causing the laser stripes to become blurred, exhibit inconsistent grayscale, and be contaminated by noise. During laser stripe image segmentation, issues such as incomplete segmentation, under-segmentation, and over-segmentation may occur, often due to noise interference, resulting in reduced stability. To address these issues, this paper innovatively proposes a laser stripe detection method based on saliency feature fusion, which combines RGB brightness feature maps and region-enhanced feature maps, and utilizes the multi-scale analysis capability of wavelet transform for feature fusion, effectively enhancing the contrast between laser stripes and background, and improving the robustness of segmentation. Figure 1 is the flowchart of the feature fusion-based laser stripe detection algorithm presented in this paper.

Fig. 1
figure 1

Laser stripe detection algorithm based on saliency feature fusion.

Full size image

First, to suppress background noise interference, the average values of the three channel images in the RGB color space are calculated. The brightness feature map is then obtained by subtracting the mean normalization from the RGB channel images. The functional expression is:

$$S_{L} = |I_{c} (x,y) - \mathop I\limits^{ - }_{c} |^{2}$$
(1)

where \(I_{c} (x,y)\) denotes the original image, \(\mathop I\limits^{ - }_{c}\) is the mean value of the original image, and c refers to the color channel of the original image,\(c \in \{ R,G,B\}\).

Next, to extract the region-enhanced feature map of the laser stripe image, binary segmentation of the laser stripe grayscale image is performed using a serialized threshold, resulting in the Boolean map \(BM = \{ BM_{1} , \ldots ,BM_{n} \}\). The functional expression is as follows:

$$BM = Thr(I,\theta )$$
(2)

where \(Thr( \cdot )\) is the threshold function,\(I\) refers to the grayscale image,\(\theta\) denotes the segmentation threshold, and \(\delta\) increases by 16 as the step size, \(\theta \in [\delta /2:\delta :255 - \delta /2]\).

In order to suppress the interference of background features and emphasize the contrast between the stripe image and the background, L2 normalization is applied to the Boolean map in this study. Then, by calculating the weighted sum of the normalized Boolean map, an enhanced feature map of the laser stripe region is obtained. The functional expression is:

$$BM_{Norm} = \frac{BM}{{||BM||_{2} }}$$
(3)

where

$$||BM||_{2} = \sqrt {BM_{1}^{2} + BM_{2}^{2} + \cdots BM_{n}^{2} }$$
(4)
$$S_{R} = \sum\limits_{i} {w_{i} } BM_{Norm}$$
(5)
$$w_{i} = \frac{{\theta_{i} }}{255}$$
(6)

where \(||\begin{array}{*{20}c} \cdot \\ \end{array} ||_{2}\) denotes the \(l_{2} {\text{ - norm}}\), \(BM_{Norm}\) denotes the normalized Boolean map, \(w_{i}\) is different weight coefficient. \(S_{R}\) is the region-enhanced feature map.

Wavelet transform is one of the important methods for image feature fusion. In this paper, the brightness feature map of the laser stripe is calculated to reduce the interference of the background on the stripe. At the same time, the region-enhanced feature map of the laser stripe area is calculated to highlight the contrast of the laser stripe. These two saliency features contain the contour information and detail features of the image, respectively. Therefore, wavelet transform is used for feature fusion in this paper14,15. Mallat proposed a fast wavelet decomposition and reconstruction algorithm, whose functional expression is:

$$\left\{ {\begin{array}{*{20}c} {C_{j + 1} = H_{r} H_{c} C_{j} } \\ {D_{j + 1}^{1} = H_{r} G_{c} C_{j} } \\ {D_{j + 1}^{2} = G_{r} H_{c} C_{j} } \\ {D_{j + 1}^{3} = G_{r} G_{c} C_{j} } \\ \end{array} } \right.$$
(7)

where \(H_{r}\), \(G_{r}\) and \(H_{c}\), \(G_{c}\) respectively denote the one-dimensional mirror filtering operators H and G acting on the rows and columns, respectively, and for a two-dimensional image, the operator \(H_{r} G_{c}\) is equivalent to a two-dimensional low-pass filter. \(D_{j + 1}^{1}\) means \(C_{j}\) is the vertical high frequency component, \(D_{j + 1}^{2}\) means \(C_{j}\) is a high frequency component in the horizontal direction, \(D_{j + 1}^{3}\) means \(C_{j}\) is a high frequency component in that diagonal direction. The wavelet transform is performed to an image \(X\), and the \(\left( {j + 1} \right)\)-th wavelet coefficients and scale coefficients of the layer will respectively expressed as \(D_{j + 1}^{1} (X)\), \(D_{j + 1}^{2} (X)\), \(D_{j + 1}^{3} (X)\) and \(C_{j} (X)\).

The corresponding wavelet transform reconstruction expression is:

$$C_{j} = H_{r}^{*} H_{c}^{*} C_{j + 1} + H_{r}^{*} G_{c}^{*} D_{j + 1}^{1} + G_{r}^{*} H_{c}^{*} D_{j + 1}^{2} + G_{r}^{*} G_{c}^{*} D_{j + 1}^{3}$$
(8)

where \(H^{*}\), \(G^{*}\) are expressed as conjugate transpose matrices of \(H\), \(G\).

The high frequency part of the wavelet transform corresponds to the edge and contour features of the image, and the low frequency part reflects the overall gray value distribution of the image. The fusion of wavelet transform should retain the details of the image as much as possible while retaining the overall outline of the image. For the high-frequency features of the laser stripe image, It reflects the features such as the edge of the image whose contrast changes greatly. Therefore, for the high-frequency features, the paper uses the maximum fusion rule. For the laser stripe image \(A\) and \(B\), the expression of the high-frequency fusion function is:

$$H(x,y) = \left\{ {\begin{array}{*{20}c} {H_{A} (x,y),if\left| {H_{A} (x,y)} \right| \ge \left| {H_{B} (x,y)} \right|} \\ {H_{B} (x,y),if\left| {H_{A} (x,y)} \right| < \left| {H_{B} (x,y)} \right|} \\ \end{array} } \right.$$
(9)

where \(H(x,y)\) represents the image fusion coefficients, \((x,y)\) is the coefficient coordinate, \(H_{A} (x,y)\) and \(H_{B} (x,y)\) represent the high frequency subband coefficients of images A and B respectively.

For the fusion of the low-frequency part of the image, it is necessary to retain the overall features of the image as much as possible, so the fusion method takes mean weighted processing, and its expression is:

$$L(x,y) = (L_{A} (x,y) + L_{B} (x,y))/2$$
(10)

where \(L(x,y)\) is the image fusion coefficient; \(L_{A} (x,y)\), \(L_{B} (x,y)\) represent the low frequency subband coefficients of images A and B respectively.

Adaptive segmentation of laser stripe

This paper uses the maximum entropy method to segment the stripes based on the fused image. According to Shannon’s theory16, the functional expression is:

$$H = - \sum\limits_{x = 1}^{N} {p(x)\lg \left[ {p(x)} \right]}$$
(11)

where \(lg( \cdot )\) denotes the logarithm base 2, and p(x) represents the probability distribution of gray level x.

Let \(T\) be the threshold value, and define the frequency of each gray value \(p_{i}\) as the gray level probability. The gray level probabilities for the target area and background area are then given as:

$$p_{0} = \sum\limits_{i = 0}^{T = 1} {p_{i} }$$
(12)
$$p_{b} = \sum\limits_{i = T}^{255} {p_{i} }$$
(13)

Then, the entropy of the target region and the background region are defined as:

$$H_{0} (t) = - \sum\limits_{i = 0}^{T = 1} {(p_{i} /p_{0} )} \lg (p_{i} /p_{0} )$$
(14)
$$H_{b} (t) = - \sum\limits_{i = T}^{255} {(p_{i} /p_{b} )\lg (p_{i} /p_{b} )}$$
(15)

The entropy function obtained from the target entropy and background entropy is:

$$H(t) = H_{0} (t) + H_{b} (t)$$
(16)

The threshold \(T\) can be expressed as:

$$T = \arg \mathop {\max }\limits_{t \in [0,1]} H(t)$$
(17)

After applying adaptive maximum entropy segmentation to the fused salient image, the final segmentation is achieved by measuring the area of the connected regions for stability. As shown in Fig. 2, the segmentation process of laser stripes in various scenes is illustrated. Scenes No. 1, No. 2, and No. 3 have uneven illumination, No. 4, No. 5, and No. 6 are low contrast, and No. 7 and No. 8 contain background noise. The figure demonstrates that the saliency detection model effectively reduces the impact of uneven illumination, background interference, and noise, while enhancing the contrast between the laser stripes and the background.

Fig. 2
figure 2

Results of laser stripe segmentation: (a) Input image; (b) Brightness feature map; (c) Region-enhanced feature map; (d) Fused feature map; (e) Final segmentation result.

Full size image

To further verify the segmentation effect of the algorithm in this paper, as shown in Fig. 3, laser stripes with inhomogeneous illumination scenes (e.g., Figs. No. 1 and No. 2), different background interference scenes (e.g., Figs. No. 3 and No. 4), low-resolution scenes (e.g., Figs. No. 5 and No. 6) and low-resolution scenes with added noise of variance 0.2 (e.g., Figs. No. 7 and No.8) were segmented separately. By comparing the five commonly used saliency methods of SR17, AC18, SIM19, MSS20, SUN21 and MVSF22. Since these saliency detection results are grayscale images, in order to align with the algorithm in this paper, the different saliency detection results are segmented using maximum entropy to obtain binary images. A comparison of the different saliency segmentation results is shown in Fig. 3. Although some saliency algorithms can correctly segment laser stripes in specific scenes, they fail to accurately delineate the stripe contours. Additionally, they are sensitive to strong edge noise from the background and uneven illumination, which impact the segmentation accuracy. The AC algorithm has a higher segmentation accuracy but has a higher time overhead. The results extracted in this paper can not only correctly locate the position of the laser stripe region, but also accurately segment the stripe contour. For image scenes with different resolutions and added noise at low resolutions, as shown in Figs. 4, 5, and 6, this method demonstrates high sensitivity to low-resolution images, effectively overcoming the impact of low resolution, and accurately segments the laser stripe contours, reflecting the advantages of the method proposed in this paper. Additionally, for noisy images in low-resolution scenes, the algorithm in this paper also performs well in segmenting the laser stripes. As shown in Table 1, the comparison of running times for different saliency algorithms indicates that the algorithm in this paper not only outperforms other saliency methods in segmentation accuracy but also performs better in terms of running time.

Fig. 3
figure 3

Comparison of segmentation results of different saliency algorithms: (a) Input image. (b) AC. (c) SR. (d) SIM. (e) MSS. (f) SUN. (g) Otsu. (h) MVSF. (i) Proposed.

Full size image
Fig. 4
figure 4

Adaptive segmentation of laser stripe: (a) Fracture stripe. (b) Large curvature stripe. (c) Neighborhood difference of fracture stripe. (d) Neighborhood difference of large curvature stripe.

Full size image
Fig. 5
figure 5

The results of the centerline extracted by segment fitting.

Full size image
Fig. 6
figure 6

Schematic diagram of system measurement.

Full size image
Table 1 Comparison of running time of different saliency algorithms (unit: second).
Full size table

Extracting the laser stripe centerline through piecewise fitting curve

To optimize the extraction process of the laser stripe center and ensure smoother extraction, this study adopts a gray-level centroid method based on gradient direction and curvature optimization to determine the initial center points of the laser stripe. Subsequently, the neighborhood differences of the initial center points are calculated for adaptive segmentation. Finally, polynomial fitting is applied to the different segments to obtain the final subpixel centers of the laser stripe.

The gray-level centroid method is based on the distribution characteristics of the laser stripe’s gray levels, and its functional expression is:

$$\begin{gathered} x_{c} = {{\sum\nolimits_{i} {I(i) \cdot x_{i} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i} {I(i) \cdot x_{i} } } {\sum\nolimits_{i} {I(i)} }}} \right. \kern-0pt} {\sum\nolimits_{i} {I(i)} }} \hfill \\ y_{c} = {{\sum\nolimits_{i} {I(i) \cdot y_{i} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i} {I(i) \cdot y_{i} } } {\sum\nolimits_{i} {I(i)} }}} \right. \kern-0pt} {\sum\nolimits_{i} {I(i)} }} \hfill \\ \end{gathered}$$
(18)

where \(I(i)\) represents the pixel gray value, \(x_{i} ,y_{i}\) denote the pixel coordinates, and \(x_{c} ,y_{c}\) are the initial center coordinates.

The gray-gravity method is vulnerable to blurred stripe boundaries or uneven intensity distributions. Gradient direction optimization leverages the grayscale gradient information of the laser stripe to enhance boundary constraints, thereby improving extraction accuracy. The functional expression is:

$$G = \sqrt {\left( {\frac{\partial I}{{\partial x}}} \right)^{2} + \left( {\frac{\partial I}{{\partial y}}} \right)^{2} }$$
(19)
$$\theta = \arctan \left( {\frac{{{{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial y}}} \right. \kern-0pt} {\partial y}}}}{{{{\partial I} \mathord{\left/ {\vphantom {{\partial I} {\partial x}}} \right. \kern-0pt} {\partial x}}}}} \right)$$
(20)

where G represents the gradient magnitude, and \(\theta\) represents the gradient direction.

A weight is constructed using the gradient magnitude to emphasize regions with significant grayscale changes, enhancing the contribution of pixels near edges to the extraction of the centerline. The functional expression is:

$$W_{grad} = \exp \left( { - \frac{{G^{2} }}{{2\sigma^{2} }}} \right)$$
(21)

where \(\sigma\) is a tuning parameter, and in this paper, \(\sigma = 0.5\).

Since laser stripes are easily affected by noise in regions with high curvature, this paper adopts a curvature optimization method to enhance the attention to regions with significant curvature changes. The curvature calculation functional expression is:

$$\kappa = \frac{{\left| {{{\partial^{2} y} \mathord{\left/ {\vphantom {{\partial^{2} y} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}} \right|}}{{\left( {1 + \left( {\frac{\partial y}{{\partial x}}} \right)^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}$$
(22)

The curvature weight is:

$$W_{curv} = 1 + \alpha \cdot \kappa$$
(23)

By combining the gradient direction weight and the curvature weight, the final pixel weight is obtained, which is used to optimize the gray-gravity method. The initial centerline coordinates are re-weighted to obtain the optimized centerline. The functional expression is:

$$y = \frac{{\sum\nolimits_{i} {W(i) \cdot y(i)} }}{{\sum\nolimits_{i} {W(i)} }}$$
(24)

where \(W\) is the final pixel weight, \(W = W_{grad} \cdot W_{curv}\).\(y(i)\) is the initial centerline of the gray-gravity method.

Although increasing the number of points on the light stripe results in a smoother fitting outcome, when the laser stripe exhibits large curvature or fractures, adding more points can lead to the loss of details at the stripe’s center. This causes the fitting to fail in accurately representing the actual center of the stripe. To address this, the paper calculates the neighborhood difference at the initial point of the stripe. If the difference exceeds a threshold (T = 1), the region is segmented. Figure 4 shows the neighborhood difference maps for stripes with large curvature and fractures. The neighborhood difference function is expressed as:

$$d = y_{i + 1} - y_{i}$$
(25)

where \(d\) denotes the neighborhood difference, \(y_{i}\) represents the longitudinal coordinate of the stripe center at a specific position. If \(\left| d \right| \ge T\), the area can be considered that to be segmented.

The polynomial function used to fit the stripe center point data \((x_{i,} y_{i} )\), where \(i = 1,2, \ldots m\), is expressed as:

$$y = a_{0} + a_{1} x + \cdots + a_{n} x^{n}$$
(26)

where \(y\) is the fitting polynomial and \(a_{i}\) is the coefficient to be fitted (\(i = 1,2, \ldots n\)).

To minimize the fitting error, the least squares method is used to solve for the coefficients, such that the sum of squared errors is minimized. The expression for the sum of squared errors is:

$$Q = \sum\limits_{i = 1}^{m} {\left( {y_{i} - \sum\limits_{j = 0}^{n} {a_{j} x_{i}^{j} } } \right)^{2} }$$
(27)

By minimizing the sum of squared errors Q, the normal equation of the least squares method is obtained:

$$\frac{\partial Q}{{\partial a_{k} }} = \sum\limits_{i = 1}^{m} {\left( {y_{i} - \sum\limits_{j = 0}^{n} {a_{j} x_{i}^{j} } } \right)x_{i}^{k} = 0} \quad (k = 0,1, \ldots ,n)$$
(28)

The function expression of Eq. (28) is represented in matrix form as:

$$X = \left[ {\begin{array}{*{20}c} 1 & {x_{1} } & {x_{1}^{2} } & \cdots & {x_{1}^{n} } \\ 1 & {x_{2} } & {x_{2}^{2} } & \cdots & {x_{2}^{n} } \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & {x_{m} } & {x_{m}^{2} } & \cdots & {x_{m}^{n} } \\ \end{array} } \right],\;\;A = \left[ {\begin{array}{*{20}c} {a_{0} } \\ {a_{1} } \\ \vdots \\ {a_{n} } \\ \end{array} } \right],\;\;Y = \left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \vdots \\ {y_{m} } \\ \end{array} } \right]$$
(29)

Thus, the equation can be simplified to:

$$X^{T} XA = X^{T} Y$$
(30)

where \(X^{T}\) is the transpose matrix of matrix \(X\).

The coefficient matrix \(A\) can be expressed as:

$$A = (X^{T} X)^{ - 1} X^{T} Y$$
(31)

where A contains the coefficients of the fitting curve.

As shown in Fig. 5, the laser stripe centerline is extracted through segment fitting. Figure 5a presents the centerline results obtained using different segment fitting methods. From the figure, it is clear that this approach accurately captures the center position of the laser stripe. In Fig. 5b, it can be seen that the fitted laser stripe successfully addresses the issue of discontinuity in the gray-gravity method, and the extracted stripe shows a smooth and continuous structure. Algorithm 1 outlines the proposed laser stripe centerline extraction method.

figure a

Analysis of results

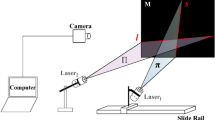
The experimental testing platform, as shown in Fig. 6, includes a Daheng MER2-U3 CCD camera and a line laser emitter. The CCD camera captures the laser stripe image, while the line laser emitter projects a concentrated laser beam onto the surface of the target.

Figure 7 presents the results of stripe center extraction using various algorithms under uneven illumination and strong background interference. A comparison of the traditional gray-gravity method, extremum method, Steger algorithm, and template method23 shows that the gray-gravity method performs poorly at curvature changes, while the Steger algorithm and template method fail to fully extract the laser stripe center. The extremum method also lacks accuracy in centerline extraction. In contrast, the algorithm proposed in this paper exhibits greater stability, accurately detects the laser stripe center at varying curvatures, and demonstrates robust performance.

Fig. 7
figure 7

Stripe center extraction with different algorithms.

Full size image

To evaluate the robustness of the proposed algorithm against noise in industrial environments, experiments were conducted to extract the laser stripe center under varying noise levels. During the tests, laser stripe images were captured at the same position under different lighting conditions, as shown in Fig. 8. Since the stripe image captured by the CCD primarily differs in background illumination, particularly in low-light conditions, centerline extraction is minimally affected by interference. The stripe center extracted under a black background was used as a benchmark. Noise with variances of 0.05, 0.25, and 0.3 was added to the images for further testing. Figure 9 presents the center extraction results under different noise levels, while Fig. 10 illustrates the error curve of center extraction under these conditions. The error curve indicates a maximum error of less than 1.07 pixels. These results confirm the algorithm’s robustness and strong anti-interference capability.

Fig. 8
figure 8

Laser stripe under different brightness background.

Full size image
Fig. 9
figure 9

Extraction of laser stripe center under different noise.

Full size image
Fig. 10
figure 10

Error extraction curve under different noise.

Full size image

To further validate the accuracy of this algorithm, 3D reconstruction experiments are conducted on various workpieces. Figure 11 shows different experimental test workpieces and Figs. 12 and 13 show the three-dimensional reconstruction results of workpiece 1 and workpiece 2. As shown in Figs. 14 and 15, which are partial enlarged view of that point cloud data of the workpiece.

Fig. 11
figure 11

Test workpiece.

Full size image
Fig. 12
figure 12

3D reconstruction result of workpiece 1.

Full size image
Fig. 13
figure 13

3D reconstruction result of workpiece 2.

Full size image
Fig. 14
figure 14

Partial enlarged view of workpiece 1.

Full size image
Fig. 15
figure 15

Partial enlarged view of workpiece 2.

Full size image

From the XY directional view, it can be observed that the traditional gray center of gravity algorithm tends to cause stripe breakage at curvature changes, resulting in unsmooth point cloud data and an inability to accurately reflect the 3D features of the workpiece. In comparison, the algorithm presented in this paper generates smoother stripes at points of curvature change, and the extracted stripe centers more accurately capture the 3D shape features of the workpiece. Table 2 shows the test results for different row widths, where the width errors for workpiece 1 are 0.13 mm, -0.01 mm, and -0.18 mm, and for workpiece 2 are -0.28 mm, 0.13 mm, and -0.23 mm.

Table 2 Point cloud extraction results of different rows.
Full size table

The stability of the algorithm was verified through repeatability tests on 100 sets of laser stripe point cloud data at the same position. Figure 16 and Table 3 demonstrate that the system’s repeatability extraction errors are small and within the allowable range.

Fig. 16
figure 16

Repeatability extraction error of different workpieces.

Full size image
Table 3 Errors of standard workpiece (unit: mm).
Full size table

Conclusion

To address the impact of background noise and uneven illumination on line laser measurement, this paper proposes a laser stripe center extraction method based on saliency feature fusion. A multi-feature fusion saliency detection model is designed to generate brightness feature maps and region-enhanced feature maps, effectively reducing background interference and enhancing the contrast between laser stripes and background. Adaptive maximum entropy combined with connected region analysis is adopted to segment the fused saliency map, solving problems of incomplete segmentation, under-segmentation, and over-segmentation. A gray-gravity method optimized by gradient direction and curvature is developed for initial center point extraction, combined with adaptive segmentation based on neighborhood differences and polynomial fitting to achieve high-precision centerline extraction. Experimental results demonstrate that the proposed algorithm successfully reduces the impact of uneven lighting and background noise. The mean error across different rows in the reconstructed results is less than 0.24 mm, and the mean repeatability extraction error is below 0.13 mm. Future work will focus on further optimizing the algorithm to enhance performance in complex scenarios.