Introduction

Strip coal pillars are widely employed in coal mines underlying urban zones to maintain ground stability1,2. However, creep-induced settlement of these pillars poses challenges for site selection during urban expansion3,4,5. Consequently, understanding the creep damage mechanisms in strip coal pillars is essential for the design and long-term maintenance of such engineering structures.

The long-term behavior of strip coal pillars has garnered increasing attention from the research community, as creep-related issues have been observed in numerous coal mines globally6. Wang et al.7 conducted numerical modeling to assess the long-term stability of strip coal pillars, concluding that residual pillars remain in an unstable state, with ongoing creep failure likely to persist.

While extensive research exists on coal creep behavior, studies specifically addressing the damage evolution in coal pillars are scarce. Coal is recognized for its pronounced creep characteristics, often modeled using viscoelastic-plastic or component-based approaches8,9,10,11. In conjunction with real-world stress conditions, Guo et al.12 employed a bridge model to evaluate the stability of residual coal pillars, while Zhang et al.13 investigated creep fracture evolution in coal pillars. Wessels et al.14 proposed a limit equilibrium model to analyze coal pillar stability. These studies collectively underscore the significant creep behavior of coal, which drives damage propagation in strip coal pillars.

However, laboratory tests on individual coal samples fail to fully capture the creep damage evolution across an entire coal pillar, and replicating such behavior in scaled models is challenging due to difficulties in obtaining materials with equivalent viscosity and strength15. Advances in numerical modeling techniques, such as finite element modeling (FEM) and discrete element modeling (DEM), have enhanced the ability to predict creep damage evolution over time16,17. Nonetheless, accelerated creep damage in localized regions of coal pillars often leads to convergence issues in simulations. Despite these challenges, numerical modeling has emerged as a reliable tool for studying coal pillar damage behavior2. For individual coal pillars, numerical simulations have revealed mechanisms of damage development, including the formation of an isolated elastic core and the accumulation of elastic energy due to surrounding rock softening18,19. In wider coal pillars, progressive failure under overburden pressure from the roof has been observed20,21, potentially triggering rock bursts and significantly increasing permeability22,23,24,25.

Despite these advancements, the characteristics of creep damage propagation in strip coal pillars remain poorly understood. In practice, the design of such structures typically relies on short-term or statistical stability assessments26,27,28. However, variations in concentrated stress induced by the roof and coal seam significantly influence the progressive creep damage in strip coal pillars29,30,31,32. The key innovation of this paper lies in the comprehensive approach combining in-situ investigation, laboratory experiments, and advanced numerical modeling to elucidate the creep damage evolution in strip coal pillars.

This paper implemented a site investigation on the engineering case, laboratory tests on the creep deformation of coal, and numerical modeling on the mechanism of coal pillar damage propagation. The evolution law and mechanism of creep damage expansion in strip coal pillars were analyzed in terms of the stress distribution in coal pillars, damage evolution, and the mechanism of damage expansion. The outcomes of this paper are significant for evaluating and maintaining strip coal pillars for long-term safety.

Engineering background of the study case

A coal mine in Rencheng, Shandong Province, was selected as a case study to investigate the characteristics of creep failure in water-immersed strip coal pillars. This coal mine represents a typical example located near an urban area. The mined coal seam in the numbered 7300 area is buried at a depth of approximately 500 m, with a dip angle of about \(6 ^{o}\), and an average coal thickness of roughly 2.5 m.

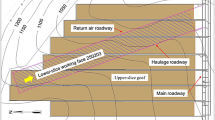
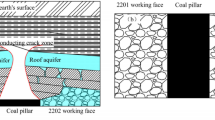
As illustrated in the schematic diagram (Fig. 1(a)) of the studied strip coal pillars beneath urban development zones, the horizontal cross-sections of these coal pillars are shown in Fig. 1(b). Three goaves, designated 7330, 7334, and 7338, were formed around 2017. Each goaf spans a width of approximately 50 m, with coal pillars of about 100 m width reserved between them. The lengths of the 7330, 7334, and 7338 goaves are approximately 180 m, 650 m, and 700 m, respectively.

As shown in Fig. 1(a), these coal pillars experience creep damage, leading to roof fracture and ground settlement. The fracture in the roof rock layers makes water in the aquifer flow into the goaves, softening coal pillars and accelerating creep failure in coal pillars. In fact, a borehole suggests the 7334 goaf is full of water. As shown in Fig. 1(c), according to the 3D transient electromagnetic result, both the 7334 and 7338 goaves have very low equal resistivity(blue color distribution), since water leads to high magnetic flux, therefore, it is easy to recognize that the goaves of 7334 and 7338 are full of water. In addition, the electrical resistivity was measured from the boreholes of CK3-3, CK4-2, and CK2-2, as the locations in Fig. 1(b), which are approximately 2.7 m, 16.5 m, and 26.5 m away from the side wall of the goaf, respectively. The electrical resistivity values in Fig. 1(d) suggest a dramatic downtrend after 16.5m, and the value gets close to the value of intact coal. Since the higher density of fracture makes larger electrical resistivity, this means a width of about 16.5 m to 26.5 m away from the side wall of the goaf was creep damaged. Therefore, this kind of coal pillar is of high potential to threaten the safety of the ground architectures.

Fig. 1
figure 1

A diagram sketch of (a) strip coal pillars under urban developing area, (b) the horizontal section of coal pillars, (c) 3D transient electromagnetic result and (d) electrical resistivity data from the boreholes in the coal seam.

Full size image

Creep performance of water-immersed coal

In order to analyze the mechanism of the water-immersed coal pillar, the creep performance of coal was investigated by multi-stage creep experiments under different water immersion durations.

Experiment apparatus

The GCTS RIR 2000 rock mechanical testing system, as shown in Fig. 2 (a), was applied to implement the uniaxial creep experiments. This system allows a maximum axial force of 2000 kN and a maximum confining pressure of 140 MPa. The axial and confining displacements were measured automatically according to the meters as displayed in Fig. 2 (b).

Fig. 2
figure 2

The involved (a) coal samples and X-ray results (b) GCTS RIR 2000 rock mechanical testing system and (c) Loading platform.

Full size image

Experiment materials and test procedures

The tested coal samples were drilled from the Rencheng Coal Mine and were cut into cylinder-shaped pieces with a diameter of 50 mm and a height of 100 mm. X-ray testing suggests the minerals in this kind of coal contain quartz, albite, calcite, iron pyrite, kaolinite, clinopyroxene, coal matrix, etc. Their weight proportions are approximately 0.39 \(\%\), 0.18 \(\%\), 0.95 \(\%\), 0.52 \(\%\), 1.59 \(\%\), 2.03 \(\%\), and 94.34 \(\%\), respectively.

Prior to the creep experiments, the test samples were immersed in the solution for various durations. The simulated mine water was prepared using a mixture of chemical reagents to replicate the typical chemical composition of mine water. Specifically, the solution was formulated with NaCl (1.63 g/L), \(\hbox {Na}_2\) \(\hbox {SO}_4\) (0.61 g/L), \(\hbox {MgSO}_4\cdot\) 7\(\hbox {H}_2\)O (0.9 g/L), and \(\hbox {FeSO}_4\cdot\) 7\(\hbox {H}_2\)O to adjust the pH to approximately 5, consistent with the acidic conditions observed in the target mining environment. In such a solution, considering the effect of water immersion finished within about 14 days, as announced by Yi et al.33, the samples immersed for 0 days, 5 days, 10 days, and 20 days were selected for the uniaxial and creep experiments. Actually, the experiment data indicate that the mechanical performance stabilizes after about an immersion duration of 10 days or longer.

Given the minor lateral confining pressure induced by water accumulation in goaf areas 7334 and 7358, only uniaxial creep experiments were conducted. The uniaxial compression tests were performed under displacement control at a loading rate of 0.5 mm/min until failure. According to the uniaxial compression test of the tested samples, the uniaxial compression strength \(\sigma _c\), three stages of the multi-stage creep experiments were defined with an increment of 30 \(\% \sigma _c\) for each stage. The creep duration of each loading stage is set as 24 h.

Experiment data analysis

The measured data in the creep experiment involves the time-dependent axial strain and stress, the creep strain curves and stress-strain curves are plotted in Fig. 3(a) and Fig. 3(b), respectively.

As displayed in Fig. 3(a), the measured strain-stress curves of the uniaxial compression experiment suggest that the longer immersion days make a more obvious compaction deformation of the coal. Take the data during elastic deformation to calculate the elastic modulus, the increased immersion time results in a decreasing tendency of the elastic modulus. After the elastic deformation, the samples were immersed for 10 days and 20 days exhibited obvious plastic deformation before peak stress, and the promoted immersion durations led to a slight drop in strength. As announced by Li et al.34, the mechanical properties of water-immersed coal kept steady after about 14 days, in our case, the tendency line of elastic modulus and strength as in Fig. 3(a) shows that the value of which are close to each other between 14 days and 20 days, therefore, it is reasonable to say both the elastic modulus and strength got relatively steady after an immersion time of 14 days. In addition, all the tested samples experienced a dramatic decrease in stress after peak stress, exhibiting brittle failure.

Fig. 3
figure 3

The results of (a) uniaxial compression experiment and (b) uniaxial creep experiment.

Full size image

The average compressive strength of the tested samples was approximately 16 MPa. Consequently, in the creep experiment, the stress increment for each loading stage was set at 4.8 MPa. Figure 3(b) presents the experimental results, demonstrating that the duration of water immersion significantly affects the long-term creep behavior of the samples. Specifically, it markedly increases the instantaneous strain, primarily due to the softening effect, which manifests as a reduction in the elastic modulus. Additionally, water immersion significantly accelerates the failure of coal samples: under a load of 16.8 MPa, accelerated creep occurred after 180 hours in non-immersed samples, whereas in samples immersed for 20 days, creep failure was observed after only 125 hours. Notably, the creep deformation curves after 10 days of immersion are similar. Both the uniaxial compression and creep tests demonstrate that the elastic behavior, strength, and creep performance stabilize after immersion periods exceeding 10 days.

It is notable that the confining pressure has a certain degree of influence on the creep performance of the coal pillar, such as the confining pressure from the broken coal mass to the intact coal body. An experimental investigation by Yan et al.35 suggests that promoted confining pressure decreases the instantaneous elastic strain, but increases the long-term strength of coal. In such a case, the immersed coal in the pillar has a degree of strength deduction, during the damage propagation, the creep strength of coal will be increased by the confining pressure.

Numerical model setup

In order to analyze the mechanism of creep failure in the coal pillar, based on the laboratory experiment, numerical modeling was conducted to identify the stress distribution and failure process in the strip coal pillar. The involved creep model and numerical model were introduced in the following subsections.

Creep model of coal

In our previous study, a fractal-order-based creep model of water-immersed coal was proposed as Fig. 4, which is composed by a Maxwell body and the parallel connection of a dashpot to a yield friction block. The spring in Fig. 4 represents the elastic behavior of materials, the viscosity describes the steady creep behavior and the parallel connection helps express the viscoplastic performance of materials. The fractal order \(\alpha\) and \(\beta\) benefit describing the nonlinear behavior of coal during creep deformation. Therefore, this model expresses the viscoelastic and viscoplastic behavior of materials by the formulation of34

$$\begin{aligned} {\varepsilon _{ij}} = \left\{ { \begin{array}{l} {\frac{1}{{2G}}{S_{ij}} + \frac{1}{{3K}}{\sigma _m}{\delta _{ij}} + \frac{{{S_{ij}}}}{{\eta _1^ * }}{t^\alpha } \quad \quad \quad \quad \quad \quad \quad \quad \quad (f < 0)}\\ {\frac{1}{{2G}}{S_{ij}} + \frac{1}{{3K}}{\sigma _m}{\delta _{ij}} + \frac{{{S_{ij}}}}{{\eta _1^ * }}{t^\alpha } + \frac{{\exp \left( {\beta t} \right) }}{{\beta \eta _2^ * }}f\frac{{\partial f}}{{\partial {\sigma _{ij}}}} \quad \quad \quad \left( {f \ge 0} \right) \mathrm{ }} \end{array}} \right. \end{aligned}$$
(1)
Fig. 4
figure 4

Components of the fractal-order-based creep model.

Full size image

where \(\varepsilon _{ij}\), \(S_{ij}\), \(\sigma _m\), \(\delta _{ij}\), and t are the strain, derivative stress invariant, volumetric stress, Kronecker symbol, and creep time, respectively. The parameters K, G, \(\eta _1^*\), \(\alpha\), \(\eta _2^*\) and \(\beta\) represent the bulk modulus, shear modulus, viscoelastic viscosity, viscoelastic fractal order, viscoplastic viscosity, and viscoplastic fractal order. Alternatively, f means the plastic potential. In this paper, the Von-Mises criteria was applied for defining the plastic potential with the formation of

$$\begin{aligned} f = \sqrt{J_2}-C \qquad \quad or \quad \qquad f = \sqrt{\frac{(\sigma _1-\sigma _2)^2+(\sigma _1-\sigma _3)^2+(\sigma _2-\sigma _3)^2}{6}}-C \end{aligned}$$
(2)

in which \(\sqrt{J_2}\) are the second derivative invariant, C means a coefficient of creep strength.

In order to check the capability of Eq. (1) in reproducing the three-dimensional creep behavior of coal, the triaxial creep data of Yan et al.35 were employed for the fitting work. The triaxial creep experiment data of water-immersed anthracite coal and the fitted results by Eq. (1) are plotted in Fig. 5. In Fig. 5, one can see that there are 4 coal samples involved in the triaxial creep tests, which are encoded by w1, w2, w3, and w4 with the axial stress of 17 MPa. 23 MPa, 26 MPa, 26 MPa and the confining pressures of 0.5 MPa. 1 MPa, 1.5 MPa and 2 MPa, respectively. Correspondingly, the derivative stress of these samples are 16.5 MPa, 22 MPa, 24.5 MPa, and 24 MPa. Obviously, with low confining pressure, the axial stress ranged from 17 MPa to 26 MPa made the coal samples creep failure around 50 h. The difference is the creep strain before the accelerated creep stage, exhibiting that the higher the confining pressure, the smaller the creep strain before the accelerated creep. In the case of a stripped coal pillar, the confining pressure in the stripped coal pillar is relatively small due to the deloading effect by coal excavation7,30. With the propagation of creep damage in the coal pillar, the creep strain will be reduced by the increased confining pressure, but it would still be damaged with the small confining pressure according to the experimental evidence from Yan et al.35.

Fig. 5
figure 5

Fitting work of the Eq. (1) on the triaxial creep experiment data35.

Full size image

In Fig. 5, the model of Eq. (1) was utilized to reproduce the triaxial creep strains. The coal sample has a uniaxial strength of about 9.58 MPa, according the Eq. (2), the parameter of C can be calculated as 5.53 MPa. The alternative parameters of Eq. (1) are listed in the table in Fig. 5. One can see that with the same creep strength, both the axial strain and radial strain of the model have a good capacity of reproducing the experimental data, in addition, the parameter of \(\beta\) is the same for all the samples of w1 to w4, the difference is the parameters of \(\eta _1^*\), \(\alpha\) and \(\eta _2^*\), which are various with different samples. This is due to the mechanical discreteness of coal, which is typically a kind of heterogeneous material. Despite these differences would influence the creep deformation to some extent, the strength criteria of this model have the capability of recovering the failure status of coal under different stress, which means the used model is suitable for calculating the three-dimensional creep processes of the coal pillar.

Numerical software and model

In order to model the creep deformation of water strip coal pillar, the software of OpenGeoSys 5.8 was applied, which is an open-source thermal-hydraulic-mechanical-chemical (THMC) coupling software compiled by the C++ program36,37. Equation (1) and Eq. (2) are inserted into this software in light of the creep module.

To simplify the numerical modeling, a three-dimensional model was set as Fig. 6 (a), the cross-section view of X-Z and X-Y coordinates through the three goaves was displayed in Fig. 6 (b) and Fig. 4(c). The dimensions of this model are 800 m \(\times\) 750 m \(\times\) 550 m. Fron the top to the bottom of this model, as shown in Fig. 6(b), there are clay soil, coarse sandy clay, sandy clay, medium coarse sandstone, medium fine sandstone, sandy mudstone, aluminum mudstone, siltstone and coal involved in the modeling. On account of the boundary conditions, take Fig. 6(a) for instance, the bottom, left, right, front, and back surfaces of this model are set as fixed displacement boundaries in the normal direction, the top surface of this model is free in displacement to simulate the ground surface. Hexahedron elements are applied in the model discretization, and there are 67585 elements involved in the modeling, in which the elements of coal pillars were limited within 0.5 m in geometric scale.

Fig. 6
figure 6

The numerical model of (a) total one, the view of (b) X-Z cross-section and (c) X-Y cross-section.

Full size image

Numerical modelling procedures

In order to investigate the process of creep damage of strip coal pillars, the numerical modeling involves the initial stress equalization, coal seam excavation, and long-term creep damage steps.

For the initial stress equalization, the stress conditions of this model were self-equalized according to gravity as the way of Suo et al.38. During the excavation step, since the majority of this study focuses on the stable stress status of the creep of coal pillars, the excavation zones were excavated at one time. Then the creep damage step was calculated with a duration of 50 years.

Parameters identification

The numerical parameters involved in Eq. (1) and Eq. (2) are identified according to the creep data of Fig. 3(b). As announced by Perry et al.39 and Zhang et al.40, water-rock interaction will be complemented within 4 days and reach a stable mechanical performance, therefore, the tested samples can be regarded as mechanically stable materials without the influence of immersion time. In addition, as the results of creep tests in Fig. 3(b), the creep deformation of the samples immersed within 10 days showed a continuous degradation in terms of elastic loading, steady creep, and accelerated creep process, and when immersion durations overpass 10 days, the evolution of creep strain is very close. Therefore, considering the influence of water immersion on the creep performance of coal pillar acts within a very short time during the creep damage, the numerical parameters can be obtained from the data of creep tests with an immersion duration of 10 days.

The parameters then can be obtained by a fitting work as displayed in Fig. 7. In the work of parameter identification, the values of bulk and shear modulus (K, and G, respectively) are obtained according to the loading stress-strain curves at each stage. The data of stable creep strain versus time were utilized for calculating the averaged viscosity \(\eta\). On account of the coefficient of creep strength, the strength of coal immersed within 10 days is about 14 MPa, according to Eq. (2), for a uniaxial compression, \(\sqrt{J_2} = \sigma _1/\sqrt{3}\), then C can be calculated as 8.08 MPa. The alternative parameters are determined by the least-square method. The parameters are obtained as listed in Table 1.

Fig. 7
figure 7

Parameters identification by fitting work of the 10 days immersed creep strain data .

Full size image
Table 1 The identified model parameters of coal.
Full size table

For alterative stratum layers, the elastoplastic behavior are calculated in the modeling. According to the laboratory tests by the Rencheng Coal mine, the mechanical coal pillar are listed in Table 2. In the modeling work, the Mohr-Coulomb criterion were applied for the stratum layers associated with the creep deformation of coal by the parameters of Table 1.

Table 2 The mechanical parameters for stratum layers.
Full size table

Numerical model validation

The numerical model and parameters are validated according to in situ measurement data (InSAR detection techniques) of ground settlement in the study area. The comparison of the InSAR data and numerical results is displayed in Fig. 8.

Fig. 8
figure 8

Ground settlement value of (a) to (c) InSAR measurement (Unit: mm), (d) to (f) numerical data (Unit: mm) and (g) to (i)data comparison along measurement lines at 1st year, 4th year and 6th year, respectively.

Full size image

In Fig. 8, the ground surface of the study area has a tiny settlement in the first year after coal mining, local deformed sites occurred above the right part of the 7334 and 7338 goaves. When it arrived at the 4th year, the right side area above the 7334 and 7338 goaves had a relatively large settlement. The great ground settlement was observed at the 6th year above the coal pillar between 7334 and 7338 goaves and the left area above the 7338 goaf. In the case of numerical modeling, ground settlement mainly occurred above the coal pillar between 7334 and 7338 goaves, with time going forward, continuous settlement expanded to the left side of the coal pillar. As a whole, the difference between the data of InSAR and numerical modeling, exhibits the discrete distribution of ground settlement among the InSAR data rather than the continuous spatial variation of the numerical modeling. This is because of the ideal conditions of numerical modeling, which do not consider the local surface movement due to uncertain reasons or errors in InSAR data. To identify the difference between the InSAR data and numerical modeling results, the settlements above the goaves are included every 10 m. Figs. 8(g) to 8(i) show the comparison of ground settlement values along the measurement lines above the goaves of 7330, 7334, and 7338. In the 1st year, as plotted in Fig. 8(g), the InSAR data show very small changes along the measurement lines, but the numerical modeling has a certain degree of settlement on the right-hand side of the model, the calculated root mean square errors (RMSE) of line \(\#\)1 to line \(\#\)3 are 10.31, 5.97 and 5.76, respectively. When it comes to the 4th year, as shown in Fig. 8(h), obvious settlements were observed in both the InSAR data and numerical modeling, suggesting the ranges of about -50 mm to -90 mm along line \(\#\)1, -40 mm to -100 mm along line \(\#\)2, and -20 mm to -110 mm along line \(\#\)3. Since the data fluctuation of InSAR data along the measurement lines, the differences between the InSAR data and numerical results are increased, The RMSE of line \(\#\)1 to line \(\#\)3 are 23.81, 23.29 and 36.56, respectively. In the 6th year, see Fig. 8(i), the settlement values of line \(\#\)1 to line \(\#\)3 were improved, especially the right-hand side of the goaves, where the InSAR data are close to the numerical modeling. Compared to the RMSE of the lines at the 4th year, the RMSE of the measurement lines at the 6th year are coming to be stable, suggesting 22.28, 24.42 and 32.2 of the line \(\#\)1 to line \(\#\)3, respectively. Despite the obvious difference between the InSAR data and numerical modeling, the tendency of settlement expansion, mainly in the settlement areas of the InSAR, and the numerical modeling results are similar, the RMSE suggest stable level afther the 4th year and the maximum RMSE is about 32.2 mm at the 6th year, this acceptable for using the numerical model for further study.

In addition, the site point measurement in subsidence of InSAR data and numerical model results are compared in Fig. 9(a), where five points were compared within the various years. The settlement of all the points experienced an almost linear decrease before the 4th year and dropped slowly thereafter. Although the data of the numerical model is sort of smaller than the InSAR data after the fourth year, their tendencies are similar. In addition, the calculated plastic strain in the coal pillar in the 6th year, as displayed in Fig. 9(b), suggests a damaged width of around 18.4 m and 16.1 m in the left and right side walls, respectively. According to the drilling hole detection in CK3-3, CK3-2, and CK4-2, the damage width of the coal pillar ranges from 16.5 m to 26.5 m(please see Fig. 1(d)), which is close to the numerical modeling data. Therefore, it is reasonable to see that the numerical model is capable of covering the conditions of long-term damage and deformation in the study area.

Fig. 9
figure 9

Comparison of (a) subsidence at various points by InSAR and numerical calculation and (b) the plastic strain distribution in numerical modeling.

Full size image

Characteristics of the creep damage in the strip coal pillar

In order to analyze the characteristics of creep damage in the strip coal pillar, the numerically calculated evolution of stress and plastic strain within 20 years has been analyzed in this section.

Evolution of stress distribution

The evolution of stress in the coal pillars at various times is plotted in Fig. 10, in which Fig. 10(a) indicates the maximum principal stress along the coal pillar between 7334 and 7338 goaves at various times, and Fig. 10(b) shows the vertical stress distribution at different years. Since the stress condition in the coal pillar between 7330 7334 and 7334 7338 goaves, which are similar to each other, the maximum principal stress in Fig. 10(a) gives the evolution of maximum principal stress along the coal pillar between 7334 7338 goaves. As demonstrated by Lu et al.41, the maximum principal stress along a strip coal pillar has a saddle-shaped distribution, in Fig. 10(a), such stress curves have a similar shape. Additionally, as pointed out by Kang et al.42, the concentrated stress ahead of the coal wall is about 1.5 to 2.5 times the intact stress of the coal seam, in 10(a). The rate of concentrated stress to the stress in the middle of the coal pillar is approximately 1.7. As a result, the numerical modeling in Fig. 10 is reliable.

Fig. 10
figure 10

Evolution of (a) maximum principal stress distribution in coal pillar and (b) the stress contour of numerical modeling at different times.

Full size image

Figure 10(a) suggests that the concentrated stress ahead of the damaged zone moved forward to the center of the coal pillar during creep durations. Interestingly, tensile stress was observed in the numerical modeling before the area of concentrated stress. This is due to the failed part of the coal pillar, which is dragged forward to the goaf by the vertical pressure43. The compression stress level in these areas increased after about the 6th year. The concentrated stress was enlarged initially and kept to a stable value of approximately 15 MPa, while this stress decreased after about the 6th year. Figure 10(b) convinces one that the area between the goaf and concentrated stress zone has a very small stress, which means these areas were damaged, therefore, the elastic area in the coal pillar underwent increasing stress, which can be seen in both Fig. 10(a) and Fig. 10(b).

Evolution of creep damage

In the numerical modeling, the plastic failure of materials was calculated using Eq. (2), which describes creep damage. The development of creep damage in the coal pillar is shown in Fig. 11, illustrating the width of the plastic zone in the coal pillar.

Fig. 11
figure 11

Evolution of plastic damage width of a coal pillar versus time.

Full size image

Obviously, the damaged width of the coal pillar in the 7338 goaf’s right, 7334 7338 goaves’ right, 7334 7338 goaves’ left, 7330 7334 goaves’ right, 7330 7334 goaf’s left, and the 7330 goaf’s left parts, have a similar tendency during the creep duration of 20 years. Specifically, these coal parts have an initial damage width of around 2.8 m, and fast damage expansion was observed before about the 4th year. but the speed of damage expansion was slowed down thereafter. Correspondingly, the damaged expansion will induce ground subsidence, as plotted in Fig. 9. The ground subsidence was slowed after the 4th year, and the subsidence value over 7338 goaf has a relatively large number after the 4th year.

The difference between these curves in Fig. 11 is the expansion width after about 4th years. The deeper the coal pillar, the wider the damage zone. In addition, the outer side of the coal seam, such as the coal on the left of the 7330 goaf and the right of the 7338 goaf, whose damage expansion was accelerated slightly after about the 15th year, the reason for this phenomenon is the stress in the middle part of overburden rock layers transferred outwards to the side coal seam44.

Mechanism of the damage expansion

The above analysis of the evolution of stress and damage suggests that the evolution of concentrated stress in the coal pillar creates different conditions for damage expansion. According to the concentrated stress and plastic strain in Fig. 10 and Fig. 11, the characteristics of stress and mechanism of damage expansion can be illustrated in Fig. 12.

As indicated in Fig. 12(a), concentrated stress occurred ahead of the damaged area, in which the part with concentrated stress over the creep strength will fail and make concentrated stress move forward. Compared to the initial damage condition, the new condition of concentrated stress has a higher peak stress due to the residual strength of the previously damaged zone, which provides lateral constraints45,46. With the damage zone expanded forward, the lateral constraints will become stronger and stronger, exhibiting the increased compression stress as displayed in Fig. 10(a). As the analysis of the triaxial creep experiment in the above section, the increased confining pressure will decrease the strain accumulation. In addition, the enlarged bearing capacity of damaged coal associated with the stress-transferring effect in the overburden rock layers, as analyzed in the above subsection, decreases the subsequent concentrated stress, thereby slowing the speed of damage propagation.

Fig. 12
figure 12

The diagrammatic sketch of (a) concentrated stress around the creep damage zone and (b) width of creep damage propagation.

Full size image

In the numerical modeling, creep damage was observed with a certain width at every time step. As displayed in Fig. 12(b), the width of damage expanded at one step in the numerical modeling is about 2.2 m. The results of the creep experiment in Fig. 3 suggest a creep strength smaller than 14.4 MPa. In the case of stress curves in Fig. 12(b), the width of coal with stress over about 12.7 MPa has a width of about 2.25 m. Considering the lateral constraint, the initial creep damage expansion has a faster speed because of the higher and wider range of concentrated stress surpassing the creep strength, the later damage expansion will be slowed down by the weakening stress integration.

Reasonably, the final condition of a coal pillar depends on the evolution of stress concentration, which may be weakened to be smaller than the creep strength or not, as a result, to be stable or, on the contrary. Specifically, in a certain depth of coal pillar, the stress transfer from previous creep failure will be weakened gradually by the damaged coal, because of its residual bearing capability, and the increased creep strength due to the increasing confining pressure. If the width of the stripped coal pillar is enough, the concentrated stress would be less than the increased creep strength. In such a case, creep damage propagation will be stopped. Otherwise, the enlarged overburden pressure on the intact coal pillar will accelerate the damage propagation and lead to the total failure of the coal pillar47. This still needs to be studied further.

Conclusions

This study investigated the characteristics of creep damage in strip coal pillars. Based on the field measurement of an engineering case, in terms of the ground settlement and fracture depth of coal pillars at various years, laboratory tests on the water-immersed coal and numerical modeling work of the studied case were conducted. According to the analysis of the evolution of stress distribution, creep damage, and damage expansion mechanism. Conclusions can be drawn as (a) concentrated stress ahead of the damaged zone moved forward to the center of the coal pillar during the creep durations, (b)the creep damage in the coal pillar expanded quickly initially but slowed down because of the constrain of damaged coal zones, which weak the overburden pressure and provide confining pressure to the intact coal pillar, (c)the expansion of creep damage depends on the the evolution of the triaxial creep strength of coal, which will be influenced by the transferred overburden pressure and the constraint of damaged coal body. The findings of this study are expected to enhance the long-term stability of water-immersed strip coal pillars, providing valuable guidance for ensuring urban safety above mined-out areas.