Introduction

Lithium-ion batteries (LIBs) are the primary power source for electric vehicles (EVs), hybrid EVs, and plug-in hybrid EVs due to their high energy density, efficiency, and long cycle life1,2,3,4,5. However, their performance and safety are highly sensitive to operating temperature. Excessive heat during charging and discharging accelerates capacity fade and may lead to thermal runaway, while excessively low temperatures impair power delivery and efficiency2,6,7,8,9,10. Maintaining LIBs within a recommended operating range of 20–45 °C is therefore essential for reliability and safety11.

Battery thermal management systems (BTMSs) have been developed to address these challenges. Active methods—such as liquid, air, or refrigerant-based cooling—are effective but increase system complexity, weight, and energy consumption12,13,14,15,16,17. In contrast, passive approaches are lighter, simpler, and more energy-efficient. Among them, phase change materials (PCMs) have attracted wide attention for their high latent heat storage, enabling them to absorb large amounts of heat while maintaining nearly constant temperature18,19,20,21,22,23. In addition to maintaining the maximum cell temperature within a safe range, it is equally important to limit the maximum allowable temperature difference (ΔT) within the battery pack. Large temperature gradients can accelerate uneven aging, reduce overall capacity, and increase the risk of localized thermal runaway24,25,26. The literature generally recommends that ΔT should not exceed 5 °C under normal operating conditions to ensure uniform performance and prolonged lifespan of the pack27,28,29. Therefore, both the absolute temperature and the internal temperature uniformity are critical design targets for a reliable BTMS30,31,32,33,34.

Recent studies have advanced PCM-based BTMS by addressing limitations such as low thermal conductivity. For example, composite PCMs enhanced with foams or fins achieved 3–5 °C reductions in peak temperature compared to pure PCMs35, while PCM–heat pipe hybrids reduced average operating temperature by 10–14% under 16 W heating loads36. In high-power conditions (3–5 C), optimized PCM–aluminum block housings demonstrated 19–30% lower peak temperature and 40–59% lower ΔT, successfully meeting the ΔT ≤ 5 °C requirement37. These benchmarks confirm that while material modifications are effective, thermal pathway design and geometry optimization are equally decisive. For cylindrical LIB cells, the circumferential area provides an underexplored avenue for thermal management. Zhang et al.38showed that full circumferential contact with PCM improved melting uniformity and minimized hot spots. Wang et al.39 demonstrated that circumferential encapsulation enhances PCM utilization efficiency, yielding more uniform temperatures than radial-only cooling. Lin et al.40 further optimized PCM housings to exploit circumferential thermal pathways, achieving 12–15 °C reductions in peak cell temperature at high discharge rates. Together, these studies highlight that cell geometry and housing design directly influence PCM effectiveness41,42,43. Despite these advances, most prior works have focused on material selection or circumferential contact without systematically analyzing how housing geometry itself governs PCM melting and thermal performance. In particular, the role of chamber shape and tapering has received little attention44,45,46,47,48.

The choice of a conical cylindrical chamber (CCC) is motivated by the need to improve both heat transfer and PCM utilization. Unlike conventional cylindrical casings with uniform cross-section, the CCC introduces tapering, which directly modifies the natural convection pathways during PCM melting49,50,51,52,53. This variation in cross-sectional area enhances buoyancy-driven circulation, reduces stagnant regions, and increases thermal contact between the battery and surrounding PCM. Furthermore, by tuning the top and bottom radii, the CCC enables a balance between PCM volume and exposed heat transfer area, thereby offering a design parameter to simultaneously lower peak battery temperature and improve PCM melting efficiency. The results of this study confirm that optimized CCC geometries can reduce maximum battery temperature by ~ 30 °C while avoiding underutilization of PCM volume, highlighting their superiority over traditional uniform casings54,55,56,57. Recent research has increasingly explored the use of PCM in BTMS; however, limited attention has been given to the influence of PCM housing geometry on thermal performance. In this study, a CCC was employed in both upright and inverted orientations along the longitudinal axis to identify the optimal configuration for enhancing BTMS performance. A CFD model based on the Finite Volume Method (FVM) was used to simulate the phase change behavior of PCM in the solid–liquid state. The present work focuses on buoyancy-driven natural convection and conduction mechanisms within the PCM, while the influence of external vibration is identified as an important aspect for future investigation.

The novelty of this work lies in introducing a conical cylindrical chamber (CCC) as a new design parameter for PCM housing, systematically evaluating its impact under varying radii, discharge rates, and PCM types. Unlike existing studies that primarily examine material modifications or simple cylindrical casings, this work demonstrates that chamber geometry alone can:

  • reduce peak LIB temperature by up to 30 °C in optimized cases,

  • prevent up to 38% PCM underutilization in suboptimal designs, and.

  • provide practical guidelines for balancing surface area and PCM volume in next-generation passive BTMS.

Thus, this study fills a critical gap by quantifying the role of chamber geometry in PCM-based BTMS and offering insights for geometry-driven design optimization.

Problem description

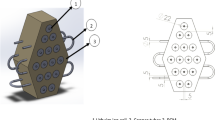
This study utilized a practical and rechargeable LIB, specifically the 18,650 model (LG INR 18650 MH1), which was encased in a conical structure (Fig. 1). The comprehensive specifications of the LIB used in this research are detailed in Table 1. The space between the LIB and its casing was filled with a PCM. During operation in discharge mode, the LIB generated heat through electrochemical reactions and internal resistance. This heat initially raised the temperature of the PCM to its melting point, triggering a phase transition from solid to liquid. In the liquid state, natural convection occurred, driven by the temperature difference between the hot source (the LIB) and the cold source (the solid phase), both of which are crucial for facilitating natural convection, alongside the influence of gravitational acceleration. As a result, the buoyancy force effects were integrated into the momentum equation. It is important to note that the current in electric vehicles varies dynamically during both acceleration and deceleration, rather than following a constant or linear pattern.

A key requirement for commercial EV battery packs is high volumetric energy density, which imposes limits on the allowable space allocated to thermal management components. The introduction of a conical cylindrical chamber (CCC) inevitably increases PCM volume relative to a purely cylindrical casing, potentially reducing the number of cells that can be accommodated within a given module footprint. However, this trade-off is justified by the significant thermal benefits demonstrated in this study, including reductions of up to ~ 30 °C in peak cell temperature and improved PCM utilization that limits ΔT within the recommended 5 °C threshold. These gains contribute directly to enhanced cycle life and safety. In practical applications, compactness can be maintained by restricting the degree of tapering, employing modular CCC inserts that fit standard module frames, and integrating CCC-based housings with hybrid cooling solutions. Thus, the CCC concept provides a tunable design parameter, allowing manufacturers to balance compactness and thermal safety according to application requirements.

To accurately model this study, discharge current amplitudes corresponding to different C-rates were applied. The C-rate is defined as the ratio of the applied current to the rated capacity of the cell; for example, 1 C corresponds to a discharge in one hour, 2 C to a discharge in half an hour, and 3 C to a discharge in 20 min. A cosine function was then utilized to represent the discharge mode current, as described below58:

$$\:I\left(t\right)=A\left(0.5+0.5cos\left(2\pi\:ft\right)\right)$$
(1)

Where A represents the C-rate, a variable ranging from 1 to 3 in this study. The frequency f is set at 0.005 Hz. The initial temperature was set to the ambient temperature of 20℃.

Fig. 1
figure 1

The proposed conical cylindrical chamber (CCC) with different radii at the top (RT) and bottom (RB). Here, RT denotes the radius of the chamber at the top surface, while RB represents the radius at the bottom surface.

Full size image
Table 1 The specification of LG INR 18,650 MH1 used in this numerical study46.
Full size table

The State of Charge (SOC) represents the ratio of the remaining capacity of the battery to its nominal capacity, expressed as a percentage. It serves as an indicator of the battery’s discharge status during operation. In this study, SOC is calculated as58:

$$SOC(t)=1 - \frac{1}{{{C_n}}}\int\limits_{0}^{t} {I\left( \tau \right)} d\tau$$
(2)

where Cn​ is the nominal capacity of the battery (3.2 Ah for the LG INR 18650 MH1), and I(τ) is the instantaneous discharge current defined in Eq. (1). At SOC = 100%, the battery is fully charged, while SOC = 0% corresponds to complete discharge.

This definition ensures consistency with standard practice in LIB studies and provides a direct link between the applied C-rate profile and the discharge process modeled in this work.

In this study, the PCM is assumed to be in direct thermal contact with the outer surface of the cylindrical battery cell. This simplifies the model by neglecting interfacial thermal resistance and enables clearer evaluation of the effect of chamber geometry on PCM melting and heat absorption. In real battery modules, a thin protective layer (e.g., aluminum shell, polymer coating, or thermally conductive epoxy) is typically introduced between the cell and PCM to ensure electrical insulation, containment of PCM, and additional mechanical safety, while still maintaining low thermal resistance. Most PCMs employed in BTMS are electrically non-conductive and chemically stable, so the assumption of direct contact does not introduce unrealistic safety risks in the thermal analysis. Nonetheless, system-level safety evaluation and long-term PCM stability are beyond the scope of this study and are recommended for future work.

Mathematical formulation

This research conducted a simulation to model the transition between solid and liquid phases in the context of incompressible laminar flow with consistent thermophysical properties. Additionally, the momentum equation incorporated the buoyancy force term, considering the presence of both a hot source and a cold source, through which the liquid phase flowed, influenced by changes in density. As a result, the governing conservation equations for mass, momentum, and energy can be expressed as follows:

Mass conservation (continuity)46:

$$\:\nabla\:.\varvec{V}=0$$
(3)

Momentum conservation (Navier–Stokes with buoyancy and mushy-zone source terms):

$$\:{\rho\:}_{PCM}\frac{\partial\:\varvec{V}}{\partial\:t}+{\rho\:}_{PCM}\left(\varvec{V}.\nabla\:\right)\varvec{V}=-\nabla\:p+{\mu\:}_{PCM}\nabla\:.\left(\nabla\:\varvec{V}\right)+{\rho\:}_{PCM}{\beta\:}_{PCM}\left(T-{T}_{Ref}\right)\varvec{g}-{10}^{5}\frac{{\left(1-\lambda\:\right)}^{2}}{{\lambda\:}^{3}+{10}^{-3}}\varvec{V}$$
(4)

Energy conservation (including latent heat term)46:

$$\:{\rho\:}_{PCM}\left({C}_{p,\:PCM}+{h}_{PCM}\frac{d\lambda\:}{dT}\right)\frac{\partial\:T}{\partial\:t}+{\rho\:}_{PCM}{C}_{p\:PCM}\left(\varvec{V}.\nabla\:T\right)=\nabla\:.\left({k}_{PCM}\nabla\:T\right)$$
(5)
$$\:\lambda\:=0.5\:erf\left(4\frac{{T}_{s}-{T}_{f}}{{T}_{l}-{T}_{s}}\right)+0.5$$
(6)

The momentum equation’s third and fourth terms on the right side correspond to the buoyancy force and the influence of the mushy zone, which are essential for determining the phase of a point, whether it is in a liquid state or not. The melting function serves to measure the volume of melting occurring at each specific cell or point, with its values ranging from 0, indicating a solid state, to 1, indicating a liquid state. In these equations, the variables V, p, T, g, t, and λ represent the velocity vector, pressure, temperature, gravitational acceleration vector, time, and melting fraction, respectively.

The solid–liquid transition of PCM was modeled using the enthalpy–porosity method, a widely adopted approach for solid–liquid phase change problems. In this formulation, the PCM is treated as a single effective continuum, and the local state (solid, mushy, or liquid) is determined by the liquid fraction λ, which varies smoothly between 0 (fully solid) and 1 (fully liquid). The liquid fraction is related to the local temperature through Eq. (5), which distributes latent heat over the melting temperature range.

In the momentum equation, the mushy zone is incorporated as a Darcy-type source term46:

$${S_{mushy}}= - c\frac{{{{(1 - \lambda )}^2}}}{{{\lambda ^3}+\varepsilon }}$$
(7)

where C = 105 is the mushy zone constant and Ɛ=10− 3 is a small numerical parameter to prevent division by zero. This term suppresses velocity in regions where λ approaches 0 (solid PCM) while allowing full convection where λ→1.

The energy equation couples sensible and latent heat through an effective heat capacity formulation46:

$$\rho \left( {{C_p}+{h_{PCM}}\frac{{d\lambda }}{{dt}}} \right)\frac{{\partial T}}{{\partial t}}+\rho {C_p}\left( {V.\nabla T} \right)=\nabla .\left( {k\nabla T} \right)$$
(8)

ensuring that latent heat absorption and release are captured during melting and solidification.

This method avoids explicit interface tracking and enables robust simulation of complex phase change phenomena with natural convection. In the present study, this approach allows simultaneous resolution of heat conduction in solid PCM, buoyancy-driven convection in liquid PCM, and suppression of flow in partially solidified regions, capturing the essential multiphase physics of the LIB–PCM thermal system.

A single cylindrical 18,650-type lithium-ion battery cell was modeled with a radius of 9 mm and a height of 65 mm, consistent with typical commercial dimensions. The cell was represented as a homogeneous heat-generating solid domain, with volumetric heat generation prescribed according to the discharge rate. The internal heat generation \({\dot {Q}_{cell}}\)​ was calculated using59:

$${\dot {Q}_{cell}}(t)=I{(t)^2}R+I(t){\left( {\frac{{\partial U}}{{\partial T}}} \right)_{SOC}}$$
(9)

where I(t) is the current, R the internal resistance, and U the open-circuit voltage. Average heat generation values for 1 C, 2 C, and 3 C discharge rates were taken from Table 3. The cell was assumed to have uniform material properties, with density, specific heat, and thermal conductivity listed in Table 1.

The battery’s curved outer surface and bottom face were in direct thermal contact with the PCM, as discussed in Sect. 3. The outer surface of the PCM chamber was exposed to ambient air and modeled as a convective heat transfer boundary with a heat transfer coefficient of h = 10 W·m⁻²·K⁻¹ and ambient temperature T ∞ = 298 K (25 °C). Symmetry conditions were applied along the vertical axis of the geometry to reduce computational cost. The initial condition for both battery and PCM domains was a uniform temperature of 298 K. Gravity was included in the vertical direction to capture buoyancy-driven convection in the liquid PCM.

Electrochemical reactions are integral processes in batteries, driving the flow of electric current. These reactions involve the transfer of electrons between the anode and cathode electrodes during discharge, where the anode undergoes oxidation, losing electrons and becoming positively charged. The electrons travel through an external circuit to the cathode, engaging in a reduction reaction that adds electrons to the cathode, rendering it negatively charged. This sequence results in an electric current flowing from the anode to the cathode. During charging, these reactions reverse, with current flowing in the opposite direction, and electrons transferring from the cathode back to the anode. This reverts the anode and cathode to their original states, enabling the battery to be recharged. The specific electrochemical reactions vary based on battery chemistry; for instance, LIBs involve the movement of lithium ions, leading to the formation and dissolution of lead dioxide and lead sulfate. These reactions generate heat within LIBs. Internal resistance, the resistance to current flow within the battery, contributes to energy loss as some stored electrical energy is converted into heat. This resistance arises from materials within the battery, including electrodes and electrolytes. Consequently, internal resistance can impact battery efficiency and current delivery to external circuits. Factors influencing internal resistance include battery chemistry, size, design, temperature, and age. The interplay of electrochemical reactions and internal resistance in LIBs results in heat generation, as expressed below59:

$$\:{\dot{Q}}_{el}=IT\frac{d{E}_{oc}}{dT}$$
(10)
$$\:{\dot{Q}}_{r}=R{I}^{2}$$
(11)

Which \(\:R\:and\:\frac{d{E}_{oc}}{dT}\) were \(\:10\:m{\Omega\:}\:and\:0.4\:\frac{mV}{K}\), respectively.

The total volumetric heat generation in the cell is obtained by summing the reversible electrochemical heat \({\dot {Q}_{el}}\) and the irreversible ohmic heat \({\dot {Q}_r}\) according to Eqs. (5) and (6). Since the discharge current I(t) is defined by a cosine function [Eq. (1)], the instantaneous heat generation varies with state of charge (SOC) rather than remaining constant. Table 2 summarizes the average heat generation values for the C-rates investigated in this study, computed for the 18,650 cell (capacity 3.2 Ah, nominal voltage 3.67 V). As expected, heat generation increases approximately with the square of the C-rate due to the dominance of ohmic heating.

Table 2 Average heat generation values at different C-rates.
Full size table

To compute the PCM thermophysical properties can refer to Table 3.

Table 3 The thermophysical properties of studied PCMs in ambient temperature46.
Full size table

Grid and time-step independence study

To ensure that the reported results are not influenced by spatial or temporal discretization, we conducted a mesh and time-step independence study using the most thermally demanding operating condition (C-rate = 3) and the CCC configuration with the largest top and bottom radii (worst-case heating). Unstructured, hexahedral-dominant meshes with local refinements were generated in the battery–PCM interfacial region and within the expected phase front. Mesh quality metrics for all cases satisfied common best practices (average skewness ≤ 0.25, maximum non-orthogonality ≤ 65°). Transient simulations were advanced with a second-order time integrator and second-order spatial schemes for all transported quantities. Nonlinear iterations were continued each time step until residuals fell below 10⁻⁶ for velocity, pressure, and temperature, and 10⁻⁸ for the enthalpy/melting fraction equation.

Table 4 summarizes the grid convergence using four systematically refined meshes. Two integral measures were monitored: (i) the maximum cell temperature \({T_{\hbox{max} }}\) reached during discharge and (ii) the average liquid fraction \(\overline {\lambda }\) of the PCM at the end of discharge (SOC = 0%). Between the Fine and Very Fine meshes, the relative changes are ≤ 0.1% for \({T_{\hbox{max} }}\)​ and ≤ 0.4% for \(\overline {\lambda }\), indicating mesh-independent results. A supporting time-step check (Δt = 0.10, 0.05, and 0.025 s on the Fine mesh) yielded variations ≤ 0.2 K in \({T_{\hbox{max} }}\)​ and ≤ 0.2% in \(\overline {\lambda }\). Based on these findings, the Fine mesh and Δt = 0.05 s were adopted for all production runs to balance accuracy and computational cost.

Table 4 Mesh independence for the worst-case operating condition (C-rate = 3). Quality metrics refer to the entire domain; \({T_{\hbox{max} }}\)is the peak battery temperature reached during discharge; \(\overline {\lambda }\) is the domain-averaged liquid fraction at SOC = 0%.
Full size table

Model validation

To establish confidence in the numerical model, a validation study was performed by comparing the predicted temporal evolution of PCM melting fraction against reference data reported by Kamkari et al.60. The test case corresponds to a horizontal configuration (Θ = 90°), widely used in the literature as a benchmark. Figure 2 shows that the present model reproduces the melting fraction–time relationship with excellent fidelity, with discrepancies not exceeding 5% throughout the melting process. This close agreement confirms the accuracy of the enthalpy–porosity method implementation and supports the use of the present CFD framework for simulating battery–PCM thermal interactions.

Fig. 2
figure 2

Validation of the numerical model by comparison of the predicted melting fraction with reference data60 for Θ = 90°60.

Full size image

Results and discussion

In this study, the effects of nine different types of battery housing on the melting of PCMs and energy saving were investigated. The results are presented in the form of contours and plots. It should be noted that the total heat generation is not constant but varies dynamically with SOC, as governed by the cosine discharge profile [Eq. (1)]. Consequently, thermal response curves shown in Figs. 4, 5 and 6 reflect both the geometry-dependent heat transfer and the inherent temporal variation in heat generation.

Figure 3 demonstrates the effect of nine types of CCC on the melting fraction of PCM. As can be seen from the figure, for cases with a top surface of 15 mm, by increasing the length of the bottom surface from 15 to 27 mm, the unmelted area increases because of the lower thermal performance of the CCC. Moreover, cases with the narrowest bottom surface, which are R2B 15, have a fraction of melted PCM near the lower surface. Considering that the heated surface is only the middle one, this phenomenon can be explained by the fact that it creates a larger temperature gradient and a stronger buoyancy force in the liquid PCM near the bottom surface. These factors enhance the natural convection and the melting process of the PCM near the lower surface. It can be said that, considering the ratio of the total area of the CCC to the melted area of the PCM, the highest melting occurred for the case with the upper side of 15 mm and the lower side of 21 mm. This is because this case has the optimal balance between the heat transfer area and the PCM volume, which maximizes the heat transfer efficiency and the melting fraction of the PCM.

Fig. 3
figure 3

Melting fraction contour of the PCM for various thicknesses at C-rate = 1.

Full size image

Figure 4 shows the velocity contour of melted PCM affected by conical configurations of battery housing. As illustrated by the figures, in most cases the maximum velocity magnitude is close to the middle wall, which is the heated one, and it can be more pronounced in the cases with the longest bottom wall, which is (R2B 27). This is because the longer bottom wall creates a larger contact area between the battery and the CCC, which increases the heat transfer and the temperature gradient in the liquid PCM near the middle wall. The increased temperature gradient and the buoyancy force induce stronger fluid motion and higher velocity magnitude in the liquid PCM. Moreover, for cases with a bottom wall of 21 mm, a small vorticity can be seen near the upper wall, which, by increasing the length of the top wall from 15 mm to 27 mm, leads to a long vorticity emerging near the middle wall near the battery. This is because the increased length of the top wall changes the shape and the orientation of the CCC, which affects the flow pattern and the distribution of vortices in the liquid PCM. The longer top wall creates a more inclined surface, which deflects the fluid flow and generates a longer vorticity near the middle wall.

Fig. 4
figure 4

The velocity contour of the PCM for various thicknesses at C-rate = 1.

Full size image

Figures 5, 6 and 7 show the battery temperature affected by different CCC types for 3 C-rates from 1 to 3. As can be seen from the plots, for C-rate = 1 the variation of the plots due to different CCC conditions is negligible. However, for the case with a bottom wall of 21 mm, by increasing the top wall length from 15 to 27 mm, the battery temperature decreases, which shows a promising operation of this configuration for PCM melting and absorbing heat from the battery. On the other hand, for cases with C-rate = 2 and C-rate = 3, it can be seen that changes in the geometry of CCC affect the battery temperature; that is, by increasing the top wall length from 15 to 27 mm, the battery temperature decreases. To illustrate the point, for the cases studied with C-rate = 2, by increasing the length of the top wall and keeping the same length of the bottom wall at 15 mm, the maximum temperature of the battery decreases from 419.248 to 339.422 K. The plateau in battery temperature observed after ~ 60–70% SoC is attributed to the decrease in heat generation as discharge progresses. During the early and mid stages, both ohmic and entropic heat contributions are significant, causing temperature rise. However, toward the later stages of discharge, the entropic term diminishes and overall heat generation decreases, while the PCM has already absorbed earlier heat. This leads to a nearly constant cell temperature, consistent with trends reported in previous PCM-BTMS studies.

Fig. 5
figure 5

The battery temperature when C-rate = 1 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image
Fig. 6
figure 6

The battery temperature when C-rate = 2 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image
Fig. 7
figure 7

The battery temperature when C-rate = 3 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image

Figures 8, 9 and 10 show the average melting fraction of PCM for different battery housing geometries and C-rates. As can be seen from the line graphs for the period of SOC, by increasing the length of the top wall from 15 to 27 mm, the average melting fraction decreases. This is because the increased length of the top wall reduces the contact area between the PCM and the CCC, which decreases the heat transfer and the temperature gradient in the liquid PCM near the bottom. However, it is more pronounced in C-rate = 1, which has a lower heat generation rate than the other C-rates. That is, for the case with C-rate = 1, R2T = 15 mm and R2B = 21 mm, the average melting fraction in the highest amount is 72.224, while it has decreased to 27.03 for the case with C-rate = 1, R2T = 27 mm and R2B = 21 mm. Moreover, for cases with C-rate = 1, the highest percentage of average melting fraction is for R2B = 15; likewise, the mentioned case for other C-rates and top wall lengths reaches 100% sooner. This is because the case with R2B = 15 has the smallest CCC area and the largest PCM volume among the cases studied, which means it can store the most heat in the PCM and reach the complete melting faster. Figure 8 presents the temperature evolution as a function of SoC during discharge. The SoC range is shown beginning at 80%, since the initial 100–80% discharge segment produced only negligible temperature rise. In this early stage, the heat generation is relatively low and the PCM remains largely in the solid state, so thermal changes are minimal. By starting the plot from 80% SoC, the figure emphasizes the region where heat generation becomes significant, the PCM begins to melt actively, and the most relevant temperature dynamics occur. This representation avoids a flat initial segment and provides clearer insight into the influence of chamber geometry and PCM behavior on thermal performance.

Fig. 8
figure 8

The average melting fraction when C-rate = 1 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image
Fig. 9
figure 9

The average melting fraction when C-rate = 2 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image
Fig. 10
figure 10

The average melting fraction when C-rate = 3 corresponding to SOC for (a) R2T = 15 mm, (b) R2T = 21 mm, and (c) R2T = 27 mm.

Full size image

Conclusion

This paper presented a numerical study of the effects of different CCC types on the melting of PCMs and energy saving for various C-rates of a LIB. The results showed that the CCC area and the PCM volume had a trade-off effect on the heat transfer and the melting process of PCM, and the optimal balance depended on the C-rate and the ambient temperature. The case with the largest CCC area and the smallest PCM volume had the lowest battery temperature and the fastest melting process, which was beneficial for the battery performance and safety. The inclination angle of the system also influenced the natural convection and the heat transfer in the liquid PCM, which in turn affected the melting fraction and the velocity magnitude of PCM. The numerical model used in this study was validated by comparing the results with the reference data, showing a good agreement. The main contributions of this paper are:

  • It provided a comprehensive analysis of the effects of different CCC types on the melting of PCMs and energy saving for various C-rates of a LIB.

  • It identified the optimal CCC configuration that achieved the highest heat transfer efficiency and the melting fraction of PCM, as well as the lowest battery temperature.

  • It revealed the influence of the inclination angle of the system on the natural convection and the heat transfer in the liquid PCM, and the corresponding effects on the melting fraction and the velocity magnitude of PCM.

Scope and future work

The present study has been deliberately restricted to a single cylindrical 18,650 cell to allow a clear evaluation of how CCC geometry influences PCM melting and passive cooling performance. Although the concept is scalable, pack-level performance depends on additional factors such as inter-cell coupling, module casing, and active cooling strategies. Drawing reliable conclusions at that level requires dedicated multi-cell simulations and experimental validation. Consequently, the application of CCCs in battery packs is identified as an important direction for future research, beyond the scope of the current single-cell study.