Hybrid machine learning models for predicting the tensile strength of reinforced concrete incorporating nano-engineered and sustainable supplementary cementitious materials

Abstract

Despite its significance for performance-based design, concrete’s tensile strength, which governs crack formation, structural damage, and the longevity of the structure, has usually received inadequate attention in predictive modeling compared to compressive strength. This paper proposes a complete machine learning approach to forecast the tensile strength of nano-engineered and sustainable concretes utilizing a novel database containing 500 data points and ten diverse input factors such as water-to-cement (w/c) ratio, curing time, coarse and fine aggregates, and content of other additives (basalt fiber, carbon nanotube, geopolymer binder, superplasticizer). The study employed and compared four state-of-the-art machine learning algorithms, including support vector regression (SVR), artificial neural networks (ANN), extreme gradient boosting (XGBoost), and a novel hybrid ensemble model (HEM) that uses a weighted meta-regressor to combine outputs from multiple base learners. The HEM model consistently outperformed the others in hold-out cross-validation, K-fold cross-validation, and generalization tests. It achieved the best predictive accuracy with a K-fold cross-validation composite score of 96. ANN came in second place, followed by SVR and XGBoost, with K-fold cross-validation ranking scores of 70, 53, and 25, respectively. In the generalization tests, HEM demonstrably followed the nonlinear trends in the tensile strength for w/c ratios (peak at 0.4 with 36.95 MPa), curing time (peak at 56 days with 38.49 MPa), and nano-clay content (peak at 5% with 38.86 MPa), surpassing the other models in every case. Sensitivity analysis using the HEM model revealed optimal input values for maximizing tensile strength, including cement content (378.7 kg/m²), w/c ratio (0.406), fine aggregate (830.5 kg/m²), coarse aggregate (1034.5 kg/m²), nano-clay (4.98%), carbon nanotubes (1.00%), geopolymer binder (18.18%), basalt fiber (2.56%), and superplasticizer (< 0.93%). The findings of this study offer not only a reasonable and precise model for forecasting tensile strength but also a predictive analytical framework for enhancing eco-friendly concrete mix designs. By combining sophisticated machine learning algorithms with materials science, the article contributes to the development of innovative, performance-oriented, more durable, and environmentally friendly infrastructure construction and maintenance.

Introduction

Concrete is one of the most widely used materials in construction worldwide due to its flexibility, strength, and cost-effectiveness¹. Its mechanical properties, which include, but are not limited to, compressive strength, tensile strength, and durability, dictate the performance and safety of structures over time^2,3,4,5. Out of all the properties, tensile strength is notably more critical as it affects the material’s ability to withstand cracking and failure under tension⁶.

Recently, the use of nanomaterials like nano-clay, carbon nanotubes, and silica fume has been received positively due to their potential improvement of concrete’s mechanical and durability properties^7,8,9,10. Due to their small size and large surface area, these new materials are believed to enhance the concrete microstructure, thereby improving its strength and performance. Supit and Shaikh¹¹; noted that workability was reduced by 60% with the addition of 2–4% nano silica and that the high surface area of nano silica was responsible due to a large amount of water being captured, thus reducing slump values.

The impact of nano-alumina on concrete workability has not yet been determined and necessitates further investigation. Some studies suggest a decrease in workability, but others, like Feng et al.¹², found an increase. The decrease is assumed to be the result of the high surface area of nano alumina, similar to nano silica, while the rise is connected to the effect of magnesium phosphate cement¹³. Due to the high specific gravity of graphene oxide, it has been proven to cause a reduction in workability owing to its high water absorption. Lee et al.¹⁴ noted a 31.8% reduction in workability at a 0.025 wt% dosage. This is such a significant decrease that even with the maximum dosage of superplasticizer, the required workability could not be attained. The same result is reported by Suchorzewski et al.¹⁵ regarding the use of carbon nanotubes, as they also reduce workability.

According to Fan et al.¹⁶, nano-clay diminishes workability. It was determined that with greater amounts of nano-clay, more water was required to achieve normal consistency, and this relationship was directly proportional. Also, Norhasri et al.¹⁷ showed that slump decreased by 15% with the addition of 9% nano metakaolin. Conversely, Morsy et al.¹⁸ reported that the incorporation of 2.5%, 5%, and 7.5% nano metakaolin resulted in increases in compressive strength of 15%, 34%, and 19%, respectively.

When producing high-performance concrete (HPC) with nanomaterials, it is crucial to develop an optimal mix design that strikes a balance between workability, strength, durability, and cost. Such optimization is typically achieved through various experimental investigations, including rheological evaluations and mechanical property tests, which involve multiple trial mixes.

While it is necessary to fathom the interactivity of nanomaterials within the cementitious matrix system, these processes are often expensive, both temporally and financially. Especially with the integration of various nanomaterials, such as nano-silica, nano-alumina, graphene oxide, carbon nanotubes, and nano-clays, the increasing sophistication of concrete systems cannot be adequately addressed using simple trial-and-error methods. This problem highlights the need for specialized, state-of-the-art optimization and predictive technologies. In this regard, machine learning methods offer a novel solution, being both quick and highly efficient. These algorithms are capable of discerning intricate, non-linear functions when enormous datasets resulting from experimental outcomes are provided^19,20,21. Moreover, with the correct input of parameters such as the type of nanomaterial, dosage, water-to-cement (w/c) ratio, and content of admixture, crucial properties of concrete, including compressive strength, slump, setting time, and durability metrics, can be easily predicted.

Incorporating machine learning into the design methodology of reinforced concrete facilitates the transformation of ideas into reality, thanks to the independent nature of computational design and the elimination of repetitive and expensive experimental work^22,23,24. In the future, the interplay between materials science and modeling will be indispensable in realizing the potential of using nanomaterials in concrete for construction as the interdisciplinary domain continues to evolve^{25,26,27,28,29}.

Even with modern advancements in using machine learning techniques to forecast the compressive strength of concrete^30,31,32, predicting its tensile strength remains relatively uncharted. Notably, considering the tensile strength of concrete governs the structure’s performance in various aspects such as crack formation and development, shrinkage, long-term durability, and structural operability. It plays a vital role in evaluating the capability of reinforced concrete structures under bending, axial, and shear forces. If the estimates or predictions concerning this property are insufficient, serviceability or structural failure will occur in due time. The ease with which concrete’s compressive strength can be measured and is almost universally requested in design specifications stands in stark contrast to the challenges posed by testing its tensile strength. Measuring tensile strength is not only more difficult, but it also necessitates the use of indirect methods, such as splitting tensile or flexural tests. This partly explains the sparse and unreliable datasets, as well as the strong machine learning models focused on the tensile strength of concrete, which further explains the sparse datasets on the tensile strength of concrete.

In addition, a scope of gap in the existing body of work pertains to evaluating the performance and generalization capability of machine learning algorithms over a broad range of concrete specimens, particularly those with engineered nanomaterials. Factors such as nano-clay content, water-to-cement ratio (w/c ratio), curing time, and supplementary cementitious materials (SCMs) interact in a multidisciplinary manner with each other, introducing a high degree of non-linearity to the tensile strength. The relationships between these variables are intricate and often defy capture by standard statistical approaches or one-dimensional predictive models. Most of these studies appear to deal with individual mix conditions or limited material sets, resulting in underfit, over-determined models that lack generalization ability and perform poorly on out-of-sample datasets or other concrete variations. There’s an industry-wide shift towards high-performance and sustainable materials, including concrete enhanced with nano-engineered additives. Consequently, there’s an outstanding need for advanced modeling techniques that reflect the diversity and complexity of modern mix designs.

To address these issues, this study presents a detailed proposal for using advanced machine learning approaches in the predictive modeling of tensile strength in a blend of nano-modified and sustainable concrete. Notably, this study examines and analyzes the results from four prominent machine learning algorithms: support vector regression (SVR), artificial neural networks (ANNs), extreme gradient boosting (XGBoost), and a custom-built hybrid ensemble model (HEM), which was explicitly designed for this study. All models were trained on the experimental data set from the survey, which contained a variety of input features, including nano-clay content, w/c ratio, curing time, SCM incorporation, and others. Each of these variables has the potential to improve the accuracy of design-based predictive models, efficient transforms, and generalized high-fidelity models.

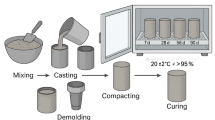
The principal objectives of this research are fivefold: (1) to develop reliable and precise machine learning-based models for predictions on the tensile strength of nano-engineered concrete; (2) to evaluate the generalization performance of each algorithm using varying conditions to test their robustness across different formulations of concrete; (3) to perform a feature importance analysis to evaluate the degree to which design elements of the mix contribute to the overall output prediction; (4) to check the predictive accuracy of the models using a withheld experimental dataset; and (5) to provide a scalable and interpretable model framework capable of supporting optimization for performance-based material selection and use in engineering design practice. The whole process of this study is shown in Fig. 1.

Fig. 1

The whole process of this study.

Research significance

Predicting tensile strength in nano-engineered concrete with accuracy is essential for driving performance-oriented designs, fine-tuning mix designs, and minimizing the need for labor-intensive laboratory tests. Although the literature is replete with investigations using traditional machine learning tools to forecast concrete strength, nearly all concentrate on compressive strength and overlook tensile strength, an equally vital measure for preserving structural soundness, particularly in elements subjected to flexural loading or those prone to early cracking.

The addition of nano-engineered and greener supplementary cementitious materials (SCMs) further complicates the microstructure, triggering nonlinear effects and intricate interactions that conventional single-model techniques struggle to resolve. Current models tend to overfit the training data, exhibit restricted extrapolation to non-standard or hybrid formulations, and, most critically, lack clarity on how mix constituents affect the final strength.

This work addresses those limitations through an innovative HEM model, augmented with Bayesian hyperparameter tuning and sensitivity quantification. The resulting system not only elevates predictive performance but also distils actionable information on the impact of key design variables, thus empowering engineers to formulate more rational and eco-efficient concrete mixtures.

This research advances the field of artificial intelligence-driven concrete design by delivering three key contributions: first, it presents a prediction tool that is both transferable and generalizable across a wide range of concrete formulations and loading scenarios; second, it establishes the tool’s robustness through systematic monotonic parameter variation and rigorous cross-validation; and third, it provides an explainable framework that can be seamlessly incorporated into intelligent design platforms and decision-support systems serving the structural materials engineering community.

The most remarkable novel contributions made in this work are as follows:

• First, the study shifts its focus to predicting the tensile strength of materials, which is critically essential yet not emphasized in machine learning-based modeling of concrete behavior.

• Second, it utilizes nano-clay and sustainable SCMs as its primary inputs, deviating from traditional SCMs and aligning with the contemporary focus on eco-efficient construction.

• Third, it conducts a significant comparison of multiple machine learning algorithms, including a mixed ensemble approach, for elevating the prediction accuracy and robustness of the problem.

• Four, it utilizes non-MLASS interpretation, focusing on providing actionable insights from mixed components using techniques such as permutation importance and SHAP analysis, which significantly enhances the interpretability of models.

• Ultimately, the study addresses fundamental issues of sustainability and performance optimization in conjunction with international efforts aimed at minimizing the ecological impact of the construction industry while enhancing material efficiency.

Concrete sample preparation, tensile strength testing, and machine learning modeling

This section describes the detailed methodologies for nano-engineered sustainable materials, incorporating curing and mechanical testing of reinforced concrete mixtures. The focus was on developing and capturing a synthetic dataset of 500 distinct concrete mixes, aimed at training, validating, and interpreting machine learning models that target splitting tensile strength.

Dataset origin and experimental procedures”

The complete collection of 500 data points was generated solely from laboratory experiments conducted by the authors. Each entry denotes an individual concrete mix formulation, meticulously formulated and subjected to tensile strength testing in tightly regulated settings. The testing program encompassed a broad spectrum of nano-engineered and fibre-reinforced concrete formulations, varying curing durations, and mix variables, thus delivering a thorough and robust dataset. No synthetic data generation or regression-based enhancement was employed; every data point originates from repeatable, standardized experimental procedures, thereby guaranteeing the authenticity and reliability of the dataset used for training and assessing the machine-learning algorithms.

Dataset specification and variable ranges

The stand-alone dataset used for this study comprises a complete range of eleven parameters, where ten are input features and one is the target output (Table 1). The inputs capture the modern and conventional dimensions of concrete mix design, that is, the physical proportions, material substitutions, chemical admixtures, and curing regimes. These variables were selected through a systematic analysis of experimental research on high-performance and sustainable concrete, ensuring both scientific and practical relevance.

The traditional mix design consists of cement content, water-to-cement (w/c) ratio, and contents of fine and coarse aggregates. This is supplemented by modern materials, such as nano-clay and carbon nanotubes, which are posited to enhance strength through nano-scale reinforcement mechanisms by refining the microstructure. Basalt fibers were added to strengthen the post-cracking tensile behavior, and the geopolymer binder content used serves as a sustainable alternative to Portland cement, often improving strength and durability over time. Superplasticizer dosage, control of workability, and additive dispensing and curing age indicate the strength development over time.

As provided in Table 1, each variable was given a scientifically justifiable range based on the latest experimental findings. For example, the cement content was adjusted between 250 and 450 kg/m³, and the w/c ratio was adjusted between 0.25 and 0.60. Both fine and coarse aggregates were varied within practical limits to represent dense and workable mixes. Representing the stronger performance observed with lower allotment, nano-clay was restricted to 5% and carbon nanotubes to 1% of the binder content. Geopolymer binders were added to the mix in amounts ranging from 0 to 30% by mass of the cementitious material. Curing ages of 7, 14, 28, and 56 days were selected to represent the strength characteristics of early and long-term curing periods. The tensile strength was treated as an output variable and predicted using a nonlinear mathematical model based on the input parameters. To ensure robustness of any predictive modeling applied, Gaussian noise was added to simulate inherent experimental variability.

Table 1 Dataset variables and characteristics.

Concrete mix design protocol

A systematic combinatorial approach was employed to design synthetic concrete mixtures in silico, considering the entire design space based on the input variable ranges. The objective was to capture the diversity of industrial concrete compositions utilized in advanced experimental research while ensuring internal consistency and practicality. Each mix followed traditional guidelines of ACI 211 ‘mix proportioning’ (i.e., ‘the delineation of specific proportions’) while also incorporating the dispersive and integrative demands of nanomaterials and fibers. The superplasticizer dosage was modified based on the demonstrated loss of workability associated with the hyper-structured nano-clay and CNTs, due to their high surface area.

To represent concrete with more realistic rheological properties, uniform distribution of the nano-additives mentioned above was assumed. Carbon nanotubes and nano-clays were considered to be pre-dispersed using high-shear mechanical mixers or ultrasonic homogenizers, which are commonly employed in small-scale nano-concrete production laboratories. The interactions between the geopolymer binders and cement hydration products were constructed on the paradigms of blended system strength gain measurements, assuming adequate alkali activation of the constituent geopolymers.

Covering the complete parameter space while respecting inter-material compatibility enables all generated mix designs to serve as a sophisticated framework for simulating practical concrete behavior, particularly in situations involving intricate material interactions where simplistic approaches fail to meet predictive needs.

Sample casting and curing

In a concrete testing laboratory, concrete specimens are prepared within cylindrical molds with standard dimensions of 150 mm in diameter and 300 mm in height, which are also used for mechanical strength testing. Concrete sample preparation used in this study attempted to adhere to traditional and best practices in concrete casting, including processes in concrete casting with traditional and nano-enhanced procedures.

The mixing procedure was considered to begin with dry constituent nano-clay, cement, geopolymer powder, as well as both fine and coarse aggregates, where the constituent of the specimen was mixed for 2 min in either a pan or a rotary drum mixer, a uniform premixed solution of water and superplasticizer was added to retain the consistency of fluidity and guarantee chemical pores activation. Following a second mixing stage that lasted around 3 min, all the nano-additives were added, ensuring adequate coating of the aggregates in the ultra-high-performance concrete (UHPC) preparation.

The concrete mix was cast into the molds in two stages: first compacted layer and second compacted layer, which can increase the quality of the air interfacial transition zone. After 24 h, the specimens were demolded and placed immediately into lime water, which was kept at a constant temperature of 23 ± 2 °C. This environment is designed according to ASTM specifications and enables the hydration of cement, as well as the activation of geopolymeric reactions. Curing durations were set to be short-term (7 and 14 days) and long-term (28 and 56 days) to capture changes in mechanical behavior and evolution of tensile strength over time.

Tensile strength testing methodology

The tensile strength of concrete is one of the most important properties when considering the cracking resistance and ductility of fiber- and nano-reinforced cementitious structures. For this analysis, the splitting tensile test, also known as the Brazilian test, was utilized. This is described in ASTM C496/C496M-17. This method is quite popular due to its ease and reproducibility in simulating cylindrical uniaxial tensile conditions, eliminating the need for sophisticated gripping devices.

During the routine procedure, the cylindrical specimen is horizontally placed between two concrete-steel loading caps on a universal testing machine. A compressive load is applied on the vertical diameter of the cylinder at a controlled speed, usually 1.2 MPa/min. This causes tensile stress in the direction perpendicular to the applied force. The fracture will occur along the vertical alignment, and the measuring instrument computes the maximum load that can be achieved without exceeding this threshold. Equation (1) is used to calculate the splitting tensile strength.

$$\:{f}_{t}=\frac{2P}{\pi\:LD}$$

(1)

Where, $\:{f}_{t}$ is the splitting tensile strength in MPa, $\:P$ the maximum available load in Newtons (N), $\:L$ the length of the cylinder in mm, and $\:D$ the diameter of the cylinder in mm.

To generate the dataset, the input variables were used to create linear and non-linear interactions between them. The tensile strength values were synthesized using a regression-based modeling approach. To imitate the variability observed in lab testing, zero-mean Gaussian noise with a standard deviation of 0.5 MPa was introduced. This ensures that the dataset is statistically sound and representative of the true performance metrics in sophisticated concrete systems.

Machine learning framework

This section discusses the computational architecture developed for estimating the tensile strength of nano-engineered and fiber-reinforced concrete mixtures. Most importantly, the goal is to define a strong, predictive model which is purely empirical and can integrate the intricate, nonlinear relationships between a multitude of material and design parameters. Usually, due to the heterogeneous nature of the input features (for instance, the use of nano-additives, fiber reinforcement, and binder systems, which have multiple sustainability aspects), and the complex interfacing relationships, conventional linear regression or empirical equations would not suffice. Thus, a supervised machine learning approach was employed, in which different models were developed, optimized, and tested in terms of their predictive accuracy, generalizability across a given dataset, and robustness with varying data types.

The framework consisted of five key phases: (1) data preprocessing and normalization, (2) model selection and architecture design, (3) hyperparameter optimization, (4) model training and validation, and (5) performance evaluation using multiple statistical metrics and visual diagnostics.

Data preprocessing and normalization

Before developing the model, all input features underwent thorough preprocessing to facilitate seamless integration with the model, ensuring consistent performance. Continuous input parameters were standardized using Z-score normalization to a mean of 0 and variance of 1. Non-ordinal categorical variables (curing duration) were one-hot encoded, avoiding the loss of non-ordinal relationships among categories.

We examined multicollinearity among the input features by computing the Variance Inflation Factor (VIF) for each predictor. The VIF measures the extent to which the estimated variance of the regression coefficients is inflated due to the linear intercorrelations among the features. A VIF exceeding 5 (with some analysts adopting a stricter cutoff of 10) typically signals a level of multicollinearity that can destabilize coefficient estimates and complicate interpretation. In the current dataset, every predictor recorded a VIF of less than 5 (Table 2), affirming that multicollinearity is sufficiently low to justify the inclusion of all variables in subsequent modeling phases without the need for exclusion or further modification.

Table 2 VIF values obtained for each feature.

We performed Principal Component Analysis (PCA) primarily to visualize the data and to explore the structure of the variance among variables. The technique provided insights into the interrelationships among predictors and helped characterize the data geometry. However, PCA was not deliberately applied for variable selection or to reduce the dimensionality of the dataset before training machine learning algorithms. We retained the complete set of original features to maintain the interpretability of the coefficients and to ensure that the physical significance of parameters essential for optimizing concrete mix design was preserved.

SHAP and permutation analysis were employed to confirm the robustness of the machine learning models and uncover actionable guidance for refining mix designs. SHAP values proved invaluable for visualizing the incremental effect of every input feature on tensile strength predictions, while expressly accounting for feature interdependencies. A noteworthy finding was the complex, nonlinear interaction between cement content and w/c ratio: rather than exerting their most substantial positive influence when individually maximized, their joint effect peaked when both variables converged toward constrained mid-range settings. This observation aligns with established insights on the trade-offs between workability and shrinkage, yet remains obscured in conventional scatter-plot analyses of experimental data. In parallel, permutation importance enabled us to gauge the accuracy decline induced when any single feature’s values were randomly permuted. This analysis highlighted the preeminence of the nano-clay dosage and curing duration.

Furthermore, the SHAP analysis revealed diminishing returns from nano-clay levels exceeding 5%, suggesting a plateau likely attributable to agglomeration or reduced dispersion—a nuanced but crucial observation for fine-tuning formulations. A further unexpected finding was the tight, localized dependence of tensile strength on superplasticizer content, where even marginal increases beyond the 1% mark induced apparent variations in strength, likely stemming from segregation phenomena. Such sharply defined behavior enhances trust in the model’s physical grounding and serves as a precise touchstone for material engineers when defining acceptable ranges and safety margins for design parameters.

Stratified sampling was applied to divide the data into training (80%) and testing (20%) sets, thereby retaining the proportional representation of all curing duration and nano-material combinations. Additionally, a k-fold cross-validation strategy (k = 5) was integrated into the model training phase to mitigate overfitting further and enhance model strength.

Model selection and architecture

Considering the nonlinear and multidimensional aspects of concrete behavior, particularly in hybrid and nano-modified systems, four advanced machine learning techniques were selected for developing algorithms.

• 1. GBRT/XGBoost: This approach integrates weaker predictions made by various base learners in a sequential structure, significantly improving accuracy for complicated tasks. XGBoost was chosen due to its advanced regularization parameters, which work effectively with fewer resources.

• 2. SVR: This approach can model non-linear relationships that exist in higher dimensions by utilizing kernel functions to project data into higher dimensions. In this case, the radial basis function (RBF) kernel was employed, as it is more adaptable in capturing trends in tensile strength for a broad range of input parameters.

• 3. ANN: The architecture of the model was constructed as a multi-layer perceptron (MLP) with three hidden layers and ReLU activation functions. Training was conducted by backpropagation using the Adam optimizer. The network structure was fine-tuned through a grid search, where the number of neurons per layer was set between 32 and 128.

• 4. HEM: XGBoost, SVR, and ANN models, referred to as base learners, were combined in a stacked ensemble approach, where their predictions were averaged with a meta-learner (this was a Ridge regression model trained on the outputs of the base learners). We chose Ridge regression chiefly for its reliability in managing multicollinearity among the predictions generated by the base learners (XGBoost, SVR, and ANN) because their outputs frequently exhibit correlated behaviors in regression stacking. By incorporating L2 regularization, the method effectively shrinks the coefficients and mitigates the likelihood of overfitting. To validate this decision, we conducted a series of empirical experiments comparing Ridge with other possible choices. Ordinary Linear Regression produced slightly inferior generalization results and proved more vulnerable to the multicollinearity present. Bayesian Ridge Regression delivered results of similar predictive accuracy, yet its greater computational burden and absence of notable improvement in the relevant metrics did not warrant its adoption. We also evaluated tree-based meta-learners, including Random Forest and XGBoost, which achieved excellent fitting performance but, due to their complex structure, tended to compromise interpretability and increase the risk of meta-level overfitting.

• 5. Using this HEM approach enabled us to combine the strengths of each algorithm while mitigating its downsides.

The models were developed using Python 3.10 and the Scikit-learn and TensorFlow/Keras libraries. An integrated approach combining custom and built-in visualization methods was employed to analyze model performance and interpretability.

Hyperparameter tuning

Each model was optimized using Bayesian optimization with Gaussian process priors. This approach was preferred over grid and random techniques because it searches multi-dimensional spaces much more efficiently with fewer evaluations.

For XGBoost, the specialist focuses on learning rate, maximum tree depth, subsample ratio, and number of estimators. SVR optimization was concentrated on kernel coefficient (γ), regularization parameter (C), and epsilon-insensitive loss width (ε). For the ANN model, the learning rate, dropout ratio, number of hidden units, and batch size were adjusted to achieve maximum performance. That was done using the Optuna library, which pruned trials that were not meeting expectations dynamically and achieved optimal configurations in 200 iterations per model. The final hyperparameters were set using nested cross-validation to ensure no overfitting.

Model training and validation

Following hyperparameter tuning, models were retrained on the whole training set and validated on the testing set. Monitoring for convergence was performed during the training process, and early stopping was activated wherever appropriate (i.e., in the ANN) to mitigate overfitting. To enhance consistency and robustness, each model was trained five times with unique random seeds (five-fold cross-validation). The reported performance was the average of all these runs. Convergence behavior, training times, memory consumption, and other relevant parameters were recorded to assess the practicality of these models for real-world situations.

Performance metrics and evaluation

To evaluate the machine learning models developed in this study, a comprehensive set of statistical evaluation metrics was employed. These metrics assess the quantifiable accuracy and generalization capacity of the models for new data. The following metrics were evaluated:

• Coefficient of determination (R²): Indicates how much of the variability in the observed tensile strength is accounted for by the predictions made using the model. An R² value close to 1 indicates that the model is a good fit.

• Root mean squared error (RMSE): Determines the square root of the mean squared difference between the predicted and actual values, and in this context, indicates the model’s average error in predicting tensile strength in MPa.

• a¹⁰‒index: Among the most recent of metrics, this metric captures the number of predicted values that fall within 10% of the actual values and measures accuracy within that threshold. As engineering accuracy is inherently grounded within set tolerances, this form of measurement is practical for evaluating prediction precision, especially from an engineering standpoint.

• Variance accounted for (VAF): A measure calculated as VAF measures the amount of discrepancy in actual values of tensile strength that has been captured within the given predictive values. Models with VAF values exceeding 90% are generally deemed robust, as such high values indicate the model is highly explanatory.

Data analysis

A successful application of machine learning hinges on data analysis, which sets the stage for building, interpreting, and optimizing the model’s performance. It is important to emphasize that no model can learn from data until its structure, quality, and distribution are discerned. With exploratory data analysis (EDA), specialists can detect patterns, outliers, and relationships among variables that determine the modeling approach. Moreover, data analysis uncovers dataset issues related to missing values, biased distributions, multicollinearity, or collusion which tarnish the model’s accuracy and generalization capabilities, thus safeguarding the quality of the dataset. Data analysis improves feature selection and engineering, determines the appropriate algorithm, and adjusts hyperparameters, all of which are critical at this stage. In complex systems of concrete, for instance, the prediction of tensile strength constitutes an advanced application where data analysis is crucial because of highly nonlinear material interdependencies. With a combination of thorough analysis, raw data undergoes processing to become insights, rendering the machine learning results more transparent and trustworthy.

Figure 2 shows a Spearman correlation heatmap which shows the monotonic relationships existing among the input features. This dataset is best analyzed using Spearman’s method because it captures both linear and nonlinear associations. Weak associations are observed among most variables, which suggests a high degree of feature independence. Cement content’s moderate inverse correlation with superplasticizer dosage is particularly interesting. This is probably due to a compensating change in mix design where lower cement content requires greater superplasticizer inclusion to maintain feasible workability.

Fine and coarse aggregates show minimal correlations and thus support their role as non-redundant variables in concrete composition. Those modern nano-engineered materials like nano-clay, basalt fiber, and carbon nanotubes, however, are noticeably more interesting because they exhibit very low correlation with traditional mix components, validating their distinct and non-overlapping influence on the material behavior. It is apparent from the findings that the tensile behavior of the concrete mix is determined by a significant variety of factors, most independent, which is why sophisticated algorithms need to be employed.

Fig. 2

Spearman correlation heatmap.

Figure 3 contains a detailed statistical summary of the machine learning model input parameters and list box plots of continuous variables, and distribution of curing time as a categorical feature under. In Fig. 3a, the box plots reveal the overall average, variation, and distribution of each input feature. Importantly, all variables do not contain any statistical outlier, since every data point is within 1.5 times the interquartile range (IQR) which suggests the uniformity and consistency of the dataset.

The distributions of cement content, fine aggregate, and coarse aggregate are moderately symmetric since their medians are bounded with whiskers in both directions which is indicative of balance in the representation of mix designs and standard engineering practices. w/c ratio demonstrates a small interquartile range along with a tight median which an indicator of controlled variation. This is often the case in the concrete mix design because w/c ratio significantly impacts the workability and compressive strength of the concrete. Such tight clustering during mix preparation suggests careful optimization.

For the engineered additives (nano-clay, basalt fiber, and carbon nanotubes), distributions showed moderate variation among samples with the medians located toward the centers and some skewness in a few cases. These distributions confirm ascertained consistent usage across different formulations, which assists in evaluating the additives’ effects on UCS. The geopolymer binder graph has a slight positive skew; this may indicate growing interest in experimental work focused on sustainable cement alternatives in certain formulations intended for a lower carbon footprint. The superplasticizer dosage, on the other hand, demonstrates a greater spread suggesting an interest in workability issues across other mix designs with more fibers or other secondary materials. In unison, the distributions lacking extreme values within these plots indicate the dataset is clean of outliers and suitable for robust predictive modeling. In addition, the described statistical characteristics provide guidance on considering scaling and normalization feature design, and selecting model architectures responsive to input variability.

In Fig. 3b, the curing time histogram shows a distinctly discrete and multimodal distribution, including frequency spikes at 7, 14, 28, and 56 days. These ‘spikes’ fall within the standard timelines of the industry’s mechanical testing benchmarks for cement-based hydraulic materials. The distribution, despite being inherently numerical, suggests that the stepwise nature and lack of continuum is more ordinal or categorical rather than continuous in nature. Such observations pose an important design issue for the model: considering curing time as a numeric continuous variable runs the risk of obscuring essential behavioral changes characteristic of specific regimes, such as strength gain plateauing after 28 days or pronounced early-age reactions prior to 14 days. As a solution, this research utilized one-hot encoding to transform the curing period into a set of binary features. This approach allows the machine learning models to consider every curing interval as a separate condition while maintaining critical curing duration distinctions. Consequently, the model learns the different impacts of each curing regime on the tensile strength without overly simplistic continuity or linearity assumptions. This approach works best in hybrid concrete systems as some reactions in their geopolymerization and pozzolanic reaction kinetics differ from the Portland cement hydration kinetics, heightening the need for discrete treatment of curing time in the modeling process.

Fig. 3

Box plot of input continuous parameters (a); and the distribution of curing time as a categorical parameter (b).

PCA holds particular significance for analysis of complex and high-dimensional data sets like the kind used in this study. Regarding the dataset in the context of nano-engineered and fiber reinforced concrete, it includes ten features as materials, chemical admixtures, and curing regimes, all of which, as factors, have quantifiable values and possess varying degrees of complexity. It is nearly impossible to form a mental picture of how these variables are related because each of them may interact with the others in finely granulated and complicated non-linear systems. PCA accomplishes this by translating data into a new coordinate system, based on the directions along which the greatest variance is observed. It also enables the effective visualization of data that would otherwise be impossible to depict, for example, multi-dimensional data such as the dataset in this study which has more than two or three principal components (PCs). The strength of the PCA graph is its ability to reveal hidden structure and relationships, discern clustering tendencies, and evaluate data quality with respect to predictive model variables, checking for collinearity, redundancy, or input variable redundancy prior to model training.

Figure 4 displays the PCA biplot which is an effective visual representation of the relation between different variables in a dataset containing various components of concrete mixes and their interaction with the tensile strength of concrete. It also demonstrates how each sample of concrete is assigned a position in the PCA based on its tensile strength, represented via color. This biplot reduces the high dimensional dataset into two principal components, PC1 and PC2, which contain most of the variance in the data. In this case, each concrete sample is represented as a point in the plot with its corresponding PC scores. The gradient in Fig. 4 has been scaled linearly according to the original tensile strength measurements (un-normalized) to facilitate easier interpretation. The gradient extends from around 24 MPa (represented in dark purple) to just above 50 MPa (represented in yellow), without any logarithmic or exponential transformations, in order to keep the visualization straightforward. For uniformity, the tensile strength values were not normalized or standardized via z-scores prior to the plot creation.

To check for the presence of inherent groups in the feature space, an initial k-means clustering was performed with k set to 3, a decision supported by the elbow criterion. The analysis, however, revealed that clusters were neither compact nor well-aligned with tensile strength values. This outcome indicates that in the composite nano-engineered sustainable concrete systems, tensile strength arises from a nuanced interaction of multiple features, rather than from physically separable categories in the PCA-reduced view. Consequently, the PCA plot shown in Fig. 4 is regarded chiefly as a dimensionality-reduction procedure that provides qualitative insight into feature contribution and overall data dispersion, rather than a definitive clustering methodology.

The primary features projected into the new PCA component space are represented by red arrows. These features are important for the evaluation of the importance of each feature to the total variance described by PC1 and PC2. The direction the arrow points towards and the arrow’s length show the effect and relationship of each feature to the PCAs. The longer the arrows, the larger the effect toward variance and the direction indicates the interrelation amongst the features. If they point in the same direction, positively related features; if in opposing directions, negatively related features but still opposing direction features indicate negative correlation.

Looking more closely at the arrows, properties like geopolymer binder, nano-clay, cement content, fine aggregate, and curing time are all pointed toward the positive end of PC1. This means that these properties contribute greatly to the variance associated with PC1 and are positively related to each other. Importantly, the samples with higher tensile strength, marked by yellow and green dots, are also located in this area indicating that these properties strengthen the association with greater tensile strength. Thus, those with richer formulations of these materials will have greater mechanical performance. In contrast, superplasticizer and w/c ratio indicators are directed toward the negative side of PC1, showing a positive correlation with inverse relationship with tensile strength PC1. Their distance from the high-tensile-strength area suggests that greater amounts of these constituents may hinder the mechanical properties sought after. Coarse aggregate and carbon nanotubes, located in the upper right quadrant, have positive loadings on both PC1 and PC2, meaning that they may contribute to primary or secondary tensile strength variations. Moreover, basalt fiber is more mid-vertical downwards, so that it aligns weakly to PC1, but strongly to PC2. This means that while its effect is rather weak in the principal component dimension PC1, it is stronger in the secondary variance component PC2.

Thus far, it seems that the PC1 axis registers the main penetrating the matrix and microstructure enhancements (binder and curing features) and PC2 captures weaker modifications, possibly attributed to the type of reinforcement or aggregate, but still noticeable. The pile up of the high tensile strength samples along the positive PC1 axis highlights instructive compositional parameters, particularly those reinforcing matrix and curing quality, under the stronger effects.

Fig. 4

PCA of input features colored by tensile strength.

Results analysis Ans comparison

An evaluation of the analysis results derived using the applied machine learning models is particularly important in confirming the value and reliability of the framework provided; therefore, does not require any additional explanations for specifying reasons. This part focuses on model evaluation and describes the analysis carried out on the algorithms using numerous statistics, graphical interfaces, and explanation components to evaluate and rank the results of the different algorithms and the hybrid ensemble. Attention is paid to measuring how well the models perform with various compositions of concrete containing nano-engineered and sustainable cementitious materials. This part relies on estimating and illustrating the precision, strength, and reasoning ability of all models which enables an understanding, anticipation, and prediction of the behavior of complex systems termed as advanced concrete systems in reality during realistic engineering practice, and as a result, reveals the other side of the story of the predictive capability of machine learning models.

Figure 5 compares the performance of four machine learning models on estimating the tensile strength of reinforced concrete with incorporated nano-engineered sustainable cementitious materials. The analysis incorporates both graphical and statistical evaluations: Fig. 5a depicts parity plots of the a¹⁰‒index value and multiple performance metric calculations while Fig. 5b contains the R² values, RMSE, VAF, a¹⁰‒index score, and cumulative scoring system designed to enhance ranking clarity. In the parity plots, the predicted vs. actual values of tensile strength are plotted for each model. The graphs also include three reference lines; one solid diagonal (x = y) line representing perfect prediction and two dashed ones that denote the ± 10% deviation margins (x = 0.9y and x = 1.1y). These plots visually help understand the prediction and generalization accuracy. Both SVR and ANN models aligned closely with the diagonal achieving an a¹⁰‒index of 0.95. This means that 95% of predictions were within 10% of actual values of tensile strength. The XGBoost model shows an a¹⁰‒index of 0.93, meaning it is slightly less precise and its predictions are more scattered. The HEM performed best with a perfect a¹⁰‒index of 1 suggesting all their predictions landed within the 10% margin of error. From an engineering reliability perspective, this demonstrates an impressive achievement.

The analysis performed in Fig. 5b strengthens the conclusions regarding the dominance of HEM. The values provided corroborate that HEM not only achieved the best R²: 0.96, RMSE: 0.91 MPa, VAF: 98%, and a¹⁰‒index: 1.00, but also suggest that it minimizes error while capturing almost all the variance in the target variable, thus rendering it accurate and robust. The ANN model came in second, achieving an R² of 0.87 and a reasonably low RMSE of 1.55 MPa, but outperformed all other metrics as well. Following ANN, SVR is rank in the a¹⁰‒index and VAF, but has poorer performance regarding RMSE (1.65 MPa) and R² (0.86), suggesting moderate performance. XGBoost shows the most significant drop in performance with an often powerful in many contexts label. It offers the lowest R²: 0.82, highest RMSE: 1.85 MPa, and the lowest composite score.

To conclude, the outcomes emphasize the HEM as the best choice for predicting the tensile strength of sophisticated, nano-modified concrete systems in a robust and generalizable way. Its exceptional a¹⁰‒index and the most accurate results in every other statistical measurement confirm that the model is fit for real-world use in the design and optimization of structural materials. The model’s success in capturing the intricate nonlinear relationships with advanced materials showcases the immense benefit of combining different methods of teaching for engineering challenges with numerous interdependent variables.

Fig. 5

Comparative analysis of statistical performance metrics for machine learning models in the hold-out validation phase.

Figure 6 summarizes the models’ performance evaluated via 5-fold cross-validation using five key metrics including R², mean absolute error (MAE), mean absolute percentage error (MAPE), RMSE, and VAF for machine learning models under 5-fold cross-validation. Each fold (Fold 1 to Fold 5) was used to train and evaluate the models, and the results represent the average performance across all folds to reflect generalization reliability. Each metric is assigned a normalized value from 1 to 4 with 4 indicating the best performance. The right most column indicates the total across all folds and metrics which together provide an aggregate index of the model’s robustness and reliability.

Regarding consistency in performance, SVR delivered fairly uniform results over all five validation folds. The R² statistics fell between 0.88 and 0.90 (with 0.90 recorded in Fold 2 and 0.88 in Folds 3 and 4). RMSE showed a tighter band, moving from 1.40 MPa in Fold 2 to 1.68 MPa in Folds 4 and 5. MAPE kept a narrow range of 0.031 to 0.037, while VAF landed between 0.88 in Folds 3 and 4 and 0.90 in Fold 2. Collectively, these numbers signal competent yet not outstanding prediction capacity. SVR finished with a composite score of 53, exceeding XGBoost but trailing ANN and HEM. The model displays solid generalization, especially in Fold 2, but the larger prediction errors in Folds 4 reveal its struggle to capture the nonlinear behavior present in complex concrete composites.

The ANN model achieved an overall score of 70, earning it second place, after maintaining solid performance in every cross-validation fold. R² values remained above 0.89 for each fold, topping out at 0.94 in Fold 3, which also recorded the lowest RMSE overall at 1.17 MPa. MAPE values varied between 0.027 and 0.038, with the minimum occurring in Fold 1, and VAF measurements peaked at Fold 5. These statistics highlight the model’s strong ability to generalize and its effectiveness in dissecting the underlying nonlinear relationships present in the input features. ANN’s consistency across Folds 1 to 5 indicates that it is well-suited to the predictive challenge, albeit slightly surpassed by the HEM’s performance. These variations may stem from suboptimal hyperparameter settings or architectural limitations, and further refinement (such as deeper tuning of the learning rate, number of neurons, activation functions, or regularization schemes) could plausibly enhance the model’s predictive accuracy. Therefore, while ANN is well-suited to the prediction task, its current configuration may not be fully optimized, leaving space for performance gains through advanced hyperparameter optimization or architectural adjustments.

XGBoost delivered the weakest performance, finishing with an overall score of 25. Its R² values were uniformly below the desired threshold, ranging from 0.84 to 0.87, and Fold 5 marked the nadir with an R² of 0.84 and the peak RMSE of 1.97 MPa across every model and fold. MAPE peaked at 0.044 in Fold 5, and VAF values predominantly hovered below 0.87, signaling a lack of dependable predictions. Even though XGBoost is generally lauded for its outstanding results with structured data, it fell short of achieving the accuracy of SVR and ANN in our analyses. Several interconnected reasons can be identified. The first is the intricate nature of the dataset, which involves nonlinear, high-order interactions among nanoscale additives (such as carbon nanotubes and nano clay), hybrid cementitious binders, and curing-dependent phenomena. This complexity likely surpasses the representational limits of sequentially fitted decision trees. While XGBoost’s ensemble of additive trees excel with monotonic or moderately nonlinear patterns, the sharp, non-smooth interactions and expanded feature dimensionality found in novel cementitious materials present a greater challenge. The second reason concerns the hyperparameter tuning, which, despite rigorous application of both grid and randomized search across max_depth, learning_rate, n_estimators, and subsample, still produced residual bias and indications of mild underfitting. This effect was particularly pronounced for tensile strength measurements that exceeded 45 MPa. The challenge appears to stem from the inherent insensitivity of tree-based methods to small perturbations in the feature space, especially when the dataset contains noise and exhibits heteroscedasticity in the target variable.

HEM turned in remarkable performance through every cross-validation fold, leading every single metric, and finishing with an overall score of 96. It reported R² values of 0.96 and 0.97 across the board. RMSE remained comfortably under 0.92 MPa, dipping to a low of 0.83 MPa in Fold 4. MAPE stayed impressively low, within 0.018 to 0.021. These figures underline HEM’s exceptional ability to generalize and to trace the nonlinear response of nano-engineered concrete with high fidelity. The ensemble design of the model likely merges the strengths of several algorithms, mitigating overfitting and capturing intricate interactions that single models would miss.

To summarize our findings, the fold-wise analysis from the 5-fold cross-validation clearly indicates that the HEM model surpasses every other approach in each fold, exhibiting both superior predictive power and remarkable stability across the dataset. The ANN ranks second, producing strong values on all metrics, and achieves its peak in Fold 3. The SVR, while yielding passable accuracy, struggles to capture the more complex input-output dynamics, a limitation that becomes pronounced in both Folds 3 and 5. The XGBoost variant, showing consistently low performance in every fold (most strikingly in Fold 5) offers no dependable predictions.

Fig. 6

Comparative analysis of statistical performance metrics for machine learning models in the 5-fold cross validation phase.

The approach suggested for evaluating the generality of the given machine learning models involves changing one input parameter, keeping the rest constant, and analyzing how the model predicts tensile strength in comparison to actual experimental results. This approach is suitable as it permits evaluation of the physical behavior of concrete to model erosion during a feature-specific monotonic change. By controlling the impact of a parameter, the model is assessed on its ability to go beyond a learned correlation and provide actual material response. In particular, the model’s generalizability is put to test concerning material response when defined conditions are fulfilled. It can also assist in validating the model’s accuracy, detection of overfitting or bias, and prediction consistency irrespective of the shift in input distribution. In particular, this method replicates the approach engineers would follow in practice (cutting a concrete mix one part at a time and observing its impact), which increases the machine learning technique’s credibility and usage in engineering design and material optimization.

In the first task of generalization performance evaluation, the w/c ratio was adjusted within the range of 0.2–0.6, while all other mix design parameters were kept constant as shown in Table 3. This configuration enables to assess the influence of w/c ratio on tensile strength in isolation, which is critical for evaluating the generalization ability of the machine learning models. Table 4 shows experimental results of tensile strength along with the predictions from the machine learning models. Figure 7 visually compares tensile strength predictions of the different models against laboratory results across a w/c ratio range from 0.2 to 0.6.

Observing both Table 4; Fig. 7, there is a notable trend that can be followed; in this case, as the w/c ratio increases, tensile strength increases up until an optimal value of 0.4, wherein it reaches its highest value of 36.95 MPa, and then starts to decrease. This behavior corresponds to conventional concrete behavior in which moderate increases in w/c ratio improves the hydration and workability of concrete, but too much water starts to increase the porosity and decrease the strength. This parabolic trend serves as an essential baseline for assessing the performance of the machine learning models in simulating realistic concrete behavior.

According to the results, the HEM demonstrates the highest level of compatibility to data from experiments, tracking the experimental curve throughout the entire range of w/c ratios. It is able to capture the peak strength at 0.4 and the decline afterwards, which shows that it strong generalization abilities. SVR does not capture the overestimation trend, and usually tends to underestimate tensile strength, indicating a bias in its predictions. XGBoost captures the trend better than SVR and provides moderate accuracy. ANN exhibits the weakest performance, particularly at the higher w/c ratio where tensile strength is grossly underestimated due to overfitting or limited robustness within the training range.

Table 3 Five new test data-points with various w/c ratios to evaluate the effect of this parameter on the tensile strength and examine the performance of machine learning techniques.

Table 4 Tensile strength values ​​obtained from laboratory tests and machine learning models for different w/c ratios.

Fig. 7

(a) Comparison of tensile strength results ​​obtained from laboratory tests and machine learning models for different w/c ratios; (b) Error values of each algorithm in estimating the tensile strength of concrete.

For the second stage of model evaluation, curing time was systematically adjusted at four levels: 7, 14, 28, and 56 days, as all other input parameters remained constant (see Table 5). This enables an assessment of how the machine learning models capture the time regression of strength development in concrete, which is dependent on tensile strength through the curing time factor. The experimental results along with forecasts from SVR, XGBoost, ANN, and HEM models are provided in Table 6. These data alongside model predictions and actual laboratory values are visually depicted in Fig. 8, which illustrates the predicted tensile strength evolution over curing periods compared to experimental data.

Concrete curing time is evident from the experimental results. There exists an observable relationship with intervening gaps as seen from the tensile strength increase. These results support the hydration and microstructural development processes that happen within a concrete structure. The increase in tensile strength is markedly significant: from 31.68 MPa at 7 days to 38.49 MPa at 56 days, the eye-catching jump occurs at the 7 to 28 days mark. Understanding this growth trend is important, particularly for further evaluations on how well each model understands the non-linear progression of concrete curing.

The HEM approach consistently aligns with measured results throughout the full curing duration, accurately mapping the steep rise in tensile strength from 7 to 28 days and the ongoing growth through to 56 days. This performance illustrates the model’s strong generalization and its capacity to track the intricate, time-driven processes of hydration and microstructural development. By comparison, the SVR model, while providing reasonable estimates for the later curing periods, tends to overpredict the tensile strength during the early ages. This early overestimation likely arises from the SVR framework’s inclination toward smoother, quasi-linear fits, a consequence of its kernel-based regression. Such a characteristic can hinder the model’s reaction to the steeply nonlinear kinetics governing early hydration and the refinement of the pore structure. As a result, SVR registers these fast microstructural shifts and the coincident rise in stiffness with diminished sensitivity. XGBoost tends to underestimate the tensile strength for most curing times, suggesting the model dampens the influence of increased duration of curing. The ANN model remains the least accurate, indicating difficulties in non-linear learning during the curing process.

Table 5 Four new test data-points with various curing time values to evaluate the effect of this parameter on the tensile strength and examine the performance of machine learning techniques.

Table 6 Tensile strength values ​​obtained from laboratory tests and machine learning models for different curing time values.

Fig. 8

(a) Comparison of tensile strength results ​​obtained from laboratory tests and machine learning models for different curing time values; (b) Error values of each algorithm in estimating the tensile strength of concrete.

During the third stage of generalization analysis, the concentration of nano-clay was changed methodically from 1% to 5%, remaining in accordance with Table 7, where all other parameters were kept constant. This attempt aims to determine the impact of nano-clay on the tensile strength of concrete while simultaneously evaluating the performance of diversified machine learning algorithms in predicting the relationship. Experimental results along with predictive results have been compiled in Table 8 and are graphically represented in Fig. 9.

Based on the laboratory test results presented in Table 8 and illustrated in Fig. 9, it is evident that the tensile strength of the specimens strongly correlates with the nano-clay content. It can be noted that the tensile strength for the concrete sample which has 1% of nano-clay stands at 32.78 MPa and the value rises up to 38.86 MPa at 5%. This illustrates the nano-clay serves as a strength augmenter for the concrete matrix beyond 5%. The possible causes for this improvement can be attributed to the pozzolanic reaction and micro-filling properties of nano-clay, which enhances the bonding at the micro level with the concrete matrix.

Each machine learning model displays this increasing trend to a different extent. As observed in this model, HEM again predicts with the highest accuracy and tends to the laboratory results the closest. Its predictions perpetually follow the experimental values at the different levels of nano-clay content. At lower concentrations of nano-clay, SVR and XGBoost modestly overpredict, whilst at higher concentrations they show some underestimation. In any event, both models replicate the underlying phenomena. On the other hand, the ANN model shows the least accuracy compared to other models. It adheres to the increasing trend, but greatly underestimates the upper limit of the tensile strength range with in the upper most bounds.

These results validate again the performance and versatility of the HEM model for sophisticated relationship mappings, like the effects of nano-clay on concrete’s tensile strength, and its potential for advanced materials optimization in engineering contexts.

Table 7 Five new test data-points with various nano-clay values to evaluate the effect of this parameter on the tensile strength and examine the performance of machine learning techniques.

Table 8 Tensile strength values ​​obtained from laboratory tests and machine learning models for different nano-clay values.

Fig. 9

(a) Comparison of tensile strength results ​​obtained from laboratory tests and machine learning models for different nano-clay values; (b) Error values of each algorithm in estimating the tensile strength of concrete.

The analysis of sensitivity investigates the impact of the individual parameters of concrete on the tensile strength of reinforced concrete structures. This helps to uncover the more important variables, the levels of these variables which have maximum impact, and their optimal values. The model accurately captures interaction among several features depending on their individual contribution by averaging other feature values. With w/c ratio, fiber types, admixtures, and cement to concrete ratios, the feature represents the augment and decline in strength while adding or removing concrete. Primarily, the model determines the precise value required to attain the most viable optimization for tensile strength. In concrete mix design, this attribute is critical for optimizing performance.

Figure 10 displays sensitivity curves for each input parameter derived from the HEM model. The sensitivity graphs obtained using the HEM algorithm can be used to determine the impact each input parameter has on the tensile strength of reinforced concrete. Considering the range for each feature in the model was set to its observed range while keeping all other inputs at their mean value, it was possible to dissect each feature to see how it impacted the final outcome. The sensitivity curves in Fig. 10 exhibit familiar parabolic and plateau behaviors that are deeply rooted in the mechanics of concrete. Cement content reaches a peak effectiveness at about 378.7 kg/m³. At low levels, more cement means better bonding and faster hydration, which boosts tensile strength. When the dosage surpasses the peak, however, autogenous and drying shrinkage introduce microcracks and non-uniform shrinkage, leading the tensile strength to fall. The w/c ratio, in contrast, demonstrates a descending parabola. A w/c of around 0.406 affords enough water to support hydration without excessive porosity, thus maximizing strength. Surplus water, however, enlarges pore volume and weakens the microstructure. Aggregate size, likewise, displays a non-linear influence. Both the coarse and fine extremes improve load transfer and minimize microvoids when contained within a defined range. Outside that range, the integrity of the matrix-aggregate bond degrades, or the packing density declines, and strength either levels off or retracts.

For nano-engineered fillers like nano-clay and carbon nanotubes, the response curve flattens past certain loadings (roughly 5% nano-clay and 1% nanotube) probably because of agglomeration and because the contributing pozzolanic and reinforcing mechanisms reach their maximal effect. Below those limits, these materials refine the microstructure and inhibit crack propagation in a quasi-exponential manner, yet when dispersion becomes uneven and contributions start canceling, the strength does not climb further. The geopolymer binder itself hits an ideal dosage around 18.18%. This quantity optimizes the chemical bonding and long-term durability, but exceeding it can alter rheological properties and introduce microstructural mismatches. The superplasticizer performs best at approximately 0.93% because larger amounts can induce segregation and bleeding, which compromise the uniformity of the matrix and, in turn, the tensile strength.

This advancement touches on the strengths of structural engineering and concrete technology. Employing machine learning sensitivity analysis enables a data-driven optimization approach while moving away from empirical mix design. Automated input calculation guarantees that concrete designs will fulfill the criteria of maximum tensile strength, highest durability, and minimal material wastage. It shifts the focus from an iterative method to increasing the performance and cost efficiency of concrete in infrastructural applications, fostering innovation. The streamlined concrete design approach promotes the development of concrete that meets the aspires of advanced infrastructure while reducing the trial-and-error reliance.

Fig. 10

Examine the sensitivity of numerical features on the tensile strength of reinforced concrete using the HEM.

Benchmarking machine learning models on a common dataset is a cornerstone practice for achieving fairness, reproducibility, and meaningful comparison. Many researchers have developed models for predicting concrete shear strength, yet disparate dataset features, varying experimental setups, and divergent preprocessing pipelines tend to cloud head-to-head evaluation. To overcome this limitation, Table 9 offers a harmonized benchmark in which every algorithm (developed in this study and in prominent prior literature) operates on the uniform synthetic dataset utilized herein (%80 for training and %20 for testing). By neutralizing the variability introduced by varying datasets, this procedure renders a genuine apples-to-apples evaluation, thereby disaggregating the models’ authentic learning abilities and generalization capacity. Moreover, it supplies a definitive gauge for positioning the proposed HEM model against both traditional and widely accepted alternatives.

Table 9 consolidates five statistical performance metrics (R², RMSE, VAF, a^a10-index), and a composite score for a decadal roster of machine learning algorithms, all tested on the identical dataset. Each statistic is furnished with a score that ranks it relative to the remainder, and the accumulation of these ranks yields a terminal benchmarking score.

HEM sets the benchmark, reporting the highest R² at 0.96 and the lowest RMSE at 0.91 MPa. These figures show it captures almost all the variance and keeps prediction errors to a minimum. Alongside, it leads in VAF at 0.98 and in the a¹⁰-index with a perfect score of 1.00, proving it explains variance exceptionally and remains reliably within 10% of true values. With a combined score of 23, it ranks first among all compared methods, confirming it as the most precise and dependable model in the evaluation.

The ANN model remains a strong competitor, totaling 20 points, with an R² of 0.87, RMSE of 1.55 MPa, and VAF and a¹⁰-index values of 0.93 and 0.95, respectively. Close behind, SVR registers a total of 19, showing strong generalization with R² at 0.86 and consistent results across metrics. These outcomes indicate that while ANN and SVR deliver solid independent predictions, neither matches the accuracy and reliability that HEM consistently achieves.

XGBoost and Gaussian process regression (GPR) land in the middle of the accuracy spectrum. GPR scores a strong R² of 0.85 and a good VAF of 0.92; XGBoost falls a tad short on both counts. With GPR totalling 16 points and XGBoost 12, the results confirm a reasonable grip on nonlinear patterns, yet they also show weaknesses in extrapolation and in capturing outlier behavior.

Conversely, simpler or shallower models, including decision tree regression (DTR), multi-layer perceptron (MLP), k-nearest neighbors (KNN), and adaptive neuro-fuzzy inference system (ANFIS), fail to deliver satisfactory accuracy. ANFIS, which intuitively combines rule-based reasoning and tuning, ends up with an R² of 0.82 and RMSE of 1.88, marking a sizeable gap behind newer techniques. The MLP also disappoints, registering R² of 0.77 and RMSE of 2.47, a likely result of insufficient depth, an ill-suited learning rate, or overall poor tuning. This gap emphasizes how critical hyperparameter optimization is, a need the HEM tackles using Bayesian optimization.

Random forest regression (RFR) demonstrates stability across measures but does not excel in any specific area, attaining an aggregate score of 15. Such uniformity confirms the robustness of ensemble averaging, yet performance plateaus since the method leverages bagging without the boosting cascades or neural interventions seen in HEM.

The comparative evaluation conducted under homogeneous experimental settings confirms HEM as an advanced forecasting platform that resolves subtle nonlinear couplings within nano-engineered concrete formulations. Its supremacy over both traditional linear models and conventional ensemble frameworks is consistent. Results further indicate that judicious ensemble architecture and rigorous hyperparameter calibration (strategies woven into the HEM design) are essential for elevating machine learning capability within structural materials science. These findings advocate for a paradigm wherein model choice is guided less by theoretical sophistication and more by robust empirical tests with uniform benchmark datasets, a principle that strengthens the integration of artificial intelligence within engineering practice.

Table 9 Benchmarking the machine learning models used in this study against literature-based algorithms for concrete shear strength prediction.

Key limitations and future directions of this stucy

Even though this study achieved encouraging outcomes, there are several important limitations that can be addressed in follow-up studies. To begin with, the dataset’s scope is quite large; however, it is limited in terms of the specific range of material compositions that were considered. In particular, the generalization of the models, primarily the HEM, is constrained due to the lack of sufficient datasets containing multiple designs, environmental factors, and extensive testing frameworks. Furthermore, although the predictive accuracy of the models was found to be quite high, the explanation provided by ensemble and neural network-focused methodologies remains difficult and requires the application of more sophisticated explainable AI (XAI) methods to improve their reliability in engineering domains. In addition, focusing on one input parameter at a time, as was done for this study, enables easier assessment of model generalization but does not reflect the actual behavior of concrete, which is complex and multi-dimensional, and is something that needs to be studied in future research using factorial or global sensitivity analysis. The application of these models across different structural scales, such as applying them to elements versus full-scale structures, as well as different load conditions, has not been investigated and constitutes an important gap in research. There is also a need to further develop these intelligent models and incorporate them into design and engineering software systems for use in civil engineering.

To overcome the constraints imposed by the current dataset’s limited size and variability, two advancing paradigms can be effectively leveraged. First, transfer learning permits us to adapt neural networks originally trained on expansive, related collections of concrete data, refining them on the narrower nano-engineered concrete compositions. This approach boosts the model’s ability to generalize while obviating the burden of generating large additional datasets. Second, federated learning enables disparate research teams to jointly refine predictive architectures, aggregating insights from their respective experiments without the transfer of sensitive raw data. This collaborative framework safeguards confidentiality and enlarges the practical dataset. By embedding both techniques in forthcoming studies, we can obtain models that are not only more resilient but also more readily deployable across the diverse, real-world concrete formulations that the construction industry demands.

Conclusions

This research applied several machine learning approaches (SVR, XGBoost, ANN, and HEM) to forecast the tensile strength of nano-engineered concrete, guided by a synthetic database of 500 records, each comprising ten engineering variables. Key findings include:

• 1. Model performance: The HEM model consistently outshone the SVR, XGBoost, and ANN configurations, achieving superior accuracy and reliability in both the independent hold-out and the 5-fold cross-validation setups.

• 2. Influence of w/c ratio: The hybrid model closely mirrored experimental observations, showing tensile strength reaching a maximum at a 0.4 w/c ratio, while the ANN predictions were overly optimistic and the SVR readings were too conservative.

• 3. Curing duration response: The ensemble model accurately traced the tensile-strength evolution from 7 to 56 days, excelling in predictions of early-age behavior, where the other techniques showed greater scatter.

• 4. Nano-clay proportion: The hybrid ensemble yielded fine, consistent predictions over a 1 to 5% nano-clay gradient, faithfully capturing the supplementary pozzolanic strength gain, in contrast to the other algorithms, which either inflated or deflated the results.

• 5. Influence analysis: Through a sensitivity probe, the HEM isolated key variables (cement dosage, w/c ratio, aggregate characteristics, and nano-additive levels) while delineating optimal operating bands that fortify tensile performance.

• 6. Predictive range: The hybrid model exhibited outstanding transferability, accurately projecting tensile strengths across a wide spectrum of concrete formulations, curing ages, and nano-modifications, thereby confirming its potential in performance-centered concrete mix design.

• 7. Practical implications: Embedding HEM into standard engineering processes will refine mix-design choices and forecast material behavior more accurately, setting the stage for next-generation, AI-fueled concrete innovations.