Impact of rotating cylinders configurations on Cu-water nanofluid heat transfer in a vented cavity: a COMSOL multiphysics base study

Abstract

This study investigates forced convection heat transfer and fluid flow in a square vented cavity filled with Cu–water nanofluid, containing three rotating cylinders. This configuration is relevant for thermal performance optimization in compact systems such as electronic cooling, battery packs, and microfluidic heat exchangers. Unlike prior studies that considered only one or two rotating cylinders, this work introduces a more complex model with three cylinders under four distinct rotation configurations, allowing comparative evaluation of individual and collective effects on flow and heat transfer. The Galerkin finite element method (FEM) was applied using COMSOL Multiphysics 6.3 to solve the dimensionless governing equations for momentum and energy transport in the nanofluid system. Simulations are conducted for specific ranges of key physical parameters, including the Reynolds number $(\operatorname{Re} )$, rotational Reynolds number $({\operatorname{Re} _\omega })$, nanofluid volume fraction $(\phi )$, and also inlet/outlet port positions across four distinct cases for cylinders rotations. The Reynolds number is fixed at $\operatorname{Re} =600$, while ${\operatorname{Re} _\omega }$ is varied (0, 50, 100), along with nanoparticle volume fractions $(\phi =1.5\% ,3\% )$.The Prandtl number is held constant at Pr = 4.1588, reflecting the thermophysical properties of the Cu–water nanofluid. At Reynolds number $\operatorname{Re} =600$and nanoparticle volume fraction $\phi =3\%$, the maximum Nusselt number of 16.405 was achieved when all cylinders rotate at ${\operatorname{Re} _\omega }=100$. Scenarios with a non-rotating central cylinder (C2) showed significant reductions in heat transfer due to suppressed flow circulation. Cylinder rotation pattern and nanoparticle concentration can be strategically adjusted to enhance localized convective heat transfer. The model provides practical insights for the design of advanced cooling systems where rotational enhancement is feasible.

Introduction

Forced convection refers to the transport of heat within a fluid due to an external source of motion, such as a fan, pump, or mechanical stirring. This mechanism plays a crucial role in thermal engineering applications where efficient thermal management is essential. From electronic cooling systems and automotive radiators to heat exchangers and HVAC systems, forced convection is widely employed to maintain operational temperatures within desired limits. It allows precise control of overheat removal in confined or high-heat-flux environments, making it indispensable in both industrial and microscale thermal systems¹. Researchers conducted a numerical analysis to explore how a rotating cylinder influences forced convection heat transfer. Their findings revealed that both an increase in the cylinder’s rotational speed and a higher Reynolds number tend to diminish the overall heat transfer efficiency. Moreover, they demonstrated a strong sensitivity of the Nusselt number to variations in rotational velocity^2,3. Authors studied that increasing Reynolds number reduced the Nusselt number due to the dominance of rotational inertia over convective enhancement⁴. They reported that introducing rotating circular cylinders in a vented cavity distorts flow symmetry and significantly influences forced convection patterns⁵. Scientists found that the presence of a rotating cylinder coupled with magneto-hydrodynamic effects improves thermal control in phase change material-filled cavities⁶. To improve the thermal performance of conventional fluids, researchers have introduced nanoparticles, solid particles typically less than 100 nm in size into base fluids, creating that is known as nanofluids. These suspensions significantly boost the thermal conductivity and heat transfer capability of the working fluid without causing major changes in flow behavior. The addition of nanoparticles facilitates faster energy transport due to their high surface area and superior thermal properties, making them particularly useful in forced convection applications where efficient thermal management is critical. They have widespread applications in engineering systems such as heat exchangers, microchannel coolers, automotive radiators, and solar thermal collectors.^7,8. Authors showed that $A{l_2}{O_3}$nanofluid enhances heat transfer in inclined cavities at higher Rayleigh numbers⁹. It was observed that a rotating cylinder improves heat transfer within a nanofluid-filled square enclosure¹⁰. Researchers investigated that a cold circular cylinder improves heat and flow control in a non-Newtonian fluid-filled cavity¹¹. Scientists reported that applying corrugation to the inner wall intensifies heat transfer in an annular cavity filled with nanofluid, where the outer cylinder rotates¹². Researchers numerically analyzed low-melting metal PCM-filled heat sinks, demonstrating improved thermal control performance for high heat flux electronic chips¹³.

As a key dimensionless parameter, the Reynolds number quantifies the ratio of inertial to viscous forces in fluid flow and is used to predict flow regimes, such as laminar or turbulent. In cavity flow simulations, it defines the intensity of the incoming forced flow^14,15. The rotational Reynolds number $({\operatorname{Re} _\omega })$, on the other hand, represents the influence of a rotating body such as a cylinder on the flow field, typically defined based on the angular velocity and cylinder radius. Both $\operatorname{Re}$ and ${\operatorname{Re} _\omega }$ critically affect flow circulation, vortex formation, and heat transfer characteristics within the cavity¹⁶. Authors determined that both reattachment length and vortex intensity behind the cylinder increase steadily as $\operatorname{Re}$ rises from 100 to 1000¹⁷. They investigated that higher rotational Reynolds numbers stabilize the wake and suppress vortex shedding in counter-rotating cylinder pairs¹⁸. Researchers found that cylinder rotation significantly boosts the average Nusselt number in a lid-driven cavity, with machine-learning models accurately capturing trends¹⁹.

COMSOL Multiphysics is a powerful finite element-based simulation platform widely used in fluid dynamics for modeling complex transport phenomena, including momentum, heat, and mass transfer. Its strength lies in its ability to handle Multiphysics coupling, enabling the simultaneous simulation of fluid flow with heat transfer, chemical reactions, electromagnetic effects, and more²⁰. In fluid dynamics applications, COMSOL offers intuitive geometry creation, automated meshing, and robust solvers, making it ideal for analyzing laminar and turbulent flows, convection in enclosures, and nanoparticle-enhanced systems. Its flexibility and accuracy have made it a preferred tool in thermal management, microfluidics, HVAC system design, and advanced cooling technologies²¹. Authors found that hybrid nanofluid and rotating rough cylinders significantly boost thermal performance under magnetic fields²². Researchers investigated that magnetic field intensity and cylinder rotation control the strength of flow circulation and heat transfer rate²³. Scientist studied that magnetic field strength and cylinder rotation significantly influence flow circulation and heat transfer. They concluded that rotation enhances convection strength while increasing entropy generation, with optimal ranges depending on Re and rotation speed²⁴.

In the present study, the effect of rotating cylinders on heat transfer enhancement in a vented cavity filled with Cu–water nanofluid is numerically explored using COMSOL Multiphysics 6.3. The nanofluid is modeled as a single-phase homogeneous mixture, where the addition of copper nanoparticles enhances the thermal conductivity and heat transfer capability of the base fluid (water) without significantly altering its flow characteristics. The study introduces multiple rotation scenarios to evaluate hydrothermal behavior. The novelties and significance of the present investigation are:

• The novelty of this research lies in extending prior two-cylinder models to a more complex system involving three rotating cylinders with different rotational combinations to evaluate their individual and collective thermal impacts.

• Four different rotation cases are studied: all cylinders rotating, one cylinder static while the others rotate (C1 static, C2 static, C3 static). This comparative setup allows assessment of individual cylinder contribution.

• What is the effect of each rotating cylinder on the overall heat transfer?

• How does the removal of one cylinder’s rotation influence the flow symmetry and thermal performance?

• Which configuration offers the highest Nusselt number?

Mathematical formulation

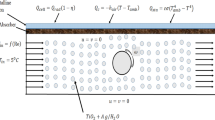
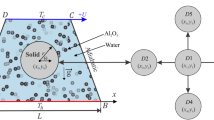
Figure 1a illustrates the steady, two-dimensional, laminar flow of an incompressible $Cu - Water$nanofluid within a square vented cavity of length $H=1m$. Three circular cylinders, each with a diameter of $0.15*H$, are positioned inside the cavity at different locations. The cavity features an inlet and an outlet port, each with a width of $W=0.2*H$. The inlet is located at the bottom-left corner of the cavity (0, W), where a cold nanofluid enters with a uniform velocity ${U_{in}}$ and initial temperature ${T_{in}}$​. The outlet is positioned near the top-right corner at location $(1,1 - W)$. All cavity walls are treated as adiabatic and subject to no-slip boundary conditions. The embedded circular cylinders are subjected to a uniform heat flux $q''$ and rotate in the clockwise direction with a constant angular velocity $\omega$. The simulations are carried out for Reynolds numbers ranging from 100 to 1000, rotational Reynolds numbers ${\operatorname{Re} _\omega }$ varying between 0 and 100, and nanofluid volume fractions $\phi$ between 0% and 3%. For simplicity, viscous dissipation and the effects of gravity are neglected, and the thermophysical properties of the nanofluid are assumed to be constant. Based on these assumptions, the governing conservation equations for mass, momentum, and energy are formulated as follows:^25,26.

Positions of cylinders are $C1=(3*H/4,3*H/4)$, $C2=(H/4,3*H/4)$, $C3=(H/4,H/4)$.

Continuity equation 

$$\frac{{\partial u}}{{\partial x}}+\frac{{\partial v}}{{\partial x}}=0$$

(1)

Momentum equation

x-momentum equation

$$u\frac{{\partial u}}{{\partial x}}+v\frac{{\partial u}}{{\partial y}}= - \frac{1}{{{\rho _{nf}}}}\frac{{\partial P}}{{\partial x}}+\frac{{{\mu _{nf}}}}{{{\rho _{nf}}}}\left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}}+\frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right)$$

(2)

y-momentum equation 

$$u\frac{{\partial u}}{{\partial x}}+v\frac{{\partial u}}{{\partial y}}= - \frac{1}{{{\rho _{nf}}}}\frac{{\partial P}}{{\partial y}}+\frac{{{\mu _{nf}}}}{{{\rho _{nf}}}}\left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}}+\frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right)$$

(3)

Energy equation

$$u\frac{{\partial T}}{{\partial x}}+v\frac{{\partial T}}{{\partial y}}=\frac{{{k_{nf}}}}{{{{\left( {\rho {c_p}} \right)}_{nf}}}}\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}}+\frac{{{\partial ^2}T}}{{\partial {y^2}}}} \right)$$

(4)

Boundary	Velocity	Temperature
Top wall	$u=0,{\text{ }}v=0$	$\frac{{\partial T}}{{\partial y}}=0$
Bottom wall	$u=0,{\text{ }}v=0$	$\frac{{\partial T}}{{\partial y}}=0$
Left wall	$u=0,{\text{ }}v=0$	$\frac{{\partial T}}{{\partial y}}=0$
Right wall	$u=0,{\text{ }}v=0$	$\frac{{\partial T}}{{\partial y}}=0$
Inlet port	$u={U_{in}},{\text{ }}v=0$	$T={T_{in}}$
Outlet port	$\frac{{\partial u}}{{\partial x}}=0,{\text{ }}\frac{{\partial v}}{{\partial x}}=0,{\text{ }}P={P_{out}}$	$\frac{{\partial T}}{{\partial x}}=0$
Rotating cylinder	$u=\omega (y - {y_c}),{\text{ v}}=\omega (x - {x_c})$

Using the similarity transformation.

Fig. 1

(a) Physical model and Mesh generation of the square cavity of the present study. Positions of cylinders are C1=(3*H/4,3*H/4), C2=(H/4,3H/4), C3=(H/4,H/4). (b) Methodological workflow for COMSOL multiphysics.

$$X=\frac{x}{H},{\text{ Y}}=\frac{y}{H},{\text{ U}}=\frac{u}{{{U_{in}}}},{\text{ V}}=\frac{v}{{{U_{in}}}},{\text{ }}\theta =\frac{{T - {T_{in}}}}{{q''H/{K_{nf}}}},{\text{ }}{{\text{P}}^*}=\frac{P}{{{\rho _{nf}}U_{{_{{in}}}}^{2}}}.$$

We get the dimensionless equations

$$\frac{{\partial U}}{{\partial X}}+\frac{{\partial V}}{{\partial Y}}=0$$

(5)

$$U\frac{{\partial U}}{{\partial X}}+V\frac{{\partial U}}{{\partial Y}}= - \frac{{\partial {P^*}}}{{\partial X}}+\frac{W}{{H\operatorname{Re} }}\left( {\frac{{{\partial ^2}U}}{{\partial {X^2}}}+\frac{{{\partial ^2}U}}{{\partial {Y^2}}}} \right)$$

(6)

$$U\frac{{\partial U}}{{\partial X}}+V\frac{{\partial U}}{{\partial Y}}= - \frac{{\partial {P^*}}}{{\partial Y}}+\frac{W}{{H\operatorname{Re} }}\left( {\frac{{{\partial ^2}V}}{{\partial {X^2}}}+\frac{{{\partial ^2}V}}{{\partial {Y^2}}}} \right)$$

(7)

$$U\frac{{\partial \theta }}{{\partial X}}+V\frac{{\partial \theta }}{{\partial Y}}=\frac{W}{{H\operatorname{Re} \Pr }}\left( {\frac{{{\partial ^2}\theta }}{{\partial {X^2}}}+\frac{{{\partial ^2}\theta }}{{\partial {Y^2}}}} \right)$$

(8)

Boundary	Velocity	Temperature
Top/Bottom/Left/Right wall	$U=0,{\text{ V}}=0$	$\frac{{\partial \theta }}{{\partial X}}=0$, $\frac{{\partial \theta }}{{\partial Y}}=0$
Inlet port	$U=1,{\text{ }}V=0$	$\theta =0$
Outlet port	$\frac{{\partial U}}{{\partial X}}=0,{\text{ }}\frac{{\partial V}}{{\partial X}}=0,{\text{ }}{P^*}=0$	$\frac{{\partial \theta }}{{\partial X}}=0$
Rotating cylinder	$U=320{\operatorname{Re} _\omega }(Y - {Y_c})/(9\operatorname{Re} )$$V=320{\operatorname{Re} _\omega }(X - {X_c})/(9\operatorname{Re} )$	$\frac{{\partial \theta }}{{\partial N}}= - 1$

Where.

${\text{Re = }}\frac{{{\rho _{nf}}{U_{in}}W}}{{{\mu _{nf}}}}$ Reynolds number, ${\text{Pr = }}\frac{{{\mu _{nf}}{c_p}_{{nf}}}}{{{K_{nf}}}}$ Prandtl number, ${\text{R}}{{\text{e}}_\omega }{\text{ = }}\frac{{{\rho _{nf}}\omega {R^2}}}{{{\mu _{nf}}}}$ Rotational Reynolds number. The expressions for the nanofluid model and its thermophysical properties are presented in Tables 1 and 2.

The Nusselt number is calculated using the following expression.

$$Nu=\frac{{hD}}{{{K_{nf}}}}=\frac{{2\pi \left( {\frac{D}{H}} \right)}}{{\int\limits_{0}^{{2\pi }} {{\theta _s}d\theta } }}$$

(9)

Table 1 Model for nanofluids is listed below²⁴.

Table 2 Thermophysical properties of nanofluids.

Result and discussion

This section presents the numerical results for the streamlines and isotherms to evaluate the influence of rotating cylinders on flow circulation and thermal performance in a square cavity filled with $Cu - Water$nanofluid. The study is carried out using COMSOL Multiphysics 6.3. The governing dimensionless parameters considered in the analysis include the Reynolds number is set at $\operatorname{Re} =600$, while the rotational Reynolds number $({\operatorname{Re} _\omega })$is varied as 0, 50, and 100 to investigate the impact of cylinder rotation on the flow structure and heat transfer characteristics. Additionally, two volume fractions of nanoparticles $(\phi =1.5\% )$ and $(\phi =3\% )$ are considered to assess the influence of nanoparticle loading on convection enhancement. The Prandtl number is kept constant at $\Pr =4.1588$, corresponding to the $Cu - Water$nanofluid properties. Four distinct rotation cases are studied: For each case, the flow structures are visualized using streamlines, while the temperature distribution is represented by isotherms. The effects of varying rotational speed and nanoparticle concentration are clearly observed in the graphical outputs.

Case 1: all the cylinder rotating clockwise

Figures 2 and 3 illustrate the streamline distributions with rotational Reynolds numbers set at ${\operatorname{Re} _\omega }=0,50,{\text{ and }}100$, and nanoparticle volume fractions of $\phi =3\%$ and $\phi =1.5\%$ respectively. In Fig. 2a $({\operatorname{Re} _\omega }=0)$a single large primary vortex dominates the cavity, exhibiting moderate circulation. As the rotation intensifies to ${\operatorname{Re} _\omega }=50$and 100 (Fig. 2b and c), strong secondary vortices develop around the cylinders, indicating enhanced momentum transfer due to rotation. In comparison, Fig. 3$(\phi =1.5\% )$ shows smoother and more symmetric flow structures at ${\operatorname{Re} _\omega }=0$, with weaker recirculation. Although vortex formation increases with ${\operatorname{Re} _\omega }$, the strength and complexity remain lower than in the 3% case. This comparison clearly demonstrates that a higher nanoparticle volume fraction amplifies rotational effects, leading to more confined and intensified vortical regions, thereby enhancing convective mixing within the cavity. Figures 4 and 5 show the isotherm contours, for $\phi =3\%$ (Fig. 4) and $\phi =1.5\%$ (Fig. 5). In Fig. 4a, with ${\operatorname{Re} _\omega }=0$, the flow is mainly conduction-dominated, and the isotherms appear smooth, horizontal, and layered, showing limited fluid motion. As we move to Fig. 4b ${\operatorname{Re} _\omega }=50$and Fig. 4c ${\operatorname{Re} _\omega }=100$, the isotherm patterns become more curved, compressed, and circulate around the cylinders, indicating a strong shift toward convection-dominated heat transfer. Physically, this rising trend in isotherm distortion occurs because increasing rotational Reynolds number injects more kinetic energy into the fluid, which strengthens circulation and mixing. The rotating cylinders drag nearby fluid, disturbing the thermal boundary layers and enhancing convective transport. Additionally, at $\phi =3\%$the presence of more nanoparticles improves the thermal conductivity of the nanofluid, supporting faster heat diffusion. In contrast, Fig. 5$(\phi =1.5\% )$shows the same trend with ${\operatorname{Re} _\omega }$, but the isotherm lines are more spread out and less intense due to the lower nanoparticle concentration, which results in weaker thermal conductivity and reduced heat transfer performance.

Case 2. C1 static, C2 and C3 rotating clockwise

Figures 6 and 7 highlight the streamline distributions for nanoparticle volume fractions $\phi =3\%$and $\phi =1.5\%$ respectively. In both cases, increasing ${\operatorname{Re} _\omega }$ from 0 to 100 enhances vortex formation near the rotating cylinders. In Fig. 6${\text{(}}\phi =3\% )$, strong secondary vortices develop around C2 and C3 at higher ${\operatorname{Re} _\omega }$, while the region near the static C1 remains less active. The higher nanoparticle concentration results in tighter and stronger vortices due to increased momentum diffusion. In Fig. 7$(\phi =1.5\% )$similar vortex trends are observed, but with noticeably weaker circulation and more diffused streamlines. Physically, the absence of rotation in C1 reduces shear generation in its vicinity, while the rotating C2 and C3 dominate the flow field, driving asymmetry and enhanced motion on their side of the cavity. The comparison shows that higher $\phi$ and cylinder rotation enhances convective mixing, while the static C1 locally suppresses flow intensity. Figures 8 and 9 show the isotherm distributions when Cylinder C1 is static, and C2 and C3 rotate clockwise at $\phi =3\%$ and $\phi =1.5\%$, respectively. In Fig. 8${\text{(}}\phi =3\% )$,the presence of more nanoparticles improves the fluid’s thermal conductivity, which helps transfer heat more efficiently. The rotating C2 and C3 stir the fluid, causing stronger mixing and tighter thermal layers near their surfaces. However, near the static C1, the absence of rotation weakens local fluid motion, resulting in wider isotherms and reduced heat transport. In Fig. 9$(\phi =1.5\% )$, similar changes occur but are less pronounced. The lower nanoparticle volume fraction leads to weaker thermal conductivity, and the isotherms are broader, indicating less efficient heat distribution. Physically, rotation injects angular momentum, which enhances convection. Meanwhile, the static C1 creates a low-shear region where heat transfer remains mainly conduction-dominated. The uneven motion results in asymmetric heat dispersion across the cavity.

Case 3. C2 static, C1 and C3 rotating clockwise

Figures 10 and 11 demonstrate the streamline graphs. In Fig. 10${\text{(}}\phi =3\% )$, higher nanoparticle concentration and rotation result in compact, stronger vortices, especially near C1 and C3. The stationary C2 interrupts the central flow, causing asymmetry and splitting the circulation zones. In Fig. 11$(\phi =1.5\% )$, although the rotational effect still promotes circulation near C1 and C3, the lower φ results in weaker momentum diffusion, leading to broader, less intense vortices. Physically, increasing ${\operatorname{Re} _\omega }$ injects more angular momentum into the system, intensifying fluid rotation around moving cylinders, while the static center cylinder acts as a barrier, weakening flow connection between the top and bottom zones. Figures 12 and 13 show the isotherm (temperature) distributions when C2 is static, and C1 and C3 rotate clockwise. In Fig. 12${\text{(}}\phi =3\% )$, increasing ${\operatorname{Re} _\omega }$ causes noticeable bending and compression of isotherms around the rotating C1 and C3, indicating enhanced convective heat transfer. The higher nanoparticle concentration improves thermal conductivity, making heat spread more effectively throughout the cavity. However, the static center cylinder (C2) weakens flow circulation near the middle, creating a less active thermal zone. This disrupts the continuity of thermal transport across the cavity. In Fig. 13$(\phi =1.5\% )$, similar trends appear but with broader and more spaced isotherms. The reduced nanoparticle content lowers the effective thermal conductivity, and weaker rotational energy limits mixing. As a result, heat remains more localized, and the transfer becomes less efficient. Physically, increasing the rotational Reynolds number intensifies shear and momentum near rotating surfaces, which enhances convective heat transfer. Moreover, the central static cylinder (C2) breaks the symmetry of the cavity, blocking the thermal pathway between the top and bottom rotating zones. This leads to thermal isolation in the middle and shifts most of the heat exchange activity toward the cavity’s upper and lower regions.

Case 4. C3 static, C1 and C2 rotating clockwise

Figures 14 and 15 depict the flow patterns. In Fig. 15$(\phi =1.5\% )$, similar flow structure is seen, but they are softer and wider because the lower $\phi$ gives weaker thermal and momentum effects. Physically, the rotating C1 and C2 energize the upper flow field, while the static C3 acts as a local barrier. The inlet (top left) supports circulation near C1, while the outlet (bottom right) helps remove flow near the weakened zone around C3, adding to the asymmetry. Figures 16 and 17 present the isotherm distributions when C3 is static, and C1 and C2 rotate clockwise. In Fig. 16${\text{(}}\phi =3\% )$, the higher nanoparticle content improves thermal conductivity, allowing stronger temperature gradients and better heat spreading. In Fig. 17$(\phi =1.5\% )$, this effect is weaker, with broader, less intense isotherms due to reduced heat-carrying capacity. Physically, rotation injects kinetic energy into the flow, disturbing thermal boundary layers and promoting convection near moving cylinders. The static C3 lacks this effect and forms a relatively stagnant region, reducing local heat transfer. Additionally, the inlet at the top-left introduces warm fluid near the rotating C1–C2, while the outlet at the bottom-right helps discharge cooler fluid near static C3 creating a strong vertical thermal gradient and asymmetry in the temperature field.

Numerical validation and grid independency test

Table 3 represents the detailed grid independence test at $\operatorname{Re} =600$, ${\operatorname{Re} _\omega }=100$, and $\phi =0.015$to ensure the reliability and accuracy of our numerical simulations. The test includes a range of mesh densities from “Extremely coarse” to “Extremely fine,” highlighting convergence behavior in Nusselt numbers for each cylinder.

Furthermore, to validate our numerical model, we have added a comparative Table 4 showing the Nusselt number values at different rotational Reynolds number against benchmark results from Ref²⁶. This confirms strong agreement between our results and the reference study, thus reinforcing the validity of our model.

Table 3 The grid independence test at $\operatorname{Re} =600$, ${\operatorname{Re} _\omega }=100$ and $\phi =0.15\%$.

Table 4 Comparison of Nusselt number.

Fig. 2

Streamlines distribution when all the cylinders are rotating and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 3

Streamlines distribution when all the cylinders are rotating and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 4

Temperature distribution when all the cylinders are rotating and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 5

Temperature distribution when all the cylinders are rotating and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 6

Streamlines distribution when C1 static and C2 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 7

Streamlines distribution when C1 static and C2 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 8

Temperature distribution when C1 static and C2 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 9

Temperature distribution when C1 static and C2 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 10

Streamlines distribution when C2 static and C1 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 11

Streamlines distribution when C2 static and C1 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 12

Temperature distribution when C2 static and C1 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 13

Temperature distribution when C2 static and C1 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 14

Streamlines distribution when C3 static and C1 = C2 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 15

Streamlines distribution when C3 static and C1 = C3 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Fig. 16

Temperature distribution when C3 static and C1 = C2 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =3\%$.

Fig. 17

Temperature distribution when C3 static and C1 = C2 are rotating, and $\operatorname{Re} =600,{\text{ }}\phi =1.5\%$.

Figures 18, 19, 20, 21 present a comparative analysis of the average Nusselt numbers associated with each rotating cylinder under various rotational Reynolds numbers and nanoparticle volume fractions. These bar graphs collectively illustrate the thermal performance across different scenarios by displaying the Nusselt number for each cylinder. Specifically, Nu₁, Nu₂, and Nu₃ represent the Nusselt numbers for cylinders C1, C2, and C3 at a nanoparticle volume fraction of 3%, while Nu₁₂, Nu₂₁, and Nu₃₂₁ correspond to the same cylinders at 1.5%. The color scheme represents the rotational Reynolds number, with yellow indicating ${\operatorname{Re} _\omega }=0$, green for ${\operatorname{Re} _\omega }=50$, and red for ${\operatorname{Re} _\omega }=100$.

Figure 18 illustrates the average Nusselt number for all three cylinders when they rotate clockwise. Among all cases, the highest Nusselt number is observed at ${\operatorname{Re} _\omega }=100$for $\phi =3\%$, highlighting the significant enhancement in convective heat transfer due to intensified and symmetric circulation induced by collective rotation. This configuration increases shear around each cylinder, thinning the thermal boundary layers and improving heat exchange. In contrast, the lowest Nusselt number is recorded for Cylinder 2 at $\phi =1.5\%$, where weaker nanoparticle loading results in reduced thermal diffusion and weaker rotational effects. Figure 19 shows the scenario where C1 is static and C2 and C3 rotate. Here, the Nusselt number of C1 remains relatively low, especially for ${\operatorname{Re} _\omega }=0$, because of reduced local flow agitation and weaker vortex development. In contrast, C2 and C3, being active rotors, show a substantial increase in Nusselt number with higher ${\operatorname{Re} _\omega }$, particularly at $\phi =3\%$, highlighting the dominance of rotational shear in enhancing local heat transfer. In Fig. 19, at $\phi =3\%$, the maximum Nusselt number $(Nu \approx 24.06)$ occurs at C3 for ${\operatorname{Re} _\omega }=100$, attributed to the strong rotational mixing and improved thermal conductivity of the nanofluid. Meanwhile, the stationary C1 consistently exhibits lower Nusselt numbers due to reduced fluid agitation near its surface. From Fig. 20, for $\phi =3\%$, the highest Nusselt number $(Nu \approx 21.04)$ is observed at C3 for ${\operatorname{Re} _\omega }=100$, highlighting intensified convective activity around the rotating lower cylinder. Interestingly, C2 consistently shows the lowest heat transfer rates, particularly at higher ${\operatorname{Re} _\omega }$, with Nu dropping to nearly 5.0. This is attributed to the central static cylinder acting as a thermal and flow obstruction, suppressing momentum exchange and vortex formation near its surface. At $\phi =1.5\%$, the overall Nusselt numbers are lower due to reduced thermal conductivity of the nanofluid. In Fig. 21, The highest Nusselt number is observed for Cylinder C3 at $\phi =3\%$ and ${\operatorname{Re} _\omega }=100$, reaching a value of 16.405. In contrast, the lowest Nusselt number, 4.1684, occurs for Cylinder C2 at $\phi =1.5\%$ and ${\operatorname{Re} _\omega }=50$. This reduction stems from weakened thermal conductivity at lower nanoparticle concentration, compounded by asymmetric flow disruption near C2 due to differential cylinder rotation.

Fig. 18

Comparisin of Nusselt number when C1 = C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 19

Comparisin of Nusselt number when C1 = 0, C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 20

Comparisin of Nusselt number when C2 = 0, C1 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 21

Comparisin of Nusselt number when C3 = 0, C1 = C2 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

To enhance the clarity of comparative understanding of the result, a series of heatmap Figs. 22, 23, 24, 25 have been added to clearly compare the Nusselt number variations across four different rotation configurations (Cases 1 to 4) for both 3% and 1.5% nanoparticle volume fractions under varying rotational Reynolds numbers. These visualizations strengthen the interpretation of the findings by providing an immediate graphical comparison of thermal performance, ensuring a clearer and more structured presentation of the study.

Fig. 22

Comparisin of Nusselt number when C1 = C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 23

Comparisin of Nusselt number when C1 = 0, C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 24

Comparisin of Nusselt number when C2 = 0, C1 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Fig. 25

Comparisin of Nusselt number when C3 = 0, C1 = C2 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

The tabulated Nusselt number data represents in Tables 5, 6, 7 and 8 for all four configurations under three rotational Reynolds numbers $({\operatorname{Re} _\omega }=0,50,100)$and two nanoparticle volume fractions (3% and 1.5%) reveals that increasing ${\operatorname{Re} _\omega }$ generally enhances heat transfer performance. In Case 1 (all cylinders rotating), the Nusselt numbers for both volume fractions consistently rise with rotational speed, reaching their highest values at ${\operatorname{Re} _\omega }=100$. In Case 2 (C1 static) and Case 3 (C2 static), the actively rotating cylinders show significant Nu improvement with higher ${\operatorname{Re} _\omega }$, while static cylinders exhibit smaller gains or non-monotonic trends due to asymmetric vortex development. Case 4 (C3 static) shows a similar pattern, where heat transfer enhancement is most notable for rotating cylinders but less pronounced for the stationary one. Across all cases, the effect of increasing nanoparticle volume fraction from 1.5% to 3% is positive, with higher thermal conductivity leading to consistently larger Nu values. These trends confirm that higher rotational speeds and increased nanoparticle concentrations synergistically boost convective heat transfer, though the degree of improvement depends on cylinder placement and flow symmetry.

Table 5 Comparisin of Nusselt number when C1 = C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Table 6 Comparisin of Nusselt number when C1 = 0, C2 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Table 7 Comparisin of Nusselt number when C2 = 0, C1 = C3 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Table 8 Comparisin of Nusselt number when C3 = 0, C1 = C2 = rotating, and $\phi =3\% {\text{ and }}\phi =1.5\%$.

Conclusion

In this study, a comprehensive numerical investigation was conducted using COMSOL Multiphysics 6.3 to examine the flow structure and thermal performance of $Cu - Water$nanofluid in a square cavity with rotating cylinders. The impact of rotational Reynolds number, nanoparticle concentration, and rotational configurations was analyzed in detail through streamline and isotherm patterns, along with local Nusselt number variations. The results demonstrate that rotational motion significantly enhances convective heat transfer by intensifying vortex strength and disrupting thermal boundary layers. This research has potential applications such as electronic cooling, energy storage devices, and compact heat exchangers.

The most important results have been summarized as follows.

• The results indicate that adjusting the rotation of the cylinders allows effective control of fluid flow and heat transfer in targeted areas within the cavity.

• Rotational motion of cylinders significantly enhances convective heat transfer, especially when all cylinders rotate clockwise, leading to the highest Nusselt number and thermal performance.

• Higher nanoparticle volume fraction $(\phi =3\% )$ consistently improves thermal conductivity, resulting in stronger vortex formation, tighter isotherms, and better heat transfer compared to $\phi =1.5\%$.

• From bar graph higher nanoparticle concentration $(\phi =3\% )$significantly enhance convective rate of heat transfer, with the highest Nusselt numbers observed when all cylinders rotate, especially at $({\operatorname{Re} _\omega }=100)$.

  • The removal of one cylinder’s rotation disrupts flow symmetry, reducing local shear and weakening heat transfer near the static cylinder while increasing asymmetry in the cavity.

  • Cylinder positioning relative to the inlet and outlet affects performance; cylinders closer to the inlet experience stronger flow impingement, enhancing local heat transfer, while those near the outlet show reduced thermal activity.

  • The highest heat transfer performance was achieved when all three cylinders rotated simultaneously at ${\operatorname{Re} _\omega }=100$and $\phi =3\%$.

  • The $3\%$ nanoparticle concentration is more effective than $1.5\%$for enhancing both flow circulation and heat transfer. It improves thermal conductivity, strengthens vortex intensity, and results in more distorted isotherms indicating stronger convection. This is further supported by higher Nusselt numbers across all cases, confirming superior thermal and flow performance at the higher concentration.

Design implications and practical considerations

This section outlines the relevance of rotating-cylinder-based nanofluid systems in real-world applications such as:

• Microelectronic device cooling: where space is constrained, and thermal hotspots must be effectively managed.

• Battery thermal management systems (BTMS): where rotating modules may help redistribute coolant flow and reduce thermal gradients.

• Compact heat exchangers or solar collectors: where optimized rotating configurations can enhance localized heat extraction.

We also acknowledge potential operational challenges, such as:

• The complexity of integrating rotating elements in miniaturized systems,

• Increased maintenance requirements due to moving parts,

• And design trade-offs regarding weight, power consumption, and manufacturability.

• Particle Agglomeration and Stability: Over time, Cu nanoparticles tend to aggregate, reducing thermal performance and increasing clogging risks in real-world systems.

• Recyclability and Environmental Impact: Copper, while widely used, poses challenges in terms of nanoparticle recovery, environmental persistence, and potential toxicity if released into water or soil systems.

• Long-Term Operational Viability: Ensuring colloidal stability through surfactants or surface modification is necessary for sustainable deployment, but it adds to material cost and complexity.

This added commentary broadens the scope of our study by connecting numerical insights with practical engineering contexts.

Future work

In future investigations, the study will be extended to include entropy generation analysis and thermodynamic performance metrics such as the Bejan number. This addition will allow for a more comprehensive assessment of thermal irreversibility and second-law efficiency. Such analysis will further support optimization strategies for advanced thermal management systems using rotating cylinders and nanofluids.