Introduction

Gallium Nitride (GaN) stands out as a promising material for the next generation of both high-power applications due to its wide bandgap of 3.4 eV and high critical breakdown electric field of 3.3 MV/cm1. Furthermore, the development of AlGaN/GaN hetero-epitaxial structures benefits from the copresence of spontaneous and piezoelectric polarization2, leading to the formation of a quantum-confined two-dimensional electron gas (2DEG) with high sheet carrier density (1013 cm− 2) and electron mobility (> 2000 cm2 V− 1 s− 1)3. These properties make high electron mobility transistors (HEMTs) based on AlGaN/GaN heterostructures highly attractive for high-frequency applications4. Schottky contacts play a critical role and control the current injection and the channel modulation5,6,7. The choice of metal and its interface quality affect the barrier height, leakage current, threshold voltage8 and overall stability9.

While the Thermionic Emission (TE) model describes ideal Schottky behavior, deviations from this trend are often observed in real contacts10,11,12. These deviations are commonly addressed introducing the ideality factor which exhibits a value grater than unity and its thermal dependence can be explained by the T0-anomaly12. Furthermore, Schottky barrier inhomogeneities, described by Tung’s model13, link the presence of spatial fluctuations of the electrical potential to a local lowering of the barrier height, defined as “patches”, which result in increased ideality factors14,15.

The barrier inhomogeneity has successfully explained deviations from ideality both on SiC16,17 and GaN18. However, in AlGaN/GaN heterostructures, the deviations from ideal TE conduction are often too pronounced to be explained by the presence of inhomogeneities. In fact, high and temperature dependent ideality factors generally indicate the presence of additional mechanisms beyond thermionic emission, such as dislocation assisted tunneling19 and recombination-generation processes20. Since Tung’s model is valid for small deviations from ideal thermionic emission, its application to AlGaN/GaN heterostructure is often not suitable, since tunneling components usually prevail the charge conduction. In AlGaN/GaN heterostructures, barrier inhomogeneity is usually analyzed through statistical methods, where gaussian distributions of barrier heights21,22 are obtained by extracting the Schottky barrier from many diodes on the same sample.

In reverse bias conditions the conduction mechanism in AlGaN/GaN heterostructures is generally linked to a high electric field in the AlGaN barrier leading to tunneling mechanism, according to Poole-Frenkel or Fowler-Nordheim conduction23,24,25.

Among the various Schottky contacts studied on AlGaN/GaN, Ni/Au bilayers are widely used19,26. Other Au-free metallization have been also proposed27 such as W and its nitrides28, TiN29, WC30, Cu31, Fe31, Al31.

Molybdenum (Mo) is a refractory metal characterized by a melting temperature of 2600 °C32. Its employment in GaN-based electronics has been very limited. Some studies33,34,35,36,37 have employed it as a Schottky contact due to its rectifying behavior on n-GaN38. The main characteristics are its thermal stability, mechanical strength33 which is fundamental for some gate geometries, and good adherence to the AlGaN and GaN surface. When kept at high temperatures for long periods of time the contact and its electrical properties do not degrade33. Also, molybdenum has a low tendency to oxidation at temperatures lower than 500 °C39 due to the low reaction enthalpy40. So, it could represent a valid alternative for Au-free Schottky contacts for GaN-based materials.

In this work, Mo Schottky contacts on AlGaN/GaN heterostructures have been studied. The current measurements in Schottky diodes acquired at different temperatures showed a TE behavior (n ~ 1.26 at 25 °C). In the explored thermal range (25–150 °C) the barrier increases (from 0.85 to 0.89 eV) while the ideality factor decreases (from 1.26 to 1.20). The conduction mechanism follows typical thermionic emission. Such behavior, uncommon for Schottky contacts on AlGaN/GaN heterostructures, makes it possible to investigate the barrier inhomogeneity in detail by means of an analytical application of Tung’s model, providing insight into the role of inhomogeneities in such materials.

Experimental

AlGaN/GaN heterostructures grown on Si substrate characterized by a 16 nm AlGaN barrier thickness and 26% concentration of Al have been used in this work. Ti/Al/Ti annealed at 600 °C for 1 min in N2 atmosphere has been used as ohmic contacts. The Schottky contact consists of a 100 nm thick Mo layer deposited by magnetron sputtering in an EvoVac PVD system (Angström Engineering) in Ar atmosphere at a base pressure of 5 × 10− 3 mbar at a rate of 0.3 nm/s with 300 W of output power. Schottky diodes have been defined by optical lithography and standard lift-off method, the anode consists of a circle having a diameter of 200 μm and it’s surrounded by a large area ohmic contact. Electrical analyses have been performed in a TS200-HP (MPI) probe station equipped with a semiconductor parameter analyzer B1500 (Keysight).

Results and discussion

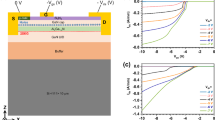
Figure 1 shows the semilogarithmic plot of the forward current density-voltage (J–V) of the Mo/AlGaN/GaN Schottky diodes in the temperature range of 25–150 °C.

Fig. 1
figure 1

Forward J–V curves at different temperatures of Mo/AlGaN/GaN Schottky diodes and schematically the structure of the device.

Full size image

An ideal homogeneous Schottky contact can be defined as a metal/semiconductor junction that electrically behaves, regardless of temperature, voltage or contact area, as predicted by the Thermionic Emission (TE) model41. The TE model predicts that the current density depends on ΦB (Schottky Barrier Height) and n (ideality factor, close to unity), both temperature independent, following the equation42:

$$\:{\text{J}}_{\text{T}\text{E}}={\text{J}}_{\text{S}}\text{exp}\left(\frac{\text{q}{\text{V}}_{\text{F}}}{\text{n}{\text{k}}_{\text{B}}\text{T}}\right)={\text{A}}^{\text{*}}{\text{T}}^{2}\text{exp}\left(-\frac{\text{q}{{\Phi\:}}_{\text{B}}}{{\text{k}}_{\text{B}}\text{T}}\right)\text{exp}\left(\frac{\text{q}{\text{V}}_{\text{F}}-\text{J}{\text{R}}_{\text{S}}\:}{\text{n}{\text{k}}_{\text{B}}\text{T}}\right)$$
(1)

where A* is the Richardsons’ constant (A* = 32 A cm− 2 K− 2 for electrons in AlGaN/GaN heterostructures7, T is the absolute temperature, q is the electron’s charge, kB is the Boltzmann’s constant, VF is the forward voltage applied to the Schottky contact and RS is the series resistance.

The experimental current can be expressed as reported in Eq. (1) according to the TE model. By performing a fit in the linear region of the semilog J–V curve it’s possible to obtain the values of ΦB and n, for each measurement temperature (Fig. 2a), both show a weak thermal dependence which is consistent with real Schottky contacts. Figure 2b reports the correlation between the barrier height and the ideality factor. A linear relationship between the barrier and the ideality factor is symptomatic of an inhomogeneous barrier13. The homogeneous barrier (ΦB0) value can be determined from the extrapolation of the barrier value at n = 117,43. From a statistical analysis conducted on wafer at room temperature the Schottky barrier height is ΦB = 0.85 ± 0.03 eV, while the ideality factor n = 1.26 ± 0.01.

From Fig. 2a, there is an evident thermal dependence of both the barrier height and the ideality factor. The barrier increases (from 0.85 to 0.89 eV) while the ideality factor decreases (from 1.26 to 1.20) with increasing temperature. By correlating the values of the barrier with the ones of the ideality factor, Fig. 2), it’s possible to extrapolate at n = 1 a homogeneous value of the barrier of ΦB0 = 1.04 eV. This value represents the barrier that a homogeneous Mo Schottky contact should have on AlGaN/GaN. Molybdenum’s work function is reported to be in the range of 4.9−5.0 eV44, so according to the Schottky-Mott rule the Schottky barrier height expected on AlGaN/GaN heterostructures, considering an electron affinity of χAlGaN = 4.1 eV30, should be ΦB = ϕm − χAlGaN = 0.8 − 0.9 eV.

Previous works report that at room temperature the Schottky barrier height on Mo/AlGaN systems is 0.80 eV (for Mo/Al0.05Ga0.95N/GaN)34 and 0.8 eV (for Mo/Al0.22Ga0.78N/GaN)33. These values align with the ones predicted by Schottky-Mott rule and the one experimentally obtained.

Fig. 2
figure 2

Values of ΦB and n at different temperatures (a), correlation of ΦB and n, extraction of ΦB0 = 1.04 eV (b).

Full size image

The weak thermal dependence of the ideality factor recorded for the Mo/AlGaN/GaN Schottky diodes, Fig. 2a, does not have any accordance with a tunneling mechanism. In fact, based on the thermal dependence of the ideality factor it’s possible to correlate it to a characteristic tunneling energy E0014,30 according to

$$\:\text{n}=\frac{{\text{E}}_{00}}{{\text{k}}_{\text{B}}\text{T}}\text{coth}\left(\frac{{\text{E}}_{00}}{{\text{k}}_{\text{B}}\text{T}}\right)$$
(2)

Based on Eq. (2), the lower the value of E00 is, the lower will be the thermal dependence of the ideality factor. Meanwhile, the higher the value of E00 and the more pronounced will be the thermal dependence of the ideality factor, and also there will be a tunneling contribution to the overall current conduction7,20,45. Instead, the weak thermal dependence of the ideality factor exhibited by the Mo/AlGaN/GaN diodes is rationalized according to the T0-anomaly, which can be expressed as46,47

$$\:\text{n}=1+\frac{{\text{T}}_{0}}{\text{T}}$$
(3)

Following Eq. (3), an ideal TE emission, with a temperature-independent unitary value of the ideality factor is obtained for T0 = 0 K. The higher the value of T0 is, the higher will be the thermal dependence of the ideality factor. Furthermore, for the same temperature the value of the ideality factor will be higher for higher values of T0. The origin of the T0-anomaly has been previously associated to defects at the interface between the metal and the semiconductor15. The introduction of this constant temperature is done since in a T0-plot41, where nkBT is plotted as a function of kBT, a Schottky contact characterized by the T0-anomaly will have the same behavior of a pure TE (n = 1) but shifted at higher values due to the higher than 1 ideality factors. For the Mo/AlGaN/GaN Schottky diodes a T0 = 80.2 K is obtained Fig. 3a, and also according to the T0-plot the experimental data lies on a parallel line to the ideal TE (n = 1) case, meaning that the conduction mechanism is due to thermionic emission, Fig. 3b.

The rationalization of the thermal dependency of the Schottky barrier can be done, according to Werner et al.14

$$\:{{\Phi\:}}_{\text{B}}={{\Phi\:}}_{\text{B}}^{0}-\frac{\text{q}{{{\upsigma\:}}_{{{\Phi\:}}_{\text{B}}}}^{2}}{2{\text{k}}_{\text{B}}\text{T}}$$
(4)

where ΦB is the value of the barrier determined according to the TE model, Fig. 2a, while ΦB0 is the homogeneous value of the barrier, and finally \(\:{\sigma\:}_{{\varPhi\:}_{B}}\) is the standard deviation associated to the barrier variation generated by the lateral inhomogeneity of the potential. Figure 3c14 reports the barrier ΦB obtained from the TE plotted as a function of q(2kBT)−1, the standard deviation of the distribution of barrier heights is the square root of the slope, while the intercept with the y-axis is the homogeneous value of the Schottky barrier. The value of the homogeneous barrier extracted from this fit is ΦB0 = 0.99 eV, which is similar to the value obtained from the linear ΦB/n correlation (Fig. 2b). Also, the value of the standard deviation is \(\:{\sigma\:}_{{\varPhi\:}_{B}}\) = 85 meV is in the low-range of the values reported in literature, that range from 60 meV21 to 150 meV48.

Fig. 3
figure 3

Thermal dependence of the ideality factor with a non tunneling dependence (a), nkBT/kBT (T0) plot with the extraction of a T0 = 80.2 K (b), thermal dependence of ΦB, a standard deviation of \(\:{{\upsigma\:}}_{{{\Phi\:}}_{\text{B}}}\) = 85 meV has been obtained (c).

Full size image

The electrical characteristics of Schottky contacts are highly influenced by various factors, including the metal stack, pre-deposition treatments and post-deposition treatments (such as post metallization annealing PMA). Additionally, the composition of the AlGaN barrier layer and its deposition approach (MOCVD or ALD) may play a crucial role in determining the dominant conduction mechanism. To provide a comprehensive comparison, Table 1 summarizes different Schottky contacts reported in literature highlighting key parameters affecting their electrical behavior. Furthermore, Table 1 highlights that for AlGaN/GaN heterostructures the conduction mechanism in forward bias generally follows a tunneling behavior with values of E00 that depend on multiple factors. The Mo/AlGaN/GaN diodes reported in this study have instead a thermionic emission conduction in the whole bias range.

Table 1 Summary of reported Schottky contacts on AlGaN/GaN heterostructures with different processing conditions and their corresponding conduction mechanisms.
Full size table

Although low ideality factors have been previously reported, their thermal dependence shows a tunneling contribution that can be described by a value of characteristic tunneling energy E00 that ranges from 30 to 85 meV. This underlies a significant tunneling contribution to the conduction at the Schottky/AlGaN interface. A low temperature thermal annealing after the metal deposition (PMA) has shown variation in the electrical properties of devices, such as leakage reduction7, also a decrease in the ideality factor and the value of E007,51, but the conduction mechanism keeps following a tunneling trend. In the case reported in this study, the Mo/AlGaN/GaN diodes show an ideality factor of 1.26 at room temperature, which is in the low range of the values reported in literature. Furthermore, the recorded ideality factor weakly decreases with increasing temperature following a behavior that is not related to tunneling but to thermionic emission, as confirmed by the nkBT/kBT plot reported in Fig. 3b.

The Richardson’s plot is reported in Fig. 4a, from a correlation of Js/T2 as a function of q/kBT, where the saturation current density is determined from the extrapolation at VF = 0 of the linear fit used for the TE model. Rewriting the saturation current density of the TE model (Eq. 1)

$$\:\text{ln}\left(\frac{{\text{J}}_{\text{s}}}{{\text{T}}^{2}}\right)=\text{ln}\left({\text{A}}^{\text{*}}\right)-\frac{\text{q}{{\Phi\:}}_{\text{B}}^{\text{e}\text{f}\text{f}}}{{\text{k}}_{\text{B}}\text{T}}$$
(5)

According to Eq. (5), from the slope of the linear fit was determined an effective barrier ΦBeff = 0.76 eV, while from the y-axis intercept a Richardson’s constant value of 0.48 A cm− 2 K− 2. The value of the Richardson’s constant is far from the one commonly used for electrons in AlGaN/GaN heterostructures (32 A cm− 2 K− 27. Reported in previous works is the correction of the Richardsons’ plot by inserting a contribution of inhomogeneities to the barrier height53 according to

$$\:\text{ln}\left(\frac{{\text{J}}_{\text{s}}}{{\text{T}}^{2}}\right)-\frac{{\text{q}}^{2}{{{\upsigma\:}}_{{{\Phi\:}}_{\text{B}}}}^{2}}{2{\left({\text{k}}_{\text{B}}\text{T}\right)}^{2}}=\text{ln}\left({\text{A}}^{\text{*}}\right)-\frac{\text{q}{{\Phi\:}}_{\text{B}}^{0}}{{\text{k}}_{\text{B}}\text{T}}$$
(6)

Following Eq. (6), from a linear fit it’s possible to extract the value of the homogeneous barrier as the slope while the Richardsons’ constant as the intercept with the y-axis. Reported to Fig. 4b there’s the result of this procedure leading to a homogeneous barrier of ΦB0 = 0.995 eV and a Richardsons’ constant of A* = 30.4 A cm− 2 K− 2. The homogeneous value is close to the one obtained both by considering the ΦB/n correlation (Fig. 2b) and the inhomogeneity of the barrier (Fig. 3c). This result underscores the impact of the inhomogeneities on the extracted parameters, demonstrating that accounting for the inhomogeneities yields a Richardsons’ constant in better agreement with the theoretical value.

Fig. 4
figure 4

Richardsons’ plot, an effective barrier ΦBeff = 0.76 eV (a), modified Richardsons’ plot (b).

Full size image

From the results obtained, the Mo/AlGaN/GaN Schottky diodes seem to behave as close-to-ideality thermionic emission. To acknowledge the deviation from ideality, Tung’s inhomogeneity model13 has been employed. Many could be the reasons behind the strong deviation from ideal TE behavior of Schottky contacts. Firstly defects, the Schottky/Semiconductor junction consists of polycrystalline materials, at least on one side if not both. The distribution of defects along the surface, the presence of structural defects and grain boundaries, both in the semiconductor and the metal, cause fluctuation of the electrical potential14. Moreover, the formation of the Schottky contact is highly sensitive to the choice of metal and to the preparation steps undertaken before and after the metal deposition. Pre-deposition processes, such as cleaning54 and plasma treatments55, as well as post-deposition processes like thermal treatments30 and oxidation56, can significantly influence the electrical properties of the contact57,58.

In real Schottky contacts the presence of a lateral inhomogeneity of the barrier is another factor that impacts their electrical behavior. An analytical model for the study of non ideal Schottky contacts has been proposed by Tung13. In this model, a real Schottky contact is assumed to have a barrier that is laterally inhomogeneous. The punctual value of the barrier oscillates around an average (homogeneous value, ΦB0) following a gaussian distribution. The regions where the barrier deviates from the homogeneous value are referred to as patches. When the radius of these patches is smaller than or comparable to the Debye length, they undergo a pinch-off effect. In this case, the current flowing through the low-barrier region is affected by the presence of the higher-barrier regions, due to the formation of a saddle point in the energy profile that arises from the local electric field. For this reason, the region parameter γ is defined in Tung’s model and the effective barrier of the patches depends on it. Furthermore the model allows to explain some other experimental evidences, such as the thermal dependence of both the Schottky barrier and the ideality factor (n > 1)17.

Both on Gallium Nitride48,59 and Silicon Carbide17,41 the barrier height inhomogeneity has been studied through I-V-T measurements on diodes but also through nanoscale analyses such as conductive AFM43,60,61.

According to the models reported in literature for the study of metal/semiconductor inhomogeneities13,15, it’s possible to correlate the value of the homogeneous barrier to the value of the effective barrier, extracted with the Richardson’s plot.

$$\:{{\Phi\:}}_{\text{B}}^{\text{e}\text{f}\text{f}}={{\Phi\:}}_{\text{B}}^{0}-{\upgamma\:}{\left(\frac{{\text{V}}_{\text{b}\text{b}}}{{\upeta\:}}\right)}^{\frac{1}{3}}$$
(7)

where ΦBeff is the effective barrier height (Fig. 4), ΦB0 is the homogeneous value of the barrier (Fig. 2b), γ is the region parameter introduced to describe the inhomogeneity of the barrier62, Vbb = ΦB0 − Vn is the band bending, where Vn is the chemical potential, and η = εs/qND with εs permittivity of the semiconductor. The region parameter depends on the effective barrier of the patch and its radius. When the patch radius is small and the effective barrier resembles the homogeneous one γ is low, indicating minimal system inhomogeneity. As the radius increases or the effective barrier decreases, the value of γ rises, underlying an increasing inhomogeneity.

Most of the studies about inhomogeneities employ just one value of the region parameter, assuming that only one is the patch, or barrier, that prevails over the others effecting with a higher weight the conduction mechanism16,17. In a more realistic analysis, a gaussian distribution of values can be employed for the study of inhomogeneities13,15,41.

In this study, a gaussian distribution has been employed, as reported in Fig. 5a. The performed analysis assumes the presence of 10 different patches. Considering a range of patches corresponds to consider a spread of γ values, and at each γ a value of an effective barrier height, according to Eq. 7. The concentration of each patch lays on a gaussian distribution defined by a maximum value of Np = 1.5 × 106, an average value of µγ = 1.0 × 10− 4 cm2/3 V1/3, and a standard deviation of σγ = 1.4 × 10− 4 cm2/3 V1/3. The standard deviation σγ, coherent with values reported in previous works41, has been analytically determined according to Tung’s model13,15 assuming low barrier circular patches embedded in a homogeneous region according to

$$\:{{\upsigma\:}}_{{\upgamma\:}}={\text{T}}_{0}\:{\text{k}}_{\text{B}}\:{{\upeta\:}}^{2/3}{\text{V}}_{\text{b}\text{b}}^{1/2}$$
(8)

The patch concentration, obtained by dividing the total number of patches by the geometrical area of the analyzed diode is 2 × 109 cm− 2, which lays in the range of typical dislocation concentrations present in AlGaN/GaN heterostructures (109-1010 cm− 2)1. Furthermore, the contribution of these patches is lower than 5%.

The average value of the distribution of γ‘s is µγ = 1.0 × 10− 4 cm2/3 V1/3. In previous works the modeling has been performed using just one value of γ and not a distribution. Nevertheless, the values reported for GaN48 is γ = 5.96 × 10− 4 cm2/3 V1/3, while for 4 H-SiC17 γ = 1.31 × 10− 4 cm2/3 V1/3, γ = 2.52 × 10− 4 cm2/3 V1/3 using Ni and Ti as Schottky contacts, respectively.

The current flowing through the laterally inhomogeneous Schottky contact can be modelled by considering the current passing through the low-barrier patches. In fact, although the barriers have a gaussian distribution14, it is reasonable to assume that the higher-barrier patches contribute in negligible magnitude to the overall conduction17. The current transport can be described as13,15,43

$$\:{\text{I}}_{\text{p}\text{a}\text{t}\text{c}\text{h}\text{e}\text{s}}=\sum\limits_{\text{i}=1}^{10}{\text{A}}^{\text{*}}{\text{T}}^{2}{\text{A}}_{\text{e}\text{f}\text{f}}{\text{N}}_{\text{p},\text{i}}\text{exp}\left(-\frac{\text{q}{{\Phi\:}}_{\text{B},\text{i}}^{\text{e}\text{f}\text{f}}}{{\text{k}}_{\text{B}}\text{T}}\right)\text{exp}\left(\frac{\text{q}{\text{V}}_{\text{F}}}{{\text{n}}_{\text{i}}{\text{k}}_{\text{B}}\text{T}}\right)$$
(9)

According to Eq. (9), the experimental current has been fitted considering as fitting parameters the mean value of the distribution (µγ) and its maximum (Np). The result of this fit for 25 °C and 150 °C is reported in Fig. 5b and c, respectively.

Fig. 5
figure 5

Gaussian distribution of ’s (a), fit of experimental data at 25 °C (b) and 150 °C (c).

Full size image

The approach employed in this study allows for an accurate description of the experimental data considering the barrier inhomogeneity model proposed by Tung13.

Figure 6 presents a 3D schematic representation of the inhomogeneous Schottky barrier. The presence of inhomogeneities leads to the formation of dips in the potential profile at the Mo/AlGaN interface. These dips, referred to as “patches”, play a dominant role in the conduction mechanism although according to Tung’s model, based on the I-V-T analysis of the Mo/AlGaN/GaN diodes, the patches account for less than 5% of the geometrical area.

Fig. 6
figure 6

3D schematic illustration of the metal/AlGaN interface showing the Schottky barrier inhomogeneity.

Full size image

Conclusions

We showed that Mo contact on AlGaN/GaN heterostructures behave in a nearly ideal thermionic emission way. Mo/AlGaN/GaN Schottky contacts were characterized through I-V-T measurements, allowing the extraction of the Schottky barrier height and ideality factor in the explored thermal range. The analysis revealed a temperature-dependent barrier height ranging from 0.85 to 0.89 eV and an ideality factor decreasing from 1.26 to 1.20 with increasing temperature. By correlating these values, the homogeneous Schottky barrier height was determined to be ΦB0 = 1.04 eV for the Mo/AlGaN/GaN diodes.

According to Tung’s model, the deviation from ideal behavior can be modelled assuming that the interface exhibits lateral inhomogeneities in the form of localized patches with barrier heights deviating from the homogeneous value. These lower-barrier patches play a dominant role in conduction even if they cover less than 5% of the geometric area of the diode. Also these patches have a concentration of 2 × 109 cm− 2, coherent with values of dislocation density of heterostructures grown on silicon The distribution of these barrier fluctuations follows a gaussian profile, further confirming the inhomogeneous nature of the contact.

This study demonstrates that Mo/AlGaN/GaN Schottky diodes behave close to ideal thermionic emission, with slight deviations attributed to barrier inhomogeneities. These findings highlight molybdenum as a promising candidate for replacing gold based Schottky contacts and contribute to the broader understanding of conduction mechanisms in AlGaN Schottky interfaces.