Introduction

The term “distributed generation sources” refers to electric energy sources directly linked to the distribution network or the consumer side. Although the nominal values of these sources vary, their output capacities are often measured in the range of a few kilowatts to several megawatts. These units are positioned in the distribution feeders and on the posts, close to the loads, respectively. The pattern of electricity consumption by customers can be altered through energy management. This adjustment is made to get more relative to the consumption curve that works best. The operational and planning costs may be reduced by using energy management to minimise consumption over time as well as by selecting the proper load curve. The objective of the energy management system (EMS) is to make decisions on the most efficient usage of generators to create power and heat in the microgrid, as well as the most efficient scheduling of the storage system, appropriate load management, and appropriate purchasing and selling from the power grid. This paper used load response algorithms to successfully execute energy management on the microgrid. Load response programs may also refer to the execution of activities that lead to a decrease in peak demand in the short term and are recommended for a short period. These kinds of activities might be considered part of short-term load reduction. The two main types of demand response programs based on incentives and time-based programs are the two main types of demand response programs1.

There has been an increase in the influence of thermal and electrical energy sources in the form of distributed generation sources in microgrids, which has led to the development of ways that have been proposed to gather these sources for a variety of purposes. In order for such networks to be commercially feasible, there needs to be favourable financial incentives for investment in the restructuring sector. Consequently, the best use of electrical or thermal sources, storage devices, and microgrids should be planned so that an acceptable case for investment can be made. Customers’ patterns of electricity consumption are altered by energy management. To obtain the ideal consumption curve, this modification is made. It lowers the cost of operation and planning by utilising energy management, reducing consumption over time, in addition to the proper load curve. The Energy Management System (EMS) is used to make decisions about the best way to use the units that generate heat and electricity in the microgrid; the ideal time to schedule the storage system; effective load management; and appropriate purchases and sales from the power grid. The response programme with real-time pricing is utilised to implement energy management in the microgrid. One of the most popular time-varying tariff programmes is changing power rates throughout various hours. This strategy encourages customers to improve their electricity consumption patterns (consumption during off-peak hours and a reduction in consumption during peak hours). It is evident that the majority of customers do not have the time or resources necessary to react to these sudden adjustments. As a result, it would seem more sensible to use different times throughout the day to apply different electricity pricing to this group of customers. In the TOU approach, different rates are assigned to various times of the day to establish the power tariff. The average cost of power generation and transmission throughout the course of each time period is typically assumed to be this tariff. The TOU tariff is typically established several months or years in advance and typically changes from one time period to another within a day or season to season2,3,4,5,6,7,8,9,10,11,12.

The more precise management of energy and storage resources inside microgrids is one of their key challenges and also helps to enhance the performance of the power system and its behaviour in both technical and economic aspects, which in turn necessitates the development of flexible control approaches. In the field of distributed generation resource management in microgrids, many studies have been done, and the papers in this section align with this paper’s goals.

Before moving on to the design and operation of microgrids in the short term, it is important to first address the structure of operation and control of microgrids, which are responsible for the functioning of these networks. The idea of numerous microgrids allows for the definition of distribution networks that include resources such as low voltage microgrids, larger dispersed generating sources, and a collection of interruptible and non-interruptible loads. In13, examining several approaches to modeling and energy management in microgrids has been addressed. This paper provides a summary of the research that has been carried out in the area of these particular kinds of microgrids. A microgrid with high dependability has been created with the use of a predictive model, as described in14. The cost of power generation in a microgrid is another objective that will be worked on during the discussion of this paper. In addition, the approach has been given a practical application for the purpose of optimization in the context of a microgrid2. The planning specific details of a decentralized microgrid are outlined in reference number15. Microgrid planning is modeled in16 in order to optimize the revenue of distributed generation resources. This is accomplished by establishing criteria for buying and selling for each of the resources and loads. In17, strategies for microgrid market involvement and simulation are discussed. In18, a 24-hour plan for the microgrid has been performed, which is based on the multi-factor technique. However, this planning does not take into consideration the link between the microgrid’s operation hours. In19, by considering each microgrid as an operator in multiple microgrids that are separate from the grid, a 24-hour program was developed. The primary goal of the program was to reduce the cost of generation as much as possible by factoring in the cost of turning the units on and off as well as the cost of the load supply that was implemented on the microgrids as a part of the individual. The values that are suitable for the offer on the multiple microgrid market have been derived. The optimization issue for the islanding mode and the one-hour time period is addressed in the reference13. In20, a daily planning procedure for optimizing a microgrid in islanding mode is provided. This procedure does not include any communication between the various hours of the planning procedure. In2, in addition to maximizing the income of generation resources from energy sales and economic studies, tuning has been implemented in the microgrid with the goals of reducing pollution and being in line with environmental goals. This optimization has been carried out with the intention of achieving both of these goals. The objective function is minimized in21 by taking into account the costs of generation, the costs of pollution, and the costs of operation and maintenance. In this particular microgrid, the method for providing the load by internal sources—including the battery, which is also represented in this approach—is the foundation upon which it is founded. In the paper referred to as18, the author used linear programming in order to effectively operate a residential microgrid and analyze the economic efficiency of using a microgrid in a building. Additionally, assess the environmental impact of utilizing a microgrid. In22, the energy management of distributed generation resources was conducted when hydrogen storage devices were present. A probabilistic model is taken into consideration for each source and load in this reference. Afterwards, self-adaptive meta-heuristic algorithms for charge search were used to conduct optimization. According to the findings, the performance of this algorithm is superior to that of the algorithm for particle assembly. The management of energy for fuel cells in a sampling system is the subject of research presented in23. To reach this goal, research has been done that takes into account the normal distribution function for the fuel cell’s output power.

According to the findings of the research that was carried out in this area, the energy management system for a microgrid operating in islanding mode was explored in24. In order to effectively manage energy, the Predictive Control Model (MPC) approach is used throughout this paper. This method first controls the network’s frequency and voltage in order to make an accurate prediction of the amount of active and reactive power that the network consumes and then puts the management system into operation. Throughout this paper, the subject of energy management is broken down into its component parts, which are the location of the units and the equitable distribution of the load. They proposed an energy management system for a microgrid that used responsive loads in conjunction with a distributed storage system in25. According to the information presented in this paper, an energy management system of multi-agent systems (MAS) that also incorporates responsive loads and storage devices was successful in lowering the amount of demand that occurred during the peak period while also lowering the costs of the system in the state that is connected to the grid. Recent studies have focused on intelligent energy management and optimization in microgrids using advanced metaheuristic and mixed-integer linear programming approaches26,27,28. These methods aim to minimize operational costs, reduce carbon emissions, optimize real-time energy scheduling, and enhance user comfort, demonstrating the applicability of AI-based and smart energy management systems in both residential and commercial microgrid scenarios. Incorporating these approaches highlights the relevance and contribution of the proposed BBO-based energy management strategy under real-time pricing conditions. To better illustrate the context of our research and the differences between previous works and our contribution, Table 1 summarizes the key characteristics of the most relevant studies in the literature and compares them with the present work.

The primary motivation for this research arises from the increasing penetration of distributed generation units and storage systems in modern microgrids, which introduces operational and economic challenges. Effective scheduling of these resources is critical to minimize operating costs while maintaining reliability. Additionally, real-time pricing programs significantly influence consumer behavior and energy consumption patterns, making them a key component of future smart grids. However, the complexity of optimizing both electrical and thermal energy resources under such dynamic pricing conditions requires advanced techniques beyond conventional optimization methods. In this context, metaheuristic approaches such as Biogeography-Based Optimization (BBO) provide a robust solution due to their capability to handle nonlinear, multi-objective, and constrained optimization problems. Therefore, this work aims to address the gap in existing literature by proposing an optimal energy management strategy for microgrids using BBO under real-time pricing, considering both electrical and thermal energy sources, storage systems, and demand response programs.

Table 1 Summary and comparison of previous works with the proposed approach.
Full size table

In this study, the optimal utilization of distributed generation sources in a microgrid was investigated using Biogeography-Based Optimization (BBO). The microgrid utilized a diesel generator, solar panels, and a combined heat and power unit (CHP) as sources of electric power generation, as well as boilers and CHPs as sources of heat generation, with the goal of reducing costs. The construction of general microgrids will take place and to achieve the goal of minimizing overall system costs, the algorithm should select the capacity for energy generation by sources that is the most appropriate given the amount of electrical and thermal energy that is requested each hour by subscribers as well as the price of energy at that particular hour.

This paper is broken up into six sections for your convenience. In the second section, the microgrid model that was investigated is described. The third section discusses the problem’s constraints and its objective function. In the fourth portion, the Biogeography-Based Optimization, sometimes known as the BBO, is discussed. Discussion of the findings of data analysis and simulations takes place in the fifth segment. In the sixth part of this essay, which is also the conclusion, the results and ideas are finally given.

The model of studied microgrid

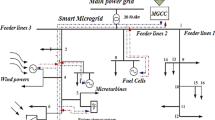
The microgrid that was investigated consists of a number of dispersed sources of thermal and electrical generation in addition to a storage device. This microgrid is linked to the power network electricity grid and has the capability to exchange electrical energy with the electricity network. A perspective of the network that was investigated can be shown in Fig. 1. Distributed electrical generating sources were used in the microgrid that was under investigation. Some examples of these sources are solar panels, diesel generators with battery storage, and boiler thermal sources with thermal storage. A combined heat and power (CHP) system is also used in this microgrid to make both heat and electricity at the same time.

Fig. 1
figure 1

The studied microgrid adapted from29.

Full size image

The lines that represent the channels for the transmission of heat are shown in red, while the lines that represent the channels for the transfer of electric energy are shown in black. In addition to that, the information flow from the sources to the control center is represented by a blue dashed line in the diagram as well. The next topic to discuss is the quantity of solar radiation, which can be seen in Fig. 2.

Fig. 2
figure 2

The quantity of solar radiation adapted from29.

Full size image

As can be seen in Fig. 2, solar panels have the potential to harvest sunlight from 7:00 in the morning until 8:00 at night, during which time they might be utilized to generate electricity from the sun. The most energy that can be gathered from the sun is 850 watts per square meter. The quantity of electrical energy that was required to meet the needs of subscribers for one full day of research is shown in Fig. 3.

Fig. 3
figure 3

The quantity of electrical power adapted from29.

Full size image

As can be seen in Fig. 3, the peak demand for electrical energy occurs at about 2700 kW at 9:00 p.m., while the lowest demand occurs at around 110 kW at 3:00 p.m. The quantity of thermal energy that has to be supplied by the microgrid during the course of the research is seen in Fig. 4.

Fig. 4
figure 4

The quantity of thermal energy adapted from29.

Full size image

The quantity of required thermal energy peaked at 1500 kilowatts at 21:00 and dropped to a low of 850 kilowatts at 3:00 in the morning. Both of these peaks occurred on the same day. Following that, the price of energy on the market during the first 24 h of the research is shown in Fig. 5. Within this particular microgrid, the least expensive electricity is around 6 cents per kilowatt and the highest price is approximately 13 cents per kilowatt. To encourage subscribers to reduce their energy consumption during peak consumption hours and delay it until low load hours, the price of energy is increased during peak consumption hours and decreased during low load hours. This encourages subscribers to reduce their consumption during peak consumption hours.

Fig. 5
figure 5

The current market price of electricity.

Full size image

Objective function and constraints

Regarding the subject of load response, the goal function that has been decided upon is the operating cost. The suggested function, which has been stated in the form of an Eq. (1), is intended to optimally use the microgrid that has been analyzed29.

$$\sum\limits_{{t = 1}}^{{24}} {(\sum\limits_{{i = 1}}^{G} {(C_{{LDG}}^{{i,t}} + SC_{{LDG}}^{{i,t}} ) + P_{{LG}}^{{i,t}} \times \rho _{{LG}}^{t} } } + \sum\limits_{{j = 1}}^{n} {C_{{CHP}}^{{j,t}} + C_{{SPL}}^{t} )}$$
(1)

In the aforementioned equation \(C_{{CHP}}^{{j,t}}\)and \(C_{{SPL}}^{t}\)is the cost of CHP electrical and thermal power, \(P_{{LG}}^{{i,t}}\) the power sought by subscribers and \(C_{{LDG}}^{{i,t}}\)is the cost of DGs. The target function specifies the operational expenses that should be reduced throughout the planning horizon. Based on this equation, the operator’s expenses are equal to the entire cost of generation (total variable cost, start-up cost) and the cost of executing load response programs. The constraints on the issue are29:

Power balance condition

The total power of all generation units must be sufficient to fulfil the load that is being demanded. When generation units are linked to the grid, the quantity of electricity bought and sold is added to the total amount of power available to provide the load.

$$P_{e}^{{Demand}} (t) + P_{e}^{{ch\arg e}} (t) = P_{e}^{{Net}} (t) + \sum\limits_{{i = 1}}^{{N_{{DG}} }} {P_{e}^{{DG}} (i,t)} + P_{e}^{{dch\arg e}} (t)$$
(2)
$$P_{e}^{{Demand}} (t) + P_{e}^{{ch\arg e}} (t) = P_{e}^{{Net}} (t) + \sum\limits_{{i = 1}}^{{N_{{DG}} }} {P_{e}^{{DG}} (i,t)} + P_{e}^{{dch\arg e}} (t)$$
(3)

which in the above relations\(P_{e}^{{Demand}}(t)\) and\(P_{{th}}^{{Demand}}(t)\)is the electrical and thermal powers requested by the subscribers, \(P_{e}^{{ch\arg e}}(t)\)and\(P_{e}^{{dch\arg e}}(t)\)is the charging and discharging powers of the electric cars, \(P_{e}^{{DG}}(i,t)\) is the electrical power of distributing products generation in hour t and\(P_{e}^{{Net}}(t)\)is the power exchanged with the network.

Constraints of minimum and maximum generation

The capacity of distributed generation is also restricted, and each generation unit that makes up the micro network has its own set of constraints for how it should be run. One of these restrictions is the maximum and lowest generation levels that are technically acceptable for each generator, which are determined by the manufacturer.

$$P_{e}^{{Min}} (i) \le P_{e}^{{DG}} (i,t) \le P_{e}^{{Max}} (i)$$
(4)
$$P_{{th}}^{{Min}} (j) \le P_{{th}}^{{DG}} (j,t) \le P_{{th}}^{{Max}} (j)$$
(5)

Binary constraints of on-off mode

On or off mode represents a range of output generation. Distributed generation always has to pay a start-up cost whenever it makes electricity. This is because of this limitation as well as the minimum and maximum generation constraints.

Biogeography-based optimization algorithm

An evolutionary algorithm based on the population of animals in a certain geographic habitat is called Biogeography-Based Optimization (BBO). This algorithm was developed based on the occurrence of animal migration to various habitats. In general, habitats that are suitable places for geographical species to settle have a High Suitable Index (HIS). The residential characteristics known as the Suitability Index Variable (SIV) are used to calculate this index. There are species that move to surround habitats from environments with a high habitat suitability index30.

Weak migration occurs in high-HSI habitats, which are already filled by other species and so can’t take in anymore. On the other hand, because of their tiny populations, ecosystems with low HSI have a high rate of migration. Because the appropriateness of a location is related to its geographical variety, the migration of new species to habitats with lower HSI might enhance the HSI of that region. Evolving algorithms, such as genetics, function by creating an initial population and then using specific operators like combination and mutation in them to generate a better population or an answer that is more correct. The difference between the original population and the population maintained at the preservation rate is equal to the number of the new population. Therefore, the two operators of migration and mutation are utilized in the biogeography algorithm to produce advantageous changes in the generation process of the population of generations or replies. The HIS biogeography optimization algorithm’s fitting function evaluates these responses.

Migration operator

Following the creation of the initial answers, techniques are employed to identify their categorization and desirability. Strong replies with low HSI indicate a habitat with few species, whereas favourable answers with high HSI indicate a habitat with numerous species. The migration rate (λ) and migration rate (µ) for each habitat in the biogeography optimization method are determined using the following relations to probabilistically distribute information across the used solutions.

$$\lambda _{i} = I\left( {1 - \frac{{k(i)}}{n}} \right)$$
(6)
$$\mu _{i} = E\left( {\frac{{k(i)}}{n}} \right)$$
(7)

where I and E are the maximum values of migration rate and emigration that the responses may have, and k(i) is the number of species in the i-th habitat. This number falls somewhere in the range between 1 and n. Additionally, the number of people in the population is denoted by the letter n. With a given degree of probability, each response may be used to alter the outcome of another. When a response is chosen for change, its migration rate (λ) is examined to see whether any of the SIVs that are provided for the response need to be adjusted. Once a SIV in response Si is chosen for modification, using the migration rate (µ) in a probabilistic manner, The appropriate responses are determined based on the migration of a randomly chosen SIV to The answer Si. Once this decision has been made, a SIV in response Si will be modified.

Mutation

The HSI value of a habitat is susceptible to change if there is a sudden shift. In addition to this, they are capable of upsetting the natural equilibrium of the number of species present. In the BBO, this is portrayed as a mutation caused by the SIV30. The pace at which mutations occur may be calculated based on the chance that a certain ecosystem will have a certain number of species.

$$m_{g} = m_{{\max }} \left( {1 - \frac{{P_{g} }}{{P_{{\max }} }}} \right)$$
(8)

where mmax refers to the highest possible value of the mutation rate that the user might choose to implement. Ps is the chance that there are precisely s different species in the environment. This trend of mutation leads to more genetic diversity in the population as a whole.

Figure  6 presents the steps involved in using the biogeography algorithm to find a solution to the issue of energy management .

Fig. 6
figure 6

A flowchart of the biogeography algorithm to tackle the issue of energy management.

Full size image

To illustrate the working mechanism of the proposed Biogeography-Based Optimization (BBO) algorithm, consider a simplified example of a microgrid with three components: a diesel generator, a CHP unit, and a battery storage system. During an iteration, the algorithm generates candidate solutions (habitats), each representing a possible scheduling plan for the 24-hour horizon. For instance, one candidate may allocate higher generation from the diesel unit during low price hours and store surplus energy in the battery for peak hours, while another candidate prioritizes CHP operation due to its combined heat and power advantage. The suitability index (SI) of each habitat is then calculated based on the total operational cost. Habitats with lower cost values share features with others through migration, improving overall population quality until the optimal scheduling plan is achieved. This example demonstrates how BBO dynamically balances power generation, storage, and grid interaction under real-time pricing signals.

Simulation and analysis of results

This section of the paper will offer appropriate software for the best usage of distributed generating sources as well as electrical and thermal storage in the microgrid based on real-time pricing. In order to accomplish this goal, the example microgrid that was presented in the second part was chosen to serve as a sample network. Within this network, an energy management strategy that prioritized cost reduction was applied to the administration of electrical and thermal resources and storage. An optimization technique based on biogeography has been utilized for the purpose of energy management in microgrids. This method takes into account the limitations of the issue and locates the ideal values for the variables in such a manner as to reduce the amount of money spent on the microgrid. A comparison has been performed between the outcomes of the biogeography algorithm and the genetic algorithm in order to validate the findings of the simulation. This was done in order to establish the accuracy of the findings (GA). The Table 2 provides information on the algorithms for biogeography and genetics algorithms.

Table 2 Parameters of biogeography and genetic algorithms.
Full size table

All simulations were conducted in MATLAB R2023a on a system with Intel Core i7 (3.2 GHz), 16 GB RAM, Windows 11. The BBO and GA algorithms were configured with population size = 50 and 200 iterations. The simulation covered a 24-hour horizon (1-hour steps) using real-time pricing and benchmark load profiles.

Research has been carried out using all three of these potential outcomes. When performing energy management on thermal sources and storages in the first scenario, load response planning is not taken into account; however, when performing energy management on electrical sources and storage in the second scenario, load response planning is taken into account. In the third and final scenario, energy management in the microgrid has been done concurrently for both electrical and thermal sources and storage.

In order to evaluate the performance of the proposed optimization algorithm and to reflect realistic operational conditions of a microgrid, three practical scenarios were developed. These scenarios were designed based on typical operating strategies observed in microgrids:

  • Scenario 1: Energy management applied only to electrical resources (diesel generator, solar panels, battery storage, and CHP in electrical mode), with thermal demand fully supplied by boilers without constraints.

  • Scenario 2: Energy management applied only to thermal resources (boilers, thermal storage, and CHP in thermal mode), with electrical demand supplied entirely by the grid.

  • cenario 3: Simultaneous energy management of both electrical and thermal resources, including CHP, boilers, solar panels, diesel generators, battery storage, and thermal storage.

These scenarios were selected because they represent common operational configurations of microgrids in practice and allow us to assess the incremental benefits of integrated management. The optimization algorithm evaluates all feasible scheduling combinations for the available components in each scenario, considering unit capacity limits, charging/discharging constraints of storage systems, and binary on/off states for generation units. The optimal profile for each scenario is determined by minimizing the total operating cost defined in the objective function (Sect. 2), while ensuring power and heat balance constraints. The matching of the best profiles is performed by comparing the cost of all feasible solutions, and the configuration with the lowest cost is selected as the optimal plan for that scenario.

The first scenario (energy management of electric resources)

In the first phase of the simulations, energy management of electrical resources and storage in the microgrid has been done by taking into consideration the load response program. This was done in order to reduce operational costs by utilizing genetic and biogeography algorithms. Therefore, it is assumed that there is no control over the heat sources, and that the boiler supplies the needed amount of thermal energy to the customers without any limits. The combined heat and power plant (CHP) simply generates electrical energy. Additionally, there is no capacity for the storage of thermal energy inside the system. The process of two algorithms converging is seen in Fig. 7, which is part of the optimization process.

Fig. 7
figure 7

The convergence of optimization techniques in electric resource management.

Full size image

The cost of energy supply without taking into account the load response program was approximately 2673 dollars, which, after optimization by the proposed Biogeography-Based Optimization (BBO), was 1862 dollars, and if the cost of the microgrid in the case of planning the power of electric resources by the genetic algorithm GA) was equal to 1934 dollars, then the total cost of energy supply was approximately 2673 dollars. After 25 rounds, the BBO algorithm arrived at its ultimate value, whereas the genetic algorithm required 28 iterations before arriving at its end. If there is a reduced amount of cost for the management approach of the BBO algorithm, then this algorithm will have a greater level of accuracy and efficiency. Figure 8 shows how much electricity was made by a diesel generator, a combined heat and power plant (CHP), a solar panel, and a battery storage over the course of 24 h of research after the BBO and GA algorithms had been used to optimize the system.

Fig. 8
figure 8

The percentage of the microgrid’s electrical resources that are used to meet the system’s demand for energy (a) GA (b) BBO.

Full size image

The above chart makes it perfectly evident that the majority of battery storage occurred between the hours of 1 and 6 in the morning, while the majority of battery discharge occurred between the hours of 7 and 9 in the evening. In the load response program, batteries play a significant part in both the movement of loads and the reduction of expenses.

The quantity of electrical energy that was traded with the power network electricity network during the time period that was under consideration is shown in Fig. 9. The presence of distributed electric sources has resulted in the amount of electric energy received from the network becoming negative during certain hours when the price of electric energy is high; consequently, these results have an impact on the sale of electricity. This phenomenon is illustrated in the figure below. The microgrid operator has been able to generate a sufficient profit from the sale of electrical energy during the hours of high power prices, which has allowed them to keep the cost of energy supply in the microgrid to a minimum. For instance, owing to the sale of electrical energy, it has resulted in a profit of around 48.3 dollars at ten o’clock in the morning.

Fig. 9
figure 9

The amount of electricity that is traded with the power network natgrid.

Full size image

The quantity of thermal energy that the boiler generates is seen in Fig. 10.

Fig. 10
figure 10

The boiler’s output of thermal energy.

Full size image

It is important to note that since there is insufficient management of thermal resources, the quantity of thermal energy that is generated by the boiler is identical to the amount of thermal energy that is needed by the customers.

The second scenario (energy management of heat sources)

In the second scenario, as opposed to the first, the only energy management that has been done is on thermal sources, and the electricity that the subscribers need is totally provided by the power network, based on their demands. This is in contrast to the first scenario. Through careful planning of the electricity coming from thermal sources, the objective here is to reduce the cost of supplying energy to the microgrid to the absolute minimum. When the CHP system is operating in thermal mode, it will not generate any electrical energy. As a consequence of this, the resources for combined heat and power (CHP) and boilers, in addition to thermal storage, are accountable for the provision of the necessary thermal energy, and energy management is performed on these resources. In the same way that the OL scenario was employed, two algorithms based on biogeography and genetics were used for the management of resource energy. Figure 11 shows how the BBO and GA algorithms come together during the process of optimizing and managing the way the microgrid’s thermal resources use energy.

Fig. 11
figure 11

The convergence of optimization methods in heat resource management.

Full size image

In the case of the cost of planning the power of thermal resources using the GA algorithm, it is equal to 2234 dollars; after optimizing and managing thermal energy using the BBO algorithm, the cost of supplying energy to the microgrid was calculated to be 2185 dollars, and it was equal to 2234 dollars after using the BBO algorithm. The convergence of the algorithms is such that the BBO method achieves its final value after 30 iterations and the GA algorithm receives its final value after 23 iterations. When compared to the GA algorithm, the BBO algorithm’s management strategy results in a much lower cost for the provision of energy in this situation. This was also the case in the scenario that came before it. The quantity of power generated by the boiler and CHP as well as the heat storage, including during optimization using BBO and GA algorithms, is given in Fig. 12. This data was collected over the time period of the research.

Fig. 12
figure 12

The contribution of various heat sources toward meeting the microgrid’s need for available energy (a) GA (b) BBO.

Full size image

The Fig. 12 indicates that there is energy storage when the thermal storage power has a negative value. According to the findings that were acquired for this figure, during the early hours of the day, when the demand for thermal energy is lower, energy is stored in devices so that it may be utilized during the times of the day when demand is at its highest (8 to 11 and 18 to 20). Because of this, it will be possible to greatly cut down on the cost of supplying electricity during peak times. because there is no need for sources of more expensive combined heat and power and boilers to provide thermal energy. As a consequence of this, the cost of obtaining energy will be decreased if an appropriate program is developed. Figure 13 shows how much electricity was used from the power network network in one day of research, shows how much energy was used.

Fig. 13
figure 13

The received electrical energy from the national grid.

Full size image

Because the microgrid does not make use of any sources of distributed electrical generation, the entire amount of electrical energy that is required by the customers is obtained from the power network grid. As a result, the price of energy supply in the microgrid has risen as a direct result of this situation, especially between the hours of 17:00 and 22:00, when there are no distributed generation sources that can help the grid supply some of the electricity, and the price of electricity is at its highest due to an increase in the amount of electricity that is being consumed and there is no way to lower it.

The third scenario (energy management of electrical and thermal resources)

It is vital to carry out the load response program, taking into consideration the thermal and electrical sources at the same time, in order to reduce the cost of supplying energy in microgrids as much as possible. because the contributions that thermal and electrical terms make to the total cost of the microgrid are almost equivalent to one another. For the third possible outcome, biogeography and genetics algorithms have been used to control the thermal and electrical resources in the Tuaman microgrid for the purpose of energy management. The energy management of a diesel generator, solar panels, and battery storage as electrical sources, a boiler and thermal storage as distributed thermal generation sources, and ultimately, a combined heat and power unit as a thermal and electrical source in the microgrid has been completed. The process of convergence of BBO and GA algorithms in the process of solving the problem of optimal energy management of electrical and thermal resources in the microgrid is displayed in Fig. 14. During the process of finding the best way to manage energy in the microgrid, this step is taken.

Fig. 14
figure 14

Algorithm convergence in electrical and thermal resource management.

Full size image

The cost of the microgrid is calculated to be 1637 dollars after optimal management of thermal and electrical energy by the BBO algorithm, whereas in the case of optimal management of resource energy by the GA algorithm, the cost is equal to 1683 dollars. The BBO algorithm and the GA algorithm both manage energy resources optimally. Both the BBO and GA algorithms reached their minimal value after 31 and 24 rounds, respectively. When compared to the GA algorithm, the fact that the suggested BBO algorithm results in lower costs for the provision of energy in the case of planning is validation of the preference for and superiority of this technique. In the continuation of the simulation process, the amount of power produced by electric sources is shown in Fig. 15, and the amount of power produced by thermal sources is shown in Fig. 16 which is over the course of one day and night, and in the event that optimization is performed using BBO and GA algorithms, respectively. These figures are shown in the case where BBO and GA algorithms are used.

Fig. 15
figure 15

The percentage of the microgrid’s electrical sources that contribute to meeting the system’s need for energy (a) GA (b) BBO.

Full size image
Fig. 16
figure 16

The contribution of heat resources toward meeting the microgrid’s need for available energy (a) GA (b) BBO.

Full size image

The storage of energy is dependent on the early morning hours of the day and the low cost of power in the microgrid, just as it was in the previous two scenarios. This is because of the need to limit the expenses associated with the supply of energy in the microgrid. In these hours, the storage generators store electrical and thermal energy at their full capacity in order to be able to handle the load during peak consumption hours and high energy costs on the market. This allows the storage generators to be accountable for the load. Other electrical and thermal sources also take up a portion of the energy that customers need, and the amount that they use is proportional to the expenses as well as the cost of energy on an hourly basis. The quantity of electrical energy that was exchanged with the national power network over the course of one day is shown graphically in Fig. 17. The first possibility that comes to mind for you is to purchase more electric energy in the early morning hours of the day in order to charge the batteries. This will allow you to make a profit from the sale of the stored electric energy during the more costly hours of the day.

Fig. 17
figure 17

The amount of electricity that is traded with the power network.

Full size image

The findings shown in Fig. 17 are virtually identical to those shown in Fig. 9, but there are some minor differences. The combined heat and power system’s ability to provide both electrical and thermal energy is the reason behind this.

Comparison and discussion

Following optimization in the form of three different scenarios, the values of the costs associated with the supply of thermal and electrical energy have been determined in the section, and they are shown in Fig. 18. The cost of electricity, the cost of thermal energy, and the overall cost, which is the sum of the two individual costs, are all shown in this figure in their own respective columns.

Fig. 18
figure 18

The cost of providing thermal and electric energy to each scenario.

Full size image

In the first scenario, as was to be anticipated, the cost of thermal energy accounted for a substantial portion of the overall cost of energy supply in the microgrid, whereas in the second scenario, the cost of electrical energy accounted for a considerable share of that cost. Because in the first situation, the thermal resources have not been subjected to any management, and in the second scenario, the electric resources have not been subjected to any management. The third scenario, in which energy management of thermal and electric sources is done concurrently, results in the lowest cost. This is also where the lowest cost is reached. Following the implementation of the suggested BBO algorithm for optimum energy management, the total cost of energy has been cut by 30% in the first scenario and by 18.2% in the second scenario. These results compare to the original situation. But the total cost of energy supply in the microgrid is cut by 38.7% when simultaneous resource management is done by adopting a load response strategy. Therefore, carrying out simultaneous management is the best course of action to take in order to achieve the lowest possible cost of energy supply in the microgrid. The outcomes of the simulation are presented in Table 3.

Table 3 Comparison of simulation results in three scenarios.
Full size table

To evaluate the performance of the proposed BBO algorithm, it was compared to the widely used Genetic Algorithm (GA) under identical microgrid conditions and real-time pricing scenarios. The comparison focused on three main metrics: total operational cost, convergence speed (iterations to reach optimal solution), and computation time. The results are summarized in Table 4. Table 4 demonstrates the comparative performance of the proposed BBO algorithm against GA for all three scenarios. BBO consistently achieves a lower total operational cost: 3.7% reduction in Scenario 1, 2.2% in Scenario 2, and 2.7% in Scenario 3. Regarding convergence, BBO generally requires fewer iterations or similar iterations compared to GA, reflecting its efficient search mechanism and balanced exploration-exploitation strategy. Computational times of BBO are slightly lower or comparable, demonstrating that the algorithm is computationally efficient even when handling multiple scenarios with complex resource interactions. Overall, these results confirm that BBO provides both cost-effective and efficient solutions for microgrid energy management under real-time pricing, outperforming GA across all metrics.

Table 4 Comparative performance of BBO and GA across three scenarios.
Full size table

To position our findings against recent approaches, Table 5 summarizes methodological features and reported foci of representative studies alongside our work. The comparison spans optimization method, pricing paradigm, treated resources, demand response (DR), storage modeling, and key takeaways. We then contrast our quantitative outcomes versus the GA baseline under identical settings.

Table 5 Comparison of this work with representative recent studies.
Full size table

Under identical constraints, data, and RTP signals:

  • Scenario 1 (Electrical resources only): BBO reduces total cost from $1,934 (GA) to $1,862, a 3.7% improvement; converges in 25 vs. 28 iterations.

  • Scenario 2 (Thermal resources only): BBO reduces total cost from $2,234 (GA) to $2,185, a 2.2% improvement; converges in 30 vs. 23 iterations with comparable computation time.

  • Scenario 3 (Electrical + Thermal): BBO reduces total cost from $1,683 (GA) to $1,637, a 2.7% improvement; converges in 31 vs. 24 iterations and achieves the lowest absolute cost overall.

These head-to-head results indicate that BBO consistently attains lower operational cost than GA for all three practical operating regimes. When viewed against the broader literature (Table 5), our contribution is distinct in: Simultaneous electrical–thermal coordination with RTP-driven DR, Explicit storage arbitrage across inter-hour dynamics, and A direct, quantitative BBO vs. GA comparison under the same Micro Grid configuration.

Conclusion

It was determined that the load response program in microgrids should be one of the primary programs for optimizing the usage of energy resources in these systems. These projects lost their efficacy as a result of a lack of cooperation with the market after the reorganization of the electricity systems. But after many decades had passed, in response to issues such as price instability and the reintroduction of demand control programs, they were used once again. This time, the load response algorithms were designed in a way that was compatible with the management structure of the reconstructed power system. It is important to note that load response programs are a significant component of demand management programs. This is due to the fact that the characteristics of these programs make them exceptionally well-suited for adjusting to the newly implemented power system management structure. In today’s world, load response programs are being looked at as a possible answer to some of the issues that are plaguing microgrids. Due to the fact that thermal and electrical resources inside the microgrid need simultaneous management.

In this study, biogeographical algorithms and genetic algorithms were used to achieve optimal utilization of distributed generation resources, electrical and thermal storage in the microgrid based on real-time pricing. This was done with the intention of lowering the cost of energy supply in the microgrid. Distributed electrical generating sources were used in the microgrid that was under investigation. These include solar panels, diesel generators with battery storage, and boiler heat sources that utilize thermal storage. In addition, a combined heat and power (CHP) system was used in this microgrid in order to generate both heat and electrical energy at the same time. Without taking into account the cost of the load response program, the cost of the energy supply was around 2673 dollars. Research was carried out using all three of these different settings. In the first scenario, load response planning is not taken into consideration when doing energy management on thermal sources and storages. However, in the second scenario, the load response plan is taken into consideration when performing energy management on electrical sources and storages. In the third and final scenario, energy management in the microgrid has been done concurrently for both electrical and thermal sources and storage.

In the first part of the simulations, the energy management of the microgrid’s electrical sources and storage was carried out by taking into consideration the load response program using the GA algorithm and the BBO algorithm. However, the heat sources were not subject to any form of control during this phase. Following optimization in the amount of 1862 dollars by the suggested Biogeography-Based Optimization (BBO), and assuming that the cost of the microgrid in the case of planning the power of electric resources by the genetic algorithm (GA) is equal to 1934 dollars, the findings of the simulation presented in this section suggest that batteries provide a significant contribution to the load response program by both shifting the load and lowering the associated expenses. Additionally, the availability of distributed electrical sources permitted some electrical energy to be sold to the national grid during certain hours when the price of electrical energy was high. This resulted in some revenue for the power network. The microgrid operator has racked up a substantial profit thanks to the valuable sale of power during peak demand times. In the first scenario, the total cost of energy went down by about 30% when the BBO algorithm was used to manage energy well. This was compared to the basic situation.This reduction was achieved in the first scenario.

The second portion of the simulations consisted of performing energy management on thermal sources, while the national network supplied the electrical energy that the customers required. After optimization using the BBO algorithm, the cost of energy supply in the microgrid was brought down to 2185 dollars, while the cost of planning the power of thermal resources was brought down to 2234 dollars by the GA algorithm. Both of these numbers reflect a reduction in cost. In this particular case, thermal storage devices were crucial in contributing to the overall cost savings. Because there was no longer a need for forms of thermal energy generation that had greater upfront costs, such as CHP and boilers. On the other hand, since the microgrid does not make use of decentralized electrical generating sources, all of the electrical energy that is required by the customers is supplied by the power network. As a result, the price of energy supply in the microgrid has increased. In the second scenario, the overall cost of energy has gone down by 18.2% because of good energy management using the BBO algorithm that was given. This decrease is measured in comparison to the parameters that were used in the first scenario.

In the third and final scenario, the load response program was carried out simultaneously considering thermal and electrical sources. This was done in order to reduce the cost of energy supply in the target microgrids as much as possible. Both genetics and biogeography were used as algorithms in this scenario, just as they were in the two situations that came before it. After the optimum management of thermal and electric energy by the BBO algorithm, the cost of energy supply in the microgrid was reduced to 1637 dollars. However, in the case of the optimal management of resource energy by the GA algorithm, the cost of energy supply was reduced to 1683 dollars. The storing of thermal and electrical energy was delayed until times when the price of energy in the microgrid was low. This was done in order to keep the expense of supplying energy to the microgrid to a minimum, as was the case in the previous two scenarios. In order to satisfy the demand during peak hours and high energy costs on the market, the storage generators stored electrical and thermal energy at their greatest capacity during these hours. This allowed them to fulfill the load during peak hours. When compared to the initial circumstances, the cost of energy has dropped by 38.7% in the third scenario as a result of effective energy management carried out by the BBO algorithm that was provided. So, if you want to get the most energy for the least amount of money in the microgrid, the best thing to do is to use simultaneous management.

However, this study has some limitations that should be acknowledged. First, the proposed model assumes deterministic load and generation profiles, which may not fully capture the uncertainties associated with renewable energy sources and demand fluctuations. Second, the communication delays and cyber-security issues in real-time implementation were not considered in this work. Third, the model focuses on a single microgrid and does not address multi-microgrid coordination or market interactions.

For future research, the integration of uncertainty modeling through stochastic or robust optimization techniques is recommended to improve reliability under variable conditions. Additionally, exploring multi-agent frameworks for managing multiple interconnected microgrids and incorporating cyber-physical security aspects can further enhance the practicality of the proposed approach. Finally, real-world experimental validation using hardware-in-the-loop (HIL) or pilot microgrid setups would strengthen the applicability of the developed optimization method.