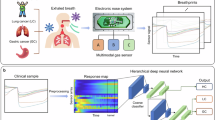
Abstract
Lung cancer is the leading cause of cancer-related mortality worldwide. Lately, electronic nose (e-nose) systems have emerged as a promising method for non-invasive lung cancer detection. These systems, however, have several limitations, including low accuracy rates and long detection times. To address these challenges, we conducted a pilot study involving the development of an affordable e-nose device that can detect more than 30 volatile organic compounds, using twelve metal oxide semiconductor sensors and one chemi-resistive alkane sensor. The device recorded data for 28 healthy controls and 18 lung cancer breath samples that were then analyzed using a multilayer perceptron neural network. The dataset was expanded through a novel use of data augmentation, where Gaussian noise was applied to generate synthetic samples while preserving the original data’s statistical properties. The model was evaluated by 5-fold cross-validation and achieved an accuracy of 96.26%, sensitivity of 92.88%, specificity of 97.75%, and an area under the curve of 0.9286. Our system outperforms existing e-nose detection methods by more than 5% and is capable of classifying in approximately 5 minutes. These findings highlight the potential of this breath analyzer system as a rapid and cost-effective tool for preliminary lung cancer screening.
Similar content being viewed by others
Introduction
Lung cancer is the deadliest form of cancer, accounting for 1 in 5 total cancer deaths1. Despite recent advances in detection, more than 75% of lung cancer patients are diagnosed after stage 3, when treatment options are limited and prognosis is poor2. However, early detection of lung cancer can substantially improve survival outcomes. For patients diagnosed at stage I, the 5-year survival rate can exceed 90%, whereas for those diagnosed at stage IV, the 5-year survival rate drops to 10% or lower3.
Although current lung cancer detection tools have high accuracy, they also have limitations. Low-dose CT (LDCT) scans are the most common, but they require expensive equipment and expose patients to radiation4,5. Additionally, a study conducted by the National Lung Cancer Screening Trial, which involved 53,454 participants, reported LDCT scans had a 96.4% false positive rate for early stages of lung cancer, highlighting another limitation of LDCT scans6. Tissue biopsies remain another standard method for accurate diagnosis, but due to their invasive nature, they carry associated risks7,8,9.
A promising diagnosis method for lung cancer utilizes gas sensors to analyze volatile organic compounds (VOCs) for breath-based detection10,11,12,13. Certain diseases, such as chronic obstructive pulmonary disease (COPD) and pulmonary fibrosis, can alter the composition of VOCs in human breath, allowing them to serve as biomarkers for those diseases14,15,16,17,18. This method is viable for lung cancer as it has a distinct VOC profile that does not overlap with other cancers or diseases19,20,21. This is the effect of the unique processes caused by lung cancer, such as altered protein expression, gene mutations, and the Warburg effect, which is an abnormal reliance of cancer cells on aerobic glycolysis19,20,22. These processes lead to the production of VOC byproducts such as toluene, benzene, and acetone, as well as the alkane VOC subgroup, which serve as analytical markers for detection23,24,25,26.
Currently, the gold standard for breath-based lung cancer detection is the gas chromatography-mass spectrometry (GC-MS)27,28,29,30. However, it is expensive, requires specialized lab equipment to operate, and has a lengthy processing time. Recently, many studies have used small-scale sensor arrays to detect and analyze various VOC compounds present in exhaled breath31,32,33. They show the promise of e-nose systems but are often limited by moderate classification accuracy, typically around 85%34,35. Additionally, some systems described can take up to 40 minutes to process one sample due to feature extraction, preventing them from being used for rapid detection purposes36. Fast results are especially valuable in primary care for screening during routine visits.
This pilot study aims to address these gaps by developing and validating an electronic breath analyzer system for highly accurate, rapid, and non-invasive lung cancer detection. In this pilot study, samples from 46 study participants were collected and analyzed using the constructed device. The dataset was then augmented to 79 samples. The resulting data were then used to train a multilayer perceptron neural network (MLP) to classify samples. Finally, 5-fold cross-validation was used to evaluate the model. Our system can provide results in under 5 minutes, underscoring its potential to serve as a preliminary screening tool to benefit both patients and clinical institutions.
Methods
Study design and population
This pilot study was designed to evaluate the effectiveness of a breath-based device for lung cancer detection. The study population consisted of 46 participants, including 28 healthy controls and 18 patients with a confirmed diagnosis of lung cancer. Data collection was conducted at the Rashtra Sant Tukdoji Regional Cancer Hospital (RSTRCH) in Nagpur, India. All participants provided one breath sample, which was collected in a 1L Tedlar gas sampling bag (CEL Scientific Corp., USA) and sent for analysis in the breath analyzer device37.
This study was approved by the RSTRCH Institutional Ethics Committee and performed in accordance with the Declaration of Helsinki. Written informed consent was obtained for each individual. were informed of the study’s purpose, procedures, and potential risks. The characteristics of the study population are presented in Table 1. The primary outcome measure was to evaluate the model’s accuracy in detecting lung cancer.
Selection of sensors
Based on prior research identifying lung cancer-indicative VOCs, we selected 12 gas sensors to capture a wide breath profile23,24,25,26. The device’s sensor array contains 12 metal oxide semiconductor (MOS) sensors and one chemiresistive alkane sensor. The alkane sensor was fabricated by following the procedures described by Tan et al. (2016)38. First, two copper electrodes were soldered onto a small printed circuit board (PCB) substrate, separated by a small gap. Then, 0.01g of tetracosane was deposited across the gap and melted at 100 degrees Celsius. Subsequently, 0.01g of carbon powder was melted on top of the tetracosane layer at 100 degrees Celsius. This process formed a stable, chemiresistive film that completes the circuit.
Table 2 shows the full list of sensors used in this study and their corresponding VOCs. The sensors primarily target different specific VOCs, with some compound cross-sensitivity. As a result, each sensor outputs a unique electrical resistance value when exposed to the same gas mixture39. This characteristic enables the sensor array to produce a distinct breathprint for control and disease groups, which can be used for analytical purposes40,41.
Design and fabrication of E-nose device
Our system is composed of two main components. The first is an airtight gas reaction chamber containing the sensors described in Table 2 and two fans positioned underneath the sensor plate to remove residual VOCs. Second, an electrical housing chamber holding the Arduino Mega 2560 R3 microcontroller (Arduino S.r.l., Monza, Italy), wiring, and battery that powers the device. The whole device costs approximately $215, with a more detailed cost breakdown shown in Table 3.
After a breath sample is transported inside the gas chamber, sensors react to the gases and output their resistance signals. Signals from the sensors are converted from analog to digital on the Arduino board and are sent to a computer through a universal serial bus (USB), where all time series voltage values are saved in comma-separated value (CSV) files.
In order to collect and read sensor data from the Arduino, we developed a computer program written in Python to decode signals coming from the Arduino and save them into corresponding CSV files for each sample on a computer. An image of our device is shown in Fig. 1.
Exhaled breath sampling process
Patient recruitment excluded those who had smoked or consumed alcohol within the last 24 hours. This was to ensure the patient’s VOC profile was not impacted by substances that could skew results21,42,43.
The sampling process starts with pumping ambient air into the gas chamber at a rate of 0.5-liter/minute, using a gas sampling pump. During this time, baseline calibration sensor readings were recorded for 30 seconds. Then, the patients breath sample is pumped into the airtight gas chamber, where it remains for 30 seconds. During the response phase, sensor readings were recorded at a sampling frequency of approximately 0.97 Hz, yielding 29 data points per sensor. This procedure ensured that sensor responses could be compared against a stable baseline for accurate discrimination.
After data collection, the gas chamber is cleared of the previous sample by opening its lid and turning on the internal fans to expel the air. The chamber is then resealed and filled with nitrogen gas. As an inert gas, nitrogen clears residual VOCs in the sensor cores through inelastic collisions without chemically interacting with the sensor core itself. This cleaning process is essential as it prevents previous breath samples from impacting subsequent readings and ensures a stable sensor baseline reading for consistency and accuracy. The cleaning cycle takes approximately 1 minute, and after this, the device is ready to process the next breath sample. A visual demonstration of this entire process is portrayed in Fig. 2.
System flow of the proposed breath analyzer for lung cancer detection. Exhaled breath samples are collected into a Tedlar bag and introduced into the device with a gas sampling pump. The breath passes through an array of MOS and alkane sensors housed within a gas chamber, where the gas responses are measured.
Data analysis and augmentation
Prior to model training, the resistance data obtained from the sensor array underwent several preprocessing steps: baseline correction, standardization, data augmentation, and dimensionality reduction. Baseline correction was performed by subtracting the mean resistance value recorded during the initial stabilization period from each sensor signal to account for environmental noise. Standardization was then applied to rescale all features to zero mean and unit variance, ensuring comparability across sensors.
Our dataset included 28 healthy and 18 lung cancer samples, which is small relative to the dimensionality of the sensor feature space (12 sensors \(\times\) 29 time points \(= 348\) features per sample). Small-N, high-d settings are susceptible to overfitting and unstable decision boundaries. To improve generalization of the model while retaining class structure, synthetic samples were generated by perturbing existing samples with isotropic Gaussian noise44,45,
This preserves the class mean while inflating variance by \(\sigma _a^2 I_d\), thereby modeling realistic variability without altering class centers. We generated \(m_{\text {LC}} = 35\) synthetic lung cancer samples and \(m_{\text {H}} = 25\) synthetic healthy samples for a final dataset of 53 lung cancer and 79 healthy samples. Only the training set was augmented to keep the test set strictly real. The noise amplitude was fixed at \(\sigma _a = 0.6\) in standardized units. To verify that augmentation did not distort class structure, we performed two complementary checks:
-
1.
Univariate shape preservation: For representative features, we compared kernel density estimates (KDEs) before and after augmentation. In standardized space, augmented curves broaden as expected (variance inflation) while retaining the location and modality of the original distributions (see Fig. 3).
-
2.
Two-sample equivalence testing: For each feature and class, we applied the Mann–Whitney U test between the original and augmented samples. In all cases, the test yielded \(p> 0.05\), indicating no significant difference between the two distributions and confirming that augmentation preserved the core statistical properties (consistent with Ultsch & Lötsch46).
Results
Prior to deep learning-based classification, we analyzed sensor response data from healthy individuals and lung cancer patients. Fig. 4a shows the response of the gas sensor array to exhaled breath from a healthy individual, while Fig. 4b shows the responses to a breath sample from a lung cancer patient.
The two graphs show the responses of the 12 gas sensors, for which sensor-specific details are available in Table 2. Each sensor demonstrated distinct sensitivity profiles but comparable response times, with certain sensors–particularly TGS2620, TGS2602, and MQ135–exhibiting markedly higher responses to the exhaled breath of lung cancer patients. Variance in response and sensitivity was due to the different target VOCs of each gas sensor. This diversity in sensor reactions allowed for a broader breath profile to be captured, resulting in increased availability of information for the machine learning model to use for prediction.
To further examine sensor performance, we performed a progressive backward ablation on the preprocessed 12-sensor matrix, using a stratified 5-fold cross-validation (CV) logistic-regression pipeline on 46 samples. Starting from all 12 sensors, at each step we removed the sensor whose removal yielded the highest CV receiver operating characteristic area under the curve (ROC-AUC). Performance peaked at \(k = 4\) (mean CV AUC \(= 0.9867 \pm 0.0267\)), yielding the minimum-optimal subset \({\textrm{TGS2602}, \textrm{TGS2620}, \textrm{MQ2}, \textrm{MQ135}}\). For interpretability, we computed SHAP values on each CV fold, fitting the scaler and model only on the training data and evaluating SHAP on the held-out test fold to avoid information leakage. Per-sensor SHAP values were summed across all 29 time points and averaged over folds, yielding a robust measure of each sensor’s contribution (Fig. 5). The resulting SHAP ranking (\(\textrm{TGS2602}> \textrm{TGS2620}> \textrm{MQ2}> \textrm{MQ135}\)) aligned closely with the ablation-derived subset, reinforcing the discriminative importance of these four sensors. Sensors such as \(\textrm{MQ9}\) and \(\textrm{MQ6}\), which were removed early in ablation, consistently showed negligible SHAP contributions across folds, indicating functional redundancy despite differences in raw signal profiles.
To examine differences between the healthy and lung cancer sample populations, we applied principal component analysis (PCA) statistical modeling to the dataset. We projected the first two principal components (PC1 and PC2), which explain 66.8% of the total variance. Fig. 6 shows the resulting 2D scatter plot, where each point represents an individual breath sample, colored by class label. The plot shows distinct clustering as the lung cancer samples are generally separated from healthy samples along PC1. While there is some overlap between the two classes in the central region, most of the points are visually separated from each other. This suggests that the variance captured by the first two principal components reflects substantial statistical differences between classes.
A multi-layer perceptron (MLP) model was implemented to classify lung cancer and healthy breath samples using multimodal sensor array resistance data. The model was developed in TensorFlow and trained on a Google Colab environment with GPU acceleration.
Each breath sample was represented as a flattened 348-element vector, corresponding to 29 measurements from each of 12 chemiresistive sensors. The dataset consisted of 28 healthy and 18 lung cancer samples that were collected under controlled conditions. Synthetic sample generation through data augmentation expanded the dataset to 79 healthy and 53 lung cancer samples. Following this process, the data was split such that 70% of both healthy and lung cancer samples were used for training. The remaining 30% of samples were kept for testing. The training set was shuffled and used to train the MLP for 100 epochs with a batch size of 8.
The MLP architecture consisted of three fully connected hidden layers with 128, 64, and 32 neurons, respectively, each followed by ReLU activation, L2 regularization (\(\lambda\) = 0.001), batch normalization, and dropout layers (dropout rate = 0.3) to mitigate overfitting. The final output layer contained a single neuron with sigmoid activation for binary classification. The Adam optimizer was then employed with a learning rate of \(1 \times 10^{-4}\), and binary cross-entropy was used as the loss function.
To justify the choice of classifier, we benchmarked the MLP against other machine learning and deep learning models: Logistic Regression, Random Forest, XGBoost, and a convolutional neural network (CNN). These results can be seen in Table 4. 5-fold cross-validation was used for the evaluation of the models. The MLP delivered the best overall performance (accuracy \(=0.963\); F1 \(=0.956\)) with strong sensitivity and specificity. Logistic Regression, Random Forest, and XGBoost clustered together and were noticeably lower than the MLP across metrics. Despite the clear separation suggested by principal component analysis, linear models (Logistic Regression) did not match the MLP, indicating that non-linear interactions across sensors and time points are informative. The CNN was more competitive with the MLP, but it offered no improvement in overall accuracy or F1 score and showed less stability. Additionally, its added architectural complexity increased the risk of overfitting without any clear benefit. For these reasons, the MLP was chosen as the primary classifier in this study.
Performance evaluation on the test set yielded an area under the ROC curve of 0.9286 (Fig. 7a). From this, the confusion matrix (Fig. 7b) demonstrated the model’s reliability, with only one false positive and one false negative on the test set. This corresponded to a sensitivity of 92.88% and a specificity of 97.75%, with an overall classification accuracy of 96.26%. The detailed cross-validation performance metrics are shown in Fig. 7c.
(a) Receiver operating characteristic (ROC) curve of the model, with an area under the curve (AUC) of 0.9286; (b) Confusion matrix of classification results showing correct predictions for healthy and cancer classes; (c) The performance metrics of the MLP model for classification of lung cancer patients and controls. All values are the averages of the results from 5-fold cross-validation.
Discussion
This pilot study demonstrates that an efficient breath analyzer combined with an MLP can accurately distinguish between lung cancer patients and healthy controls. The device achieved a mean area under the ROC curve (AUC) of 0.9286, an accuracy of 96.26%, a sensitivity of 92.88%, and a specificity of 97.75%. The high sensitivity and specificity signify the accuracy and precision in detecting lung cancer using this device. These performance metrics highlight the device’s potential as a rapid, non-invasive screening tool that could facilitate early detection, improve clinical outcomes by enabling timely intervention, and aid in primary care screening.
The device performance is competitive with existing multimodal sensor-based systems. Previous studies show accuracy rates between 85% to 92%. For example, Li et al. (2019) achieved 91.6% accuracy and Ozsandikcioglu et al. (2020) achieved a classification accuracy of 88.56%, both using a small-scale sensor array34,47. Our system’s accuracy of 96.26% outperforms these previous studies by roughly 5%.
A novel approach in our study is the use of data augmentation to overcome the challenge of limited clinical breath samples. This method enabled us to expand the training dataset while preserving its original structure, as confirmed by the Mann-Whitney U test (p> 0.05)19,48. Our model also did not overfit, indicating that our synthetic data exhibited ample variability. Additionally, our study incorporated a unique combination of small-scale MOS sensors, enabling the device to detect a broader range of VOCs. This contributed to the system’s higher prediction accuracy.
Our system is also original due to its fast prediction; the whole pipeline only requires 5 minutes from analyzing a patient’s sample to performing nitrogen cleaning. This marks a notable improvement over previous multimodal sensor studies with upwards of 40 minutes for prediction, as they absorb VOCs from exhaled breath instead of leaving the breath untreated36. Rapid detection using the system presented in this study offers particular value in primary care settings, where patients can be screened during routine visits. Unlike conventional blood or imaging tests, which require several days for processing and follow-ups, the breath analyzer system enables immediate identification of high-risk individuals during a quick in-office visit. By integrating such a device into routine check-ups, primary care physicians could expedite diagnostics, intervene earlier, and identify asymptomatic lung cancer cases, ultimately improving patient outcomes.
Accurate early-stage lung detection is another strength of the system. With the majority of the lung cancer group consisting of early-stage patients (stages I and II), the model achieved an average accuracy of 96.26% through 5-fold cross-validation. This demonstrates the consistency of our device and model across different training and testing sets, proving the system’s viability for early-stage lung cancer detection.
Lastly, our device is portable and does not depend on lab equipment, unlike other studies in this field. All these characteristics, combined with the device’s low cost of approximately $215, make our system more suitable for lung cancer preliminary screening in both clinical and non-clinical settings. It also has the potential to improve lung cancer detection in underserved regions where conventional diagnostic tools are limited or unaffordable.
While the device yielded promising results, there are a few limitations that should be acknowledged. The study population mainly consisted of South Asian individuals, and the study sample size was limited. Furthermore, the sensor array was largely homogenous, relying on MOS sensors.
Future work should aim to validate these findings in a larger, more diverse patient population. This presents an opportunity to further improve the system’s accuracy by researching the use of type-different sensors in our array, such as electrochemical or catalytic combustion sensors. Secondly, we implemented an MLP neural network; however, this can be expanded to evaluating other convolutional or recurrent neural networks for better performance. Additionally, a key challenge to widespread implementation will be gaining clinical adoption against established standards like LDCT or tumor biopsies, which will require further robust validation. However, we believe that the promising results of this pilot study provide an opportunity for further research to be conducted, thereby enhancing our understanding of the novel device’s utility.
Conclusion
The findings display the potential of our small-scale sensor device for VOC breath analysis-based lung cancer detection. The device demonstrated high accuracy across all stages of lung cancer while remaining low-cost, portable, and capable of rapid analysis. These features suggest that the system could be deployed not only in hospitals and clinics but also in resource-limited and underserved settings, where access to affordable diagnostic tools is often limited. By enabling earlier detection, the device may help identify high-risk individuals prior to the development of symptoms and thereby support clinicians in developing more timely and effective treatment plans. In addition, the results provide evidence to inform large-scale screening initiatives, contribute to the standardization of breath-based diagnostic protocols, and advance a practical approach for further investigation. Collectively, these attributes position our system as a promising tool with the potential to significantly impact lung cancer prevention and early diagnosis in healthcare.
Data availability
The datasets generated during the current study are not publicly available due to the sensitive nature of patient medical information and restrictions imposed by patient consent. However, de-identified data may be made available from the corresponding author on reasonable request.
Code availability
The Python scripts used for decoding and saving sensor readings to a CSV file database, data augmentation, and model training/evaluation are provided as Supplementary File 1.
References
Siegel, R. L., Kratzer, T. B., Giaquinto, A. N., Sung, H. & Jemal, A. Cancer statistics, 2025. Ca 75, 10 (2025).
Nooreldeen, R. & Bach, H. Current and future development in lung cancer diagnosis. International journal of molecular sciences 22, 8661 (2021).
Ning, J. et al. Early diagnosis of lung cancer: which is the optimal choice?. Aging (Albany NY) 13, 6214 (2021).
Smith-Bindman, R. et al. Projected lifetime cancer risks from current computed tomography imaging. JAMA internal medicine 185, 710–719 (2025).
Pozzessere, C., von Garnier, C. & Beigelman-Aubry, C. Radiation exposure to low-dose computed tomography for lung cancer screening: should we be concerned?. Tomography 9, 166–177 (2023).
Chudgar, N. P. et al. Results of the national lung cancer screening trial: where are we now?. Thoracic surgery clinics 25, 145 (2015).
Zhang, Y., Shi, L., Simoff, M. J., J Wagner, O. & Lavin, J. Biopsy frequency and complications among lung cancer patients in the united states. Lung cancer management 9, LMT40 (2020).
Chiu, Y.-W. et al. Costs of biopsy and complications in patients with lung cancer. ClinicoEconomics and Outcomes Research 191–200 (2021).
Lokhandwala, T. et al. Costs of diagnostic assessment for lung cancer: a medicare claims analysis. Clinical lung cancer 18, e27–e34 (2017).
Peng, G. et al. Detection of lung, breast, colorectal, and prostate cancers from exhaled breath using a single array of nanosensors. British journal of cancer 103, 542–551 (2010).
Phillips, M. et al. Prediction of lung cancer using volatile biomarkers in breath. Cancer biomarkers 3, 95–109 (2007).
Mazzone, P. J. et al. Exhaled breath analysis with a colorimetric sensor array for the identification and characterization of lung cancer. Journal of Thoracic Oncology 7, 137–142 (2012).
Le, T. & Priefer, R. Detection technologies of volatile organic compounds in the breath for cancer diagnoses. Talanta 265, 124767 (2023).
Horvath, I., Lazar, Z., Gyulai, N., Kollai, M. & Losonczy, G. Exhaled biomarkers in lung cancer. European Respiratory Journal 34, 261–275 (2009).
Van de Kant, K. D., van der Sande, L. J., Jöbsis, Q., van Schayck, O. C. & Dompeling, E. Clinical use of exhaled volatile organic compounds in pulmonary diseases: a systematic review. Respiratory research 13, 117 (2012).
Li, X. et al. Volatile organic compounds in exhaled breath: a promising approach for accurate differentiation of lung adenocarcinoma and squamous cell carcinoma. Journal of Breath Research 18, 046007 (2024).
VA, B., Subramoniam, M. & Mathew, L. Noninvasive detection of copd and lung cancer through breath analysis using mos sensor array based e-nose. Expert review of molecular diagnostics 21, 1223–1233 (2021).
Markar, S. R. et al. Assessment of a noninvasive exhaled breath test for the diagnosis of oesophagogastric cancer. JAMA oncology 4, 970–976 (2018).
Setlhare, T. C., Mpolokang, A. G., Flahaut, E. & Chimowa, G. Determination of lung cancer exhaled breath biomarkers using machine learning-a new analysis framework. Scientific Reports 15, 26085 (2025).
Vousden, K. H. & Ryan, K. M. p53 and metabolism. Nature Reviews Cancer 9, 691–700 (2009).
Gao, Y., Chen, B., Cheng, X., Li, Q. & Xi, M. Volatile organic compounds in exhaled breath: Applications in cancer diagnosis and predicting treatment efficacy. Cancer Pathogenesis and Therapy 2, E08-E16 (2025).
Zhou, D. et al. The significance of glycolysis in tumor progression and its relationship with the tumor microenvironment. Frontiers in Pharmacology 13, 1091779 (2022).
Jia, Z., Patra, A., Kutty, V. K. & Venkatesan, T. Critical review of volatile organic compound analysis in breath and in vitro cell culture for detection of lung cancer. Metabolites 9, 52 (2019).
Lv, W. et al. Identification of volatile biomarkers for lung cancer from different histological sources: A comprehensive study. Analytical Biochemistry 690, 115527 (2024).
Keogh, R. J. & Riches, J. C. The use of breath analysis in the management of lung cancer: is it ready for primetime?. Current Oncology 29, 7355–7378 (2022).
Choueiry, F., Barham, A. & Zhu, J. Analyses of lung cancer-derived volatiles in exhaled breath and in vitro models. Experimental Biology and Medicine 247, 1179–1190 (2022).
Wang, P. et al. Identification of lung cancer breath biomarkers based on perioperative breathomics testing: A prospective observational study. EClinicalMedicine 47 (2022).
Sani, S. N. et al. Lc-ms/ms based volatile organic compound biomarkers analysis for early detection of lung cancer. Cancers 15, 1186 (2023).
Selvamuthukumar, K. et al. Recent advances in breath-based volatile compounds analysis by various analytical techniques for screening of lung cancer disease. Microchemical Journal 114003 (2025).
Nardi-Agmon, I. et al. Exhaled breath analysis for monitoring response to treatment in advanced lung cancer. Journal of Thoracic Oncology 11, 827–837 (2016).
Montuschi, P., Mores, N., Trové, A., Mondino, C. & Barnes, P. J. The electronic nose in respiratory medicine. Respiration 85, 72–84 (2012).
Santini, G. et al. Electronic nose and exhaled breath nmr-based metabolomics applications in airways disease. Current topics in medicinal chemistry 16, 1610–1630 (2016).
Moura, P. C., Raposo, M. & Vassilenko, V. Breath volatile organic compounds (vocs) as biomarkers for the diagnosis of pathological conditions: A review. Biomedical journal 46, 100623 (2023).
Ozsandikcioglu, U., Atasoy, A. & Sevim, Y. Lung cancer detection utilizing mixed sensor based electronic nose. IEEE Access (2025).
Jia, Z., Thavasi, V., Venkatesan, T. & Lee, P. Breath analysis for lung cancer early detection-a clinical study. Metabolites 13, 1197 (2023).
Lee, B. et al. Breath analysis system with convolutional neural network (cnn) for early detection of lung cancer. Sensors and Actuators B: Chemical 409, 135578 (2024).
Mochalski, P., King, J., Unterkofler, K. & Amann, A. Stability of selected volatile breath constituents in tedlar, kynar and flexfilm sampling bags. Analyst 138, 1405–1418 (2013).
Tan, J.-L., Yong, Z.-X. & Liam, C.-K. Using a chemiresistor-based alkane sensor to distinguish exhaled breaths of lung cancer patients from subjects with no lung cancer. Journal of thoracic disease 8, 2772 (2016).
Dey, A. Semiconductor metal oxide gas sensors: A review. Materials science and Engineering: B 229, 206–217 (2018).
Nakhleh, M. K. et al. Diagnosis and classification of 17 diseases from 1404 subjects via pattern analysis of exhaled molecules. ACS nano 11, 112–125 (2017).
Issitt, T. et al. Volatile compounds in human breath: critical review and meta-analysis. Journal of Breath Research 16, 024001 (2022).
Fan, X. et al. Exhaled voc detection in lung cancer screening: a comprehensive meta-analysis. BMC cancer 24, 775 (2024).
Fowles, J. & Dybing, E. Application of toxicological risk assessment principles to the chemical constituents of cigarette smoke. Tobacco control 12, 424–430 (2003).
Xie, Z., Tian, Y. & Jia, P. A few-shot se-relation net-based electronic nose for discriminating copd. Sensors (Basel, Switzerland) 25, 4780 (2025).
Shorten, C. & Khoshgoftaar, T. M. A survey on image data augmentation for deep learning. Journal of big data 6, 1–48 (2019).
Ultsch, A. & Lötsch, J. Augmenting small biomedical datasets using generative ai methods based on self-organizing neural networks. Briefings in Bioinformatics 26, bbae640 (2025).
Li, W., Liu, H., Xie, D., He, Z. & Pi, X. Lung cancer screening based on type-different sensor arrays. Scientific reports 7, 1969 (2017).
Takamori, S. et al. Differential diagnosis of lung cancer and benign lung lesion using salivary metabolites: A preliminary study. Thoracic Cancer 13, 460–465 (2022).
Acknowledgements
The authors would like to thank Dr. Vitthalrao Vijaykumar Wanjari for assisting in the collection of patient breath samples and all the volunteers for their participation in the study.
Author information
Authors and Affiliations
Contributions
K.K. and K.G. conceived the experiment. D.I., V,V.W., K.K, and K.G. conducted the experiment. D.I. and G.B. analyzed the results. D.I., K.K., K.G., and G.B. wrote the main manuscript text. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iyer, D., Gobinath, K., Kowkuntla, K. et al. Breath-based lung cancer detection using an ML-driven low-cost sensor array. Sci Rep 15, 41475 (2025). https://doi.org/10.1038/s41598-025-26416-z
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-26416-z