Introduction

Incitement and motivation

The global energy sector is currently in the midst of a significant transformation, which is being driven by the pressing necessity to transition from fossil fuels to more sustainable, cleaner energy sources. Solar photovoltaic (PV) systems have emerged as one of the most promising and rapidly expanding solutions for meeting the world’s increasing energy demands, and they are among the various renewable energy technologies. In its 2024 Renewables Market Update, the International Energy Agency (IEA) stated that solar PV capacity additions are anticipated to account for nearly 60% of global renewable capacity growth between 2023 and 2028, with annual installations surpassing 500 GW by 20281. This growth is driven by technological advancements in PV modules, power electronics, and grid integration strategies, as well as supportive policies and declining costs.

Photovoltaic energy systems (PVES) are particularly appealing because of their compatibility with decentralized energy architectures, low operational costs, and scalability. In addition to their use in residential and commercial applications, they are also being deployed in utility-scale grid-tied configurations that make a substantial contribution to national electricity grids. However, the integration of large-scale PV systems into the grid, poses significant technical challenges. The intermittent and nonlinear nature of solar irradiance, the necessity of maximum power point tracking (MPPT) in dynamic weather conditions, and adherence to grid codes regarding power quality and system stability are among these challenges2. It is imperative to guarantee the efficiency and reliability of PV systems as their role expands. In particular, it is essential to optimize MPPT performance in order to maximize energy yield and guarantee grid stability in the face of rapidly changing irradiance and temperature conditions3. As revealed by the literature, several directions have been pursued in the search for MPPT solutions for Photovoltaic energy conversion systems (PVECS). Perturb and observe (P&O) and incremental conductance (INC) have gained recognition as classical algorithms4. One of their strengths is their ability to effortlessly monitor the maximum power point (MPP) by emphasizing simplicity and a reduced number of sensors. Nevertheless, they have a multitude of issues, such as the costly necessity of a trade-off between speed and oscillations at steady-state, slow convergence speed, and subtle performance under variable climatic conditions5. The performance of PVEC has been the subject of significant attention from researchers over the years, which has resulted in the opening of numerous avenues for improvement6. The subsequent discourse will systematically review these avenues.

Literature review

In order to tackle the problem of MPPT several solutions have been conceived and tested under different settings and PVES configuration. In this context, Djilale et al., (2025) studied the problem faced by the classical as well as the traditional variable step-size P&O algorithms7. They emphasized the performance impact of incorrect decision-making steps resulting from rapid changes in irradiance, temperature, and resistive load setting on the MPP. They suggested a modified variable step-size P&O method and demonstrated that it effectively addressed the concerns articulated. Their prescription is crucial for reducing response time and undershoots, as well as ensuring stable operation around the MPPT. All of these investigations were restricted to a standalone PVECS connected to a resistive load. Chellakhi et al., (2024) proposed an indirect MPPT strategy for a standalone PVECS in light of low cost applications8. The technique employed a PID controller and an enhanced INC algorithm. Electronics simulations on the Proteus platform demonstrated a static and dynamic efficiency that surpassed that of other schemes implemented on the same platform. A model reference adaptive controller was proposed by Mana et al., (2023) for a PVES connected to a resistive load. This is an adaptive controller that follows a decoupled design ensuring strengthen stability. They conducted simulations in MATLAB/Simulink, utilizing a boost converter as the DC-DC converter circuitry. Their principal outcomes indicated that the adaptive controller excelled better than the P&O/INC in terms of tracking efficiency and capture time. Several nonlinear control techniques have been studied for tackling the problem of MPPT such as the Neuro-Fuzzy fractional order sliding mode controller proposed by Ullah et al., (2025)9, the backsteeping controller proposed by Harrison et al., (2023)10 the neural network (NN)-based adaptive global sliding mode proposed by Haq et al., (2022)11, and the Gaussian Process Regression-based higher order sliding mode in12. It should be noted that the main problem with the use of nonlinear methods rests on the necessity to measure certain variables which are often very expensive. One of these variables is solar irradiance, whose real-time measurement and integration is not only expensive but complex also13. Therefore, the necessity of circumventing the requirement for solar irradiance measurement must be addressed in order to advance the deployment of nonlinear techniques for MPPT. Nevertheless, it is evident that they are capable of providing the most optimal performance in comparison to other methods from a strict control perspective. Although the utilization of nonlinear MPPT methods for standalone systems has garnered significant attention, there is still much to be accomplished for grid-integrated systems. Even though the primary objectives remain MPPT in such systems, certain demands must be met concurrently, such as grid power quality, adherence to Total Harmonic Distortion (THD) regulation, and DC voltage regulation, all these in order to avoid interference with other electrical equipment in the network and maintain grid stability. In the light of grid-integrated settings, Elallali et al., (2022) proposed a nonlinear strategy involving sliding mode-based Lyapunov method and PI controller14. On the PV side, they employed a three-level neutral point clamped (NPC) inverter on the AC side, while on the PV side; they employed a P&O MPPT algorithm. The main challenges with their controller are on the PV side, where the P&O algorithm has flaws such as slow tracking convergence and oscillations around the MPP, which affect overall grid performance. Zaghba et al., (2023) studied a single phase-grid connected system with focus on MPPT15. They proposed a Fuzzy-oriented MPPT algorithm optimized under diverse climatic conditions. With this system, they demonstrated that a dual solar tracking system outperformed a fixed tracking system in terms of efficiency by 25%. It is clear that the authors did not compare their proposed system to existing schemes, making it impossible to quantify its MPPT performance.

Metaheuristics-based intelligent algorithms have become increasingly relevant in the field of MPPT, particularly in partially shaded environments. They are, in fact, regarded as the most proficient in monitoring the global maximum power point16. One of the most frequently referenced metaheuristic algorithms has been particle swarm optimization (PSO) in the context of MPPT17. While its competent as a global optimization algorithm cannot be argued, several of its limitations have been uncovered in the literature. One of them is the problem of slow tracking response, which appears as a general problem circulating among metaheuristics. Several other metaheuristics have been developed drawing inspiration from social and physical phenomena- each of these have been applied to PVEC in the light of MPPT. For instance, the differential evolution (DE) optimization algorithm, which leverages evolutionary principles, was applied to a standalone system for tracking the global maximum power point18. The authors carried out investigations in PSIM platform and showed that DE was better than the P&O in navigating the intricate search space in search for the MPP, converging in just 1.2 seconds. The DE encounters an issue in that its mutation process lacks a convergent direction, as its particles are compared randomly19, this has a deteriorating effect on its convergence performance. The mutation process is modified in the improved differential evolution (IDE) proposed in20 to ensure that particles are compared and convergence is guaranteed toward the best particle, thereby addressing this issue. The authors of the latter work showed that the IDE was able to excel well under partial shading as well as load variation conditions, with reduced tracking time. As recently enunciated by Wei et al., (2025), metaheuristics face many problems that in navigating the large search space of PVES21. This contributes to their slow tracing performance, premature tracking convergence and real-time adaptability constraints. This is typically the problem encountered by search-based algorithms, which must systematically locate the MPP in a search procedure. While the latter work focuses on search space reduction, it still relies on searching, implying that theoretical efficiency is limited. Furthermore, it was limited to a standalone DC system and did not address grid-integrated challenges.

Scope, development and contribution

To address the issues discussed above, this paper proposes a nonlinear control strategy for a grid-tight PV system. To avoid the need for costly sensors, the proposed controller incorporates an online irradiance computational model, which allows for the estimation of the latter variable without relying on costly measurements. Based on this estimate, an intelligent NN forecasts the best reference maximum power point voltage. This is used by the controller to ensure strong MPPT. The proposed controller’s strength lies in its ability to achieve MPPT while meeting other requirements such as grid power quality and DC link voltage stability. It performs exceptionally well in variable climatic conditions, ensuring very fast MPP tracking and improving grid stability. Lyapounov laws ensure the controller’s stability during operation. The proposed controller’s superiority claims are supported by comparative results with the P&O, PSO, and IDE, which show that the proposed MPPT achieves higher power yield, grid stability, and improved power quality. Implementation takes place on a 100 kW system in MATLAB/Simulink, which includes a Boost converter, grid inverter, and electrical network. The major contributions of this work are summarized as follows:

  1. (1)

    A new nonlinear MPPT controller for a grid-tied system is proposed. This controller excels without the need for additional sensors, such as irradiance measurement.

  2. (2)

    The proposed controller attains efficient MPP while ensuring DC link stability and grid power quality.

  3. (3)

    The proposed controller is recommended for grid-tight systems operating under rapidly changing meteorological conditions.

  4. (4)

    It reveals superiority over existing algorithms including the classical P&O and metaheuristics (PSO and IDE)

Modelling and implementation of the grid-integrated PVES

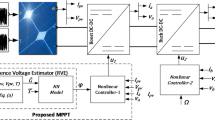
This section aims at introducing the grid-integrated PVES studied in this paper. Figure 1 presents the structure of such a system. There are two sections involved: the DC section and the AC side. The former side constitutes the solar array, DC-DC converter and its controller, while the latter side is made of the controlled inverter, connected to the electrical network and a load.

Fig. 1
figure 1

Structure of the grid-integrated PVES.

Full size image

A solar power system designed to work in tandem with the main electrical grid relies heavily on an inverter to convert the direct current (DC) output from PV panels into alternating current (AC) suitable for grid operation. This type of system, known as a grid-connected or grid-interactive setup, includes a specialized inverter that not only matches the grid’s voltage and frequency, but also allows for real-time synchronization with the utility supply. When solar generation exceeds on-site consumption, the excess energy can be transferred back to the grid and credited to the user via net metering systems22, resulting in cost savings and lower demand for fossil-fuel-based power. Modern inverters in such systems frequently include MPPT, a feature that continuously adjusts the PV modules’ electrical operating point to maximize energy extraction. Unlike off-grid setups, these systems eliminate the complexity and cost of battery storage, providing a more cost-effective and efficient solution. For example, in a 2021 study on the financial performance of rooftop solar installations in Vietnam23, researchers compared grid-tied systems with and without battery storage. The findings revealed that systems without battery storage had a significantly higher Net Present Value (NPV) of 3,402$ than those with batteries, which were 308$. Furthermore, the internal rate of return (IRR) was significantly higher at 14.8% versus 5.6%, and the payback period was shorter at 7.6 years versus 13.8 years for battery-powered systems. These highlight that, while batteries can improve energy independence, they also incur higher costs and require longer payback periods. As a result, grid-tied solar systems without battery storage are a more economically viable option.

Additionally, a smart or bi-directional energy meter is typically installed to monitor both incoming grid electricity and outgoing solar energy contributions24. The heart of the inverter circuit is typically a voltage source converter (VSC), which is prized for its simple design low cost of operation and flexibility in controlling active and reactive power independently25. This VSC usually consists of six semiconductor switches, such as IGBTs or MOSFETs, which are pulse-width modulated (PWM) to achieve precise grid synchronization.

Modelling of the solar array

The solar array, the source of the system must be modelled in order to understanding its performance under a broad array of climatic conditions. In this study, a single diode model (SDM) is considered as the fundamental building block. This model is chosen among other models for its simplicity and satisfactory accuracy26,27,28.

The electrical circuit of the SDM is presented in Fig. 2. It is made up of a photocurrent source, \({I}_{ph}\) that responds directly to solar irradiance \(G(W/{m}^{2})\) and temperature \(T(^\circ{\rm C} )\). A diode placed in parallel to the current source models the semi-conducting nature of the cell, while the resistive components, \({r}_{p}\) and \({r}_{s}\), models the parasitic effect of the panel. The current-voltage mathematical equation of the SDM can be derived as follows:

$${I}_{pv}=\frac{G}{1000}({i}_{ph\left(STC\right)}+{k}_{i}\Delta T)-{I}_{s}\left[\mathit{exp}\left(\frac{\left({V}_{pv}+{I}_{pv}{r}_{s}\right)}{a}\right)-1\right]-\frac{{V}_{pv}+{I}_{pv}{r}_{s}}{{r}_{p}}$$
(1)

where, \({I}_{pv}\), \({V}_{pv}\) denote the PV current and voltage respectively, \({i}_{ph\left(STC\right)}\) stands for the photocurrent at standard test conditions (STC), which is usually a constant, \(\Delta T\) is the temperature difference from standard temperature, \(25^\circ{\rm C}\), and \({k}_{i}\) is the temperature coefficient of short-circuit current. The parameter \(a\) is temperature dependent and written as \(a=n{k}_{s}KT/q\), whereby, \({k}_{s}\) denotes the number of cells in series, \(K\) and \(q\) stand for the Boltzmann’s and charge constant respectively. From this building block, any dimension of PV array can be constructed, with \({N}_{s}\) number of series connections and \({N}_{p}\) number of parallel conditions. In essence, the overall model’s equation for an \(({N}_{s}, {N}_{p})\) array can be written as follows:

Fig. 2
figure 2

Solar array and its SDM fundamental building block.

Full size image
$${I}_{pv}={N}_{p}\frac{G}{1000}\left({i}_{ph\left(STC\right)}+{k}_{i}\Delta T\right){N}_{p}-{N}_{p}{I}_{s}\left[\mathit{exp}\left(\frac{\left({V}_{pv}+{I}_{pv}{r}_{s}\right)}{a{N}_{s}}\right)-1\right]-\frac{{V}_{pv}+{I}_{pv}{r}_{s}\left(\frac{{N}_{s}}{{N}_{p}}\right)}{{r}_{p}\left(\frac{{N}_{s}}{{N}_{p}}\right)}$$
(2)

A 100 kW PV array was constituted with 5 series modules connected in 66 parallel strings. The complete characteristics of the array can be seen in Table 1. Using Eq. (1) along with characteristics of the array, the actual solar array can be implemented and studied under diverse climatic conditions. A plot of the power-voltage (P-V) curve of the array under diverse climatic conditions is presented in Fig 3. It can be seen the PV array has a nonlinear behavior. I t is also clear that each-curve has a knee point regarded as the MPP; this is the greatest potential of the solar array. At standard test conditions \((T=25^\circ{\rm C} , G=1000W/{m}^{2})\), it can be seen that he array has a maximum power of \(1.0038\times {10}^{5}\) W. Ideally, it is desired that the array delivers its maximum power. However this is openly available due to impedance mismatch29. In addition, it is not a straightforward task to ensure MPPT especially as the MPP is unique per climatic condition. This suggests that as climatic conditions change, the maximum power \({P}_{mpp}\) will be prone to changing. A plot of the maximum power of the array for 1000 pair of \(G,T)\) as presented in Fig 4, indicates the uniqueness of the MPP as a function of climatic conditions. It is imperative to track the MPP amidst the stochastic variations in climatic conditions.

Table 1 Parameters of the solar array.
Full size table
Fig. 3
figure 3

Power-voltage (P-V) curves of the array. (Left) Different values of irradiances (G). (Right) Different values of Temperatures (T).

Full size image
Fig. 4
figure 4

3D scatter plot of maximum power as a function of G and T for 1000 unique climatic conditions.

Full size image

Modelling of the Boost DC-DC converter

A DC-DC converter is required to connect the PV to the other end of the system. Additionally, it is required to change the PV source’s input impedance. It is obvious that when the converter’s input impedance equals the desired MPP impedance, the system is said to be operating at MPP. It is possible to change the circuit’s impedance and move closer to MPP by controlling the converter’s gate. The Boost converter, among other converters, is highly praised within the context of MPPT30,31. It has been shown that the Boost converter delivers higher power yield than the Buck converter when use for MPPT applications32. The electrical structure of such a converter is presented in Fig 5. It features different storage components, including a coupling capacitor, \({C}_{pv},\) and inductor, \(L\). The other end of the converter is the DC-bus. The converter operates in two modes: when the switch is off and when it is on. In each of these modes, the circuit’s current and voltage equations can be calculated. In this study, we are interested in the dynamic model of the converter, which can be obtained by averaging the converter’s equation over one switching period, \({T}_{sw}\). According to33, the average model is obtained as follows:

$$\left\{\begin{array}{c}{\dot{x}}_{1}=\frac{{I}_{pv}}{{C}_{pv}}-\frac{{i}_{L}}{{C}_{pv}}\\ {\dot{x}}_{2}=\frac{{x}_{1}}{L}-\left(1-u\right)\frac{{x}_{3}}{L}\end{array}\right.$$
(3)

where, \({x}_{1},{x}_{2},\) ad \({x}_{3}\) represents the average values of the PV voltage, inductor current and DC-link voltage over one period. It should be noted that such a model is derived under the premise that the converter is almost lossless. This will allow smooth exploitation by a nonlinear controller for MPPT control.

Fig. 5
figure 5

Electrical structure of the Boost converter.

Full size image

The converter can be designed based on MPP resistance as prescribed by34. For this study, the converter’s parameters were found to be \({C}_{pv}=100 \mu F\), and \(L=5 mH\). It should be noted that for MPPT, the converter must be controlled. We shall present the control of the converter in the subsequent discourse.

Modelling and control of the Grid-Inverter

Control of the inverter is paramount in order to ensure grid power quality while tracking the maximum power point. We employed dq control and Phase Locked Loop (PLL) theory to develop the inverter’s control scheme. In advanced inverter control schemes (as illustrated in Figure 6), the traditional three-phase AC signals are mathematically converted into two orthogonal components that rotate within a reference frame. This transformation commonly referred to as the dq-axis transformation, enables independent control of active (d-axis) and reactive (q-axis) power, simplifying power regulation. A PLL is employed to synchronize the inverter’s output frequency and phase with that of the utility grid, ensuring harmonious operation. To maintain this synchronization, the system continuously adjusts the d and q axis current components using feedback controllers. These controllers compare real-time output with reference values and make necessary corrections to keep the system aligned with desired performance targets. The output current is regulated using PWM, which adjusts the inverter’s switching behavior to deliver precise power levels. Additionally, DC-link capacitors act as filters by suppressing high-frequency voltage fluctuations, contributing to a more stable and clean power output. The entire approach ensures that the inverter’s output is not only well-regulated but also compatible with grid requirements, facilitating seamless grid integration. This control strategy supports essential functions such as MPPT, which optimizes energy extraction from solar panels. Moreover, it complies with utility grid standards, making it a reliable solution for connecting photovoltaic systems to the power grid. To apply this method, it is necessary to develop a mathematical model of the inverter, for which the αβ components of grid voltage and current are extracted, as referenced in35.

Fig. 6
figure 6

Control structure of the grid-inverter.

Full size image

The αβ components of grid voltage and current can be expressed as follows:

$$\left[\begin{array}{c}{V}_{\alpha }\\ {V}_{\beta }\\ 0\end{array}\right]=\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{2}}{3}& -\frac{\sqrt{3}}{2}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{V}_{a}\\ {V}_{b}\\ {V}_{c}\end{array}\right]$$
(4)
$$\left[\begin{array}{c}{I}_{\alpha }\\ {I}_{\beta }\\ 0\end{array}\right]=\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{2}}{3}& -\frac{\sqrt{3}}{2}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{I}_{a}\\ {I}_{b}\\ {I}_{c}\end{array}\right]$$
(5)

Applying the transformation in the dq plain, we obtain the following equations:

$$\left[\begin{array}{c}{V}_{d}\\ {V}_{q}\\ 0\end{array}\right]=\left[\begin{array}{ccc}\text{cos}\theta & \text{sin}\theta & 0\\ -\text{sin}\theta & \text{cos}\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{2}}{3}& -\frac{\sqrt{3}}{2}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{V}_{a}\\ {V}_{b}\\ {V}_{c}\end{array}\right]$$
(6)
$$\left[\begin{array}{c}{I}_{d}\\ {I}_{q}\\ 0\end{array}\right]=\left[\begin{array}{ccc}\mathit{cos}\theta & \mathit{sin}\theta & 0\\ -\mathit{sin}\theta & \mathit{cos}\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{2}}{3}& -\frac{\sqrt{3}}{2}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{I}_{a}\\ {I}_{b}\\ {I}_{c}\end{array}\right]$$
(7)

The following Equations are obtained after soling Eqs. (6,7):

$$\left[\begin{array}{c}{V}_{d}\\ {V}_{q}\\ 0\end{array}\right]=\sqrt{\frac{2}{3}} \left[\begin{array}{ccc}\text{cos}\theta & -\frac{1}{2}\text{cos}\theta +\frac{\sqrt{3}}{2}\text{sin}\theta & \frac{1}{2}\text{cos}\theta -\frac{\sqrt{3}}{2}\text{sin}\theta \\ -\text{sin}\theta & -\text{sin}\theta +\frac{\sqrt{3}}{2}\text{cos}\theta & -\text{sin}\theta -\frac{\sqrt{3}}{2}\text{cos}\theta \\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{V}_{a}\\ {V}_{b}\\ {V}_{c}\end{array}\right]$$
(8)
$$\left[\begin{array}{c}{I}_{d}\\ {I}_{q}\\ 0\end{array}\right]=\left[\begin{array}{ccc}\text{cos}\theta & -\frac{1}{2}\text{cos}\theta +\frac{\sqrt{3}}{2}\text{sin}\theta & \frac{1}{2}\text{cos}\theta -\frac{\sqrt{3}}{2}\text{sin}\theta \\ -\text{sin}\theta & -\text{sin}\theta +\frac{\sqrt{3}}{2}\text{cos}\theta & -\text{sin}\theta -\frac{\sqrt{3}}{2}\text{cos}\theta \\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{c}{I}_{a}\\ {I}_{b}\\ {I}_{c}\end{array}\right]$$
(9)

It should be noted that the introduced variables are defined as follows: \({V}_{a},{V}_{b}, {V}_{c}\) are the phase voltages of the grid, \({I}_{a}, {I}_{b}, {I}_{c}\) are line currents of the grid, \({V}_{\alpha }\), \({V}_{\beta }\) are αβ components of grid voltage, \({I}_{\alpha }\), \({I}_{\beta }\) are αβ components of grid current, \({V}_{d}, {V}_{q}\) are the dq components of the grid voltage while \({I}_{d}, {I}_{q}\) are the corresponding components of the grid current.

Essentially, the control architecture illustrated in Figure 6 operates by first sensing the grid voltage and current, which are then converted into rotating reference frame components (dq-axis) using Park’s transformation. The regulation of the direct-axis current reference (\({I}_{d, ref}\)) is achieved by monitoring the DC-link voltage originating from the solar source connected to the inverter. This DC voltage serves as a feedback signal, and a PI controller is employed to dynamically adjust \({I}_{d, ref}\) to maintain stable power flow. To ensure that the system delivers only active power, the quadrature-axis current reference (\({I}_{q, ref}\)) is set to zero, effectively nullifying reactive power injection. A PLL is integrated into the system to determine the grid voltage angle or frequency, allowing the inverter to stay phase-aligned with the grid and maintain synchronization. The dq-axis currents are regulated through PI controllers, which generate the necessary voltage references for each axis (\({V}_{d}\) and \({V}_{q}\)). These reference voltages guide the inverter in producing the correct output to match grid conditions and deliver efficient power transfer.

$$\left\{\begin{array}{c}{V}_{d, ref}={V}_{d}+{I}_{d}\omega L-{u}_{d}(t)\\ {V}_{q, ref}={V}_{q}-{I}_{d}\omega L-{u}_{q}(t)\end{array}\right.$$
(10)

In this context, ω represents the angular frequency, L denotes the grid inductance, and \({u}_{d}\left(t\right)\) and \({u}_{q}\left(t\right)\) correspond to the control outputs generated by the PI controllers for the direct and quadrature axis currents, respectively. The actual dq-axis currents are continuously compared against their reference values. Any deviations detected are corrected by the PI controllers to ensure that both power delivery and grid compliance criteria are met, as governed by the following equations:

$$\left\{\begin{array}{c}{u}_{d}\left(t\right)={k}_{p}\left({I}_{d,ref}-{I}_{d}\right)+{k}_{i}{\int }_{0}^{t}({I}_{d,ref}-{I}_{d})dt\\ {u}_{q}\left(t\right)={k}_{p}\left({I}_{q,ref}-{I}_{q}\right)+{k}_{i}{\int }_{0}^{t}({I}_{q,ref}-{I}_{q})dt\end{array}\right.$$
(11)

It is important to note that \({k}_{p}\) and \({k}_{i}\) represent the proportional and integral gains of the PI controller, respectively. These parameters are typically fine-tuned through iterative testing and performance evaluation to achieve optimal system response.

Proposed MPPT controller

This section presents the proposed controller, which achieves MPPT in the grid-integrated system. This is a decoupled control structure in which the \({V}_{mpp}\) is computed from the main nonlinear controller. Fig. 7 shows the general structure of the controller. The controller consists of two stages: the first stage seeks the \({V}_{mpp}\) and the second stage enforces the same reference. It should be noted that the first stage is inspired by the visualization in Fig. 4, which shows that the MPP voltage can be precisely mapped using temperature and irradiance. This suggests that if temperature and irradiance measurements are available, the voltage can be accurately computed. However, measuring irradiance is extremely complex and expensive. To reduce the number of sensors in the system and the cost, an algorithm is developed to approximate the temperature and then MPP voltage. The controller enforces the desired operation of the system based on the voltage values. The following section presents the development of each of these stages.

Fig. 7
figure 7

Structure of the proposed controller.

Full size image

Development of stage 1- computation of MPP voltage

This section discusses the creation of the first stage of the control structure. Here, the structure first attempts to approximate the irradiance and then predicts the MPP voltage. To achieve the former, we use a mathematical construction approach. Equation (1) can be rewritten as follows:

$${I}_{pv}={N}_{p}\frac{\widehat{G}}{1000}\left({i}_{ph\left(STC\right)}+{k}_{i}\Delta T\right){N}_{p}-{N}_{p}{I}_{s}\left[\mathit{exp}\left(\frac{\left({V}_{pv}+{I}_{pv}{r}_{s}\right)}{a{N}_{s}}\right)-1\right]-\frac{{V}_{pv}+{I}_{pv}{r}_{s}\left(\frac{{N}_{s}}{{N}_{p}}\right)\widehat{G}}{{r}_{p,ref}\left(\frac{{N}_{s}}{{N}_{p}}\right)1000}$$
(12)

It should be noted that we have introduced \(\widehat{G}\) which denotes the estimated irradiance. Also, a more efficient form of the parallel resistance, \({r}_{s}\) has ben introduced as a function of the irradiance. For convenience, the following nonlinear functions are established:

$$\left\{\begin{array}{c}N({I}_{pv}, {V}_{pv})=\frac{{V}_{pv}+{I}_{pv}{R}_{s}\left(\frac{{N}_{s}}{{N}_{p}}\right)}{1000\left(\frac{{N}_{s}}{{N}_{p}}\right){r}_{p,ref}}\\ M{(I}_{pv}, {V}_{pv},T)={{N}_{p}I}_{s}\left[\mathit{exp}\left(\frac{\left({V}_{pv}+{I}_{pv}{R}_{s}\right)}{a{N}_{s}}\right)-1\right]\\ \widehat{G}=F({I}_{pv}, {I}_{pv}, T)\end{array}\right.$$
(13)

By inserting the following functions into (5) alongside (2), one obtains:

$${I}_{pv}={N}_{p}\frac{G}{1000}\left({I}_{ph,ref }+{K}_{i}\left(T-{T}_{ref}\right)\right)-M{(I}_{pv}, {V}_{pv},T)-\widehat{G}N({I}_{pv}, {V}_{pv})$$
(14)

Rearrangements yield the following:

$$\widehat{G}=F\left({I}_{pv}, {I}_{pv}, T\right)=\frac{{I}_{pv}+M{(I}_{pv}, {V}_{pv},T)}{\left[{N}_{p}\frac{G}{1000}\left({I}_{ph,ref }+{K}_{i}\left(T-{T}_{ref}\right)\right)-N({I}_{pv}, {V}_{pv})\right]}$$
(15)

Consequently, Equation (15) serves as an explicit formulation enabling the real-time computation of solar irradiance dynamically. Although Equation (1) presents an implicit relationship, the subsequent algebraic transformation simplifies it into a practical expression for estimating irradiance directly. With irradiance estimation in place, we can proceed to develop a NN model aimed at predicting the MPP voltage. For this task, a Radial Basis Function (RBF) NN is employed. RBF networks are highly effective for function approximation tasks, especially when modeling complex, nonlinear relationships, thanks to their use of localized activation functions. Their strength lies in the mathematical structure, primarily the use of Gaussian-based activation combined with linear parameter tuning during training, which facilitates robust performance and interpretability across diverse applications. The architecture of an RBF network typically consists of three layers. The input layer accepts the relevant measurements, which are then processed by the hidden layer using radial basis neurons. Finally, the output layer delivers the estimated MPP voltage. The response of an RBF neuron is governed by the distance between the input vector and a predefined center, and this behavior is commonly approximated using a Gaussian function.

$$\phi \left(x\right)=exp\left(\frac{{\Vert x-c\Vert }^{2}}{2{\sigma }^{2}}\right)$$
(16)

where x=[T,\(\widehat{G}\).] is the input vector, c is the center of the function, and σ is the standard deviation, which governs the function’s breadth. Each neuron in the buried layer computes the radial basis function for a specific input vector x. The output of the i-th neuron is expressed as follows:

$${h}_{i}\left(x\right)={\phi }_{i}\left(\Vert x-c\Vert \right)=exp\left(\frac{{\Vert x-c\Vert }^{2}}{2{\sigma }^{2}}\right)$$
(17)

The output layer is a linear combination of the concealed layer’s outputs:

$$y\left(x\right)=\sum_{i=1}^{N}{w}_{i}exp\left(\frac{{\Vert x-c\Vert }^{2}}{2{\sigma }^{2}}\right) +{w}_{o}$$
(18)

where,\({w}_{i}\) denotes the weight link between the i-th hidden layer and the output, and,\({w}_{o}\) represents the output bias. The symbol N represents the total number of neurons in the hidden layer. It is worth mentioning that the selected RBF NN comprises three hidden layers and a neuron structure of (5 5). The Levenberg-Marquardt method was used to train the model, as shown in36. It is worth noting that the training was done offline, which was a purposeful move to lower the system’s complexity before deployment. Offline training allows the computationally demanding components of model building to be controlled independently, reducing the system’s workload while in real-time operation. The NN model was trained using specially designed patterns that included 1000 irradiance and temperature data as shown in Fig. 8. The dataset had irradiance values ranging from 1 to 1000 W/m2 and temperatures ranging from 10 to 50°C. After training, testing, and validation, the validated model had a regression value of 0.999 and a mean squared error of 0.00020406 at the best training performance. Therefore, the irradiance estimation function and the NN model combined create the MPP voltage estimation model. In the following discourse, the design of nonlinear controllers utilized to coordinate the isolated system is presented.

Fig. 8
figure 8

Performance of the neural network.

Full size image

Design of the proposed controller

In this section, the controller is designed that is supposed to stabilize the system in light of MPPT. The controller is designed by employing Lyapunov recursive principles. It should be noted that the controller is going to materialize the dynamics of the solar system seen in Eq. (3). The controller is thus constructed as follows:

We commence by stating that the cont4oller is feed with the reference voltage of the system from stage 1, and this voltage is considered as the first stage of the system and written as follows:

$${x}_{1ref}={V}_{mpp}$$
(19)

Control goal: Track the reference voltage, \({x}_{1ref}\)

We define the first tracking error caused by controller action and its dynamics as follows:

$${e}_{1}={x}_{1}-{x}_{1ref}$$
(20)
$${\dot{e}}_{1}={\dot{x}}_{1}-{\dot{x}}_{1ref}=\frac{{i}_{PV}}{{C}_{1}}-\frac{{x}_{2}}{{C}_{1}}-{\dot{x}}_{1ref}$$
(21)

To improve controller resilience against unmodeled dynamics and perturbations, we apply an integral action p to this mistake, resulting in the macro-variable.

$$e={e}_{1}+p, p={\int }_{o}^{t}({x}_{1}-{x}_{1ref})dt$$
(22)

The controller must guarantee that the mistake, \({e}_{1}\), diminishes with time. At this level, we use the Lyapunov functions to verify that the controller converges to its reference. To that purpose, it is obvious to select the Lyapunov candidate as specified in Equation (18) along with its respective derivative Eq. (19).

$${V}_{1}=\frac{1}{2}{e}_{1}^{2}+\frac{k}{2}{p}^{2} , k>0$$
(23)
$$\dot{{V}_{1}}={e}_{1}{\dot{e}}_{1}+kp\dot{p}$$
(24)

Inserting the error and Lyapunov dynamics into this equation once has:

$$\dot{{V}_{1}}={e}_{1}\left(\frac{{i}_{PV}}{{C}_{1}}-\frac{{x}_{2}}{{C}_{1}}-{\dot{x}}_{1ref}\right)+kp\left({x}_{1}-{x}_{1ref}\right)={e}_{1}(\frac{{i}_{PV}}{{C}_{1}}-\frac{{x}_{2}}{{C}_{1}}-{\dot{x}}_{1ref}+kp)$$
(25)

The following equation ensures that \(\dot{{V}_{1}}\) is negative definit, provided that \(K>0\)

$$\frac{{i}_{PV}}{{C}_{1}}-\frac{{x}_{2}}{{C}_{1}}-{\dot{x}}_{1ref}+kp=-{K}_{1}{e}_{1}, K>0$$
(26)

A virtual reference for \({x}_{2}\) and its error is found from the above equation as:

$$\varphi ={C}_{1}({K}_{1}{e}_{1}+\frac{{i}_{PV}}{{C}_{1}}-{\dot{x}}_{1ref}+kp)$$
(27)
$${e}_{2}={x}_{2}-\varphi$$
(28)

Rearranging Equation (25), so that:

$${x}_{2}={e}_{2}+\varphi$$
(29)

Inserting the above equation into the first error dynamics, along with the expression of the virtual reference one has:

$${\dot{e}}_{1}=\frac{{i}_{PV}}{{C}_{1}}-\frac{{e}_{2}+{C}_{1}({K}_{1}{e}_{1}+\frac{{i}_{PV}}{{C}_{1}}-{\dot{x}}_{1ref}+kp)}{{C}_{1}}-{\dot{x}}_{1ref}$$
(30)

If we simplify this, we get:

$${\dot{e}}_{1}=-{K}_{1}{e}_{1}-\frac{{e}_{2}}{C1}-kp$$
(31)

In this context, Equation (19), the initial Lyapunov dynamics may be represented as:

$$\dot{{V}_{1}}={e}_{1}{\dot{e}}_{1}+kp\dot{p}={e}_{1}\left(-{K}_{1}{e}_{1}-\frac{{e}_{2}}{C1}-kp\right)+kp\dot{p}==-{K}_{1}{e}_{1}^{2}-\frac{{e}_{1}{e}_{2}}{{C}_{1}}$$
(32)

The error system (\({e}_{1}, {e}_{2}\)) must be reduced to zero. However, the second part of the above equation is not guaranteed negative. We must address this issue and verify that \(\dot{{V}_{1}}\) is a negative definite system. The dynamics of the virtual reference may be derived from the dynamics of its error as follows:

$$\dot{\varphi }={C}_{1}\left({K}_{1}{\dot{e}}_{1}+\frac{{\dot{\dot{i}}}_{PV}}{{C}_{1}}-{\ddot{x}}_{1ref}+k\dot{p}\right)$$
(33)

Solving this equation along with Equation (16) and (31) we have:

$$\dot{\varphi }={C}_{1}\left(K1\left(-{K}_{1}{e}_{1}-\frac{{e}_{2}}{C1}-kp\right)+\frac{{\dot{\dot{i}}}_{PV}}{{C}_{1}}-{\ddot{x}}_{1ref}+k({x}_{1}-{x}_{1ref}\right)$$
(34)

Inserting Equation (34) into the dynamics of the second error \([{\dot{e}}_{2}={\dot{x}}_{2}-\dot{\varphi }]\), we get:

$${\dot{e}}_{2}={\dot{x}}_{2}-{C}_{1}\left(K1\left(-{K}_{1}{e}_{1}-\frac{{e}_{2}}{C1}-kp\right)+\frac{{\dot{\dot{i}}}_{PV}}{{C}_{1}}-{\ddot{x}}_{1ref}+k({x}_{1}-{x}_{1ref})\right)$$
(35)

Further simplification of Equation (35) yields:

$${\dot{e}}_{2}={\dot{x}}_{2}-{C}_{1}\left(-{K}_{1}^{2}{e}_{1}-\frac{{K}_{1}{e}_{2}}{{C}_{1}}-k{K}_{1}p+\frac{{\dot{\dot{i}}}_{PV}}{{C}_{1}}\right)+{C}_{1}\left({\ddot{x}}_{1ref}-k{e}_{1}\right)$$
(36)

We introduce a new Lyapunov function \({V}_{f}\), to ensure that the error system (\({e}_{1},{e}_{2})\), now converges to zero. This candidate and its derivative are as follows:

$${V}_{f}={V}_{1}+\frac{1}{2}{e}_{2}^{2}$$
(37)
$${\dot{V}}_{f}={\dot{V}}_{1}+{e}_{2}{\dot{e}}_{2}$$
(38)

Inserting Equation (31) in (38) results to:

$${\dot{V}}_{f}=-{K}_{1}{e}_{1}^{2}-\frac{{e}_{1}{e}_{2}}{{C}_{1}}+{e}_{2}{\dot{e}}_{2}=-{K}_{1}{e}_{1}^{2}+{e}_{2}\left({\dot{e}}_{2}-\frac{{e}_{1}}{{C}_{1}}\right)$$
(39)

The negative definiteness of the above equation is ensured by the following definition:

$${\dot{e}}_{2}-\frac{{e}_{1}}{{C}_{1}}=-{K}_{2}{e}_{2}$$
(40)

Under this condition, Equation (31) paired with Equation (40) yields:

$${\dot{V}}_{f}=-{K}_{1}{e}_{1}^{2}-{K}_{2}{e}_{2}^{2}$$
(41)

Thus, (41) meets the requirements of a negative definite system. Equations (3) and (36) may now be used to determine the nonlinear control law (40). By doing this, one has:

$$u=1-\frac{L}{{x}_{3}}\left({K}_{2}{e}_{2}+\frac{{x}_{1}}{L}+{K}_{1}^{2}{C}_{1}{e}_{1}+{K}_{1}{e}_{2}+k{K}_{1}{C}_{1}p-{\dot{\dot{i}}}_{PV}+{C}_{1}{\ddot{x}}_{1ref}-{C}_{1}k{e}_{1}-\frac{{e}_{1}}{{C}_{1}}\right)$$
(42)

This is therefore the nonlinear action of the controller that ensures that the control goal is archived. It is clear that the system of errors will converge to zero which is the basis of the stability of the controller

Stability condition, performance requirements, and physical constraints

In this section, we present the Stability condition, performance requirements, and physical constraints of the overall system under the control action of the controller.

We note that from the Lyapunov function derivative, \({\dot{V}}_{f}=-{K}_{1}{e}_{1}^{2}-{K}_{2}{e}_{2}^{2}\)

Stability requirements: \({K}_{1}>0, {K}_{2}>0\) (ensures negative definiteness)

The error dynamics are governed by:

$$\left\{\begin{array}{c}{\dot{e}}_{1}=-{K}_{1}{e}_{1}-\frac{{e}_{2}}{C1}-kp\\ {\dot{e}}_{2}=-{K}_{2}{e}_{2}+\frac{{e}_{1}}{{C}_{1}}\end{array}\right.$$
(43)

To achieve exponential convergence, enforce eigenvalues with negative real parts. For simplicity, assume decoupled dynamics:

$$\left\{\begin{array}{c}{\dot{e}}_{1}\approx -{K}_{1}{e}_{1}\\ {\dot{e}}_{2}\approx -{K}_{2}{e}_{2}\end{array}\right.$$
(44)

This leads to the time constants: \({\tau }_{1}=\frac{1}{{K}_{1}}, {\tau }_{2}=\frac{1}{{K}_{2}}\)

Design Equations are thus: \({K}_{1}\ge \frac{1}{{\tau }_{desired}}, {K}_{2}\ge \frac{1}{{\tau }_{desired}}\)

Where \({\tau }_{desired}\) is the desired settling time.

Also, note that the integral term \(p={\int }_{o}^{t}({x}_{1}-{x}_{1ref})dt\) ensures zero steady state. To avoid oscillations or windup: \(k\le \frac{1}{{\tau }_{integral}}\), where \({\tau }_{integral}\) is the integral time constant

Physical constrains on control input: The duty cycle (Eq. 42) must satisfy \(0\le u\le 1\).

The overall grid-integrated system is presented in Fig. 9. It is clear how the PV power is injected into the grid, where there a 10 kVar load. In the subsequent section of this work, we shall be presenting the results if simulations of the prescribed system. Note that the objective is to achieve optimal MPPT while ensuring power quality.

Fig. 9
figure 9

Overall grid-integrated system with proposed MPPT controller.

Full size image

Results and Discussion

The system presented in the last figure was implemented in MATLAB/Simulink environment. It is essentially a 100 kW grid-connected system. We note that at the DC link, the desired reference voltage is chosen to be 500 V. The parameters of the controller was found to be \({K}_{1}=1.35\times {10}^{5}, {K}_{2}=1000, k=1000.\) A series of simulations were undertaken to ascertain the performance of the system as documented below:

Scenario 1- Rapid step variation in Irradiance

The system was originally observed under fast step-changing settings. The system was subjected to step-changes in irradiation. Initially, the system had an irradiance of G= 1000, which was reduced to 500 after 0.2 seconds. The unit of irradiance has been omitted for the sake of simplicity in the documentation. The major outcomes of this test are shown in Figs. (10-14). When running at G=10000, the system accurately monitored the predicted MPP voltage (273.5V) and the expected 100 kW (exactly 100.40 kW) (see Fig 10). The MPP was traced in 8ms. The control duty cycle grew successfully while remaining within physical constraints. After the irradiance change was implemented at 0.1 s, it is clear that the new PV voltage was properly monitored, and the system continued to operate at the new MPP of 49.71 kW. It can be observed that the control action was quickly altered in only 7 ms, allowing the PV to follow the new reference voltage. The evolution of the DC-link voltage as seen in Fig. 12 indicates that the system operated consistently at the desired 500 V amidst the change of irradiance at 0.1s. Initially the desired voltage was stabilized in just 49 ms and the system needed just about 42 ms to restore the DC link voltage to 500 V after the change of irradiance at 0.1 s.

Fig. 10
figure 10

Plot of voltage, power and duty cycle (PV side) for a rapid step change in G.

Full size image
Fig. 11
figure 11

Reference DC voltage on the actual DC link voltage for a rapid step change in G.

Full size image
Fig. 12
figure 12

Plot of voltage and current (Grid side) for a rapid step change in G.

Full size image
Fig. 13
figure 13

Display of the THD (voltage) of the system.

Full size image
Fig. 14
figure 14

Plot of active power and reactive power (grid side) for a rapid step change in G.

Full size image

From the grid side, it is evident that the system performed consistently as planned; synchronization of the grid’s voltage and current (see Fig. 12). Furthermore, the THD is lower than 0.1 percent (see Fig 13). The grid voltage remained constant at 25 kV despite the decline in irradiance. The current fed into the grid clearly decreased in response to a decrease in irradiance. Figure 14 further clearly shows that the grid ran at the required power level. The active power was around 100 kW for 0.1s, after which the grid current fell owing to a decrease in irradiance. The active power clearly varies with the system’s irradiance levels.

Scenario 2- Continuously changing climatic conditions

The system was also seen under severe environmental settings, with a constantly fluctuating irradiance and temperature profile. A real-climatic environmental profile was created and utilized to assess the system. The goal was to evaluate the system’s performance in situations comparable to those seen in practice. The major outcomes of this test are shown in Figures (15-19). Figure 15 depicts the climatic conditions, which range from G=250 to 1000 and temperature 25 to 50. Figure 16 shows that the desired reference voltage was followed during the entire time of operation. It is clear that the MPP was likewise on track. The graphic indicates that the system’s power development is smooth. Furthermore, the duty cycle remained within the limits, indicating continuity in control and no saturation in the control action. Even after abrupt shifts in irradiance circumstances, the PV voltage remained consistent with the required reference, indicating that the controller is resilient.

Fig. 15
figure 15

Continuously changing climatic conditions of irradiance and temperature.

Full size image
Fig. 16
figure 16

Voltage, power and duty cycle (PV side) under continuously changing climatic condition.

Full size image
Fig. 17
figure 17

Reference DC voltage on the actual voltage under continuously changing climatic condition.

Full size image
Fig. 18
figure 18

Plot of voltage and current (Grid side) under continuously changing climatic condition.

Full size image
Fig. 19
figure 19

Active power and reactive power (grid side) under continuously changing climatic condition.

Full size image

Despite the tough environmental circumstances, the DC link voltage remained constant at 500 V (see Fig 17). This suggests that the DC connection performed satisfactorily due to the strong control system.

It is apparent that the current injected into the grid was desirably synchronized with the voltage (see Fig 18). This suggests that the grid met the necessary specifications. Figure 19 clearly illustrates that the reactive current remained null after the transitory duration (approximately 140 ms), as intended. The active power follows the PV power that is sent to the grid segment. This demonstrates that the system worked in perfect harmony, since the control goal was met.

Comparison with state-of-the-art methods under continuously changing climatic conditions

Finally, the performance of the suggested MPPT controller for the grid-integrated system is compared to literature state-of-the-art approaches. The implemented state-of-the-art approaches include the traditional perturb and observe (P&O), metaheuristics such as the classical PSO, and the more recently created IDE algorithm. To quantify the performance of the MPPTs, we used two measurement indices: (1) the power yield (on PV side and grid side) measured as the mean power, and (2) the Integral of Absolute Error (IAE). The IAE, determined using Eq. (44), assesses how accurately the DC connection performs at the specified value.

$$IA{E}_{dc}=\underset{0}{\overset{T}{\int }}\left|{V}_{dc}-{V}_{dc,ref}\right|$$
(44)

Figures 20, 21 show the qualitative findings from the deployment of the different MPPT controllers on the same platform, whereas Fig 22 provide the quantitative results (24). Figure 20's power graphs enable for a visual comparison of the algorithms’ power performance. The PSO algorithm obviously performed the poorest in terms of power; it was impeded mostly by oscillations and slow convergence, which were most likely due to exploration-exploitation difficulties. In contrast, the IDE showed oscillations, but at a smaller level than the PSO. The P&O obviously outperforms the previously mentioned MPPTs in terms of reaction time. However, when compared to the proposed, it is clear that it converges more slowly. Furthermore, the power injected into the grid by the proposed MPPT is greater than that of the P&O and the other algorithms, as seen in Fig 23.

Fig. 20
figure 20

Plot of PV power for different MPPT algorithms-continuously changing climatic condition.

Full size image
Fig. 21
figure 21

DC link voltage considering different MPPTs-continuously changing climatic condition.

Full size image
Fig. 22
figure 22

Grid Active power for different MPPT algorithms-continuously changing climatic condition.

Full size image
Fig. 23
figure 23

Power Yield of PV and grid side considering different MPPTs continuously changing climatic condition.

Full size image

The DC link profile shown in Figure 21 shows that all algorithms kept the DC bus at 500 V. However, a deeper examination at the curves reveals that the suggested MPPT controller retains the best level of DC link stability. Initially, it was observed that it stabilized the DC connection faster than the other techniques. The IAE measurements in Fig 24 show that the suggested controller improved the stability and quality of the DC connection, obtaining the lowest IAE of only 10.6156.

Fig. 24
figure 24

IAE of the DC link for different MPPTs- continuously changing climatic condition.

Full size image

Finally, the grid active power under the management of the different MPPT algorithms shows that the suggested MPPT enabled the maximum active power injection into the electrical network, reported as (78.69 kW). This verifies the efficiency and durability of the suggested MPPT controller for the 100.0 kW grid connection.

Conclusion

This study has introduced and validated a novel MPPT control strategy for a grid-integrated photovoltaic energy system operating under rapidly changing environmental conditions. The proposed solution incorporates a sensor-efficient neural network and a nonlinear controller to overcome major limitations found in traditional and metaheuristic-based MPPT algorithms. By eliminating the need for real-time irradiance sensors, the design significantly reduces system complexity and cost, while ensuring fast and accurate tracking of the MPP. The first component of the controller leverages a mathematical irradiance estimation model, which enables the generation of MPP voltage references without relying on physical irradiance measurements. This estimate feeds into a RBF neural network that has been trained offline to map temperature and estimated irradiance to the optimal operating voltage of the solar array. This two-stage intelligent estimation structure provides a reliable and computationally efficient way to dynamically track the MPP. In the second stage, a nonlinear controller, guided by Lyapunov stability theory, was designed to enforce the computed reference voltage. Extensive simulations on a 100 kW grid-connected photovoltaic system validate the effectiveness of the proposed control framework. Under both step and continuously varying irradiance scenarios, the system maintained DC-link stability at the reference voltage of 500 V, while rapidly adjusting to changes in environmental conditions. The proposed MPPT controller demonstrated superior performance in terms of power yield, control accuracy, and grid synchronization when benchmarked against three widely used MPPT strategies Quantitative comparisons confirmed these observations. On the PV side, the proposed controller achieved a power yield of 80.41 kW, surpassing P&O (79.71 kW), IDE (73.44 kW), and PSO (59.34 kW). Similarly, grid-side active power was highest for the proposed controller at 78.69 kW, again outperforming all other methods. Furthermore, the controller achieved the lowest IAE of the DC link voltage at 10.6156, indicating enhanced voltage regulation and reduced deviation from the reference value. In conclusion, the proposed MPPT controller offers a powerful, efficient, and sensor-reduced solution for grid-tied PV systems, delivering fast MPP convergence, strong voltage stability, and superior energy yield under real-world conditions. These advantages make it a promising candidate for future deployment in large-scale solar energy systems, particularly those requiring high reliability and performance in the face of environmental variability. Future work could extend the proposed system and control solution to partial shading scenarios.