Introduction

Karst landforms are one of the major landform types globally, covering approximately 15% of the Earth’s land area. They are characterized by high ecological sensitivity, low environmental carrying capacity, and frequent natural disasters, making them highly sensitive and vulnerable ecological systems1. Under the combined influence of landform features and human activities, karst regions exhibit multiple types of disasters, high frequencies, long disaster chains, and significant regional disparities2,3. Furthermore, with the increasing frequency and scale of extreme climate events globally, coupled with the continued urbanization and concentration of population and wealth in urban areas, karst small towns (KST) will exhibit higher vulnerability and susceptibility4. However, due to the limitations imposed by landform conditions and socio-economic development levels, issues such as the ineffectiveness of disaster prevention measures, delayed disaster response, and insufficient resource allocation directly constrain the improvement of disaster response, recovery, and adaptation capabilities in KST5,6,7. The fundamental cause of the constraints on disaster response, recovery, and adaptation in KST lies in the mismatch between resource allocation and disaster needs during the rapid urbanization process8,9. Effectively addressing the imbalance between resource availability and disaster needs in KST has become key to enhancing their disaster response, recovery, and adaptation capabilities10,11.

In the academic circle, scholars believe that the main body of small towns is organic towns, and their main dispute lies in whether the main composition of small towns should include small cities, county seats or towns and townships12. Globally, definitions of small towns vary significantly due to differences in social structures, land use patterns, economic development levels, and regional contexts. For instance, the United States defines small towns as settlements with a population ranging from 200 to 50,00012. Some economically underdeveloped developing countries define small towns as settlements with residents ranging from 5,000 to 20,00013. In China, small towns, defined as those with populations ranging from 5,000 to 250,000, are considered the foundation of the urban–rural system pyramid. They serve as critical nodes for linking urban and rural areas, alleviating the pressure on large cities, and promoting rural revitalization14. This study adopts this concept. But no matter how small towns are defined, problems such as insufficient disaster prevention capacity, limited response capacity and lack of Disaster-resilient resources (DR) are common issues in disaster prevention and control of KST. Enhancing the disaster adaptability and resilience of KST is a global practical challenge.

DR encompass various supplies, equipment, technologies, funds, and human resources that can provide support and assistance in a disaster15. The tight balance state (TBS) of DR refers to a situation where resource reserves and disaster management demands reach basic equilibrium. In this state, DR is capable of meeting disaster management demands despite not being in oversupply. The ability of hazard-affected bodies to “adapt to” and “withstand” disasters is exceptionally strong in the TBS; maintaining such equilibrium is crucial for enhancing the disaster resistance and adaptation capacities of the affected entities.

Existing studies primarily use aggregation functions, the ARC-D Toolkit, DPOR, and other methods to quantify urban resilience across regional16, urban17, community18, and individual dimensions19. These approaches fail to comprehensively consider the full range of disaster causality and long-term impacts, lacking a systemic understanding of resource allocation and the dynamic evolution of disasters20,21. Some researchers have examined different stages of disaster and discussed effective methods or measures for improving urban preparedness at each stage22,23,24,25. However, their studies often neglect the dynamic adaptation process of KST during the disaster. Furthermore, their discussions primarily focus on large cities or megacities, with relatively little targeted research on KST26,27,28,29. Furthermore, existing research primarily focuses on disaster-inducing factors30,31, disaster assessment32, and disaster governance33, exploring ways to enhance the resilience of KST. However, studies based on the resource base of these towns are relatively scarce. Studies focusing on the interaction between DR and disaster management demands remain largely underexplored, and the conclusions or methods derived are unable to provide insights for enhancing the disaster resilience of KST. We focused on a typical karst region in China to explore the TBS in KST and the mechanism to maintain such a state by employing the DPSIR-TOPSIS, coupling coordination degree model (CCDM), and obstacle factor diagnosis models, in order to provide a scientific reference for the improvement of disaster adaptability and resilience of KST worldwide.

Materials

Study area

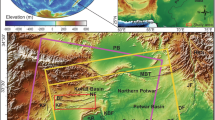
The typical karst region in China, situated in central Guizhou Province, encompasses approximately 30.5% of the province’s total land area (Fig. 1). Renowned for its karst diversity, this region exhibits the most complex geological structures, the widest distribution of carbonate rock strata, and the most fragile ecological environment in Guizhou. The province’s karst terrain extends over 109,084 square kilometers, accounting for 61.9% of its total area, ranking it among the three largest contiguous karst regions worldwide. Characterized by rugged mountainous and hilly landscapes, a subtropical humid monsoon climate, and frequent heavy rainfall, the region is highly susceptible to surface erosion and deformation34. Furthermore, socio-economic development has exacerbated human-environment conflicts35. Guizhou exhibits a unique array of disaster characteristics, including extensive disaster-prone environments, diverse triggering factors, intricate disaster chains, and heterogeneous disaster-bearing entities. These challenges have created a persistent dilemma: the coexistence of frequent geological disasters and limited resources34. Despite continued efforts to strengthen disaster prevention and mitigation networks, enhance disaster management capabilities, and allocate more disaster-resilient resources, the province remains constrained by economic limitations and its challenging terrain. Between 2011 and 2020, Guizhou experienced over 1,800 geological disasters36. In 2020 alone, small towns within the study area endured direct economic losses totaling $7.86 billion, representing 62% of the province’s total direct economic losses from natural disasters that year.

Fig. 1
figure 1

The research area. Provincial administrative boundary data is sourced from the National Platform for Common GeoSpatial Information Services (https://www.tianditu.gov.cn/), and the zoning data for the typical karst region in China is sourced from the Guizhou Provincial Department of Natural Resources (https://zrzy.guizhou.gov.cn/). The software used is ArcGlS 10.2 (https://www.malavida.com/en/soft/arcgis/).

Full size image

Data sources

The statistical indicators in this study involved data related to infrastructure, disaster statistics, and land use across 28 cities in the typical karst region of China. In total, 1,036 indicators were considered in the analysis. The “China City Statistical Yearbook (2017–2021)” served as a primary source for the specific indicator data. Given variations in data collection scales and formats among the towns and cities in the research area, supplementary information was sourced from each city’s and county’s statistical yearbooks and their statistical bulletins from 2017 to 2021, and other relevant materials. In instances where individual indicators lacked data, the mean value method was employed to supplement the data based on adjacent years.

Methods

Research methodology

The essence of the TBS is to resist, respond, and adapt to the impact and changes of a disaster through reasonable coordination of the limited DR (Fig. 2). Research on this topic and the mechanisms to maintain such an equilibrium involves three aspects: (1) quantifying the TBS in KST; (2) identifying the interactions of internal elements within the TBS system and the mechanism underlying such interactions; and (3) examining the cause of the TBS in KST disaster-ready resources and proposing corresponding strategies to optimize resource allocation.

Fig. 2
figure 2

Study framework.

Full size image

The DPSIR model

The DPSIR model offers flexibility in integrating multiple dimensions of environmental issues, emphasizing the continuous feedback loops between the components of the system37. This allows it to effectively capture the dynamic relationships influencing environmental outcomes, providing a systematic approach to understanding how factors such as society, economy, environment, and disasters contribute to changes in the state of KST38. Furthermore, the DPSIR model can incorporate both quantitative and qualitative data, making it adaptable to various research methodologies. This flexibility enables it to integrate both quantitative and qualitative data, making it adaptable to various research methodologies39. By using the DPSIR model, the complex interactions between socio-economic activities and environmental factors within systems like KST can be better understood. It enables a deeper exploration of the interactions and feedback mechanisms influencing the TBS in KST, ultimately supporting more informed decision-making in disaster risk reduction and resilience planning. This capability allows for a comprehensive analysis of disaster resilience in KST, facilitating wiser decisions in mitigating disaster risks and improving adaptive capacity in such regions. The TBS analysis framework of KST based on the DPSIR model is shown in Fig. 3.

Fig. 3
figure 3

TBS analysis framework based on DPSIR model.

Full size image

The evaluation indicator framework of the TBS

The TBS is a complex system. It emphasizes the resistance, response, and adaptive capabilities of these resources throughout the entire disaster process. This is aimed at mitigating intense fluctuations and changes within the system40. Consequently, drawing on the research contributions of scholars such as Beccari, Chen et al. and Parsons et al. in the field of enhancing urban disaster resilience20,41,42, and integrating the DPSIR model’s five subsystems of Driving Forces (D), Pressures (P), States (S), Impacts (I), and Responses (R), we constructed an assessment and mechanistic research indicator framework (Table 1). This framework is established based on principles of scientific rigor, practicality and feasibility, and consideration of the specific conditions in the typical karst terrain of China.

D: Potential drivers that facilitate changes of the TBS, which propel pressure on and development of the state43. The enhancement of urban construction standards, growth of overall economic strength, and development of the social environment contribute to the bolstering of a city’s disaster response capabilities. This improvement involves an increase in the sufficiency of disaster prevention facilities and disaster-preparedness resources, thereby augmenting the overall stability of the system. However, it also leads to the complexity of the disaster environment, an escalation of potential losses, and an increased burden on the city resulting from efforts made to achieve disaster preparedness44,45.

P: The direct reason that causes changes in the TBS and leads to influences on the entire system, particularly negative consequences46. The growth and concentration of populations and wealth increase the disaster frequencies and contribute to potential pressure that cause disaster changes. The occurrence of a disaster and the actions that should be taken to prevent place direct pressure on the TBS47.

S: The resources or elements that render the stability of the entire system susceptible to changes due to the dynamics of pressures48. The states involve two dimensions: first, the vulnerability of the social public health resource reserves becomes further exposed during the disaster process, consequently affecting the stability of the overall system; second, the household DR reserves, as indicated by Zhang et al. are prone to the impact of disasters with weak recovery capabilities49.

I: The negative social, economic, environmental, and other influences caused by changes in the TBS50.

R: Response entails actions aimed at alleviating and adapting to the adverse impacts resulting from changes in TBS. These actions also involve measures to prevent or reverse unfavorable changes. The significance of response lies in its comprehensive provision of disaster information, enhancement of disaster response capabilities, and the improvement of stability in the TBS51. The capacity for allocation DR is a crucial indicator for assessing urban disaster response capabilities. Ensuring the effective distribution of essential DR, such as food, water, shelter, and pharmaceuticals, to corresponding environments is paramount. Importantly, the reserve of disaster-resilient skills reflects a city’s ability to learn from and utilize past experiences in disaster prevention and mitigation.

Additionally, to analyze the relationship between DR and disaster demand within the TBS, the five subsystems of DPSIR are categorized into two classes: supply and demand. The Supply (Sup) class includes D, S, and R, representing the specific components and mechanisms of DR supply in KST. The Demand (Dem) class includes P and I, indicating the losses caused by disasters and the consumption of DR in disaster prevention and mitigation efforts in KST.

Table 1 The evaluation indicator framework of the TBS.
Full size table

The entropy weight TOPSIS model

The TOPSIS model ranks a finite set of evaluation objects based on the proximity gap between these objects and an ideal reference object, thereby conducting a relative performance assessment among all evaluation objects52,53. Traditional TOPSIS models employ weight calculation methods such as the Delphi approach and the Analytic Hierarchy Process, which exhibit a significant degree of subjectivity. This subjectivity can impact the objectivity of the results in the assessment of the TBS. The introduction of the entropy weight method to modify TOPSIS provides an effective means to consider the variability of each indicator, while mitigating the influence of subjective factors54.

  1. (1)

    The standardization of evaluation indicators.

    The standardization of positive indicators is calculated using the following equation 

    $$yij={{\left[ {x(i,j) - xmin(j)} \right]} \mathord{\left/ {\vphantom {{\left[ {x(i,j) - xmin(j)} \right]} {\left[ {xmax(j) - xmin(j)} \right]}}} \right. \kern-0pt} {\left[ {xmax(j) - xmin(j)} \right]}}$$
    (1)

    The standardization of negative indicators is calculated using the following equation 

    $$yij={{\left[ {x{\text{max}}(j) - x(i,j)} \right]} \mathord{\left/ {\vphantom {{\left[ {x{\text{max}}(j) - x(i,j)} \right]} {\left[ {x{\text{max}}(j) - x{\text{min}}(j)} \right]}}} \right. \kern-0pt} {\left[ {x{\text{max}}(j) - x{\text{min}}(j)} \right]}}$$
    (2)

    In Eqs. (1) and (2): \(x{\text{(}}i,j{\text{)(}}i={\text{1}},{\text{2}}, \ldots ,m\); \(j={\text{1}},{\text{2}}, \ldots ,n{\text{)}}\). \(yij\) refers to Indicator j of Town i in the typical karst region, and \(x\hbox{max} \left( j \right)\) and \(x\hbox{min} \left( j \right)\) represent the maximum and minimum values of Indicator j, respectively.

  2. (2)

    Calculations in the TOPSIS approach.

    First, the information entropy of Indicator j, \(Hj\), is calculated through the following equation 

    $$Hj=-k\sum\limits_{{i=1}}^{m} {pij\ln (pij)}$$
    (3)

    In Eq. (3), m represents the number of cities (similarly hereinafter), which is 28; \(k={1 \mathord{\left/ {\vphantom {1 {\ln m}}} \right. \kern-0pt} {\ln m}}\), k > 0, and ln is a natural logarithm; \(pij={{yij} \mathord{\left/ {\vphantom {{yij} {\sum\limits_{{i=1}}^{m} {yij} }}} \right. \kern-0pt} {\sum\limits_{{i=1}}^{m} {yij} }}\), and when \(pij=0\), \(pij\ln pij=0\).

    Subsequently, the standard deviation of Indicator j, \(Gj\), is calculated using the following equation 

    $$Gj=1 - Hj$$
    (4)

    Finally, the weight of Indicator J, \(Wj\), is calculated as below.

    $$Wj={{Gj} \mathord{\left/ {\vphantom {{Gj} {\sum\limits_{{i=1}}^{n} {Gj(n=1,2, \ldots ,30)} }}} \right. \kern-0pt} {\sum\limits_{{i=1}}^{n} {Gj(n=1,2, \ldots ,30)} }}$$
    (5)

    In Eq. (5), n stands for the number of indicators in the evaluation indicator framework of the TBS in the typical karst region in China (similar hereinafter), which is 30.

  3. (3)

    Developing a weighted normalized matrix, V, for the assessment of the TBS in the typical karst region in China.

    $$V=\left| {Vi} \right|m \times n=Wj \times Yij$$
    (6)

    In Eq. (6), \(Yij\) represents the standardized matrix.

  4. (4)

    Identifying the positive and negative ideal solutions.

    The best and worst solutions of the evaluation indicators of the TBS in the typical karst region in China were calculated, yielding \({Z^+}\), the best solution, and \({Z^ - }\), the worst solution, based on the following equation 

    $${Z^+}=\left\{ {\hbox{max} \sum\limits_{{1 \leqslant i \leqslant m}} {Zij} } \right.\left| {i=1,2,} \right. \ldots ,\left. m \right\}=\left\{ {z{1^+}} \right.,z{2^+}, \ldots ,\left. {z{m^+}} \right\}$$
    (7)
    $${Z^ - }=\left\{ {\hbox{min} \sum\limits_{{1 \leqslant i \leqslant m}} {Zij} } \right.\left| {i=1,2,} \right. \ldots ,\left. m \right\}=\left\{ {z{1^ - }} \right.,z{2^ - }, \ldots ,\left. {z{m^ - }} \right\}$$
    (8)
  5. (5)

    The distance between each town and the best solution,\(D{j^+}\), and that between each town and the worst solution,\(D{j^ - }\), were calculated respectively.

    $$D{j^+}=\sqrt {\sum\limits_{{i=1}}^{m} {{{(zij - z{i^+})}^2}} }$$
    (9)
    $$D{j^ - }=\sqrt {\sum\limits_{{i=1}}^{m} {{{(zij - z{i^ - })}^2}} }$$
    (10)

Defining the nearness degree between each town and the ideal solutions, identified as \(Ci\).

$$Ci=\frac{{D{i^ - }}}{{D{i^ - }+D{i^+}}}$$
(11)

In Eq. (11), \(Ci\) is between 0 and 1. A higher proximity to 1 indicates a shorter distance between the relevant town and the positive ideal solution, and a longer distance between it and the negative ideal solution. This signifies higher stability in the TBS. On the contrary, a closer proximity to 0 indicates a longer distance between the town and the positive ideal solution, as well as a shorter distance between it and the negative ideal solution, indicating lower stability of the TBS.

The coupling coordination degree model

The coupling degree measures the intensity of the interaction between two or more subsystems within a system. It can reflect the interaction, influencing mechanisms, and level of benign coupling between different subsystems. However, the TBS is a dynamic and complicated system. A conventional coupling degree model can only reflect the coupling intensity of the system without the ability to showcase the system’s coordination level. Thus, we introduced the CCDM39. The model is as follows:

$$C={\text{n}}{\left\{ {\frac{{U1 \times U2 \times \cdot \cdot \cdot \times U{\text{n}}}}{{{{\left[ {U1+U2+ \cdot \cdot \cdot +U{\text{n}}} \right]}^{\text{n}}}}}} \right\}^{\frac{1}{{\text{n}}}}}$$
(12)
$$T={\beta _1}{U_1}+{\beta _2}{U_2}+ \cdot \cdot \cdot +{\beta _{\text{n}}}{U_{\text{n}}}$$
(13)
$$H=\sqrt {C \times T}$$
(14)

Among these values, n represents the number of the objects of the study, \({U_1},{U_2},{U_3}, \cdot \cdot \cdot {U_{\text{n}}}\) represents the comprehensive value of each object, \(\beta 1,\beta 2,\beta 3 \cdot \cdot \cdot \beta {\text{n}}\) stands for a pending parameter, and \(\beta 1+\beta 2+\beta 3+ \cdot \cdot \cdot +\beta {\text{n=1}}\). This study adopts a CCDM to examine the overall coupling coordination degree (CCD) of the five subsystems of the DPSIR and the CCD each of the two subsystems. The CCD is a key indicator in this study for assessing the dynamic interactions and overall coordination of KST in disaster scenarios. A higher value indicates better synchrony and overall performance between the two subsystems. The five subsystems consist of D, P, S, I, and R, and each is equally important when the overall coupling coordination degree is being examined. If the coupling coordination between each of the two subsystems is being analyzed, C represents the coupling degree and ranges between 0 and 1. T stands for the coordination degree, and H represents the coupling coordination degree. H ranges between 0 and 1. A larger H indicates better coordinated development of the system, and a smaller H indicates the contrary. The CCD are presented below (Table 2).

Table 2 Grade classification of CCD.
Full size table

The obstacle factor diagnosis model

The obstacle factor diagnosis model can precisely and comprehensively recognize influencing factors that constrain the development of the system55. The indicator contribution degree \(Mi\), the indicator deviation degree \(Si\), and the constraint degree of a performance-level indicator \(Hi\) are introduced to build a model for the diagnosis of obstacle factors of the TBS.

$$ni=\frac{{Si \times Mi}}{{\sum\limits_{{i=1}}^{m} {\left( {Si \times Mi} \right)} }}$$
(15)

In the equation, \(Hi\) stands for the constraint degree of a performance-level indicator, which refers to the degree of influence such an indicator has on the TBS. A larger \(Hi\) indicates a higher degree of influence. \(Mi\) represents the indicator contribution degree, the value of which is the weight of the indicator, calculated through the entropy weight method. \(Si\) stands for the indicator deviation degree, which signifies the distance between an indicator and an ideal TBS of each town. \(Si=1-Xi\), and \(Xi\) stands for the normalization value of Indicator i.

The characteristics and mechanism analysis of TBS

The characteristics and mechanism of the TBS

Figure 4a presents an overview of the TBS values in the study area, including the maximum (Max), minimum (Min), average (Avg), and standard deviation (SD). Figure 4b, a box plot, illustrates the distribution of TBS values in the region, highlighting the interquartile range (IQR), median, and outliers (Max and Min). The box plot visually represents the median, quartiles, anomalies, and data variability. The overall TBS of the region is stable but at a low level, the five-year average is just 0.355 and there are obvious differences among KST. Besides the mutual differences show a gradually increasing trend (SD: increases from 0.289 to 0.308). The data in the box plot is mainly concentrated below the median, indicating that the base number of KST with low TBS is large (Fig. 4). However, due to the cliff-like lead of the outlier (Guiyang), the overall TBS level of the region has been improved.

Fig. 4
figure 4

The stability of the TBS in the typical karst region in China from 2017 to 2021.

Full size image

The spatial mechanisms of the TBS in KST within the typical karst region in China from 2017 to 2021 revealed an evolving pattern characterized by a “high in the south and low in the north” transition to a regional multi-center structure (Fig. 5). From 2017 to 2019, the southern cluster centered around downtown Guiyang, Longli, and Kaili exhibited a higher TBS compared to the northern cluster centered around the Honghuagang and Huichuan, indicating a gradual expansion trend toward the north. In the years 2020 to 2021, a “regional multi-center structure” essentially formed, with downtown Guiyang as the absolute center, the Honghuagang and Huichuan and Renhuai as northern centers, and the towns of Kaili and Xixiu as southern centers. The spatial evolution of the TBS is intricately linked to the urbanization development strategy of Guizhou Province. In 2010, the Guizhou Province proposed a spatial development framework centered on Guiyang, with support from cities such as Zunyi, Anshun, Duyun and Kaili. The geographical proximity of the southern clusters to developed regions such as the Guangdong–Hong Kong–Macao Greater Bay Area enables positive influence from these regions, thereby promoting urbanization and economic development within the region. Consequently, a spatial pattern featuring differentiation between the northern and southern regions gradually emerged. In 2017, Guizhou province introduced the “Development Plan for Urban Agglomerations in the Typical Karst Area in China,” which emphasized the strategy to expand and strengthen the core towns while actively constructing major cities including Zunyi, Bijie and Anshun. This strategic approach aimed to facilitate the overall coordinated development of the social and economic aspects of the northern and southern clusters, optimizing the urbanization discrepancies between them. Regional centers such as Xixiu t and Honghuagang have begun to stand out and have played a catalytic role in the socio-economic development of the surrounding areas. Regrettably, however, the current resource siphoning phenomenon in the central areas is far stronger than the radiation and driving capacity they can exert. The areas surrounding central towns are generally characterized by low-value KST.

Fig. 5
figure 5

The spatial evolution of the stability of the TBS from 2017 to 2021. Boundary data is sourced from the Guizhou Provincial Department of Natural Resources (https://zrzy.guizhou.gov.cn/). The software used is ArcGlS 10.2 (https://www.malavida.com/en/soft/arcgis).

Full size image

The CCD results of the TBS

The CCD exhibits characteristics of high coupling and low coordination differentiation. The coupling degree remains at a high coordination level (average value of 0.75), while the coordination degree is at a mild dissonance level (average value of 0.43). This indicates that within TBS, there is a strong interdependence and connectivity among subsystems, but there is a lack of coordination and mismatch in their interactions and cooperation. This differentiation may result in TBS showing vulnerability in disaster response, limiting the system’s ability to respond and recover. The average CCD value is 0.56, which is at a moderate coordination level (Fig. 6a), indicating challenges in the effective allocation and management of DR, necessitating better integration and coordination of resources and actions across different subsystems.

Fig. 6
figure 6

The CCD results of the TBS from 2017 to 2021.

Full size image

To further reveal the causes of this situation, the study conducted a CCD analysis of the five subsystems of DPSIR as well as the Sup and Dem categories, as shown in Fig. 6b. W With the full outbreak of COVID-19 in 2019, the rapid increase in R led to the swift depletion of DR. However, due to the strict isolation and control measures implemented by the government, DR could not be replenished in time. As a result, except for R×P and R×D, which showed an upward trend, the CCD of other subsystems exhibited a downward trend. The decline was most pronounced in S×I, P×S, I×R, and R×S. The upward trend in R×P and R×D indicates that, under increased disaster pressure, the response mechanisms of the system were adjusted and optimized due to policies and measures being more aligned with actual disaster needs, enhancing the system’s disaster response capability. The significant decrease in S×I, P×S, and R×S reflects the lack of ability of KST to cope with high-intensity, large-scale sudden disaster risks, especially the S subsystem, which struggles to make timely and effective adjustments to address the pressures brought by disaster risks. The decline in I×R suggests that although R has strengthened, KST still lack the capacity to respond effectively to the negative impacts of disaster risks. While Sup×Dem has decreased, it remains at a moderate coordination level, highlighting the TBS system characteristic of KST, which indicates that the system may degrade but not collapse.

The CCD is gradually evolving from a “high in the south and low in the north” pattern to a multi-center regional structure (Fig. 7), which aligns with the spatial evolution of the TBS. High TBS values also correspond with high CCD values. This indicates that advancing the coupling and collaborative relationships between subsystems is a key measure for effectively enhancing the TBS of KST, as well as strengthening their disaster adaptation and recovery capabilities. The number of KST in each CCD stage remains relatively stable, possibly because the current typical karst region emphasizes economic development while neglecting disaster management and the configuration and improvement of DR for KST. The TBS of KST surrounding Qingzhen is higher than that of Qingzhen itself, significantly influenced by resource siphoning, ultimately making it the only moderate dissonance small town.

Fig. 7
figure 7

The spatial evolution of the stability of the CCD from 2017 to 2021. Boundary data is sourced from the Guizhou Provincial Department of Natural Resources (https://zrzy.guizhou.gov.cn/). The software used is ArcGlS 10.2 (https://www.malavida.com/en/soft/arcgis).

Full size image

The obstacle factor diagnosis results of the TBS

A constraint diagnosis at the subsystem level can directly reflect the constraint degrees of the five subsystems. However, due to the high generality at this level, disparities between specific indicators might be obscured if the analysis of obstacle factors of TBS is based solely on subsystem constraint degrees. Therefore, to thoroughly investigate the obstacle factors affecting TBS, further diagnosis at the indicator level is necessary. Considering the large number of indicators, only the eight with the highest constraint degrees were selected for visualization. The results of obstacle factor diagnosis at both the system and indicator levels from 2017 to 2021 are shown in Fig. 8.

Fig. 8
figure 8

The diagnostic results of obstacle factors.

Full size image

The diagnostic results indicated that D (Obstacle degree: 123) was the most influential obstacle factor, followed by R (Obstacle degree: 116), S (Obstacle degree: 99), P (Obstacle degree: 91), and I (Obstacle degree: 71). In 2020, the COVID-19 pandemic fully erupted in the study area, prompting the government to initiate a provincial-level emergency response to major public health incidents. This response involved the coordinated allocation of medical resources across society, the isolation and control of potential transmission sources, and widespread public mobilization to fight the pandemic. These measures led to R replacing D as the primary obstacle factor, highlighting the critical role of the government, as the policymaker and administrator of KST, in ensuring the rapid flow and effective distribution of DR across various subsystems. Throughout the research period, the average P value of KST was 18.19, showing an increasing trend. This suggests that with ongoing urbanization, the disaster environment in KST will become more complex. However, due to the current low concentration of population and wealth in KST, the impacts of disasters and secondary disasters remain relatively minor.

The main obstacle indicator is ROD (Obstacle degree: 92), which is reflected in limited expenditure on science and technology and inadequate disaster prevention and rescue capabilities. The lack of advanced disaster monitoring and early warning technologies, along with inefficient prevention and control measures, contributes to increased disaster frequency and casualties. Regarding the limitations of D, it was determined that there were reductions in obstacles related to UCC (decreased from 12 to 9), accompanied by an increase in obstacles related to SDL (increased from 5 to 7). This indicates that while extensive urbanization has improved the level of urbanization in KST, the construction of social public facilities has not kept pace with urban development. Strengthening the construction of public service facilities in KST and achieving interconnectivity and sharing of core public service facilities are effective means to enhance TBS. Although the hindrance degree of PMR (decreased from 10 to 7) and FAR (decreased from 11 to 9) has reduced, other indicators, such as ROD, EDL (increased from 7 to 9), ECI (increased from 7 to 10), and SOI (increased from 2 to 4), have shown significant increases. This suggests that, despite the increase in DR, the lack of effective resource allocation for DR has severely limited the improvement of resilience capacity in KST.

Discussion

Compared with KST, the economic development level, urbanization development and infrastructure construction in other urban areas are more advanced and complete, which enables them to have more DR to prevent and respond to disasters, and they are also stronger in terms of resource utilization capacity and resource allocation efficiency56,57. There are unique characteristics between the DR and disaster demands in KST. DR can basically meet the disaster demands, but there is no redundancy in DR, which puts forward a higher requirement for the DR resource allocation capacity of KST, and the disaster environment in KST is also more complex and frequent58,59. Therefore, this study examined the TBS of KST.

Using the DPSIR model to study the TBS of KST is a fast and effective method. This model fully considers the five subsystems: D, P, S, I, and R, allowing for a comprehensive and quantitative analysis of TBS. This approach enhances our understanding of the dynamic relationship between DR allocation and disaster demands within KST. It promotes the optimization of DR allocation and the formation of a systematic disaster adaptation and recovery structure, thereby achieving sustainable development of KST.

Central KST can radiate and enhance the DR allocation capacity and efficiency of edge towns, improving the effectiveness of disaster governance. This finding aligns with disaster research results from other urban areas60,61. However, the current siphoning capacity of central towns is significantly stronger than their radiation-driven capacity. The reason for this discrepancy may be due to several factors, including the challenges posed by the karst topography, which complicates infrastructure development and increases construction costs, as well as the highly imbalanced socio-economic development across regions62. As a result, the radiation capacity of central KST is weakened, while their well-developed socio-economic status strengthens their siphoning ability over surrounding KST. Policymakers and government managers need to address this issue and implement active and effective measures to improve it. These measures could include promoting the construction of a regional division of labor and cooperation mechanism, strengthening regional infrastructure, and ensuring a balanced layout of public facilities.

The CCD results of the subsystems indicate that building a small-town system with central towns as the main body and edge towns as supplements is feasible. This approach can promote cross-regional allocation and sharing of DR, further enhancing the radiation-driven efficiency of central towns. However, effectively coordinating the relationship between central and edge towns presents significant challenges. The strong coupling relationship of the subsystems may amplify the siphoning effect of central towns, which is detrimental to the region’s coordinated development. Therefore, it is necessary to formulate a scientific, reasonable, and forward-looking regional development strategy. This strategy should clarify the functional positioning and development direction of both central and edge towns, avoiding blind competition and disorderly development within the region.

The diagnostic results of the obstacle factors highlight a major dilemma faced by KST in rapidly urbanizing areas: how to coordinate the relationship between the rate and quality of urbanization development. The extensive urbanization in the study area has indeed stimulated short-term economic growth and urban expansion, but it has also led to serious issues such as inadequate DR allocation and lagging public service infrastructure development. These problems have consequently reduced the efficiency of disaster prevention and control in these towns63. Therefore, it is imperative to focus on improving the quality of urbanization, transitioning from extensive to intensive development. Our research indicates that enhancing the social development level of KST, such as by strengthening public service facilities and increasing capital investment in infrastructure, are effective measures to boost disaster adaptability and resilience. Moreover, the research underscores the government’s proactive role in DR allocation. By intervening in regional DR circulation and optimizing DR allocation at the KST, the government can improve the targeting and scientific accuracy of DR distribution, thereby reducing the losses and impacts caused by disasters.

The research requires the integration of multiple dimensions of KST and the continuous feedback loops between system components. The DPSIR model, when applied to the study of disaster resilience and DR management in KST, helps reveal the relationships between D, P, S, I, and R. However, it is undeniable that the DPSIR model gives limited consideration to socio factors, local knowledge, and community behaviors in the disaster adaptation process. These factors, however, can also enhance the disaster resilience of KST. The indicators we selected are primarily objective data, such as urbanization development, economic level, and investment in disaster prevention funds, to maximize the applicability and objectivity of the indicator framework and quantitative results. However, differences in the social, economic, and political backgrounds, as well as the disaster environments of KST, and subjective factors like residents’ risk awareness and community cohesion, can also significantly enhance the disaster adaptability and resilience of KST. Moreover, further exploration is warranted into the dynamic and complex relationship between resources and disasters. This includes refining the indicator model and expanding data sources. Future research can delve deeper into these issues, enhancing our understanding and ability to mitigate disaster risks effectively.

Conclusion

As disaster-prone areas without adequate disaster prevention capabilities, KST need to enhance their ability to sustain the TBS, particularly against the backdrop of escalating global urban disaster risks. Based on the urban-rural statistical data and disaster statistical data in typical karst landform areas of China, the entropy weight DPSIR model, CCDM and obstacle factor diagnosis model were comprehensively adopted to study the TBS of KST. The main conclusions obtained are as follows:

  1. (1)

    The TBS is at a low level, with a five-year average of only 0.355. The disparities between KST are gradually increasing. Guiyang’s TBS significantly outpaces other KST, thereby raising the regional overall TBS level.

  2. (2)

    Under the positive guidance of the urbanization strategy in Guizhou Province, the spatial mechanism of TBS has evolved from a “high in the south, low in the north” pattern to a regional multi-center structure. Central KST exhibit both siphoning and radiative driving capabilities, with siphoning capacity being stronger than radiative driving capacity.

  3. (3)

    The average CCD value is 0.56, indicating a moderate coordination level and showing a differentiated feature of high coupling but low coordination. There is strong interdependence and connectivity between subsystems, but their interactions and cooperation lack coordination and are mismatched. Strengthening the coupling and collaborative relationships between subsystems is a key measure for effectively improving the TBS of KST and enhancing their disaster adaptation and recovery capabilities.

  4. (4)

    The diagnosis results of obstacle factors show that D is the main constraint factor, followed by R, S, P, and I. The government can adopt proactive interventions to enhance the targeting of DR allocation and circulation. The lack of advanced disaster monitoring and early warning technologies is a major cause of increased disaster socio-economic losses in KST.