Optimizing ternary hybrid nanofluids using neural networks, gene expression programming, and multi-objective particle swarm optimization: a computational intelligence strategy

Abstract

The performance of nanofluids is largely determined by their thermophysical properties. Optimizing these properties can significantly enhance nanofluid performance. This study introduces a hybrid strategy based on computational intelligence to determine the optimal conditions for ternary hybrid nanofluids. The goal is to minimize dynamic viscosity and maximize thermal conductivity by varying the volume fraction, temperature, and nanomaterial mixing ratio. The proposed strategy integrates machine learning, multi-objective optimization, and multi-criteria decision-making. Three machine learning techniques—GMDH-type neural network, gene expression programming, and combinatorial algorithm—are applied to model dynamic viscosity and thermal conductivity as functions of the input variables. Then, the high-performing models provide the foundation for optimization using the well-established multi-objective particle swarm optimization algorithm. Finally, the decision-making technique TOPSIS is employed to identify the most desirable points from the Pareto front, based on various design scenarios. To validate the proposed strategy, a ternary hybrid nanofluid composed of graphene oxide (GO), iron oxide (Fe₃O₄), and titanium dioxide (TiO₂) was employed as a case study. The results demonstrated that the combinatorial approach excelled in accurately modeling (R = 0.99964–0.99993). The optimization process revealed that optimal VFs span a broad range across all mixing ratios, while optimal temperatures were consistently near the maximum value (65 °C). The decision-making outcomes indicated that the mixing ratio was consistent across all design scenarios, with the volume fraction serving as the key differentiating factor.

Introduction

Optimizing thermal equipment through heat transfer enhancement (HTE) techniques increases thermal efficiency, reduces energy consumption, and compacts devices¹. The various HTE strategies can be grouped into two main classes: active and passive. In the first type, external forces such as electric/magnetic fields², surface/fluid vibration³, or fans/pumps⁴are the main elements for HTE. However, implementing complex and expensive external mechanisms is considered a serious challenge. In contrast, passive strategies that create geometric modifications such as surface roughness/treatment⁵and extended surfaces^6,7or add porous materials⁸, micro/nano-sized materials, and twisted tapes⁹help improve system performance. Among the passive methods, dispersing metal, metal oxide, and carbon-based nanomaterials is an appealing and widely used idea. Choi and Eastman¹⁰introduced this idea, which subsequently exhibited considerable promise in enhancing diverse fluids’ thermal, rheological, and tribological characteristics over time. This concept gave rise to a new fluid classification known as hybrid nanofluids, created by dispersing multiple nanomaterials into the base fluid¹¹.

Hybrid nanofluids show promising prospects for modifying thermophysical properties (TPPs), particularly thermal conductivity (TC) and dynamic viscosity (DV)¹². In recent years, the interest of numerous researchers has been drawn towards binary and ternary hybrid nanofluids¹³. Even with its nascent stage, the research on ternary hybrid nanofluids (THNF) holds great potential for widespread industrial applications, as indicated by the promising outcomes of limited studies¹⁴. Recent laboratory experiments on the thermophysical characteristics of THNFs are presented in Table 1.

Hybrid nanofluids, particularly ternary hybrids, offer versatile applications due to their tunable thermophysical properties, achieved by varying the ratio of nanomaterials. In heat exchangers, they enhance energy efficiency through superior thermal conductivity. Their customizable viscosity and thermal performance make them ideal for electronic cooling systems, managing high heat loads in compact spaces. In thermal energy storage systems, their adaptable properties optimize heat retention and transfer, improving renewable energy systems’ reliability. Additionally, ternary hybrid nanofluids find applications in solar energy technologies, enhancing the efficiency of solar collectors¹⁵. Their flexibility in tailoring thermophysical properties makes them highly suitable for diverse industrial needs.

Table 1 Recent experimental studies on measuring the DV and TC of THNFs.

In order to develop highly efficient nanofluids, especially THNFs, it is essential to have a comprehensive understanding of their thermophysical properties. The complex nature of nanofluids arises from the interaction of multiple parameters, including those of the base fluid and nano-additives, which collectively influence their TPPs. By utilizing artificial intelligence (AI) tools, robust regression-based models between TPPs and independent variables can be established³⁰. Depending on their accuracy, these models can serve as the foundation for effective optimization³¹.

To predict and analysis of nanofluids, researchers have utilized various ML algorithms, which are a subset of AI. The recent studies on this subject are presented in detail in Table 2. These studies have demonstrated that employing machine learning tools offers an efficient and accurate approach to reducing the costs of experiments and computational simulations³². In this regard, in order to predict the DV of THNFs, Sepehrnia et al.³³ designed various ML models, including the COMBI algorithm and a GMDH-type ANN. The accuracy and complexity of these methods were evaluated, with the COMBI algorithm demonstrating the highest precision, achieving an R² value of 0.9995. In a separate study, Ibrahim et al.³⁴ achieved R² values ranging from 0.994 to 0.995 for their TC prediction models, which were developed using an artificial neural network framework. Furthermore, Esfe et al.³⁵ utilized a multilayer perceptron neural network (MLPNN) to predict the TC of oil/MWCNT nanofluid. By constructing a two-layer MLPNN model, they attained an R² value of 0.998. Additionally, they applied a similar approach to predict the DV using MLPNN, resulting in an R² of 0.9449. Shahsavar et al.²⁹ developed a ML model to predict the TC of THNFs. They introduced a method that used a genetic algorithm (GA) to optimize the structure and training variables for Gaussian process regression (GPR). This GA-GPR approach yielded a highly accurate model with an R² value of 0.999. In conclusion, the findings summarized in Table 2 indicate that machine learning algorithms typically generate models with a high degree of accuracy.

Table 2 Recent studies on predicting DV and TC using ML techniques.

As highlighted in the reviewed literature, the development of ML models has enabled accurate predictions of the TPPs of hybrid nanofluids. These models serve as effective objective functions in the optimization processes for nanofluids. Recent studies have demonstrated the success of this approach in multi-objective optimizing both single and binary nanofluids. Esfe et al.³⁹ introduced a multi-algorithm approach that synergistically combined particle swarm optimization (PSO), GA, and ANN to optimize the dynamic viscosity and thermal conductivity of water-based nanofluids containing various oxide nanoparticles. This hybrid optimization strategy aimed to identify optimal operating conditions for maximizing the desired thermophysical properties of the nanofluid. In a similar study, a comprehensive study conducted by Amani et al.⁴⁰ explored the synergistic potential of combining decision-making techniques, GA, and ANN to optimize the TPPs of eco-friendly nanofluids. Furthermore, Said et al.⁴¹employed a combination of fuzzy logic and PSO to enhance the TC and DV of an ethylene glycol-water-based nanofluid incorporating hybrid oxide nanoparticles. In another work, Esfe and Tilebon⁴² employed a hybrid approach combining the NSGA-II algorithm with classical regression modeling to identify optimal parameter settings for the production of oil/MWCNT-Al₂O₃ TPPs. Maqsood et al.⁴³ conducted a multi-criteria optimization of MWCNT-based nanofluid parameters. Their optimization strategy incorporated artificial neural network modeling. Despite extensive efforts in this field, previous research has not established a definitive approach for the optimal design of ternary nanofluids based on their thermophysical properties, which has resulted in a significant research gap.

A thorough examination of the literature reveals that the pivotal properties of nanofluids, including thermal conductivity and dynamic viscosity, significantly influence the operational efficiency of diverse applications. The optimization of these TPPs is essential for developing high-performance fluids that offer both technological and economic benefits across various fields, including heat exchangers, electronic cooling systems, thermal energy storage, and solar energy technologies. Motivated by the need for advanced optimization of TPPs in ternary hybrid nanofluids, this study introduces a novel computational intelligence (CI)-based framework. For the first time, machine learning models, multi-objective optimization (MOO), and multi-criteria decision-making (MCDM) techniques are integrated to design THNFs, addressing a critical gap in the emerging field of ternary hybrid nanofluid optimization. This approach advances the field from early single-objective designs to robust multi-objective optimization of TPPs, focusing on volume fraction (VF), temperature, and nanomaterial mixing ratio (MR). Additionally, less-explored modeling methods, such as the combinatorial algorithm (COMBI) and gene expression programming (GEP) techniques, are employed to capture the complex non-linear relationships between inputs and outputs. A distinctive innovation is the incorporation of a weighting system for design scenarios, allowing decision-makers to tailor the optimization process to specific real-world applications.

Proposed strategy

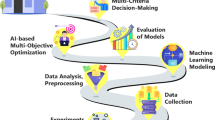
The proposed hybrid CI-based strategy consists of four distinct steps. In the first step, a comprehensive data analysis is applied. The first step aims to introduce data extraction references, determine the data distribution, data statistical description, and quantitative and qualitative evaluation of the correlation of input and output variables. Three machine-learning techniques are applied to the data in the second step: GMDH-type ANN, GEP, and COMBI, which have yet to be extensively explored in previous studies. These techniques model DV and TC in terms of input variables. In the third step, the high-performing models for each TPP serve as the foundation for MOO with the widely recognized multi-objective particle swarm optimization (MOPSO) algorithm. Finally, the MCDM technique (TOPSIS) is employed to identify the desirable points from the Pareto front in the fourth step. Decision-making is made based on each objective’s importance coefficients (weight). By assigning weights to TPPs, the designer can identify and select the optimal points that lead to maximum efficiency based on the system’s conditions and requirements.

A detailed road map of the described four steps of the CI-based strategy is shown in Fig. 1. This approach can lead to reliable results in optimizing the thermophysical properties of ternary hybrid nanofluids. The detailed report and results of each design step will be discussed separately in the following sections.

Fig. 1

A schematic of the road map of CI-based strategy.

Data analysis

The experimental data from Sepehrnia et al.²⁸ and Shahsavar et al.²⁹ were used to test the proposed method. These studies examined the DV and TC of THNF containing a base of hydraulic oil and a combination of graphene oxide (GO), iron oxide (Fe₃O₄), and titanium dioxide (TiO₂). Both studies covered a broad range of temperatures (15–65 °C) and volume fractions (0.05–1%), with different mixing ratios of the nanomaterials. Four nanomaterials mixing scenarios were analyzed. In the first scenario, equal mass ratios were used for all the nanomaterials. In the remaining three scenarios, one of the nanomaterials had double the mass of the others. These MRs were labeled as 111, 211, 121, and 112 for simplicity. In these notations, the first, second, and third digits represent graphene oxide, iron oxide, and titanium dioxide in that order. The descriptive statistics of input and output data used in the experiments are provided in Table 3.

Based on Table 3, the temperature ranges from a minimum of 15 °C to a maximum of 65 °C, with a mean and median value of 40 °C. The variance in temperature is 300, with a standard deviation of 17.32 °C, indicating a moderate spread around the mean. The average deviation is 15 °C, suggesting that temperature values do not deviate too far from the central value in most cases. A low coefficient of variation (CV) of 0.43 further confirms the relatively consistent distribution of temperature values in the dataset. Also, temperature data has a skewness of zero, indicating a perfectly symmetrical distribution. This suggests that temperature values are evenly spread around the mean, with no extreme outliers or significant asymmetry. Furthermore, temperature data has a kurtosis of −1.28, which indicates a flatter distribution than the normal one, with lighter tails. Temperature data has a Kolmogorov-Smirnov (K-S) value of 0.14, suggesting that its distribution does not deviate significantly from a normal distribution. This is consistent with the skewness and kurtosis values, which indicate symmetry and moderate tails.

According to the Table 3, VF data shows more variability, ranging from 0.05 to 1%, with a mean of 0.442% and a median of 0.375%. The variance for VF is 0.123, and the standard deviation is 0.351%, reflecting a broader distribution compared to temperature. The coefficient of variation for VF is relatively high at 0.794, indicating significant dispersion around the mean. This suggests that the volume fraction values are widely distributed across the dataset, which is expected given that VF influences the THNF properties more strongly than temperature. Also, VF data shows a skewness of 0.407, which is a mild positive skew. This indicates that the distribution is slightly right-skewed, meaning there are more small values, with a few larger volume fractions pulling the distribution’s tail to the right. VF data also shows a similar pattern to temperature with a kurtosis of −1.326, indicating that the VF values form a flatter distribution with fewer extreme values, confirming the moderate spread of volume fractions in the data. Furthermore, VF has a higher K-S value of 0.208, suggesting that the VF distribution deviates more from normality than temperature, which aligns with the skewness and kurtosis values indicating a mild right skew and flatter distribution.

Table 3 Descriptive statistics of inputs and outputs.

Based on the information provided in Table 3, DV varies significantly across the different mixing ratios. The DV ranges from a minimum of 67.086 mPa.s (MR 111) to a maximum of 1674.3 mPa.s (MR 211). The mean values for DV range from 156.65 mPa.s (MR 111) to 715.76 mPa.s (MR 121), indicating that MR 121 and MR 211 exhibit higher viscosities compared to MR 111 and MR 112. In terms of variability, MR 211 shows the highest standard deviation (339.45), followed by MR 112 (317.13). This indicates that DV for these MRs is more dispersed compared to MR 111 and MR 121, which have standard deviations of 72.383 and 279.59, respectively. The coefficient of variation is also highest for MR 112 (0.5612), followed by MR 211 (0.5196), MR 111 (0.4621), and MR 121 (0.391). This suggests that MR 112 shows the highest relative variability in DV, while MR 121 shows the lowest. The skewness and kurtosis values indicate the distribution’s shape. Positive skewness across all MRs (ranging from 0.967 to 1.444) suggests that the DV distributions are right-skewed, meaning there are more lower values and a long tail of higher values. Kurtosis values close to zero or slightly positive indicate that the distributions are relatively normal, with a few outliers and extreme values, especially in MR 112 (kurtosis of 1.757). Also, the K-S statistic for DV is relatively low for all MRs, with the highest value being 0.171 for MR 112. MR 111 has the lowest K-S statistic at 0.132, suggesting that its distribution is closest to normal. However, the slightly higher K-S values for MR 112 (0.171) and MR 211 (0.168) reflect the greater deviation from normality, which is supported by their higher skewness and kurtosis values. The box plots, violin plots, and histograms presented in Fig. 2 clearly validate the observations and analysis from Table 3. It should be noted that violin plots are graphical tools used to represent the probability density of random variables based on sample data. By merging nonparametric density estimates with summary statistics, they facilitate the comparison of variable distributions. Their benefits include highlighting unique distribution features such as peaks and amplitudes, retaining raw data for further analysis, and offering a concise yet insightful depiction of sample distributions.

TC also varies across the different MRs. TC ranges from a minimum of 0.1063 W/m.K (MR 112) to a maximum of 0.169 W/m.K (MR 111). The mean values range from 0.1253 W/m.K (MR 112) to 0.134 W/m.K (MR 111), with MR 111 consistently showing higher thermal conductivity than the other MRs. MR 211 also shows higher thermal conductivity with a mean of 0.1323 W/m.K. In terms of variability, MR 111 has the highest standard deviation (0.0138), while MR 121 has the lowest (0.012). The coefficient of variation is also consistent across all MRs, with MR 111 having the highest CV (0.1031) and MR 121 the lowest (0.094). This indicates relatively low variability in TC compared to DV. Skewness values for TC are positive, ranging from 0.573 to 0.623, indicating a slight right skew, while kurtosis values close to zero suggest a near-normal distribution. The K-S statistics for TC are all lower than for DV, with the highest value being 0.106 for MR 112. This indicates that TC values follow a distribution that is closer to normal compared to DV. The lower K-S values align with the relatively low skewness and kurtosis for TC, suggesting that it is more symmetrically distributed. The visual representations of TC data for different MRs, including box plots, violin plots, and histograms shown in Fig. 3, effectively support and confirm the data analysis results given in Table 3.

Fig. 2

Detailed depiction of DV data includes box plots, histograms of frequency distribution, and violin plots for MRs of (a) 111, (b) 112, (c) 121 and (d) 211.

Fig. 3

Visual analysis of TC data includes box plots, histograms of frequency distribution, and violin plots for MRs of (a) 111, (b) 112, (c) 121, and (d) 211.

Assessing the intensity and orientation of linear connections between variables prior to modeling can offer valuable insights into the nature and degree of their association. One effective tool for this analysis is the Pearson correlation coefficient (PCC), a statistical metric designed to fulfill this objective. This measure ranges from − 1 to 1, with − 1 representing a perfect negative correlation, zero signifying no correlation, and + 1 indicating a perfect positive correlation⁴⁴. The PCC is determined using the following formula:

$$\:{R}_{p}=\frac{\sum\:_{i=1}^{N}\left({X}_{i}-\stackrel{-}{X}\right)\left({Y}_{i}-\stackrel{-}{{Y}}\right)}{\sqrt{\sum\:_{i=1}^{N}{\left({X}_{i}-\stackrel{-}{X}\right)}^{2}\sum\:_{i=1}^{N}{\left({Y}_{i}-\stackrel{-}{{Y}}\right)}^{2}}}$$

(1)

In the formula, $\:N$, $\:{X}_{i}$, $\:{Y}_{i}$, $\:\stackrel{-}{X}$, and $\:\stackrel{-}{{Y}}$ represent the total number of observations, the individual X and Y values, the average of X and Y variables, respectively.

Figure 4 displays the PCC between input and output variables. According to Fig. 4 (a), temperature has moderate negative correlations with the DV for various MRs, with coefficients ranging from − 0.57 to −0.67, suggesting that as temperature increases, the DV values tend to decrease. On the other hand, VF shows moderate to strong positive correlations with the DV variables, with correlation values between 0.63 and 0.72, implying that an increase in VF generally corresponds to an increase in DV values. Furthermore, the DV for different MRs (111, 112, 121, and 211) exhibit very strong positive correlations with each other, with values ranging from 0.98 to 0.99, highlighting that DV for various MRs are closely related and likely vary in tandem.

Furthermore, Fig. 4 (b) shows that temperature has strong positive correlations with the TC, with coefficients ranging from 0.72 to 0.75 for various MRs, indicating that an increase in T is associated with increased TC values. Similarly, VF has moderate positive correlations with the TC variables, with values ranging from 0.64 to 0.68, implying that a higher VF also correlates with higher TC values. The TC for different MRs (111, 112, 121, and 211) all exhibit perfect positive correlations with each other, with correlation values of 1.00, highlighting that TC in various mixing ratios move in perfect synchrony and are highly interdependent.

Fig. 4

PCC between inputs and outputs for each MR.

Machine learning modeling

Modeling based on machine learning is implemented through GMDH-NN, GEP, and COMBI algorithms. All three techniques have shown remarkable precision in modeling the TPPs of nanofluids in recent research^13,45. These methods were selected for their ability to model the complex, non-linear relationships between input variables and the thermophysical properties of ternary hybrid nanofluids. GMDH and COMBI are categorized as white-box models, offering transparency in their functional relationships, while GEP, closer to a gray-box model, provides insights into variable importance. Both GEP and COMBI are novel in the context of THNFs, with COMBI excelling in handling intricate non-linear patterns due to its diverse operators and high accuracy. GMDH’s stability and self-organizing nature, coupled with GEP’s flexibility, make them ideal for optimization tasks. These novel applications address gaps in the field and advance the modeling of nanofluids. This section aims to introduce the three ML methods, outline their approach to model development, and present a comparative analysis of their results.

GMDH-type neural network (GMDH-NN)

ANNs, one of the most prominent computational models, result from a conceptual understanding of the function of neurons in the human brain. ANNs have reported excellent performance in modeling very complex phenomena⁴⁶. One of the well-known types of ANNs is the group method of data handling (GMDH) neural networks, considered a feed-forward ANN⁴⁷. This technique shows little dependence on the data quality and has acceptable stability in the modeling. GMDH-NN is based on a powerful self-organizing mechanism that involves sub-models in the modeling process, which, while increasing efficiency, prevents excessive model complexity.

In order to represent a complex phenomenon involving numerous datasets, it is essential to utilize an advanced function, symbolized as $\:f$, that defines the relationship between the inputs $\:\left({x}_{i1},{x}_{i2},\dots\:{x}_{in}\right)$ and outputs $\:{y}_{i}$ in the following manner:

$$\:{y}_{i}=f\left({x}_{i1},{x}_{i2},\dots\:{x}_{in}\right)\:\:\:\:\:\:\:\:(i=\text{1,2},\dots\:,M)$$

(2)

The GMDH neural network seeks to develop a function, denoted as $\:\widehat{f}$, capable of accurately forecasting the output values. Its primary objective is to reduce the difference between the observations ($\:{y}_{i}$) and predictions ($\:{\widehat{y}}_{i}$). This relationship can be mathematically formulated as follows:

$$\:{\widehat{y}}_{i}=\widehat{f}\left({x}_{i1},{x}_{i2},\dots\:{x}_{in}\right)\:\:\:\:\:\:\:(i=\text{1,2},\dots\:,M)$$

(3)

$$\:\sum\:_{i=1}^{M}{\left[{\widehat{y}}_{i}-{y}_{i}\right]}^{2}\:\:\underrightarrow{\:\:\:\:\:\:\:\:\:}\min$$

(4)

Various orders of the Kolmogorov-Gabor polynomial (Eq. 5)⁴⁸ can be utilized to establish a mathematical relationship.

$$\:y={\alpha\:}_{0}+\sum\:_{i=1}^{n}{\alpha\:}_{i}{x}_{i}+\sum\:_{i=1}^{n}\sum\:_{j=1}^{n}{\alpha\:}_{ij}{x}_{i}{x}_{j}+\sum\:_{i=1}^{n}\sum\:_{j=1}^{n}\sum\:_{k=1}^{n}{\alpha\:}_{ijk}{x}_{i}{x}_{j}{x}_{k}+\dots\:$$

(5)

Previous research has indicated that employing the quadratic version of Eq. (5) strikes an optimal balance between model precision and intricacy⁴⁸. This version is presented as follows:

$$\:y=G\left({x}_{i},{x}_{j}\right)={a}_{0}+{\alpha\:}_{1}{x}_{i}+{\alpha\:}_{2}{x}_{j}+{\alpha\:}_{3}{x}_{i}{x}_{j}+{\alpha\:}_{4}{x}_{i}^{2}+{\alpha\:}_{5}{x}_{j}^{2}$$

(6)

It is essential to highlight that the coefficients are determined through the application of the least-squares approach.

The GMDH modeling begins by establishing an input layer, where each neuron represents an individual input variable. These neurons act as the foundational elements for subsequent layers. Intermediate layers are developed by connecting pairs of neurons from various layers using quadratic polynomials, as outlined in Eq. 6. Previous research has demonstrated that employing this equation achieves optimal models, particularly for regression tasks involving TC and DV⁴⁹. This framework enables the identification of intricate relationships and interactions among variables. The output layer comprises a single neuron that synthesizes information from prior layers to produce the final output. The GMDH algorithm employs a self-organizing mechanism to evaluate the performance of neurons in intermediate layers. Only neurons that positively contribute to improving the model’s efficiency and precision are retained, while less effective neurons are excluded. This selective process ensures that the final model incorporates only the most relevant and impactful components.

Combinatorial (COMBI) algorithm

The model development algorithm in the COMBI technique works similarly to GMDH-NN. Unlike the GMDH, the COMBI algorithm has a single-layer structure and utilizes a self-organizing mechanism to choose influential terms from a polynomial function. The degree of polynomial function can change from linear to high-degree functions. The variety of terms (sub-models) is provided by applying different operators on the input variables, which is the strength of this algorithm. While the COMBI technique typically entails higher computational costs than GMDH, it often yields superior accuracy. The COMBI method can be succinctly outlined through the subsequent four stages¹³:

• 1. In order to raise diversity in the interaction between inputs and outputs, additional terms are incorporated into the main polynomial, as exemplified below:

  $$y=\sum_{i=1}^{n}{\beta}_{i}g\left({x}_{i}\right)$$

  (7)

$$\:y=\sum_{i=1}^{n}\sum_{j=1}^{n}{\beta\:}_{ij}g\left({x}_{i}\right)\bullet\:g\left({x}_{j}\right)$$

(8)

$$\:y=\sum_{i=1}^{n}\sum_{j=1}^{n}{\beta\:}_{ij}g\left({x}_{i}\right)/g\left({x}_{j}\right)$$

(9)

The function $\:g$ employs a wide range of operators on variables, thereby enhancing the representation of variables in the modeling process. This expanded set of operators, such as square, cubic, sigmoid, trigonometric, exponential, cube root, square root and others, allows for a more accurate correlation with the outputs.

• 2. During the training process, the least squares method computes the model coefficients.

• 3. Throughout the validation procedure, the mean absolute error (MAE) criterion is employed to assess the precision of the sub-models.

• 4. The ultimate model is constructed by blending the most efficient terms while maintaining the intricacy within established boundaries.

The time-consuming nature of the COMBI algorithm impacts its efficiency and has prompted efforts to strike a balance between precision and intricacy. Less complex models typically demonstrate reduced accuracy. Nevertheless, to guarantee the applicability of the models developed, a strict limitation is enforced on their complexity.

Gene expression programming (GEP)

GEP is an evolutionary-based machine learning approach that draws inspiration from Darwin’s theory of evolution⁵⁰. GEP offers a significant advantage over other algorithms, such as ANN, by allowing the initial definition of the model’s structure, followed by determining coefficients and optimal structure during the training phase. In contrast, the structure is predetermined in ANN, and then coefficients are obtained. Furthermore, GEP incorporates an intelligent mechanism that automatically designates input variables of higher importance. GEP combines branch structures of varying sizes and shapes, resembling decomposition trees with linear and constant-length chromosomes similar to GA⁵¹. GEP employs GA operators such as permutation, combination, mutation, crossover, selection, and reproduction. The initial population solutions are developed as the first step of GEP. This can be performed by either a random procedure or by considering specific data. Afterward, the chromosomes are converted into tree terms and assessed using the fit function. The evolutionary process stops with achieving a specific number of generations or attaining a fitness threshold.

The modeling process through GEP can be summarized in the following five steps:

• 1. Importing data and introducing inputs and output to the GEP algorithm.

• 2. Dividing the data into testing and training sets.

• 3. Selecting algorithm settings such as general settings (number of chromosomes and genes, linking function, possibility of increasing generations and complexity, maximum complexity (genes)), fitness function (criterion, parsimony pressure rate, and variable pressure rate), genetic operators and numerical constants.

• 4. Choosing a collection of functions that consist of boolean, test, and arithmetic operators. Typically used functions include addition, subtraction, multiplication, division, power, exponential, natural logarithm, square root, cube root, sine, cosine, tangent, arcsine, arccosine, arctangent, etc.

• 5. Running the algorithm until the stop condition (number of generations or fitness threshold) is reached, and the final model is then constructed.

Models development and evaluation criteria

Three ML techniques, GMDH-NN, GEP, and COMBI, are compared and evaluated under statistical criteria to select the best predictive models as a basis for the optimization phase of the CI-based strategy.

A method centered on the whole search (WS) is included in the modeling process to optimize the structure and hyper-parameters of machine learning algorithms. In the COMBI modeling, the WS strategy tries to find the best operators and functions applied to the input variables. Also, the WS strategy controls and optimizes the number of additional sub-models to restrain the complexity. This strategy leads to the optimal selection of GEP algorithm parameters such as the number of chromosomes and genes, linking function, fitness function (criterion, parsimony pressure rate, and variable pressure rate), genetic/numerical constants, and operators and functions applied to the input variables. In GMDH-NN, the quantity of layers and their neurons form the structure of the neural network, which strongly affects the complexity and accuracy of the output models. These two parameters are controlled by applying constraints on the complexity.

As repeatedly emphasized, developing simple but accurate models is very crucial. This ideal is achieved when the complexity (the number of terms or sub-models) is limited. To achieve this objective, after a series of trial and error analyses, COMBI and GEP models were restricted to a maximum of twelve sub-models. Also, the GMDH-NN algorithm was forced to produce models with a maximum of two layers. These limitations result in straightforward models that are comparable and can be effectively applied in practical situations.

In all three algorithms, 80% of the data are responsible for training and 20% for evaluation. Ranking of models and optimization of structures/hyper-parameters is done based on testing data. In addition, another dataset as a subset of the training data undergoes the leave-one-out CV algorithm, which is based on the cross-validation technique and is responsible for checking the generalizability and preventing overtraining. It should be noted that fixed data sets are applied for testing and training in all three algorithms, guaranteeing justice in the modeling process.

Considering $\:{Y}_{i,Exp}$, $\:{Y}_{i,Pred}$, and $\:n$ as observations, predictions, and the number of data, respectively, five statistical metrics are applied to evaluate the efficacy of ML models as follows:

$$Mean\, squared\, error:\:MSE=\frac{1}{n}\sum_{i=1}^{n}{\left({Y}_{i,Exp}-{Y}_{i,Pred}\right)}^{2}$$

(10)

$$Mean\, absolute\, percentage\, error: \:MAPE\left(\%\right)=\frac{1}{n}\sum\:_{i=1}^{n}\left|\frac{{Y}_{i,Pred}-{Y}_{i,Exp}}{{Y}_{i,Exp}}\right|\times\:100$$

(11)

$$Correlation\, coefficient:\:R=\frac{\sum\:_{i=1}^{n}\left({Y}_{i,Exp}-\stackrel{-}{{Y}_{i,Exp}}\right)\left({Y}_{i,Pred}-\stackrel{-}{{Y}_{i,Pred}}\right)}{\sqrt{\sum\:_{i=1}^{n}{\left({Y}_{i,Exp}-\stackrel{-}{{Y}_{i,Exp}}\right)}^{2}\sum\:_{i=1}^{n}{\left({Y}_{i,Pred}-\stackrel{-}{{Y}_{i,Pred}}\right)}^{2}}}$$

(12)

$$Coefficient\, of\, determination:\:{R}^{2}=1-\sum\:_{i=1}^{n}\frac{{\left({Y}_{i,Pred}-{Y}_{i,Exp}\right)}^{2}}{{Y}_{i,Exp}^{2}}$$

(13)

$$Willmott's\, Index\, of\, Agreement: \:{I}_{A}=1-\frac{\sum\:_{i=1}^{n}{\left({Y}_{i,Exp}-{Y}_{i,Pred}\right)}^{2}}{\sum\:_{i=1}^{n}{\left(\left|{Y}_{i,Pred}-\stackrel{-}{{Y}_{i,Exp}}\right|+\left|{Y}_{i,Exp}-\stackrel{-}{{Y}_{i,Exp}}\right|\right)}^{2}}$$

(14)

MAPE and MSE are used as metrics to quantify the error of the models. When these metrics tend towards zero for a particular model, it indicates that the model is highly valid in its predictions. Furthermore, the agreement between the experimental and predicted values is measured using metrics such as R, R², and I_A. These criteria provide a value between 0 and 1, where a value closer to 1 indicates a higher level of validity. Also, the computation of relative error (RE) offers the opportunity to visually represent the deviation of data points in more detail using margin of deviation (MOD) diagrams. These diagrams visually represent the deviation of predictions from their target values. They illustrate acceptable ranges by highlighting upper and lower limits, ensuring quality control and compliance. Each data point is individually evaluated by calculating the RE using the following equation:

$$\:{RE}_{i}\left(\%\right)=\frac{{Y}_{i,Exp}-{Y}_{i,Pred}}{{Y}_{i,Exp}}\times\:100$$

(15)

Modeling results

The statistical criteria, MOD diagrams, and violin plots are utilized to comprehensively compare the effectiveness and functionality of the top-performing models obtained from each machine learning method. This thorough evaluation allows for a detailed assessment of the models’ capabilities.

Table 4 shows the statistical criteria for comparing the best DV predictive models resulting from the WS strategy in optimizing GMDH, GEP, and COMBI algorithms. According to the table, all three methods generally provide appreciable outcomes, which result from the optimal selection of hyper-parameters and the suitable structure of the models. The testing phase results indicate the COMBI algorithm’s superiority over the other two algorithms, especially in the MRs of 111 and 121. This comparison is also graphically displayed as spider plots in Fig. 5, which clearly indicates the superiority of the COMBI algorithm in the testing phase. The spider (radar) chart in Fig. 5 visually displays statistical criteria data on a two-dimensional graph. Each axis represents a statistical criterion, radiating from a central point. Points are plotted and connected, forming a polygon, allowing for a brief overview to identify the strengths and weaknesses of ML predictive models.

Also, for MRs of 111 and 121, the GEP algorithm performs better than GMDH. While in the MRs of 112 and 211, the GMDH algorithm performs much better than the GEP and exhibits a slight weakness compared to the COMBI algorithm. The superiority of COMBI and GMDH models to the GEP model for mixing ratios of 112 and 211 is obviously detected in Fig. 5. The main criterion for comparing ML-based models is the testing phase; however, comparing models in the training phase is not completely worthless. Based on the information presented in Table 4, it can be observed that during the training phase, COMBI models exhibit a significant advantage over other models for all MRs, similar to what was marked in the testing phase. The superiority of GMDH and GEP models over each other is qualitatively similar to the testing phase.

A detailed analysis of the three ML techniques in DV modeling is possible by calculating the relative deviation of the predicted values from observations for all data points. Figure 6 provides the MOD plots of various models for different mixing ratios. MOD diagrams are displayed as a range encompassing the maximum positive and negative REs, as outlined below:

$$\:MR=111\left\{\begin{array}{c}-1.99\le\:{MOD}_{COMBI}\le\:2.78\\\:-17.26\le\:{MOD}_{GMDH}\le\:10.60\\\:-8.71\le\:{MOD}_{GEP}\le\:5.45\end{array}\right.$$

(16)

$$\:MR=112\left\{\begin{array}{c}-5.57\le\:{MOD}_{COMBI}\le\:5.43\\\:-6.51\le\:{MOD}_{GMDH}\le\:16.20\\\:-8.46\le\:{MOD}_{GEP}\le\:11.58\end{array}\right.$$

(17)

$$\:MR=121\left\{\begin{array}{c}-2.94\le\:{MOD}_{COMBI}\le\:0.95\\\:-8.79\le\:{MOD}_{GMDH}\le\:8.37\\\:-9.84\le\:{MOD}_{GEP}\le\:15.66\end{array}\right.$$

(18)

$$\:MR=211\left\{\begin{array}{c}-5.32\le\:{MOD}_{COMBI}\le\:2.62\\\:-5.29\le\:{MOD}_{GMDH}\le\:11.02\\\:-5.84\le\:{MOD}_{GEP}\le\:18.03\end{array}\right.$$

(19)

The comparison of the RE of the data points in all MRs validates the findings of Table 4; Fig. 5, which indicate the absolute superiority of the models produced by the COMBI. This means that according to Fig. 6, the distribution of the RE of the COMBI model data points is closer to the zero-error line, and according to Eqs. (16)-(19), the RE of the data in the COMBI models has a smaller range. In addition, the MOD graphs show the overestimation and underestimation of models in predicting experimental data. According to the figure, in the mixing ratio of 111, the COMBI model shows a proper balance between overestimated and underestimated values. While in this mixing ratio, the underestimation of the values by GEP and GMDH models is evident. In the MR of 112, the COMBI model has a similar trend to the MR = 111. In contrast, the overestimation of experimental values by GEP and GMDH models is intense. In MR = 121, the GMDH model is balanced regarding overestimating and underestimating observations. In comparison, the COMBI model tends to underestimate the observations. Also, in this MR, the overestimating of experimental values by the GEP model is quantitatively and qualitatively more significant. In the MR of 211, the overestimating of observations by GEP and GMDH models can be clearly seen. At the same time, the COMBI model is relatively balanced, although, in one test data point, the underestimation of the laboratory value is apparent.

In addition, Fig. 6 presents a comparison of the probability density function (PDF) for the predictions generated by various ML methods with the PDF of observations using violin plots. According to the figure, in all MRs, the COMBI models are more compatible with the experimental data than other models. Table 5 provides the equations of the most accurate models developed for predicting the DV based on the input parameters, T and VF, across different MRs.

Table 4 Statistical metrics of the best models of each ML algorithm in DV prediction.

Fig. 5

Spider charts for comparing the statistical criteria of various models in predicting dynamic viscosity.

Fig. 6

Detailed comparison of the superior GMDH, COMBI, and GEP models in predicting the dynamic viscosity.

Table 5 The formula of the best developed models in DV prediction.

The statistical criteria for comparing the best TC predictive models obtained through the WS strategy in optimizing GMDH, GEP, and COMBI algorithms are presented in Table 6. This table provides a comprehensive overview of the performance and effectiveness of the developed models. Based on the data presented in the table, all three techniques generally yield satisfactory outcomes. These positive results are attributed to the careful selection of hyper-parameters and the appropriate structure of the models. The outcomes derived from the testing phase clearly demonstrate the dominance of the COMBI algorithm over the other two algorithms. The superiority of the COMBI algorithm in the testing phase is visually depicted through spider plots in Fig. 7. Furthermore, in the case of MR 111, the GEP algorithm outperforms the GMDH algorithm. However, for MRs 112, 121, and 211, the GMDH algorithm performs significantly better than GEP, although it exhibits a slight weakness compared to the COMBI algorithm. The superiority of the COMBI and GMDH models over the GEP models is evident from the findings presented in Fig. 7. Moreover, Table 6 indicates that during the training phase, COMBI models consistently demonstrate a significant advantage over other models across all MRs, similar to the findings observed during the testing phase. The relative superiority of GMDH and GEP models over each other remains qualitatively similar to what was observed in the testing phase.

By calculating the RE of the predicted values from the observations for all data points, conducting a comprehensive analysis of the three machine learning techniques in TC modeling becomes feasible. In order to achieve this objective, Fig. 8 displays the MOD diagrams of developed models for different mixing ratios. The MOD results can be presented by expressing a range that encompasses the maximum negative and positive RE, as illustrated below:

$$\:MR=111\left\{\begin{array}{c}-0.58\le\:{MOD}_{COMBI}\le\:0.44\\\:-1.41\le\:{MOD}_{GMDH}\le\:1.08\\\:-1.16\le\:{MOD}_{GEP}\le\:1.29\end{array}\right.$$

(20)

$$\:MR=112\left\{\begin{array}{c}-0.78\le\:{MOD}_{COMBI}\le\:0.53\\\:-0.83\le\:{MOD}_{GMDH}\le\:1.26\\\:-1.93\le\:{MOD}_{GEP}\le\:1.08\end{array}\right.$$

(21)

$$\:MR=121\left\{\begin{array}{c}-0.30\le\:{MOD}_{COMBI}\le\:0.41\\\:-0.87\le\:{MOD}_{GMDH}\le\:1.16\\\:-2.80\le\:{MOD}_{GEP}\le\:4.08\end{array}\right.$$

(22)

$$\:MR=211\left\{\begin{array}{c}-0.46\le\:{MOD}_{COMBI}\le\:0.48\\\:-0.90\le\:{MOD}_{GMDH}\le\:0.93\\\:-2.03\le\:{MOD}_{GEP}\le\:2.15\end{array}\right.$$

(23)

The comparison of the relative errors for both the testing and training data points across all mixing ratios further validates the findings presented in Table 6; Fig. 7. These findings consistently demonstrate the clear superiority of the COMBI algorithm-generated models. Based on the observations from Fig. 8, it can be inferred that the RE distribution of the data points in the COMBI model is closer to the zero-error line. Additionally, considering Eqs. (20)-(23), it can be concluded that the range of RE in the COMBI models is comparatively smaller. Based on the figure, it can be observed that in the mixing ratio 111, all three models exhibit a balance between overestimating and underestimating the experimental values. In the case of the mixing ratio 112, both the COMBI and GMDH models exhibit a similar trend to that observed in the MR = 111. However, the GEP model stands out with its pronounced underestimation of the experimental values. For the mixing ratio 121, both the GMDH and COMBI models demonstrate a balanced pattern in terms of overestimating and underestimating observations. However, in this particular mixing ratio, the GEP model exhibits an error exceeding 2% in four data points, indicating overestimation. On the other hand, there is only one data point where the absolute error is greater than − 2%, indicating underestimation. In the case of the mixing ratio 211, the COMBI and GMDH models demonstrate a relatively balanced performance. However, the GEP model tends to underestimate the observations.

Furthermore, Fig. 8 uses violin plots to compare the PDF of the outputs generated by various models and the observed values. The figure reveals that across all mixing ratios, the COMBI models demonstrate a higher level of compatibility with the experimental data compared to other models. Additionally, Table 7 provides the equations for the most accurate models developed to predict the TC for different MRs.

Overall, it can be stated that the COMBI algorithm outperforms other methods for various mixing ratios, specifically 111 and 121, due to its unique capability to model complex, non-linear interactions among input variables and output properties. Unlike GMDH-NN, COMBI utilizes a diverse range of operators, including trigonometric, exponential, and polynomial functions, enabling it to capture intricate relationships in the dataset with higher precision. This flexibility is particularly advantageous for datasets dominated by non-linearity, as observed in these mixing ratios. For instance, in the case of MR = 111, where equal mass portions of nanomaterials result in subtle yet complex interactions between thermal conductivity and viscosity, COMBI’s enhanced feature selection mechanism ensures that the most relevant terms are included in the final model. Similarly, for MR = 121, the algorithm’s ability to adapt its structure optimally balances model complexity with predictive accuracy. These advantages are reflected in the algorithm’s lower error metrics (MSE, MAPE) and superior statistical measures (R, R², I_A) for these mixing ratios. The robustness of COMBI across diverse scenarios highlights its effectiveness in nanofluid modeling.

Table 6 Statistical metrics of the best models of each ML algorithm in TC prediction.

Fig. 7

Spider charts for comparing the statistical criteria of various models in predicting thermal conductivity.

Fig. 8

Detailed comparison of the superior GMDH, COMBI, and GEP models in predicting the thermal conductivity.

Table 7 The formula of the best developed models in TC prediction.

Regression modeling was performed on a computer equipped with a Core i7 processor operating at 2.3 GHz and 8 GB of RAM. The average modeling times were 16 min for GMDH-NN, 32 min for COMBI, and 10 min for GEP. COMBI required significant computational cost due to its exhaustive search for optimal submodels but achieved superior accuracy in capturing high complex non-linear relationships. In contrast, GEP was the fastest but often exhibited lower accuracy compared to GMDH and COMBI. GMDH struck a balance between computational cost and accuracy, utilizing its self-organizing structure to identify key relationships effectively. Scalability varied across methods, with COMBI being less efficient for large datasets due to its intensive computations, while GMDH and GEP demonstrated better scalability and computational efficiency.

Multi-objective optimization (MOO)

In real-world applications, one of the major challenges in producing nanofluids is to incorporate nanomaterials in a way that significantly enhances the TC of the base fluid while keeping the DV at an acceptable level. For hybrid nanofluids, mixing ratio, system temperature, and volume fraction are three main factors in determining thermophysical properties. The Pareto front approach is favorable for exploring the problem space and identifying optimal conditions when multiple objectives are involved. Rather than identifying a singular optimal solution, this approach offers a spectrum of optimal points. Every point along the Pareto front may be viewed as a viable design option, depending on the relative significance assigned to each objective. In this section, the well-known MOPSO algorithm introduced by Coello and Lechuga⁵² is used to identify Pareto optimal points.

Multi-objective particle swarm optimization (MOPSO)

MOPSO is a well-known meta-heuristic algorithm that draws inspiration from the collective behavior observed in fish schooling or bird flocking, where individuals, referred to as particles, navigate the problem space in search of optimal solutions. The movement is influenced by their individual best position (personal best) and the best position discovered by the entire population (global best). The personal and global best positions are continuously updated during optimization, considering the objectives at hand. MOPSO employs Pareto dominance, a concept that evaluates the fitness of particles across multiple objectives. A particle is deemed dominant if it surpasses another particle in at least one objective without performing worse in any other objective. This dominance aids in recognizing non-dominated solutions and constructing the Pareto front. One of the primary benefits of MOPSO is its capacity to offer various solutions along the Pareto front, enabling decision-makers to select the most appropriate solution according to their preferences. In order to preserve variety, MOPSO employs methods like niching or crowding distance to ensure that particles do not converge towards one particular area. Like the original particle swarm optimization (PSO) algorithm, MOPSO also includes equations for updating position and velocity. These equations are adjusted to accommodate multiple objectives. The position update equation determines the new location of a particle, while the velocity update equation ensures a balance between exploiting and exploring the search space.

Overall, MOPSO is a highly effective algorithm for addressing multi-objective optimization problems, offering optimal solutions that showcase the trade-offs between conflicting objectives. Figure 9 illustrates the optimization procedure of the MOPSO algorithm. The bi-objective optimization problem in this study for each nanomaterial mixing ratio can be formulated as follows:

$$\:\left\{\begin{array}{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:Minimize\:DV={f}_{1}\left(VF,T\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:Maximize\:TC={f}_{2}\left(VF,T\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:Subject\:to\:\left\{\begin{array}{c}0.05\le\:VF\le\:1\:\left(Real\right)\\\:15\le\:T\le\:65\:\left(Real\right)\:\:\:\end{array}\right.\:\\\:\:\end{array}\right.\:$$

(24)

Fig. 9

Flowchart of MOO process by the MOPSO algorithm.

Pareto optimal results

Pareto solutions in multi-objective optimization of ternary hybrid nanofluids for different mixing ratios are depicted in Fig. 10. Variation in mixing ratios leads to various optimal points, which can be the basis for different decisions based on the importance of the problem’s objectives. Given that the objective of the current problem is to maximize TC and minimize DV, it becomes evident that the points leaning toward the upper-left side of the graph hold greater significance. Therefore, the Pareto points, influenced by the mixing ratio of 111, become doubly important in the decision-making process.

Figure 11 illustrates the change of optimal values in terms of VF and T for different mixing ratios. It is evident that an increase in the VF of optimal points results in a simultaneous increase in both DV and TC. On the other hand, the temperature in the optimal points remains relatively unchanged. Optimum points accept a wide range of VFs in all MRs. In contrast, the temperature of the optimum points is limited to a minimal range around the maximum value. The noteworthy point in Fig. 11 is the presence of at least one optimal point among different mixing ratios, which has increased TC despite the DV stability. These points possess a volume fraction close to the maximum value, making them highly preferable for decision-makers when the TC of the nanofluid holds significant importance.

The nanomaterials mixing ratio can significantly affect the volume fraction of optimal points. For example, in the mixing ratio of 111, the probability of achieving optimal points is higher in low VFs. About 93% of the optimal points in this MR have a VF of less than 0.5%. This value equals 68%, 65%, and 62% for 112, 121, and 211 mixing ratios, respectively. In addition, in the MR of 111, only one optimal solution (0.5% of the optimal solutions) has a VF of more than 0.6%. Meanwhile, 18%, 28%, and 29% of the optimum points in the mixing ratios of 112, 121, and 211, respectively, experience a VF > 0.6%. This trend is not visible for temperature because the increase in temperature leads to improving the problem’s objectives. That is, with the increase in temperature, the thermal conductivity grows, and the dynamic viscosity drops. Optimal solutions in the MR of 111 accept temperatures in the range of 64.8 to 65 °C. The optimal temperature for the MR of 112 is in the range of 63.9 to 65 °C. Also, for the MRs of 121 and 211, the optimal temperature ranges of 62.7 to 65 °C and 64.9 to 65 °C are observed, respectively.

The Pareto front analysis not only identifies the trade-offs between maximizing thermal conductivity and minimizing dynamic viscosity but also offers valuable insights into the most effective operating conditions for ternary hybrid nanofluids in real-world applications. For instance, the analysis reveals that the optimal volume fractions for MR = 111 tend to be low, suggesting that, in industrial heat exchangers, these optimal points can achieve high thermal conductivity while maintaining manageable viscosity for efficient fluid flow. In electronic cooling systems, where minimizing viscosity is crucial for fluid circulation, the identified optimal points may guide the selection of the appropriate thermal fluid composition that balances performance with ease of circulation. Furthermore, the consistent temperature values near the maximum (65 °C) across all MRs emphasize the potential of these optimal points for high-temperature applications, such as solar energy collectors and thermal energy storage systems, where enhanced heat transfer is critical. These insights provide practical guidance for industrial designers and decision-makers seeking to optimize nanofluid-based systems.

Fig. 10

Pareto optimal points for THNF with various MRs.

Fig. 11

Alteration of optimal values of (a) DV and (b) TC in terms of VF and T for various MRs.

Multi-criteria decision-making (MCDM)

Designers face a substantial challenge when selecting the most desirable solution from the available optimal points on the Pareto front. In order to address this issue, multi-criteria decision-making (MCDM) methods can prove to be beneficial. One widely recognized MCDM approach is the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). This method relies on an aggregate function, where the proximity to the ideal point serves as the foundation for choosing the desirable points.

TOPSIS approach

The procedure for prioritizing for $\:m$ alternatives and $\:n$ criteria using the TOPSIS method comprises six consecutive steps, outlined as follows:

• (1) Forming decision-making matrix (DMM).

• (2) Applying the Euclidean approach to normalizing the DMM;

$$\:{{R=(r}_{ij})}_{m\times\:n},\:\:\:\:{r}_{ij}=\frac{{x}_{ij}}{\sqrt{\sum\:_{k=1}^{m}{x}_{kj}^{2}}}\:\:\:i=1,\:2,\dots\:,\:m\:\:\:\:j=1,\:2,\:\dots\:,\:n$$

(25)

• (3) Weighting the normalized DMM.

$$\:{S}_{ij}={r}_{ij}\bullet\:{w}_{j},\:\:\:\:\:i=1,\:2,\dots\:,\:m\:\:\:\:j=1,\:2,\:\dots\:,\:n$$

(26)

• (4) Specifying the best and worst alternatives considering the advantageous or disadvantageous effects of criteria;

$$\begin{aligned}{A}_{best}&=\left\{\langle min\left({t}_{ij}|i=1,2,...,m\right)|j\in\:{J}_{-}\rangle,\langle max\left({t}_{ij}|i=1,2,...,m\right)|j\in\:{J}-{+}\rangle \right\}\\&\equiv\:\left\{\left.{t}_{bj}\right|j=1,2,...,n\right\}\end{aligned}$$

(27)

$$\begin{aligned}\:{A}_{worst}&={\langle max\left({t}_{ij}|i=1,\:2,\dots\:,\:m\right)|j\in\:{J}_{-}\rangle,\langle min\left({t}_{ij}|i=1,\:2,\dots\:,\:m\right)|j\in\:{J}_{+}\rangle}\\&\equiv\:{\left.{t}_{wj}\right|j=1,\:2,\:\dots\:,\:n}\end{aligned}$$

(28)

where.

$$\:{J}_{+}=\left\{j=1,\:2,\:\dots\:,\:n|j\right\},\:\:{J}_{-}=\left\{j=1,\:2,\:\dots\:,\:n|j\right\}\:$$

(29)

$\:{J}_{+}$ and $\:{J}_{-}$ are correspond to criteria that have advantageous or disadvantageous effects, respectively.

• (5) Calculating the Euclidean distance for both $\:{A}_{best}$ and $\:{A}_{worst}$;

$$\:{D}_{i,best}=\sqrt{\sum\:_{j=1}^{n}{\left({t}_{ij}-{t}_{bj}\right)}^{2}}\:,\:\:\:\:\:{D}_{i,worst}=\sqrt{\sum\:_{j=1}^{n}{\left({t}_{ij}-{t}_{wj}\right)}^{2}}\:,\:\:\:\:\:i=1,\:2,\dots\:,\:m$$

(30)

• (6) Ranking the alternatives by assigning them an $\:{S}_{i,worst}$ value

$$\:{S}_{i,worst}=\frac{{D}_{i,worst}}{{D}_{i,best}+{D}_{i,worst}},\:{0\le\:S}_{i,worst}\le\:1,\:\:\:i=1,\:2,\dots\:,\:m$$

(31)

The selection of the best alternative in the TOPSIS method is based on identifying the case with the highest $\:{S}_{i,worst}$ value.

Selection of desirable points

As mentioned, the Pareto front is a set of optimal solutions that are not superior to each other but are superior to other solutions in the problem space. Passing from one solution to another in the Pareto front does not improve all objectives simultaneously but improves one objective at the cost of another. That is, various optimal points from the Pareto front distinguish the relative importance of the objectives. TOPSIS helps the decision maker choose desirable optimal points by assigning an importance factor (weight) to each objective. This process makes achieving optimal points that describe various operating conditions possible.

Table 8 displays the optimal points derived from both single-objective optimization and MCDM approaches, corresponding to different weightings assigned to the objectives. Also, Fig. 12 displays the location of the proposed points on the Pareto front. The information presented in Table 8 clearly indicates that all the proposed points have equal nanomaterials mass portion (MR = 111) and maximum temperature (T = 65 °C), irrespective of whether the decision-making process focuses on a single objective or incorporates dual objectives. From this preliminary analysis, it can be concluded that VF is the only optimization variable differentiating between diverse optimization scenarios.

Single-objective optimization is achieved by assigning a unity value to the weight of one objective and setting the weight of the other objective to zero. While single-objective problems may not directly apply to real-world scenarios, they can still provide valuable theoretical insights into the operating conditions necessary to achieve optimal performance for any thermophysical property. Point A considers the coefficient of importance of DV and TC as 1 and 0, respectively. In such situations, the lowest possible VF (0.05%) leads to optimal conditions because the minimization of DV can be achieved at the highest temperature and the lowest nanomaterials concentration. Point B describes a case where the focus is only on maximizing TC, and DV is insignificant. The purpose can be achieved in this scenario by utilizing the largest VF (1%).

Considering the two-criterion decision-making, the scenarios become concrete and practical. Point C describes a scenario where the importance of DV and TC is equal ($\:{W}_{DV}={W}_{TC}=1$). In this case, the maximum VF leads to the desirable solution. Also, the same trend is observed with increasing importance of TC (point D). In fact, a result similar to TC-focused single-objective optimization is observed in two-objective optimization by giving equal importance to the objectives or assigning more weight to TC. This trend reverses with the increase of the weight of DV, where at points E, F, and G, the desirable value of VF drops with the increase of the weight of DV relative to TC.

Table 8 The proposed MCDM-based optimal points for various design scenarios.

Fig. 12

Position of proposed desirable points on the Pareto fronts.

Conclusion

Understanding the thermophysical characteristics of hybrid nanofluids is crucial for evaluating their effectiveness in real-world applications. Enhancing these properties enables the creation of more efficient heat transfer fluids, which can be applied in numerous sectors. This study proposed an innovative hybrid approach, using computational intelligence (CI), to determine the best conditions for ternary hybrid nanofluids. The CI-based strategy integrates machine learning, AI-based multi-objective optimization, and multi-criteria decision-making techniques to improve the performance of THNFs. The proposed CI-based strategy encompasses four distinct steps. The initial step involves conducting a comprehensive data analysis, including:

• Establishing data extraction references,

• Determining data distribution,

• Providing statistical descriptions of the data,

• Evaluating the correlation between inputs and outputs.

In the second step, three machine-learning techniques, namely GMDH-NN, GEP, and COMBI, are employed to model the DV and TC based on the input variables. In the third step, the well-performing models for each TPP serve as the basis for MOO using the widely recognized MOPSO algorithm. Finally, the fourth step involves utilizing the MCDM technique known as TOPSIS to identify the most desirable points from the Pareto front.

The main discoveries of the proposed CI-based strategy can be condensed into the following:

• 1. All three ML techniques demonstrated satisfactory performance. However, the COMBI algorithm stood out for its exceptional reliability in accurately modeling both TPPs.

• 2. The MOO process indicated that the optimum points accept a wide range of VFs in all mixing ratios. In contrast, the temperature of the optimum points was limited to a minimal range around the maximum value.

• 3. About 93% of the optimal points of the Pareto front in MR of 111 had a VF of less than 0.5%. This ratio was equal to 68%, 65%, and 62% for 112, 121, and 211 mixing ratios, respectively.

• 4. All the MCDM-based proposed points had equal nanomaterials mass portion (MR = 111) and maximum temperature (T = 65 °C), irrespective of whether the decision-making process focuses on a single objective or incorporates dual objectives. VF was the only optimization variable differentiating between diverse scenarios.

• 5. A similar optimal point was observed in TC-focused single-objective optimization with two-objective optimization by giving equal importance to the objectives or assigning more weight to TC.

Future research could explore additional computational algorithms and nanomaterial combinations to further enhance the performance of ternary hybrid nanofluids. For instance, AI techniques such as deep neural networks or hybrid approaches combining novel metaheuristic algorithms with machine learning models could be investigated to improve modeling accuracy and optimization efficiency. Furthermore, exploring novel nanomaterials, such as graphene oxide (GO) and MXene combined with carbon nanotubes (CNTs) or boron nitride (BN), may provide new opportunities for fine-tuning the thermal and rheological properties of nanofluids. These advances could lead to more efficient and versatile nanofluid-based solutions for a wide range of industrial applications, including advanced cooling systems and renewable energy technologies.