Enhancing photovoltaic efficiency in Half-Tandem MAPbI₃/ MASnI₃ Perovskite solar cells with triple core-shell plasmonic nanoparticles

Abstract

Significant progress has been made through the optimization of modelling and device architecture solar cells has proven to be a valuable and highly effective approach for gaining a deeper understanding of the underlying physical processes in solar cells. Consequently, this research has conducted a two-dimensional (2D) perovskite solar cells (PSCs) simulation to develop an accurate model. The approach utilized in this study is based on the finite element method (FEM). Initially, a new configuration was introduced by incorporating a CH₃NH₃SnI₃ layer as the absorber within the PSC structure, forming a parallel architecture. As a result, the power conversion efficiency (PCE) of PSC increased up to 26.89%. The light trapping process plays an essential role in enhancing the performance of PSCs. For this purpose, we utilized arrays of metal nanostructures on the active layer (AL) which resulted in significantly enhancing light absorption within these layers. In this research, the influence of nanoparticles position within the AL, the radius of nanoparticles and their composition (gold (Au) and silver (Ag)) on enhancing absorption in PSCs are examined by determining the cross-sectional area of light scattering and absorption on Au and Ag nanoparticles. The optimal position for the plasmonic nanoparticles was determined to be inside the MASnI₃ as the complementary AL, 60 nm for the radius and Ag as champion composition. As a result of these modifications, the PCE reached 29.52%, representing an approximate 64% improvement compared to the planar structure. Subsequently, dielectric-metal-dielectric nanoparticles were introduced into the MASnI₃ layer, replacing the previously embedded metallic nanoparticles, in order to enhance their chemical and thermal stability. According to optical-electrical simulation results, the short-circuit current density (J_sc) of the proposed parallel PSC, featuring triple core-shell nanoparticles composed of TiO₂@Ag@TiO₂ and SiO₂@Ag@SiO₂, has been improved by approximately 40% and 41.5%, respectively, compared to a PSC lacking nanoparticles. Moreover, under optimal conditions for the PSC, the open-circuit voltage (V_oc), J_sc, fill factor (FF), and PCE were simulated at 1.01 V, 35.17 mA/cm², 84.16, and 30.18%, respectively. This approach paves the way for advancements in the development of perovskite solar cells, offering significant potential for practical applications and enhanced efficiency.

Introduction

Organic-inorganic halide perovskites have garnered significant attention over the past ten years because of their exceptional photovoltaic properties. For instance, the highest efficiency achieved by a perovskite solar cell (PSC) is an impressive 26.7% in power conversion efficiency (PCE), nearly matching the 27.3% record held by silicon solar cells¹. However, the PCE of single-junction solar cells is ultimately constrained by the Shockley-Queisser limit, capping it at around 30%. To overcome this limitation, multijunction solar cells that integrate various photovoltaic materials could potentially increase the theoretical efficiency to 44% for dual junctions². Furthermore, organic-inorganic perovskites are considered the most promising candidates for top cells in multijunction solar cells, due to their unique properties. Notably, the band gap of perovskite materials can be readily adjusted through compositional engineering^3,4. Moreover, the soft and defect-tolerant properties of perovskite thin films eliminate the necessity for lattice matching^5,6. Typically, PSCs consist of light-absorbing AL, flanked by two layers of hole and electron transport materials (HTM and ETM), which can be either organic or inorganic. Front contacts, often FTO or ITO due to their high optical transparency and low electrical resistance, are positioned on the bottom or top of the device. The principle behind PSCs is that sunlight hits the AL and gets absorbed because of the specific band gap of the perovskite material used. Light absorption in the AL creates excitons, which, when subjected to an electric field, are split into holes and electron^7,8. Subsequently, these charge carriers travel within the perovskite, migrate into the hole transfer layer (HTL) and electron transfer layer (ETL), and subsequently flow across these layers to the metal contacts, producing an electric current^9,10,11.

Importantly, photovoltaic systems based on perovskites offer two key benefits: high PCE and low manufacturing costs. Moreover, perovskite materials also possess several appealing characteristics, such as minimal non-radiative carrier recombination, suitable carrier diffusion lengths under illumination, and strong absorption of visible sunlight^12,13,14. To further enhance the PCE of PSCs, various approaches have been employed, such as interface engineering, process refinement, and manufacturing techniques, along with the implementation of mesoporous scaffold designs, among others. These techniques are designed to reduce electrical losses in PSC and avoid the loss of generated charge carriers. Approaches to enhance light absorption by improving light trapping in the AL have also been investigated. These approaches have focused on refining the optical elements within the cell^15,16,17.

PSCs generally capture light within the 300–800 nm range, however, the absorption coefficient of the AL diminishes for wavelengths exceeding 650 nm. In addition, intervals from 700 to 2500 nm, known as near infrared light, constitute a substantial portion of the solar spectrum that is not yet utilized. Therefore, utilizing this wavelength range can enhance efficiency. Materials capable of capturing light with wavelengths longer than 800 nm could potentially serve as supplementary absorbers to boost the solar cell efficiency. A key aspect of evaluating materials related to perovskite is the energy band gap. It can be attributed to the role of perovskites as light absorption layer in solar cells. Especially, their energy band gap influences the range of wavelengths or the quantity of light they can absorb. Moreover, both experimental and computational analyses indicate that MAPbI₃possesses a direct band gap across all phases, with a value of 1.55 eV^18,19,20.

To address this gap, alternative perovskite materials with smaller band gaps can be employed to broaden the absorption range. For instance, a smaller band gap allows for the absorption of low-energy photons. To fully harness the energy of sunlight, perovskite materials can be combined in half tandem within the structure of perovskite solar cells. It is important to note that due to the toxicity of Pb, research has been conducted to replace it with tin (Sn). Experimental studies have measured the MASnI₃band gap to be approximately 1.3 eV, which narrows the band gap and broadens its absorption range^19,21,22,23. MASnI₃ with a thickness of 100 nm was used, successfully extending the absorption range up to 1000 nm and increasing the J_sc from 17.57 mA/cm² to 21.97 mA/cm². Another study introduced a novel structure incorporating a layer of MASnI₃ as a secondary absorber layer within the PSC design based on MAPbI₃. In this new design, when the thickness of MASnI₃^24,25, the authors employed GeSe, which has a narrower bandgap and a broader absorption spectrum, to enhance light absorption, resulting in an increase in J_sc from 19.76 mA/cm² to 22.64 mA/cm².

One of the effective strategies in enhancing the efficiency of solar cells is the utilization of plasmonic nanostructures. The presence of plasmonic nanostructures within the absorber layer enhances optical absorption via two mechanisms. First, the scattering of incident light extends the length of optical path that photons travel within the cell. Essentially, photons traverse a longer path inside the cell, which raises the probability of photon absorption by absorbent material. The formation of surface plasmons around nanostructures generates a strong electromagnetic field in their vicinity. Since absorption is proportional to the square of the field strength, optical absorption within the solar cell is enhanced^26,27. Plasmonic nanostructures significantly enhance light collection in solar cells, carrier generation, boosting light absorption, and overall PCE. Recently, various research efforts have focused on the plasmonic characteristics of metal structures and their application in solar cells. can improve the PCE can be improved by plasmonic nanostructure throughout all three phases: light entry, absorption, and trapping. By modifying the shape, composition and size of metal plasmonic nanostructures, it is possible to trap specific wavelengths of sunlight within the solar cell, allowing these structures to serve as an additional light source^28,29. The behavior of metal plasmonic nanostructures can be categorized into two types: First, radiation effects, in which, following the localized surface plasmon resonance (LSPR) development, the electric field generated by LSPR serves as an additional source, enhancing absorption in the AL of the PSC. Second, non-radiative effects, where the energy formed by the LSPR is conducted to the nearby semiconductor, resulting in enhanced current generation^30,31.

This study explains two mechanisms behind plasmonic enhancement. The LSPRs related to metal nanostructures dissipate radially through photon emission. This phenomenon can be attributed to the lifespan limitation of these nanostructures. This radiative decay process generates electromagnetic fields within the nanostructures, exhibiting both near-field effects and light scattering in the far-field. Here, we will primarily concentrate on the mechanisms and concepts of plasmonic improvement in solar cells, particularly examining the processes associated with the radiative effects^32,33. Light that strikes the metal nanostructures is scattered in the far-field. The area over which the electric field is scattered due to the plasmonic properties of these nanostructures can exceed the physical dimensions of the nanostructure itself. This characteristic is highly influenced by the geometry and material properties of the nanostructures. Far-field scattered light can ultimately enhance and boost absorption of the AL³⁴. When it comes to light scattering, the dimensions of the metal nanostructures play a crucial role. To analyze this scattering phenomenon from nanostructures, Mie’s theory can be employed for justification³⁵. When incoming light interacts with plasmonic nanostructures, it generates a localized electromagnetic field around them, known as the near-field effect. Incorporating metal nanostructures within PSC enhances light trapping and concentrates the light more effectively within a small volume of the AL. The electromagnetic field intensity generated by plasmonic nanostructures significantly exceeds that of the incoming light into the AL. Thus, metal nanostructures can serve as an additional source to enhance absorption and increase photon flux in PSCs^36,37.

In recent years, extensive research has focused on enhancing absorption in perovskite solar cells using plasmonic nanoparticles. Stuart and Hall were the first to observe and report the phenomenon of enhanced light-to-semiconductor coupling resulting from the presence of metallic nanoparticles^38,39. They employed nanoparticle arrays to confine light within a silicon optical detector, achieving a photocurrent enhancement of up to 20-fold. In our previous work⁴⁰, the authors aimed to explore how the size, quantity, and composition of randomly distributed plasmonic nanoparticles within the AL could enhance the PCE without altering the thickness of the absorbing layer. Simulation results showed an 11.12% increase in the device’s photocurrent (from 18.24 to 20.27 mA/cm²) by leveraging the near field plasmonic enhancements of random plasmonic nanoparticles, with 50 nanoparticles of 10 nm radius integrated into the AL. Fard et al.⁴¹ performed a three-dimensional simulations revealing integrating Ag-based nanoparticles can improve PCE by 29.89% (increasing from 18 to 23.39%) for front-side illumination and by 29.63% (rising from 17.22 to 22.33%) for rear-side illumination. Ag-based nanoparticles demonstrated the most significant enhancement in PCE, achieving a J_sc of 41.30 mA/cm² and an PCE of 35.34% with an albedo of 0.5%.

The subsequent aspect to address is the morphology of plasmonic nanostructures. Research conducted by Catchpole and Polman indicates that sphere and cylindrical plasmonic nanostructures are the most effective design for improving PCE in solar cells²⁹. In this context, choosing the appropriate metal and size for plasmonic nanostructures is crucial for enhancing the PCE of PSC. Our objective is to apply plasmonic science through nanostructures to enhance PSC. Employing plasmonic nanostructures enhances absorption rates and generation of carriers, while also aiding in the efficient transfer of generated carriers. Hence, this method may significantly boost the PCE.

Perovskite is known for its susceptibility to decomposition and its corrosive nature. Additionally, when sunlight interacts with the free electrons in metallic nanoparticles, those electrons that do not participate in the absorption process and remain on the nanoparticle surface contribute to heating the nanoparticles through phonon radiation and relaxation processes. This ultimately results in nanoparticles functioning as centers for exciton recombination. Furthermore, the breakdown of nanoparticles reduces the efficiency of the PSC^42,43,44,45. To address this issue, a highly stable dielectric material like TiO₂ and silica (SiO₂) are applied around the nanoparticles, transforming pure metallic nanoparticles into core-shell structures. Employing this model enhances the chemical and thermal stability of nanoparticles. Thus, dielectric materials serve as barriers to prevent direct interaction between metals and semiconductors^38,46. A recent experimental study on thermal stability showed that SiO₂used as shell effectively preserved and stabilized their structure at around 700 °C⁴⁷. Du et al.⁴⁸  investigated the fluorescence and improved absorption of P₃HT through coating bare Ag and Ag@TiO₂ in form of core-shell nanoparticle configuration. The Ag nanoparticles’ thermal stability was significantly enhanced because of utilization of the TiO₂as shell. Metal-dielectric nanoparticles have been utilized in various PSCs. Fu et al. in⁴⁹ showed an increase in PCE about 2%, from 14.5 to 16.3%, with the using of Au/SiO₂ with core-shell nanoparticles configuration.

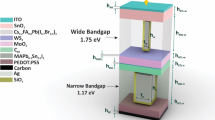
This report introduces an innovative structure, parallel MAPbI₃/ MASnI₃ PSC, featuring a metal core and a semiconductor shell, designed for the AL to achieve optimal photovoltaic performance (such as J_sc, V_oc, and PCE). A key challenge in PSCs is narrowing the absorption spectrum in the 650 to 800 nm wavelength range. Implementing this proposed structure allows us to overcome the current challenge and enhance absorption. First, to maximize PCE in this structure, an additional layer of perovskite material (CH₃NH₃SnI₃) was introduced to enhance absorption. This research involves simulating the proposed design for plasmonic nanoparticles in the absorber layer and then evaluating the nanoparticles placement to maximize PCE. Additionally, the core’s (metal) radius and composition were optimized, with subsequent analysis of how variations in composition and radius impacted the optical model, focusing on light absorption and carrier generation. This research is focused on comparing pure metallic nanoparticles of the same size with various composition of dielectric-metal-dielectric (Au, Ag, TiO₂@Ag@TiO₂ SiO₂@Ag@SiO₂) nanoparticles. The results of this study offer a comprehensive guide for achieving high-efficiency PSCs through the use of triple core-shell nanoparticles. The choice of triple core-shell plasmonic nanoparticles, specifically TiO₂@Ag@TiO₂ and SiO₂@Ag@SiO₂, was driven by their ability to enhance optical absorption through plasmonic effects while maintaining superior thermal and chemical stability compared to uncoated metallic nanoparticles. The TiO₂ and SiO₂ shells provide excellent stability by preventing accumulation and oxidation of the Ag core, which is critical for the long-term performance and reliability of PSCs. This design also minimizes the adverse effects of plasmonic hot spots, which could otherwise lead to increased recombination losses.

The structure of the paper is organized as follows: The first section introduces the fundamental principles of solar cell performance and explores how plasmonic science has been applied to enhance solar cell efficiency. Additionally, we discuss several preliminary studies that have utilized plasmonic effects to improve the PCE of solar cells. The second section details the proposed structure and simulation outcomes. The third section covers the mathematical equations, physical modeling and solution techniques associated with the proposed structure. The conclusion is provided in the fourth and final section.

Results and discussion

Proposed structure of PSC

The manuscript primarily addresses design guidelines for the optoelectronic device structure of half tandem perovskite/perovskite solar cell achieving a PCE above 30%, considering parameters related to realistic devices such as experimental validation of optoelectrical properties for all layers that are being utilized in solar cells. At the beginning of this section, we validate our simulation based on combined optical and electrical properties using values from the device fabricated experimentally in⁴⁶. The planar PSC in⁴⁶ was fabricated as follows: First, the FTO glass substrates were cleaned in a sequential process involving distilled water, soap solution, ethanol, acetone, and a final rinse with distilled water. The substrates were then exposed to UV ozone treatment for 15 min. Afterward, a 100 nm layer of TiO₂ was deposited onto the FTO glass via spin coating at 450 °C, using a 0.35 M solution of titanium diisopropoxide bis(acetylacetonate) in isopropanol. To prepare the perovskite solution, 1 M PbI₂ and 1 M CH₃NH₃I were dissolved in a solvent mixture of DMF and DMSO in a 4:1 ratio and stirred for 1 h at 60 °C. The perovskite film was created using a spin-coating technique, where the precursor solution was spun at 6,000 rpm for 60 s. Chlorobenzene (500 µL) dripped onto the surface 8 s after the spin-coating process began. The precursor-coated substrates were then heated on a hot plate at 100 °C for 1 h to facilitate the crystallization of the perovskite. The HTL was spin-coated at 3,000 rpm for 30 s using a solution of 2,2′,7,7′-tetrakis (N, N-di-p-methoxyphenylamine)−9,9′-spirobifluorene (spiro-OMeTAD) in chlorobenzene (0.058 M), along with 4-tert-butylpyridine (0.19 M), lithium bis(trifluoromethylsulfonyl)imide (0.031 M), and tris[2-(1 H-pyrazol-1-yl)−4-tert-butylpyridine] cobalt (III) tris[bis(trifluoromethanesulfonyl)imide] (5.6 × 10⁻³M). Subsequently, a 50 nm layer of Au was deposited onto the HTL to create the electrodes^50,51.

Fig. 1

Schematic of (a) experimented and (b) simulated PSC with a planar configuration⁴⁷, (c) normalized spectral absorption for each layer in the PSC with planar structure, (d) energy band diagram for two states of V = 0 V and V = V_oc.

A single-junction PSC was simulated and validated as part of this study, this validation has been performed based on the⁵⁰. The planar structure is composed of 100 nm TiO₂ as ETL, the thickness of MAPbI₃ layer approximately 300 nm, and the thickness of Spiro-OMeTAD equal to ~ 250 nm as HTL. The solar cell was constructed on the substrate made FTO, with an Au metal as contact applied via thermal evaporation. Figure 1(a) shows the experimental planar structure which has been derived from the⁵⁰. A similar structure of cell structure is modeled both optically and electrically using FEM and FDTD methods. Thus, we replicated the exact structure from the experimental work in the simulation, as illustrated in Fig. 1(b). Figure 1(c) shows the absorption spectra of each layer along with the overall reflection spectrum of the planar structure. This figure illustrates how much the entering light is absorbed and reflected by each layer across different wavelengths. Calculation of light ratio absorbed by the AL to the entire incident light reveals that only 67% of the entering light is absorbed by the AL. The spectrum indicates that AL does not absorb all the energy from the incoming light, with a significant portion of the energy being lost. Calculations reveal that 20% of the light is lost due to the parasitic absorption in other layers, while 13% is lost due to front reflection. We expect that most of the light will be absorbed by the AL. However, a portion of the light is absorbed by the FTO, TiO₂, and spiro-OMeTAD layers, which does not contribute effectively to the device’s performance. Our objective is to minimize this non-effective (parasitic) absorption and convert it into effective absorption by employing a light-trapping configuration. The current output is not limited by carrier recombination during transport within the cell, thanks to the AL and the high diffusion length of carriers. Thus, the low current in the PSC with planar configuration is primarily caused by insufficient light absorption in the AL. To enhance the current density and the associated output power, energy losses within the AL need to be minimized. Therefore, a photonic structure such as light trapping is employed to increase light entry through reduction in reflection and confinement of light within the absorbing layer by minimizing parasitic losses in the inactive layers. The energy levels of the proposed structure studied are depicted in Fig. 1(d), where the MAPbI₃ layer is positioned between the ETL and HTL. Subsequently, the generated pair hole-electrons are selectively transferred to the transport layers and contact respectively, with the V_oc being determined by the disparity between the quasi-Fermi levels at the electron-hole and selective contacts. A comprehensive study was conducted to select absorber materials, utilizing a wide bandgap perovskite (MAPbI₃) with bang gap equal to 1.5 eV chosen as the top cell, a low bandgap perovskite (MASnI₃) with band gap equal to 1.3 eV chosen as the bottom cell. Figure 2(a) illustrates the relationship between J_sc as a function of V_ocfor the planar-structured PSC. This figure demonstrates the validation of our results against experimental data⁵¹. As evident, the two outcomes are well-aligned, ensuring the reliability of the information presented in this study. The PCE, FF, V_oc, and J_scfor this configuration were equal to 17.94%, 83.60%, 1.01 V, and 21.33 mA/cm², respectively. Overall, the simulation outcomes closely align with this in reference⁵¹, indicating that future analyses are likely to be accurate. Additionally, to gain a clearer understanding of the effects when bias is applied to the device, the electron-hole concentration for two conditions (V = 0 V and V = V_oc) is presented in Fig. 2(b). In the electrical model, three regions AL, ETL and HTL were taken into account for the transport of generated carriers. After generation in the AL, the hole-electron pair is transferred to the HTL and ETL based on the carrier diffusion length characteristics of the perovskite. In the electron concentration condition (left panel), when the V = 0 V, In the AL, a gradient of electron concentration is visible, with a high concentration (in the red-yellow range) near the TiO₂ interface and decreasing toward the spiro-OMeTAD interface. In the TiO₂ layer, electron concentration is moderate (purple color), indicating electron collection. spiro-OMeTAD shows minimal electron concentration (very low values, near the lower boundary of the color scale). On the other hand, when the V = V_oc, the perovskite region shows a higher electron concentration throughout, especially near the TiO₂ interface (red). The electron concentration in TiO₂ is also high (red), suggesting efficient electron transfer. spiro-OMeTAD remains with very low electron concentration, as expected for a hole-transport material. While in the hole concentration condition (right panel), when the V = 0 V, in the perovskite region, there is a moderate concentration of holes near the spiro-OMeTAD interface (red-yellow region), while the hole concentration drops near TiO₂. The spiro-OMeTAD layer has a significant hole concentration (red), consistent with its role as a hole-transport material. TiO₂ shows very low hole concentration (dark purple). When the V = V_oc, the perovskite layer has a high concentration of holes near the spiro-OMeTAD interface, with a sharp drop-off towards TiO₂. spiro-OMeTAD continues to show high hole concentration, indicating efficient hole transfer. Hole concentration in TiO₂ remains negligible. At V = V_oc, both electron and hole concentrations increase, reflecting a situation of charge buildup in the AL under open-circuit conditions, with efficient separation and transport toward the respective transport layers (ETL and HTL). Figure 2(c) provides the generation rate of charge carriers as a function of position within a layered structure of a solar cell, including spiro-OMeTAD, AL, TiO₂, and FTO, for various incident light wavelengths ranging between 400 nm and 800 nm. The black and red curves (400 and 500 nm) in Fig. 2(c) show the highest generation rates, peaking around 550 nm (near the TiO₂-Perovskite interface). This suggests that shorter wavelengths (UV/blue light) are more effective at generating carriers, particularly near the Perovskite and TiO₂ layers. The most important reason can be attributed to the peak point of AL absorption. The absorption peak for the perovskite is the 550 nm wavelength. Shorter wavelengths (400 nm and 500 nm) are much more efficient in generating carriers due to close to the absorption peak of AL, particularly near the TiO₂-Perovskite interface, making them crucial for optimal solar cell performance. Longer wavelengths (700 nm and 800 nm) show diminishing carrier generation, with most of it happening in the AL. The overall optical generation rate depicted in Fig. 2(d) provides insight into the locations and quantities of electron and hole generation. The generation rate within AL is evident here, supporting the previous claims. For example, at the 500 nm wavelength, the generation rate is significantly higher compared to other wavelengths, particularly at the TiO₂ and AL interface.

Fig. 2

(a) J-V characteristics of the perovskite solar cell (PSC) structure obtained from both experimental measurements and analytical simulations (b) Electron and hole concentration profiles at V = 0 V and V = V_oc (c) Generation rate as a function of position across the four layers of the planar structure (d) Generation profiles corresponding to different wavelengths (400 to 800 nm).

Influence of adding MASnI3 layer to improve the PCE and increase carrier generation rate

A key approach to enhancing the performance of PSCs is to extend device absorption spectrum into the invisible range. The V_oc of the half tandem solar cell is the sum of the V_oc from the bottom and top cells, offering a key benefit for enhancing the PCE. Due to the band gap of MAPbI₃ which is equal approximately 1.55 eV, light absorption in this device is significantly reduced for wavelengths exceeding 800 nm. Optimally, solar cells should capture both the visible and a portion of the near-infrared spectrum, enhancing efficiency by absorbing a larger segment of the solar spectrum. The maximum efficiency of theoretical for the solar cell with the single-junction configuration with a band gap of approximately 1.3 eV which is able to absorb photons with energies above this threshold (λ = 1227 nm), is around 30%. In traditional PSCs, the MAPbI₃ band gap of approximately 1.55 eV allows the absorption of only photons with energies below this threshold, corresponding to wavelengths shorter than 850 nm. Based on this, incorporating a material with a band gap smaller than 1.55 eV into the structure would enable the absorption of lower-energy photons in the solar cell. To accomplish this, we introduced an additional layer of MASnI₃, positioned between the HTL and MAPbI₃ layer. To achieve the desired improvement in device performance, we incorporated an additional layer of MASnI₃, strategically positioned between the HTL and the MAPbI₃ layer. The introduction of this MASnI₃ layer leverages its narrower bandgap (approximately 1.3 eV) compared to MAPbI₃, enhancing the device’s absorption capabilities, particularly in the infrared region. This addition optimizes charge carrier separation and reduces recombination losses, leading to improved power conversion efficiency. The precise placement of MASnI₃ between the HTL and MAPbI₃ not only facilitates efficient charge transfer but also minimizes energy band misalignments, contributing to the overall performance enhancement of the PCE. This configuration typically involves a MAPbI₃ paired with another material layer like MASnI₃, where one sub-cell primarily absorbs high-energy photons, while the additional layer, with a narrower bandgap, enhances absorption in the lower-energy region of the spectrum.

MASnI₃ shares a similar crystal structure with MAPbI₃ but features a band gap of approximately 1.3 eV. After simulating this configuration, absorption and optical generation rate (G_opt) were attained and are shown in Fig. 3. As illustrated in Fig. 3(a), the absorption range increased within the 300 to 800 nm wavelength, which can be attributed to the beneficial impact of the MASnI₃ layer on overall absorption. Between the wavelengths of 800 and 1000 nm, an additional segment appears in the absorption spectrum of the AL, resulting from the inclusion of the MASnI₃ layer. In this context, the G_opt in Fig. 3(b) exhibits behavior similar to the absorption spectrum, with additional G_opt observed at wavelengths beyond 800 nm, contributing to an increase in J_sc. Figure 4 presents electric field profile of planar structure for PSCs, depicting the structure without the MASnI₃ layer, and showing the structure with the MASnI₃ layer included. As illustrated in Fig. 1b, the addition of this layer to the structure leads to an increase in J_photon followed by that increase the J_sc. We obtained the electric field profile for two wavelengths: 560 nm, corresponding to the peak absorption of MAPbI₃, and 900 nm, where MAPbI₃ shows no absorption. Figure 4(b) provides an example of the G_opt values obtained at various wavelengths. Figure 4(b) illustrates the optical generation rate for a planar structure with complementary AL, serving as the unit cell of the PSC for wavelengths of 560 nm and 900 nm. These two chosen wavelengths are based on the following: At 560 nm, the light absorption and subsequently G_opt inside the AL reach their maximum, as shown in Fig. 3(a). In contrast, 900 nm is chosen as a representative wavelength above 800 nm to demonstrate that G_opt in the AL nears zero, as depicted in Fig. 4(b), due to the near-zero absorption coefficient in the AL. Based on Fig. 4(b), a comparison of the G_opt profiles for the planar structures in presence of MASnI₃ reveals that the inclusion of the MASnI₃ layer leads to an increase in G_opt, which in turn boosts the J_sc. It is important to highlight that when comparing the G_opt at 900 nm for PSCs with the MASnI₃ layer to the structure without it, it becomes evident that light absorption occurs at this wavelength within the MASnI₃ layer. Thus, incorporating this layer into the planar structure of the PSC successfully extends the light absorption range, achieving the intended objective. In this scenario, the current density as a function of voltage for the solar cell with the MASnI₃ layer was determined, as shown in Fig. 5. This figure presents the Jsc-Voc diagram of the PSC in two configurations: the planar structure with and without the MASnI₃ layer, respectively. As shown in this figure, the highest J_sc and PCE were achieved with the structure incorporating MASnI₃, with values of 32.21 mA/cm² and 26.89%, respectively.

Fig. 3

Illustration of (a) light absorption rate and (b) carrier generation rate in the AL versus wavelength for the structures with the planar configuration for two conditions (with and without MASnI₃ layer).

Fig. 4

(a) Electric field and (b) generation profile in two different structures including with and without MASnI₃.

Influence of adding metallic nanoparticles and optimization of morphology and position

Plasmonics is a fundamental area within the field of nano-photonics, focused on studying the behavior of electromagnetic fields at scales smaller than the wavelength. Studies indicate that working at scales smaller than the wavelength reveals intriguing and unexpected behaviors. One of the appealing aspects of this field is that all the governing principles can be explained using classical physics. Plasmonic structures positively influence the PCE and absorption of PSCs. By optimizing the geometry and selecting appropriate materials, it is possible to achieve the goal of enhancing the PCE of PSCs. Plasmonic nanoparticles are utilized in one of their key applications, which is in PSCs. First, we performed our modeling based on the structure shown in Fig. 6(a). Since the device is periodic, we analyzed a unit cell of the entire structure to minimize simulation time. The position and dimensions of the structure as well as the radius of the nanoparticle are shown in Fig. 6(a). According to this figure, we divided the position of the nanoparticle into four parts including without nanoparticle, nanoparticle placed in MASnI₃, nanoparticle placed in MAPbI_3, and nanoparticle placed in both MASnI₃/MAPbI₃. Next, we aim to analyze the proposed structure to achieve an optimized PSC. To begin, we placed the nanoparticle with 60 nm radius inside the MASnI₃. Considering Fig. 6(b), the rate of absorption in the AL rises within the wavelength range of 600–1000 nm, while below 600 nm, the behavior of absorption for both the planar structure and the metallic (Au) nanoparticle spectra is identical (black and red lines). This is due to the interaction of light with the Au nanoparticle within the 600–1000 nm wavelength range. At a wavelength of 600 nm, light reaches the MASnI₃ layer, where its interaction with the nanoparticles begins, causing changes from this point onward. When the nanoparticle was positioned within the MAPbI₃ and both ALs (MASnI₃/MAPbI₃), the absorption rate significantly dropped. As shown in Fig. 6(b), the absorption rate began to fluctuate, likely due to the plasmonic effect generated at the onset of the MAPbI₃ layer. When the nanoparticle is embedded in the MAPbI₃, it obstructs light from penetrating the entire device, preventing the light from reaching the second AL. This is the primary cause of the significant reduction in the absorption rate. We expect that light will be confined within both AL. To illustrate this, the reflectance and transmittance rates as a function of wavelength are presented in Fig. 6(c) and Fig. 6(d), respectively. We anticipate that light will be confined to both ALs. The inclusion of nanoparticles within the MASnI₃ layer leads to a slight increase in reflectance (Fig. 6(c)), though this increase is minimal compared to the planar configuration. This suggests that light is confined within the AL, resulting in the excitation of the nanoparticles. However, when the nanoparticle was positioned in the MAPbI₃ or both ALs, the reflection increased significantly. To provide further clarity, the transmittance rate for our proposed structure is displayed in Fig. 6(d). When the nanoparticle placed inside the MAPbI₃, light transmittance is significantly reduced, suggesting that light struggles to penetrate the AL, and the high density of the nanoparticle obstructs its passage to the end of the AL. The combined effect of increased reflectance and reduced transmittance results in a substantial reduction in light absorption for the nanoparticle inside both MAPbI₃ and MASnI₃, with absorption levels falling below those of the planar configuration. To explain the behavior of the absorption range related to AL, the profile of the electric field in the AL, with the nanoparticle placed at different positions, is presented in Fig. 7. As illustrated in Fig. 7, the given profile of the electric field exhibited an uniform and standard distribution when nanoparticles were not utilized. The electric field is stronger at the front and rear of the AL, attributed to the light entering the layer and the light reflection from the underlying layer, respectively. When the nanoparticle is introduced into the MASnI₃ and light reaches this layer, an interaction occurs between light and nanoparticles, resulting in excitation of nanoparticles. This plasmon effect is a result of the small size of the nanoparticle, manifesting as LSPR in the near-field region. In other words, the electric field generated by the LSPR is concentrated around the nanoparticle. As depicted in Fig. 7, each nanoparticle functions as a secondary light source. Nanoparticles enhance absorption across various regions of AL. In essence, each nanoparticle behaves like an optical island. To further examine if the electric field intensity increases with a larger nanoparticle radius, we embedded the nanoparticle inside the MAPbI₃. As illustrated in Fig. 7, placing the nanoparticle inside the MAPbI₃ resulted in a higher electric field compared to nanoparticle which has been embedded inside MASnI₃, leading to greater absorption in the AL (MAPbI₃). The key point here is the focus on enhancing the absorption rate in both ALs (MASnI₃/MAPbI₃). While nanoparticles do increase the absorption rate in MAPbI₃, they hinder light from entering MASnI₃, as a significant portion of the light is reflected by the nanoparticles embedded in MAPbI₃. Consequently, as evident, the electric field is less pronounced, particularly within the MASnI₃ layer. When the Au nanoparticle is positioned in the MAPbI₃ (Fig. 7), light entering the MAPbI₃ excites the nanoparticle plasmon, producing an electric field in the form of a far-field response. The electric field in the upper portion of the MAPbI₃ increases, resulting in enhanced absorption in that region. However, in the lower half of this layer (beneath the nanoparticle), the electric field is weaker than in the PSC with a planar configuration because of limited light transmission. In the next step, we embedded the nanoparticle within both ALs, and it is clear that the nanoparticle inside the MAPbI₃ still obstructs light from entering the entire device. However, compared to the previous case where the nanoparticle was only placed in MAPbI3, this configuration shows an improved absorption rate (Fig. 6). To provide a more detailed explanation of these occurrences, the electric field distribution for nanoparticles at three positions with the planar structure is depicted as a vector in Fig. 8. This illustration depicts the electric field distribution in terms of vectors within AL and indicates the changes in direction in the electric field. The $\:X$-direction corresponds to the transverse axis of the device, the $\:Y$-direction corresponds to the extended axis, and the $\:Z$-direction indicates the third-dimensional axis, which cannot be visualized in a two-dimensional representation. Figure 8 aids in providing a clearer understanding of how the nanoparticle contributes to enhancing absorption in the AL. As shown in Fig. 8, in absent of nanoparticles inside the AL, the distribution of electric field vectors displays uniform behavior. When the nanoparticle is positioned at MASnI₃, direction of electric field vectors is modified by the LSPR excitation around the nanoparticle, leading to the accumulation and confinement of the electric field in this region. Notably, at the top of the AL, the behavior of the electric field vectors is identical to that in the planar configuration. However, the intensity of electric field vectors differs from that observed in the planar configuration. This variation in intensity is evident due to the light scattering triggered by the nanoparticle. When the nanoparticle is positioned inside MAPbI₃, changes in the distribution of electric field vectors at the upper surface of the AL are observed. In contrast, the distribution of electric field vectors in the bottom section of the AL exhibits an intensity that is very similar to the planar configuration. The alterations in the electric field in this configuration are minimal and can be ascribed to the increased light reflection caused by the nanoparticle. In Fig. 8, when the nanoparticle is positioned in both AL, the overall electric field vectors undergo changes throughout the entire AL. This alteration is partially due to the LSPR formation and the associated near-field effects. The other part of these changes is attributed to the scattering of light caused by the nanosphere. This scattering can be beneficial, as the light is scattered by the nanosphere is redirected toward AL, thereby enhancing the absorption within the layer. In the bottom section of the AL, the vectors related to electric field are influenced by nanoparticles, altering their behavior in this region and leading to a reduction in electric field intensity.

Fig. 5

Evaluation of J_sc-V_oc for PSC in two different structures including with and without MASnI₃.

Fig. 6

(a), (b), (c) and (d) simulated structure, absorption, reflectance and transmittance rate of AL in presence of nanoparticles, respectively.

Fig. 7

Electric field profile in the proposed structure for different position (including without nanoparticles, nanoparticles placed in MASnI₃, nanoparticles placed in MAPbI_3, and nanoparticles placed in both MAPbI₃/ MASnI₃) based on the optical simulation comparison of J_sc-V_oc for PSC in four different structures.

Fig. 8

Changes in electric field vectors relative to the x and y dimensions of the active layers for four different structures including without nanoparticles, nanoparticles placed in MASnI₃, nanoparticles placed in MAPbI_3, and nanoparticles placed in both MAPbI₃/ MASnI₃.

Fig. 9

Comparison of J_sc-V_oc for PSC in four different structures including without nanoparticles, nanoparticles placed in MASnI₃, nanoparticles placed in MAPbI_3, and nanoparticles placed in both MAPbI₃/ MASnI₃.

Table 1 Output electrical results for proposed PSC in four configurations.

Overall, when the nanoparticle is embedded in the MASnI₃, the electric field intensity increases, and the electric field vectors are modified due to the formation of LSPR around the nanoparticle. Following the acquisition of optical results, we proceed to obtain electrical results using the FEM method. For this, the J-V characteristics of the proposed PSC with the nanoparticle inside different AL configurations are presented in Fig. 9. The J_sc values for the planar, nanoparticles placed in MASnI₃, nanoparticles placed in MAPbI₃, and both MAPbI₃/ MASnI₃ configurations are equal to 32.21, 33.46, 31.69, and 31.46 mA/cm², respectively. As shown, the highest current is achieved with the nanoparticle positioned inside MASnI₃, where the PCE reached 28.64%. The remaining results for the proposed PSC are summarized in Table 1. According to Table 1, by incorporating additional AL as complementary material into device architecture, we observed a significant improvement in the PCE, increasing from 17.94 to 26.89%. This improvement can be attributed to the broader absorption spectrum enabled by the added layer, which complements the primary material’s absorption by capturing photons from different parts of the solar spectrum. The introduction of this complementary AL not only expands the wavelength range for efficient light absorption but also enhances charge carrier separation and reduces recombination losses. As a result, the half tandem-like configuration boosts the overall energy conversion efficiency of the solar cell, illustrating the potential of material combinations in optimizing photovoltaic performance. By comparing the results of this work with those in reference⁵², it is evident that the obtained PCE is 33.78% higher than that reported in reference⁵². Although our structure is similar to the one described in reference⁵³, it is important to note that reference^52,53 utilize a full tandem configuration, whereas our structure is a half tandem. Despite this difference, our PCE is comparable to that of full tandem, which highlights the efficiency of our design. Moreover, this advantage allows us to reduce construction costs while maintaining competitive performance. Figure 10 illustrates the changes in absorption in terms of the wavelength function in the AL for diverse radii (R) of the Au nanoparticle. The plasmonic nanoparticle was positioned in the MASnI₃, and its radius was increased from 40 to 120 nm. We increased the nanoparticle radius to 60 nm, resulting in a higher absorption rate in comparison with the 40 nm radius. The behavior between 300 and 600 nm remains identical, but noticeable changes occur as the wavelength approaches 1000 nm. These changes result from light interacting with the nanoparticle within the 600 to 1000 nm wavelength range, where the light reaches the nanoparticle and initiates interaction. Additionally, this scenario was repeated and adjusted the nanoparticle radius to 120 nm with 20 nm step, which led to a decrease in AL absorption compared to the previous cases with 40 nm and 60 nm radio and the numerical results for the photocurrent are displayed in the bar graph in Fig. 10(b). According to this figure, the best radius was 60 nm. The photocurrent for 40, 60, 80, 100 and 120 nm were equal to 33.42, 33.46, 33.37, 33.02, 32.52 (mA/cm²) respectively.

We investigated the response of plasmonic response for Ag and Au nanoparticles to enhance absorption rate further. In this part, based on the optimized position and radius, we altered the composition of nanoparticles to Ag and Au and observed alterations in the AL absorption behavior. When Ag was used instead of Au, the absorption spectrum increased between 600 and 800 nm (Fig. 11(a)). Figure 11(b) and 11(c) present the frequency dependence of the dielectric function for Au and Ag, as reported in the literature⁵⁴. Based on the dielectric functions of these two metals, it can be concluded that Ag exhibits greater absorption compared to Au. Thus, incorporating Ag into the plasmonic nanoparticle results in greater light scattering excitation compared to Au, leading in an enhancement of J_sc in the PSC. Using Ag in PSCs is also more cost-effective. Additionally, the light scattering properties are influenced by the nanoparticle composition, with Ag exhibiting stronger radiative characteristics due to lower Ohmic losses compared to Au. This phenomenon is best explained by the complex dielectric related to functions of bulk for the metal nanoparticles (Au and Ag), that include a real component referred to Fig. 11(a) and an imaginary component referred to Fig. 11(b). The dielectric function real component ($\:\epsilon\:_{i}$) determines the response of polarization inside the metal. The dielectric function imaginary component ($\:\epsilon\:_{r}$) defines the optical parasitic, referring to intraband losses. As shown in Fig. 11(c), Au exhibits high Drude losses in the invisible region, while these losses are lower in the visible spectrum. Additionally, Au experiences significant losses at reduced wavelengths. In contrast, the lower imaginary dielectric function for the Ag metal over all wavelengths indicates reduced optical parasitic (i.e., plasmon damping), resulting in greater reduced plasmon linewidths and scattering efficiency. This key variation in the optical properties of Ag and Au has been instrumental in our decision to select Ag metal as the nanoparticle material, ultimately enhancing absorption in the AL. Figure 11(d) presents the J–V curve for Ag and Au used in the metallic plasmonic nanoparticle architecture of the PSC. For the Ag nanoparticle with a 60 nm radius, the obtained J_sc, V_oc, FF, and PCE values were 34.43 mA/cm², 1.01 V, 84.12%, and 29.52%, respectively. The detailed electrical parameters for the two structures (Au and Ag) have been mentioned inside Fig. 11(d). According to Fig. 11, the use of Ag as the core material was specifically chosen for its low optical losses and strong scattering properties, which are highly beneficial for light trapping within the AL of the solar cell. Simulation results indicated that these nanoparticles effectively enhance light absorption, particularly in the near-infrared region, where PSCs often exhibit reduced performance. After optimizing the proposed structure and getting the maximum PCE via incorporating the plasmonic nanoparticle, the triple core-shell nanoparticle is introduced to improve the PCE of PSC. It is important to account for the optical losses of the nanoparticle in various semiconductor materials used as solar cell absorbers. In addition, PSCs, which are prone to decomposition, face other challenges including the thermal and chemical instability of the nanoparticle. Triple core-shell nanoparticles were selected to address and overcome these existing challenges.

Fig. 10

(a) Characterized absorption rate of the active layers in the presence of metal nanoparticles for five different radii (40, 60, 80, 100, 120 [nm]) and (b) the photocurrent for various radii.

Fig. 11

(a) The absorption ranges comparison of the PSC incorporating Ag and Au metallic plasmonic nanoparticles, (b) the real and (c) imaginary components of the dielectric function for Ag and Au, and (d) J-V curve for the metallic plasmonic nanoparticle architecture in PSC utilizing both metals, Ag and Au.

Influence of adding triple core-shell nanoparticles

Figure 12 presents both 3D and 2D schematics of the proposed PSC structure with the inclusion of triple core-shell nanoparticles. Along with the schematic, the composition and the radii of the core and shell layers are also specified. In this nanoparticle design, the inclusion of a metal nano shell between two dielectric layers decreases the total metal thickness. The radius of the dielectric core chosen TiO₂/SiO₂ within the metal shell of the triple-shell nanoparticle was designed less than pure metal because we did not want to change the optimized radius set at 50 nm. Additionally, the thickness of the metal nano shell (Au or Ag) and the outer dielectric layer (TiO₂/SiO₂) selected for both was 10 nm. It means that the radii for the metal and outer dielectric spheres have been chosen to be 60 and 70 nm, respectively. The core-shell design with TiO₂ and SiO₂ensures not only enhanced light-matter interactions but also better compatibility with the perovskite lattice constant, minimizing any potential destructive effects such as ion diffusion or degradation of the AL. Furthermore, these materials were selected based on their ability to act as optical spacers and improve the distribution of the plasmonic near-fields, thus contributing to better light harvesting efficiency. As reported in the study⁵⁵, when the dielectric thickness exceeds 3 nm, hot electrons cannot overcome the Schottky barrier, preventing their injection into the perovskite conduction band and effectively halting the hot electron transfer (HET) process. In contrast to the first non-radiative effect (HET), the dielectric layer does not obstruct the plasmon resonant energy transfer (PRET) process. This process occurs as long as strong fields surround the metal nanoparticle within the perovskite material and there is a spectral overlap between perovskite absorption and LSPR. To better understand what is happening when the triple core-shell is used inside the AL across different models, the absorption rate, generation rate, and electrical distribution were obtained and analyzed. Figure 13 presents the absorption spectrum comparison between pure metal nanoparticle and triple core-shell nanoparticle. Figure 13(a) depicts the overall Ag nanoparticle absorption, demonstrating an enhancement in the total absorption rate. However, after accounting for optical losses, it becomes evident that the absorption spectrum of the AL improves for wavelengths above 600 nm. TiO₂/Ag/TiO₂ triple core-shell nanoparticles outperform metallic Ag nanoparticles across the entire wavelength spectrum, with a particular enhancement in absorption for wavelengths between 600 and 800 nm. SiO₂/Ag/SiO₂ triple core-shell nanoparticles notably enhance the absorption spectrum above 700 nm compared to the absorption of spherical Ag nanoparticles. As previously noted, intense local fields are generated around the nanoparticle, with these fields being influenced by the size and shape of the nanoparticle. Additionally, the local distribution of the electric field varies across different wavelengths. To provide a clearer understanding of the electric field distribution at various wavelengths, the profile for TiO₂/Ag/TiO₂ and SiO₂/Ag/SiO₂ is analyzed from a cross-sectional perspective, as shown in Fig. 13(b) and 13(c). The AL as an absorber layer exhibits strong absorption in the key wavelengths. At 500 nm, the triple core-shell nanoparticle starts stimulating and following that the LSPR is formed around the triple core-shell nanoparticle, but this distribution is not enough to improve the absorption rate of the AL. In other words, at wavelengths below 500 nm, it is no existence of interaction between the light and the nanoparticle, and the incident light is reflected upon striking the TiO₂/Ag/TiO₂ triple core-shell nanoparticle. Scattering effects are evident at the 700 nm wavelength, as shown in Fig. 13(b). After a brief period of metal electron oscillation, both far-field and near-field effects become visible at the 700 nm wavelength (Fig. 13(b)). At this wavelength, the near-field effects are intensified while scattering effects diminish. At 900 nm, pronounced near-field effects are observed. Figure 13(c) illustrates the electric field distribution of the SiO₂/Ag/SiO₂ structure. Comparing the electric fields of both TiO₂/Ag/TiO₂ and SiO₂/Ag/SiO₂ reveals that the LSPR is stronger for the SiO₂/Ag/SiO₂, especially at 900 nm, as confirmed by the absorption rate displayed in Fig. 13(a). Due to the intense localization, SiO₂/Ag/SiO₂ nanoparticles can act as secondary incident light sources by recharging the photon flux at various wavelengths, facilitating the transfer of electrons from the valence band to the conduction band. Additionally, intense electromagnetic fields which surround the triple core-shell nanoparticle enhance charge carrier mobility and overcome exciton binding energy, contributing to the efficiency of the PSC. Notably, triple core-shell nanoparticles exhibit no optical losses and possess a more effective mechanism of plasmon hybridization compared to pure metallic nanoparticles. In the last section, we obtained the J_sc-V_oc for the triple core-shell nanoparticle. As shown in Fig. 14, triple core-shell Ag nanoparticles outperform pure Ag nanoparticles. Furthermore, Fig. 14 highlights that the highest PSC performance is achieved with SiO₂/Ag/SiO₂ nanoparticles. According to this figure, the J_sc, V_oc, FF and PCE were 35.17 mA/cm², 1.01 V, 84.16% and 30.18%. The rest of the electrical parameters are listed in Table 2. In this table, we present a comparison between the results of our study and documented in previous research. It can be concluded that the designed configuration enhanced key cell characteristics, including J_sc, V_oc, FF and PCE. This configuration and material choice were part of a broader strategy to optimize the balance between light trapping and carrier dynamics. By minimizing recombination losses and increasing photon absorption in the AL, the device achieves a significant improvement in PCE.

Fig. 12

3D and 2D schematic of proposed structure PSC in presence of triple core/shell nanoparticle.

Fig. 13

(a) The comparison of the absorption rate of the active layers in presence of TiO₂@Ag@TiO₂ and SiO₂@Ag@SiO₂ nanoparticles, (b) and (c) electric filed distribution of TiO₂@Ag@TiO₂ and SiO₂@Ag@SiO₂ nanoparticles respectively.

Fig. 14

J_sc-V_oc for the plasmonic TiO₂@Ag@TiO₂ and SiO₂@Ag@SiO₂ nanoparticles architecture in PSC.

Table 2 A comparison between the outcomes of our work and those reported in previous studies is provided.

Methods

Theory

Optical model

In the framework of classical electrodynamics, optical phenomena are explained by Maxwell’s equations. In fact, Maxwell’s equations are differential equations that, together with boundary conditions for each specific situation, determine the fields produced by sources of charge and current. The differential form of these equations in the SI system can be written as follows:

$$\:\frac{\partial\:\text{H}}{\partial\:\text{t}}=\frac{-1}{\mu\:}\nabla\:\times\:E\:$$

(1)

$$\:\epsilon\:\frac{\partial\:E}{\partial\:t}=-\nabla\:\times\:H-\sigma\:E$$

(2)

Here, $\:H$ denotes the intensity of the magnetic field, $\:E$ represents the intensity of the electric field, $\:\mu\:$ stands for permeability, $\:\epsilon\:$ indicates permittivity, and $\:\sigma\:$refers to electrical conductivity. By applying the aforementioned equations, it is possible to derive the internal electric field. Subsequently, the rate of optical generation of electron-hole pairs within the active region can be determined as⁶¹:

$$\:{G}_{OPT}=\frac{\epsilon^{\prime\prime}{E}^{2}}{2\hslash\:}$$

(3)

The G_opt at a specific wavelength is influenced primarily by two factors: the imaginary component of the permittivity ($\:\epsilon\:{\prime\:}{\prime\:}$) and the strength of the built-in electric field ($\:E$). As per Eq. (3), an increase in G_opt is directly related to a rise in $\:E$, which can be achieved by enhancing the absorption of incoming light.

Electrical model

At this stage, we use the outcomes from the optical model as inputs for the electric model. The J-V characteristics for photovoltaic system can be expressed through:

$$\:J\left(V\right)={J}_{dark}-{J}_{sc}={J}_{0}\left(exp\left(\frac{eV}{nKT}\right)-1\right)-q{G}_{OPT}\left({L}_{n}+{L}_{p}\right)$$

(4)

The J_dark refers to the photovoltaic system current when there is no sunlight, meaning no carriers are generated. To determine J_sc, it’s necessary to first measure the carrier concentration within the device. To achieve this, it is essential to resolve the continuity equations through Poisson equation within the PSC, as outlined below:

$$\:\nabla\:.\left({\epsilon\:}_{0}.{\epsilon\:}_{r}\nabla\:\phi\:\right)=-\rho\:$$

(5)

$$\:\frac{\partial\:n}{\partial\:t}=\frac{1}{q}\nabla\:{j}_{n}+{G}_{n}-{U}_{N}\:$$

(6)

$$\:\frac{\partial\:p}{\partial\:t}=\frac{1}{q}\nabla\:{j}_{p}+{G}_{p}-{U}_{p}$$

(7)

where $\:\phi\:$ represents the electrostatic potential, $\:q$ denotes the electron charge, $\:{\epsilon\:}_{0}$ is the permittivity of free space, and $\:\rho\:$ indicates the charge density. $\:{U}_{N}$ and $\:{U}_{P}$ refer to the rates at which electrons and holes recombine, respectively, while $\:{J}_{n}$ and $\:{J}_{P}$ denote the current densities for electrons and holes, respectively. $\:{G}_{n}$ and $\:{G}_{p}$ represent the total generation rates for electrons and holes, respectively, and it is assumed that $\:{G}_{n}$ equals $\:{G}_{p}$, both being equal to G_tot. G_tot can be derived by integrating Eq. (3) across the full wavelength spectrum, as shown in:

$$\:{G}_{total}={\int\:}_{{\lambda\:}_{min}}^{{\lambda\:}_{max}}{G}_{opt}\left(\lambda\:\right)d\lambda\:$$

(8)

By utilizing the two models described earlier, we can determine J_sc and V_oc.

Plasmon

Mie theory describes the local field amplifications, scattering and absorption cross-sections and far-field scattering patterns from a nanoparticle excited by a plane wave. The expressions for the scattering and absorption cross-sections are defined as follows:

$$\:{C}_{scat}=\frac{1}{6\pi\:}{\left(\frac{2\pi\:}{\lambda\:}\right)}^{4}{\left|\alpha\:\right|}^{2}$$

(9)

$$\:{C}_{abs}=\frac{1}{6\pi\:}Im\left[\alpha\:\right]$$

(10)

where

$$\:\alpha\:=3 V\left[\frac{{\epsilon\:}_{P}/{\epsilon\:}_{m}-1}{{\epsilon\:}_{P}/{\epsilon\:}_{m}+2}\right]$$

(11)

is the particle polarizability. In this formula, $\:{\epsilon\:}_{p}$ represents the particle’s dielectric function, $\:V$ denotes the volume of the particle, and $\:{\epsilon\:}_{m}$ refers to the dielectric function of the surrounding medium. It is evident that the particle’s polarizability significantly increases when $\:{\epsilon\:}_{p}$ equals − 2 $\:{\epsilon\:}_{m}$. This phenomenon is referred to as surface plasmon resonance (SPR). During SPR, the scattering cross-section can surpass the geometric cross-section of the particle.

Mesh structure

A mesh controlled by the user is specified for the entire geometry. Each domain is individually meshed with a maximum element size of 48.2 nm and a minimum element size of 1.75 nm. The element growth rate is capped at 1.25, with a curvature factor of 0.2. A triangular mesh is applied to the interface between the FTO and TiO₂ layers. The tessellation setting is configured to automatic. The surfaces are meshed by employing a swept mesh approach, with a method called the face meshing specified as quadrilateral. The TiO₂ layer needs a fine mesh; therefore, the number of mesh elements on its surface is configured to 120. Regarding the perovskite layer, a distribution of sweep type was specified, using 40 elements on one face and an element ratio of 0.1. A symmetric distribution is chosen to ensure consistent meshing across all the perovskite layer faces. This meshing approach is also applied to the Spiro-OMeTAD layer. As the shell is the thinnest, the sweep mesh elements are uniformly distributed with 5 elements assigned to each face. In this study, the mesh quality is assessed based on the growth rate and the elements skewness. Elements that deviate from the ideal mesh shape, whether by having larger or smaller angles, are penalized. A skewness value of 1 represents the optimal mesh quality, while a value of 0 indicates a degenerate mesh element.

Simulation details

As previously stated, the nanostructures development relies on both electrical and optical modelling. In the optical aspect, light trapping occurs based on the spacing of nanostructures, specifically the distance between each nanostructure within a unit cell. Hence, the spacing between nanostructures must be smaller than the incident wavelength to enhance the absorption of light and generation of electron-hole pairs, resulting in an improvement in the G_opt. Electrical models describing the processes of collection and carrier transport take place. Enhancing the built-in electric field can lead to increased carrier transport. Initially, we simulated the device using an optical module by the Finite-Difference Time-Domain (FDTD) method to determine the carrier generation and absorption rates within the AL when nanostructures are present. Next, after modifying the nanostructures (triple core-shell metallic plasmonic nanoparticles) in the optical module, we used the resulting generation of carrier rate as input for the electrical module which has been done by finite element method (FEM). During the simulation phase, we analyzed three device models: (I) a planar configuration, (II) two ALs as parallel structure and (III) triple core-shell. The structure of our model consists of (from top to bottom): indium-doped tin oxide (ITO) serving as the transparent conducting oxide, titanium dioxide (TiO₂) functioning as the ETL, perovskite (MAPbI₃) as the AL, CH₃NH₃SnI₃ as complementary AL to increase the absorption rate, spiro-OMeTAD as the HTL, TiO₂ and SiO₂ forming the shell, Au and Ag acting as the core within the triple core-shell nanoparticles, and Au metal as the back contact. We positioned a plane wave source atop the front contact (ITO) to simulate the incoming sunlight. We utilized the AM1.5G ranges simulated as the source of light. In the simple structure (planar), we used a wavelength spectrum from 300 to 800 nm while we increased this range to 1000 nm when we utilized the MASnI₃ with the resolution of 20 nm. To minimize computational demands and simulation duration, we modelled a small segment of the device and employed periodic boundary conditions (PBC) on the edges of all layers in the simulation. The intricate refractive indices for ITO, spiro-OMeTAD, MAPbI₃, MASnI₃, TiO₂ and SiO₂, were sourced from existing research^{22, 62–72}. By applying the optical module (Eq. (3)), we determined the G_opt for each wavelength. Subsequently, we used Eq. (8) to compute the cumulative number of carriers generated across the entire wavelength range. By inputting the carrier generation profile into the electrical model, we can determine the J-V curve of the PSC. The electrical model focuses solely on the HTL, ETL and perovskite regions. The primary mechanism for carrier recombination in the device is Shockley–Read–Hall (SRH) recombination. Additionally, the top contact (ITO) is treated as ohmic, while the bottom contact (Au) is modelled as Shockley. In our simulations, the surface recombination velocities for holes and electrons are set to $\:{S}_{n}={S}_{n}={10}^{7}cm/s$. The electrical properties of the materials used in this study were sourced from prior studies^{73,74,75,76,77,78}and shown in Table 3.

Table 3 Electrical parameters required for PSC.

Conclusion

This study explores the improvement in PCE of a thin-film organic-inorganic halide PSC cell by incorporating triple core-shell spherical metallic-dielectric nanoparticles into the AL. Maxwell’s equations were solved and electrical calculations were conducted using a 2D FEM. Due to the 1.55 eV band gap of the MAPbI₃ in the planar structure, absorption and G_opt at wavelengths beyond 800 nm are nearly negligible. To address this issue, MASnI₃ with a favorable band gap of 1.3 eV was utilized in a half tandem configuration to enhance G_opt at wavelengths exceeding 800 nm. For this structure, the electrical parameters were J_sc = 32.21 mA/cm², V_oc = 1 V, FF = 82.81, and PCE = 26.89%. This report applied plasmonic principles to improve G_opt and enhance light absorption in the 300 to 1000 nm wavelength range. To achieve this, the mechanism of LSPR was employed as an additional resource, facilitated by the configuration of plasmonic nanoparticles. 2D simulations for both electrical and optical properties were utilized to thoroughly investigate the impact of plasmonic nanoparticles on PSC parameters. To achieve this, key factors such as the core material, radius, shell composition as well as the nanoparticles position and the processes for carrier transfer and collection were taken into account for assessment. By employing the triple core-shell approach along with plasmonic principles, we successfully improved the performance of the proposed PSC design, particularly in terms of PCE, compared to the planar configuration. Moreover, a radius of 60 nm and Ag as core composition were optimized for the metallic plasmonic nanoparticle and the J_sc for this step was $\:\sim\:$3.5 times greater than without nanoparticles. Then, the position of nanoparticles was investigated and when nanoparticles were embedded in the MASnI₃, the PCE increased to 28.64% from 26.89%. Additionally, utilizing triple core-shell nanoparticles ensures chemical and thermal stability while lowering the spectroscopic expenses typically associated with pure metallic nanoparticles. The optimal configuration of the proposed PSC designed by triple core-shell plasmonic nanoparticles (SiO₂@Ag@SiO₂) achieved values of 1.01 V for V_oc, 35.17 mA/cm² for J_sc, 84.16 for FF, and 30.18% for PCE. The findings presented in this paper offer valuable insights and practical guidance for the design, fabrication, and application of PSCs. Lastly, it should be noted that the PSC architecture by triple core-shell developed in our study can be produced using existing and feasible manufacturing methods, as detailed in the referenced literature^{58,62,79,80,81,82,83} for further information.