Introduction

Creep is one of the important mechanical properties of rocks, which are related to their crystal structures and the external environment. The rock masses of deep caverns tend to show local fracture characteristics after excavation, with obvious time-dependent behaviors1. In view of the creep damage characteristics and fracture characteristics of rocks, indoor tests and on-site monitoring methods are usually used to carry out research in such areas. Using numerical methods to study the creep characteristics of deep rocks is gradually becoming more common. In particular, the particle flow method can reflect the microscopic fracture characteristics of rocks, which has obvious advantages on the study of local fracture evolution of surrounding rocks in deep caverns2,3,4. How to construct a particle flow model that conforms to the actual rock mechanical properties and creep characteristics, and to study the time-dependent evolution law of deep rock fracture is the key and difficult problem in the current research.

In the study of particle flow about rock creep behavior, Potyondy5 developed a parallel bond stress corrosion (PSC) model to simulate the change of rock mechanical properties with time. In subsequent studies, the inversion of cracking, deformation, accelerated failure and instability in rocks using stress corrosion method had been widely used6,7. Cui et al.8 obtained the long-term strength fitting curves of marble based on the results of indoor tests, and the parameters of the stress corrosion model of marble were inversely analyzed using the particle flow method. Liu et al.9 simulated the creep damage process of brittle rocks based on a grain stress corrosion model, described the continuous degradation of parallel bond radius during stress corrosion by correcting the damage rate law, which could better predict the damage time of rocks at low stresses. Combining the equivalent crystalline model with the stress corrosion model, Li et al.10 developed a creep particle flow model considering the influence of different crystal sizes and shape distributions. Ghasemi et al.11 investigated the effect of stress corrosion process on the long-term strength of crystalline rocks and the process of fracture expansion by using the particle flow method, and concluded that there exists a “stress threshold” for fracture initiation during fracture deformation in crystalline rocks. With the above studies, the stress corrosion model can explain the creep damage mechanism of rocks at the microscopic level, and the microscopic fracture time-dependent behavior of rock materials is better simulated by the attenuation of intergranular connection bonds.

In the study of creep damage in deep hard rock, Chen et al.12 conducted graded creep tests on Beishan granite, and combined particle flow simulation and acoustic emission tests to study the effects of temperature and confining pressure on its creep behavior. Hu et al.13 proposed a creep damage model considering the time scale, and used particle flow to simulate triaxial compression and creep tests on rock samples to investigate the long-term creep deformation behavior of fracture-bearing prefabricated hard rock. Wang et al.14 proposed a new unified tectonic model by combining with the time-dependent damage law and the viscoplasticity theory, represented the nonlinear creep deformation characteristics and long-term mechanical properties of hard rocks. Considering the influence of the time factor on the evolutionary process of the rock rheological characteristics, Li et al.15 established the variable-order fractional-order creep damage model, and verified the applicability of this model in other complex stress environments. Das et al.16 validated the ability of the smooth particle hydrodynamics method to predict cracking of brittle rocks during simulated impacts by using the strain history of each particle to predict the damage evolution. By constructing creep damage models, the above studies better describe the rock creep failure process, analyze the rock long-term mechanical properties, and contributed to understanding the creep characteristics and damage evolution laws of rock.

During the rock graded loading process, both the creep rate and the plastic strain gradually increase with the stress level. When the stress corrosion model is used to simulate the rock graded loading, the creep rate is smaller than the actual rock creep rate at high stress levels, which leads to a large difference in the strain value and does not simulate the whole process of multistage loading well. In this paper, taking the deep mining project of Xincheng Gold Mine as background, the mechanical properties and creep characteristics of granite were obtained by indoor tests. A variable radius particle clump model was constructed using the particle flow method. Considering the change of bond parameter during the loading process, a bond-degradation creep model for deep granite was proposed, and the applicability of the model was verified. The fracture evolution law of deep roadway surrounding rock was studied based on the bond-degradation creep model.

Cohesion-weakening-friction-strengthening (CWFS) model

Basic principles of the CWFS model

Conventional rock yield criterion all use linear strength mobilization method to simulate the rock failure process, assuming that cohesion and friction strengths are activated together during the rock failure process and both remain constant throughout the failure process17. However, after the initial fracture occurs within the rock, the expansion of the tension fractures parallel to the maximum compressive stress direction hinders effective normal stress transfer on the microscopic fracture surface, at which time the normal effective compressive stress is 0, and the frictional strength component is also 0. As microfractures develop, the intergranular cohesion strength gradually decreases until the parallel bonds fracture, at which time the friction strength is activated until the fractures are produced. Hajiabdolmajid et al.18 proposed a cohesion-weakening-friction-strengthening (CWFS) model based on the plastic strain and the Mohr-Coulomb strength criterion, which suggested that the cohesion and friction strengths of rock were not be activated together, but showed a nonlinear variation law with the plastic strain. In a study by Martin19, the test curves of granite were studied and the general trends of cohesion strength and friction strength were obtained, as shown in Fig. 1.

Fig. 1
figure 1

Variation of granite cohesion strength and friction strength.

Full size image

In the CWFS model, the variable strength components (cohesion and friction strength components) depend on the change of the plastic strain, and the failure criterion is:

$$f(\sigma )=f(c,{\varepsilon ^p})+f({\sigma _n},{\varepsilon ^p})\tan \varphi$$
(1)

where f(σ) is the shear strength component, f(c, εp) is the cohesion strength component, f(σn, εp)tanφ is the friction strength component, and εp is the equivalent plastic strain.

This nonlinear yield criterion considers the cohesion c and the friction angle φ in the variable strength component as functions of the plastic strain, which reflects the microscopic mechanisms of fracture initiation, extension, and merging involved in the rock failure process, and describes the rock brittle behavior20.

Improved CWFS model

Scholars recognize the expression of the cohesion strength component in the CWFS model, but the expression of the friction strength component is still controversial21,22,23. The rock brittle failure process involves tensile fracture, the friction strength component induced by this tension is unstable at different sites24,25, and the friction strength component have different activated degrees. The friction component in the conventional CWFS model only considers the variable strength component at different failure stages and the plastic strain of the rock, ignoring the effect of contact stress on the friction component, which varies in real time with stress loading. When the contact force between particles is compressive stress, the friction is strengthened, and when the contact force is tensile stress, the friction is weakened. Figure 2 shows the activated rock strength components at different stages of the loading process.

Fig. 2
figure 2

Nonlinear Mohr-Coulomb strength criterion based on the CWFS model.

Full size image

In the variable strength component of rock, the cohesion component is related to the parallel bond strength. When the parallel bonds between particles breaks, the strength component degenerates to a state determined by the friction component, a change function of c with respect to the plastic strain εp. The friction component is related to the stress state and magnitude at the contact site and is gradually activated with the breaking of parallel bonds. Due to the limitation of the continuous medium model, the change trend of the effective constraint of the friction component cannot be directly represented in the PFC. However, the effective constraint can be reflected as the contact stress between the particles in the microstructure, and the friction angle φ is taken to be a function of the plastic strain εp and the intergranular stress σn. In the PFC2D program, the effective normal stress σn at each contact site can be obtained separately using the FISH language. The upper and lower limits of the variation range of the cohesion c and friction angle φ are called the initial and residual values of the variable strength components. The parameter variations equations are shown in Eqs. (2) and (3).

$$c({\varepsilon ^p})=\left\{ {\begin{array}{*{20}{c}} {{c_i}}&{({\varepsilon ^p}<\varepsilon _{c}^{i})}&{} \\ {{c_i} - ({c_i} - {c_r})\frac{{{\varepsilon ^p}{\text{-}}\varepsilon _{c}^{i}}}{{\varepsilon _{c}^{p}{\text{-}}\varepsilon _{c}^{i}}}}&{(\varepsilon _{c}^{i} \leqslant {\varepsilon ^p}<\varepsilon _{c}^{p})}&{} \\ {{c_r}}&{(\varepsilon _{c}^{p} \leqslant {\varepsilon ^p})}&{} \end{array}} \right.$$
(2)
$$\varphi ({\sigma _n},{\varepsilon ^p})=\left\{ {\begin{array}{*{20}{c}} {{\varphi _i}}&{({\varepsilon ^p}<\varepsilon _{\varphi }^{i})}&{} \\ {{k_1}({\varphi _i} - {\varphi _r})\frac{{{\varepsilon ^p} - \varepsilon _{\varphi }^{i}}}{{\varepsilon _{\varphi }^{p} - \varepsilon _{\varphi }^{i}}}{e^{ - (\sigma /{\sigma _c})}}}&{(\varepsilon _{\varphi }^{i} \leqslant {\varepsilon ^p}<\varepsilon _{\varphi }^{p})}&{} \\ {{\varphi _r}}&{(\varepsilon _{\varphi }^{p} \leqslant {\varepsilon ^p})}&{} \end{array}} \right.$$
(3)

where ci is the initial cohesion, cr is the residual cohesion; φi is the initial friction angle, φr is the residual friction angle; εic and εiφ are the plastic strains corresponded to the initial cohesion ci and initial friction angle φi, εpc and εpφ are the plastic strains corresponded to the residual cohesion cr and residual friction angle φr; k1 represents the strengthened coefficient of the rock friction parameter, which is determined to take the value of 0.368 according to the continuous optimization and debugging based on the rock test results.

Model parameter determination

To describe the change process of the rock strength parameters, besides the conventional mechanical parameters, the parameters in the above equations need to be determined in the CWFS model. Figure 3 shows a set of stress-strain curve of the rock conventional compression test, the whole failure process can be divided into five stages, such as no fractures development zone, microfractures development zone, fractures penetration zone, post-peak failure zone, and total failure zone. According to the basic characteristics of the rock failure process, a parameterization method was proposed in this paper, which simplified the weakened curve of cohesion strength and the strengthened curve of friction strength to linear26, and the CWFS model parameters could be obtained by monitoring the changes of the energy and fractures in the rock compression process.

Fig. 3
figure 3

Rock stress-strain curve and variable strength component activation points.

Full size image

When the microfractures are not generated in the rock, both the cohesion and friction strength components are not activated, there is only elastic deformation inside the rock, and the initial friction angle φi = 0. The strength components are activated when the first fracture initiation, at which moment the strains correspond to the initial cohesion plastic strain εic and the initial friction plastic strain εiφ. According to the Mohr-Coulomb strength criterion, the relationship between the cohesion and the friction angle is

$${\sigma _1}=2c\tan \left( {45+\varphi /2} \right)+{\sigma _3}{\tan ^2}\left( {45+\varphi /2} \right)$$
(4)

In uniaxial loading, the initial cohesion ci = σ1/2, and the c and φ values vary with strain growth during loading. When the stress reaches a peak value, the specimen breaks down, and the curve drops sharply. The cohesion component gradually withdraws from the influence on the rock strength and becomes a residual value, corresponding to the plastic strain as the residual cohesion plastic strain εpc. At that moment, the friction component is still growing and the post-peak strength is supported by friction force. As the specimen is further broken, the internal stress reaches the residual friction strength, and the corresponding plastic strain is the residual friction plastic strain εpφ. The FISH language is used to record the friction strength energy and cohesion strength energy of the specimens. The friction and cohesion strength cannot reach full activation at the same time, and the friction strength required more plastic strain than cohesion strength for full activation, which is the main effect of the friction composition on the post-peak strength27.

Sensitivity analysis of model parameters

Different parameter residual values have a significant influence on the rock failure strength. To study the influence of parameter residual values on the peak strength, a set of initial values was selected: ci = 40MPa, φi = 0°, the residual cohesion cr ranged from 10~100% of ci, and the residual friction angle φr ranged from 10°~50°. Keeping one parameter constant, the influence of another parameter change on the peak strength was studied. The influence trends and the fitting curves are shown in Fig. 4.

Fig. 4
figure 4

Fitting curves for the influence of parameter residual values on peak strengths.

Full size image

The fitting curve results showed that the peak strength increased slowly with the increase of friction angle when the residual friction angle was in the range of 10°~30°, with an increase of 4.65%. When the residual friction angle exceeded 30°, the increasing trend of the peak strength gradually accelerated and the increase is about 25.19%. The peak strength increased with the increase of residual cohesion, showing an S-shaped curve with a first fast and then slower growth. When the residual cohesion was 20~40% of the initial cohesion, it tended to a linear increase, with a growth rate of 86.9%. When the residual cohesion was in the range of 50~90% of the initial cohesion, the peak strength growth tended to be stable, with a growth rate of 13.95%. Through the comparative analysis, the influence of cohesion on peak strength was more significant. The influence of cohesion on peak strength tended to stabilize when the residual cohesion exceeded 50% of the initial cohesion. The larger the activated residual friction angle, the greater the post-peak strength reserve when the rock tended to the limit state.

Bond-degradation creep model based on variable radius particle clump

The crystal structure of rocks is different, and the tension-compression ratio is also different. When particle modeling is adopted, ball particles cannot better reflect the tension-compression ratio of rocks28. Guan R29 demonstrated that the clump particle model could significantly increase the sliding friction, causing the microscopic fracture characteristics and the tension-compression ratio of rocks to be closer to the test results. In this paper, a variable radius ratio clump model was constructed based on the granite mechanical properties obtained by indoor tests.

Granite indoor test results

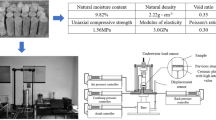
Granite specimens were taken from the − 1080 m prospecting roadway of the Xincheng Gold Mine. The granite blocks with uniform texture were selected on site and processed indoors into ϕ50 × 100 mm and ϕ50 × 25 mm standard specimens. The TAW-2000 electro-hydraulic servo rigidity testing machine was used to carry out granite Brazilian splitting tests, triaxial compression tests and triaxial creep tests. The confining pressures of granite triaxial compression tests were set to 0, 5, 15, and 30 MPa, and the loading method was stress-controlled. The creep tests were conducted using a constant stress graded loading, which were divided into 5 loading levels, each lasting 48 h. The stress-strain curves of the granite Brazilian splitting tests and triaxial compression tests are shown in Fig. 5, and the axial creep curves under different confining pressures are shown in Fig. 6.

Fig. 5
figure 5

Granite stress-strain curves of Brazilian splitting tests and triaxial compression tests: (a) Brazilian splitting tests; (b) Triaxial compression tests.

Full size image
Fig. 6
figure 6

Granite axial creep curves under different confining pressures: (a) σ3 = 0MPa; (b) σ3 = 5MPa; (c) σ3 = 15MPa; (d) σ3 = 30MPa.

Full size image

Variable radius ratio clump model

The method and principle of variable radius ratio clump model construction are shown in Fig. 7. In the clump, two types of particles were generated, large particles (R) and small particles (r), corresponding to the radius range of the clump and the ball radius in the clump, respectively.

Fig. 7
figure 7

Clump model construction method and bond breakage mechanism.

Full size image

First, large particles with randomly populated distribution were generated in the specified range according to the particle size ratio of Rmax/Rmin = a, whose location information were recorded, and then the particles were deleted, as shown in Fig. 7(1). Then, small particles were generated using a randomized algorithm in the same range according to the particle size ratio of rmax/rmin = b, and the location information of the large particles was consulted to determine whether the center point of the generated small particles was located within the radius of the large particles at that location, as shown in Fig. 7(2). The small particles within the same large particle range were regarded as a group, the small particles not inside any large particle were uniformly recorded as a group, and the small particles within the same large particle range were combined into a clump using the FISH language, as shown in Fig. 7(3). By adjusting the particle size R, r and the particle size ratio a, b, the method can change the size of the clump model and the number of particles inside it, which can more accurately describe the complex geometrical morphology and particle distributions within the rock materials.

Conventional mechanical parameter calibration

The rock micro-parameters were calibrated based on the indoor test results, and the model parameters were corrected by debugging methods. Though smaller particle sizes can better simulate the rock fracture process, a large total number of particles will lead to longer calculation time30. Based on the internal mineral particle size and morphology of the granite specimens observed by the microscope, the minimum clump radius was determined to be 0.8 mm, with the particle size ratio a of 1.25; and the minimum ball radius was determined to be 0.3 mm, with the particle size ratio b of 1.66. The numerical models for uniaxial compression and Brazilian splitting tests of granite specimens are shown in Fig. 8, and the model parameters determined by debugging correction are shown in Table 1.

Fig. 8
figure 8

Numerical models of granite specimens.

Full size image
Table 1 Model mechanical parameters.
Full size table

The numerical calculation results of uniaxial compression and Brazilian splitting of granite based on the above model parameters are compared with the indoor test results as in Fig. 9.

Fig. 9
figure 9

Comparison of granite test results.

Full size image

Comparison results showed that the uniaxial compressive strength of granite measured in the indoor test was 82.1 MPa, and the uniaxial compressive strength of granite obtained by numerical calculation was 85.9 MPa, with a relative error of 4.63%. The tensile strength of granite measured in the indoor test was 6.2 MPa, and the tensile strength of granite obtained by numerical calculation was 5.8 MPa, with a relative error of 6.45%. The granite tension-compression ratio calculated from the indoor tests was 0.076, and the granite tension-compression ratio obtained from the numerical calculations was 0.068, with a relative error of 10.52%. Through comparative analysis, the stress-strain curves obtained from numerical calculations were in good agreement with those obtained from indoor tests, and the calculated tension-compression ratios of granite were closer to those obtained from indoor tests. In addition, the granite failure morphology obtained from numerical calculations was also consistent with the granite failure morphology of indoor tests, which accurately reflected the microscopic fracture characteristics of the granite.

Bond-degradation creep (BDC) model and verification

In the PSC model, the radius attenuation rate of the corrosion process is related to three parameters: σa, which is the corrosion initiation threshold and affects the transient deformation of the rock; β1 and β2, which are the different material parameters. The relevant studies showed that the creep failure time tf accelerated to decrease with the increase of material parameters β1 and β2, and both parameters showed a nonlinear change trend31. In this paper, the CWFS model was combined with the stress corrosion method to establish a bond-degradation creep (BDC) model with variable radius particle clump. By debugging the model parameters and comparing with the test results, a set of suitable material parameters were obtained: β1 = 3 × 10–14, β2 = 18, and σa = 1.5 MPa.

To better describe the difference between the BDC model and the PSC model, the driving stress ratio γd was introduced to reflect the stress level, which was represented by the ratio of the applied external stress and the compressive strength, as shown in Eq. (5):

$${\gamma _{\text{d}}}{\text{=}}\frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _f} - {\sigma _3}}}$$
(5)

σ1 and σ3 are the axial load and confining pressure in the rock triaxial creep tests, respectively, and σf is the peak load in the rock triaxial compression tests. Creep tests were performed at a limiting pressure of σ3 with a deviatoric stress of σ1-σ3, and the driving stress ratio γd provided a good indication of the degree of stress level during creep graded loading. Figure 10 showed the comparisons of the creep calculation results between the PSC model and the BDC model at γd values of 0.75, 0.8, 0.85 and 0.9 for confining pressures of 0 MPa, 15 MPa, and 30 MPa. The calculation results for the BDC model were shown in solid lines and those for the PSC model were shown in dashed lines.

Fig. 10
figure 10

Creep calculation results of the PSC model and BDC model.

Full size image

The creep failure time tf is the time from the beginning of loading to the accelerated creep failure of the rock under constant axial pressure, which can reflect the time-varying characteristics of rocks under different stress levels32. Due to the large difference in the order of magnitude of tf, the log(tf) form was taken for the study, and the variations of creep failure time for the PSC model and BDC model at different driving stress ratios are shown in Fig. 11.

Fig. 11
figure 11

Creep failure time of the PSC model and BDC model under different driving stress ratios.

Full size image

As shown in Fig. 11, the failure times for both models decreased exponentially with the increase of the driving stress ratio. The failure time of the specimen at high stress levels could vary by 4 orders of magnitude compared with that at lower stress levels. At low driving stress ratios, the difference of failure times between the two models for the same confining pressure was small. As the stress levels increased, the attenuation of the internal particle bonding parameter was increased, which showed macroscopically that the slopes of the BDC model curves changed faster, the failure time was shorter, and the specimens became more prone to failure at high stress levels. Lateral restraint could improve the bearing capacity of the rock under long-term loading, and the creep failure time of the specimen increased and the creep rate decreased with the increase of the confining pressure.

Creep characteristic analysis of the BDC model

Comparative analysis of creep curves

The PSC model and BDC model were used for the numerical calculations of the granite triaxial creep, and the results were compared with the indoor test results. The numerical creep curves and test creep curves of granite under different confining pressures are shown in Fig. 12.

Fig. 12
figure 12

Numerical creep curves and test creep curves of granite under different confining pressures: (a) σ3 = 0MPa; (b) σ3 = 5MPa; (c) σ3 = 15MPa; (d) σ3 = 30MPa.

Full size image

As shown in Fig. 12, the final strain value difference between the numerical calculation results of the PSC model and the test results was 13.2%, while the final strain value difference between the numerical calculation results of the BDC model and the test results was only 5%. At low stress levels, the numerical calculation curves of the two models had a high overlap. With the increase of stress levels, the damage inside the specimen accumulated, and the BDC model showed larger strain rate and amplitude, and the brittle mutation properties of specimen failure were significant. The PSC model did not consider the effect of the internal shear failure strength of the rock attenuating with the bonding parameter on the creep properties. When the BDC model was used for calculation, more stress corrosion points and microfractures were generated inside the specimen with the decrease of shear failure strength, which was the reason for the difference between the numerical calculation results with the PSC model calculation results. From the curve comparison results, the BDC model curves were in good agreement with the indoor test curves, which was more applicable to simulate the creep mutation properties of granite.

Comparative analysis of creep rate

The creep rate curves of granite under different confining pressures could be obtained by first-order derivation of the creep curves. The creep curve at a confining pressure of 0 MPa was selected for analysis, as shown in Fig. 13. When the axial stress reached 75 MPa, the creep curve showed the typical three stages of creep failure, where εs, εc, and εf corresponded to the creep deformation at ts, tc, and tf, respectively.

Fig. 13
figure 13

Comparison of steady state creep rate between the PSC model and BDC model.

Full size image

Due to the uneven distribution of the crystal structure within the rock material and the differences in the specimens caused by the particle size and initial defects, the creep curves fluctuated during loading33. However, the overall trends of the creep curves of the two models were relatively consistent. When the rock specimens entered the steady state creep rate, the shear failure strength decreased with the decrease of the bonding parameter, and the difference in creep rate between the two models was nearly 2 times. With the increase of loading time, the stress corrosion in the specimens gradually accumulated. When the stress level increased, the parameters attenuation accelerated and the damage intensified, leading to a significant difference between the creep rates of the two models.

Comparative analysis of fractures extension

The creep curves at the confining pressure of 0 MPa were selected, and the number of tension and shear fractures and the expansion trends of the PSC model and BDC model during loading are shown in Fig. 14.

Fig. 14
figure 14

Microfractures number versus time of the PSC model and BDC model.

Full size image

As shown in Fig. 14, the expansion of microfractures during the granite creep process could be divided into three stages. The AB stage was a slow expansion stage, in which both models produced a small number of fractures and the fractures expansion was slow, and the shear fractures growth rate of the BDC model was slightly higher than that of the PSC model. The BC stage was an equal-velocity expansion stage, where the fractures expansion time was about 60% of the loading process, and the internal stress corrosion and parameters damage in the rock reached the initiation value. As the stress level increased, the parameters of the BDC model entered the accelerated damage stage. At this time, the parameters attenuated greatly, and the shear failure strength of the specimen decreased sharply, resulting in a significant increase in the shear fractures number of the specimen, which was about 3 times of the shear fractures number of the PSC model. The number of tension fractures produced by the two models was close at this stage. With the stress level gradually tended to creep failure strength, fractures expansion entered the accelerated expansion stage (CD stage), most of the inter-particle contact had undergone varying degrees of corrosion, a large number of microfractures existing inside the specimen gradually expanded and penetrated at this time. In addition, fractures could expand automatically in this stage, and the generation of new fracture no longer required the higher level of stress, with fractures expansion occurring throughout the loading stage. As the driving stress ratio γd increased, the shear failure strength no longer decreased, and the number of tension fractures gradually dominated. With the corrosion proceeding, the specimen gradually formed a macroscopic shear zone and lost the bearing capacity, and the brittle mutation failure occurred.

In terms of the number of microfractures, the BDC model showed more tension than shear fractures, and the result was consistent with the study result of granite by Li et al.34, indicating that the fractures within the rock during the specimen failure was mainly dominated by tensile failure. At the final failure of the specimen, the number of shear fractures in the BDC model increased about 173% compared to the PSC model, which accounted for about 45.8% of the total number of fractures in the model, and the number of tension fractures in the BDC model increased about 10% compared to the PSC model.

Time effect of surrounding rock fracture in deep roadway

Engineering background

The Xincheng Gold Mine is located in Laizhou City, Shandong Province, and the geographic location of the mine area is shown in Fig. 15. At present, the maximum mining depth of the Xincheng Gold Mine exceeds 1100 m, which has entered the deep mining stage. In this paper, taking the − 1080 m horizontal prospecting roadway of Xincheng Gold Mine as the engineering background, the time effect characteristic of the surrounding rock local fracture in the deep roadway was studied.

Fig. 15
figure 15

Geographic location of Xincheng Gold Mine.

Full size image

During the deep mining process of Xincheng Gold Mine, with the growth of time, the surrounding rock occurred local deformation failure under the high ground stress state after the roadway excavation, which was specifically shown as the shear failure of the roadway vault and the plate crack failure of the roadway sidewall, as shown in Fig. 16. Through the field measurement, the failure length of the roadway vault anchors was about 0.8~1.0 m, and the shedding surrounding rock thickness in the plate crack failure area of the roadway sidewall was 1.0~1.2 m.

Fig. 16
figure 16

Failure characteristics of the roadway surrounding rock in the Xincheng Gold Mine: (a) Shear failure of the roadway vault; (b) Plate crack failure of the roadway sidewall.

Full size image

Numerical model construction

When the particle flow is used to simulate deep roadway excavation, the particle number in the numerical model can be hundreds of thousands to millions, which is a huge amount of computation. In this paper, based on the above variable radius particle clumping model, a numerical model based on the actual engineering size was established using the gradient particle density method. The model was divided into 4 areas, with higher particle density and smaller particle radius in the area close to the roadway, and gradually increasing particle radius and decreasing total number of particles in the area away from the roadway. The model could satisfy the computational accuracy requirements as well as significantly improve the computational efficiency. The model was in the state of hydrostatic pressure, and the original rock stress was σ0 = 30 MPa, and the displacement constraint was used at the bottom. The model dimensions and boundary conditions are shown in Fig. 17a, the schematic diagram of the gradient particle density model is shown in Fig. 17b, and the particle radius ranges for each area are shown in Table 2. The conventional mechanical parameters of the model were taken as calibrated in Table 1, and the bond-degradation parameters were taken as: β1 = 3 × 10–14, β2 = 18, and σa = 1.5 MPa.

Fig. 17
figure 17

Numerical model of deep roadway: (a) Model dimensions and boundary conditions; (b) Schematic diagram of the gradient particle density model.

Full size image
Table 2 Particle radius ranges of roadway surrounding rock area.
Full size table

Evolution law of roadway surrounding rock fracture

The fracture evolution of the surrounding rock is the main behavior for the progressive failure of the roadway, the initiation, expansion, aggregation and interaction of the microfractures reduce the mechanical properties of the surrounding rock, and ultimately form the macroscopic fracture. The local fracture evolution characteristics of the surrounding rock after the roadway excavation are shown in Fig. 18.

Fig. 18
figure 18

Local fracture evolution characteristics of roadway surrounding rock: (a) 30d; (b) 60d; (c) 90d; (d) 120d.

Full size image

Numerical results showed that after 30 days of the roadway excavation, the rock stress was fully released, and the plastic zone range of the surrounding rock was small. Microfractures first sprouted at the arch top and arch foot of the roadway, and the thickness of the microfracture area was about 0.3R (0.45 m). After 60 days, microfractures at the arch top and arch foot of the roadway continued to develop, expand and gather, and some of the particles began to spread out. A small range of shear fracture occurred at the arch top and left arch foot of the roadway, and the thickness of the fracture area was about 0.4~0.5R (0.6~0.75 m). At 90 days, the left side surrounding rock of the roadway began to produce a fracture area, which was mainly dominated by local plate crack failure, and the thickness of the plate crack failure area was about 0.6R (0.9 m). The fractures on the right arch top gradually increased and gathered, the spread particles continued to increase, and the surrounding rock showed a shear failure trend. When reaching 120 days, the range of the roadway plate crack failure was gradually extended from the arch foot to the arch waist, and the boundary of the plate crack failure area was gradually clear. Then, rib spalling occurred, and the thickness of spalled surrounding rock was about 0.8R (1.2 m). An obvious shear failure area with a thickness of about 0.7R (1.05 m) appeared at the arch top of the roadway, and the broken surrounding rock in the area gradually collapsed.

Comparative analysis showed that the fracture characteristics of roadway surrounding rock obtained by numerical calculation were similar to those of deep roadway surrounding rock in Xincheng Gold Mine. The evolution characteristics of the surrounding rock fracture after the roadway excavation were consistent with the high stress roadway surrounding rock failure law in the actual mining engineering, reflecting that the deep roadway surrounding rock fracture has obvious time effect.

Conclusions

Aiming at the time effect of brittle failure of the deep hard rock, a variable radius ratio clump model was constructed, and a bond-degradation creep (BDC) model suitable for deep granite was proposed. The creep process of granite under high stress was simulated, and the fracture evolution law of deep roadway surrounding rock was analyzed. The conclusions are as follows:

  1. 1.

    The variable radius clump modeling method could reflect mechanical properties of the tension-compression ratio of different types of rocks by adjusting the radius ratio of the clump particle. By comparing and analyzing the stress-strain curves and failure patterns of granite indoor tests and numerical calculations, the clump modeling method could better reflect the tension-compression ratio of the rock, and the rock failure characteristics were more consistent with the actual situation.

  2. 2.

    The bond-degradation creep model for variable radius particle clump of deep granite could control the creep rate by changing the activation degree of the bond parameters, such as cohesion and friction angle, under different plastic strains. Compared with the parallel bond stress corrosion model, the creep failure time of the variable radius particle clump bond-degradation creep model was shorter and more microfractures were generated during failure, and the numerical curves were in better agreement with the test curves. The proposed model could better simulate the creep damage process of granite under high stresses.

  3. 3.

    The fracture characteristics of the deep roadway surrounding rock calculated by the granite bond-degradation creep model showed obvious shear failure of the arch roof and plate crack failure of the sidewall, with aging deformation characteristics. The numerical calculation results were basically similar to the actual engineering situation. The granite bond-degradation creep model was more suitable for analyzing the fracture evolution law of the surrounding rock in deep hard rock caverns.