Introduction

Mycoplasma pneumoniae (MP) is a common pathogen of community-acquired pneumonia worldwide, predominantly among children and adolescents1,2, and in late 2023, it became the major pathogen causing respiratory tract infection in children in China3. MP infections manifest a range of clinical symptoms and disease severities, including fever, cough, sore throat, and malaise, commonly affecting the respiratory system and contributing to a substantial portion of the global disease burden (8.6% from 2017 to 2020)4. Because MP is easily spread through droplets or direct contact in densely populated, enclosed, or poorly ventilated environments, numerous outbreaks have been reported in crowded places, such as schools, universities, hospitals and health care facilities5. Owing to the long incubation period, strong infectivity, prolonged illness, high rate of macrolide resistance and high proportion of asymptomatic patients, outbreaks occurring in schools are difficult to prevent and control quickly6,7. Physical barriers, continuous surveillance, case isolation, school closures, suspension of group activities, ventilation and disinfection are important for the prevention and control of respiratory infection disease outbreaks8,9,10. Some scholars have also proposed that the duration of school closure should be at least longer than the average incubation period to control the outbreaks quickly11. However, nonuniform standards for the duration of school closure during outbreaks lead to longer epidemic times and an increased number of infected students, which greatly affect normal teaching work and arouse widespread concerns, even the staff of the local CDC bases school closure measures on experience. Public health officials often have little success in controlling MP outbreaks because of the long incubation period of the organism, late detection of outbreaks, and incomplete understanding of the effectiveness of various infection control strategies, which are difficult to characterize via conventional epidemiological methods and experience. Mathematical modelling has been frequently used in the design and evaluation of infectious disease control strategies, such as influenza12, Mpox13, COVID-1914,15, mumps16, and dengue17. Given the lack of quantitative evaluation of the effectiveness of intervention measures during MP outbreaks in China, this study aimed to perform a quantitative evaluation of different intervention measures through the construction of a transmission dynamics model based on an outbreak of MP and to explore the best method to control outbreaks in schools.

Results

Transmissibility of MP

The simulation results revealed that the present model fit well (R2 = 0.617, P < 0.05) with the reported epidemic curve when β was 0.314936 and κ was 0.99982. The value of R0 was determined to be 3.29, suggesting that if intervention measures were not taken in a timely manner, the epidemic would spread rapidly in school.

Effectiveness of interventions

In the baseline scenario of MP outbreaks without interventions, the present model revealed that the duration of the outbreak would last 143 days, with a TAR of 75.78% (122/161) and a TIR of 95.65% (154/161). The simulation results revealed that most of the entire grade would be infected, the actual TIR would be greater than 17.39%, and the DO would be 42 days after the local CDC implemented measures.

When a four-, seven- and ten-day isolation policy was implemented after receiving the report on November 4, our model predicted an increase in the duration of the outbreak (DO) to 9, 20, and 34 days, respectively, compared with the baseline without interventions. Moreover, the TAR was 75.78%, 75.16%, and 75.16%, and the TIR was 95.65%, 95.65%, and 95.03%, respectively, which were all close to those of no interventions (Fig. 1a; Table 1).

Fig. 1
figure 1

Effectiveness of different interventions on MP outbreaks. (a) The effects of different durations of school closure. The starting time of the school closure was November 4. (b) Effects of different proportions of case isolation. The starting time of the case isolation was November 4. (c) Effects of different initial times of implementing case isolation. (d) Effects of different degrees of ventilation and disinfection. The starting time of ventilation and disinfection was November 4. (e) Effects of different initial ventilation and disinfection times. (f) Comparisons of the effects of implementing single and combined interventions. The vertical axis indicates the number of accumulated infections.

Full size image
Table 1 Evaluation of the different intervention measures on the MP outbreak. TAR: total attack rate; TIR: total infection rate; DO: duration of outbreak; 90% Iso + 90% VD: 90% of cases isolated and 90% of transmission risk reduced by ventilation and disinfection; C4d + 90% Iso + 90% VD: school closure for 4 days, 90% of cases isolated and 90% of transmission risk reduced by ventilation and disinfection; C10d + 90% Iso + 90% VD: school closure for 10 days, 90% of cases isolated and 90% of transmission risk reduced by ventilation and disinfection.
Full size table

In addition, 60%, 70%, 80%, 90%, and 100% case isolation resulted in lower TAR values (the lowest values were 15.53% and 19.88%), but the DO was prolonged to 194 days (Fig. 1b; Table 1). Moreover, the TAR and TIR increased gradually as case isolation measures were implemented later (Fig. 1c; Table 1).

The model revealed that 60%, 70%, 80%, 90% and 100% ventilation and disinfection resulted in the following reductions: the TAR was reduced from 75.78 to 40.37%, 24.84%, 14.91%, 9.94% and 8.07%, respectively; the TIR was reduced from 95.65 to 50.31%, 31.06%, 18.63%, 13.04% and 9.94%, respectively; and the DO was reduced from 143 days to 192, 194, 184, 92, and 48 days, respectively (Fig. 1d; Table 1). Ventilation and disinfection measures that were taken later after receiving the report resulted in higher values of TAR, TIR, and DO; in other words, the simulated results of the best execution time of ventilation and disinfection revealed better effectiveness of strategy when an earlier intervention was simulated (Fig. 1e; Table 1).

We also evaluated the effects of 90% Iso + 90% VD (90% of cases are isolated and 90% of transmission risk is reduced by ventilation and disinfection), C4d + 90% Iso + 90% VD (school closure for 4 days, 90% of the cases are isolated and 90% of the transmission risk is reduced by ventilation and disinfection), and C10d + 90% Iso + 90% VD (school closure for 10 days, 90% of the cases are isolated and 90% of the transmission risk is reduced by ventilation and disinfection). All combinations achieved good control of MP outbreaks, with DO values ranging from 58 to 65 days. The TAR values were 8.70% (14/161), 8.70% (14/161), and 8.07% (13/161), which were decreased by 67.08%, 67.08%, and 67.71%, respectively, in comparison with those without interventions. The TIR values were always 10.56% (17/161), which was 85.09% lower than the baseline value (Fig. 1f; Table 1).

Sensitivity analysis

When ω varied in the range of 0.0476–0.1428, the TIR fluctuated in the range of 95.46–95.82%, and the result was relatively stable. When γ varied in the range of 0.0476–0.1428, the TIR fluctuated in the range of 99.86–84.49%, and the result was relatively stable. When p varied in the value range of 0–1, the TIR was always 95.81% (Fig. 2).

Fig. 2
figure 2

Sensitivity analysis of the ω, γ, and p parameters based on the selected outbreak.

Full size image

Discussion

To our knowledge, this is the first study to characterize the transmission dynamics and control of an MP outbreak. In our study, SEIAR models were established on the basis of an outbreak of MP infection in a primary school in Zhejiang Province. The results of the statistical test revealed high goodness-of-fit of our models with no intervention to the reported data, suggesting that the SEIAR models were suitable for this study and can be used to simulate the incidence of outbreaks and to evaluate the effectiveness of interventions. The sensitivity analysis suggested that the present model was sensitive to the parameters ω, γ, and p, which had almost no effect on the TIR. The present model revealed that MP may lead to a high total attack rate (75.78%) and total infection rate (95.65%) within 143 days without any interventions. Furthermore, the basic reproductive rate (R0) for MP was estimated to be 3.29, whereas it has been estimated to be 1.0–21.0 for influenza18, 2.0–3.0 for SARS-CoV, and 1.8–3.6 for COVID-1919.

According to our study, school closure was not predicted to be an effective control method; the values of the TAR and TIR were comparable to those in the situation of no intervention, and the DO was prolonged. There are two possible reasons for this inefficacy. First, the incubation period of MP infection was long; although the transmission route in schools was briefly interrupted after school closure, the previously exposed population continued to spread the epidemic as a potential source of infection after resuming classes, and infection from schools also spread in households, further amplifying the outbreak20. Second, the number of infected students was already large when discovering and reporting the clusters or outbreaks. In our study, the class incidence rate (excluding the asymptomatic infections) was 37.70%, and the grade infection rate (excluding the asymptomatic infections) was 8.07% when the report was received on November 4. Studies have shown that the best effect of school closure is achieved when the total population incidence is less than 1%21, and the effect is insignificant when the infection rate is 20%22. The general rules provided by the WHO also show that when the infection rate of the population is less than 1%, school closures can reduce the peak infection rate by 30-50%, and when the infection rate of the population is more than 1%, the effect of school suspension is limited. A dynamic study of norovirus has also revealed that school closures alone do not contain norovirus outbreaks and that overlooked personal hygiene may serve as a hotbed for infectious disease transmission23. At present, the National Health and Health Commission has not issued relevant guidelines and standards for MP epidemic prevention and control, and most staff members refer to the influenza standards for class dismissal or set the length of school closure on the basis of work experience. The different simulated models of school closure duration indicated that school closure measures should not be overly relied on when dealing with the epidemic because the measures may not be applicable to all epidemic situations, and each epidemic should be treated according to specific circumstances.

In the case of symptom-based isolation for MP, the model predicted that the policy would reduce the total attack rate by 60.25% and the total infection rate by 75.77% but that the DO would be 21 days longer than the baseline. Therefore, isolation of symptomatic patients is not a good way to control the development of MP epidemics. Asymptomatic infection, accounting for up to 21.2% of infections, plays an important role in the transmission of MP20,24, which may significantly reduce the effectiveness of countermeasures. Patients should only be isolated if they show related symptoms, and it is difficult to detect these hidden infections without full testing. Researchers have also reported that the proportion of the asymptomatic population strongly affects prevention and control25. When the proportion of the asymptomatic population is too high, isolation of patients alone cannot completely control the epidemic situation26. In addition, it is better to isolate patients as soon as possible. If case isolation measures are not taken immediately after receiving a report, the TAR and TIR will gradually increase as the measures are delayed. This finding highlights the importance of early detection, early reporting and early isolation in epidemic management.

Fortunately, taking effective ventilation disinfection measures to ensure that the disinfection effect reaches the quality standard (disinfection effect of 90%) can significantly reduce the TAR, TIR, and DO. In this study, the most effective single-intervention strategy was ventilation and disinfection, when the disinfection effect reached 90%, the TAR decreased by 65.84%, the TIR decreased by 82.61%, and the DO decreased by 51 days. These findings suggested that ventilation and disinfection can reduce the amount of virus in the environment and weaken the coefficiency of disease transmission. In real epidemic management, staff not only use a single intervention measure but also adopt a combination of intervention measures, including closure, isolation, ventilation and disinfection. Evaluation of the effects of simulated combination intervention measures revealed that the effects of the three combined measures of 90% Iso + 90% VD, C4d + 90% Iso + 90% VD, and C10d + 90% Iso + 90% VD were similar, which significantly reduced the TAR, TIR and DO. Moreover, the effects of the combined measures were significantly better than that of 90% ventilation disinfection or 90% case isolation alone. The present results suggested that the key to MP epidemic control lies in case isolation and ventilation disinfection rather than school closure, which has little effect on MP infection epidemic control. In addition, it is difficult to achieve 100% case isolation because the course of MP infection can last as long as 3 weeks, and some students do not meet the standards for resuming classes but hide their illness due to academic pressure. Considering the three factors of teaching pressure, operation accessibility and intervention effects, classes may not be suspended immediately, but comprehensive prevention and control measures for MP epidemics, such as ventilation, disinfection, case isolation and self-protection (such as wearing masks), should be taken as soon as possible. Further, the isolation ratio of patients should be increased as much as possible on the basis of ensuring qualified disinfection to minimize the TAR, TIR and DO. Earlier implementation of interventions result in lower values of TAR, TIR, and DO during the outbreak.

The TAR of the studied epidemic was 17.39% after a series of countermeasures were taken by the local CDC, which achieved good prevention and control effects, mainly because of the strict case isolation and ventilation disinfection measures taken after receiving the report. However, according to the simulation results of the SEIAR model, the TAR can decrease to 8.70% if 90% VD + 90% Iso can be achieved. The simulation results revealed that the effectiveness of prevention and control measures for the selected outbreak could be improved. The spatial transmission dynamics model with improved epidemic prevention and control effectiveness has been widely used in recent years to understand epidemiological burden, trends, and transmission dynamics, to facilitate policy decisions, and to evaluate infection prevention and control measures27. In this study, the SEIAR model was used to simulate the effects of different interventions for MP infection, and good results were achieved in the future management of MP epidemics. The simulation results of the SEIAR model can be used to improve the efficiency of epidemic management.

Several limitations should be noted in this study. First, the existing data mainly were derived from a single outbreak with limited and small-scale data, which may not be fully applied to other scenarios or population. Second, considering the ethical issues, we were unable to implement a comparative experiment on different intervention measures for students to verify the predictive performance of the model. Third, the model was established in a situation in which the recovery rate of population, susceptibility, and contact rate were consistent, and the mobility of the population, herd immunity, and health education were not considered. Second, the transmission rate was set at a constant value, and other parameters were derived from literature reports, which might have a certain impact on the research results. In reality, the individual differences (e.g., immunity, activity status and so on) in humans make the parameters different. In the future, more relevant epidemic data should be collected and meta-analysis could be used to estimate more accurate parameters. The stochastic model may be used to provide a more accurate estimation for the epidemic. Finally, owing to hypersensitivity to the number of cases for one parameter, the implications of our conclusion should be limited to the value setting in this research.

Methods

Data source

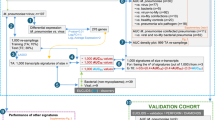
On November 4, 2023, the local CDC confirmed that an outbreak of MP infection occurred in Class A of Grade 2 in a primary school in Zhejiang Province. There were 41 students in the class and 161 students in the grade. To investigate the outbreak and find probable cases, the school absenteeism records and daily health monitoring records were reviewed, the head teachers and school doctors in the school were interviewed, the outpatient and inpatient records were reviewed and doctors in the hospitals were interviewed. The information regarding demographics, the process of illness, signs and symptoms, clinical treatment and hospitalization was collected by telephone follow-up. All probable cases were detected in oropharyngeal swabs by qPCR. This event was confirmed as MP infection on the reporting day (November 4), and some essential intervention measures, such as school closure for 4 days (from November 4 to November 7), case isolation, environmental disinfection, ventilation, health education, and hand hygiene, were implemented immediately. Retrospective record review was performed to identify cases diagnosed as early as October 7. The local CDC tracked the implementation of intervention measures and new cases daily. Finally, the outbreak was effectively controlled and the last case occurred on November 17. A total of 28 cases were reported within 42 days from the onset of the first case (October 7) to the last case (November 17) in Grade 2. The cumulative incidence was 17.39% (28/161). The timeline of this outbreak was shown in Fig. 3. From October 7 to November 4, a total of 13 cases were reported without intervention, and from November 5 to November 17, a total of 15 cases were reported with intervention. In this study, the period between October 7 and November 4 was regarded as a nonintervention period, which was used to fit the SEIAR model without intervention measures.

Fig. 3
figure 3

Timeline of the MP outbreak in a primary school in Zhejiang Province.

Full size image

SEIAR model

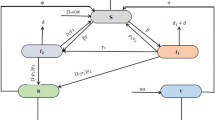
The present study utilized the susceptible-exposed-infectious/asymptomatic-recovered (SEIAR) model to simulate MP transmission. In this model, the population is divided into the following five compartments on the basis of the natural history of MP: susceptible (S), exposed (E), infectious (I), asymptomatic (A), and recovered (R). According to whether intervention measures were taken, the SEIAR model was constructed without intervention measures and with intervention measures (school closure, case isolation, ventilation and disinfection, and combinations of multiple interventions).

Model with no intervention

To simulate the SEAIR model without interventions, the following assumptions should be considered during the outbreak of MP infection: there are no population movements or deaths, the susceptibility and exposure rates do not change after health education, students are generally susceptible and have an equal chance of being infected, there are no repeated infections within a short time, the transmission rate from susceptible to infection is the same as that of asymptomatic individuals, and the transmission rate from infection to recovery is the same as that from asymptomatic to recovered individuals. The model framework is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the development of the SEIAR model.

Full size image

The SEIAR model can be expressed using the following differential equations. dS/dt, dE/dt, dI/dt, dA/dt, and dR/dt refer to the change rates of the S, E, I, A, and R populations at time t, respectively. β is the transmission rate from S to E. ω and γ refer to changing rates from E to I and from I to R, respectively. κ refers to the relative risk of transmission by an asymptomatic individual versus by a symptomatic individual. p refers to the proportion of asymptomatic infections. The values and meanings of these parameters are listed in Table 2.

Table 2 Description and values of the parameters in the SEIAR model.
Full size table
$$\:\text{d}\text{S}/\text{d}\text{t}=-\frac{{\upbeta\:}\text{S}(\text{I}+\text{k}\text{A})}{\text{N}}$$
$$\:\text{d}\text{E}/\text{d}\text{t}=\frac{{\upbeta\:}\text{S}(\text{I}+\text{k}\text{A})}{\text{N}}-{\upomega\:}\text{E}$$
$$\:\text{d}\text{I}/\text{d}\text{t}=(1-\text{p}){\upomega\:}\text{E}-{\upgamma\:}\text{I}$$
$$\:\text{d}\text{A}/\text{d}\text{t}=\text{p}{\upomega\:}\text{E}-{\upgamma\:}\text{A}$$
$$\:\text{d}\text{R}/\text{d}\text{t}={\upgamma\:}(\text{I}+\text{A})$$
(1)

School closure

In the studied school outbreak, school closures were performed on November 4, and both symptomatic–susceptible and asymptomatic–susceptible contacts were stopped, resulting in a β value of zero. After the school closures ended, I and A returned to school. Because the epidemic may have continued to spread, school closures were simulated for 4, 7, and 10 days. The model with school closures is expressed as follows:

\(\:\text{d}\text{S}/\text{d}\text{t}=\)0

$$\:\text{d}\text{E}/\text{d}\text{t}=-{\upomega\:}\text{E}$$
$$\:\text{d}\text{I}/\text{d}\text{t}=(1-\text{p}){\upomega\:}\text{E}-{\upgamma\:}\text{I}$$
$$\:\text{d}\text{A}/\text{d}\text{t}=\text{p}{\upomega\:}\text{E}-{\upgamma\:}\text{A}$$
$$\:\text{d}\text{R}/\text{d}\text{t}={\upgamma\:}(\text{I}+\text{A})$$
(2)

Patient isolation

During the school outbreak, any new patients were isolated once they showed symptoms, but some patients still concealed their illness and attended classes while they were sick. Asymptomatic infection is typically difficult to identify because there are no symptoms of the infection that can be observed. Thus, x was defined as the proportion of isolated patients, indicating that the route of transmission between the isolated symptomatic–susceptible route was partially blocked; in this scenario, individuals in compartment S could be infected only via the (1-x) percentage of symptomatic–susceptible contact and asymptomatic–susceptible contact. In this study, y was set in five scenarios, namely, 100%, 90%, 80%, 70%, and 60%, and the effects of case isolation were simulated on the 1st, 3th, 5th, 10th, and 15th day after receiving the report. The mathematical model is expressed as follows:

$$\:\text{d}\text{S}/\text{d}\text{t}=-\frac{\beta\:\text{S}\left[\right(1-\text{x})\text{I}+\text{k}\text{A}]}{\text{N}}$$
$$\:\text{d}\text{E}/\text{d}\text{t}=\frac{\beta\:\text{S}\left[\right(1-\text{x})\text{I}+\text{k}\text{A}]}{\text{N}}-{\upomega\:}\text{E}$$
$$\:\text{d}\text{I}/\text{d}\text{t}=(1-\text{p}){\upomega\:}\text{E}-{\upgamma\:}\text{I}$$
$$\:\text{d}\text{A}/\text{d}\text{t}=\text{p}{\upomega\:}\text{E}-{\upgamma\:}\text{A}$$
$$\:\text{d}\text{R}/\text{d}\text{t}={\upgamma\:}(\text{I}+\text{A})$$
(3)

Ventilation and disinfection

In the studied school outbreak, taking ventilation and disinfection measures reduced the amount of pathogens in the environment and further affect the risk of transmission. Thus, y was assumed as the proportion of transmission risk reduced by ventilation and disinfection, which reduced the transmission rate to (1-y)β. In this study, y was set in five scenarios, namely, 100%, 90%, 80%, 70%, and 60%, and the effects of ventilation and disinfection were simulated on the 1st, 3th, 5th, 10th, and 15th day after receiving the report. The model with ventilation and disinfection is expressed as follows:

$$\:\text{d}\text{S}/\text{d}\text{t}=-\frac{(1-\text{y})\beta\:\text{S}(\text{I}+\text{k}\text{A})}{\text{N}}$$
$$\:\text{d}\text{E}/\text{d}\text{t}=\frac{(1-\text{y})\beta\:\text{S}(\text{I}+\text{k}\text{A})}{\text{N}}-{\upomega\:}\text{E}$$
$$\:\text{d}\text{I}/\text{d}\text{t}=(1-\text{p}){\upomega\:}\text{E}-{\upgamma\:}\text{I}$$
$$\:\text{d}\text{A}/\text{d}\text{t}=\text{p}{\upomega\:}\text{E}-{\upgamma\:}\text{A}$$
$$\:\text{d}\text{R}/\text{d}\text{t}={\upgamma\:}(\text{I}+\text{A})$$
(4)

Combinations of multiple interventions

The duration of MP infection could be as long as 3 weeks, and some infected students did not meet the standards for return to school, but they hid their symptoms and returned to class due to academic pressure. A patient isolation rate of 100% was difficult to reach in practice. Therefore, it was more close to the actual situation when we set the patient isolation rate as 90% for comparison. The qualification criterion for disinfection was that the natural bacterial extinction rate was not less than 90% according to the general principle of disinfection for infectious focus (GB19193-2015). Based on this criterion, we assumed 90% disinfection in our study to evaluate its role in controlling the outbreak. For MP outbreaks in schools, it was recommended that if necessary, four days of school suspension could be implemented referring to the guidelines for the disposal of influenza-like illness outbreaks issued by the National Health Commission of People’s Republic of China (2018 version). As for the average incubation period of MP infection was about 10 days, longer than influenza, we also examined the policy of 10 days of school closure. Consequently, we simulated the following combined interventions to compare their impacts, in which 90% Iso, 90% VD, C4d, and C10d refer to 90% of the cases being isolated, 90% of transmission risk being reduced by ventilation and disinfection, school closure for 4 days, and school closure for 10 days, respectively. The present study evaluated the following combinations: 90% Iso + 90% VD, C4d + 90% Iso + 90% VD, and C10d + 90% Iso + 90% VD. The model including school closures is referred to model (2) above, and the model with 90% Iso + 90% VD is expressed as follows:

$$\:\text{d}\text{S}/\text{d}\text{t}=-\frac{0.1\times\:\beta\:\text{S}(0.1\times\:\text{I}+\text{k}\text{A})}{\text{N}}$$
$$\:\text{d}\text{E}/\text{d}\text{t}=\frac{0.1\times\:\beta\:\text{S}(0.1\times\:\text{I}+\text{k}\text{A})}{\text{N}}-{\upomega\:}\text{E}$$
$$\:\text{d}\text{I}/\text{d}\text{t}=(1-\text{p}){\upomega\:}\text{E}-{\upgamma\:}\text{I}$$
$$\:\text{d}\text{A}/\text{d}\text{t}=\text{p}{\upomega\:}\text{E}-{\upgamma\:}\text{A}$$
$$\:\text{d}\text{R}/\text{d}\text{t}={\upgamma\:}(\text{I}+\text{A})$$
(5)

Indicators for assessing the effectiveness of interventions

Commonly, R0 is defined as the expected number of secondary infections that result from the introduction of a single infected individual into a completely susceptible population under ideal conditions31. Therefore, R0 is an important indicator that reflects the transmissibility of a virus and indicates the potential ease or difficulty in controlling the transmission of the disease. If R0 ≥ 1, an outbreak will occur, and essential control measures need to be taken. If R0 < 1, the outbreak will end. The effectiveness of interventions were evaluated using the following three outcome measures: (1) total attack rate (TAR), which represents the proportion of the population attacked during the outbreak; (2) total infection rate (TIR), which represents the proportion of the population infected during the outbreak; and (3) duration of outbreak (DO), which represents the number of days between the occurrence of the first case and the last case. It is the cumulative number of dominant cases, At is the cumulative number of recessive cases, and N is the total number of people. These values were calculated via the following equations:

$$\:{R}_{0}=\frac{\beta\:S}{N}（\frac{1-\text{p}}{{\upgamma\:}}+\frac{\text{k}\text{p}}{{\upgamma\:}}）$$
(6)
$$\:\text{T}\text{A}\text{R}=\frac{{\text{I}}_{\text{t}}}{\text{N}}\times\:100\text{\%}$$
(7)
$$\:\text{T}\text{I}\text{R}=\frac{{\text{I}}_{\text{t}}+{\text{A}}_{\text{t}}}{\text{N}}\times\:100\text{\%}$$
(8)

Sensitivity analysis

Considering that three parameters of the SEIAR model, p, ω, and γ were obtained from existing research results, resulting in potential uncertainty in the present simulation results. Small changes in these parameters may lead to large changes in the number of infected patients. Thus, sensitivity analysis was performed by changing three parameters on the basis of the methods adopted in previous research26. The values of TIR were compared when each parameter was split into 1,000 values, and the range of which was based on Table 1.

Statistical analysis

Berkeley Madonna 8.3.18 (University of California at Berkeley, Berkeley, USA) and Microsoft Office Excel 2021 were employed for model simulation and graph plotting. Curve fitting was performed via the Runge–Kutta method of order four with the tolerance set at 0.001. The goodness of fit was assessed by SPSS 23.0 (IBM Corp, Armonk, NY, USA) according to previously published methods14. Statistical significance was indicated by R2 ≥ 0.5 and P < 0.05, and the model fit was good.