Introduction

Thallium halide crystals, with their excellent physical and chemical properties, play an important role in optics1,2 and detection technology3. Whether as a material for the preparation of optical parts, an additive material for the coating of optical thin films, or a common semiconductor material, they have become a research hotspot in related fields. Thallium bromide (TlBr) belongs to compound semiconductors, which can be used as good electron transport semiconductors4. In order to better put TlBr into practical applications, fundamental research on the spectroscopic properties and transition properties of TlBr and TlBr+ are particularly important.

The spectroscopic and transition properties of thallide of group VII diatomic molecules have been extensively studied. As early as 1986, the A0+  ↔ X1Σ+ transition of the TlCl molecule was investigated by using the frequency-doubled laser radiation method. The results indicated that the rotational structure was more complete at the lower vibrational energy levels of the A0+ state, but the upper vibrational energy levels have shown typical fragmentation bands of predissociation5. Later in 1994, the potential energy curves (PECs), transition properties and radiation lifetimes of the ground state and the low excited states of the TlCl molecule were calculated by using the MRD-CI method and employing the relativistic effective core potential for the constituent atoms, and the spin–orbit coupling (SOC) effects were considered. Radiative lifetime of the a0 + state was 0.808 μs6. In 2001, Melville and Coxon calculated infrared and other relevant data of the ground state X1Σ of the TlCl molecule, and the PEC of the X1Σ state was fitted by using the least-squares method7. In 2009, the PECs and spectroscopic parameters of the low-lying states of TlX (X = F, Cl, Br, I, and At) were systematically researched by Zou and Liu8. In 2018, the possibility of laser cooling of the TlCl molecule was studied by using the MRCI + Q method. The radiative lifetime of the a0 + state was also reported, which was 6.04 μs, and Franck–Condon factors (FCFs) of the \(a^{3} \prod_{{0^{ + } }} \to X^{1} \sum_{{0^{ + } }}^{ + }\) transition was 0.985, which was the highly diagonal FCFs, therefore, the optical cycling scheme for laser cooling of TlCl molecule was proposed9. In 2020, the PECs of 13 Λ–S states and 24 Ω states of TlF molecule were calculated using the MRCI + Q method by Yan et al.10. In 2021, the PECs and spectroscopic parameters of thirteen Λ–S states of the TlBr molecule were calculated, and the transition dipole moment (TDM) of the \(a^{3} \prod_{{0^{ + } }} \to X^{1} \sum_{{0^{ + } }}^{ + }\) transition was also obtained, the FCF f00 was only 0.4079, which was so small to construct a quasicycling transition for laser cooling of TlBr molecule. Therefore, TlBr could not be used as a candidate for laser cooling11.

The PECs of halide diatomic molecular cations have studied widely, such as BBr+12, AlBr+13, GaBr+13, InBr+14, CF+15, SeCl+16, SBr+17, and GeCl+18, et al., however, the PECs of thallide of group VII molecular cations were a few not many. In 2021, the PECs and transition properties of four states (X2Σ+, 12Π, 22Σ+, and 22Π) of TlF+ cation were calculated, and the results indicated that the 2Σ+ is the ground state and the 2Π is the first excited state, the vertical excitation energy (Te) was only 456.2 cm−1 at the spin-free level. The SOC effects were taken into account in the calculations, the \(2^{2} \prod_{1/2} \to X^{2} \sum_{1/2}^{ + }\) quasicycling transition was created for laser cooling of the TlF+ cation19. In our previous work, the PECs and TDMs of fourteen Λ–S states of TlCl+ cation were investigated. Contrary to the TlF+ cation, the 2Π was the ground state and the 2Σ+ was the first excited state, Te was 1421.25 cm−1. Due to the FCF being very small of the calculated transitions, the TlCl+ cation was not suitable for laser cooling20.

From the above summary, we found that the spectroscopy and transition properties of many thallide of group VII diatomic molecules and molecular cations have been widely studied, but the spectroscopy properties of TlBr+ cation have not been reported. TlF+ cation was suitable to laser cooling, and TlCl+ cation was not suitable at spin-free level. This study aims to investigate the PECs and TDMs of the low-lying states of the TlBr+ cation, and discuss the possibility of laser cooling of the TlBr+ cation.

Computational details

The electronic structures of the 14 Λ–S states are calculated using the MOLPRO 2010 program package21. Because of the restriction of the program, the C∞v symmetry is reduced to the C2v subgroup in the calculation. The C2v subgroup has four irreducible representations (A1, B1, B2, and A2), therefore, A1 → Σ+, B1 + B2 → Π, and A1 + A2 → Δ. The nuclear bond lengths for single-point energy calculations were selected from 1.8 to 6.0 Å, to make the results more accurate and credible, the step was set as 0.02 Å from 2.1 to 3.6 Å.

Tl and Br were used in ECP60MDF_AVQZ22 and ECP10MDF_AVQZ23 pseudopotential basis set, which included 60 effective core potential (Kr + 4d4f electrons) of Tl atom and 10 effective core potential (Ne electrons) of Br atom, respectively. The primary and contracted atomic basis sets are (15s12p13d3f2g)/[7s6p5d3f2g] for Br and (15s12p12d3f2g)/[7s7p5d3f2g] for Tl. To obtain a more accurate result, for the Tl atom, the (n−1)d orbitals were re-contracted, and one Rydberg s function contracted from seven universal Rydberg functions24, therefore, (21s12p12d3f2g)/[7s7p5d3f2g] basis set for Tl was used in the calculations.

The initial wave function of the ground state was calculated by using a restricted Hartree–Fock (RHF) method, based on the guessed wave function, a multi-reference wave function is obtained by using the complete active space self-consistent field (CASSCF)25,26 method, and MRCI27,28 approach was performed for the electronic correlation energy calculations, the Davidson correction (+ Q) was included to overcome the size-consistence problem. The active space includes Br(4s4p) and Tl(6s6p7s) shells, nine electrons are distributed in a (5, 2, 2, 0) active space, and the Br(3s3p3d) and Tl(5s5p5d) orbital is closed-shell, which keeps doubly occupation. Spin–orbit coupling effects via the Breit-Pauli operator29,30 were considered following MRCI + Q calculations.

The equilibrium internuclear distance (Re), dissociation energy (De), harmonic frequency (ωe), anharmonic vibrational frequency (ωeχe), rotational constant (Be), vertical excitation energy (Te), emission coefficients (\(A_{{\nu ^{\prime } \nu ^{{\prime \prime }} }}\)), Franck–Condon factors (FCFs), and radiative lifetimes (τ) were obtained by using LEVEL8.0 program31.

Results and discussion

PECs and spectroscopic parameters of Λ–S and Ω states

14 Λ–S states (X2Π, A2Σ+, B2Σ+, 12Σ−, 22Σ−, 22Π, 32Π, 12Δ, a4Σ+, 14Σ−, 24Σ−, 14Π, 24Π, b4Δ) correlating with the lowest second dissociation channels are calculated at MRCI + Q level. The first dissociation channel derived from the ground atomic state of Br(2Pu) and ground ion state Tl+(1Sg), leads two lowest states X2Π and A2Σ+. Due to the energy difference of ionization energy between the Br atom and Tl atom being smaller than that of the first excitation energy of Tl+ and Br, the second channel is Tl(2Pu) + Br+(3Pg), which corresponding 12 Λ–S states. The atomic states and Λ–S states corresponding to two dissociation limits are listed in Table 1. Our result of the energy difference between the two dissociation limits is in good agreement the experimental value collected by Moore32, the error is 2.11%.

Table 1 Calculated dissociation relationships of the Λ–S states of TlBr+ cation.
Full size table

The potential energy curves (PECs) of the 14 Λ–S states are plotted in Fig. 1, Similar to the TlCl+ cation, several crossing phenomena occurs at the 40,000–60,000 cm−1 region. Avoided crossings primarily arise between different electronic states that belong to the same irreducible representation, causing discontinuities in the potential energy curve. It is predicted that the inclusion of SOC effects will lead a complex potential energy profile for TlBr+ cations. The avoid phenomenon between 22Π and 32Π, 12Σ− and 22Σ−, and 14Σ− and 24Σ− states occurs at about 3.5–4.5 Å, the PECs of these states are near the horizontal (when the spin and orbital symmetry of the two states is the same, the two states that curve at the spin-free level avoid crossing). To the best of our knowledge, the spectroscopic properties of low-lying states of TlBr+ cation are not known experimentally and theoretically. For comparison, the spectroscopic parameters of the three lowest states of TlX+ (X = F, Cl, Br) are also listed in Table 2. The spectroscopic parameters of 13 bound Λ–S states are collected in Table 3.

Fig. 1
figure 1

The PECs of 14 Λ–S states.

Full size image
Table 2 Spectroscopic parameters of three lowest Λ–S states of TlX+ (X = F, Cl, Br) cation.
Full size table
Table 3 Spectroscopic parameters of the Λ–S states of TlBr+ cation.
Full size table

From Fig. 1 and Table 2, it can be seen that the X2Π is the ground state and the A2Σ+ is the first excited state for TlBr+. Similar to TlF+ and TlCl+ cation, the PECs between two electronic states occur crossing phenomenon, and the energy level between 12Π and 12Σ+ states is very close, the Te is only 1909.67 cm−1, but the order of energy level of TlBr+ is the same as that of TlCl+, but different with that of TlF+. For the first 2Π state, which is a weakly bound state for TlX+ (X = F, Cl, Br), the De of TlBr+ is only 0.2460 eV, which increases with increasing the atomic weight of halide (TlCl+: 0.1967 eV, TlF+: 0.086 eV). The Re of TlBr+ is 3.4344 Å, which is a little bigger than that of TlCl+ (3.3452 Å) and TlF+ (3.123 Å). For the first two 2Σ+ states, the ωe and De decrease with increasing the atomic weight of halide, but the Re and Te increase with increasing the atomic weight of halide. Remarkable, the well depth of the first 2Σ+ state is smaller than that of the first 2Π state, and the second 2Σ+ state are the strongly bound state of three cations. Compared with other MBr+ (M = B, In, Al, Ga, Tl) cations, the X2Σ+ is the ground state, and the A2Π is the first excited state of BBr+12, AlBr+13, GaBr+13, InBr+14. The Te of the first excited state of the InBr+ cation is small, which is only 1165 cm−1.

The main configurations at the respective Re are also listed in Table 3, with weights higher than 2%. The 1σ molecular orbital is mainly composed of Tl (6s) atomic orbital, the 2σ (1π) and 3σ (2π) molecular orbitals are mainly composed of Br (4p) and Tl (6p) atomic orbitals, respectively, and the 4σ molecular orbital is contributed with Tl (7 s) atomic orbital. The dominant electronic occupation of ground state X2Π is 1σ22σ23σ21π3 with a contribution of 90.2%, the a4Σ+, b4Δ, 14Σ−, 12Δ, and 12Σ− states derived from a same configuration 1σ22σ23σ11π32π1, the contributions are bigger than 87%, therefore, the Re of the five states are close, about 2.8 Å. The a4Σ+–X2Π, b4Δ–X2Π, 14Σ−–X2Π, 12Δ–X2Π, and 12Σ−–X2Π electronic transitions arising from 3σ → 2π electron promotion. Similarly, the Re of 14Π and 32Π, 24Σ− and 22Σ− are close. The 14Π–X2Π (32Π–X2Π) and 24Σ−–X2Π (22Σ−–X2Π) electronic transitions arising from 3σ → 4σ and 1π → 4σ electron promotions, respectively. Three electronic states (A2Σ+, B2Σ+ and 22Π) show the multi-configurational character, which is the heavy mixture of several Λ–S states. The dominant electronic occupations of the A2Σ+ state are composed of two parts, 1σ22σ23σ11π4 and 1σ22σ13σ21π4 with a contribution of 50.8% and 39.0%; The mainly configurations of B2Σ+ state are relatively complex, i.e., 1σ22σ23σ11π4 (19.9%), 1σ22σ13σ21π4 (49.5%), 1σ22σ23σ11π32π1 (17.8%), 1σ22σ24σ11π4 (7.8%).

When spin–orbit coupling effects are considered, Br(2Pu), Tl(2Pu), and Br+(3Pg) atomic states should be split, two dissociation limits change to eight, and 14 Λ–S states split into 30 Ω states, which corresponding to fifteen = Ω1/2, ten = Ω3/2, four = Ω5/2 and one = Ω7/2. The atomic states and Ω states corresponding to eight dissociation limits are listed in Table 4.

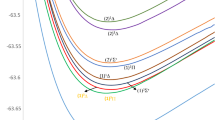
Table 4 Calculated dissociation relationships of the Ω states of TlBr+ cation.
Full size table

The PECs of Ω states are plotted in Fig. 2a–c, and the spectroscopic parameters of these states are listed in Table 5. The ground state X2Π splits into X2Π3/2 and X2Π1/2, and the X2Π3/2 is the lowest one. The X2Π3/2 state is derived from its dominant parent the X2Π state with a percentage of 99% at Re. Therefore, the spectroscopic parameters of the X2Π3/2 and X2Π states possess nearly the same values. The first excited state \(A{}^{2}\Sigma_{1/2}^{ + }\) is placed at 1092.94 cm−1 above the ground state, which is derived from the X2Π and A2Σ+ states along the whole range of internuclear distances R, the contributions of these two Λ–S states are exhibited in Fig. 3, the contribution of the X2Π increases with increasing internuclear distances from 2.0 to 3.46 Å, which reaches a maximum 62.3%. And the A2Σ+ and X2Π states contribute the same amount to \(A{}^{2}\Sigma_{1/2}^{ + }\) near the Re, which indicates the energies of the A2Σ+ and X2Π states will be equal, i.e. the PECs occur a crossing. Due to the influence of strong mixing with the X2Π state at Franck–Conden region, the PECs of the \(A{}^{2}\Sigma_{1/2}^{ + }\) and X2Π1/2 states undergo an avoided crossing, and the PEC shape of the \(A{}^{2}\Sigma_{1/2}^{ + }\) state changes a great deal compared with that of the A2Σ+ state, the spectroscopic parameters are profoundly different between these two states, i.e. ΔRe equals 10.1% and Δωe equals 136.6%, respectively. The X2Π1/2 state is derived from the X2Π with a percentage of 61.9% and the A2Σ+ with a percentage of 38.1% at Re. Similar to the \(A{}^{2}\Sigma_{1/2}^{ + }\) state, the spectroscopic parameters are different between the X2Π1/2 and X2Π. The splitting constants (ASO) is very large, ASO = 4271.35 cm−1. It shows that SOC effects play a very important role in the spectroscopic properties of TlBr+ cation. Indeed, both Tl and Br atoms are classified as heavy elements, and the strength of the SOC effect is typically proportional to the nuclear charge of the atom. Therefore, it is necessary to specially treat the SOC effect in the feasibility of laser cooling for TlBr+.A lot of the crossing phenomenon between the Λ–S states can be found in Fig. 1. According to the avoid crossing rule (as the total angular momentum quantum number J of the two Ω states is the same, the two states that curve intersect at the spin-free level avoid crossing), several avoid crossing phenomena exist in the energy region between 30,000 and 60,000 cm−1 when SOC effects are considered. Due to the 22Π state crossings with other low-lying Λ–S states, the avoided crossing phenomenon for the = Ω1/2 and = Ω3/2 is very common. The crossing and avoided crossing phenomenon below 50,000 cm−1 will be discussed in detail. For the = Ω1/2 states, the avoid crossings between the \(B{}^{2}\Sigma_{1/2}^{ + }\) and \(a{}^{4}\Sigma_{1/2}^{ + }\) states occur at about 2.24 Å and 3.46 Å, on the other hand, the avoid crossings between the \(a{}^{4}\Sigma_{1/2}^{ + }\) and \(b^{4} \Delta_{1/2}\) states occur at about 2.48 Å and 3.6 Å, which lead the PEC of the shallow potential wells and the deformations of the \(a{}^{4}\Sigma_{1/2}^{ + }\), \(B{}^{2}\Sigma_{1/2}^{ + }\) and \(b^{4} \Delta_{1/2}\) states. For the = Ω3/2 states, the energy levels of the \(a{}^{4}\Sigma_{3/2}^{ + }\), \(b{}^{4}\Delta_{3/2}\) and \({1}{}^{{2}}\Delta_{3/2}\) states are very close, and the avoided crossing phenomenon is not very obvious in Fig. 2b. From Fig. 2c, it can be seen that the avoided crossing phenomenon does not exist for the four = Ω5/2 states. Only one = Ω7/2 state, which is derived from the b4Δ state, therefore, there does not occur the avoided crossing phenomenon. And the spectroscopic parameters of the \(b{}^{4}\Delta_{{{7}/2}}\) and b4Δ state possess nearly the same values. Although these avoided crossings introduce some distortion, they ensure that the energy difference between the various electronic states of the molecule varies monotonically and does not result in energy instability due to crossing. This reduces the occurrence of unstable electronic state transitions.

Fig. 2
figure 2

The PECs of the Ω states. (a) = Ω1/2; (b) = Ω3/2; (c) = Ω5/2 and 7/2.

Full size image
Table 5 Spectroscopic parameters of the Ω states of TlBr+ cation.
Full size table
Fig. 3
figure 3

The contributions of the Λ–S states for the \(A{}^{2}\Sigma_{1/2}^{ + }\) state.

Full size image

Dipole moments and transition dipole moments of the Λ–S and Ω states

Dipole moments (DMs) for the eight doublet states and six quartet states as functions of the internuclear distance R at the spin-free level are plotted in Fig. 4a,b, respectively. The value of DMs reflect the polarity of the molecule, which are positively correlated with the molecular polarity. The value of DM of the ground state X2Π at Re is 0.9890 a.u. (2.5140 Debye), which is larger than that of TlF+ (X2Σ+: 0.797 a.u.) and TlCl+ (X2Π: 0.327 a.u.), it indicates that the polarity of TlBr+ cation possesses the largest one compared with the other two. As the polarity of a molecule increases, its dipole moment and transition dipole moment also become larger, which affects spectral features like the positions and intensities of peaks. Furthermore, in laser cooling, a higher molecular polarity, accompanied by a stronger electric transition dipole moment, can impact the molecule’s deceleration and cooling efficiency within the laser field. On the other hand, for the first 2Π states, DM at Re increases with increasing the atomic weight of the halide. From Fig. 4a,b, the avoid-crossing phenomenon is also found in the curves of DMs. The avoid crossing between the 22Π and 32Π, 12Σ− and 22Σ−, and 14Σ− and 24Σ− states occurs at about 3.9 Å, 4.4 Å, and 4.3 Å, respectively. The function of DMs of 14 Λ–S states shows a linear behavior up to approximately 5 Å.

Fig. 4
figure 4

Dipole moments of the Λ–S states. (a) Doublet states; (b) Quartet states.

Full size image

Transition dipole moments (TDMs) for the transitions between doublet Λ–S states are also calculated, which are plotted in Fig. 5a,b. The magnitude of TDMs directly affect the intensity of the spectrum. If TDM is zero, transition will be forbidden. The 32Π → X2Π and 22Π → X2Π transitions have the larger TDMs near the equilibrium nuclear distance. Because of the avoid crossing between 32Π and 22Π states, therefore, TDMs of the 32Π → X2Π and 22Π → X2Π, 32Π → A2Σ+ and 22Π → A2Σ+ transitions must be shown the avoid crossing phenomenon. The TDM of the A2Σ+ → X2Π transition close to zero at about 3.8 Å. This occurs because the two states arise from the same dissociation channel Tl+(1Sg) + Br(2Pu). In this case, the TlBr+ cation is formed by Tl+ and Br. However, the TDMs of the transitions between the other 12 states for the second dissociation channel Tl(2Pu) + Br+(3Pg), which originates from the 2P → 3P transition of the Br atom as the nuclear distance tends to infinity, also approach zero as the nuclear distance increases. Because the separation of the ionized species (Tl and Br+) weakens the interaction between the states, and the overlap of the electronic wave functions decreases.

Fig. 5
figure 5

Transition dipole moments of the Λ–S states. (a) Transitions from the excited states to the ground state; (b) Transitions between the several excited states.

Full size image

When SOC effects are considered, TDMs of the \(A{}^{2}\Sigma_{1/2}^{ + } \to X{}^{2}\Pi_{3/2}\), \(X{}^{2}\Pi_{{{1}/2}} A{}^{2}\Sigma_{1/2}^{ + }\) and \(X{}^{2}\Pi_{{{1}/2}} \to X{}^{2}\Pi_{3/2}\) transitions are also calculated, which are plotted in Fig. 6. Because the X2Π3/2 state is derived from its dominant parent X2Π state, the TDM curve of the \(A{}^{2}\Sigma_{1/2}^{ + } \to X{}^{2}\Pi_{3/2}\) transition is similar to that of the A2Σ+ → X2Π transition. Notable, the TDM of the \(X{}^{2}\Pi_{{{1}/2}} \to X{}^{2}\Pi_{3/2}\) transition is the largest at the Franck–Condon region, the value reaches 0.18 a.u. (0.452 Debye). This indicates that, of the three transitions, \(X{}^{2}\Pi_{{{1}/2}} \to X{}^{2}\Pi_{3/2}\) transition has the greatest probability of leaping, i.e. absorbing or emitting photons with the greatest intensity.

Fig. 6
figure 6

Transition dipole moments of the Ω states.

Full size image

Franck–Condon factors, emission coefficients, and radiative lifetimes

The highly diagonally distributed FCFs and large emission coefficients (105–108 s−1) are criteria for laser cooling, the FCFs and emission coefficients are also calculated by using the LEVEL8.0 program, the results of the Λ–S states and Ω states are listed in Tables 6 and 7, respectively.

Table 6 Emission coefficients \(A_{{\nu ^{\prime } \nu ^{{\prime \prime }} }}\) (unit of s−1) and Franck–Condon factors \(f_{{\nu ^{\prime } \nu ^{{\prime \prime }} }}\) of the A2Σ+ → X2Π, 32Π → X2Π and 32Π → A2Σ+ transitions.
Full size table
Table 7 Emission coefficients \(A_{{\nu ^{\prime } \nu ^{{\prime \prime }} }}\) (unit of s−1) and Franck–Condon factors \(f_{{\nu ^{\prime } \nu ^{{\prime \prime }} }}\) of the \(A{}^{2}\Sigma_{1/2}^{ + } X{}^{2}\Pi_{3/2}\) and \(X{}^{2}\Pi_{{{1}/2}} X{}^{2}\Pi_{3/2}\) transitions.
Full size table

Radiative lifetimes are expressed as the following formula33,

$$\tau_{{\upsilon^{\prime}}} = \left( {A_{{\upsilon^{\prime}}} } \right)^{ - 1} = \frac{{4.936 \times 10^{5} }}{{\left| {TDM} \right|^{2} \sum\nolimits_{{_{{\nu^{\prime\prime}}} }} {f_{{\nu^{\prime},\nu^{\prime\prime}}} \left( {\Delta E_{{\nu^{\prime},\nu^{\prime\prime}}} } \right)^{3} } }}$$

where, TDM is the transition dipole moment in units of a.u., fν′ν″ is the Franck–Condon factors and the ΔEν′ν″ is the energy difference between two states in units of cm−1.

From Table 3, the difference of Re between the X2Π and A2Σ+ states is 0.3074 Å, it is shown with a little overlap of the wavefunctions. Therefore, f00 of the A2Σ+ → X2Π transition is small, which equals 0.1199. On the other hand, the energy level between the X2Π and A2Σ+ states are close, Te of the A2Σ+ state is only 1909.67 cm−1. So the total emission coefficient of the A2Σ+ → X2Π transition is only 13.75 s−1. FCFs of the 32Π → X2Π transition is 0.8705, which is highly diagonally distributed. FCFs of the 32Π → X2Π transition are sufficiently large for laser cooling. The total emission coefficients of the 32Π → X2Π transition is 9.181 × 107 s−1, which can provide a significant rate of rapid cycling. Notable, several intermediate states in the 32Π → X2Π transition can be found, and the total emission coefficients of the 32Π → A2Σ+ transition reaches 5.010 × 106 s−1. The vibrational branching loss ratio is used to evaluate the influence of the quasicycling transition for laser cooling. The vibrational branching loss ratio to the low-lying intermediate state A2Σ+ can’t be negligible at level = ηγ/γΣ = 5.46 × 10–2. γ and γΣ represents the total emission coefficient of the 32Π → A2Σ+ and 32Π → X2Π transitions, respectively.

When SOC effects are considered, the FCF of the \(A{}^{2}\Sigma_{1/2}^{ + } X{}^{2}\Pi_{3/2}\) and \(X{}^{2}\Pi_{{{1}/2}} X{}^{2}\Pi_{3/2}\) transitions is 0.9751 and 0.7879, but the total emission coefficient of \(A{}^{2}\Sigma_{1/2}^{ + } X{}^{2}\Pi_{3/2}\) and \(X{}^{2}\Pi_{{{1}/2}} X{}^{2}\Pi_{3/2}\) transitions is only 0.6304 s−1 and 5.888 × 103 s−1, respectively. The emission coefficients are both small for laser cooling of the TlBr+ cation. The energy levels of high excited states are intricate, the transition properties are not discussed in this paper.

In conclusion, TlBr+ cation is not a candidate for laser cooling.

Conclusion

In this paper, potential energy curves of 14 Λ–S states and 30 Ω states of TlBr+ cation were investigated by using the MRCI + Q method. The X2Π is the ground state and the A2Σ+ is the first excited state, these two states are weakly bound states. The spectroscopic constant of the ground state and low excited bound Λ–S and Ω states were fitted. The avoided crossing phenomenon for the = Ω1/2 and = Ω3/2 in 30,000–50,000 cm−1 region are also discussed. In addition, Franck–Condon factors, emission coefficients, and radiative lifetimes of Λ–S and Ω states are also calculated. At spin-free level, the 32Π → X2Π transition has high diagonally distributed f00 and large emission coefficients, but the influence of intermediate state A2Σ+ to build the 32Π → X2Π quasicycling transition of for laser cooling of TlBr+ cation can’t be negligible. When SOC effects are considered, the \(A{}^{2}\Sigma_{1/2}^{ + } X{}^{2}\Pi_{3/2}\) and \(X{}^{2}\Pi_{{{1}/2}} X{}^{2}\Pi_{3/2}\) transitions have high diagonally distributed f00, but the total emission coefficient of the \(A{}^{2}\Sigma_{1/2}^{ + } X{}^{2}\Pi_{3/2}\) and \(X{}^{2}\Pi_{{{1}/2}} X{}^{2}\Pi_{3/2}\) transitions is too small. The results indicate that TlBr+ cation is not a candidate for laser cooling. All results are reported for the first time.