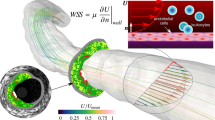
Abstract
Local hemodynamics play an essential role in the initiation and progression of coronary artery disease. While vascular geometry alters local hemodynamics, the relationship between vascular structure and hemodynamics is poorly understood. Previous computational fluid dynamics (CFD) studies have explored how anatomy influences plaque-promoting hemodynamics. For example, areas exposed to low wall shear stress (ALWSS) can indicate regions of plaque growth. However, small sample sizes, idealized geometries, and simplified boundary conditions have limited their scope. We generated 230 synthetic models of left coronary arteries and simulated coronary hemodynamics with physiologically realistic boundary conditions. We measured the sensitivity of hemodynamic metrics to changes in bifurcation angles, positions, diameter ratios, tortuosity, and plaque topology. Our results suggest that the diameter ratio between left coronary branches plays a substantial role in generating adverse hemodynamic phenotypes and can amplify the effect of other geometric features such as bifurcation position and angle, and vessel tortuosity. Introducing mild plaque in the models did not change correlations between structure and hemodynamics. However, certain vascular structures can induce ALWSS at the trailing edge of the plaque. Our analysis demonstrates that coronary artery vascular structure can provide key insight into the hemodynamic environments conducive to plaque formation and growth.
Similar content being viewed by others
Introduction
Coronary artery disease (CAD) is a leading cause of global mortality1. CAD is caused by the progressive occlusion of coronary arteries by atherosclerotic plaque buildup on the arterial wall. The growth and rupture of plaques can lead to myocardial ischemia and infarction, stroke, and other potentially fatal major adverse cardiac events (MACE)2. Given the high prevalence of CAD, predicting MACE risk is of high clinical importance. While metrics like fractional flow reserve (FFR) are suitable for guiding mild-to-severe CAD treatment3, there is less consensus on assessing de novo plaque growth and early-stage CAD risk. Plaque topology and location can be considered, alongside hemodynamics, to improve our understanding of these risks. Atherosclerotic lesions commonly form at bifurcations in the proximal and medial left coronary arteries4. Secondary flows often develop at bifurcations, which indicates that the local hemodynamic environment can prime plaque formation5. These observations have led to considering hemodynamic metrics like wall shear stress (WSS) to understand how plaques develop and progress. For example, endothelial WSS has been reported as a risk factor for atherosclerosis in several studies6,7,8. However, while the site-specificity of plaque at bifurcations is well characterized, there is less understanding of how coronary artery anatomy itself affects local hemodynamics that contribute to atherosclerotic risk.
Clinical research studies have explored how vascular anatomy relates to adverse CAD outcomes using computerized tomography angiography (CTA)9,10,11,12. However, the results from existing work are often contradictory or clinically inconclusive. Some studies suggest that left main coronary artery (LMCA) length is significantly shorter in CAD patients compared to healthy individuals10,11. In contrast, others find no clear distinction between groups13,14. Bifurcation angle has also been considered in relation with CAD. Some studies suggest that patients with severe CAD have significantly larger bifurcation angles than healthy patients15,16,17,18. However, the statistical strength of these findings can be weak14,19, and studies are often conducted retrospectively with small sample sizes14,17,18,19. Tortuosity, or exaggerated vessel curvature, has been found to only marginally affect plaque formation, with benign clinical implications20. Given these conflicting or ambiguous results, there remains a gap in understanding how vascular anatomy correlates with atherosclerotic risk. This gap is partly due to the nature of these investigations that have considered geometrical features in isolation but not their combined effect. An ongoing prospective study9 is investigating a broad range of geometric features and their relationship with CAD, but the results are still unknown. Despite this effort, CTA studies are still limited by the heterogeneity of patient-specific anatomies, which can contribute to confounding associations. Furthermore, imaging studies alone cannot describe the hemodynamic environment that can contribute to adverse hemodynamic conditions that enable CAD progression.
Computational fluid dynamics (CFD) studies can provide hemodynamic data to quantify relationships between anatomy and hemodynamics21,22,23. Apart from studying patient-specific anatomies, computer-generated synthetic anatomies enable precise control over geometric variations and their subsequent effect on hemodynamics. Most computational studies have focused on quantifying WSS. Areas of low WSS (ALWSS), defined as less than 0.5 to 1 Pa, have been measured to determine areas prone to plaque growth24, while areas of high WSS (AHWSS), defined as greater than 7 Pa, have been used to predict areas prone to plaque rupture25. Computational studies examining hemodynamic changes to bifurcation angles have led to conflicting conclusions, similar to observational ones. Data from some works suggest that bifurcation angles have little effect on ALWSS26,27,28,29, while others have found the opposite30,31,32,33. The sensitivity of hemodynamics to arterial tortuosity has also been evaluated via computational modeling. Some papers suggest tortuosity can reduce ALWSS31,34,35,36, while others argue that higher tortuosity increases ALWSS37,38. Varying branch-wise diameters between parent–child branches can alter the distribution and magnitude of ALWSS39,40. However, changes in diameter have not been studied in combination with bifurcation positions, angles, and tortuosity. Arterial segment lengths have seldom been studied, but prior work suggests a weak to moderate correlation between short vessel lengths and low WSS33,41. Computational models have also been used to quantify flow in diseased coronary arteries. Previous studies have examined how plaque alters local hemodynamics along with variations in angles and local curvature28,42,43,44,45. Common limitations of these works include small sample sizes (10 on average), an inconsistent mix of idealized and patient-specific geometries, and frequent use of non-physiological coronary boundary conditions (BC). Non-physiological BCs can lead to underestimations in pressure and incorrect periodic velocity waveforms46. In addition, most studies have focused on a subset of all the vascular features mentioned, while none have thoroughly investigated these features and their combined effect on hemodynamics. As such, we do not understand which coronary artery geometric features induce the most adverse hemodynamic conditions which can lead to plaque formation and growth.
This study aimed to answer two key questions: (1) Which coronary artery geometric features are most prone to adverse hemodynamics, and (2) is the effect of vascular geometric variations conserved when atherosclerotic plaque is present? Our computational study overcomes the aforementioned limitations regarding sample size and modeling choices. Using a custom modeling pipeline, we generated 230 synthetic left coronary artery (LCA) anatomical models through a parametric sweep of LCA geometric features informed by published angiographic data47. These features included bifurcation angles, bifurcation positions, branch-wise diameter variations, and tortuosity. We employed CFD to assess the sensitivity of local hemodynamics, particularly ALWSS, to these structural variations in the LCA (where plaque is most common4). Through this study, we identified several geometric features of the LCA most prone to generating atherosclerotic-promoting flow.
Methods
Design of computational experiments
The baseline LCA structure and the arterial segments included in our vascular models are shown in Fig. 1a. The LCA structure was derived from model 0066_H_CORO_H in the Vascular Modeling Repository48. We extracted the LCA from this model to include the LMCA, the LAD, and the left circumflex (LCx) artery while removing the right coronaries and aorta. This model was post-processed to remove unidentified downstream branches and smooth branch centerlines to eliminate patient-specific irregularities and tortuosity. Five simulation phases were conducted based on parametric sweeps of the following geometric parameters applied to the baseline LCA model: (1) LAD/LCx bifurcation position and angle (n = 25), (2) diameter variations of the LAD and LCx for values representative of females and males (n = 32), (3) arterial tortuosity (n = 9), (4) combined variations in bifurcation positions, angles, diameters, and tortuosity (n = 68), and (5) mild plaque combined with changes in underlying geometry (n = 96). In each phase, all geometric features were unchanged unless otherwise indicated. For example, inlet and outlet diameters were fixed as we imposed tortuosity. When changing the bifurcation angle, position, or vessel tortuosity, we held inlet and outlet diameters, as well as the diameter ratio between bifurcating branches (\({R}_{D}={D}_{LAD}/{D}_{LCx}\)), constant. Lumen cross-sectional areas were assumed to be circular, except for diseased cases with stenosis. Prior studies indicate that non-symmetric cross-sectional areas do not substantially alter wall shear stress trends49.
(a) Baseline LCA structure. The diagram of the LCA is from a lateral, or looking towards the myocardium, view. (b) Histograms of average population distributions for the segment lengths, angles, and diameters varied in this study. Most features were referenced from Medrano-Gracia et al.47. Patient-specific models from the Vascular Model Repository48 were used to estimate anatomical characteristics not established in the literature, such as left main branch segment lengths. Terminal branch lengths were kept constant in all models.
In each phase, all combinations of selected geometric features determined the number of anatomical models and corresponding simulations. For example, in phase one (LAD/LCx bifurcation), we considered five positions and five angles, resulting in 25 simulations. The positions of this bifurcation corresponded to the LMCA length. Phase two consisted of 16 simulations with varying LAD and LCx diameter values in models representative of females and males according to vessel diameter. These branch diameters were measured in a proximal position downstream of the LAD/LCx bifurcation. Phase three included three variations of tortuosity in the LAD and LCx (n = 9). Based on data from these three phases, in phase four we combined diameters, bifurcation position, angles, and tortuosity to determine their superimposed effect on coronary hemodynamics. We replicated phase one (n = 25) twice and phase three (n = 9) twice, once for a set of models with skewed LAD dominance and the other with skewed LCx dominance, resulting in 68 models. As a general classification, we considered a branch to be dominant if its diameter exceeded its neighbor. A neutral ratio was considered near 1. The term skewed dominance was used if the diameter ratio \({R}_{D}\) was \(\le\) 0.65 (dominant LCx) and \(\ge\) 1.40 (dominant LAD). These skewed ratios were the most extreme \({R}_{D}\) ratios from phase two which also induced the largest ALWSS, indicating that they led to the most atheroprone hemodynamic environments in this phase. These ratios were also used to set LAD and LCx diameters in phase four to create skewed LAD and LCx dominant models with varied bifurcation positions, angles, and tortuosity. In phase five, we first analyzed sensitivity to plaque topology in baseline LCA geometry (n = 32). Then, we incorporated plaque with a predefined topology into parametric sweeps of geometric features, including bifurcation angles, positions, and diameters (n = 64). In phase five, we reduced the number of bifurcation positions/angles from five to four as the results from phase one determined that was sufficient for statistical analysis. The geometric range of models are shown in Supplementary Fig. S1.
The geometric parameters were predominantly bound by angiographic measurements from a CTA study of the LCA47 (Fig. 1b) to ensure that the synthetic models were representative of real LCA anatomies. In this angiographic study, bifurcation angles, segment lengths, and diameters were statistically described by their mean, standard deviation, and range. Diameter tapering over vessel length was also approximated from this study for the LMCA, LAD, LCx, and side branches. Additionally, the ratio of diameters for branching vessels at distal junctions (excludes LAD/LCx) was set to 0.85 based on this paper. Sex-disaggregated data for males and females regarding LAD diameters (3.7 ± 0.6 mm vs. 3.0 ± 0.6 mm) and LCx diameters (3.6 ± 0.6 mm vs. 2.8 ± 0.7 mm) were available and used to build models. The mean LAD/LCx bifurcation angle was 75.2 + 23.3°. With these considerations, we constructed normal distributions of each feature to sample the values used in each parametric sweep. These parameters varied within \(\pm\) 2 standard deviations. These values were used to construct LCA models. Further details of each phase’s parametrization are shown in Supplementary Table S1.
The aforementioned study did not provide all the geometric information needed to generate LCA anatomies. For example, LAD and LCx medial segment lengths were unreported47. Instead, we measured medial segment lengths in eight patient-specific coronary models from the Vascular Modeling Repository. Using this data, medial segments were approximately 2/3 of the proximal branch length. LAD/Distal-2 and LCx/Obtuse-marginal 2 bifurcation angles in the baseline model were assumed to be identical to their proximal counterparts. We set the LMCA length and standard deviation (2.3 ± 1.3 cm) based on ten coronary models from the Vascular Modeling Repository. To verify the anatomy of the coronary models from the Vascular Modeling Repository was consistent with the population included in the CTA study47 we extracted the proximal LAD and LCx lengths and checked bifurcation angles. These values were within the distributions provided for these parameters in the study.
Bifurcation angles were measured between two vectors originating from the point where the branch’s centerlines intersect. These vectors were tangential to the curvature of each branch’s centerline near their intersection. For tortuosity, we used a definition by Eleid et al.50, where tortuosity was scored from 0 (none) to 2 (three inflections with peak-to-peak angles from 90° to 180°). We used this definition of tortuosity in our models so our results were comparable to clinical studies reporting tortuosity. Further details regarding tortuosity generation can be found in Supplementary material and Fig. S2.
To construct diseased LCA models, plaque length and stenosis were defined based on data from the PREDICTION6 and PROSPECT51 clinical studies. They reported plaques ranging from 10 to 40% diameter reduction, or stenosis, while the length of the plaque varied between 0.9 cm and 2.6 cm. The average stenosis and plaque lengths were 30% and 1.7 cm, respectively52. These plaques would be considered angiographically nonsignificant53. We considered angiographically nonsignificant plaque topologies as we were interested in investigating the hemodynamic sensitivity to arterial structure variability in early CAD and its potential links to plaque growth. For plaques longer than 0.9 cm, a constant stenosis was assumed over two-thirds of the lesion length. First, we separately studied plaque topologies (length and stenosis) in the proximal LAD or LCx in the baseline model within the ranges described and kept other geometric features constant. Subsequently, we introduced a mild plaque (30% stenosis and 1.7 cm long) in models with varied coronary geometric features of healthy variants of phases one, two, and four. The spatial placement of plaque was informed by hemodynamic simulation results from healthy models. In particular, we placed plaque in regions where we observed low WSS, as longitudinal studies suggest that low WSS is an indicator for de novo plaque growth6,7. In models from phase one, we placed the plaque in the proximal LCx where the largest ALWSS region was observed in the healthy set. To recreate diseased models from phases two and four, the location of ALWSS markedly differed based on branch dominance. Therefore, we introduced plaque in the proximal LCx for LAD dominant models, whereas plaque was placed in the proximal LAD for LCx dominant models. In all diseased models, plaques were placed at the same circumferential position in either the proximal LAD or LCx, immediately downstream of the LAD/LCx bifurcation. This circumferential position was based on the generalized ALWSS location observed in healthy geometries. Plaque was not incorporated in models with tortuosity (phase three) due to inconsistent and sporadic localization of ALWSS changes.
Numerical approach
We used SimVascular54, an open-source cardiovascular modeling and simulation software, to construct synthetic LCA models, generate finite element meshes, and solve the incompressible Navier–Stokes equations that govern blood flow. SimVascular includes an advective-stabilized finite element flow solver55 with backflow stabilization56, implicit boundary condition coupling57, and a specialized linear solver58. We employed a tetrahedral mesh with a boundary layer averaging 3 million elements. Mesh parameters were selected based on a mesh-independence study. The time step for each simulation was set to 0.001 s. Transient flow was simulated over four cardiac cycles to reach a converged periodic solution with a < 1% difference in outlet pressure and flow from the previous cycle. The final cardiac cycle was used for data analysis. Simulations were run on high-performance computing hardware, requiring 1000 CPU hours on average.
Automated computational pipeline
We developed an automated pipeline to generate synthetic 3D LCA models, meshes, and simulation files using the SimVascular Python API54. This pipeline’s inputs were a baseline adult LCA model as defined in the Design of computational experiments section and a parametric description of LCA geometric features. These features included LAD and LCx diameters, segment lengths, bifurcation angles, tortuosity characteristics such as number of inflections and amplitude, and lumen eccentricity. Stenosis and plaque length were prescribed for the diseased models. These parameters informed changes to the baseline LCA centerline coordinates and segmentations. Then, these segmentations were lofted to form 3D models with smoothing operations. Finally, a tetrahedral mesh was generated from the 3D model. The outputs from the pipeline were the mesh and input files for the SimVascular flow solver. Hemodynamic metrics were extracted from simulation results with a Python VTK59 script.
Boundary conditions and assumptions
We prescribed a coronary flow waveform at the inlet at a baseline heart rate of 70 beats per minute (Fig. 2) and imposed a parabolic velocity profile. Outlet surfaces were coupled to a 0D lumped-parameter network (LPN) model to represent coronary physiology and achieve realistic LCA pressure waveforms46,60. Total resistance was calculated as the ratio of mean arterial pressure drop over mean inlet flow60. Based on this estimated total resistance, resistances at each flow outlet were scaled by their diameter using Murray’s law with an exponent of 2.661. Each outlet resistance was split by a 0.34:0.48:0.18 ratio into distal arterial resistance (\({R}_{a}\)), microvascular resistance (\({R}_{A-m}\)), and venous resistance (\({R}_{V}\))60. Total capacitance was tuned to achieve physiological pressure decay between systolic and diastolic pressure (70–120 mmHg). Arterial capacitance (\({C}_{A}\)) and microvascular capacitance (\({C}_{im}\)) were scaled to 0.11 and 0.89, respectively, of the total capacitance. As left ventricle contraction leads to elevated pressures in the coronary intramyocardial beds during systole, a pressure source term (\({P}_{im}\)) was included in the LPN to account for this effect. Walls were assumed to be rigid, and zero velocity no-slip conditions were applied to the walls. Prior studies have shown that wall deformation has a minor effect on WSS for healthy coronary arteries62,63. Heart-induced motion on the LCA was neglected, as prior work suggests that it inconsequentially alters time-averaged WSS63. We assumed laminar flow as the average Reynolds number in our models was near 200. Blood was modeled as a Newtonian fluid (density = 1.06 g/cm3, dynamic viscosity = 0.04 dynes \(\cdot\) s/cm2) as the average shear rate in our simulations exceeded 100/s64.
Automated computational pipeline to generate models, meshes, and simulation files, perform simulations, and extract hemodynamic metrics. Geometric changes imposed on the baseline LCA were defined by a numerical description of the geometric parameters considered: diameters (\(\text{D}\)), lengths(\(\text{L}\)) angles (\(\alpha\)), tortuosity (\(\uptau\)), and plaque (\(\uprho\)). Specialized coronary LPNs were coupled to the 3D geometry flow outlets (\({\Gamma }_{\text{h}}\)) and a coronary inflow waveform was prescribed at the inlet (I). Dirichlet no-slip conditions were applied on \({\Gamma }_{\text{w}}\), and a parabolic inlet velocity profile was prescribed on \({\Gamma }_{\text{g}}\).
Baseline cardiac output, mean intramyocardial pressure, total capacitance, and heart rate were set using published averages for adult females and males65,66,67. In simulations with varied diameter ratios, allometric power law scaling was applied to the inlet flow (i.e., cardiac output), intramyocardial pressure, and heart rate based on the ratio of a model’s volume to the sex-differentiated baseline volume. A model’s volume was assumed to correlate with the cardiac mass it would supply, as mass is more prevalent in the literature. Intramyocardial pressure and cardiac output were scaled by a power of 0.25 and heart rate was scaled by a power of − 0.2568,69,70. Allometric scaling was used only when diameter ratio \({R}_{d}\) changed, and not due to volume changes induced by tortuosity, shifted bifurcation positions and angles. Tortuosity would have biased the scaling due to the increased volume of longer, tortuous vessels. Similarly, bifurcations shifted downstream would elongate a branch, increase the volume, and thus bias scaling. The total downstream vascular resistance remained constant by scaling both inlet flow and pressure.
Hemodynamic metrics and statistical analysis
For each simulation, we computed time-averaged wall shear stress (TAWSS), the area exposed to low wall shear stress (ALWSS) defined as the area where TAWSS < 0.5 Pa, and the area exposed to high wall shear stress (AHWSS) defined as the area where TAWSS > 7 Pa. Low and high TAWSS thresholds of 0.5 Pa and 7 Pa were selected based on estimations from experimental studies in the literature24. These hemodynamic metrics were calculated in different regions of interest for each model following the same definition: in a spherical region at each bifurcation, along the entire surface of the LAD and LCx branches, along arterial segments with plaque, and immediately at the distal end of plaque in diseased models. Then, ALWSS and AHWSS were normalized by the model surface area within the measurement region (sphere or arterial segment wall surface). For example, the ALWSS at each bifurcation was normalized by the surface area of the LCA model within the measurement sphere. As such, we report ALWSS as a percentage. To ensure that the sphere at bifurcations fully encapsulated ALWSS across the vast range of models, the LCA model-to-sphere surface area ratio was maintained near 0.25. ALWSS at the LAD/LCx bifurcation was also categorized by branchwise location; i.e. proximal LAD or LCx. Finally, flow rates were measured at each outlet in ml/s. Given that outlet resistances were held constant for each set of experiments (apart from varied diameters in phase 2), we wanted to quantify if other geometric features altered significantly flow distributions through the LAD and LCx. Additional details regarding hemodynamic measurement regions and normalization are depicted in Supplementary Fig. S3.
In diseased models, we computed pressure based measurements such as instantaneous wave-free ratio (iFR), the ratio of pressure immediately distal to the plaque and inlet pressure mid-diastole71. Prior studies have reported that the diagnostic potential of iFR (hemodynamic significance threshold = 0.89) may be similar to FFR without requiring induced hyperemia72. To gauge the sensitivity of various hemodynamic metric magnitudes to changes in geometry, we computed percent changes between the smallest and largest values for a given phase of simulations, as well as percent changes with respect to the baseline model from phase 1.
We performed statistical analyses to assess the sensitivity of hemodynamic parameters to vascular structure. Partial correlation test was used when two or more geometric features were correlated in opposite directions with a hemodynamic metric, or the magnitude of these correlations had different strengths73. When this method was used, correlation coefficients (R) were reported to effectively display the direction of correlation (positive or negative). We considered a very strong correlation for R \(\ge \left|0.8\right|\), a strong correlation for \(\left|0.8\right|>\) R \(\ge \left|0.6\right|\), a moderate correlation for \(\left|0.6\right|>\) R \(\ge \left|0.4\right|\), and weak linear correlation for R \(<\left|0.4\right|\)74. Multi-linear regression was used when two or more geometric features correlated in the same direction with a hemodynamic metric, as well as having correlation coefficients for all independent variables in a similar range. In these cases, the adjusted coefficient of determination (R2) was reported. We considered a very strong correlation for R2 \(\ge 0.7\), a strong correlation for \(0.7>\) R2 \(\ge 0.4\), a moderate correlation when \(0.4>\) R2 \(\ge 0.2\), and a weak correlation when R2 \(<0.2\). Quadratic regression was used to assess ALWSS correlations with diameter ratio to improve model fit with the behavior of the data, for which adjusted coefficient of determination (R2) was reported. We used the Mann–Whitney U test to determine if any two groups had significantly different medians. Similarly, we used the Kruskal–Wallis test to determine if three or more groups originated from the same distribution. A p-value < 0.05 was specified to determine the statistical significance of correlations and group differences. We compared statistical correlations for tortuosity score versus average-absolute-curvature37 for tortuous models. For this analysis we used Python’s scipy, pingouin, and statmodels libraries.
Results
Hemodynamic sensitivity to variations in healthy coronary artery geometry
Bifurcation position and angle have a mild effect on ALWSS if the LAD/LCx diameter ratio is neutral
For a neutral LAD/LCx diameter ratio (\({R}_{d}\)= 0.94), bifurcation position and angle showed non-significant or weak correlations with ALWSS at the LAD/LCx bifurcation. ALWSS measured at the LAD/LCx bifurcation ranged between 0.2 and 5.7% based on changes in bifurcation angle and position (Fig. 3a). The largest ALWSS at the bifurcation corresponded to the smallest bifurcation angle and the shortest LMCA tested (case 1). Bifurcation position (LMCA length) negatively correlated with ALWSS in the proximal LAD (R = -0.72, p < 0.001), but no statistically significant correlation was observed in the proximal LCx (R = -0.14, p = 0.513). A larger bifurcation angle moderately correlated with an increase in ALWSS in the proximal LAD (R = 0.51, p = 0.0113) and a decrease in ALWSS in the proximal LCx (R = -0.52, p = 0.00863). Outlet flow distributions exhibited small changes (< 6% change) with bifurcation position and angle.
Sensitivity of ALWSS at the LAD/LCx bifurcation to bifurcation position and angle in (a) healthy and (b) diseased models at a neutral LAD/LCx diameter ratio (\({\text{R}}_{\text{d}}\) = 0.94). TAWSS contours are observed from a proximal view, as in looking underneath the myocardium. (a) More proximal bifurcation positions increased ALWSS at the LAD/LCx bifurcation. Proximal bifurcation positions consistently induced ALWSS for small (case 1) and large (case 2) angles in the proximal LAD. (b) ALWSS at the LAD/LCx bifuraction in models with proximal LCx plaque. Trends observed in the healthy model are conserved, except for a significant reduction in ALWSS in the proximal LCx. ALWSS measured in the LAD did not significantly differ between healthy and diseased models, as shown by comparing cases 1 and 3, as well as cases 2 and 4. Case 5 is referred to in Fig. 7.
Skewed LAD and LCx dominance increases ALWSS at the LAD/LCx bifurcation
Skewed dominance increased ALWSS at the LAD/LCx bifurcation, with respect to the baseline model, in the full range of vessel diameters tested — females and males (Fig. 4). ALWSS demonstrated a strong quadratic fit with diameter ratio in both groups (R2 = 0.91, p < 0.001 and R2 = 0.94, p < 0.001). ALWSS at the LAD/LCx bifurcation ranged from 0 to 11.5% in models representative of male LCAs and from 0 to 9.8% in models representative of female LCAs. However, there was no significant difference in ALWSS between models with diameters representative of females and males (1.8 ± 2.7% vs. 1.8 ± 2.9%, p = 0.985). The largest ALWSS at the bifurcation corresponded to the smallest LAD and the largest LCx for both groups (Fig. 4 cases 2 and 4). ALWSS was larger when LCx was the dominant branch at the bifurcation. Skewed dominance led to ALWSS formation in the smaller-of-the-two branches at the bifurcation — LAD or LCx. As expected, LAD and LCx flow distribution strongly correlated with LAD and LCx diameters (R2 > 0.95, p < 0.001), inducing substantial changes in the flow split (> 100% change from baseline in the diameter range tested).
Sensitivity of ALWSS at the LAD/LCx bifurcation to varying diameter ratio in healthy male and female models. The same trends were observed in both sexes, with the skewed LAD and LCx dominance increasing ALWSS. ALWSS was maximized in the proximal LAD for geometries with the largest LCx and smallest LAD diameter (cases 2 and 4). Similarly, dominant LAD models with the largest LAD and smallest LCx diameter (cases 1 and 3) led to a ALWSS formation exclusively in the proximal LCx.
Vessel tortuosity has a minor influence on ALWSS at the LAD/LCx bifurcation if the LAD/LCx diameter ratio is neutral
At a neutral diameter ratio, tortuosity in the LAD and LCx caused local variations in WSS distribution. However, ALWSS at the LAD/LCx bifurcation did not correlate with LAD and LCx tortuosity (R2 = − 0.31, p = 0.952). Furthermore, ALWSS at the LAD/LCx bifurcation only varied by 1.6 points (from 0.4 to 2.0%). Imposing tortuosity marginally altered the LAD/LCx outlet flow distribution (< 4% change from baseline). Regardless of the tortuosity-classification used, similar statistical conclusions were obtained. For example, we observed statistically insignificant correlation coefficients for both tortuosity score and average-absolute-curvature with ALWSS at the LAD/LCx bifurcation (R2 = − 0.31, p = 0.952 and R2 = − 0.32, p = 0.970).
Changes in bifurcation position and angle, and branch tortuosity with a skewed LAD/LCx diameter ratio reveal the most adverse vascular structures regarding ALWSS
We simulated variations in the LAD/LCx bifurcation position and angle in dominant LAD (\({\text{R}}_{\text{d}}\) = 0.65) and dominant LCx models (\({\text{R}}_{\text{d}}\) = 1.40) (Fig. 5a). Our results show that skewed LAD/LCX diameter ratios strengthen the correlations between these geometrical variations with ALWSS observed in phase 1. Bifurcation position moderately correlated with ALWSS at the LAD/LCx bifurcation in both LAD dominant (R = − 0.43, p = 0.0355) and LCx dominant models (R = − 0.48, p = 0.0184). Depending on branch dominance, we observed a positive or negative correlation between the bifurcation angle and ALWSS at the LAD/LCx bifurcation. A larger bifurcation angle decreased ALWSS in LAD dominant models (R = − 0.73, p < 0.001), while it increased ALWSS in LCx dominant models (R = 0.86, p < 0.001).
Sensitivity of ALWSS at the LAD/LCx bifurcation to varying LAD/LCx bifurcation angle and position in LAD dominant (\({\text{R}}_{\text{d}}\)=0.65) and in LCx dominant (\({\text{R}}_{\text{d}}\)=1.40) (a) healthy and (b) diseased models. (a) LCx dominant models had greater ALWSS than the LAD dominant ones (p < 0.001). Large bifurcation angles led to the largest ALWSS magnitude in LCx dominant models (case 3). However, the LAD dominant cases exhibited the opposite behavior (case 1); smaller angles increased ALWSS at the bifurcation (cases 2 and 6). Changing the bifurcation position only moderately changed ALWSS. (b) The same trends were observed in both the healthy and diseased models. However, ALWSS at the LAD/LCx bifurcation was significantly lower in the diseased cases.
ALWSS was significantly larger in the LAD and LCx dominant models compared to those with a neutral diameter ratio with the same LAD/LCx bifurcation position and angle (6.8 ± 3.6% vs. 1.7 ± 1.3%, p < 0.001 for LAD dominance and 16.7 ± 4.7% vs. 1.7 ± 1.3%, p < 0.001 for LCx dominance). ALWSS at the LAD/LCx bifurcation was significantly smaller in LAD dominant models compared to LCx dominant ones (6.8 ± 3.6% vs. 16.7 ± 4.7%, p < 0.001). Similar to phase one, LAD/LCx outlet flow distribution was marginally affected by changes in bifurcation position or angle (< 6% change).
In LAD dominant models (\({R}_{d}\)=0.65), we observed a strong correlation between LAD and LCx branch tortuosity and ALWSS at the LAD/LCx bifurcation (R2 = 0.95, p < 0.001) (Fig. 6). Proximal LAD and LCx ALWSS correlated with tortuosity in their respective branch at this bifurcation. For example, at the proximal LAD, ALWSS increased with LAD tortuosity (R = 0.94, p < 0.001) but not LCx tortuosity (R = − 0.094, p = 0.825). Similarly, proximal LCx ALWSS did not statistically correlate with LAD tortuosity (R = -0.55, p = 0.159) but strongly correlated with LCx tortuosity (R = 0.94, p < 0.001). Similar trends were observed when considering the whole arterial branch. In LAD dominant models, LAD tortuosity strongly correlated with ALWSS throughout the LAD (R = 0.80, p = 0.0182), while LCx tortuosity did not correlate (R = − 0.034, p = 0.937). LCx tortuosity strongly correlated with ALWSS throughout the LCx branch (R = 0.90, p = 0.00241), while LAD tortuosity only showed moderate correlation with ALWSS (R = − 0.49, p = 0.222).
In LCx dominant models (\({R}_{d}\)=1.40) with tortuosity, LAD and LCx tortuosity did not statistically correlate with ALWSS at the LAD/LCx bifurcation (R = − 0.59, p = 0.124 and R = 0.29, p = 0.438) (Fig. 6). Also, ALWSS throughout the entire LAD and LCx branches weakly correlated with tortuosity (R2 = 0.26, p = 0.404 and R2 = 0.28, p = 0.378). Compared to neutral ratio models with tortuosity, ALWSS was significantly larger in tortuous models with LAD dominance (8.8 ± 2.0% vs.1.2 ± 0.5%, p < 0.001) and LCx dominance (10.1 ± 1.8% vs. 1.2 ± 0.5%, p < 0.001).
We found that correlation coefficients R2 were similar when we performed multilinear regression with tortuosity score or average-absolute-curvature. For example, in LAD dominant models with tortuosity we observed very strong correlation coefficients for both tortuosity score and average-absolute-curvature with ALWSS at the LAD/LCx bifurcation (R2 = 0.95, p < 0.001 and R2 = 0.88, p < 0.001).
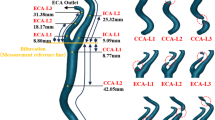
Hemodynamics at distal bifurcations are predominantly sensitive to upstream vessel diameters
LAD and LCx diameters determined ALWSS magnitude at distal bifurcations. Varied LAD/LCx bifurcation positions and angles induced minor changes in ALWSS at distal bifurcations (18% change on average from baseline) compared to changes observed at LAD/LCx bifurcation itself (500% change on average from baseline). This observation was true for neutral diameter and skewed diameter ratios. Interestingly, ALWSS at distal bifurcations was statistically larger in LAD dominant models compared to LCx dominant ones, including the LAD/Distal-1 (5.4 ± 0.2% vs. 3.3 ± 0.1%, p < 0.001), LAD/Distal-2 (6.8 ± 0.3% vs. 3.9 ± 0.2%, p < 0.001), LCx/Obtuse-marginal-1 (8.3 ± 0.3% vs. 3.7 ± 0.3%, p < 0.001), except the LCx/Obtuse-marginal-2 (1.1 ± 0.05% vs. 5.3 ± 0.1%, p < 0.001). LAD dominant models also had statistically larger ALWSS at distal bifurcations compared to neutral ratio models, including the LAD/Distal-1 (5.4 ± 0.2% vs. 2.9 ± 0.3%, p < 0.001), LAD/Distal-2 (6.8 ± 0.3% vs. 2.9 ± 0.2%, p < 0.001), LCx/Obtuse-marginal-1 (8.3 ± 0.3% vs. 2.6 ± 0.1%, p < 0.001), except the LCx/Obtuse-marginal-2 (1.067 ± 0.05% vs. 1.142 ± 0.04%, p < 0.001). Distal ALWSS increased in tortuous models, but the range of magnitude change was small (< 3%) compared to changes induced by diameter variations (up to 8%).
In phase two, we observed strong correlations between branch diameter and ALWSS at distal bifurcations (Supplementary Fig. S4). For example, ALWSS at the LAD/D2 bifurcation very strongly correlated with both LAD and LCx diameters in females and males (R2 = 0.95, p < 0.001 and R2 = 0.94, p < 0.001). ALWSS at this bifurcation ranged from 0 to 4.8% in females and 1 to 8.9% in males. Similarly, ALWSS at the LCx/OM2 bifurcation strongly correlated with both LAD and LCx diameters in females and females (R2 = 0.82, p < 0.001, R2 = 0.94, p < 0.001). ALWSS at this bifurcation varied from 0 to 3.5% in females and 0 to 7.5% in males.
Streamlines indicate disturbed flow regions induced by variations in coronary artery geometry
Qualitative analysis of the flow streamlines identified regions of disturbed flow near the bifurcations. In LCx dominant models, a large disturbed flow region formed in the proximal LAD as the flow from the LMCA turned towards the LCx (Fig. 7, right). At a neutral diameter ratio (Fig. 7, left), regions of disturbed flow were the smallest in general. For LAD dominant geometries (Fig. 7, center), smaller angles increased disturbed flow regions in the proximal LCx. We observed similar disturbed flow in the proximal LCx for models at a neutral diameter ratio or a dominant LAD. However, the effect of the bifurcation on local flow perturbations was more pronounced in LCx dominant models. The relationship between disturbed flow to low shear stress and its effect on the progression of CAD and vascular remodeling has previously been established in the literature7,24. As expected, these regions of disturbed flow qualitatively coincide with segments of the arterial wall where we identified areas of low WSS.
Time-averaged streamlines colored by velocity magnitude for various geometries from Figs. 3 and 6. At the same bifurcation position (2.2 cm), changes in bifurcation angle and diameter ratio induced different flow patterns. The effect of the bifurcation on the local flow is more pronounced in LCx dominant models.
Hemodynamic sensitivity to variations in diseased coronary artery geometry
Isolated plaque study indicates the formation of plaque trailing edge ALWSS
Although ALWSS decreased overall, a mild plaque did not affect the trends observed in the healthy model. The plaque also created new areas of low WSS at its trailing edge for certain combinations of stenosis and length. The variations in atherosclerotic plaque length and stenosis we tested did not significantly affect ALWSS at the LAD/LCx bifurcation This was true regardless of whether the plaque was placed in the LAD (R2 = 0.027, p = 0.331) or the LCx (R2 = – 0.024, p = 0.46). In general, ALWSS at this bifurcation was < 0.3%. However, ALWSS distal to the plaque (trailing edge) was observed when LAD stenosis was 40%. For models with LCx plaque, we observed trailing edge ALWSS with the same stenosis degree but only when plaque length was > 1.7 cm. Both plaque length and stenosis correlated with AHWSS along LAD (R2 = 0.64, p < 0.001) plaques and, to a smaller extent, LCx plaques (R2 = 0.34 p = 0.024). AHWSS ranged from 0 to 43% in LAD plaques and 2 to 24% in LCx plaques. At the average plaque stenosis length and width, AHWSS was 10.2% and 3.8% along the LAD and LCx plaque, respectively. Outlet flow distribution between the LAD and LCx was unaffected by plaque length and stenosis tested (< 3% change from healthy baseline outflow). For all these simulations, iFR was above the threshold for hemodynamic significance (iFR > 0.89).
Hemodynamic sensitivity to varying geometric structure with plaque
ALWSS trends from changes in LAD/LCx bifurcation position and angle with a neutral LAD/LCx diameter ratio are similar in healthy and diseased models
The correlation of ALWSS at the LAD/LCx bifurcation with bifurcation position and angle at a neutral diameter ratio (\({R}_{d}\)= 0.94) was similar in healthy and diseased models with proximal LCx plaque (Fig. 3b). At the LAD/LCx bifurcation, position negatively correlated with ALWSS in the proximal LAD (R = − 0.78, p < 0.001), while there was no statistical correlation in the proximal LCx (R = 0.10, p = 0.718). Bifurcation angle moderately, but not to statistical significance, correlated with ALWSS in the proximal LAD (R = − 0.50, p = 0.0547), while it negatively correlated with ALWSS in the proximal LCx (R = – 0.70, p = 0.00399). ALWSS in the proximal LAD was not statistically different in healthy and diseased models (1.07 ± 0.98% vs. 1.15 ± 0.96%, p = 0.799), while it was significantly reduced in the proximal LCx where plaque was present (0.63 ± 0.81% vs. 0.17 ± 0.27%, p = 0.0166). Similar to the healthy models, outlet flows were unaffected by LAD/LCx bifurcation position and angle changes in diseased geometries (< 5% change from healthy baseline outflow). Furthermore, for the plaque topology we considered, there was no significant difference in outlet flow between healthy and diseased models (for example, LCx outlet flow was 0.32 ± 0.0053 cm3/s vs. 0.32 ± 0.0057 cm3/s, p = 0.792). For all these simulations, iFR surpassed the hemodynamic significance threshold (iFR > 0.89).
ALWSS trends from changes in the LAD/LCx diameter ratio are similar in healthy and diseased models
Diameter ratio changes at the LAD/LCx bifurcation, from neutral to skewed, affected ALWSS at the LAD/LCx bifurcation similarly in healthy and diseased models. However, plaque trailing edge ALWSS was observed in some cases. We observed a moderate quadratic correlation between ALWSS and diameter ratio in LAD and LCx plaque models, although not at statistical significance (R2 = 0.26, p = 0.0532). Incorporating plaque decreased ALWSS at the LAD/LCx bifurcation (Figs. 4 and 8). For the geometry with the most dominant LCx (\({R}_{d}\)=1.40), plaque in the proximal LAD decreased ALWSS from 11.5% to 4.8%. In the most dominant LAD model (\({R}_{d}\)=0.65), ALWSS was reduced to a lesser extent, from 3.7% to 2.9%, when a plaque in the proximal LCx was present. However, when considering a mild plaque in the proximal LAD or LCx, ALWSS at the LAD/LCx bifurcation was not significantly different between healthy and diseased models (1.8 ± 2.9% healthy vs. 1.7 ± 1.5% LAD plaque, p = 0.474).
Sensitivity of ALWSS at the LAD/LCx bifurcation to varying diameter ratio in diseased models. Compared to its healthy counterpart, ALWSS in the proximal LCx is reduced when compared to healthy geometries due to the presence of plaque (case 1). Similarly, ALWSS in the proximal LAD is reduced in comparison to healthy cases due to the presence of proximal LAD plaque (case 2).
Introducing plaque in skewed LAD and LCx dominant models induced ALWSS at the plaque trailing edge in some cases (Supplementary Fig. S5). Trailing edge ALWSS strongly correlated with both LAD and LCx diameters in diseased models (R2 = 0.69, p < 0.001). We observed trailing edge ALWSS predominantly in models with LCx plaque. We observed no correlation between LAD and LCx diameters and AHWSS along the plaque (R2 = 0.042, p = 0.299).
Compared to healthy models, introducing a mild plaque did not significantly affect LCA flow distribution in models with skewed LAD or LCx dominance. For example, LAD outlet flow was not statistically different between healthy and diseased models (0.80 ± 0.25 cm3/s vs. 0.80 ± 0.245 cm3/s if the plaque was in the LAD, p = 0.706). Similarly, LCx outlet flow was not statistically different between healthy and diseased models (0.46 ± 0.22 cm3/s vs. 0.46 ± 0.22 cm3/s if the plaque was in the LCx, p = 0.865). For all these simulations, iFR was above the threshold for hemodynamic significance (iFR > 0.89).
ALWSS trends from changes in LAD/LCx bifurcation position and angle with skewed dominance are similar in healthy and diseased models
Trends observed in ALWSS for healthy models with varying bifurcation position, angle, and skewed dominance were conserved when a mild plaque was introduced (Fig. 5b). For example, in LAD dominant models with plaque, LAD/LCx bifurcation position and angle negatively correlated with ALWSS at the LAD/LCx bifurcation (R = − 0.56, p = 0.029 and R = − 0.72, p = 0.00270), similar to healthy cases. In LCx dominant models with plaque, ALWSS negatively correlated with LAD/LCx bifurcation position (R = − 0.64, p = 0.00960) but positively correlated with angle (R = 0.77, p < 0.001), similar to their healthy counterparts. In diseased models we observed statistically lower ALWSS at the LAD/LCx bifurcation in LAD dominant models compared to LCx dominant ones (3.7 ± 2.3% vs. 8.8 ± 4.2%, p < 0.001).
We observed statistically significant changes in ALWSS at the proximal location of each branch where the plaque was introduced. For example, in LAD dominant models ALWSS in the proximal LCx was greater in healthy versus diseased models with LCx plaque (6.2 ± 3.0% vs. 3.0 ± 1.5%, p < 0.001). Furthermore, in LCx dominant models, ALWSS in the proximal LAD was greater in healthy models compared to diseased models with plaque in the LAD (16.4 ± 4.8% vs. 8.5 ± 4.2%, p < 0.001). Finally, changes in outlet flow distribution were small for bifurcation position and angle variations in LAD and LCx dominant models with plaque (< 7% change). There was no statistically significant difference in outlet flows between healthy and diseased models (in LCx dominant models, LAD outlet flow was 0.329 ± 0.0060 cm3/s vs. 0.327 ± 0.0062 cm3/s, p = 0.269). For all these simulations, iFR was above the threshold for hemodynamic significance (iFR > 0.89).
Discussion
Our analysis suggests that vascular structure has a profound effect on ALWSS magnitude and location in the LCA. Skewed LAD and LCx dominance has an impact on ALWSS and exacerbates the influence of other geometric features, such as LAD/LCx bifurcation position and angle, on ALWSS. Skewed LAD and LCX dominance induces ALWSS in the smaller of the two branches. We observe a strong quadratic correlation between ALWSS and diameter ratio. This finding aligns with prior computational work, which suggests that the smaller branch at the bifurcation is more prone to low WSS exposure40. Interestingly, geometries with skewed LAD/LCx dominance/diameter-ratios correspond to an upstream/downstream diameter ratio (\({D}_{LMCA}/({D}_{LAD}+{D}_{LCx}))\) of 0.66, on average. This upstream/downstream ratio range is within published population averages of this parameter (0.678 ± 0.0665)75, implying that skewed dominance may be common and worth considering when assessing ALWSS and potential plaque growth risk. Comparatively, a neutral LAD/LCx diameter ratio in our simulations corresponded to an upstream/downstream ratio of around 0.57. LAD/LCx bifurcation angle and position, and tortuosity induced significantly larger ALWSS in models with skewed LAD and LCx dominance (phase four) compared to models with neutral ratios (phases one and three). Models with skewed LAD and LCx dominance did not universally conserve the trends between ALWSS and geometric parameters at a neutral diameter ratio. An exception was the proximal bifurcation position (i.e., shorter LMCA), which consistently correlated with greater ALWSS. This finding aligns with prior observational studies that suggest shorter LMCA lengths in CAD patients11.
Branch dominance may explain why LAD/LCx bifurcation angle does not consistently correlate with ALWSS. The qualitative differences observed in the streamlines of Fig. 7 suggest that branch dominance substantially influences flow patterns at the LAD/LCx bifurcation, which can be amplified by the bifurcation angle. This finding may explain why prior studies have reported conflicting results regarding the relationship between adverse hemodynamics and bifurcation angles. These differences may be attributed to the lack of consideration of LAD and LCx diameters and how they impact flow at the LAD/LCx bifurcation.
LAD/LCx diameter ratio influenced the distribution of WSS in tortuous models. While no significant changes were observed between ALWSS and tortuosity for a neutral diameter ratio, in LAD dominant models, tortuosity significantly correlated with ALWSS at the LAD/LCx bifurcation, and throughout the surfaces of the LAD and LCx branches. Interestingly, we observed weak correlations between tortuosity and ALWSS in LCx dominant models, both locally at the LAD/LCx bifurcation and throughout the LAD and LCx branches. These results suggest that LCA configurations with a dominant LAD and higher tortuosity may be more prone to plaque formation not only at the LAD/LCx bifurcation, but also downstream, in proximal and medial regions of the LAD. The increased branchwise low WSS exposure is largely attributed to increased curvature in tortuous arteries, which generates secondary flows along these segments.
ALWSS at the distal bifurcations was predominantly sensitive to increases in branch diameter and, to a lesser extent, tortuosity. While this suggests that LCA configurations with the largest LAD and LCx diameters are most prone to increased ALWSS at distal bifurcations, this finding may be biased by the volume allometric scaling. Inlet flow in the smallest volume models may have been disproportionally large relative to their diameter, which may have resulted in higher mean velocities and less ALWSS compared to models with larger volumes.
Introducing a mild plaque did not alter the statistical trends we observed between geometric features and hemodynamics in healthy models but, as expected, significantly reduced ALWSS in branches where plaque was present. In particular, the location of ALWSS at the LAD/LCx bifurcation were similar in healthy and diseased models. In both healthy and diseased models, LCx dominant cases with small bifurcation angles and proximal positions were the most hemodynamically adverse geometries. This implies that when a mild plaque has formed, certain bifurcation positions, angles, and diameter-ratios can induce a hemodynamic environment that is prone to the growth of proximal plaque.
Trailing edge ALWSS was primarily influenced by plaque stenosis. However, variation in vascular structure can induce ALWSS at the trailing edge of mild plaques, suggesting potential areas of distal plaque growth. For example, trailing edge ALWSS was observed for LCx plaque with increases in both LAD and LCx diameters. This observation is likely due to the velocity profile skewing towards the outer wall, generating a lower velocity gradient at the inner wall immediately after the plaque which can lead to low WSS. Since the plaque topology is kept constant, this effect is modulated by the LAD and LCx diameters, which drive flow distribution in the LCA.
High TAWSS is related to vulnerable plaque rupture risk. For plaque \(\le\) 30% stenosis, most vascular features did not induce AHWSS along the plaque. For example, AHWSS was not observed along the stenosed plaque surface with variations in LAD/LCx bifurcation angle and position for all the tested diameter ratios. Although we observed AHWSS in diseased models with varied diameter ratios, no statistical correlations were apparent. This may indicate that changes in geometric features do not induce AHWSS along the plaque surface. Instead, the degree of stenosis itself may be more consequential to AHWSS.
Limitations
The pathlines in the baseline LCA model may have biased the hemodynamic parameters we measured. In particular, the continuity of the LAD and LCx branch pathlines with their shared upstream branch (LMCA) likely influenced hemodynamics at the LAD/LCx bifurcation. Specifically, the LAD was \(\rm C{^1}\) continuous with the LMCA, while the LCx was not. As such, the angle between the LCx and the LMCA induced higher flow rotationality in the proximal LCx, which was notably weaker in the proximal LAD. An increase in flow rotation (measured by helicity) has been suggested to increase WSS35, which aligns with our observations of decreased ALWSS with greater helicity. This difference likely led to a lower magnitude of ALWSS in the proximal LCx compared to the proximal LAD. However, we chose to maintain \(\rm C{^1}\) continuity between the LMCA and the LAD, as the geometries we generated with continuous LMCA and LCx had a substantially different topology. Despite a potential slight overestimation of ALWSS, maintaining LAD and LMCA branch centerline continuity avoided confounding effects from changing the general topology of the LAD/LCx bifurcation.
Flow entering the coronary arteries is unsteady and undeveloped76. Given an average inlet flow of 2.2 cm3/s in our simulations, the estimated entrance length was 3.9 cm based on approximations for hydrodynamic entrance length for a fully developed laminar flow77. Given that our LMCA length was typically less than this value, assuming parabolic inlet flow may have affected our predicted ALWSS and AHWSS values at the LAD/LCx bifurcation and proximal LAD and LCx arteries segments. However, we expect the trends found in this study to still hold. Also, this will not be an issue if the full coronary anatomy is considered.
Given the synthetic nature of this study, we cannot definitively confirm how well our findings would translate to a clinical population. This ambiguity is, in part, due to the nature of the selected threshold values for low WSS. Previous studies have suggested the importance of ALWSS to endothelial dysfunction78 and subsequent plaque growth6, but they generally treat ALWSS as a categorical variable without statistically establishing a low WSS threshold that separates patients as low and high risk for progressive CAD. With this analysis, we have gained valuable insight into the vascular phenotypes most conducive to plaque-promoting hemodynamics. However, some of our conclusions are likely sensitive to the selected threshold of 0.5 Pa. Future work will involve conducting a longitudinal study to correlate ALWSS measured in patient-specific CFD models with plaque growth over time. These data can be used to propose ALWSS cutoff values for early risk stratification.
Finally, we did not investigate how microvascular dysfunction can alter the hemodynamic environment in the epicardial LCA. Given the synthetic nature of our study, imposing microvascular dysfunction is nontrivial as patients with or without obstructive CAD may experience this condition79. In future work, boundary conditions that reflect microvascular pathologies can be implemented to evaluate the combined effect of microvascular dysfunction and vascular structure on adverse hemodynamics.
Conclusions
Coronary hemodynamics are highly sensitive to vascular structure, and plaque-promoting hemodynamics can be correlated to specific geometric features. We determined LCA structures that exhibit adverse hemodynamic phenotypes through a rigorous computational study. The results of our analysis demonstrate that coronary artery vascular structure can provide key insight into the hemodynamic environments that are conducive to plaque formation and growth. Future studies would further evaluate these findings in patient-specific vasculatures.
Data availability
The source code for the vascular modeling and simulation pipeline is available on GitHub to use at github.com/BioSiMMLab/CoronaryModelPipeline. All data from the simulations is available on Kilt Hub, a cloud-storage system from Carnegie Mellon University at the request of the authors.
References
Roth, G. A. Global, regional, and national age-sex-specific mortality for 282 causes of death in 195 countries and territories, 1980–2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet 392, 1736–1788 (2018).
Heitzer, T., Schlinzig, T., Krohn, K., Meinertz, T. & Münzel, T. Endothelial dysfunction, oxidative stress, and risk of cardiovascular events in patients with coronary artery disease. Circulation 104, 2673–2678 (2001).
Tonino, P. A. L. et al. Fractional flow reserve versus angiography for guiding percutaneous coronary intervention. NEJM 360, 213–224 (2009).
Bergström, G. et al. Prevalence of subclinical coronary artery atherosclerosis in the general population. Circulation 144, 916–929 (2021).
VanderLaan, P. A., Reardon, C. A. & Getz, G. S. Site specificity of atherosclerosis. Arterioscler. Thromb. Vasc. Biol. 24, 12–22 (2004).
Stone, P. H. et al. Prediction of progression of coronary artery disease and clinical outcomes using vascular profiling of endothelial shear stress and arterial plaque characteristics. Circulation 126, 172–181 (2012).
Stone, P. H. et al. Effect of endothelial shear stress on the progression of coronary artery disease, vascular remodeling, and in-stent restenosis in humans. Circulation 108, 438–444 (2003).
Papafaklis, M. I. et al. Effect of the local hemodynamic environment on the de novo development and progression of eccentric coronary atherosclerosis in humans: Insights from PREDICTION. Atherosclerosis 240, 205–211 (2015).
Rampidis, G. et al. Correlation of coronary artery geometry with the complexity and severity of coronary atherosclerosis: rationale and design of the GEOMETRY-CTA study. Eur. Heart J. Cardiovasc. Imaging 22, jeab111.018 (2021).
Gazetopoulos, N. et al. Length of main left coronary artery in relation to atherosclerosis of its branches. A coronary arteriographic study. Br. Heart J. 38, 180–185 (1976).
Saltissi, S., Webb-Peploe, M. M. & Coltart, D. J. Effect of variation in coronary artery anatomy on distribution of stenotic lesions. Heart 42, 186–191 (1979).
Rampidis, G. et al. Relationship between coronary arterial geometry and the presence and extend of atherosclerotic plaque burden: A review discussing methodology and findings in the era of cardiac computed tomography angiography. Diagnostics 12, 2178 (2022).
Ohkawa, S. et al. Stenotic lesions and length of the left main coronary artery in the aged. Jpn. Heart J. 30, 779–788 (1989).
Ajayi, N. O., Lazarus, L., Vanker, E. A. & Satyapal, K. S. The impact of left main coronary artery morphology on the distribution of atherosclerotic lesions in its branches. Folia Morphol. 72, 197–201 (2013).
Sun, Z. & Cao, Y. Multislice CT angiography assessment of left coronary artery: correlation between bifurcation angle and dimensions and development of coronary artery disease. Eur. J. Radiol. 79, e90-95 (2011).
Gaafar, A., Kawi, M. A. & Mohammed, A. Coronary artery bifurcation angle degree; bifurcation lesion development and the prognostic impact. Med. J. Cairo Univ. 89, 787–796 (2021).
Cui, Y. et al. Quantification of left coronary bifurcation angles and plaques by coronary computed tomography angiography for prediction of significant coronary stenosis: A preliminary study with dual-source CT. PLoS One 12, e0174352 (2017).
Moon, S. H. et al. Clinical usefulness of the angle between left main coronary artery and left anterior descending coronary artery for the evaluation of obstructive coronary artery disease. PLoS One 13, e0202249 (2018).
Konishi, T., Funayama, N., Yamamoto, T., Hotta, D. & Tanaka, S. Relationship between left main and left anterior descending arteries bifurcation angle and coronary artery calcium score in chronic kidney disease: A 3-dimensional analysis of coronary computed tomography. PLoS One 13, e0198566 (2018).
Kahe, F. et al. Coronary artery tortuosity: a narrative review. Coron. Art. Dis. 31, 187–192 (2020).
Hakim, D. et al. The role of endothelial shear stress, shear stress gradient, and plaque topography in plaque erosion. Atherosclerosis 376, 11–18 (2023).
Gijsen, F. et al. Expert recommendations on the assessment of wall shear stress in human coronary arteries: existing methodologies, technical considerations, and clinical applications. Eur. Heart J. 40, 3421–3433 (2019).
Samady, H. et al. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation 124, 779–788 (2011).
Malek, A. M., Alper, S. L. & Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 282, 2035–2042 (1999).
Dhawan, S. S. et al. Shear stress and plaque development. Expert Rev. Cardiovasc. Ther. 8, 545–556 (2010).
Zhang, Q., Steinman, D. A. & Friedman, M. H. Use of factor analysis to characterize arterial geometry and predict hemodynamic risk: application to the human carotid bifurcation. J. Biomech. Eng. 132, 114505 (2010).
Beier, S. et al. Impact of bifurcation angle and other anatomical characteristics on blood flow - A computational study of non-stented and stented coronary arteries. J. Biomech. 49, 1570–1582 (2016).
Chiastra, C. et al. Healthy and diseased coronary bifurcation geometries influence near-wall and intravascular flow: A computational exploration of the hemodynamic risk. J. Biomech. 58, 79–88 (2017).
Malvè, M. et al. Tortuosity of coronary bifurcation as a potential local risk factor for atherosclerosis: CFD steady state study based on in vivo dynamic CT measurements. Ann. Biomed. Eng. 43, 82–93 (2015).
Liu, B., Zheng, J., Bach, R. & Tang, D. Influence of model boundary conditions on blood flow patterns in a patient specific stenotic right coronary artery. BioMed. Eng. OnLine 14, S6 (2015).
Rabbi, M. F., Laboni, F. S. & Arafat, M. T. Computational analysis of the coronary artery hemodynamics with different anatomical variations. Inform. Med. Unlock. 19, 100314 (2020).
Chaichana, T., Sun, Z. & Jewkes, J. Computation of hemodynamics in the left coronary artery with variable angulations. J. Biomech. 44, 1869–1878 (2011).
Pinho, N. et al. Correlation between geometric parameters of the left coronary artery and hemodynamic descriptors of atherosclerosis: FSI and statistical study. Med. Biol. Eng. Comput. 57, 715–729 (2019).
Pinho, N. et al. The impact of the right coronary artery geometric parameters on hemodynamic performance. Cardiovasc. Eng. Tech. 10, 257–270 (2019).
Vorobtsova, N. et al. Effects of vessel tortuosity on coronary hemodynamics: an idealized and patient-specific computational study. Ann. Biomed. Eng. 44, 2228–2239 (2016).
Shen, C. et al. Secondary flow in bifurcations – Important effects of curvature, bifurcation angle and stents. J. Biomech. 129, 110755 (2021).
Kashyap, V. et al. Accuracy of vascular tortuosity measures using computational modelling. Sci. Rep. 12, 865 (2022).
Myers, J. G., Moore, J. A., Ojha, M., Johnston, K. W. & Ethier, C. R. Factors influencing blood flow patterns in the human right coronary artery. Ann. Biomed. Eng. 29, 109–120 (2001).
Doutel, E., Pinto, S. I. S., Campos, J. B. L. M. & Miranda, J. M. Link between deviations from Murray’s Law and occurrence of low wall shear stress regions in the left coronary artery. J. Theor. Biol. 402, 89–99 (2016).
Huo, Y. et al. Which diameter and angle rule provides optimal flow patterns in a coronary bifurcation?. J. Biomech. 45, 1273–1279 (2012).
Ashrafee, A. et al. Design of experiment approach to identify the dominant geometrical feature of left coronary artery influencing atherosclerosis. Biomed. Phys. Eng. Express 10, 035008 (2024).
Peng, C. et al. The impact of the geometric characteristics on the hemodynamics in the stenotic coronary artery. PLoS One 11, e0157490 (2016).
Doutel, E., Viriato, N., Carneiro, J., Campos, J. B. L. M. & Miranda, J. M. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries—numerical and in vitro approaches. J. Biomech. 35, e3207 (2019).
Vardhan, M., Das, A., Gouruev, J. & Randles, A. Computational fluid modeling to understand the role of anatomy in bifurcation lesion disease. In 2018 IEEE 25th International Conference on High Performance Computing Workshops (HiPCW), 928–933 (2018).
Wong, K. K. L., Jianhuang, W., Liu, G., Huang, W. & Ghista, D. N. Coronary arteries hemodynamics: effect of arterial geometry on hemodynamic parameters causing atherosclerosis. Med. Biol. Eng. Comput. 58, 1831–1843 (2020).
Kim, H. J., Vignon-Clementel, I. E., Figueroa, C. A., Jansen, K. E. & Taylor, C. A. Developing computational methods for three-dimensional finite element simulations of coronary blood flow. Finite Elem. Anal. Des. 46, 514–525 (2010).
Medrano-Gracia, P. et al. A computational atlas of normal coronary artery anatomy. EuroIntervention 12, 845–854 (2016).
Vascular Model Repository. https://www.vascularmodel.com/.
Xiong, G. & Taylor, C. A. Influence of vessel roughness on wall shear stress in image-based blood flow modeling. In 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 33–36 (2010).
Eleid, M. F. et al. Coronary artery tortuosity in spontaneous coronary artery dissection. Circ. Cardiovasc. Interv. 7, 656–662 (2014).
Stone, G. W. et al. A prospective natural-history study of coronary atherosclerosis. NEJM 364, 226–235 (2011).
Antoniadis, A. P. et al. Arterial remodeling and endothelial shear stress exhibit significant longitudinal heterogeneity along the length of coronary plaques. JACC Cardiovasc. Imaging 9, 1007–1009 (2016).
Mehta, S. R. et al. Complete revascularization with multivessel PCI for myocardial infarction. New England J. Med. 381, 1411–1421 (2019).
Updegrove, A. et al. SimVascular: An open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 45, 525–541 (2017).
Brooks, A. N. & Hughes, T. J. R. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 32, 199–259 (1982).
Esmaily Moghadam, M. et al. A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations. Comput. Mech. 48, 277–291 (2011).
Esmaily Moghadam, M., Vignon-Clementel, I. E., Figliola, R. & Marsden, A. L. A modular numerical method for implicit 0D/3D coupling in cardiovascular finite element simulations. J. Comput. Phys. 244, 63–79 (2013).
Esmaily-Moghadam, M., Bazilevs, Y. & Marsden, A. L. A new preconditioning technique for implicitly coupled multidomain simulations with applications to hemodynamics. Comput. Mech. 52, 1141–1152 (2013).
VTK - The Visualization Toolkit. https://vtk.org/.
Kim, H. J. et al. Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann Biomed. Eng. 38, 3195–3209 (2010).
Murray, C. D. The physiological principle of minimum work. PNAS 12, 207–214 (1926).
Chiastra, C., Migliavacca, F., Martínez, M. Á. & Malvè, M. On the necessity of modelling fluid–structure interaction for stented coronary arteries. J. Mech. Behav. Biomed. Mater. 34, 217–230 (2014).
Fogell, N. A. T. et al. Considering the influence of coronary motion on artery-specific biomechanics using fluid-structure interaction simulation. Ann. Biomed. Eng. 51, 1950–1964 (2023).
Pedley, T. J. The Fluid Mechanics of Large Blood Vessels (Cambridge University Press, 1980).
Argiento, P. et al. Exercise stress echocardiography of the pulmonary circulation. Chest 142, 1158–1165 (2012).
Ramaekers, D., Ector, H., Aubert, A. E., Rubens, A. & Van de Werf, F. Heart rate variability and heart rate in healthy volunteers. Is the female autonomic nervous system cardioprotective?. Eur. Heart J. 19, 1334–1341 (1998).
Vasan, R. S., Larson, M. G., Levy, D., Evans, J. C. & Benjamin, E. J. Distribution and categorization of echocardiographic measurements in relation to reference limits. Circulation 96, 1863–1873 (1997).
Weinberg, P. D. & Ross Ethier, C. Twenty-fold difference in hemodynamic wall shear stress between murine and human aortas. J. Biomech. 40, 1594–1598 (2007).
Choi, J., Kim, E., Kim, H. Y., Lee, S. & Kim, S. M. Allometric scaling patterns among the human coronary artery tree, myocardial mass, and coronary artery flow. Physiol. Rep. 8, e14514 (2020).
St Pierre, S. R., Peirlinck, M. & Kuhl, E. Sex matters: A comprehensive comparison of female and male hearts. Front. Physiol. 13, 831179 (2022).
Sen, S. et al. Development and validation of a new adenosine-independent index of stenosis severity from coronary wave-intensity analysis: Results of the ADVISE (ADenosine vasodilator independent stenosis evaluation) Study. J. Am. Coll. Cardiol. 59, 1392–1402 (2012).
Götberg, M. et al. Instantaneous wave-free ratio versus fractional flow reserve to guide PCI. NEJM 376, 1813–1823 (2017).
Baba, K., Shibata, R. & Sibuya, M. Partial correlation and conditional correlation as measures of conditional independence. Aust. New Zealand J. Stat. 46, 657–664 (2004).
Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 18, 91–93 (2018).
Finet, G. et al. Fractal geometry of arterial coronary bifurcations: a quantitative coronary angiography and intravascular ultrasound analysis. EuroIntervention 3, 490–498 (2008).
Ilegbusi, O. J., Hu, Z., Stone, P. H. & Feldman, C. L. Flow Phenomena in the Human Aortic Root and Entrance Region of Coronary Arteries During Diastole 113–114 (American Society of Mechanical Engineers Digital Collection, 2022).
Langhaar, H. L. Steady flow in the transition length of a straight tube. J. Appl. Mech. 9, A55–A58 (1942).
Siasos, G. et al. Local low shear stress and endothelial dysfunction in patients with nonobstructive coronary atherosclerosis. J. Am. Coll. Cardiol. 71, 2092–2102 (2018).
Marano, P., Wei, J. & Merz, C. N. B. Coronary microvascular dysfunction: what clinicians and investigators should know. Curr. Atheroscler. Rep. 25, 435 (2023).
Acknowledgements
We acknowledge the support of NSF ACCESS – project MDE22003 for running high-performance computing experiments.
Author information
Authors and Affiliations
Contributions
A.G. and N.G.G. conceptualized the study and conceived the experimental designs; A.G. conducted computational experiments, analyzed the results, developed the software pipeline to generate geometries and simulations, generated the figures. N.G.G. supervised the study, A.G. and N.G.G. wrote, reviewed and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Garcha, A., Grande Gutiérrez, N. Sensitivity of coronary hemodynamics to vascular structure variations in health and disease. Sci Rep 15, 3325 (2025). https://doi.org/10.1038/s41598-025-85781-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-85781-x