A two-tier optimization strategy for feature selection in robust adversarial attack mitigation on internet of things network security

Abstract

Adversarial attacks were commonly considered in computer vision (CV), but their effect on network security apps rests in the field of open investigation. As IoT, AI, and 5G endure to unite and understand the potential of Industry 4.0, security events and incidents on IoT systems have been enlarged. While IoT networks efficiently deliver intellectual services, the vast amount of data processed and collected in IoT networks also creates severe security concerns. Numerous research works were keen to project intelligent network intrusion detection systems (NIDS) to avert the exploitation of IoT data through smart applications. Deep learning (DL) models are applied to perceive and alleviate numerous security attacks against IoT networks. DL has a considerable reputation in NIDS, owing to its robust ability to identify delicate differences between malicious and normal network activities. While a diversity of models are aimed at influencing DL techniques for security protection, whether these methods are exposed to adversarial examples is unidentified. This study introduces a Two-Tier Optimization Strategy for Robust Adversarial Attack Mitigation in (TTOS-RAAM) model for IoT network security. The major aim of the TTOS-RAAM technique is to recognize the presence of adversarial attack behaviour in the IoT. Primarily, the TTOS-RAAM technique utilizes a min-max scaler to scale the input data into a uniform format. Besides, a hybrid of the coati–grey wolf optimization (CGWO) approach is utilized for optimum feature selection. Moreover, the TTOS-RAAM technique employs the conditional variational autoencoder (CVAE) technique to detect adversarial attacks. Finally, the parameter adjustment of the CVAE model is performed by utilizing an improved chaos African vulture optimization (ICAVO) model. A wide range of experimentation analyses is performed and the outcomes are observed under numerous aspects using the RT-IoT2022 dataset. The performance validation of the TTOS-RAAM technique portrayed a superior accuracy value of 99.91% over existing approaches.

Introduction

As the Internet of Things (IoT) expands and emerges in the following few years, the security threats in IoT will rise. There should be greater rewards for effective IoT breaches and, therefore, better motivation and incentive for attackers to discover unique and innovative methods to deal with IoT techniques¹. Conventional models and strategies for protecting against cyber risks in the standard Internet will agree that it is insufficient in preserving the new security susceptibilities, which will be predictable in the IoT¹. Therefore, security investigators and specialists should be required to estimate prevailing procedures and increase upon them to make more effective security solutions to direct the security vulnerability in the developing IoT. Processing security challenges in some networks include three comprehensive tactics: detection, mitigation, and prevention². Effective security solutions for a network of IoT would require the implementation of each of these three procedures. To manage improving privacy and security companies, current distributed or IoT methods are requisite to prevent and detect network intrusions more intelligently³. As illustrated in Fig. 1, the architecture of an IoT system consists of various layers, including sensors, communication networks, and cloud platforms. Several investigation efforts are keen on developing machine learning (ML) or DL-based techniques for NIDS, to avoid some misuse or deviance in IoT infrastructures and systems⁴.

Fig. 1

Architecture of IoT.

While NIDS is well demoralized in identifying mischievous network events, the significant susceptibilities of recent NIDS are the need for skill to identify unknown network intrusion kinds, owing to the imbalanced or limited intrusion data within the model training method⁵. However, adversarial attacks are a hot investigation subject in CV, and their implementations in wireless communications are only sometimes known. Generally, adversarial attacks are classified into three stages, like gray-, black-, and white-box attacks, depending on how the attacker becomes aware of the learning method⁶. During white-box attacks, the complete model architecture, data of input, labels, and parameters are entirely vulnerable to the attacker. With gray-box attacks, the assailant contains partial data about the training method⁷. By black-box attacks, the assailant recognizes nearly zero near the network, excluding the input data, which provides a more genuine illustration of actual risk setups. As web attacks propagate quickly in diversity and sophistication, investigators of network security are dynamically exploring novel security techniques depending on DL. Whereas standard web attack detection techniques display flaws in environmental big data, increasing DL offers new solutions to safety issues in such environments⁸. DL solutions have assisted in facilitating and advancing the growth of IoT network securities. Nevertheless, ML-based IDS solutions are susceptible after antagonistic hackers exploit and target the model. Adversarial ML approaches aimed to construct improper data classification compelling the applied method⁹. In an adverse environment, predicting the movements an adversary might take toward an applied model is critical. To generate the finest model, an earlier study showed the significance of using adversarial samples in a dataset once training an ML model.

This study introduces a Two-Tier Optimization Strategy for Robust Adversarial Attack Mitigation in (TTOS-RAAM) model for IoT network security. The major aim of the TTOS-RAAM technique is to recognize the presence of adversarial attack behaviour in the IoT. Primarily, the TTOS-RAAM technique utilizes a min-max scaler to scale the input data into a uniform format. Besides, a hybrid of the coati–grey wolf optimization (CGWO) approach is utilized for optimum feature selection. Moreover, the TTOS-RAAM technique employs the conditional variational autoencoder (CVAE) technique for the detection of adversarial attacks. Finally, the parameter adjustment of the CVAE model is performed by utilizing an improved chaos African vulture optimization (ICAVO) model. A wide range of experimentation analyses is performed and the outcomes are observed under numerous aspects using the RT-IoT2022 dataset. The major contribution of the TTOS-RAAM technique is listed below.

• The TTOS-RAAM model utilizes a min-max scaler to normalize the input data, enhancing the effectualness of the preprocessing step. This confirms that features are scaled to a consistent range, improving subsequent approaches’ performance. By standardizing the data, it supports more precise and stable model predictions.

• The TTOS-RAAM method employs the CGWO approach to choosing the most relevant features for attack detection. This methodology improves the model’s capability to detect critical patterns while mitigating computational complexity. Concentrating on optimal features enhances the accuracy and efficiency of adversarial attack detection.

• The TTOS-RAAM approach utilizes the CVAE technique to detect adversarial attacks, enabling the detection of anomalous patterns in network traffic. This improves the model’s resilience to malicious behaviors by distinguishing between normal and suspicious activity. By utilizing CVAE, the model improves its capability to detect subtle, complex attack scenarios.

• The TTOS-RAAM model integrates the ICAVO technique to fine-tune its parameters, optimizing the search process. This methodology improves convergence speed and enhances overall performance. By adjusting parameters effectually, ICAVO assists in attaining a more accurate and efficient model for attack detection.

• The TTOS-RAAM model uniquely incorporates CGWO for feature selection, CVAE for adversarial attack detection, and ICAVO for parameter optimization, forming a hybrid approach that improves accuracy and efficiency in intrusion detection. This approach enables dynamic feature selection, robust anomaly detection, and optimized parameters, with the novelty being the synergy of these techniques to improve precision and adaptability in handling complex IoT network threats.

Related works

Khazane et al.¹⁰ offer a complete analysis of learning regarding the defence mechanisms and adversarial attacks, with a specific concentration on 3 projecting IoT security methods: DISs, IDSs, and MDSs. The study begins by creating a classification of adversarial attacks in the IoT context. Next, several approaches to developing adversarial attacks have been classified and described in a 2D structure. In addition, the author defines current solutions for improving IoT security against adversarial attacks. Han et al.¹¹ present a boundary-generative adversarial network (GAN) depending on the Grid IoT. This advanced method intensely enhances the precision of attack behavior recognition as well as resolves the supervised DL and unsupervised anomaly detection challenges. Rabieinejad et al.³ propose an advanced two-level privacy-preserving structure in this study. This structure cooperatively integrates federated learning (FL) with partly homomorphic encryption, which the author helps across other techniques like differential privacy and completely homomorphic encryption. The predilection for partly homomorphic encryption is based upon its greater balancing between model performance and computation efficiency. Sánchez et al.¹² study the efficiency of hardware behaviour-based distinct device recognition, how it is impacted by feasible context- and DL/ML-focused attacks, and how its strength could be enhanced by using defence methods. It presents a long short-term memory with a convolutional neural network (LSTM-CNN) structure depending on hardware performance for distinct device recognition. Next, the utmost standard DL/ML classification methods are equated by the suggested structure by utilizing a hardware performance dataset gathered from devices operating the same software. Elsisi et al.¹³ present a novel IoT model for the indoor positioning of AGVs by utilizing a deep CNN. The presented technique handles signal handling by changing the RSSI signal into an image. The 1-D RSSI signal is changed into two-dimensional image data to create novel features depending on CWT. Next, the presented DCNN is executed for the indoor positioning method.

Zhao et al.¹⁴ study advanced techniques, especially FL and GAN, to boost intrusion detection abilities. FL, a decentralized ML model, allows distinct network users to perform method training locally, reducing confidentiality risks related to centralized data transfers. But FL tackles data privacy issues, it cascades less in defending against the reconstruction attacks malicious tries to restructure the sensitive data from training models. The author incorporates GAN into the FL structure to address this vulnerability, offering a new technique for IoT anomalous traffic intrusion detection. Scholarvib et al.¹⁵ introduce a complete exploration of various DL structures appropriate for IoT botnet-based attack detection. The research starts with an analysis of present DL methods and their limits in tackling the distinctive challenges modelled by IoT botnet attacks. Afterwards, different DL structures, like GANs, CNNs, and RNNs, are studied extensively. Ma et al.¹⁶ presented a GAN-VS, which decreases the patch area and makes the patch more natural and less noticeable. A visual attention method integrated with GAN is presented to identify the crucial areas of image identification, and only patches are created in the critical areas to decrease patch region and enhance attack efficacy. In any seed patch, an adversarial patch could be made with a higher degree of content and stylistic comparison to the attacked image by style transfer network and GAN. He, Kim, and Asghar¹⁷ review recent literature on NIDS, adversarial attacks, and defences, focusing on DL models in NIDS and adversarial learning, including attack types and defence mechanisms. Nasr, Bahramali, and Houmansadr¹⁸ show that adversarial perturbations can defeat deep neural network (DNN)-based traffic analysis in real-time, without prior knowledge of traffic, while preserving feature integrity. Heidari, Navimipour, and Unal¹⁹ propose a blockchain-based radial basis function neural networks (RBFNN) model to improve data integrity and storage for smart decision-making in IoDs, enabling decentralized predictive analytics and sharing of DL methods. Vakili et al.²⁰ suggest a service composition method using Grey Wolf Optimization (GWO) and MapReduce framework to compose services with optimized QoS.

Rashid et al.²¹ propose a FL methodology for intrusion detection in IoT networks. The model is updated through federated training, optimizing the overall system while maintaining data security. Heidari et al.²² aim to evaluate the availability and reliability of Wireless Sensor Networks (WSNs) under long-term failure scenarios using fault trees and Markov chain analysis. Zhang et al.²³ present a two-stage intrusion detection model by utilizing LightGBM for classification and CNN for fine-grained attack detection. Amiri et al.²⁴ explore the integration of nature-inspired algorithms with IoT in healthcare. Abou El Houda et al.²⁵ propose a privacy-aware FL framework for jamming attack detection, featuring secure aggregation to protect against reverse-engineering attacks. Zanbouri et al.²⁶ propose a blockchain-based IIoT system optimized with the GSO approach to address scalability challenges, improve resource allocation, and reduce inefficiencies. Zhang et al.²⁷ introduce a hierarchical, personalized federated deep reinforcement learning methodology for dynamic spectrum access, utilizing a client-edge-cloud framework to optimize model convergence. Amiri, Heidari, and Navimipour²⁸ present a novel taxonomy of DL applications for climate change mitigation. It classifies methods into six key areas and highlights advanced research to stimulate further exploration of ML solutions for climate change challenges. Alsirhani et al.²⁹ present an intrusion detection strategy for intelligent grids combining DL and feature-based techniques, using the African Vulture Optimization (AVO) model for feature selection and DBN-LSTM for classification to detect normal and attack packets. Nandhini and SVN³⁰ improve network intrusion detection by utilizing Principal Component Analysis (PCA) for dimensionality reduction, Improved Harris Hawks Optimizer (IHHO) for efficient feature selection, and a two-stage classifier combining Support Vector Machine (SVM) and k-Nearest Neighbour (KNN) to improve classification accuracy and reduce false alarm rates. Li et al.³¹ propose a Hybrid DoS Attack Intrusion Detection System (HDA-IDS) that integrates signature-based and anomaly-based detection, introducing the CL-GAN model, which integrates CNN-LSTM with GAN for improved detection of DoS and botnet attacks.

These existing studies review various IoT security models, concentrating on adversarial attacks and defence mechanisms, comprising GANs for attack recognition and FL for privacy preservation. It explores the incorporation of DL, nature-inspired models, and secure aggregation schemes for effectual intrusion detection, botnet attack prevention, and dynamic spectrum access. The research underscores the threats of scalability, computational overhead, and handling imbalanced datasets, as well as the requirement for improved model convergence and real-time performance. Despite significant advancements, there are still concerns regarding these methods’ privacy, security, and real-world applicability. The research gaps identified encompass the lack of standardized evaluation metrics for IoT security methods, limited studies on incorporating nature-inspired algorithms with DL for dynamic and privacy-preserving applications, and challenges in addressing scalability and real-time performance in large-scale IoT environments. Moreover, there is a requirement for more comprehensive solutions that balance model accuracy, computational efficiency, and robustness against adversarial attacks.

Proposed methodology

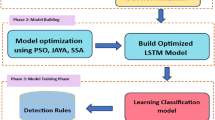
This article presents a TTOS-RAAM model for IoT network security. The technique’s main intention is to recognize adversarial attack behaviour in IoT. The method comprises data preprocessing, hybrid feature selection, CVAE-based attack detection, and an ICAVO-based hyperparameter tunes model to accomplish this. Figure 2 signifies the overall flow of work of the TTOS-RAAM technique.

Fig. 2

Workflow of TTOS-RAAM model.

Data preprocessing

Initially, the TTOS-RAAM technique involves a min-max scaler to scale the input data into a uniform format. Min-Max Scaler is a normalization model generally used to rescale data features to an exact collection, generally [0, 1]. In the context of adversarial attack alleviation in IoT networks, the Min-Max Scaler is vital in normalizing input data, making it harder for adversarial attacks to develop irregular data distributions³². By regularizing the data, the Min-Max Scaler certifies steady input ranges through IoT devices, which can increase the resilience of ML methods besides adversarial perturbations. This scaling method aids in upholding the performance and integrity of IoT networks by decreasing the impact of adversarial inputs.

Hybrid feature selection

Next, a hybrid of the CGWO approach is utilized for the optimum choice of features³³. The two-tier optimization strategy refers to the incorporation of two distinct optimization models that work together to improve the system’s overall performance. The first tier comprises CGWO, which is utilized for optimal feature selection. This model concentrates on detecting the input data’s most relevant features, enhancing subsequent processes’ accuracy and efficiency. The second tier employs ICAVO for parameter adjustment. ICAVO fine-tunes the model’s parameters, confirming optimal performance and faster convergence. These two optimization models operate together to create a robust and adaptive system, with CGWO concentrating on feature selection and ICAVO refining the model’s parameters, making the methodology more efficient and effective in detecting adversarial attacks and enhancing overall performance.

The CGWO approach was chosen for its ability to effectively balance exploration and exploitation during feature selection, which is significant in high-dimensional IoT data. Unlike conventional optimization techniques, CGWO integrates a hybrid strategy that improves search efficiency and the likelihood of finding the most relevant features for attack detection. Its flexible and adaptive nature makes it appropriate for dynamic and complex IoT environments. Moreover, the capability of the CGWO to avoid local minima and converge to global optima confirms optimal feature selection, which improves the overall model accuracy. Compared to other techniques, CGWO presents faster convergence and superior performance in selecting the most informative features, thus enhancing the efficiency of IDSs. Figure 3 illustrates the working flow of the CGWO model.

Fig. 3

Workflow of CGWO model.

This part concentrated on increasing a hybrid model by joining the COA, and GWO featured systems. Grey wolves are capable of recognizing and attacking their target. To improve their abilities, they allow grey wolves to climb trees such as coatis. Hence, grey wolves are stated as coati-wolves within the presented method. These coati-wolves next hit the dropped prey and search for it. This method allows the coati-wolves to travel in various directions within the hunt space, improving the model’s exploration skill during the analytical space. To offer the mathematic technique of the presented COAGWO, the algorithmic population is initiated in the following:

$$\left[ {\begin{array}{*{20}l} {S_{1} } \hfill \\ \vdots \hfill \\ {S_{i} } \hfill \\ \vdots \hfill \\ {S_{N} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {s_{{1,1}} } \hfill & \ldots \hfill & {s_{{1_{{\dot{j}}} }} } \hfill & \ldots \hfill & {s_{{1,m}} } \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} \hfill & \vdots \hfill \\ {s_{{i,1}} } \hfill & \ldots \hfill & {s_{{i_{{\dot{j}}} }} } \hfill & \ldots \hfill & {s_{{i,m}} } \hfill \\ \vdots \hfill & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {s_{{N,1}} } \hfill & \ldots \hfill & {s_{{N_{{\dot{j}}} }} } \hfill & \ldots \hfill & {s_{{N,m}} } \hfill \\ \end{array} } \right]$$

(1)

with

$$\:{s}_{i,j}=L{B}_{j}+r\left(U{B}_{j}-L{B}_{j}\right),\:i=\text{1,2},\dots\:,N,\:j=\text{1,2},\dots\:,m$$

(2)

$\:{S}_{i}$ signifies the $\:jth$ coati-wolf location, $\:{s}_{i,j}$ means the $\:jth$ decision variable value presented by the $\:jth$ coati-wolf, $\:N$ denotes population numbers, $\:m$ characterizes decision variable counts, $\:r\in\:\left[\text{0,1}\right]$ means randomly generated real numbers, and $\:L{B}_{j}$ and $\:U{B}_{j}$ are the lower and upper limits of the $\:j$$\:th$ variable of decision, correspondingly. Here, every coati-wolf is measured as the possible solution, and the function of the objective has been estimated using their values for variable training.

$$F = \left[ {\begin{array}{*{20}l} {F_{l} } \hfill \\ \vdots \hfill \\ {F_{i} } \hfill \\ \vdots \hfill \\ {F_{N} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F\left( {S_{l} } \right)} \hfill \\ \vdots \hfill \\ {F\left( {S_{i} } \right)} \hfill \\ \vdots \hfill \\ {F\left( {S_{N} } \right)} \hfill \\ \end{array} } \right]$$

(3)

whereas $\:F$ stands for a vector which provides a value of the objective function for each coati-wolve, and $\:{F}_{i}$ signifies the value of the objective function towards $\:ith$ coati‐wolf.

Exploration stage 1: In the case of partial coati-wolves climbing the tree whereas the other half notices the prey till it falls, they present a mathematic representation of the behaviour of coati‐wolves as they develop off a tree as below:

$$\:{S}_{i}^{P1}:{s}_{\text{i},\text{j}}^{P1}={s}_{i,j}+r.\left({s}_{p,j}-I.{s}_{i,j}\right)$$

$$\:\text{f}\text{o}\text{r}\:i=\text{1,2},\dots\:,\frac{N}{2}\:\text{a}\text{n}\text{d}\:j=\text{1,2},\dots\:,m.$$

(4)

The victim falls to the field and is located randomly within the hunt zone. Coati-wolves discover the search space out in the field that is pretended using Eqs. (5) and (6):

$$\:{S}_{p}^{G}:{s}_{p.j}^{G}=L{B}_{j}+r.\left(U{B}_{j}-L{B}_{j}\right),j=\text{1,2},\dots\:,m,$$

(5)

$$\:{S}_{i}^{P1}:{s}_{i,j}^{P1}=\left\{\begin{array}{l}{s}_{i,j}+r.\left({s}_{p,j}^{G},-I.{s}_{i,j}\right),\:{F}_{{s}_{p,j}^{G}}<{F}_{i}\\\:{s}_{i,j}+r.\left({s}_{i,j}-{s}_{p,j}^{G}\right),\:else,\end{array}\right.$$

$${\text{for}} i=\frac{N}{2}+1,\frac{N}{2}+2,\ldots\:,N\:and\:j=\text{1,2},\ldots\:,m$$

(6)

In the update procedure, when the objective function demonstrates development, every coati-wolf transfers near the unique position; otherwise, the coati-wolf halts at the present location. This updation state has been presented for every coati-wolf $\:i=\text{1,2},\dots\:,N$ in

$$S_{i} = \left\{ {\begin{array}{*{20}l} {S_{i}^{{P1}} ,} \hfill & {F_{i}^{{Pl}} < F_{i} } \hfill \\ {S_{i} ,} \hfill & {else} \hfill \\ \end{array} } \right.$$

(7)

Here, $\:{S}_{i}^{P1}$ signifies the original place designed for the $\:ith$ co-function, $\:{s}_{i,j}^{P1}$ signifies its $\:jth$ dimension, and $\:{F}_{i}^{P1}$ characterizes the value of the objective function. $\:{S}_{p}^{G}$ signifies the victim’s position within the search space, $\:{s}_{p,j}^{G}$, which stands for its $\:j\:th$ dimension, and $\:{F}_{{s}_{p,j}^{G}}$, which means a value of the objective function. Moreover, $\:I$ exist selected at random from $\:\{1,\:2\}.$

Exploration stage 2:

$$U=\left|\overline{C}{s}_{p,j}-{s}_{i,j}\right|$$

(8)

$$\:{s}_{i,j}={s}_{p,j}-\overline{A}U\:$$

(9)

Now $\:{s}_{i,j}$ signifies the coati-wolf location vector, and $\:{S}_{p}\left(t\right)$ means vector demonstrating the prey’s position,

$${S}_{p}\left(t\right)=\left[{s}_{p,1}\:\cdots\:\:{s}_{p,j}\right]$$

(10)

in that $\:{s}_{p,j}$ stans for its $\:jth$ dimension whereas

$$\overline{A}=2a\times\:{r}_{1}-a\:and\:\overline{C}=2{r}_{2}$$

(11)

Here $\:{r}_{1}\in\:\left[\text{0,1}\right]$ and $\:{r}_{2}\in\:\left[\text{0,1}\right]$ are randomly generated numbers, which is defined as:

$$\:a=2-\frac{2t}{T}$$

(12)

In the process of updation, when the objective function illustrations develop, every coati-wolf travels near a different position; then, the coati-wolf breaks by the existing place. These upgrade conditions are

$$\:{s}_{i,j}^{cw1}={s}_{j}^{\alpha\:}-{A}_{1}^{-}\left|{C}_{1}^{-}{s}_{j}^{\alpha\:}-{s}_{i,j}\right|\:$$

(13)

$$\:{s}_{{i}_{\dot{j}}}^{cw2}={s}_{j}^{\beta\:}-{A}_{2}^{-}\left|{C}_{2}^{-}{s}_{j}^{\beta\:}-{s}_{i,j}\right|\:$$

(14)

$$\:{s}_{\text{i},\text{j}}^{cw3}={s}_{\dot{j}}^{\delta\:}-{A}_{3}^{-}\left|{C}_{3}^{-}{s}_{\dot{j}}^{\delta\:}-{s}_{i,j}\right|\:$$

(15)

Now, the coefficients of $\:\overline{A}$ and $\:\overline{C},$$\:i=\text{1,2},3$, are comparable to $\:\overline{A}$ and $\:\overline{C}$.

Exploitation stage: This exploitation stage examines the finest solutions depending on obtainable data. These involve focusing on the most recognized solution parts and creating additional developments in those fields. This method allows the algorithm to generate more enhancements to the optimization problem. If the prey movement halts, it is struck by the coati-wolves. As can be understood from $\:Reject\mathcal{X}$, the range of values $\:\overline{A},\overline{\:A}$, and $\:\overline{A}$ are $\:[-2a,\:2a]$. If $\:a$ turns into a smaller value, the $\:\overline{A}$th variation decreases. While$\:\:\left|\overline{A}\right|<1$, algorithmic exploitation begins. Eq. $\:\left(16\right)$ terms the exploitation stage of the optimizer difficulty.

$$\:{s}_{i,j}=\frac{{s}_{i,j}^{cw1}+{s}_{i,j}^{cw2}+{s}_{i,j}^{cw3}}{3}\:$$

(16)

The fitness function (FF) considers the classification precision and the select feature counts. It increases the classifier precision and decreases the collection dimension of the chosen features. Hence, the subsequent FF has been applied to estimate individual solutions, as represented in Eq. (17).

$$\:Fitness=\alpha\:*\:ErrorRate+\left(1-\alpha\:\right)*\frac{\#SF}{\#All\_F}\:$$

(17)

Here, $\:ErrorRate$ signifies the classification error rate with the chosen features. $\:ErrorRate$ refers to the computed as the incorrect percentage classified to the number of classifications completed, stated as a value between 0 and 1, $\:\#SF$ is the selected number of features, and $\:\#All\_F$ characterizes the total attribute counts in the new set. $\:\alpha\:$ is applied to control the significance of classification qualities and subset length. In the investigations, $\:\alpha\:$ is the group to 0.9.

CVAE-based attack detection

Furthermore, the TTOS-RAAM approach utilizes the CVAE technique to detect adversarial attacks³⁴. The CVAE method is chosen for adversarial attack detection because it can model intrinsic, high-dimensional data and generate robust representations of normal behaviour. Unlike conventional models, CVAE learns a probabilistic data dispersion, enabling it to distinguish subtle deviations from normal patterns, which is critical for detecting adversarial attacks. By conditioning the autoencoder on specific network conditions, CVAE adapts to diverse attack scenarios, making it more versatile. Additionally, the capacity of the CVAE model to reconstruct normal data allows it to detect anomalies or adversarial modifications effectually. Its robustness to small perturbations and ability to generalize across diverse attack types make it superior to other detection methods, giving improved accuracy and resilience in IoT environments. Figure 4 represents the framework of the CVAE method.

Fig. 4

Structure of the CVAE method.

AE was a neural network approach that learned dense data illustrations like vectors and images while protecting their features. Including an encoder and a decoder, which are related over a latent vector $\:z$, both elements are DNNs with parameters$\:\:\theta\:$ and$\:\:\varphi\:$, correspondingly. The basic idea of an AE is that it has an input and reduces it to a lower-dimension space named “latent vector space.” Then, the decoder recreates data by using latent vectors. Furthermore, it creates novel data by entering randomly created latent vectors. The AE parameter has been learned with backpropagation (BP) so that the loss function $\:L$, termed loss reconstruction, is minimalized. Usually, the loss of reconstruction has been established by MSE by loss of reconstruction.

$$\:{L}_{MSE}=\frac{1}{N}{\sum\:}_{i=1}^{n}({x}_{i}-\widehat{{x}_{i}}{)}^{2},\:$$

(18)

Now, $\:{x}_{j}$ signifies the $\:ith\:$distributed material, and $\:\widehat{{x}_{i}}\:$means the equivalent rebuilt distributed material. An AE is usually applied for tasks, namely compression, noise removal, and data feature extraction. Nevertheless, because of its non-probabilistic nature, the AE latent space is inappropriate for making new material distribution.

The VAE is a probabilistic method that includes a decoder and encoder that can unravel the latent structure of data. Corresponding to AE, the VAE serves the network, which rebuilds from input $\:x$ data over the variable latent $\:z$. Still, when the AE executes a predetermined change, the VAE performs a probabilistic change. VAE accepts that the variables of the latent track are a standard distribution, and the space of latent is made to take a continuous and smooth structure. This work additionally uses a CVAE, which can consider the labels of every distribution. Using CVAE has the potential to wrap the topological framework into a lower-dimension space of latent and make a new material distribution from the unique labels and latent variables $\:z$.

During the CVAE framework, the making process of the latent variable $\:z$ is described as $\:z\sim\:p\left(z\right)=\mathcal{N}(0,I)$, whereas $\:I$ signifies the identity matrix. The making system of an input $\:x$ is expressed in $\:x\sim\:{p}_{\theta\:}\left(x|z,\:c\right)$, using $\:c$ performing as the label. Consequently, a method has been accurately made to instantaneously estimate the truth approximate distribution $\:{q}_{\varphi\:}\left(z|x,\:c\right)$ and posterior distribution $\:{p}_{\theta\:}\left(z|x,\:c\right).$ During the complex learning method of the CVAE, the parameters$\:\:p$ and $\:\theta\:$ are exposed to optimizer with the subsequent Eq., eventually searching to maximize the$\:\:\text{l}\text{o}\text{g}\:$chance of $\:p\left(x\right)$:

$$\text{l}\text{o}\text{g}p(x,\:c)={D}_{KL}\left({q}_{\varphi\:}\right(z|x,\:c)\Vert\:{p}_{\theta\:}\left(z\right|x,\:c\left)\right)+\mathcal{L}\left(\theta\:,\:\varphi\:;x,\:c\right)$$

(19)

Here$\:,\:\varphi\:$ and$\:\:\theta\:$ denote the parameters of the encoder and decoder networks. The primary word signifies the Kull-backLeibler divergence (KLD). This KLD represents a theoretical amount of contiguity among dual density$\:\:q\left(x\right)$, and $\:p\left(x\right)$ is asymmetric, namely, $\:{D}_{KL}\left(q\right|\left|p\right)\ne\:D\left(pq\right)$ and non-negative. This is minimalized if $\:q\left(x\right)=p\left(x\right)$. This KLD is decomposed in such a way

$${\begin{array}{*{20}l} {D}_{KL}({q}_{\varphi\:}\left(z|x,c\right)\left.‖{p}_{\theta\:}\left(z|x,c\right)\right)&={E}_{{q}_{\varphi\:}\left(z|x,c\right)}\left[\text{l}\text{o}\text{g}{q}_{\varphi\:}\left(z|x,c\right)\right]-\text{l}\text{o}\text{g}{p}_{\theta\:}\left(z|x,c\right)\\&={D}_{KL}({q}_{\varphi\:}\left(z\right|x,c)\Vert\:p(z\left)\right)-{E}_{{q}_{\varphi\:}\left(z|x,c\right)}\left[\text{l}\text{o}\text{g}{p}_{\theta\:}\left(x|z,c\right)\right]+\text{l}\text{o}\text{g}\:p\left(x,c\right) \end{array}}$$

(20)

Whereas $\:{q}_{\varphi\:}\left(z\right|x,\:c)$ is similar to the encoder, which understands latent variables with inputs and $\:{p}_{\theta\:}\left(x|z,\:c\right)$ equivalent in a decoder, which creates the shape of a variable of latent. The 2nd term characterizes the lesser limit on the marginal possibility. As of Eqs. (19) and (20), which is said below:

$$\mathcal{L}(\theta\:,\:\varphi\:;x,\:c)=-{D}_{KL}\left({q}_{\varphi\:}\right(z|x,\:c)\Vert\:p\left(z\right))+{E}_{{q}_{\varphi\:}\left(z1x,c\right)}\left[\text{l}\text{o}\text{g}{p}_{\theta\:}\left(x|z,\:c\right)\right]$$

(21)

To maximize the $\:\text{l}\text{o}\text{g}\:$possibility, maximizing$\:\mathcal{\:}\mathcal{L}\left(\theta\:,\:\varphi\:;x,\:c\right)$ is necessary. Besides, the 1st term $\:{D}_{KL}\left({q}_{\varphi\:}\right(z|x,\:c)\Vert\:p\left(z\right))$ of Eq. (8) is calculated in the following:

$$\:{D}_{KL}\left({q}_{\varphi\:}\right(z|x,\:c)\Vert\:p\left(z\right))=-\frac{1}{2}\sum\:\left(1+\text{l}\text{o}\text{g}{\sigma\:}^{2}+{\mu\:}^{2}+{\sigma\:}^{2}\right)$$

(22)

ICAVO-based parameter tuning

At last, the parameter adjustment of the CVAE approach is performed by employing the ICAVO technique³⁵. The ICAVO model is chosen for parameter adjustment of the CVAE approach due to its exceptional capability to fine-tune model parameters using chaotic search mechanisms, improving exploration and preventing premature convergence. Unlike conventinal optimization methods, ICAVO integrates global search capabilities with efficient local refinement, making it ideal for adjusting the complex parameters of CVAE. This outcome improved performance, faster convergence, and more accurate detection of adversarial attacks. ICAVO’s ability to navigate high-dimensional search spaces ensures that optimal parameters are found, resulting in improved model stability and efficiency. ICAVO presents superior robustness and precision in fine-tuning compared to other optimization techniques, making it specifically appropriate for dynamic IoT environments where adaptability and accuracy are critical. Figure 5 demonstrates the architecture of the ICAVO model.

Fig. 5

Steps involved in the ICAVO method.

The AVO is an optimization stimulated by nature and vultures’ searching behaviour. A particular kind of larger bird occurs that must not be sterilized. Nevertheless, they normally prey on injured or sick animals. These animals are known for their remarkable capability and power to reach big heights. These individuals are constantly in motion, flying from one place to another to search for the healthiest nutrition. Moreover, they participate in consistent races with other vultures to eat the found nutrition.

Like all other bio-inspired techniques, the current technique starts using an animal chosen randomly. Therefore, every animal’s strength is determined using a randomly formed quantity in the measured cost value. Following this, the best animals within the clusters are maintained and evaluated. The current process is described in the equation:

$$R = ~\left\{ {\begin{array}{*{20}l} {Best\,vulture\,~1,} \hfill & {if\,p_{i} = m_{1} } \hfill \\ {Best\,vulture~\,2,} \hfill & {if\,p_{i} = m_{2} } \hfill \\ \end{array} } \right.$$

(23)

$${m}_{1}+{m}_{2}=1$$

(24)

Where $\:{m}_{2}$ and $\:{m}_{1}$ are calculated before optimization in an interval of $\:0$ and 1.

The Roulette wheel intends to select the best animals among the clusters.

$${p}_{i}=\frac{{L}_{i}}{{\sum\:}_{j=1}^{m}{L}_{i}}$$

(25)

Now, $\:L\:\text{r}\text{e}\text{p}\text{r}\text{e}\text{s}\text{e}\text{n}\text{t}\text{s}\:$the satisfaction rate of the animals’.

Therefore, the satisfaction rate of the animals’ is reached. These animals go to higher mountains to find nutrition sources. If they don’t have sufficient strength to search, they start a fight on the problem of being with stronger animals to gain nutrition. The current explanation has been considered subsequently:

$$t=z\times\:\left({\text{s}\text{i}\text{n}}^{w}\left(\pi\:\times\:0.5\times\:\frac{ite{r}_{i}}{{\text{m}\text{a}\text{x}}_{iter}}\right)+\text{c}\text{o}\text{s}\left(\pi\:\times\:0.5\times\:\frac{ite{r}_{i}}{{\text{m}\text{a}\text{x}}_{iter}}\right)-1\right)$$

(26)

$$L=\left(2\times\:{\beta\:}_{1}+1\right)\times\:V\times\:\left(1-\frac{ite{r}_{i}}{{\text{m}\text{a}\text{x}}_{iter}}\right)+t$$

(27)

Whereas the current iteration is explained by $\:ite{r}_{i}$, a stochastic quantity, which is in the interval of 1 and $\:0$, is established by $\:{\beta\:}_{1}$, and the continuous amount is represented by $\:w$ that is applied for defining the operation of optimization and determining steps of analysis and operation. The complete iteration counts are stated by $\:{\text{m}\text{a}\text{x}}_{iter}$, and $\:V$ is positioned and selected based on a stochastic way in the range 1 and $\:0$. Besides, a stochastic amount is demonstrated by $\:z$, which is within the range of 2 and $\:-2$. During this case, if $\:V$ attains 0, the animal should be hungry. Alternatively, when $\:V$ intensifies to one, the animal can eat.

Finally, myriad stochastic parts are estimated using two methods to propose the system’s analysis term. The food-searching route is described by the animals based on the following Eqs:

If $\:{P}_{1}\ge\:ran{d}_{{P}_{1}}$:

$$\:P\left(i+1\right)={R}_{i}-D\left(i\right)\times\:L$$

(28)

If $\:{P}_{1}<$ rand:

$$P\left(i+1\right)={R}_{i}-L+{\beta\:}_{2}\times\:\left(\left(ub-lb\right)\times\:{\beta\:}_{3}+lb\right)$$

(29)

Whereas,

$$D\left(i\right)=\left|X\times\:R\left(i\right)-P\left(i\right)\right|$$

(30)

The$\:\:X$ value defines the stochastic difference in the nutrition quantity that the animal would protect from another animal within the group. This protected food is established $\:X=2\times\:\beta\:$, and two stochastic sizes are stated $\:{\beta\:}_{i}\left(i=\text{1,2},3\right)$ that are between 1 and $\:0$. The top animal is pointed out by $\:R$, and the lowest and highest parameter limits are illustrated by $\:lb\:$and $\:up.$

The other word of the current technique is utilized, which is satisfied after $\:\left|H\right|<1$. It contains two potions that have two tactics: siege fighting and rotating. P3 and P2 calculate the current strategies $\:{P}_{3}$ and $\:{P}_{2}$ dual variables within intervals 1 and $\:0$. The main segment of the application initiates after the amount of $\:\left|H\right|$ exists in the interval 1 and 0.5. When $\:\left|H\right|\ge\:1$, it demonstrates that this animal is satisfied.

$$P\left(i+1\right)=D\left(i\right)\times\:\left(L+{\beta\:}_{4}\right)-d\left(t\right)$$

(31)

$$d\left(t\right)={R}_{i}-P\left(i\right)$$

(32)

Where $\:{\beta\:}_{4}$ designates a stochastic amount, which is between $\:0$ and 1.

Moreover, the curved movement of an animal is described in the following Eqs:

$${F}_{1}=R\left(i\right)\times\:\left(\frac{{\beta\:}_{5}\times\:P\left(i\right)\times\:0.5}{\pi\:}\right)\times\:\text{c}\text{o}\text{s}\left(P\left(i\right)\right)$$

(33)

$$\:{F}_{2}=R\left(i\right)\times\:\left(\frac{{\beta\:}_{6}\times\:P\left(i\right)\times\:0.5}{\pi\:}\right)\times\:\text{s}\text{i}\text{n}\left(P\left(i\right)\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(34)

$$P\left(i+1\right)={R}_{i}-\left({F}_{1}+{F}_{2}\right)$$

(35)

Now, dual numbers of stochastic, which are in the ranges 1 and $\:0$, are represented by $\:{\beta\:}_{6}$ and $\:{\beta\:}_{5}.$ When $\:\left|H\right|$ is equal or bigger to 0.5, the vulture movement invites different individuals to the food source when the amount of $\:\left|H\right|$ is lower than 0.5. Besides, blockade and antagonistic battles are applied to discover the nutrition. Firstly, a dimension depending on stochastic selection is explained by $\:{\beta\:}_{{P}_{3}}$ between 1 and 0. After $\:{\beta\:}_{{P}_{3}}\ge\:{P}_{3}$, myriad animals contest to gain food. Formerly, $\:{\beta\:}_{{P}_{3}}<{P}_{3}$, the robust siege-battle method is used. Then, the animals get hungry, which makes a struggle between all the animals to get food. It is depicted in the subsequent Eqs.

$${A}_{1}=BestVultur{e}_{1}\left(i\right)-\frac{BestVultur{e}_{1}\left(i\right)\times\:P\left(i\right)}{BestVultur{e}_{1}\left(i\right)-P(i{)}^{2}}\times\:L$$

(36)

$${A}_{2}=BestVultur{e}_{2}\left(i\right)-\frac{BestVultur{e}_{2}\left(i\right)\times\:P\left(i\right)}{BestVultur{e}_{2}\left(i\right)-P(i{)}^{2}}\times\:L$$

(37)

where the best incredible animals inside the dual clusters are established by $\:BestVulture\left(i\right)$ and $\:BestVulture\left(i\right)$. Furthermore, the present vector’s position of the animal is shown by $\:P\left(i\right)$:

$$P\left(i+1\right)=\frac{{A}_{1}+{A}_{2}}{2}$$

(38)

After $\:\left|L\right|<0.5$, prior stronger animals drop their power and get their skill that neighbourhood of another animal. Simultaneously, every animal wings in various directions to gain nutrition.

$$P\left(i+1\right)=R\left(i\right)-\left|d\left(t\right)\right|\times\:L\times\:LF\left(d\right)$$

(39)

Here, the Levy fight is specified by $\:LF$ that the following Eqs may measure.:

$$LF\left(x\right)=\frac{u\times\:\sigma\:}{100\times\:|v{|}^{2}}$$

(40)

$$\sigma\:={\left(\frac{r\left(1+\beta\:\right)\times\:\text{sin}\left(\frac{\pi\:\beta\:}{2}\right)}{r\left(1+{\beta\:}_{2}\right)\times\:\beta\:\times\:2\left(\frac{\beta\:-1}{2}\right)}\right)}^{\frac{1}{\beta\:}}$$

(41)

Now, a fixed amount is indicated by $\:\beta\:$; also, stochastic numbers are reported by $\:v$ and $\:u$ that are between 1 and $\:0.$

The principal phase involves the transmission of the chaos map method, which uses unpredictable, chaotic parameters instead of stochastic parameters. Chaos series, discovered to be present within dynamic and non-linear processes, are non‐convergent, bounded, and non‐periodic. By incorporating chaotic variables inside metaheuristic techniques, the hunt space may be proficiently noticed due to the turbulence series’ active environment. In short, using the chaotic parameters inside the chaos map improves the hunt space findings in the method, allowing quick and more effectual findings.

Optimizer techniques can use different chaos maps to make various series by improving the initial positions. The present analysis utilizes a sinusoidal chaotic mapping operation to increase the AVO model’s convergence rate. It attains this to balance the exploration and exploitation stages that permit the solution space that evaluated more proficiently and avoid local targets. Replacing the previous $\:r$ randomly generated value with values at random from the Chaos operation is how chaos mapping is applied within the AVO technique. The AVO method includes the sinusoidal chaotic mapping operation to search the solution space, increasing its performance to avoid local targets. The statistical sinusoidal mapping formulation is used to study the $\:{\beta\:}_{i}$. Using this equation, outcomes in the subsequent formulations:

$$\beta_{i}^{{t + 1}} = \gamma \times (\beta_{i}^{t} )^{2} {\text{sin}}\left( {\pi \beta_{i}^{t} } \right)$$

(42)

The randomly generated amount made in the current iteration has been described by $\:{\beta\:}_{i}^{t}$. A changeable variable $\:\gamma\:$ equivalents 2.3. The variable $\:{\beta\:}_{i}^{0}$ is obtained by errors and trials and equivalents 0.5.

This model experiences any variation that is based on the OBL process. The process of OBL has been computed using a device that instructs $\:bio$-inspired procedures for alteration. It creates different positions for candidate’s explanations for particular tasks. This novel location for individuals might result in promising results for cost value. It is critical to current improved explanations, rapidly estimate a candidate explanation, and join clear, varied explanations to choose the finest explanation as a possible individual for upcoming. The explanation for a candidate, $\:{y}_{i}$, the several explanations $\:\left({Y}_{i}^{{\prime\:}}\right)$ have been considered in the following Eq:

$$\:{Y}_{i}^{{\prime\:}}=a+b-{Y}_{i\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}$$

$${Y}_{i}=\in\:\left[\underset{\_}{y},\overline{y}\right]$$

(43)

$\:y$ and $\:\underset{\_}{y}$ denote the explanation space’s maximum and minimum limit, respectively.

The ICAVO model progresses an FF to obtain superior classification performance. It controls a positive integer to indicate the improved performance of the candidate solutions. This work calculates the classifier error value minimization for FF, as specified in Eq. (44).

$$\:fitness\left({x}_{i}\right)=ClassifierErrorRate\left({x}_{i}\right)=\frac{No.\:of\:misclassified\:instances}{Total\:no.\:of\:instances}\times\:100$$

(44)

Result analysis

The performance assessment of the TTOS-RAAM model is examined using the RT-IoT2022 dataset³⁶. The RT-IoT2022 dataset is a comprehensive resource that captures normal and adversarial network behaviours in real-time IoT environments. It integrates data from IoT devices (e.g., ThingSpeak-LED, Wipro-Bulb, MQTT-Temp) and simulated attack scenarios (e.g., Brute-Force SSH, DDoS attacks, Nmap patterns). The dataset comprises bidirectional network traffic monitored utilizing Zeek and Flowmeter, giving valuable insights for advancing Intrusion Detection Systems (IDS) for IoT networks. The total feature count is 84, and the chosen features are 47. The dataset involves 123,052 samples with ten classes, as depicted in Table 1. The suggested technique is simulated using the Python 3.6.5 tool on PC i5-8600k, 250GB SSD, GeForce 1050Ti 4GB, 16GB RAM, and 1 TB HDD. The parameter settings are provided: learning rate: 0.01, activation: ReLU, epoch count: 50, dropout: 0.5, and batch size: 5.

Table 1 Details of dataset.

Figure 6 determines the confusion matrices created by the TTOS-RAAM model below 80:20 and 70:30 of TRAP/TESP. These results detect that the TTOS-RAAM technique accurately recognizes all 10 class labels.

Fig. 6

Confusion matrices of (a-c) 80%TRAP and 70%TRAP and (b-d) 20%TESP and 30%TESP.

Table 2; Fig. 7 illustrate the attack detection results of the TTOS-RAAM model under 80%TRAP and 20%TESP. The outcomes stated that the TTOS-RAAM model correctly differentiated normal and attack samples. On 80%TRAP, the TTOS-RAAM method provides an average $\:acc{u}_{y}$ of 99.88%, $\:sen{s}_{y}$ of 98.80%, $\:spe{c}_{y}$ of 99.88%, $\:{F}_{score}\:$of 97.80%, and $\:AU{C}_{score}$ of 99.34%. Additionally, on 20%TESP, the TTOS-RAAM approach gains an average $\:acc{u}_{y}$ of 99.91%, $\:sen{s}_{y}$ of 98.74%, $\:spe{c}_{y}$ of 99.90%, $\:{F}_{score}$ of 98.11%, and $\:AU{C}_{score}$ of 99.32%.

Table 2 Attack detection outcome of TTOS-RAAM model under 80%TRAP and 20%TESP.

Fig. 7

Average of TTOS-RAAM technique under 80%TRAP and 20%TESP.

Figure 8 represents the training and validation accuracy results of the TTOS-RAAM approach on 20%TESP and 80%TRAP. The accuracy outcomes are calculated for 0–25 epochs. This figure underlines that the training and validation accuracy results have an increasing tendency, which describes the ability of the TTOS-RAAM model to perform superiorly across different iterations. Additionally, the training and validation accuracy stay nearer across the epochs, which points out lower minimum overfitting and displays the higher performance of the TTOS-RAAM process, guaranteeing continuous prediction on unseen instances.

Fig. 8

$\:Acc{u}_{y}$ curve of TTOS-RAAM model at 80%TRAP and 20%TESP

In Fig. 9, the training loss and validation loss graph of the TTOS-RAAM technique on 20%TESP and 80%TRAP have been indicated. The loss values are calculated for 0–25 epochs. The training and validation accurateness values show a reducing tendency, describing the capacity of the TTOS-RAAM technique in balancing a trade-off between generalization and data fitting. The constant decline in loss rates also assures a better outcome of the TTOS-RAAM methodology and tuning of the predictive results on time.

Fig. 9

Loss curve of TTOS-RAAM methodology at 80%TRAP and 20%TESP.

In Fig. 10, the PR investigation study of the TTOS-RAAM model under 80%TRAP and 20%TESP analyses its values by plotting Precision against Recall for each class label. The figure demonstrates that the TTOS-RAAM model consistently obtains increased PR values over several classes, pointing out its capability to keep an essential part of true positive predictions between every positive prediction (precision) but also taking a greater portion of actual positives (recall). The gradual increase in PR results between all class labels represents the efficiency of the TTOS-RAAM technique in the classification process.

Fig. 10

PR curve of TTOS-RAAM model at 80%TRAP and 20%TESP.

In Fig. 11, the ROC investigation of the TTOS-RAAM methodology under 80%TRAP and 20%TESP has been examined. The outcomes indicated that the TTOS-RAAM model attains better ROC results across each class, depicting important proficiency in selecting class labels. This rising tendency to increase ROC values over numerous class labels indicates the efficient performance of the TTOS-RAAM methods in predicting class labels, underlining the strong nature of the classification process.

Fig. 11

ROC curve of TTOS-RAAM model at 80%TRAP and 20%TESP.

Table 3; Fig. 12 portray the attack detection results of the TTOS-RAAM methodology under 70%TRAP and 30%TESP. The outcomes showed that the TTOS-RAAM approach correctly differentiated normal and attack samples. On 70%TRAP, the TTOS-RAAM methodology provides an average $\:acc{u}_{y}$ of 99.83%, $\:sen{s}_{y}$ of 97.03%, $\:spe{c}_{y}$ of 99.87%, $\:{F}_{score}\:$of 96.10%, and $\:AU{C}_{score}$ of 98.45%. Besides, on 30%TESP, the TTOS-RAAM approach gives an average $\:acc{u}_{y}$ of 99.84%, $\:sen{s}_{y}$ of 97.08%, $\:spe{c}_{y}$ of 99.88%, $\:{F}_{score}$ of 96.09%, and $\:AU{C}_{score}$ of 98.48%.

Table 3 Attack detection outcome of TTOS-RAAM model under 70%TRAP and 30%TESP.

Fig. 12

Average of TTOS-RAAM approach at 70%TRAP and 30%TESP.

In Fig. 13, the training and validation accuracy results of the TTOS-RAAM model on 30%TESP and 70%TRAP are stated. The accuracy performance is calculated for 0–25 number of epochs. The figure points out that the training and validation accuracy results demonstrate an increasing trend that reports the ability of the TTOS-RAAM model to improve performance over different iterations. Besides, the training and validation accuracy stay nearer across the number of epochs, demonstrating lesser minimum overfitting and showing the TTOS-RAAM technique’s greater performance, ensuring continual prediction on unseen instances.

Fig. 13

$\:Acc{u}_{y}$ curve of TTOS-RAAM model at 0%TRAP and 30%TESP

Figure 14 describes the training loss and validation loss graph of the TTOS-RAAM method on 70%TRAP and 30%TESP. The loss outcomes are calculated through 0–25 epochs. It is signified that the training and validation $\:acc{u}_{y}$ results indicate a lesser tendency, informing the TTOS-RAAM methodology’s capacity to balance a trade-off between data fitting and generalization. The steady decline in loss values ensures better performance of the TTOS-RAAM methodology and the ability to tune the predictive outcomes on time.

Fig. 14

Loss curve of TTOS-RAAM technique under 70%TRAP and 30%TESP.

In Fig. 15, the PR examination study of the TTOS-RAAM model in terms of 70%TRAP and 30%TESP provides an interpretation of its outcomes by plotting Precision against Recall for all the class labels. This figure illustrates that the TTOS-RAAM method continually gains better PR values over several classes. It shows its capability to preserve an important proportion of true positive predictions between every positive prediction (precision) while taking a bigger portion of actual positives (recall). The consistent growth in PR products between all class labels represents the efficiency of the TTOS-RAAM method in the classification process.

Fig. 15

PR curve of TTOS-RAAM method at 70%TRAP and 30%TESP.

Figure 16 shows the ROC examination of the TTOS-RAAM method under 70%TRAP and 30%TESP. The outcomes demonstrated that the TTOS-RAAM technique obtains greater ROC results over every class, representing the important skill of differentiating the class labels. This rising tendency of better ROC values across different classes indicates the efficient performance of the TTOS-RAAM methodology in predicting class labels, emphasizing the strong nature of the classification process.

Fig. 16

ROC curve of TTOS-RAAM method under 70%TRAP and 30%TESP.

The relative study of the TTOS-RAAM technique with recent approaches is represented in Table 4^37,38,39.

Figure 17 establishes the comparison results of the TTOS-RAAM technique in terms of $\:acc{u}_{y}$ and $\:{F}_{score}$ with existing methods. According to $\:acc{u}_{y}$, the TTOS-RAAM model has a greater $\:acc{u}_{y}$ of 99.91% whereas the modified Birectional LSTM (Modified Bi-LSTM), LSTM, Gated Recurrent Unit (GRU), DNN, Bi-LSTM, Multi-Layer Perceptron (MLP), DIS-IoT, CNN, SVM, and XGBoost methodologies have lower $\:acc{u}_{y}$ of 98.36%, 98.80%, 98.98%, 99.20%, 99.37%, 99.40%, 99.70%, 95.07%, 96.68%, and 98.25%, correspondingly. According to $\:{F}_{score}$, the TTOS-RAAM model has a greater $\:{F}_{score}$ of 98.11% whereas the Modified Bi-LSTM, LSTM, GRU, DNN, Bi-LSTM, MLP, DIS-IoT, CNN, SVM, and XGBoost methodologies have least $\:{F}_{score}$ of 96.94%, 94.73%, 94.56%, 96.24%, 94.85%, 96.69%, 97.61%, 95.14%, 96.67%, and 98.37%, respectively.

Table 4 Comparative analysis of TTOS-RAAM approach with recent models.

Fig. 17

$\:Acc{u}_{y}$ and $\:{F}_{score}$ of TTOS-RAAM approach with recent models

Figure 18 establishes the comparison results of the TTOS-RAAM technique in terms of $\:sen{s}_{y}$ and $\:spe{c}_{y}$ with existing methods. According to $\:sen{s}_{y}$, the TTOS-RAAM model has a greater $\:sen{s}_{y}$ of 98.74%; however, the Modified Bi-LSTM, LSTM, GRU, DNN, Bi-LSTM, MLP, DIS-IoT, CNN, SVM, and XGBoost methodologies have lower $\:sen{s}_{y}$ of 94.84%, 95.45%, 95.65%, 98.00%, 94.90%, 94.39%, 95.84%, 93.09%, 94.66%, and 96.41%, correspondingly. Depending on $\:spe{c}_{y}$, the TTOS-RAAM technique has a greater $\:spe{c}_{y}$ of 99.90%. In contrast, the modified Modified Bi-LSTM, LSTM, GRU, DNN, Bi-LSTM, MLP, DIS-IoT, CNN, SVM, and XGBoost methods have a minimum $\:spe{c}_{y}$ of 98.68%, 98.87%, 99.30%, 99.20%, 99.63%, 99.40%, 99.70%, 93.56%, 95.29%, and 96.99%, correspondingly.

Fig. 18

$\:Sen{s}_{y}$ and $\:Spe{c}_{y}$ of TTOS-RAAM approach with recent approaches

Table 5; Fig. 19 demonstrates the ablation study of the TTOS-RAAM model. In the ablation study, several classifiers were evaluated based on their performance metrics, including $\:acc{u}_{y}$, $\:sen{s}_{y}$, $\:spe{c}_{y}$, and $\:{F}_{score}$. The Modified Bi-LSTM model attained the highest performance with an $\:acc{u}_{y}$ of 98.36%, $\:sen{s}_{y}$ of 94.84%, $\:spe{c}_{y}$ of 98.68%, and $\:{F}_{score}$ of 96.94%. The CGWO model achieved slightly improved values with an $\:acc{u}_{y}$ of 97.79%, $\:sen{s}_{y}$ of 94.16%, $\:spe{c}_{y}$ of 98.11%, and $\:{F}_{score}$ of 96.42%. The ICAVO-CVAE model demonstrated a slightly lower achievement with an $\:acc{u}_{y}$ of 97.06%, $\:sen{s}_{y}$ of 93.47%, $\:spe{c}_{y}$ of 97.38%, and $\:{F}_{score}$ of 95.89%, while the CVAE model exhibited the lowest performance, achieving an $\:acc{u}_{y}$ of 96.52%, $\:sen{s}_{y}$ of 92.74%, $\:spe{c}_{y}$o f 96.87%, and $\:{F}_{score}$ of 95.35%.

Table 5 Result analysis of the ablation study of the TTOS-RAAM approach.

Fig. 19

Result analysis of the ablation study of the TTOS-RAAM approach.

Conclusion

This work introduces a new TTOS-RAAM approach for IoT network security. The primary objective of the TTOS-RAAM approach is to recognize the presence of adversarial attack behaviour in the IoT. At first, the TTOS-RAAM technique involves a min-max scaler to scale the input data into a uniform format. Moreover, a hybrid of the CGWO approach is exploited to achieve the optimum choice of features. Furthermore, the TTOS-RAAM technique uses the CVAE technique to detect adversarial attacks. Finally, the parameter adjustment of the CVAE method was executed using the ICAVO method. A wide range of experimentation analyses is performed, and the outcomes are observed under numerous aspects using the RT-IoT2022 dataset. The performance validation of the TTOS-RAAM technique portrayed a superior accuracy value of 99.91% over existing approaches. The limitations of the TTOS-RAAM technique comprise the reliance on specific datasets that may not represent the full diversity of real-world IoT environments, potentially limiting the generalizability of the findings. Furthermore, the models evaluated in the study may need help handling real-time data and large-scale network traffic, where performance might degrade under high-volume conditions. The study also needs to address the challenge of model interpretability, critical in deploying IoT security systems in practical applications. Moreover, while adversarial attacks are considered, more advanced or growing attack strategies must be fully explored. Future works should develop more scalable and adaptable models operating in dynamic IoT environments. Additionally, improving model transparency and addressing the trade-offs between accuracy and computational efficiency will be critical to real-world deployment. Exploring hybrid security solutions that integrate multiple defence mechanisms could also enhance resilience against evolving threats. Furthermore, incorporating real-time data processing and decision-making capabilities will be crucial for timely responses in fast-paced environments. Lastly, confirming the robustness of models against adversarial attacks and data anomalies will be significant to maintaining reliability and security in diverse applications.