Introduction

The practice of layered waterflooding represents a significant means of supplementing formation energy, addressing interlayer contradictions, and enhancing oil recovery1,2. Conventional mechanical layered waterflooding techniques include bridge eccentricity and bridge concentricity, which can are capable of meeting the requirements of different periods in the waterflooding development process3. However, with the expansion and deepening of oilfield development, certain limitations of conventional layered waterflooding technology have become evident. These include complex processes, high labor intensity, and the inability to measure and adjust special wells (such as casing deformation wells, edge wells, and high angle wells). This has resulted in the inability to maintain a high water injection qualification rate in the long term. The conventional approach to developing these special wells has been through the use of the generalized waterflooding or chemical profile control methods. However, the long-term application of the generalized waterflooding method has leaded to water rushing along the high permeability layer4,5,6, as shown in Fig. 1, which resulting in wasted resources, increased operational costs, and diminished efficiency. Furthermore, the chemical profile control method has also faced high costs, environmental pollution, and even irreversible reservoirs damage7,8. Therefore, the fine profile control of special waterflooding wells represents a significant challenge affecting the fine development of oil fields.

Fig. 1
figure 1

Waterflooding advantage pathway in special well development.

Full size image

The inability to perform effective packer operations precludes the implementation of the mechanical layered waterflooding process in such special waterflooding wells, as shown in Fig. 2, and the ball-pitching plugging-selection profile control technology represents an effective and low-cost means of adjusting the profile of waterflooding wells, which mainly uses polymer balls to plug the perforation9,10,11. The operation process entails the injection of a specific quantity, density, and diameter of plugging-selection balls into the target layer, accompanied by waterflooding. The balls are capable of opting the perforations with high capacity for water absorption, thereby facilitating the plugging process. The plugging ball maintains a stable plugging effect on the perforation due to the waterflooding pressure difference, thereby reducing the effective flow area and enhancing the water absorption capacity of the medium and low permeability formation. This ultimately achieves the objective of adjusting the water absorption profile. The objective is to achieve the effect of fine profile control, which has broad application prospects in the fields of special well waterflooding, horizontal well fracturing and selective acidification of polluted reservoirs12,13,14,15. The ball-pitching plugging-selection profile control process is primarily concerned with wellhead ball-pitching, downhole plugging, and well-washing recovery. The wellhead ball-pitching refers to describe the process of pitching these plugging-selection balls into the operating string at the wellhead position. The downhole plugging refers to the perforations plugging with strong water absorption capacity by using plugging-selection balls. The well-washing recovery refers to describe the recycling and reuse process of plugging-selection balls with backwashing method, which is particularly pertinent given the dynamic variability of well conditions. Once the well-washing recovery has been completed, other waterflooding technologies may also be conducted.

Fig. 2
figure 2

The ball-pitching plugging-selection profile control technology.

Full size image

In recent years, numerous scholars from domestic and international research institutions have conducted extensive research and exploration in this field. Nozaki et al. proposed the polyacrylamide (PAM) balls for plugging the high water-bearing layers, while the plugging mechanism of hydrolyzed-polypropylene-phthalamide (HPAM) balls was researched from adsorption theory, dynamic trapping theory, and physical blocking theory11,16,17,18. For research on the migration and plugging law of plugging-selection balls, Li et al. carried out the theoretical and experimental research on the ball-pitching plugging-selection profile control technology in waterflooding wells, and analyzed the change in plugging trajectory of a single plugging ball19; Tao et al. developed a visual simulation device for plugging balls with near water density, with the aim of studying plugging efficiency under different working conditions20. For research on the horizontal fracturing field of temporarily plugging, the efficiency and migration law of plugging balls were researched in fracturing stimulation21; The movement law and plugging effect of temporary plugging balls were investigated in staged fracturing22,23. The findings of these research have significant implications for analyzing the fine profile control mechanism of waterflooding well throwing and plugging selection.

The majority of current research is concentrated on the experiment devices and data analysis of hydraulic fracturing of horizontal wells, with relatively limited investigation into the migration law and plugging effect of special waterflooding wells. The contribution of this paper is to present a novel analysis of the migration law of profile control balls in special waterflooding wells, with a particular focus on the exploration of plugging efficiency under different operating parameters. The migration law of profile control balls in the process of pitching and plugging is influenced by various factors, including the physical properties of the profile control balls (such as, density and size), and injection conditions (such as, flow rate and viscosity). The objective of this article is to utilize a combination of theoretical analysis (the coupling method of CFD (Computational Fluid Dynamics) and DEM (Discrete Element Method)) and experiment (indoor experiments and downhole applications) methods to investigate the migration law and plugging efficiency of plugging-selection balls. This will enable an analysis of the position, velocity, and sealing effect of plugging-selection balls during waterflooding are analyzed, as well as an exploration of the influence of ball density, ball number, ball diameter, waterflooding flow rate and fluid viscosity on the plugging efficiency is explored, which has theoretical and guiding significance for the optimization design of the process parameters for fine profile control process of layered waterflooding wells.

Numerical simulation and analysis

The ball-pitching plugging-selection process occurring within the wellbore encompass a range of motion phenomena, including fluid motion, particles motion, and fluid–solid coupling motion processes. For CFD (Computational Fluid Dynamics) and DEM (Discrete Element Method) coupled method, the control equations are employed to describe the behavior of the water phase and the plugging-selection ball separately. The CFD-DEM coupling method was employed to construct a numerical model, which was then used to elucidate the migration law and plugging effect of plugging-selection balls within the wellbore.

CFD-DEM coupled method

Fluid phase (CFD) control equations

The control equations for the fluid phase are typically as follows:

(1) Continuity equation: which is used to describe the principle of conservation of mass, and the continuity equation is expressed as:

$$\frac{{\partial \rho_{w} }}{\partial t} + \nabla \cdot (\rho_{w} {\mathbf{u}}_{{\mathbf{w}}} ) = 0$$
(1)

where, \(\rho_{w}\) is the fluid density; \(t\) is time; \({\mathbf{u}}_{w}\) is the fluid velocity vector, and \(\nabla\) is the gradient operator.

(2) Momentum equation: known as the Navier–Stokes equation, which is used to describe the variation in fluid momentum over time and the momentum transport due to pressure gradients and viscous stresses. The momentum equation is expressed as:

$$\frac{{\partial (\rho_{w} {\mathbf{u}}_{{\mathbf{w}}} )}}{\partial t} + \nabla \cdot (\rho_{w} {\mathbf{u}}_{{\mathbf{w}}} \times {\mathbf{u}}_{{\mathbf{w}}} ) = - \nabla P + \nabla \cdot \tau + {\mathbf{f}}$$
(2)

where, \(P\) is the pressure; \(\tau\) is the viscous stress tensor, and \({\mathbf{f}}\) represents volume forces (such as gravity).

(3) Energy equation: which is used to describe the variation in the internal energy of the fluid, including heat conduction, convection, and radiation. The energy equation is expressed as:

$$\frac{{\partial (\rho_{w} E)}}{\partial t} + \nabla \cdot [{\mathbf{u}}_{{\mathbf{w}}} (\rho_{w} E + P)] = \nabla \cdot (k\nabla T - \sum {h_{j} J_{j} } + \tau \cdot {\mathbf{u}}_{{\mathbf{w}}} ) + {\mathbf{u}}_{{\mathbf{w}}} \cdot {\mathbf{f}}$$
(3)

where, \(E\) is the total energy per unit mass of the fluid (including internal and kinetic energy), \(k\) is the thermal conductivity, \(T\) is the temperature, \(h_{j}\) and \(J_{j}\) are the enthalpy and diffusion flux.

Particle phase (DEM) equations

The DEM equations are primarily based on Newton’s second law and Euler’s second law, which are used to describe the mechanical behavior of plugging-selection balls24, including:

(1) Translational motion: which is used to describe the relationship between the acceleration and the amount external force of plugging-selection ball. In the case of the single ball, the equation is expressed as:

$$m_{i} \frac{{d{\mathbf{v}}_{i} }}{dt} = {\mathbf{F}}_{i} = F_{G} + F_{P} + F_{D} + F_{S} + F_{R}$$
(4)

where, \(m_{i}\) is the ball mass, \({\mathbf{v}}_{i}\) is the ball velocity, and \({\mathbf{F}}_{i}\) is the amount external force acting on the ball; \(F_{G}\) and \(F_{P}\) are the gravity and pressure gradient force of plugging-selection ball; \(F_{D}\), \(F_{S}\) and \(F_{R}\) are the drag force, shear force and rotating lift during migration process of plugging-selection ball in waterflooding.

(2) Rotational motion: which is used to describe the relationship between the angular acceleration and the amount external torque of plugging-selection ball. In the case of the single ball, it is expressed as:

$${\mathbf{I}}_{i} \frac{{d\omega_{i} }}{dt} = {\mathbf{M}}_{i}$$
(5)

where, \({\mathbf{I}}_{i}\) is the moment of inertia, \(\omega_{i}\) is the angular velocity, and \({\mathbf{M}}_{i}\) is the amount external torque.

CFD-DEM coupling analysis

For the CFD-DEM coupling method, the forces (e.g., drag force, pressure gradient force, shear force, and rotating lift) exerted by the waterflooding phase were incorporated into the DEM model, and the plugging-selection ball phase was accounted for through boundary conditions and source terms (e.g., particle obstruction, and momentum exchange) in the CFD model. This approach enables the coupling simulations to more accurately describe the complex behavior of particle–fluid two-phase flows.

The coupling of fluid and ball particles is described by the coupling method of DEM and CFD, in which the plugging ball adopts the H-M contact model25,26. The normal force and tangential force in the process of plugging selection are as follows:

$${\text{the}}\;{\text{normal}}\;{\text{force:}}\;F_{n} = \frac{4}{3}E^{ * } \sqrt {R^{ * } } \delta_{n}^{3/2}$$
(6a)
$${\text{the}}\;{\text{tangential}}\;{\text{force:}}\;F_{t} = - S_{t} \delta_{t}$$
(6b)

where, \(F_{n}\) is the normal force; \(F_{t}\) is the tangential force; \(E^{ * }\) is the Young’s modulus of plugging-selection ball; \(R^{ * }\) is the radius of plugging-selection ball; \(\delta_{n}^{{}}\) is the tangential overlap.

Numerical model

Prior to establishing the numerical model, it is essential to make reasonable assumptions based on actual working conditions: the distance from the sealing ball to the target layer is relatively short, therefore the compressibility of the fluid is not considered; both waterflooding and balls reach the target layer through the operation string, therefore the influence of casing deformation is not considered; the potential for perforation deformation caused by long-term operations is not considered due to the unpredictability of such occurrences; the heat transfer phenomenon between the fluid and the ball is ignored due to the small change in thermal density of the ball. The simplified physical model was constructed for the purpose of fine profile control process of layered waterflooding well, as illustrated in Fig. 3. The model incorporates horn mouth, casing, and perforation, and comprises three equally-spaced waterflooding layers, with the total depth of 5 m. Each waterflooding layer comprises six spiral-distributed perforations, with the perforation diameters of 8 mm. The inner diameter of the casing is 120 mm, while the inner diameter of the trumpet mouth outlet is 70 mm.

Fig. 3
figure 3

The technology and physical model of ball-pitching plugging-selection profile control.

Full size image

The case study was conducted with a spiral distributed single-layer waterflooding layer (including six perforations), and the physical model was meshed with the tetrahedral unstructured method, as illustrated in Fig. 4, with the near-perforations area being encrypted. The boundary conditions are as follows: the inlet boundary is defined as the mass-flow inlet, the outlet boundary is defined as the pressure outlet, and the wall boundary is defined as standard non-slip.

Fig. 4
figure 4

Mesh division and boundary conditions.

Full size image

In numerical simulation, the flow field was divided into several grid elements, and the velocity field and pressure fields associated with the waterflooding phase were solved with the CFD method. Meanwhile, the plugging-selection ball phase was discretized into several calculation units, and the movement trajectory of balls was simulated with the DEM method. The relevant parameters pertaining to the casing, perforation, water, and plugging-selection ball were presented in Table 1.

Table 1 The model parameter settings.
Full size table

In light of the complexity and efficiency of large-scale calculations, a parallel algorithm had been implemented with the objective of accelerating the calculation process. The trajectory of plugging-selection ball and the velocity–pressure fields of the waterflooding were calculated in parallel, thereby enhancing the calculation efficiency. The parameter range of plugging-selection ball during the simulation process was shown in Table 2.

Table 2 The parameter range of plugging-selection ball.
Full size table

Migration law and plugging effect analysis

Based on the established models and analysis methods, the ball-pitching plugging-selection process was dynamically simulated to investigate the migration law and plugging effect of plugging-selection balls in wellbore.

Flow field analysis

For the layered profile control of a special waterflooding well, the flow field analysis of single layer was conducted to study the velocity distribution nephogram of flow field inside the wellbore under different water absorption abilities of perforations, as shown in Fig. 5. In the case of waterflooding well with balanced water absorption capacity, the velocity in the upper layer was higher than in the bottom layer; In the case of waterflooding well with water absorption capacity of upper-strong and lower-weak, the diversion effect was concentrated in the upper-section; Conversely, in the case of waterflooding well with water absorption capacity of upper-weak and lower-strong, the diversion effect was primarily observed in the lower-layer. The findings indicated that the diversion effect was primarily observed in the layers with strong water absorption capacity, resulting in high flow velocity. Besides, the waterflooding would flow preferentially towards the layers with strong water absorption capacity, thereby forming the advantageous channel.

Fig. 5
figure 5

The velocity distribution nephogram under different flow rates.

Full size image

Figure 6 illustrated the flow field trajectory nephogram and flow rate vibration of different perforations before and after ball-pitching. The results indicated that, before ball-pitching, the waterflooding entered the wellbore from the string and is discharged from each perforation, with the waterflooding flow rate of each perforation being essentially uniform; After ball-pitching, there was a significant change in the flow rate of each perforation, with a decrease in the flow rate of the plugging perforation and an increase in the flow rate of non-plugging perforation.

Fig. 6
figure 6

Flow field trajectory nephogram and flow rate vibration before and after ball-pitching.

Full size image

Migration law of plugging-selection balls

Figure 7 illustrated the migration law of plugging-selection balls within the wellbore before and after ball-pitching. The results indicated that, before ball-pitching, the plugging balls were carried by waterflooding to the perforations, and these balls gradually moved around from the casing center after flowing out the horn mouth; Begain plugging-selection, #1–2 perforation was blocked by single ball, and other balls continued to move with waterflooding; After ball-pitching, the plugging balls blocked the most perforations, in which #1–2, #1–4 and #1–6 perforations were blocked by single ball, #1–3 and #1–5 perforations were blocked by double balls, and #1–1 perforation was not blocked. The migration analysis of plugging-selection balls revealed that, the plugging-selection process was not a top-to-bottom process, and the plugging process was affected by the parameters of waterflooding and plugging-selection balls.

Fig. 7
figure 7

The migration trajectory of plugging balls.

Full size image

Figure 8 illustrated the plugging effect and migration law with varying numbers of plugging-selection balls. The force exerted on the plugging-selection ball remained essentially unaltered due to the constant flow, ball diameter and ball density. When the balls number was relatively low, all balls participated in the plugging process, while this was insufficient to meet the plugging requirements for all perforations. As the balls number increased, the plugging efficiency of the plugging process improved markedly, accompanied by the phenomenon of multiple balls competing for single perforation or balls drifting. Therefore, the balls number should exceed that of perforations number.

Fig. 8
figure 8

Plugging effect and migration law of plugging ball under different balls numbers.

Full size image

Plugging effect analysis of perforations

Given the characteristics of the plugging-selection ball and the operational parameters of waterflooding wells, it was not feasible to achieve comprehensive plugging of all perforations through the utilization of plugging-selection balls27,28. Consequently, the plugging efficiency of these balls was employed to evaluate plugging effect, which was defined as follows:

$$\eta = \frac{{N_{f} }}{{N_{p} }}$$
(7)

where, \(\eta\) is the plugging efficiency; \(N_{f}\) is the blocked perforations number; \(N_{p}\) is the perforations number.

The plugging efficiency was used to describe the proportion of successfully plugged perforations by plugging-selection balls. The plugging efficiency was inversely proportional to the number of perforations that the plugging-selection balls were unable to plug. Consequently, the greater the number of perforations that the plugging-selection balls were able to plug, the higher the plugging efficiency.

Verification analysis of plugging efficiency

Laboratory experiments were conducted to validate the simulation results, and to further examine the influence of flow rate, ball density, diameter, and quantity on plugging efficiency.

Verification experiment

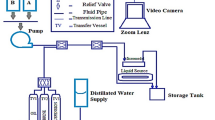
To investigate the migration law and plugging effect of plugging-selection balls, the schematic diagram of indoor experiment was devised based on the ball-pitching plugging-selection profile control process and similarity analysis method, which mainly comprises the ball-pitching tee, pressure system, measurement system, water circulation system, and centrifugal pump, as shown in Fig. 9. Three short sections were used to simulate the casing of the plugging-selection layer, with each layer comprising six spiral-distribution perforations; One-way valves were used to regulate the flow rate and pressure of perforation outlet; The centrifugal pump was used to provide hydraulic power for the whole system.

Fig. 9
figure 9

The schematic diagram of indoor experiment.

Full size image

In the experiment, the centrifugal pump was used to drive the waterflooding into the experimental pipeline; Water circulation was used to collect waterflooding from the plugging-selection layer and provide water source for the centrifugal pump; The plugging-selection balls were pitched into pipeline through the pitching tee; The one-way valve and flowmeter at the perforation outlet were used to control the measurement system, thus simulating the water absorption capacity of different formations. The experimental device parameters were shown in Table 3.

Table 3 The experimental device parameters.
Full size table

Two balls were utilized for simulation and experiments of plugging perforations, with the flow ratio before plugging and after plugging being monitored, as illustrated in Fig. 10. The flow ratio of various perforations showed that, before and after ball-pitching, the flow ratios of #1–1 perforation and #1–2 perforations exhibited a marked decline, while the other flow ratio increased. The comparative analysis results demonstrated that the ball-pitching plugging-selection profile control process can effectively regulate the formation flow.

Fig. 10
figure 10

Plugging effect and flow ratio before plugging and after plugging.

Full size image

Influencing factors of plugging efficiency

Flow rate of waterflooding

The effectiveness of the plugging process was largely dependent upon waterflooding flow, with the flow rate of waterflooding exerting a direct influence on the flow velocity and the movement law of plugging ball. The objective of this study was to examine the plugging effect at the flow rates of waterflooding were 0.5 m3/h, 1.0 m3/h, 1.5 m3/h, 2.0 m3/h, 2.5 m3/h, 3.0 m3/h, 3.5 m3/h, and 4.0 m3/h, respectively. The experiments and simulations were conducted at the waterflooding density of 1000 kg/m3, the ball density of 980 kg/m3, the ball diameter of 10 mm, and plugging modes of upper + middle layer and upper + middle + lower layer. Figure 11 illustrated the variation of plugging efficiency across different flow rates.

Fig. 11
figure 11

Influence of flow rate of waterflooding on plugging efficiency.

Full size image

As can be seen from Fig. 11, the observed trend in changes in plugging efficiency under experiment and simulation methods was consistent across different plugging modes. At low flow rates, the velocities of both water and plugging ball were relatively low, and the plugging effect was mainly concentrated in upper layer. As the flow rate increased, the plugging efficiency improved. When the flow rate was high, the rapid waterflooding speed caused the plugging ball to traverse the perforation, resulting in poor plugging effect of upper layer. It can thus be concluded that the optimal plugging effect is achieved at the flow rate of approximately 2 m3/h.

Density of plugging-selection ball

The density of plugging ball is a significant variable that influences the motion equation. The motion law and plugging effect of plugging-selection ball were investigated when the ball density ratios were 860 kg/m3, 900 kg/m3, 940 kg/m3, 980 kg/m3, 1020 kg/m3, 1060 kg/m3, and 1120 kg/m3, respectively. The experiments and simulations were conducted at the density and flow rate of waterflooding of 1000 kg/m3 and 2 m3/h, the ball diameter of 10 mm, and plugging modes of middle + lower layer and upper + middle + lower layer. Figure 12 illustrated the plugging efficiency of plugging-selection ball.

Fig. 12
figure 12

Influence of the density of plugging-selection ball on plugging efficiency.

Full size image

The analysis results indicate that an increase in the density of plugging ball was initially associated with an enhancement in the plugging efficiency, followed by a subsequent decline. When the density was small, the settling velocity of plugging-selection ball was also small, and gradually reached the dynamic suspension stage. At this time, the plugging efficiency was low, resulting in the obstruction of the upper perforations. When the density of plugging-selection ball was higher than that of the waterflooding, the high-density ball exhibited a high settling velocity, and was readily settled at the well bottom, resulting in low plugging efficiency; When the density of ball and waterflooding was similar, the plugging ball was easier to be carried near the perforations, thus achieving the desired plugging effect.

Diameter of plugging-selection ball

The diameter change of plugging-selection ball had an impact on the motion equation in the vicinity of the casing and hole. The motion law and plugging effect were investigated when the diameter of plugging-selection ball was 6 mm, 8 mm, 10 mm, 12 mm, 14 mm, and 16 mm. The experiments and simulations were conducted at the waterflooding density and flow rate of 1000 kg/m3 and 2 m3/h, the ball diameter of 10 mm, the experiment time of 60 s, plugging modes of upper + middle layer and upper + middle + lower layer. Figure 13 illustrated the variation in plugging efficiency.

Fig. 13
figure 13

Influence of diameter of plugging-selection ball on plugging efficiency.

Full size image

When the diameter of plugging-selection ball was less than that of the perforation, these balls would pass through the perforations, which ultimately precluded the possibility of achieving the plugging purpose; When the diameter of plugging-selection ball exceeded that of perforation, the plugging efficiency was essentially stable. It was therefore recommended to utilize 10 mm ball for plugging 8 mm perforation.

Number of plugging-selection ball

In the plugging process, the matching relationship between the number of the plugging ball and the perforation was an important factor affecting the plugging effect. The plugging effect of plugging-selection ball was evaluated at ball-perforation number ratios of 0.4, 0.7, 1.0, 1.3, 1.6, and 2.0, respectively. The density and flow rate of waterflooding were 1000 kg/m3 and 2 m3/h, the ball diameter was 10 mm, the experiment time was 30 s, and the plugging modes of upper + middle layer and upper + middle + lower layer were adopted. The plugging efficiency and effective utilization rate were shown in Fig. 14.

Fig. 14
figure 14

Influence of ball-perforation number ratio of waterflooding on plugging efficiency.

Full size image

The analysis results demonstrated that when the ball-perforation number ratio was low, it was not possible to meet the plugging requirements, as it was not feasible to block all the perforations; When the ball-perforation number ratio was equal, the plugging efficiency was improved. In practical applications, due to long-term operation, the perforation or casing may undergo irregular deformation, which serves to exacerbate the phenomenon of multiple balls competing for single perforation. It could be reasonably deduced that, when the ball-perforation number ratio exceed 1.0, it was possible to meet the plugging requirements, especially for multi-layers plugging.

Typical well application

A case study in Liaohe Oilfield well was presented to illustrate the practical application of selective plugging ball technology, and to discuss its potential for widespread adoption in special waterflooding wells.

Overall situation

The typical application well was located in Block X of Liaohe Oilfield, with the proven oil bearing area of 0.72 km2 and the recoverable reserve of 31.5 × 104 t. There were six operational waterflooding wells and 24 working oil wells in Block X. Among the six waterflooding wells, one of them used 3-stage and 3-layer mechanical separate injection method, while other five wells used general injection method (unable to apply mechanical layered waterflooding technology). At present, all of the waterflooding wells faced difficulties of multiple layers, thin interlayers, falling objects, and casing deformation, as shown in Table 4, making it difficult to adopt conventional injection separation and low reservoir utilization.

Table 4 The overall situation of typical application well.
Full size table

Application effect analysis

The implementation of the ball-pitching plugging-selection profile control technology on 5 wells (Waterflooding #4 without the application conditions) allowed for a detailed analysis and evaluation of the fine profile control effect from aspects of fluid production variation, reservoir utilization degree, and economic benefits.

Waterflooding pressure variation

As a consequence of the water-absorbing layer’s capacity to elevate the waterflooding pressure to a certain degree following sealing, monitoring the waterflooding pressure could facilitate the verification of the efficacy of implemented measures to a certain extent. As illustrated in Fig. 15, monitoring the water injection pressure at the wellhead is a viable approach. Prior to pitching, the pressure gauge at the wellhead registered 7.6 MPa, while post-pitching, the gauge indicated a pressure of 9 MPa. The rise in waterflooding pressure, maintained at the same daily volume, provides evidence that the high permeability layer has been successfully plugged. The same analysis results have been consistently replicated in numerical simulations and indoor experiments.

Fig. 15
figure 15

Pressure variation before and after plugging-selection.

Full size image

Fluid production variation

The implementation of the low-cost ball-pitching plugging-selection profile control technology was evidenced by the comprehensive production variation curve, as shown in Fig. 16. After ball-pitching, the formation of water breakthrough channels was effectively suppressed, accompanied by a reduction in both fluid and water production. The oil production of Block X initially declined, followed by an increase, which indicated the decline trend of oil production had been effectively controlled.

Fig. 16
figure 16

Comprehensive fluid production variation curves.

Full size image

Reservoir utilization degree

Table 5 presented the reservoir utilization status analysis of typical application well. After ball-pitching for the waterflodding wells, 19 injection layers were newly activated, 16 injection layers were restricted, and 5 injection layers were strengthened. In terms of vertical improvement, the oil layer thickness was enhanced by 79.2%.

Table 5 The reservoir utilization status analysis.
Full size table

Economic benefits

Comparative analysis of the cost and applicability of different profile control technologies in special waterflooding wells, as presented in Table 6, indicated that, in terms of direct economic benefits, the ball-pitching plugging-selection profile control technology saved more than 200% of costs; in terms of indirect economic benefits, the decline trend of oil production was significantly suppressed, and the injection and production water volume was alleviated, which promoted energy conservation and environmental protection construction in oil fields.

Table 6 Comparative analysis of cost and applicability of different profile control technologies.
Full size table

Application promotion services

The ball-pitching plugging-selection profile control technology has been successfully deployed in over 300 special waterflooding wells, as presented in Table 7. The implementation of mechanical layered waterflooding technology in these wells was hindered by such factors of casing deformation, corrosion and sand production. As a result, the ball-pitching plugging-selection profile control technology was implemented. The average improvement rate of water absorption profile is 92.4%, with the potential to open up to nine new water absorption layers in a single well, resulting in an average increment in vertical utilization degree of 17.9%. The impact of the aforementioned oil wells has resulted in an indirect increment in oil production of over 20,000 tons.

Table 7 The application promotion services analysis.
Full size table

Conclusion

  1. 1.

    The effects of waterflooding flow rate, and density, diameter, quantity of plugging-selection balls on the plugging effect of perforation were investigated through numerical simulations and experiments. The findings indicate that the optimal well plugging effect was achieved when the flow rate of waterflooding was 2 m3/h, the density of ball and waterflooding was similar, the plugging-selection ball diameter was 10 mm, and the ball-perforation number ratio exceeded 1.0.

  2. 2.

    The numerical simulation results indicated that the diversion effect was primarily observed in the layers with strong water absorption capacity, and the migration process of plugging-selection balls showed single and multiple plugging effects, which were contingent upon the parameters of waterflooding and plugging-selection balls.

  3. 3.

    The application of typical wells indicated that, the ball-pitching plugging-selection profile control technology could increase oil production, finely control reservoir utilization, and enhance economic benefits.

Although this technology has yielded significant outcomes, it was postulated that there was still potential for further optimization. Furthermore, advanced technologies such as artificial intelligence and big data can be employed to enhance the effectiveness of this technology in enhancing oil recovery.