Introduction

Fractional calculus within mathematical models have been applied extensively in many natural science and engineering domains1. Nonlinear fractional differential equations are an emerging area of study with its definition first acknowledged in 16952. It is widely used to comprehend the convoluted physical interpretation of fields such as fractional dynamics, fluid motion, stochastic motion, neural material science, strong state material science, geo-optical filaments, nonlinear optical science, mathematical physics, solid-state physics, statistical physics, nuclear physics and biomechanics3. One of the most significant areas of study for fractional differential equations is the desire for accurate and numerical solutions. These studies can serve as significant sources of information for further research in the same field. In applied research, the fractional calculus is crucial to comprehending a broad variety of intricate physical mechanisms4. The Nonlinear evolution equations have several application possibilities which makes them quite significant. Among the most phenomenal areas of study in current science are nonlinear events. Nonlinear evolution equations are widely used to show how isolated waves move5. Partial differential equations are now essential for researchers and scientists to understand physical events due to technological advancements6. The nonlinear partial differential equations are an essential instrument for investigating the characteristics of intricate physical phenomena7. Studying the precise solutions of NLPDE is crucial for understanding a wide range of physical processes seen in engineering and scientific disciplines, including biology, the kinetics of chemicals, fiber optics, plasma physics and oceanographic. Evaluating the behaviors of the problems under consideration requires the acquisition of precise and analytical answers for the nonlinear partial differential equation in the aforementioned sectors. The following are a few instances of recent advancements in the analysis and accurate outcome of NLPDE. By employing the variational iterative methodology, Wazwaz and Kaur were able to produce optical solitaires and singularity solitaire approaches of the self-focusing nonlinear Schrödinger problem8.

In the domains of electromagnetic theory, engineering, mathematical biology, signal processing and other sciences fractional differential equations are utilized to explain a broad range of physical phenomena9. An essential class of differential equations are fractional partial differential equations (FPDEs) and fractional ordinary differential equations (FODEs)10,11. The dynamics of intricate systems can be modelled by them. Numerous techniques including integral transforms, Adomian approaches and numerical algorithms are available in the literature to solve FPDEs12. And also there are numerous techniques present to resolve FODEs13. Both fractional differential equations (FDEs) and (FPDEs) have gained popularity in recent years as a result of the numerous applications that they have in the fields of engineering and physics14. A soliton sometimes known as a solitary wave, is a localised particle-like solution of a nonlinear equation that characterises finite energy excitations. It has various distinguishing characteristics including: A single wave’s profile is not destroyed during propagation; rather, the interaction of multiple solitary waves results in their elastic scattering which maintains the wave’s overall number and shape. Every now and then, the idea of a soliton is discussed in a broader context as a localised solution of finite energy15. Solitons are a type of wave that is localized, nonlinear and self-reinforcing. They are sometimes referred to as shallow-water waves or solitary waves. Even after colliding with other solitons, they maintain their shape. Because of the combined impacts of fractional derivatives and nonlinearity, soliton behavior in the nonlinear time-fractional Phi-four equation is unique. In the nonlinear time-fractional phi-four equation, solitons behave as confined, stable and non-dispersive structures that withstand external disturbances and maintain their integrity while propagation.

The advancement of fractal theory has expanded the possibilities for the theory of fractional derivatives. As a result, many different kinds of fractional derivative concepts have been developed. The significance of the derivative at the fractional order has led to the proposal of several definitions such as the Davidson derivative16 , Weyl derivative17 , Atangana derivative, Hadamard derivative18 , Miller-Ross derivative19 , Marchaud derivative20 , Sonin-Letnikov derivative, Erdélyi-Kober derivative, Grünwald-Letnikov derivative, Conformable derivative21 and Katugampola derivative. Introducing fractional derivatives in time enables more advanced behaviors that capture certain anomalous diffusion processes. Because fractional derivatives are included, the behavior and solutions of the time-fractional Phi-Four equation can be more intriguing and intricate than those of the regular Phi-Four equation. The time-fractional Phi-four equation is a PDE that extends the normal Phi-four equation by include fractional derivatives with respect to time. In the domains of mathematical physical science, including nonlinear optics and physics of condensate matter, the basic Phi-four equation is widely recognised and frequently employed to explain specific occurrences. More intricate behaviours that capture certain anomalous diffusion processes are possible when fractional derivatives are included in time. The behaviour and solutions of the time-fractional Phi-four equation can be more interesting and intricate than those of the regular Phi-four equation because of the addition of fractional derivatives. The fractional derivative introduces non-locality and memory effect which can lead to anomaly spread and other peculiar behaviours22. It is possible to utilise the proposed equation in a variety of applications in the fields of engineering, computational physics and wave analytics. Since it is more precise, efficient and versatile than other comparable equations23. The fractional Klein-Gordon equation is of great significance in the fields of physical mathematics, solid state physics, particle and atomic physics and especially condensed matter-related physics24. The suggested equation has recently been examined using a variety of analytical techniques including the unified method25 , modified extended tanh function method26 , modified Kudryashov method27 and q-homotopy analysis transform method28.

Kink-solitary wave type soliton solutions have been obtained by Unified method29. Lump, mixed lump, kink, lump periodic type soliton solutions have been obtained by modified extended tanh function method30 and Kink, lump soliton solutions have been obtained by q-homotopy analysis transform method31. While by employing Bernoulli Sub-ODE and Extended direct algebraic method we extract dark, M-shaped, W-shaped, bell, anti-bell, bright, dark bright, kink, periodic, sharp dark and anti kink type soliton solution.

In this work, the recent explicit soliton solutions to the time-fractional Phi-four equation32,33 are obtained. The time-fractional Phi-four equation is solved by extended direct algebraic method and Bernoulli sub-ODE method to generate the missing travelling wave solutions. One particular manifestation of the K-Gordon equation is known as the Phi-four equation. The Phi-four equation is a specific case of the Klein-Gordon (KG) equation, which corresponds to the nonlinear Schrödinger equation34. The Phi-four solutions can be used to examine a variety of quantum phenomena, including matter waves dictating reality in the form of waves, which are essential constituents of quantum mechanics. The Phi-four equation can be used to study ultrashort pulse propagation in optical transmission lines and particle physics events. Through the years, the collaboration of kink, lump and periodic solitary wave propagation has been an important factor in the development of experimental inventions in the fields of nuclear and theoretical physics35,36. The purpose of this paper is to examine the most current exact and straightforward outcomes for the conformable time-fractional Phi-four equation which may be represented as in the following way:

$$\begin{aligned} D_t^{2\xi }r(k,t) - r_{kk}(k,t) + \Omega ^2 r(k,t) + \Theta r^3(k,t) = 0,\,\,\, \Theta > 0,\,\,\, 0<\xi \le 1. \end{aligned}$$
(1.1)

Here \(\Omega\) and \(\Theta\) are real parameters. We utilise the BSODE and EDA method by employing the fractional travelling wave transformation with the assistance of the conformable order derivative. The Bernoulli sub-ODE approach is an analytical technique used for obtaining exact solutions to nonlinear partial differential equations. The Bernoulli sub-ODE approach can be used to identify traveling wave solutions, peaked wave solutions and solitary wave solutions. The given approach produces exact solutions. The previous articles have been investigating the precise solutions of the time-fractional Phi-four equation using various methods, including the unified method, modified khater method, \((G^{\prime }/G, 1/G)\)-expansion method and the MTHF method etc. Bright singular, dark, singular periodic soliton solutions have been obtained by using modified khater method37. Double lump, lump, periodic, cusp soliton solutions have been obtained by using \((G^{\prime }/G, 1/G)\)-expansion method38. While the methods applied in this article produces kink, anti-kink, periodic, W-shaped, M-shaped, bell, anti-bell, dark, smooth dark bright, sharp dark soliton solutions. To the best of our knowledge, there is a lack of meaningful research on our proposed methods for extracting the time- fractional Phi-four equation using the conformable derivative logic. Furthermore, our proposed approach is highly successful and provides a comprehensive and practical framework for obtaining precise solutions to FPDEs in the form of travelling waves. The primary advantage of our favoured scheme over other existing systems is its ability to deliver a concise and straightforward answer. With the help of the computer software Mathematica, we were able to illustrate the answers that were established by determining the productive values of the appropriate parameters and describing sketches in order to visualise the physical explanation.

These two suggested techniques have been devised by a number of writers in order to determine the precise solution of different NLEEs in the derivative sense. Nevertheless, no successful research using these techniques has yet been discovered on our favoured time-fractional Phi-four equation. Here the new exact solution we have found for the time-fractional Phi-four equation is more precise, effective and user-friendly. It may be used to a number of computational physics, engineering and fields connected to wave analysis. Time-Fractional Phi-four equation describes the electromagnetic interactions and processes of fission and fusion in nuclear physics, particle physics, solid-state physics, plasma physics and chemical kinematics. We may therefore assert that our suggested examine dynamical analysis of the time-fractional Phi-four equation using the suggested methodology is innovative in the sense of conformable derivative. The recent articles on Time-fractional Phi-four equation are given in39,40.

The following is the paper’s structure: The concepts and features of fractional derivatives are given in “Preliminaries”. The BSODE and EDA analytical techniques are performed and utilized regarding the proposed model in the “Descriptions of methods”. The mathematical analysis of the time-fractional Phi-four equation is presented in the indicated “Mathematical computation”. Implementation of the approaches to the time-fractional Phi-four equation is mentioned in “Application of methods”. Graphs are employed in “Results and discussion” to supplement computations and illustrate the discussion of the results. Physical interpretation and applications are given in “Physical interpretation and applications”. Section “Conclusions” provides a few concluding notes to conclude the investigation.

Preliminaries

This section provides the fractional derivatives definitions as well as some of their fundamental properties.

\(\beta\) - Derivative

Definition 1

Another type of C-D is \(\beta\)-D that can be expressed as:

$$\begin{aligned} _0^ED_t^\xi h(t) = \mathop {\lim }\limits _{\varkappa \rightarrow 0} \frac{{h(t + \varkappa {{(t + \frac{1}{{\Gamma (\xi )}})}^{1 - \xi }}) - h(t)}}{\varkappa }, \,\,\,\,\,\,\,\,\,\,0 < \xi \le 1. \end{aligned}$$

The characteristics of \(\beta\)-D are as follows:

  1. 1.

    It is a linear operator.

    \(_0^ED_u^\xi (gj(u) + iv(u)) = g _0^ED_u^\xi j(u) + i _0^ED_u^\xi v(u)\), \(\forall g,i \in \Re\).

  2. 2.

    It fulfills the requirements of the product rule.

    \(_0^ED_u^\xi (j(u) * v(u)) = v(u)_0^ED_u^\xi j(u) + j(u)_0^ED_u^\xi v(u)\).

  3. 3.

    The quotient rule is applicable to it.

    \(_0^ED_u^\xi \left\{ {\frac{{j(u)}}{{v(u)}}} \right\} = \frac{{v(u)_0^ED_u^\xi j(u) - j(u)_0^ED_u^\xi v(u)}}{{{v^2}(u)}}\).

  4. 4.

    The value of the \(\beta\)-D of a constant is equal to zero.

    \(_0^ED_u^\xi (c) = 0\), for any constant   (c).

M-truncated derivative

Definition 2

Let \({h: [0,\infty ) \rightarrow \Re }\) with order \(\xi \in (0,1)\) has the following defined M-TD:

\(_zD_{M,t}^{\xi , \hbar }h(t) = \mathop {\lim }\limits _{\varkappa \rightarrow 0} \frac{{h({t+_z}{P_\hbar }(\varkappa {t^{ -\xi }})) - h(t)}}{\varkappa }\),  for t  >  0,

where \(_z{P_\hbar }\mathrm{ }\left( . \right) ,\mathrm{ }\hbar \mathrm{ } > \mathrm{ }0\) is truncated Mittag-Leffler function with single parameter stated as

\(_z{P_\hbar }\mathrm{ }\left( t \right) \mathrm{ } = \mathrm{ }\sum \limits _{n = 0}^z {\frac{{{t^n}}}{{\Gamma \left( {\hbar \mathrm{ }n\mathrm{ } + \mathrm{ }1} \right) }}}\).

Theorem 2.1

Assume that \(0 < \xi \le 1,\hbar>\) 0 for any \(g,{{ i }} \in \Re\)  and  j, v be \(\xi\)  -  differentiable at point  u > 0. So,

  1. 1.

    \(_zD_{M,u}^{\xi ,\hbar } (gj(u) + iv(u)) = g _zD_{M,u}^{\xi ,\hbar } j(u) + i_zD_{M,u}^{\xi ,\hbar } v(u)\), \(\forall g,i\in \Re\).

  2. 2.

    \(_zD_{M,u}^{\xi ,\hbar } (j(u) * v(u)) = v(u)_zD_{M,u}^{\xi ,\hbar } j(u) + j(u)_zD_{M,u}^{\xi ,\hbar } v(u)\).

  3. 3.

    \(_zD_{M,u}^{\xi ,\hbar } \left\{ {\frac{{j(u)}}{{v(u)}}} \right\} = \frac{{v(u)_zD_{M,u}^{\xi ,\hbar } j(u) - j(u)_zD_{M,u}^{\xi ,\hbar } v(u)}}{{{v^2}(u)}}\).

  4. 4.

    It is defined as follows for an M-TD of a differentiable function j(u).

    \(_zD_{M,u}^{\xi ,\hbar }j(u) = \frac{{{u^{1 - \xi }}}}{{\Gamma (\hbar + 1)}}\frac{{dj}}{{du}}.\)

Conformable derivative

Definition 3

Let h = \({h(t): [0,\infty ) \rightarrow \Re }\) be the conformable derivative of order \(\xi\) with respect to the independent variable t is defined as

$$D_t^\xi h(t) = \mathop {\lim }\limits _{\varkappa \rightarrow 0} \frac{{h(t + \varkappa {{t}^{1 - \xi }}) - h(t)}}{\varkappa },\;\;\;\forall t > 0, \,\,\, \xi \in (0,1].$$

This well-defined fractional derivative can be obtained by meeting a few well-known prerequisites.

Theorem 1

Assume that the derivative \(\xi\) has an order within (0, 1]. Furthermore, suppose that for all positive values of t, \({j = j(t)}\) and \({v = v(t)}\) are \(\xi\)-differentiable functions.

Afterwards,

  1. 1.

    \({D_t^\xi (g_1 j(t) + g_2 v(t)) = g_1 D_t^\xi (j(t)) + g_2 D_t^\xi (v(t))}, ~~\forall {g_1, g_2 \in \Re }.\)

  2. 2.

    \({D_t^\xi (t^q) = qt^{q-\xi },\;\;\;\; \forall q \in \Re }.\)

  3. 3.

    \({D_t^\xi (\Delta ) = 0, \;\;\;\;\; \forall \; w(t) = \Delta }.\)

  4. 4.

    \({D_t^\xi (j(t)v(t)) = j(t) D_t^\xi (v(t)) + v(t) D_t^\xi (j(t))}.\)

  5. 5.

    \({D_t^\xi (\frac{j(t)}{v(t)}) = \frac{v(t) D_t^\xi (j(t)) - j(t) D_t^\xi (v(t))}{(v(t))^2}}.\)

  6. 6.

    \({D_t^\xi (j(t)) = t^{1-\xi } \frac{dj(t)}{dt}}.\)

The Taylor series expansion, laplace transforms and the chain rule are only a few of the fundamental types of laws that conformable differential operators follow.

Theorem 2

Consider \({j = j(t)}\) to be a \(\xi\) - conformable differentiable function. Additionally, consider that v is well-defined and differentiable within the range of k. So,

$$\begin{aligned} D_t^\xi (j \circ v) (t) = t^{1-\xi } v^{\prime } (t) j^{\prime }( v(t)). \end{aligned}$$

Descriptions of methods

Bernoulli sub-ODE method

This section provides an explanation of the Bernoullli Sub-ODE method given in41,42. The BSODE method for locating travel-wave solutions of NLEEs is covered in this section. Assume that a NLPDE is given by with two independent variables, let’s say t and k

$$\begin{aligned} \wp (s,s_t,s_k,s_{tt},s_{kk},s_{kt}, ... ... ...) = 0, \end{aligned}$$
(3.1)

where \({s(\nu )}\) = s(k, t) is a function that is unknown, \(\wp\) is a polynomial of s(k, t) and its partial derivatives which includes the highest order derivatives and nonlinear terms in their composition. The important steps are outlined below.

1. Creating a single variable by merging the independent variables k and t i.e, \({\nu }\) = \(k{\pm }\) ct, our assumption is that

$$\begin{aligned} s(\nu ) = s(k,t),\,\, \nu = k\pm c(t). \end{aligned}$$
(3.2)

By utilizing the (3.2) for the transformation of travelling waves, we are able to change the (3.1) into the following ODE:

$$\begin{aligned} \wp (s,s^{\prime },s^{\prime \prime }, ... ... ...) = 0, \end{aligned}$$
(3.3)

where \({\wp }\) is a polynomial in \({s(\nu )}\) and its derivatives, while \({s^{\prime }(\nu )}\) = \({\frac{ds}{d\nu }}\), \({s^{\prime \prime }(\nu )}\) = \({\frac{d^{2}s}{d\nu ^{2}}}\) and so on.

2. Assuming that the (3.3) posses a formal solution

$$\begin{aligned} s(\nu ) = \mathop \sum \limits _{m=0}^l b_{m}P_{m}, \end{aligned}$$
(3.4)

where P = \({ P(\nu )}\) fulfill the requirements of the equation;

$$\begin{aligned} P^{\prime } + \eta P = \delta P^{2}. \end{aligned}$$
(3.5)

In which \({b_m(0\le m \le l}\) ; \({l \in N}\)) are constant to be determined and \({\eta \ne 0}\).

When \({\delta \ne 0}\), (3.5) can be classified as a form of bernoulli equation, we are able to acquire the solution as

$$\begin{aligned} P = \frac{\eta }{\delta + \eta F \exp (\eta \nu )}, \end{aligned}$$
(3.6)

where F is an indeterminate constant.

When \({\delta = 0}\), (3.6) can be changed to

$$\begin{aligned} P = \frac{1}{F} \exp (-\eta \nu ). \end{aligned}$$
(3.7)

Putting \({F = \frac{\delta }{\eta }}\) into (3.6), we obtain

$$\begin{aligned} P = -\frac{\eta }{2 \delta } \Bigg (\tanh (\frac{\eta }{2} \nu ) - 1\Bigg ). \end{aligned}$$
(3.8)

Putting \({F = - \frac{\delta }{\eta }}\) into (3.6), we obtain

$$\begin{aligned} P = -\frac{\eta }{2 \delta } \Bigg (\coth (\frac{\eta }{2} \nu ) - 1\Bigg ). \end{aligned}$$
(3.9)

3. By accounting for the uniform distribution of the nonlinear components and the highest order derivatives that appear in (3.1) or (3.3), it is possible to ascertain the value of the positive integer l.

4. Substituting (3.4) into (3.3) yields a polynomial in \(P(\nu )\). Gathering all terms with the same power and zeroing off the coefficients. We derive an algebraic system of equations that can be solved with the Mathematica software.

Extended direct algebraic method

This section provides an explanation of the extended direct algebraic method given in43,44. Let us take into consideration a general nonlinear PDE that is given by

$$\begin{aligned} \wp (w,w_{t},w_{k},w_{tt},w_{kk},w_{kt}, ...) = 0, \end{aligned}$$
(3.10)

with the use of the transformation described below:

$$\begin{aligned} w(\nu ) = w(k,t), \,\,\ \nu = k \pm ct, \end{aligned}$$
(3.11)

The equation (3.10) can be transformed into an ODE with the following structure:

$$\begin{aligned} \wp (S,S^{\prime },S^{\prime \prime }, ...) = 0. \end{aligned}$$
(3.12)

We make the assumption that (3.12) possesses a solution in the following format:

$$\begin{aligned} S(\nu ) = \mathop \sum \limits _{z=0}^W a_{z}U^{z}(\nu ), \end{aligned}$$
(3.13)

where

$$\begin{aligned} U^{\prime }(\nu ) = \ln \sigma (\alpha + \omega U(\nu ) + \phi (U(\nu ))^2) ; (\sigma \ne 0,1), \end{aligned}$$
(3.14)

where \({\alpha }\), \({\omega }\) and \({\phi }\) are constants having real values. The general form of the solution of (3.14) according to these factors is provided as elaborated below:

1. For \({\omega ^2}\) - 4\({\alpha }\) \({\phi }\) \({<}\) 0 and \({\phi }\) \({\ne }\) 0, we have

$$\begin{aligned} U_1 (\nu )= & - \frac{\omega }{2 \phi } + \frac{\sqrt{-\gamma }}{2 \phi } \tan _\sigma \Bigg (\frac{\sqrt{-\gamma }}{2}\nu \Bigg ), \end{aligned}$$
(3.15)
$$\begin{aligned} U_2 (\nu )= & - \frac{\omega }{2 \phi } - \frac{\sqrt{-\gamma }}{2 \phi } \cot _\sigma \Bigg (\frac{\sqrt{-\gamma }}{2}\nu \Bigg ), \end{aligned}$$
(3.16)
$$\begin{aligned} U_3 (\nu )= & - \frac{\omega }{2 \phi } + \frac{\sqrt{-\gamma }}{2 \phi } ( \tan _\sigma ({\sqrt{-\gamma } \nu }) \pm \sqrt{\zeta \varrho } \sec _\sigma (\sqrt{-\gamma }\nu )), \end{aligned}$$
(3.17)
$$\begin{aligned} U_4 (\nu )= & - \frac{\omega }{2 \phi } + \frac{\sqrt{-\gamma }}{2 \phi } ( \cot _\sigma ({\sqrt{-\gamma } \nu }) \pm \sqrt{\zeta \varrho } \csc _\sigma (\sqrt{-\gamma }\nu )), \end{aligned}$$
(3.18)

and

$$\begin{aligned} U_5 (\nu ) = - \frac{\omega }{2 \phi } + \frac{\sqrt{-\gamma }}{4 \phi } \Bigg ( \tan _\sigma \Bigg (\frac{\sqrt{-\gamma }}{4} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\sqrt{-\gamma }}{4}\nu \Bigg )\Bigg ). \end{aligned}$$
(3.19)

2. For \({\omega ^2}\) - 4\({\alpha }\) \({\phi }\) \({>}\) 0 and \({\phi }\) \({\ne }\) 0, we have

$$\begin{aligned} U_6 (\nu )= & - \frac{\omega }{2 \phi } - \frac{\sqrt{\gamma }}{2 \phi } \tanh _\sigma \Bigg (\frac{\sqrt{\gamma }}{2}\nu \Bigg ), \end{aligned}$$
(3.20)
$$\begin{aligned} U_7 (\nu )= & - \frac{\omega }{2 \phi } - \frac{\sqrt{\gamma }}{2 \phi } \coth _\sigma \Bigg (\frac{\sqrt{\gamma }}{2}\nu \Bigg ), \end{aligned}$$
(3.21)
$$\begin{aligned} U_8 (\nu )= & - \frac{\omega }{2 \phi } + \frac{\sqrt{\gamma }}{2 \phi } (- \tanh _\sigma ({\sqrt{\gamma } \nu }) \pm \iota \sqrt{\zeta \varrho }\, {{{\textrm{sech}}}}_\sigma (\sqrt{\gamma }\nu )), \end{aligned}$$
(3.22)
$$\begin{aligned} U_9 (\nu )= & - \frac{\omega }{2 \phi } + \frac{\sqrt{\gamma }}{2 \phi } (- \coth _\sigma ({\sqrt{\gamma } \nu }) \pm \sqrt{\zeta \varrho }\, {{{\textrm{csch}}}}_\sigma (\sqrt{\gamma }\nu )), \end{aligned}$$
(3.23)

and

$$\begin{aligned} U_{10} (\nu ) = - \frac{\omega }{2 \phi } - \frac{\sqrt{\gamma }}{4 \phi } \Bigg ( \tanh _\sigma \Bigg (\frac{\sqrt{\gamma }}{4} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\sqrt{\gamma }}{4}\nu \Bigg )\Bigg ). \end{aligned}$$
(3.24)

3. For \({\alpha }\) \({\phi }\) \({>}\) 0 and \({\omega }\) = 0, we have

$$\begin{aligned} U_{11} (\nu )= & \sqrt{ \frac{\alpha }{\phi }} \tan _\sigma (\sqrt{\alpha \phi }\nu ), \end{aligned}$$
(3.25)
$$\begin{aligned} U_{12} (\nu )= & - \sqrt{ \frac{\alpha }{\phi }} \cot _\sigma (\sqrt{\alpha \phi }\nu ), \end{aligned}$$
(3.26)
$$\begin{aligned} U_{13} (\nu )= & \sqrt{ \frac{\alpha }{\phi }}( \tan _\sigma (2 \sqrt{\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\sec _\sigma (2 \sqrt{\alpha \phi }\nu )), \end{aligned}$$
(3.27)
$$\begin{aligned} U_{14} (\nu )= & \sqrt{ \frac{\alpha }{\phi }}(- \cot _\sigma (2 \sqrt{\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\csc _\sigma (2 \sqrt{\alpha \phi }\nu )), \end{aligned}$$
(3.28)

and

$$\begin{aligned} U_{15} (\nu ) = \frac{1}{2} \sqrt{\frac{\alpha }{ \phi }} \Bigg ( \tan _\sigma \Bigg (\frac{\sqrt{\alpha \phi }}{2} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\sqrt{\alpha \phi }}{2}\nu \Bigg )\Bigg ). \end{aligned}$$
(3.29)

4. For \({\alpha }{\phi }\) \({<}\) 0 and \({\omega }\) = 0, we have

$$\begin{aligned} U_{16} (\nu )= & -\sqrt{- \frac{\alpha }{\phi }} \tanh _\sigma (\sqrt{-\alpha \phi }\nu ), \end{aligned}$$
(3.30)
$$\begin{aligned} U_{17} (\nu )= & -\sqrt{- \frac{\alpha }{\phi }} \coth _\sigma (\sqrt{-\alpha \phi }\nu ), \end{aligned}$$
(3.31)
$$\begin{aligned} U_{18} (\nu )= & \sqrt{- \frac{\alpha }{\phi }}(- \tanh _\sigma (2 \sqrt{-\alpha \phi }\nu ) \pm \iota \sqrt{\zeta \varrho }\, {\textrm{sech}}_\sigma (2 \sqrt{-\alpha \phi }\nu )), \end{aligned}$$
(3.32)
$$\begin{aligned} U_{19} (\nu ) = \sqrt{- \frac{\alpha }{\phi }}(- \coth _\sigma (2 \sqrt{-\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\, {\textrm{csch}}_\sigma (2 \sqrt{-\alpha \phi }\nu )), \end{aligned}$$
(3.33)

and

$$\begin{aligned} U_{20} (\nu ) = - \frac{1}{2} \sqrt{-\frac{\alpha }{ \phi }} \Bigg ( \tanh _\sigma \Bigg (\frac{\sqrt{-\alpha \phi }}{2} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\sqrt{-\alpha \phi }}{2}\nu \Bigg )\Bigg ). \end{aligned}$$
(3.34)

5. For \({\omega } = 0\) and \({\alpha } = {\phi }\) , we have

$$\begin{aligned} U_{21} (\nu )= & \tan _\sigma (\alpha \nu ), \end{aligned}$$
(3.35)
$$\begin{aligned} U_{22} (\nu )= & -\cot _\sigma (\alpha \nu ), \end{aligned}$$
(3.36)
$$\begin{aligned} U_{23} (\nu )= & \tan _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho } \sec _\sigma (2 \alpha \nu ), \end{aligned}$$
(3.37)
$$\begin{aligned} U_{24} (\nu )= & -\cot _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho } \csc _\sigma (2 \alpha \nu ), \end{aligned}$$
(3.38)

and

$$\begin{aligned} U_{25} (\nu ) = \frac{1}{2} \Bigg (\tan _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg )\Bigg ). \end{aligned}$$
(3.39)

6. For \({\omega }\) = 0 and \({\phi }\) = \({-\alpha }\) , we have

$$\begin{aligned} U_{26} (\nu )= & -\tanh _\sigma (\alpha \nu ), \end{aligned}$$
(3.40)
$$\begin{aligned} U_{27} (\nu )= & -\coth _\sigma (\alpha \nu ), \end{aligned}$$
(3.41)
$$\begin{aligned} U_{28} (\nu )= & -\tanh _\sigma (2 \alpha \nu ) \pm \iota \sqrt{\zeta \varrho }\, {\textrm{sech}}_\sigma (2 \alpha \nu ), \end{aligned}$$
(3.42)
$$\begin{aligned} U_{29} (\nu )= & -\coth _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho }\, {\textrm{csch}}_\sigma (2 \alpha \nu ), \end{aligned}$$
(3.43)

and

$$\begin{aligned} U_{30} (\nu ) = -\frac{1}{2} \Bigg (\tanh _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg )\Bigg ). \end{aligned}$$
(3.44)

7. For \({\omega ^2} = 4{\alpha }{\phi }\) , we have

$$\begin{aligned} U_{31} (\nu ) = \frac{-2 \alpha (\omega \nu \ln (\sigma ) + 2)}{\omega ^2 \nu \ln (\sigma )} \end{aligned}$$
(3.45)

8. For \({\omega } = {m}\), \({\alpha } = {mq}\) (\(q {\ne }\) 0) and \({\phi } = 0\), we have

$$\begin{aligned} U_{32} (\nu ) = \sigma ^{m\nu } - q \end{aligned}$$
(3.46)

9. For \({\alpha } = {\phi } = 0\) , we have

$$\begin{aligned} U_{33} (\nu ) = \alpha \nu \ln (\sigma ) \end{aligned}$$
(3.47)

10. For \({\omega } = {\alpha } = 0\) , we have

$$\begin{aligned} U_{34} (\nu ) = \frac{-1}{\phi \nu \ln (\sigma )} \end{aligned}$$
(3.48)

11. For \({\omega }\) \({\ne }\) 0 and \({\alpha } = 0\), we have

$$\begin{aligned} U_{35} (\nu ) = - \frac{\zeta \omega }{\phi (\cosh _\sigma (\omega \nu ) - \sinh _\sigma (\omega \nu ) + \zeta )}, \end{aligned}$$
(3.49)

and

$$\begin{aligned} U_{36} (\nu ) = - \frac{\omega (\sinh _\sigma (\omega \nu ) + \cosh _\sigma (\omega \nu ))}{\phi (\sinh _\sigma (\omega \nu ) + \cosh _\sigma (\omega \nu ) + \varrho )}. \end{aligned}$$
(3.50)

12. For \({\omega } = {m}\), \({\phi } = {mq}\) (\(q {\ne }\) 0) and \({\alpha } = 0\), we have

$$\begin{aligned} U_{37} (\nu ) = - \frac{\zeta \sigma ^{m \nu }}{\zeta - q \varrho \sigma ^{m \nu }}. \end{aligned}$$
(3.51)

Here the generalized trigonometric and hyperbolic functions are defined as:

$$\begin{aligned} & \sinh _\sigma (\nu ) = \frac{\zeta \sigma ^\nu - \varrho \sigma ^{-\nu }}{2}, \cosh _\sigma (\nu ) = \frac{\zeta \sigma ^\nu + \varrho \sigma ^{-\nu }}{2}, \tanh _\sigma (\nu ) = \frac{\zeta \sigma ^\nu - \varrho \sigma ^{-\nu }}{\zeta \sigma ^\nu + \varrho \sigma ^{-\nu }}, \end{aligned}$$
(3.52)
$$\begin{aligned} & \coth _\sigma (\nu ) = \frac{\zeta \sigma ^\nu + \varrho \sigma ^{-\nu }}{\zeta \sigma ^\nu - \varrho \sigma ^{-\nu }}, {\textrm{sech}}_\sigma (\nu ) = \frac{2}{\zeta \sigma ^\nu + \varrho \sigma ^{-\nu }}, {\textrm{csch}}_\sigma (\nu ) = \frac{2}{\zeta \sigma ^\nu - \varrho \sigma ^{-\nu }}, \end{aligned}$$
(3.53)
$$\begin{aligned} & \sin _\sigma (\nu ) = \frac{\zeta \sigma ^{\iota \nu } - \varrho \sigma ^{-\iota \nu }}{2\iota }, \cos _\sigma (\nu ) = \frac{\zeta \sigma ^{\iota \nu } + \varrho \sigma ^{-\iota \nu }}{2}, \tan _\sigma (\nu ) = -\iota \frac{\zeta \sigma ^{\iota \nu } - \varrho \sigma ^{-\iota \nu }}{\zeta \sigma ^{\iota \nu } + \varrho \sigma ^{-\iota \nu }}, \end{aligned}$$
(3.54)
$$\begin{aligned} & \csc _\sigma (\nu ) = \frac{2\iota }{\zeta \sigma ^{\iota \nu } - \varrho \sigma ^{-\iota \nu }}, \sec _\sigma (\nu ) = \frac{2}{\zeta \sigma ^{\iota \nu } + \varrho \sigma ^{-\iota \nu }}, \cot _\sigma (\nu ) = \iota \frac{\zeta \sigma ^{\iota \nu } + \varrho \sigma ^{-\iota \nu }}{\zeta \sigma ^{\iota \nu } - \varrho \sigma ^{-\iota \nu }}. \end{aligned}$$
(3.55)

Mathematical computation

Take into consideration the following time-fractional Phi-four equation with a sense of conformable derivative:

$$\begin{aligned} D_t^{2\xi }r(k,t) - r_{kk}(k,t) + \Omega ^2 r(k,t) + \Theta r^3(k,t) = 0,\,\,\, \Theta > 0,\,\,\, 0<\xi \le 1. \end{aligned}$$
(4.1)

In order to derive soliton solutions for (4.1), the subsequent transformation

$$\begin{aligned} r(k,t) = R(\nu ), ~~ where ~~~~ \nu = fk - \frac{et^\xi }{\xi } \end{aligned}$$
(4.2)

has been employed.

By using the definition of conformable derivative

$$\begin{aligned} D_t^\xi r(t) = t^{1 - \xi } \frac{dr}{dt}, \end{aligned}$$
(4.3)

we get

$$\begin{aligned} D_t^{2\xi }(r) = e^2R^{\prime \prime }, \end{aligned}$$
(4.4)

and by differentiating r, we have

$$\begin{aligned} r_{kk} = f^2 R^{\prime \prime } \end{aligned}$$
(4.5)

By using the transformation in (4.2) along with (4.4) and (4.5) , (4.1) turns into an ODE as:

$$\begin{aligned} ( e^2 - f^2 ) R^{\prime \prime } + \Omega ^2 R + \Theta R^3, \end{aligned}$$
(4.6)

where \(\Omega\) and \(\Theta\) are real parameters.

Application of methods

Bernoulli sub-ODE method

As a result of the homogeneous balancing of the uppermost order derivative term \(R^{\prime \prime }\) and the nonlinear component \(R^3\) in (4.6), we have determined that N = 1. As a result, the method that we have proposed facilitate us to make use of the auxiliary solution of the form:

$$\begin{aligned} s\left( \nu \right) = {b_0} + {b_1}P\left( \nu \right) , \end{aligned}$$
(5.1)

where P fulfills (5.1) in the manner

$$\begin{aligned} {P^\prime (\nu ) } + \eta P(\nu ) = \delta (P(\nu ))^2, \end{aligned}$$
(5.2)

where the constants \({b_0},{b_1}\) will be found later.

Substituting (5.2) into (4.6) yields,

$$\begin{aligned} & {\Omega ^2}{b_0} + \Theta b_0^3 + {\Omega ^2}P\left( \nu \right) {b_1} + {e^2}{\eta ^2}P\left( \nu \right) {b_1} - {f^2}{\eta ^2}P\left( \nu \right) {b_1} - 3{e^2}\eta \delta P{\left( \nu \right) ^2}{b_1} + 3{f^2}\eta \delta P{\left( \nu \right) ^2}{b_1} + 2{e^2}{\delta ^2}P{\left( \nu \right) ^3}{b_1}\\ & \quad - 2{f^2}{\delta ^2}P{\left( \nu \right) ^3}{b_1} + 3\Theta P\left( \nu \right) b_0^2{b_1} + 3\Theta P{\left( \nu \right) ^2}{b_0}b_1^2 + \Theta P{\left( \nu \right) ^3}b_1^3. \end{aligned}$$

Comparing the coefficient of \({P(\nu )^l}(l = 0,1,2,3)\), we have

$$\begin{aligned} & P^0:{\Omega ^2}{b_0} + \Theta b_0^3 = 0.\nonumber \\ & P^1:{\Omega ^2}{b_1} + {e^2}{\eta ^2}{b_1} - {f^2}{\eta ^2}{b_1} + 3\Theta b_0^2{b_1} = 0.\nonumber \\ & P^2: - 3{e^2}\eta \delta {b_1} + 3{f^2}\eta \delta {b_1} + 3\Theta {b_0}b_1^2 = 0.\nonumber \\ & P^3: 2{e^2}{\delta ^2}{b_1} - 2{f^2}{\delta ^2}{b_1} + \Theta b_1^3 = 0. \end{aligned}$$
(5.3)

For all mathematical statements to be considered algebraic equations, they must all equal zero.

Set 1: Let \({b_0} = - \frac{\sqrt{-e^2 \eta ^2 + f^2 \eta ^2}}{\sqrt{2\Theta }},{b_1} = \frac{\sqrt{2}\sqrt{-((e^2 - f^2) \eta ^2)}\delta }{\sqrt{\Theta }\eta }\). Subsequently, the following solutions are derived.

In the case where \(\delta \ne 0\) , the solution is;

$$\begin{aligned} P = \frac{\eta }{\delta + \eta F \exp (\eta \nu )}, \end{aligned}$$
(5.4)

where F is an indeterminate constant. We now substitute the values of \(P, b_0\) and \(b_1\) into (5.1), we get the following:

$$\begin{aligned} {s_{1,1}}(k,t) = - \frac{\sqrt{-e^2 \eta ^2 + f^2 \eta ^2}}{\sqrt{2\Theta }} + \frac{\sqrt{2}\sqrt{-((e^2 - f^2) \eta ^2)}\delta }{\sqrt{\Theta }\eta } (\frac{\eta }{\delta + \eta F \exp (\eta \nu )}) . \end{aligned}$$
(5.5)

When \(\delta = 0\), the answer to the (5.4) can be reduced to the following:

$$\begin{aligned} P = \frac{1}{F \exp (- \eta \nu )}. \end{aligned}$$
(5.6)

Putting \(F = \frac{\delta }{\eta }\) , we obtain

$$\begin{aligned} P = \frac{-\eta }{2\delta } \Bigg (\tanh \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg ). \end{aligned}$$
(5.7)

Putting \(F = \frac{-\delta }{\eta }\) , we obtain

$$\begin{aligned} P = \frac{-\eta }{2\delta } \Bigg (\coth \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg ). \end{aligned}$$
(5.8)

After that we get the following by substituting the values of \(b_0\) and \(b_1\) into (5.1) along with (5.7) and (5.8),

$$\begin{aligned} & {s_{1,2}}(k,t) = - \frac{\sqrt{-e^2 \eta ^2 + f^2 \eta ^2}}{\sqrt{2\Theta }} + \frac{\sqrt{2}\sqrt{-((e^2 - f^2) \eta ^2)}\delta }{\sqrt{\Theta }\eta }\Bigg (\frac{-\eta }{2\delta } \Bigg (\tanh \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg )\Bigg ). \end{aligned}$$
(5.9)
$$\begin{aligned} & {s_{1,3}}(k,t) = - \frac{\sqrt{-e^2 \eta ^2 + f^2 \eta ^2}}{\sqrt{2\Theta }} + \frac{\sqrt{2}\sqrt{-((e^2 - f^2) \eta ^2)}\delta }{\sqrt{\Theta }\eta }\Bigg (\frac{-\eta }{2\delta } \Bigg (\coth \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg )\Bigg ). \end{aligned}$$
(5.10)

Set 2: Let \(b_0 = 0 , b_1 = \frac{\sqrt{2}\Omega \delta }{\sqrt{\Theta }\eta }\). Subsequently, the following solutions are derived.

In the case when \(\delta \ne 0\) , the solution is;

$$\begin{aligned} P = \frac{\eta }{\delta + \eta F \exp (\eta \nu )}, \end{aligned}$$
(5.11)

where F is an indeterminate constant. We now substitute the values of P, \(b_0\) and \(b_1\) into (5.1), we get the following:

$$\begin{aligned} s_{2,1}(k,t) = \frac{\sqrt{2}\Omega \delta }{\sqrt{\Theta }\eta } \Bigg ( \frac{\eta }{\delta + \eta F \exp (\eta \nu )}\Bigg ). \end{aligned}$$
(5.12)

When \(\delta = 0\) ,the answer to the (5.11) can be reduced to the following:

$$\begin{aligned} P = \frac{1}{F \exp (- \eta \nu )}. \end{aligned}$$
(5.13)

Putting \(F = \frac{\delta }{\eta }\) , we obtain

$$\begin{aligned} P = \frac{-\eta }{2\delta } \Bigg (\tanh \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg ). \end{aligned}$$
(5.14)

Putting \(F = \frac{-\delta }{\eta }\) , we obtain

$$\begin{aligned} P = \frac{-\eta }{2\delta } \Bigg (\coth \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg ). \end{aligned}$$
(5.15)

After that, we get the following by substituting the values of \(b_0\) and \(b_1\), into (5.1), along with (5.14) and (5.15).

$$\begin{aligned} s_{2,2}(k,t)= & \frac{\sqrt{2}\Omega \delta }{\sqrt{\Theta }\eta } \Bigg (\frac{-\eta }{2\delta } \Bigg (\tanh \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg )\Bigg ), \end{aligned}$$
(5.16)
$$\begin{aligned} s_{2,3}(k,t)= & \frac{\sqrt{2}\Omega \delta }{\sqrt{\Theta }\eta } \Bigg (\frac{-\eta }{2\delta } \Bigg (\coth \Bigg (\frac{\eta }{2}\nu \Bigg ) - 1\Bigg )\Bigg ), \end{aligned}$$
(5.17)

Extended direct algebraic method

As a result of the homogeneous balancing of the uppermost order derivative term \(R^{\prime \prime }\) and the nonlinear component \(R^3\) in (4.6), we have determined that N = 1. As a result, the method that we have proposed enables us to make use of the auxiliary solution of the form:

$$\begin{aligned} S(\nu ) = a_0 + a_1 U(\nu ), \end{aligned}$$
(5.18)

where the constants \(a_0\) and \(a_1\) will be found later and U fulfill (5.18) in the manner

$$\begin{aligned} U^{\prime }(\nu ) = \ln \sigma (\alpha + \omega U(\nu ) + \phi (U(\nu ))^2). \end{aligned}$$
(5.19)

Substituting (5.19) into (4.6) yields,

$$\begin{aligned} & \Omega ^2a_0 + \Theta {a_0}^3 + \Omega ^2 U(\nu )a_1 + e^2\alpha \omega \ln (\sigma )^2 a_1 - f^2\alpha \omega \ln (\sigma )^2a_1 + e^2\omega ^2 U(\nu )\ln (\sigma )^2a_1 - f^2\omega ^2 U(\nu )\ln (\sigma )^2a_1 \nonumber \\ & + 2e^2 \alpha \phi U(\nu ) \ln (\sigma )^2a_1 - 2f^2 \alpha \phi U(\nu ) \ln (\sigma )^2a_1 + 3e^2 \omega \phi U(\nu )^2\ln (\sigma )^2a_1 - 3f^2 \omega \phi U(\nu )^2\ln (\sigma )^2a_1 \nonumber \\ & + 2e^2\phi ^2 U(\nu )^3\ln (\sigma )^2a_1 - 2f^2\phi ^2 U(\nu )^3\ln (\sigma )^2a_1 + 3\Theta U(\nu )a_0^2a_1 + 3\Theta U(\nu )a_0a_1^2 + \Theta U(\nu )^3a_1^3. \end{aligned}$$
(5.20)

Comparing the coefficient of \({U(\nu )^y},y = 0,1,2,3\) we have

$$\begin{aligned} & U^0: \Omega ^2a_0 + \Theta a_0^3 + e^2\alpha \omega \ln (\sigma )^2a_1 - f^2\alpha \omega \ln (\sigma )^2a_1 = 0.\nonumber \\ & U^1: \Omega ^2a_0 + e^2\omega ^2\ln (\sigma )^2a_1 - f^2\omega ^2\ln (\sigma )^2a_1 + 2e^2\alpha \phi \ln (\sigma )^2a_1 - 2f^2\alpha \phi \ln (\sigma )^2a_1 + 3\Theta a_0^2a_1 = 0.\nonumber \\ & U^2: 3e^2\omega \phi \ln (\sigma )^2a_1 - 3f^2\omega \phi \ln (\sigma )^2a_1 + 3\Theta a_0a_1^2 = 0.\nonumber \\ & U^3: 2e^2\phi ^2\ln (\sigma )^2a_1 - 2f^2\phi ^2\ln (\sigma )^2a_1 + \Theta a_1^3 = 0. \end{aligned}$$
(5.21)

For all mathematical statements to be considered algebraic equations, they must all equal zero.

By utilizing the computer software Mathematica, we are able to solve these algebraic equations and we get,

$$\begin{aligned} a_0 = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} , a_1 = \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} , \beta = \frac{\sqrt{e^2 - f^2}\sqrt{\omega ^2 - 4\alpha \phi }\ln \sigma }{\sqrt{2}}. \end{aligned}$$
(5.22)

Here \(\Delta = \omega ^2 - 4\alpha \phi\).

After going through a variety of values of \(U(\nu )\) from (3.15) to (3.51), we obtain numerous corresponding outcomes.

1. For \({\omega ^2}\) - 4\({\alpha }\) \({\phi }\) \({<}\) 0 and \({\phi }\) \({\ne }\) 0, we have

$$\begin{aligned} S_1(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } + \frac{\sqrt{-\Theta }}{2 \phi } \tan _\sigma \Bigg (\frac{\sqrt{-\Theta }}{2}\nu \Bigg )\Bigg ),\\ S_2(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } - \frac{\sqrt{-\Theta }}{2 \phi } \cot _\sigma \Bigg (\frac{\sqrt{-\Theta }}{2}\nu \Bigg )\Bigg ),\\ S_3(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } + \frac{\sqrt{-\Theta }}{2 \phi } ( \tan _\sigma ({\sqrt{-\Theta } \nu }) \pm \sqrt{\zeta \varrho } \sec _\sigma (\sqrt{-\Theta }\nu ))\Bigg ),\\ S_4(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg ( - \frac{\omega }{2 \phi } + \frac{\sqrt{-\Theta }}{2 \phi } ( \cot _\sigma ({\sqrt{-\Theta } \nu }) \pm \sqrt{\zeta \varrho } \csc _\sigma (\sqrt{-\Theta }\nu ))\Bigg ) \end{aligned}$$

and

$$\begin{aligned} S_5(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg ( - \frac{\omega }{2 \phi } + \frac{\sqrt{-\Theta }}{4 \phi } \Bigg ( \tan _\sigma \Bigg (\frac{\sqrt{-\Theta }}{4} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\sqrt{-\Theta }}{4}\nu \Bigg )\Bigg ). \end{aligned}$$

2. For \({\omega ^2}\) - 4\({\alpha }\) \({\phi }\) \({>}\) 0 and \({\phi }\) \({\ne }\) 0, we have

$$\begin{aligned} S_6(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } - \frac{\sqrt{\Theta }}{2 \phi } \tanh _\sigma \Bigg (\frac{\sqrt{\Theta }}{2}\nu \Bigg )\Bigg ),\\ S_7(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } - \frac{\sqrt{\Theta }}{2 \phi } \coth _\sigma \Bigg (\frac{\sqrt{\Theta }}{2}\nu \Bigg )\Bigg ),\\ S_8(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } + \frac{\sqrt{\Theta }}{2 \phi } (- \tanh _\sigma ({\sqrt{\Theta } \nu }) \pm \iota \sqrt{\zeta \varrho }\, {\textrm{sech}}_\sigma (\sqrt{\Theta }\nu ))\Bigg ),\\ S_9(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }} \Bigg (- \frac{\omega }{2 \phi } + \frac{\sqrt{\Theta }}{2 \phi } (- \coth _\sigma ({\sqrt{\Theta } \nu }) \pm \sqrt{\zeta \varrho }\, {\textrm{csch}}_\sigma (\sqrt{\Theta }\nu ))\Bigg ) \end{aligned}$$

and

$$\begin{aligned} S_{10}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \frac{\omega }{2 \phi } - \frac{\sqrt{\Theta }}{4 \phi } \Bigg ( \tanh _\sigma \Bigg (\frac{\sqrt{\Theta }}{4} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\sqrt{\Theta }}{4}\nu \Bigg )\Bigg )\Bigg ). \end{aligned}$$

3. For \({\alpha }\) \({\phi }\) \({>}\) 0 and \({\omega } = 0\), we have

$$\begin{aligned} S_{11}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\sqrt{ \frac{\alpha }{\phi }} \tan _\sigma (\sqrt{\alpha \phi }\nu )\Bigg ),\\ S_{12}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \sqrt{ \frac{\alpha }{\phi }} \cot _\sigma (\sqrt{\alpha \phi }\nu )\Bigg ),\\ S_{13}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\sqrt{ \frac{\alpha }{\phi }}( \tan _\sigma (2 \sqrt{\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\sec _\sigma (2 \sqrt{\alpha \phi }\nu ))\Bigg ),\\ S_{14}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\sqrt{ \frac{\alpha }{\phi }}(- \cot _\sigma (2 \sqrt{\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\csc _\sigma (2 \sqrt{\alpha \phi }\nu ))\Bigg ) \end{aligned}$$

and

$$\begin{aligned} S_{15}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\frac{1}{2} \sqrt{\frac{\alpha }{ \phi }} \Bigg ( \tan _\sigma (\frac{\sqrt{\alpha \phi }}{2} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\sqrt{\alpha \phi }}{2}\nu \Bigg )\Bigg )\Bigg ). \end{aligned}$$

4. For \({\alpha }\) \({\phi }\) \({<}\) 0 and \({\omega }\) = 0, we have

$$\begin{aligned} S_{16}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (-\sqrt{- \frac{\alpha }{\phi }} \tanh _\sigma (\sqrt{-\alpha \phi }\nu )\Bigg ),\\ S_{17}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (-\sqrt{- \frac{\alpha }{\phi }} \coth _\sigma (\sqrt{-\alpha \phi }\nu )\Bigg ),\\ S_{18}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (-\sqrt{- \frac{\alpha }{\phi }}( \tanh _\sigma (2 \sqrt{-\alpha \phi }\nu ) \pm \iota \sqrt{\zeta \varrho }\, {\textrm{sech}}_\sigma (2 \sqrt{-\alpha \phi }\nu ))\Bigg ),\\ S_{19}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (-\sqrt{- \frac{\alpha }{\phi }}( \coth _\sigma (2 \sqrt{-\alpha \phi }\nu ) \pm \sqrt{\zeta \varrho }\, {\textrm{csch}}_\sigma (2 \sqrt{-\alpha \phi }\nu ))\Bigg ) \end{aligned}$$

and

$$\begin{aligned} S_{20}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \frac{1}{2} \sqrt{-\frac{\alpha }{ \phi }} \Bigg ( \tanh _\sigma \Bigg (\frac{\sqrt{-\alpha \phi }}{2} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\sqrt{-\alpha \phi }}{2}\nu \Bigg )\Bigg )\Bigg ). \end{aligned}$$

5. For \({\omega }\) = 0 and \({\alpha }\) = \({\phi }\) , we have

$$\begin{aligned} S_{21}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(\tan _\sigma (\alpha \nu )),\\ S_{22}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(-\cot _\sigma (\alpha \nu )),\\ S_{23}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(\tan _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho } \sec _\sigma (2 \alpha \nu )), \end{aligned}$$
$$\begin{aligned} S_{24}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}( -\cot _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho } \csc _\sigma (2 \alpha \nu )) \end{aligned}$$

and

$$\begin{aligned} S_{25}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\frac{1}{2} \Bigg (\tan _\sigma (\frac{\alpha }{2} \nu \Bigg ) - \cot _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg )\Bigg )\Bigg ). \end{aligned}$$

6. For \({\omega }\) = 0 and \({\phi }\) = \({-\alpha }\) , we have

$$\begin{aligned} S_{26}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(-\tanh _\sigma (\alpha \nu )),\\ S_{27}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}( -\coth _\sigma (\alpha \nu )),\\ S_{28}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(-\tanh _\sigma (2 \alpha \nu ) \pm \iota \sqrt{\zeta \varrho }\, {\textrm{sech}}_\sigma (2 \alpha \nu )),\\ S_{29}(k,t)= & \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(-\coth _\sigma (2 \alpha \nu ) \pm \sqrt{\zeta \varrho }\, {\textrm{csch}}_\sigma (2 \alpha \nu )) \end{aligned}$$

and

$$\begin{aligned} S_{30}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (-\frac{1}{2} \Bigg (\tanh _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg ) + \coth _\sigma \Bigg (\frac{\alpha }{2} \nu \Bigg )\Bigg ). \end{aligned}$$

7. For \({\omega ^2}\) = 4\({\alpha }\) \({\phi }\) , we have

$$\begin{aligned} S_{31}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\frac{-2 \alpha (\omega \nu \ln (\sigma ) + 2)}{\omega ^2 \nu \ln (\sigma )}\Bigg ). \end{aligned}$$

8. For \({\omega }\) = m, \({\alpha }\) = mf (\(f {\ne }\) 0) and \({\phi }\) = 0 , we have

$$\begin{aligned} S_{32}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(\sigma ^{m\nu } - f). \end{aligned}$$

9. For \({\alpha }\) = \({\phi }\) = 0 , we have

$$\begin{aligned} S_{33}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}(\alpha \nu \ln (\sigma )). \end{aligned}$$

10. For \({\omega }\) = \({\alpha }\) = 0 , we have

$$\begin{aligned} S_{34}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (\frac{-1}{\phi \nu \ln (\sigma )}\Bigg ). \end{aligned}$$

11. For \({\omega }\) \({\ne }\) 0 and \({\alpha }\) = 0 , we have

$$\begin{aligned} S_{35}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \frac{\zeta \omega }{\phi (\cosh _\sigma (\omega \nu ) - \sinh _\sigma (\omega \nu ) + \zeta )}\Bigg ). \end{aligned}$$

and

$$\begin{aligned} S_{36}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \frac{\omega (\sinh _\sigma (\omega \nu ) + \cosh _\sigma (\omega \nu ))}{\phi (\sinh _\sigma (\omega \nu ) + \cosh _\sigma (\omega \nu ) + \varrho )}\Bigg ). \end{aligned}$$

12. For \({\omega } = {m}\), \({\phi } = {mf}\) (\(f {\ne }\) 0) and \({\alpha } = 0\) , we have

$$\begin{aligned} S_{37}(k,t) = \frac{\iota \sqrt{e^2 - f^2}\omega \ln \sigma }{\sqrt{2\Theta }} + \frac{\iota \sqrt{2}\sqrt{e^2 - f^2}\phi \ln \sigma }{\sqrt{\Theta }}\Bigg (- \frac{\zeta \sigma ^{m \nu }}{\zeta - f \varrho \sigma ^{m \nu }}\Bigg ). \end{aligned}$$

Results and discussion

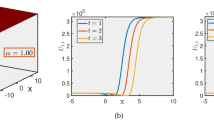
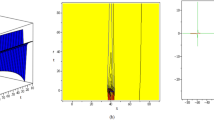
In this study we have solved the time-fractional Phi-four equation analytically by employing fractional derivative such as conformable derivative. The effective methods EDAM and BSODEM were used to acquire these solutions. The methods have produced several solutions and 2D graphics have been employed to compare the results for the derivative operator. Solitary waves are generated by using the previously mentioned methods in many forms such as periodic, M-shaped, W-shaped, dark, sharp dark, smooth dark-bright, kink, anti-kink, bell, smooth bell and anti-bell type of solitons. Variations in the value of the fractional parameter resulted in a modest alteration of the solitary wave without changing its curve form. The trigonometric and hyperbolic function solution in \(|s_{1,2}(k, t)|\), we determine the dark soliton solution for the 2D and 3D graphs by considering the values \(\Theta = 0.05\), \(\eta = 1.14\), \(\delta = 0.55\), \(e = 0.0095\), \(f = 0.99\) having the interval \(-6 \le k \le 6, -3 \le t \le 3\) as shown in Fig. 1 by BSODEM. For the trigonometric and hyperbolic function solution in 2D and 3D graphs of \(|s_{2,2}(k, t)|\), we calculate the kink type soliton solution for \(\Theta = 0.05\), \(\eta = 0.14\), \(\delta = 1.55\), \(\Omega = 1.09\) having \(-10 \le k \le 10, -3 \le t \le 3\) range and is shown in Fig. 2 by BSODEM. Figure 3 represents trigonometric solution in \(|S_1(k,t)|\) and gives the periodic soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0.06\), \(\alpha = 1.03\), \(f = 4\), \(\sigma = 2\), \(\zeta = 1.9\), \(\varrho = 0.09\), \(\phi = 1.05\) within the range \(-1 \le k \le 2, -1 \le t \le 1\) by EDAM. For the trigonometric function solution of \(S_5(k, t)\), we calculate the bell-shaped soliton solution for \(e = 0.07\), \(\Theta = 0.09\), \(\omega = 0.06\), \(\alpha = 1.03\), \(f = 1\), \(\sigma = 2\), \(\zeta = 1.4\), \(\varrho = 1.02\), \(\phi = 1.05\) within the interval\(-1 \le t \le 1\), \(-2 \le k \le 2\) in Fig. 4 by EDAM. Figure 5 represents trigonometric and hyperbolic solution in \(S_8(k,t)\), we get the anti-kink soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 2.6\), \(\alpha = 0.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.04\), \(\varrho = 1.5\), \(\phi = 1.5\) within the range \(-6 \le k \le 6, 0 \le t \le 4\) by using EDAM. For the trigonometric function solution of \(|S_{11}(k, t)|\) and \(|S_{12}(k,t)|\), we calculate the M-shaped and smooth bell-shaped soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.04\),\(\zeta = 1.9\), \(\varrho = 0.2\), \(\varrho = 0.05\), \(\phi = 1.5\) within the interval \(-1 \le t \le 1, -2 \le k \le 2\) and \(-1 \le k \le 1, -1 \le t \le 1\) by using EDAM as shown in Figs. 6 and 7. Figure 8 represents trigonometric solution in \(S_{14}(k,t)\), we obtain the anti-bell soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.5\), \(\varrho = 0.01\), \(\phi = 1.01\) by using EDAM within the range \(-1 \le k \le 1, -1 \le t \le 1\). For the trigonometric function solution of \(S_{15}(k, t)\), we calculate the periodic soliton solution by taking into account the values \(\Theta = 0.09\), \(e = 2.1\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.01\), \(\varrho = 0.09\), \(\phi = 1.5\) by using EDAM within the interval \(0 \le k \le 2, 0 \le t \le 3\) in Fig. 9. Figure 10 represents trigonometric and hyperbolic solution in \(|S_{16}(k,t)|\), we get the sharp dark soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = -1.3\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.09\), \(\varrho = 0.003\), \(\phi = 1.5\) within the range \(-3 \le k \le 2, 0 \le t \le 1\) by using EDAM. For the trigonometric function solution of \(|S_{22}(k, t)|\), we get the W-shaped soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.03\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.9\), \(\varrho = 0.05\), \(\phi = 1.05\) within the interval \(0 \le k \le 3, 0 \le t \le 1\) by using EDAM as shown in Fig. 11. Figure 12 represents trigonometric solution in \(S_{25}(k,t)\), being we get the smooth dark-bright soliton solution for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 0.25\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.01\), \(\varrho = 0.019\), \(\phi = 0.25\) within the range \(0 \le k \le 5, -2 \le t \le 2\) by using EDAM.

Figure 1
figure 1

Analytical result of \(|s_{1,2}(k,t)|\) gives dark soliton by using BSODE method, for \(f = 0.99\), \(\Theta = 0.05\), \(\eta = 1.14\), \(\delta = 0.55\), \(e = 0.0095\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 2
figure 2

Analytical result of \(|s_{2,2}(k,t)|\) gives kink-type soliton by using BSODE method, for \(\Omega = 1.09\), \(\Theta = 0.05\), \(\eta = 0.14\), \(\delta = 1.55\), \(e = 0.95\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 3
figure 3

Analytical result of \(|S_1(k,t)|\) gives periodic soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0.06\), \(\alpha = 1.03\), \(f = 4\), \(\sigma = 2\), \(\zeta = 1.9\), \(\varrho = 0.09\), \(\phi = 1.05\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 4
figure 4

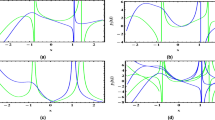
Analytical imaginary result of \(S_5(k,t)\) gives bell-shaped soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0.06\), \(\alpha = 1.03\), \(f = 1\), \(\sigma = 2\), \(\zeta = 1.4\), \(\varrho = 1.02\), \(\phi = 1.05\), (a): 3D imaginary plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 5
figure 5

Analytical real result of \(S_8(k,t)\) gives anti-kink soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 2.6\), \(\alpha = 0.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.04\), \(\varrho = 1.5\), \(\phi = 1.5\), (a): 3D real plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 6
figure 6

Analytical result of \(|S_{11}(k,t)|\) gives M-shaped soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.04\), \(\varrho = 0.2\), \(\phi = 1.5\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 7
figure 7

Analytical result of \(|S_{12}(k,t)|\) gives smooth bell-shaped soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.9\), \(\varrho = 0.05\), \(\phi = 1.5\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 8
figure 8

Analytical imaginary result of \(S_{14}(k,t)\) gives anti-bell shaped soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 2\), \(\sigma = 2\), \(\zeta = 1.5\), \(\varrho = 0.01\), \(\phi = 1.01\), (a): 3D imaginary plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 9
figure 9

Analytical imaginary result of \(S_{15}(k,t)\) gives periodic soliton by using EDA method, for \(\Theta = 0.09\), \(e = 2.1\), \(\omega = 0\), \(\alpha = 1.3\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.01\), \(\varrho = 0.09\), \(\phi = 1.5\), (a): 3D imaginary plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 10
figure 10

Analytical result of \(|S_{16}(k,t)|\) gives sharp dark soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = -1.3\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.09\), \(\varrho = 0.003\), \(\phi = 1.5\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 11
figure 11

Analytical result of \(|S_{22}(k,t)|\) gives W-shaped soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 1.03\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.9\), \(\varrho = 0.05\), \(\phi = 1.05\), (a): 3D plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image
Figure 12
figure 12

Analytical real result of \(S_{25}(k,t)\) gives smooth dark-bright soliton by using EDA method, for \(\Theta = 0.09\), \(e = 0.07\), \(\omega = 0\), \(\alpha = 0.25\), \(f = 3\), \(\sigma = 2\), \(\zeta = 1.01\), \(\varrho = 0.019\), \(\phi = 0.25\), (a): 3D real plot, (b): t-variant, (c): \(\xi\)-variant.

Full size image

Physical interpretation and applications

Physical interpretation

Time-fractional Phi-four equation is a complex model that has attracted the interest of mathematicians and physicists due to its applications in physics and other disciplines. This equation can accurately represent numerous complex changes in nature. A dark soliton represented in Fig. 1 is a localized perturbation in a wave medium characterized by a minimal amplitude at its center, but preserving a continuous phase structure. These solitons represent solutions to nonlinear partial differential equations, including the nonlinear Schrödinger equation, which characterize wave propagation in certain nonlinear mediums. A kink soliton demonstrated in Fig. 2 is a solution to specific nonlinear field equations that signifies a localised, stable transition between two distinct states of a system. These solutions hold particular importance in domains such as condensed matter physics, field theory and nonlinear dynamics. Periodic solitons pictured in Figs. 3 and 9 are type of wave pattern that repeats in space and time periodically. The waves keep their form and coherence across vast distances because the system is nonlinear. They simulate tsunamis, coastal areas and shallow water waves in fluid dynamics. They detail the steady streams of light in lasers and optical fibers in the field of nonlinear optics. The bell and smooth bell-shaped solitons displayed in Figs. 4 and 7 are used extensively in various scientific fields due to its limited stable wave patterns. These solitons are isolated wave transmissions that have the capacity to travel great distances without changing form. To demonstrate how light waves travel across optical fibers, bell-shaped solitons are employed in NL optics. Figure 5 illustrates an anti-kink, which is a phase shift that reverses the direction of a kink. For example, if a kink moves from a smaller prospective to a greater one,the anti-kink moves from a higher prospective to a fewer one. Anti-kinks, like kinks, are localized patches where the energy density differs from the surrounding environment. Typically, an M-shaped soliton displayed in Fig. 6 is a localized disruption with a specific form resembling the letter M. This arrangement usually indicates two peaks in an energy environment. A harmonious interaction between dispersion and nonlinearity may result in the formation of multi-peak patterns. It can be found in many different contexts, including fluid dynamics, plasma physics and nonlinear optics. It represents localized areas of high density or intensity that are separated by a trough. An anti-bell-shaped soliton represented in Fig. 8 is a solitary wave characterized by an inverted profile relative to a conventional bell shape, including a core depression surrounded by raised areas. The anti-bell-shaped soliton signifies a localized deficit in energy, density or intensity maintained by the equilibrium of nonlinear phenomena and dispersion. It is essential for comprehending phenomena such as phase transitions, energy redistribution and wave stability in nonlinear systems. A sharp dark soliton shown in Fig. 10 is a localized density dip or depletion in a medium such as nonlinear optical medium or water waves that propagates without changing its shape due to a balance between nonlinearity and dispersion. This type of soliton is characterized by its ability to propagate without changing its composition. The W-shaped solitons depicted in Fig. 11 are distinguished by a trough and two peaks that combine to create the letter W. A lower energy level is shown by the fall whereas regions of high energy or intensity are represented by the two heights. This can be particularly important in fields like plasma physics or Bose-Einstein condensed matter where these energy dispersions may affect stability and dynamics. Smooth dark-bright soliton displayed in Fig. 12 is a hybrid or mixed wave phenomena that combines the properties of bright and dark soliton in one solution. The smooth dark-bright soliton is a localized structure where the peak of the brilliant soliton and the dip of the dark soliton interact closely. This generally results in a smoother transition between the two zones. These solitons can be used to simulate pulse propagation in nonlinear optical fibers, potentially mitigating difficulties such as dispersion and nonlinear distortion.

Applications

The time-fractional Phi-four equation is a PDE that extends the normal Phi-four equation by include fractional derivatives with respect to time. In order to represent heat and mass transfer in materials with complex structures such as fractals or heterogeneous media, the time-fractional Phi-four equation can be utilized. Fractional derivatives are responsible for the non-local thermal or diffusive effects that take place in materials with memory. These effects are characterized by the fact that heat or mass does not spread in a straightforward manner. A broad variety of phenomena can be modeled with the help of the time-fractional phi-four equation which is a useful tool for modeling situations in which traditional models with integer-order time derivatives are unable to describe complex time-dependent behaviors. Its applications can be found in a wide variety of fields including as economics, engineering, biology and physics.

Conclusions

In this paper, the EDA and BSODE methods are used to offer analytical solutions to the time-fractional Phi-four equation. The time-fractional Phi-four equation is a prominent feature in the field of compact matter mechanics. The time-fractional Phi-four equation has been widely employed in particle and nuclear physics to investigate quantum phenomena including wave-particle duality and solitons in a plasma without collisions. The methods applied on time-fractional Phi-four equation are standard and computable enabling for us to accomplish intricate and time-consuming algebraic computations. Both methodologies are extensively utilized and effective when applied to differential equations. In terms of fractional functions, we have successfully acquired exact solutions as well as single wave solutions with these approaches. We have derived wave solutions of solitons for each of the analyzed equations which include a few unknown factors. The principles of fractional derivative specifically conformable derivative is utilized to produce many types of soliton solutions such as periodic, dark, sharp dark, bell, smooth bell, anti-bell, M-shaped, W-shaped, kink, anti-kink, smooth dark bright type solitons. Specific findings are shown in 2D and 3D graphs to show the physical appearance of the solutions when appropriate parameter choices are selected. This endeavor aims to identify new precisely specified solitons for time-fractional Phi-four equation that have never been found before. The identified solutions will facilitate the investigation of issues pertaining to the field of engineering, waves caused by tides, tsunamis and physical theory. Finally, the Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 were displayed using the mathematica tools to illustrate how the time-fractional Phi-four equation’s analytical solution is impacted by the fractional derivative.