Introduction

Electrostatic interactions are responsible for several natural phenomena, such as thunderstorms, sandstorms or volcanic plumes and significantly influence several industrial processes involving particulate materials1. Examples of the latter include electrophotography2, electrostatic powder coating and particle separation3. In biological systems, electrostatic interactions between charged lipid membranes and aqueous solutions give rise to various unusual behaviours that can be explained in terms of polarization and dipole orientations4,5. Electrostatic charge exchange between contacting solid surfaces (a phenomenon called “tribocharging”6) is usually identified as the primary cause of charge accumulation. In powder processing, electrostatic interactions often cause severe and unpredictable consequences, such as inhomogeneities, component segregation, particle adhesion to walls, and agglomeration, in turn affecting the safety of the workforce and facilities7 as well as product quality8,9. Manifestations are commonly observed in granular streams10, vibrated beds11, rotating drums12, pneumatic conveying lines13,14, hopper chute assembly15, during powder dispersion16,17 and deagglomeration18,19, or even just granule sliding20,21 or active fluctuations22. In gas–solid polymerization reactors, the agglomeration of particles is known to be the main cause of the “sheeting” phenomenon, caused by polymer particle melting due to accumulation at the reactor walls23,24,25,26,27.

Particle-scale simulation tools, such as the Discrete Element Method (DEM), are considered key resources in the dynamic modeling of industrial particulate processing. As opposed to methods for spatial fields or solids continua like the Finite Element Method, which naturally applies to deforming solid bodies, the DEM was developed for granular material and involves tracking individual particles in their motion. The approach results extremely flexible, offering the possibility to incorporate a broad variety of force contributions (see the section Methods for a more detailed description). Among the conventional models proposed to include tribocharging effects in DEM simulations are the condenser model28,29,30, the charge relaxation model31,32,33, the mosaic model34,35 and the nonuniform charge model36. In most of the references cited, charged particles are considered to interact by the Coulomb law, approximating them as point charges whose level is the actual particle net charge. Polarizable particles, however, may behave differently, as the local surface charge distribution may significantly affect the intensity or even the sign of the interaction. For example, a charged body close to a neutral body is known to attract it, as in the well-known example of a charged amber rod that lifts small paper bits by attraction. Additionally, the induced polarization can cause particles charged by the same polarity to attract37, as was observed in experiments38 and shown by theoretical calculations39,40.

This work aims to propose a realistic particle-scale model that includes polarization effects on the interaction forces between spherical particles of varying sizes and charges. Property combinations that lead to behaviors not predicted by conventional Coulomb models are investigated. Macroscopic effects in systems with hundreds of thousands of particles are discussed, along with the model’s current limitations.

Effective dipole model of the interaction between polarizable particles

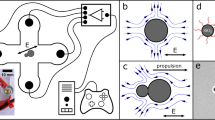
Polarizable materials tend to exhibit uneven charge distributions across the surface. For example, close charged particles show accumulation of opposite charges around the closest point, as schematically depicted in Fig. 1a. In addition to the effect of their net charges, polarization can significantly influence the interaction force, particularly at close distances, and should be correctly accounted for. The actual charge distribution can be directly calculated by somewhat sophisticated approaches, as discussed below. As anticipated, the point-charge approximation estimated via the application of Coulomb’s law, whose schematic representation is shown in Fig. 1b, is widely used. We propose modeling the interactions by combining each particle’s net charge \(q_i\) with an effective dipole \(p_i\), aiming at accounting for the uneven inducted charge distribution, as depicted in Fig. 1c. A comprehensive method, the point charge approximation and the proposed effective dipole models are described in detail below.

Fig. 1
figure 1

Graphic representation of charged particles and their models: (a) realistic charge distribution, (b) point charge approximation and (c) charge and effective dipole model.

Full size image

Electrostatic interactions with polarization

A rigorous treatment of the charge distributions on the surfaces of interacting particles requires detailed consideration of the local inhomogeneities (see Fig. 1a). Among the different possibilities, two methods worth mentioning are: the multipole expansion method proposed by Bitchoutskaia et al.41 and Lindgren et al.42,43 and the hybrid model, combining the method of moments and the image charge method, proposed by Gan et al.44,45. The latter was developed to account for many interacting polarizable particles in a physically sound way and with a computationally efficient strategy for such complex configuration. Here, we briefly recall the method of Lindgren et al. for two spheres. The approach allows the actual charge distribution on the interacting surfaces to be calculated, and the net force \(F_e\) can then be derived by summing all the microscopic contributions. The key formula is summarized in Eq. (1).

$$\begin{aligned} F_{e} = K \frac{q_i q_j}{h^2} - q_i \sum _{m=1}^{\infty } \sum _{l=0}^{\infty } {A_{i,l} \frac{(k_j-1) m (m+1)}{(k_j+1) m + 1}} \frac{(l+m)!}{(l! m!)} \frac{r_j^{2m+1}}{h^{2m+l+3}} - \frac{1}{K} \sum _{l=1}^{\infty } A_{i,l} A_{i,l+1} \frac{(k_i+1)(l+1) + 1}{(k_i-1) r_i^{2l+3}} \end{aligned}$$
(1)

where \(K=1/(4\pi \varepsilon _0)\) is the Coulomb constant with \(\varepsilon _0\) as the vacuum permittivity; \(q_i\) and \(q_j\) are the net charges of the particles; \(r_i\), \(r_j\), \(k_i\) and \(k_j\) are their radii and dielectric constants, respectively; \(k=\varepsilon /\varepsilon _0\); h is the distance between the centers of the particles, and \(A_{i,l}\) are coefficients that describe the mutual polarization experienced by the particles. The dependence of the \(A_{i,l}\) coefficients on the particle charges and interparticle distance prevents their a priori calculations. The first term in Eq. (1) is the Coulomb force, and the second and third terms include the polarization contributions. With this equation, it is possible to capture the attractive interaction (negative electrostatic force) between two like-charged particles. In Figs. 2 and  3a different cases are illustrated. As noted, the formula requires infinite summations, which can be truncated to a finite number of terms to obtain reasonable estimates of the actual force. Unfortunately, the number of terms required to satisfy a prescribed precision can easily reach 30 or higher, depending on the level of charge and the particle separation distance.

Fig. 2
figure 2

Electrostatic force (positive = repulsive) between two particles as a function of the surface-to-surface separation distance (d) calculated using different models (CM: Coulomb point-charge approximation; RM: rigorous method based on multipole expansion, using 10 terms in the summation (see Eq. 1); DM: effective dipole model). (a) Different-size and opposite charged particles: \(r_1 ={100}\,\upmu \hbox {m}\); \(r_2 = {40}\,\upmu \hbox {m}\); \(q_1 = {0.5}\,\hbox {pC}\); \(q_2 = {-4}\,\hbox {pC}\); \(k_1 = k_2 = 4\). (b) Same-size, charged-neutral particle pair: \(r_1 = r_2 ={50}\,\upmu \hbox {m}\); \(q_1 = {0}\,\hbox {pC}\); \(q_2 = {4}\,\hbox {pC}\); \(k_1 = k_2 = 4\). (c) Different-size and like-charged particles: \(r_1 ={100}\,\upmu \hbox {m}\); \(r_2 = {40}\,\upmu \hbox {m}\); \(q_1 = {0.5}\,\hbox {pC}\); \(q_2 = {4}\,\hbox {pC}\); \(k_1 = k_2 = 4\). (d) Different-size and like-charge particles (“Mix charge” pair in later DEM simulations): \(r_1 ={350}\,\upmu \hbox {m}\); \(r_2 = {250}\,\upmu \hbox {m}\); \(q_1 = {4}\,\hbox {pC}\); \(q_2 = {40}\,\hbox {pC}\); \(k_1 = 4\); \(k_2 = 3\). (e) Different-size and like-charge particles (“Mix size” pair in later DEM simulations): \(r_1 ={600}\,\upmu \hbox {m}\); \(r_2 = {150}\,\upmu \hbox {m}\); \(q_1 = {20}\,\hbox {pC}\); \(q_2 = {40}\,\hbox {pC}\); \(k_1 = 4\); \(k_2 = 3\).

Full size image
Fig. 3
figure 3

Surface plot of the dimensionless electrostatic force (ratio by Coulomb’s value) between two particles (dielectric constants \(k_1=k_2=4\)) at \(d = {0.5}\,\upmu \hbox {m}\) separation distance, considering \(r_1 = {1}\,\upmu \hbox {m}\) and \(q_1 = {1.602 \times 10^{-4}}\,\hbox {pC}\), versus the particles’ size and charge ratios; (a) rigorous model (RM), with summation terms up to the 20-th order; (b) effective dipole (DP) model. The transparent plane with black line intersections denotes zero force.

Full size image

The characteristics of the formula above show that if such an approach is acceptable for the interaction between two particles, computations become largely unfeasible in DEM simulations involving tens of thousands of particles or more.

Coulomb model

If the particles are assumed to behave as point charges, their interaction can be computed by classical Coulomb’s law of attraction/repulsion. The intensity of the electrostatic interaction force between particles i and j is expressed as follows:

$$\begin{aligned} F_{e,c} = K \frac{q_i q_j}{h^2} \end{aligned}$$
(2)

The attractive/repulsive force is directly proportional to the product of the two net charges and inversely proportional to the squared distance between the particles. Notably, only particles with opposite-sign charges can experience an attractive force. Thus, the point-charge approximation is unable to capture the attraction between like-charged particles and between charged and neutral particles.

Effective dipole model

Given the limited applicability of rigorous methods such as the multipole expansion method described earlier to many-particle systems, a physically and mathematically simpler approach based on effective dipoles (Fig.1b) is proposed, with the aim of adequately capturing polarization effects.

Chan46 proposed a theory to explain the like-charge attraction of polarizable ions on the basis of an effective dipole description. The tendency of ions to polarize is captured by defining a polarizable volume (\(\alpha _i^3\) \(r_i^3\)), through which the dipole moment is calculated. The effective dipole model approximation proposed in this work follows the same strategy but is adapted to suit solid objects rather than ions. The volume polarizability is expressed in terms of the material’s dielectric constant (\(k_i\)):

$$\begin{aligned} \alpha ^3_i = \frac{k_i - 1}{3} \end{aligned}$$
(3)

Let us consider a system of two particles, each characterized by a net charge, initially placed at an infinite distance from one another. As the two particles are gradually brought closer (without touching), they begin to interact. The electric field produced by a charged particle influences the charge distribution on the neighboring charged particle. As a result, the particle retains its initial net charge, but the distribution of charge on its surface becomes nonuniform. This charge distribution can be represented by the dipole moment. In turn, the electric field present on the second particle counterinduces a dipole moment on the original particle that changes its electric field. Computationally its evaluation would require an iterative procedure that can depend on the order of calculations, e.g. for many interacting particles47. Fortunately, by setting equilibrium equations involving both charges and dipoles, appropriate formulas can lead directly to steady-state effective dipole values, making the calculation both simpler and independent of the dynamics. The effective dipole moment (\(p_i\)) is introduced, whose modulus is defined as:

$$\begin{aligned} p_i = 4\pi \varepsilon _0 \frac{k_i - 1}{3} r_i^3 E_i=\frac{(k_i - 1)r_i^3}{3h^2}\frac{q_j-2\frac{(k_j-1)r_j^3}{3h^3}q_i}{1-4\frac{(k_i-1)(k_j-1)r_i^3r_j^3}{9h^6}} \end{aligned}$$
(4)

where \(E_i\) is the electric field. The sign of the dipole then depends on the direction assumed for the vector connecting the particle centers. These effective dipoles, one for each particle, aim to represent the nonuniform charge distributions on the particle surfaces by a simple method. There is one temporary dipole for each particle–particle interaction, which eventually affects the electrostatic force calculation. By combining the mutual polarization induced by two interacting spheres46, it is possible to express the total electrostatic force in a compact form via Eq. (5)

$$\begin{aligned} F_{e} = K \frac{q_i q_j}{h^2} \left[ \frac{1 - 2(f_{ij} + f_{ji})(1 + 2y) + 2y(3 + 4y)}{(1 - 4y)^2} \right] \end{aligned}$$
(5)

where

$$\begin{aligned} f_{ij} = \frac{k_i - 1}{3} \left( \frac{r_i}{h}\right) ^3 \frac{q_j}{q_i} \end{aligned}$$
(6)

and

$$\begin{aligned} y = f_{ij}f_{ji} = \frac{(k_i - 1)(k_j - 1)}{9} \left( \frac{r_i r_j}{h^2}\right) ^3. \end{aligned}$$
(7)

When a charged particle interacts with a neutral one, it is necessary to manipulate Eq. (5) to obtain a solution. Indeed, if \(q_i=0\) or \(q_j=0\), the form of Eq. (5) yields an undefined result. This is resolved by substituting \(f_{ij}\) and \(f_{ji}\), yielding the correct explicit expression:

$$\begin{aligned} F_{e} = \frac{K}{[(1-4y)h]^2} \left\{ q_i q_j \left[ 1 + 2y(3 + 4y)\right] - 2 \left[ \frac{k_i - 1}{3} \left( \frac{r_i}{h}\right) ^3 q_j^2 + \frac{k_j - 1}{3} \left( \frac{r_j}{h}\right) ^3 q_i^2 \right] (1 + 2y) \right\} \end{aligned}$$
(8)

Compared with the multipole expansion method of Eq. (1), the effective dipole approach is much more manageable and compact. It does not require iterations or summations of several terms. On the other hand, its accuracy requires testing.

Comparison of selected binary interaction pairs

Electrostatic interaction forces between two particles with prescribed properties are considered at various interparticle distances, \(d=h-r_i-r_j\). The interactions are evaluated through the three models discussed in the above section. The results of the investigations are presented in the following graphs in which the line “Coulomb model” (CM) is obtained with the point-charge approximation, the “rigorous model” (RM) is obtained with the multipole expansion method described by Bitchoutskaia41 and Lindgren42,43 and “dipole model” (DP) with the effective dipole approximation.

The first particle pair involves two spheres charged with opposite polarities, differing in size and charge levels. The behavior of this system is reported in Fig. 2a. With all models the electrostatic force is attractive. Quantitatively, with the RM and DM models, the calculated force is greater in modulus than the value obtained using the point-charge approximation. In Fig. 2b, the plot shows results for the interaction between a neutral and positively charged particles of the same size. According to the point-charge approximation, no interaction is obtained, as expected. With the other two models, when the distance between particles is less than approximately \({100}\,\upmu \hbox {m}\), an attractive force is observed. Electrostatic interactions between like-polarity charged particles are shown in Fig. 2c. The force profile modeled via Coulomb’s point-charge approximation is always repulsive, with the value increasing as the separation distance decreases. Both the DP and RM models follow the same trend at large distances, indicating that the effect of surface polarization is negligible. However, they exhibit different profiles when the separation distance falls below \({200}\,\upmu \hbox {m}\). At approximately \({100}\,\upmu \hbox {m}\), the electrostatic force crosses zero and, further below it, becomes negative, indicating interparticle attraction. Interestingly, at very short distances, not only is a sign change observed, but the magnitude of this attractive force significantly exceeds the Coulombic repulsive force. For reference, the gravitational force on glass particle 1 is approximately \({0.1}\,\upmu \hbox {N}\).

Figure 2d,e show two plots of the force profiles versus the distance for two particle pairs utilized below in DEM simulations (see Sect. “DEM simulation of charged binary mixture under shaking”) of the “Mix charge” and “Mix size” cases, respectively.

Influence of the particle size and charge

For the investigated cases, RM and DP prove to be accurate methods for calculating complex binary electrostatic interactions. A wider range of size ratios and charge ratios are explored here to assess the ability of the effective dipole model to capture the repulsive/attractive transition at the contact between polarizable particles charged with the same polarity. In Fig. 3 the ratio of the electrostatic force to the Coulomb value is shown for two polarizable particles placed at an interparticle separation distance \(d = {0.5}\,\upmu \hbox {m}\), plotted as a function of the charge ratio and size ratio.

By definition, the dimensionless electrostatic force would systematically be equal to 1 with the Coulomb model. The results obtained with the multipole expansion method and the effective dipole approximation model, reported in Fig. 3a,b, respectively, yield a force sign inversion for some combination of size ratio and charge ratio (see the black lines, denoting zero force on the map). Notably, Coulomb’s law is accurate when the size ratio and the charge ratio are similar, e.g., the largest particle is also the most highly charged. On the other hand, strong attractive forces can be observed when the smaller particle carries a greater charge.

With the dipole model, it is possible to compute analytically a good estimate of the distance at which the force reverses sign as a function of the particles’ radii, charges and dielectric constants. Assuming a negligible value of y, whose maximum value cannot exceed 1/6446, the following expression is obtained:

$$\begin{aligned} d_{(F_e=0)} = \root 3 \of {2\left( \frac{k_i-1}{3}r_i^3\frac{q_j}{q_i}+\frac{k_j-1}{3}r_j^3\frac{q_i}{q_j}\right) }-(r_i+r_j) \end{aligned}$$
(9)

Overall, the RM and the DP offer significant improvements over the point-charge approximation. Compared with the rigorous method, the effective dipole model provides a reasonable estimate of the electrostatic interaction, accurately capturing both the transition between attraction and repulsion and the magnitude of the force. However, it is important to note that the exact multipole expansion method is not practical for DEM simulations with many interacting particles. In contrast, the dipole model delivers accurate results while keeping the computational load manageable.

DEM simulation of charged binary mixtures under shaking

The effective dipole model has been implemented in a DEM code (see the Section “Methods”) and tested to evaluate its impact on the calculation of electrostatic interactions in systems with several thousands of particles.

Two binary mixtures of dielectric particles of different sizes and charges are simulated during motion inside a shaker. The particles have fixed charges that do not change upon collision, i.e., tribocharging is not considered. All the particles carry charges of the same polarity (positive). The shaker is a box with dimensions of \({5} \times {5} \times {5}\,\hbox {cm}^3\) and undergoes combined oscillatory motion in the vertical, y (\(f_s\) = 30 Hz, \(A_s\) = 1 mm), and horizontal, x (\(f_s\) = 30\(\sqrt{3}\) Hz, \(A_s = {200}\,\upmu \hbox {m}\)) directions, with \(f_s\) and \(A_s\) being the shaking frequency and amplitude, respectively. Nonresonant frequencies are used.

The shaker is filled with 3 g of powder, consisting of 50% (w/w) fine particles and 50% (w/w) coarse particles. The two binary mixtures are referred to as “Mix Charge” and “Mix Size” to denote their prevailing ratio. “Mix Charge” is characterized by a high fine-to-coarse charge ratio (\(q_1/q_2 = 10\)) and a moderate coarse-to-fine size ratio (\(D_{p,2}/D_{p,1}=1.4\)). For “Mix Size”, a higher coarse-to-fine size ratio (\(D_{p,2}/D_{p,1}=4\)) and a lower fine-to-coarse charge ratio (\(q_1/q_2 = 2\)) are used. The physical and mechanical properties of the particles and their mixtures are listed in Table 1. The values of the dielectric constants are similar to those of polymeric materials. For the calculation of electrostatic interactions in the two systems, both the classical Coulomb point-charge formulation and the effective dipole model were used, resulting in a total of four simulations. According to the effective dipole model, with the selected dielectric constants, charges, and particle sizes, the attractive electrostatic force at contact is ca. \({13}\,\upmu \hbox {N}\) for both binary mixtures. This force is approximately 20 times greater than the gravitational force on fine particles in the “Mix Charge” and 100 times greater than that in the “Mix Size”. A plot showing the full dependence of the force with the interparticle distance is shown in Fig. 2d,e for both mixtures.

Table 1 Particle properties for the DEM simulations of two binary mixtures (“Mix Charge” and “Mix Size”). The properties differing in the two systems are highlighted in bold.
Full size table

Figure 4 shows the results for the “Mix Charge” simulation, whereas Fig. 5 presents the results for the “Mix Size” simulation. At the start of each simulation, the particles are assigned an initial random kinetic energy, causing them to disperse uniformly throughout the shaker chamber. As the simulation progresses, the particles settle under the effect of gravity, collide with the bottom wall of the shaker, and begin to move in response to agitation. A periodic motion is observed after approximately 0.5 s , although, as will be shown in the results analysis, some differences can still be seen beyond this point. A total of 2 s of agitation was simulated for all the configurations considered.

Fig. 4
figure 4

“Mix Charge” simulations. (a) Coulomb model; location of the particles at 2 s. (b) Dipole model; location of the particles at 2 s. (c) Distribution of the coordination number of coarse particles at 2 s obtained with the Dipole model. (d) Coulomb model; coarse (black) and fine (gray) particles attached to at least one other particle. (e) Dipole model; coarse (black) and fine (gray) particles attached to at least one other particle. (f) Coulomb model; vertical position of fine and coarse particles (area between the q1 and q3 quartiles). (g) Dipole model; vertical position of fine and coarse particles (area between the q1 and q3 quartiles). (h) Evolution of the mean coordination number of coarse particles.

Full size image
Fig. 5
figure 5

“Mix Size” simulations. (a) Coulomb model; location of the particles at 2 s. (b) Dipole model; location of the particles at 2 s. (c) Distribution of the coordination number of coarse particles at 2 s obtained with the Dipole model. (d) Coulomb model; coarse (black) and fine (gray) particles attached to at least one other particle. (e) Dipole model; coarse (black) and fine (gray) particles attached to at least one other particle. (f) Coulomb model; vertical position of fine and coarse particles (area between the q1 and q3 quartiles). (g) Dipole model; vertical position of fine and coarse particles (area between the q1 and q3 quartiles). (h) Evolution of the mean coordination number of coarse particles.

Full size image

Figure 4a,b show the particle positions of the binary mixture “Mix Charge” after 2 s of agitation, as computed using the Coulomb model and the effective dipole model, respectively. With the Coulomb point-charge model (CM), the fine particles occupy a larger volume within the box: because of the repulsive electrostatic interactions they cannot form aggregates with coarse particles. In contrast, the Dipole model yields results showing a more compact particle arrangement, with both coarse particles (in black) and fine particles (in gray) moving as a cohesive group. The formation of agglomerates can be noted in the detailed Fig. 4e. To quantify this spatial dispersion, the vertical position of the two particle phases over time is analyzed in Fig. 4f for the Coulomb model and in Fig. 4g for the effective dipole model. The colored areas represent the range between the first and third quartiles of the vertical position distribution for each particle phase. The curves describing the vertical position all show the same oscillating frequency as the shaker vertical frequency (30 Hz). In the Coulomb model (Fig. 4f), fine particles tend to be located in the upper part of the shaker. The same occurs with the effective dipole model, but as the simulation progresses, the oscillation of the fine particles aligns with that of the coarse particles, eventually almost overlapping (Fig. 4g).

The analysis of particle motion suggests that the attractive forces related to polarization phenomena, may play a crucial role in particle dynamics, potentially leading to adhesion and/or agglomeration. This aspect is analyzed in terms of the coordination number, CN, of each particle, i.e. the number of contacts, see (Fig.4c). Figure 4d (Coulomb model) and e (effective dipole model) show the positions of all the coarse particles (black) and only the fine particles (gray) with \(CN > 0\), named those that are in contact with at least one other particle, at \(t = {2}\,\hbox {s}\). In the Coulomb model, only 54 particles (0.2% of the total) meet this definition, which is likely due to random collisions with other particles at the given moment. However, in the effective dipole model, 65% of the fine particles are in contact with at least one other particle. From the detailed view on the right (Fig. 4e), complex structures are formed, with the fine particles surrounding and adhering to the coarse particles. Fig. 4c shows the cumulative distribution of the CN for coarse particles at 2 s calculated using the effective dipole model. Only 5% of the coarse particles have no contacts, and some coarse particles are in contact with up to 10 other particles. Figure 4h shows the time evolution of the average CN of coarse particles, which is, on average, 260 times greater with the dipole model than with the Coulomb interaction.

Similar considerations apply to the “Mix Size” simulation (Fig. 5), where the abovementioned effects are even more pronounced, likely because of a combination of three factors: the fine particles are more numerous, they are smaller (0.3 mm vs 0.5 mm), and the 40 pC charge assigned to such small particles has a greater impact.

According to the predictions of the Coulomb model, fine particles, owing to their low inertia and strong repulsive forces, tend to fill all available space throughout the simulation, dispersing within the shaker chamber (Fig. 5a,f) and generally remaining distant from the coarse particles (Fig. 5d). With the dipole model, fine particles stay in contact with coarse particles (Fig. 5b) and move along with them (Fig. 5g). The CN of the coarse particles oscillates around an average of 35 (Fig. 5h), exceeding 40 for some particles (Fig. 5c). Approximately 51% of the fine particles form aggregates with the coarse particles, and interestingly, that the arrangement of fine particles on the coarse particles leads to the formation of compact hexagonal structures, as shown in the detailed view of Fig. 5e, likely resulting from the balance between the fine-coarse attractive forces and the repulsive forces between the fine particles.

Discussion

A new model based on the concept of an effective dipole, accounting for charge polarization on the particle surface, is described and implemented in a DEM code. The proposed model is compared with the point-charge approximation (Coulomb’s law) and a more rigorous mathematical method used as a reference. The use of the dipole model, rather than the rigorous mathematical approach, offers the advantage of a feasible mathematical complication with little compromise on accuracy. The model that incorporates the use of the induced dipole moment envisages the possibility of an attractive force between like-charged particles and can capture the sign reversal for specific combinations of size and charge ratios in two-particle interactions. From a macroscopic perspective, this provides for the ability to capture the mechanism underlying the formation of aggregates or layers of particles that remain stuck in industrial equipment, such as solids adhered to packaging bags and mixing equipment or fouling in fluidized beds.

The evaluation of electrostatic interactions is carried out considering a two-body model: the interaction of individual particle pairs is taken into account, and in multiple interactions the superposition principle is applied. While this principle has always been applied in DEM to evaluate the forces acting on a particle, in the case of electrostatics it introduces an approximation. To properly account for long-range interactions specific strategies for three-body or many-body models48,49 are necessary, which significantly increase the computational burden. One possibility offering high efficiency (linear scaling with the number of particles) was recently proposed by Gan et al.45.

Another limitation of the presented model lies in the choice of the material’s dielectric constant. Considering that the original volume polarizability fraction \(\alpha _i\) is limited to 1, the corresponding dielectric constant cannot exceed 4; see Eq. (3). Therefore, the variety of materials that can be simulated is limited accordingly.

Within the limits of its applicability, however, the dipole model can capture macroscopic effects not detectable by Coulomb’s law, such as adhesion between particles of different sizes or attraction between like-charged and neutral particles. Phenomena such as charge amplification6 and size-dependent bipolar charging37 have also been observed in industrial systems, although the underlying causes and behavior are not yet well understood50. Polarization could play a role in the formation of multiple layers on the walls of a fluidized-bed reactor, with attractive forces occurring between particles of different sizes but made of the same material. These particles, expected to carry the same polarity, nonetheless experience attraction. By combining the dipole model with a tribocharging model, it may be possible to capture this phenomenon in multiphase simulations.

From a computational point of view, tests of simulations based on the effective dipole model show no appreciable additional burden compared with corresponding simulations based on the conventional point-charge approximation.

DEM simulations are conducted on an agitated multiparticle system for two binary mixtures characterized by different size ratios and charge ratios. The use of the concept of polarization proves essential for an accurate description of the electrostatic interactions between like-charged particles, as it leads to the possible formation of agglomerates.

For the two binary mixtures considered in this work, the parameters are chosen to emphasize the phenomenon of particle aggregation. The charge of the fine particles in the “Mix charge” is set just below the Pauthenier limit51, for a dielectric particle (\(k=3\)) with a diameter of 0.5 mm in nitrogen, and is therefore realistic. On the other hand, in the “Mix size” the same fine particle charge level is used, which is more than twice its Pauthenier limit. Additionally, in a real system, the charge evolves over time due to collisions, whereas in the simulations each particle retains its initial charge. As a result, in a real system, the polarization effects may be less pronounced, although still active and important.

Finally, the simulations do not account for electrostatic interactions with the walls or for other far-field contributions. These are desirable future developments of this work.

Methods

Among the methods employed to simulate static or flowing particulate materials, the Discrete Element Method (DEM) has emerged as the most commonly adopted solution, owing to its accuracy, versatility and detail of the results. Introduced by Cundall and Strack52, it is conceived to track dynamically each particle (element) in a system as a separate (discrete) entity that interacts with other particles and walls, and a broad variety of other phenomena, such as flowing fluids, external force-fields, interfacial interactions and so on. The basic idea is similar to Molecular Dynamics (MD) simulations, but interactions are frequently limited to contacts (i.e. very short-range). The equations of translation and rotation for each particle are solved in 3D over tiny time-steps for each particle, by defining all actions of interest by their corresponding force model.

The governing equations for the translational and rotational motion of each simulated particle are as follows:

$$\begin{aligned} m_i\frac{dv_i}{dt}= & F_{g,i} + \sum _{j} F_{c,ij} + \sum _{j} F_{e,ij} + F_{sh,i} \end{aligned}$$
(10)
$$\begin{aligned} I_i \frac{d\omega _i}{dt}= & \sum _{j} T_{c,ij} + \sum _{j} T_{r,ij} \end{aligned}$$
(11)

where \(m_i\), \(v_i\), \(\omega _i\), and \(I_i\) are the mass, velocity, angular velocity, and moment of inertia of the i-th particle, respectively. The gravitational force \(F_{g,i}\), the contact forces with other particles and walls \(F_{c,ij}\), the electrostatic forces \(F_{e,ij}\) and the fictitious force induced by the shaking motion, as described below, are considered. For the rotational motion in Eq. (11), the torques considered are the contact torque \(T_{c,ij}\), directly related to the tangential contact forces and the particle radius, and the rolling friction torques \(T_{r,ij}\), a dissipative term calculated via the constant directional torque model, as reported elsewhere53.

The simulations of the particles’ motion in the shaker discussed earlier are based on the DEM approach, as coded in the open-source software package MFiX-DEM54 with several in-house developed extensions. The Hertz-Mindlin no-slip model55 for the contact model is used. The electrostatic forces are computed via either Coulomb’s law (Eq. 2) or the effective dipole model (Eq. 4), with a cutoff distance \(d = 2\cdot (r_i + r_j)\), to limit the computational load required by the long-range interactions.

The shaker is simulated in a moving reference frame by applying a time-dependent inertial force to the particles. The shaking motion is described by two periodic harmonic oscillations with amplitude \(A_s\), frequency \(f_s\), and phase displacement \(\phi\) (set to \(90^{\circ }\)), named \(s(t) = A_s \sin (2\pi f_s t + \phi )\). In turn, this motion induces a fictitious force \(F_{sh,i}\) on each particle, whose modulus is given by:

$$\begin{aligned} F_{sh,i} = m_i \cdot 4\pi ^2 A_s f_s^2 \sin {(2\pi f_s t + \phi )} \end{aligned}$$
(12)

In evaluating the contact force for coarse–fine mixtures, the “thick-wall” strategy was employed for wall contacts to limit possible particles escaping the domain56.

The following models have been implemented in a customized version of the open-source MFiX-DEM code (version 18.1.5): fictitious shaking force, Coulomb’s model, effective dipole model, rolling friction model and “thick-wall” contact. Finally, custom code was developed to compute the coordination number and corresponding postprocessing tools.