Introduction

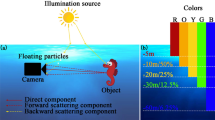
Due to the absorption and scattering effects, underwater imaging always suffers from degradation, which varies in different environments1,2. The absorption effect related to wavelength leads to color distortions of images such as greenish, bluish, yellowish, etc., and the light scattered by the particles in the medium leads to low contrast and blurring of images3. Figure 1 shows degraded images captured in diverse underwater environments, selected from the UIEB dataset4. Such degradation affects object detection and recognition, it thus makes underwater image recovery (UIR) a highly important technique5,6,7,8,9.

Fig. 1
figure 1

Images captured in diverse underwater environments.

Full size image

There are various methods to recover degraded color underwater images. For instance, Tolie et al.10 developed a novel deep learning-based approach, Deep Inception and Channel-wise Attention Modules (DICAM), to recover underwater images, considering both the proportional degradations and non-uniform color casts. To enhance the image texture with high quality, Yuan et al.11 proposed a multi-scale fusion enhancement method where two new fusion inputs are created based on different color methods. Jha et al.12 constructed a novel color-balanced locally adjustable (CBLA) approach to enhance these underwater scenes locally, thus preserving the information contained. Huang et al.13 designed relative global histogram stretching (RGHS) based on adaptive parameter acquisition to solve problems in various shallow-water images.

Since the veiling light or backscattering light is partially polarized, polarization imaging is found to be an effective way for clear underwater imaging14,15,16. Schechner et al.17 introduced polarization in recovering distorted underwater images. Encouraged by this, some underwater polarization image restoration methods based on physical models have been proposed recently and proved the usefulness of polarization information18,19,20,21. However, the revised models are unable to accurately describe the optical imaging process, which results in shortcomings in the restoration of images with different water bodies (e.g., yellowish, greenish, bluish, and whitish). For example, the restored colors are not consistent with the fact totally, there are red-shifts in the restored image, or performance is imbalanced on images of different water types. Considering the powerful feature learning and fitting capabilities of deep learning techniques22,23,24, two deep learning-based methods for underwater polarimetric color images have been proposed25,26, which have notable advancement in recovery performance, but due to inadequate consideration of multiple water types, varying turbidity of water bodies, and the rich color palette of the imaging scene, the methods exhibit limited generalization ability which is significant for the vision applications. Therefore, there is a need for a highly generalizable method that can handle underwater images imaged in varied water bodies while utilizing polarization information, including images of scenes with a high level of color variation in heavy turbid water.

In this paper, we collect an underwater polarization imaging dataset with ground truths consisting of three water types (viewed as domains) and present an underwater polarimetric image recovery network employing domain-adversarial learning, named UPD-Net, to recover images in different underwater environments. Both the network structure and the loss functions are specially designed to improve the recovery ability and domain generalization capability of the proposed method. In addition, we perform experiments on images in both source (learned) and unseen (unlearned) domains to verify the effectiveness and generalizability of this network. The contributions of this article are summarized as follows:

  • We establish a polarimetric image dataset that to the best of our knowledge is the richest underwater color polarization image dataset, which includes three water types, four turbidity levels, and five colorful scenes.

  • We propose a UPD-Net: the designed network combines the water-type classifier and the multi-encoder-decoder, and the designed training strategy combines domain adversarial training and generative adversarial training. Experiments demonstrate that the method has good recovery performance and domain generalization ability.

Related works

Deep learning-based UIR

Typically, deep learning-based UIR tasks can be broadly categorized into two groups: convolutional neural network (CNN) and generative adversarial network (GAN). To eliminate the degradation of underwater images, Jiang et al.27 proposed a target-oriented perceptual adversarial fusion network, dubbed TOPAL. Islam et al.28 presented a conditional generative adversarial network-based model for real-time underwater image enhancement. They formulate an objective function that evaluates the perceptual image quality based on its global content, color, local texture, and style information. Considering the characteristics of uneven degradation and loss of color channel of underwater images, Shen et al.29 developed a novel dual attention transformer-based underwater image enhancement method, designated as UDAformer. The Water-Net for underwater image enhancement was designed by Li et al.4 and trained on the UIEB dataset. Despite the promising outcomes obtained by CNN and GAN-based methods in UIR tasks, a common limitation of these methods is the neglect of polarization in underwater imaging, which may lead to incomplete recovery due to the underuse of valuable polarization information.

Polarization-based UIR

In recent, polarization has gained increasing attention in UIR tasks. Polarization-based recovery methods for underwater images in grey or color scales can be divided into two main categories: physical model-based and deep learning-based methods30,31,32,33,34. With regard to the less studied area of color image recovery, the majority of the methods are based on physical models. For instance, Fu et al., proposed a method of descattering and absorption compensation in 2020. The difference between the recovery results and the ground truths is more pronounced in the bluish simulated water type than in the whitish and yellowish types18. In 2020, a method was presented by Liu et al., to address image blurring and color distortion by accounting for crosstalk effects between the RGB channels while estimating the transmittances in RGB channels. However, the recovered colors in all three simulated water types (bluish, yellowish and greenish) are not sufficiently accurate compared to the ground truths19. In 2021, Hu et al. devised a method based on a polarization filter and histogram attenuation prior, taking into account the differences in the histogram distributions of the three channels (RGB) to create a “cut-tail” HS. However, the recovery results of this method are of a noticeably inferior quality in yellowish simulated waters in comparison to greenish and blueish waters: the recovered colors exhibit red-shifts20.

To compensate for the poor recovery performance based on physical methods and to leverage the potential of deep learning, two deep learning-based methods for color polarimetric image recovery have recently been proposed. In 2022, Ding et al.25 proposed a learning-based method that employs multi-polarization fusion adversarial generative networks to learn the relationship between polarization information and object radiance. In 2022, Hu et al.26 proposed another network that recovers images in white water with mild or severe turbidities. Nevertheless, while these deep learning-based methods achieve better performance, they also exhibit a limitation in their ability to generalize across different water types. Furthermore, the diversity of experimental water types used in these studies is not as extensive as that observed in physical model-based methods. In general, proposing a deep learning-based model with domain generalization capability is indeed a difficult task.

Domain generalization

Domain generalization is the challenge of allowing models trained on data from one or more source domains to generalize to other previously unseen domains35. Domain-adversarial learning represents a valuable strategy in fields such as image style transfer and image classification, where data from disparate domains can be mapped to the same feature space through it36,37,38,39,40. Training a model that is capable of handling different water types is challenging. In this work, we consider the water types as distinct domains and employ two strategies, namely domain-adversarial learning and generative-adversarial learning, to propose a novel network that is trained on a limited number of domains and exhibits stable recovery across unseen domains. This approach addresses the limitations of previous methods in terms of both recovery performance and domain generalizability.

Method

Dataset

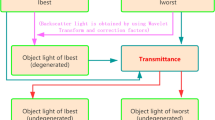
According to the basic underwater imaging physical model described in Eq. (1)17, the light intensity \({\text{I}}\left( {{\text{x}},{\text{~y}}} \right)\) captured by the camera is composed of two parts: the direct transmission \({\text{D}}\left( {{\text{x}},{\text{~y}}} \right)\) from the object, which is absorbed and scattered in the water, and the backscattered light \({\text{B}}\left( {{\text{x}},{\text{~y}}} \right)\), \({\text{I}}\left( {{\text{x}},{\text{~y}}} \right)\) can be expressed as

$$\begin{aligned} I\left( {{\text{x}},{\text{y}}} \right) & =D\left( {{\text{x}},{\text{~y}}} \right)+B\left( {{\text{x}},{\text{~y}}} \right) \\ & =L\left( {{\text{x}},{\text{~y}}} \right) \cdot t\left( {{\text{x}},{\text{~y}}} \right)~+{{\text{B}}_\infty }\left[ {1 - {\text{t}}\left( {{\text{x}},{\text{y}}} \right)} \right], \\ \end{aligned}$$
(1)

where \(\left( {{\text{x}},{\text{~y}}} \right)\) denotes the coordinates of the pixels in the image, \({\text{L}}\left( {{\text{x}},{\text{~y}}} \right)\) is the radiance of the object without attenuation by the particles in water, \({\text{t}}\left( {{\text{x}},{\text{~y}}} \right)\) indicates transmittance of the medium, and \({{\text{B}}_\infty }\left( {{\text{x}},{\text{~y}}} \right)\) is the backscattered light at an infinite distance. Not only is the background light partially polarized, but the object light also contributes to the polarization21; underwater images of different polarization states contain more information than single \({\text{I}}\left( {{\text{x}},{\text{y}}} \right)\), thus we employ multi-polarization images to remove \({\text{B}}\left( {{\text{x}},{\text{~y}}} \right)\) and recover \({\text{L}}\left( {{\text{x}},{\text{~y}}} \right)\). The multi-polarization images are captured by a polarization color camera (LUCID, TRI050S-QC) with 2048 × 2448 pixels. The pixel array consists of micro-polarizers with four polarization orientations, 0°, 45°, 90°, and 135°. The Stokes parameter\(\left[ {{{\text{S}}_{0,}}{\text{~}}{{\text{S}}_{1,{\text{~~}}}}{\text{~}}{{\text{S}}_2}} \right]\) can be expressed as

$$\begin{array}{*{20}{c}} {{{\text{S}}_0}\left( {{\text{x}},{\text{y}}} \right)={{\text{I}}_0}\left( {{\text{x}},{\text{y}}} \right)+{{\text{I}}_{90}}\left( {{\text{x}},{\text{y}}} \right)={{\text{I}}_{45}}\left( {{\text{x}},{\text{y}}} \right)+{{\text{I}}_{135}}\left( {{\text{x}},{\text{y}}} \right),} \end{array}$$
(2)
$$\begin{array}{*{20}{c}} {{{\text{S}}_1}\left( {{\text{x}},{\text{y}}} \right)={{\text{I}}_0}\left( {{\text{x}},{\text{y}}} \right) - {{\text{I}}_{90}}\left( {{\text{x}},{\text{y}}} \right),} \end{array}$$
(3)
$$\begin{array}{*{20}{c}} {{{\text{S}}_2}\left( {{\text{x}},{\text{y}}} \right)=2{{\text{I}}_{45}}\left( {{\text{x}},{\text{y}}} \right) - {{\text{S}}_0}\left( {{\text{x}},{\text{y}}} \right),} \end{array}$$
(4)

where \({{\text{S}}_0}\left( {{\text{x}},{\text{y}}} \right)\) refers to the total light intensity, \({{\text{S}}_1}\left( {{\text{x}},{\text{y}}} \right)\) and \({{\text{S}}_2}\left( {{\text{x}},{\text{y}}} \right)\) are the intensity differences between different polarization states41. The Stokes vector not only represents light intensity but also includes polarization information, for linearly polarized light, the linear degree of polarization (DoLP) can be calculated as

$$\begin{array}{*{20}{c}} {DoLP=\frac{{\sqrt {{\text{S}}_{1}^{2}+{\text{S}}_{2}^{2}} }}{{{{\text{S}}_0}}}.} \end{array}$$
(5)

Since three directions contain all the polarization information42, we only use images of 0, 45, and 90 degrees. To obtain the dataset with ground truths, we built the underwater imaging setup in a laboratory environment, as shown in Fig. 2. We provide polarized illumination so that the captured images contain polarization information, which is consistent with the fact17.

Fig. 2
figure 2

Experimental setup for underwater imaging.

Full size image

The photographed sample is placed inside a transparent PMMA tank (40 × 40 × 40 cm), which is poured into clean water, followed by colored ink and milk to simulate the absorption and scattering effects. In this setting, we collect 240 sets of images consisting of polarimetric images captured in colored turbid water and corresponding intensity images captured in clean water, which are regarded as ground truths. We pour blue, green, and yellow ink to simulate multiple water types, and we pour milk of different amounts to simulate different levels of turbidity. Hence, the dataset consists of images from three domains, each of which is subdivided into four turbidity levels. In addition, a variety of objects such as plastic disk and color card, metal coin and ruler, and seashells are used to ensure diversity of content. We expand another 720 sets of images by rotating, and all images are resized to 160 × 160. Ultimately, this dataset, which simultaneously has different turbidity, water types, and colorful scenarios, is the richest dataset known to us and is large, with a total of 960 images and 320 of each water type. Examples of our acquired images are shown in Fig. 3, where domain 1 and domain 2 are trained by UPD-Net, thus called source domains, domain 3 is only for testing the generalizability of the trained model, thus called the unseen domain, and it is worth mentioning that, we also acquire polarization images in a real lake (viewed as domain 4). Total images of bluish and greenish domains are divided into training, validation, and testing sets by 2:1:1.

Fig. 3
figure 3

Examples of acquired images in four domains.

Full size image

Network

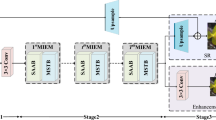
Innovatively introducing domain-adversarial learning for the first time into underwater polarimetric imaging, we propose an underwater polarimetric color image recovery network for different environments, named UPD-Net, as shown in Fig. 4. It is a generative adversarial network consisting of multi-encoder (E), decoder 1 (D1), decoder 2 (D2), discriminator (J), and water-type classifier (C). Among them, E and D1 form the generator (G), D1 and D2 have the same network structure. Multi-encoder and dual-decoder are designed by improving on U-Net43, a commonly used network based on a single encoder-decoder that outputs images utilizing local and global information via skip connections. Because of the need for multi-polarization information fusion, we designed a Multi-encoder U-Net, where each encoder is responsible for generating a feature vector of one polarimetric image, and three vectors are connected to the latent vector by the concatenation concat. To be able to preserve not only the desired content but also the polarization information that needs to be mined and exploited during the encoding process, we include a parallel decoder D2 in addition to the decoder D1, which is used to output the DoLP image, which is a representation of the polarization information. This oversees that our network mines more polarization information from the raw polarimetric images.

Fig. 4
figure 4

(a) The architecture of the UPD-Net; (b) the generator; (c) the water-type classifier.

Full size image

Since the network aims not only at satisfactory image recovery but also to generalize to images of different water types, which are viewed as multiple domains, we introduce a novel application of a water-type classifier along with the generator and the discriminator. The water-type classifier is a neural network that aims to classify the water type of the given input images from the latent vector extracted from E. The distribution of images in different water types is different, and such diversity makes it hard to train a single model to recover images of various types, especially the ones unseen in training. Whereas the scene content unrelated to the water body is what the model needs to recover, thus the encoders are expected to produce domain-agnostic feature representations, specifically, the feature vectors are ideally only related to scene content and not to the water body. To achieve this goal, the water-type classifier is expected to become increasingly incapable of determining the water type of the input image based on the encoded feature representations during the training process. This process, known as domain-adversarial learning strategy, is similar to generative-adversarial learning strategy, the generator is expected to generate images that are increasingly not recognized by the discriminator as generated images but are mistaken for ground truths, whereas the E is similar to the generator and the C is similar to discriminator. Employing these two adversarial learning strategies, we use the learned domain-agnostic features to generate recovered underwater images closed to ground truths.

To optimize the water-type classifier, we adopt classification loss \({{\text{L}}_{\text{c}}}\):

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{c}}}\left( {I,T} \right)= - \mathop \sum \limits_{{{\text{t}}=1}}^{{\text{T}}} {{\text{y}}_{\text{t}}}{\text{log}}\left[ {{\text{C}}{{\left( {\text{Z}} \right)}_{\text{t}}}} \right],} \end{array}$$
(6)

where \({\text{I}}\) is distorted images, \({\text{Z}}={\text{E}}\left( {\text{I}} \right)\) and \({\text{T}}\) is the number of types, which is 2 in this work, \({\text{~}}{{\text{y}}_{\text{t}}}=1\) if \({\text{c}}={\text{C}}\) else \({{\text{y}}_{\text{t}}}=0\). \({{\text{L}}_{\text{c}}}\) is the cross entropy of the distribution of the water type \({\text{t}}\) predicted by \({\text{C}}\).

To optimize the generator, we adopt four losses: a Domain Adversarial Loss (\({{\text{L}}_{\text{d}}}\)), an MSE Loss (\({{\text{L}}_{\text{m}}}\)), an SSIM Loss (\({{\text{L}}_{\text{s}}}\)), and a Generative Adversarial Loss (\({{\text{L}}_{\text{g}}}\)).

Domain Adversarial Loss,

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{d}}}\left( I \right)=\mathop \sum \limits_{{{\text{t}}=1}}^{{\text{T}}} {\text{C}}{{\left( {\text{Z}} \right)}_{\text{t}}}{\text{log}}\left[ {{\text{C}}{{\left( {\text{Z}} \right)}_{\text{t}}}} \right],} \end{array}$$
(7)

MSE Loss,

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{m}}}=\frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}}=1}}^{{\text{N}}} {{\left( {{\text{I}}_{{\text{i}}}^{{{\text{out}}}} - {\text{I}}_{{\text{i}}}^{{{\text{gt}}}}} \right)}^2},} \end{array}$$
(8)

SSIM Loss,

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{s}}}=\frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}}=1}}^{{\text{N}}} ({\text{SSIM}}\left( {{\text{I}}_{{\text{i}}}^{{{\text{out}}}}} \right) - {\text{SSIM}}{{\left( {{\text{I}}_{{\text{i}}}^{{{\text{gt}}}}} \right)}^2},} \end{array}$$
(9)

Generative Adversarial Loss,

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{g}}}=\frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}}=1}}^{{\text{N}}} {\text{log}}\left[ {{\text{J}}\left( {{\text{I}}_{{\text{i}}}^{{{\text{gt}}}}} \right)} \right]+\frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}}=1}}^{{\text{N}}} {\text{log}}\left[ {1 - {\text{J}}\left( {{\text{G}}\left( {{\text{I}}_{{\text{i}}}^{{{\text{raw}}}}} \right)} \right)} \right],} \end{array}$$
(10)

and Polarization Loss,

$$\begin{array}{*{20}{c}} {{{\text{L}}_{\text{p}}}=\frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}}=1}}^{{\text{N}}} {{\left( {{\text{DoLP}}_{{\text{i}}}^{{{\text{out}}}} - {\text{DoLP}}_{{\text{i}}}^{{{\text{gt}}}}} \right)}^2},} \end{array}$$
(11)

where\({\text{~}}{{\text{L}}_{\text{d}}}\) is the negative entropy of the distribution of the water type \(\left( {\text{t}} \right)\) predicted by \({\text{C}}\), and backpropagated only to update the E. \(\{ {\text{I}}_{{\text{i}}}^{{{\text{out}}}},{\text{~i}}=1,{\text{~}}2,{\text{~}} \ldots {\text{~*}},{\text{~N}}\}\) means the output recovered image and \(\left\{ {{\text{I}}_{{\text{i}}}^{{{\text{gt}}}},{\text{i}}=1,{\text{~}}2,{\text{~}} \ldots {\text{~*}},{\text{~N}}} \right\}\) the corresponding ground truth, \({{\text{L}}_{\text{m}}}\) and \({{\text{L}}_{\text{s}}}\) are calculated based on pixel-wise and structural differences, respectively. \(\{ {\text{I}}_{{\text{i}}}^{{{\text{raw}}}},{\text{~i~}}={\text{~}}1,{\text{~}}2,{\text{~}} \ldots {\text{~*}},{\text{~N}}\}\) denotes the input raw image, \({\text{G}}\) attempts to fake the discriminator and \({\text{J}}\) tries to recognize the generated images from the ground truths. Additionally, \(\{ {\text{DOLP}}_{{\text{i}}}^{{{\text{out}}}},{\text{~i}}=1,{\text{~}}2,{\text{~}} \ldots {\text{~*}},{\text{~N}}\}\) means the output DOLP image and \(\left\{ {{\text{DOLP}}_{{\text{i}}}^{{{\text{gt}}}},{\text{i}}=1,{\text{~}}2,{\text{~}} \ldots {\text{~*}},{\text{~N}}} \right\}\) the corresponding ground truth. \({{\text{L}}_{\text{m}}}\) and \({{\text{L}}_{\text{p}}}\) are calculated based on pixel-wise. We use the following summation of the above loss functions, as the Total-loss \({\text{L}}\), to backpropagate through the generator:

$$\begin{array}{*{20}{c}} {{\text{L}}={\text{\varvec{\upalpha}}}{{\text{L}}_{\text{d}}}+{\text{\varvec{\upbeta}}}{{\text{L}}_{\text{m}}}+\gamma {{\text{L}}_{\text{s}}}+\delta {{\text{L}}_{\text{g}}}+{{\text{L}}_{\text{p}}},} \end{array}$$
(12)

where \(\:{\upalpha\:}\), \(\:{\upbeta\:}\), \(\:{\upgamma\:}\), \(\:{\updelta\:}\), and ρ are the weights of \({{\text{L}}_{\text{d}}}\), \({{\text{L}}_{\text{m}}}\), \({{\text{L}}_{\text{s}}}\), \({{\text{L}}_{\text{g}}}\) and \({{\text{L}}_{\text{p}}}\), respectively, and the setting of the weights depends on the pre-training performance. Our network is implemented in the PyTorch framework, trained and tested by the NVIDIA GeForce RTX 4090 GPU. We utilize the Adam optimizer with a batch size of 4 to update the network parameters. The learning rate is initially set to 5e–5 and decays exponentially at a rate of 0.6. In the training process, we first train the generator to ensure that the feature vectors generated by the encoders are meaningful by utilizing \({{\text{L}}_{\text{m}}}\), \({{\text{L}}_{\text{s}}}\), \({{\text{L}}_{\text{g}}}\) and \({{\text{L}}_{\text{p}}}\). Then, we use classification loss to train the water-type classifier to reach a certain threshold of classification accuracy. Finally, the total loss \({\text{L}}\) is utilized to help the multi-encoder generate domain-agnostic feature representations to recover images in different domains. To avoid the common problems of mode collapse in generative adversarial networks and blurring of details in the generated images, we take measures to keep the network stable, such as doing batch normalization on the training data, lowering the weight of the Generative Adversarial Loss during the training process, and applying a low learning rate for the generator.

Experiments

We carry out a comparison of our UPD-Net with eight state-of-the-art (SoTA) underwater image restoration methods: Schechner15, RGHS13, CBLA12, TEBCF11, TOPAL27, FUnIE-GAN28, DICAM10 and UDAformer29 using quantitative and qualitative metrics. The first four are physical-based underwater image restoration methods, and Schechner is based on polarization imaging; the last four are recently proposed deep learning-based methods, and these networks have been retrained on our data from two source domains. The quantitative and qualitative results are presented in Table 1; Figs. 5 and 6. Table 1 shows the comparative results in terms of Peak Signal-to-Noise Ratio (PSNR)44 and Structural Similarity Index (SSIM)45. Note that higher PSNR or SSIM values indicate better quality. As can be seen in Table 1, our method performs best on PSNR and SSIM metrics among all image restoration methods. Learning-based methods involved in the comparison usually perform significantly weaker on the unseen domain than on the trained domain, but the gap is insignificant for our method. These high numerical results show that our method not only achieves satisfactory recovery results on the source domains but also performs stably on the unseen domain, achieving our two goals: excellent recovery performance and high domain generalization ability. It is worth mentioning that we also evaluated the output DoLP images on these two metrics. Compared to the ground truth, the results have an average SSIM score of 0.89 and an average PSNR score of 34.61 dB. This suggests that not only the content information that needs to be utilized and restored, but also the polarization information that needs to be utilized is preserved during the encoding process.

Table 1 SSIM and PSNR values of the recovery results.
Full size table

To further prove the performance of our method, we conduct a stability analysis of the different methods on the source data. As shown in Fig. 5, we statistically analyze the PSNR and SSIM results of the recovered images and represent them in box plots. For each box, the whiskers above and below indicate the maximum and minimum, respectively. The top and the bottom edges of the box are the 75th percentile and 25th percentile, respectively. The center of the box is the median. The smaller the box, the less fluctuating the recovery performance of the method. As can be observed, our method obtains better quantitative values on average and has a stable performance.

Fig. 5
figure 5

Box plot of different methods for testing data from source domains.

Full size image

Many no-reference quality assessment are introduced to reduce the dependency on reference data46. For a more comprehensive and objective assessment of image quality, we employ two methods: natural image quality evaluator (NIQE)47 and blind MPRIs-based (BMPRI)48 measure. The results on the source domains are shown in Table 2. Note that lower NIQE and higher BMPRI values indicate better quality. As you can see from the table, our method still achieves the best results, followed by the method DICAM. Overall, from the analysis of various indicators, our proposed method exhibits effective recovery and high stability on underwater color images.

Table 2 NIQE and BMPRI values of the recovery results in source domains.
Full size table

Quality assessment methods can be categorized into subjective and objective ones, and the human visual system is the ultimate receiver of visual signals48. More visually, Fig. 6 shows the results of the comparison between the eight SoTA methods and our proposed method in three domains. The first column is the RGB representation of the input, and the last column is the ground truth captured in clear water. For the five deep learning-based methods, the first eight rows are trained source domains and the last three rows of yellowish domains are domains that are not involved in training. First, Schechner does not color correct the image on any domains, but only improves the contrast, and TOPAL performs inadequate color correction only on the greenish domain. Next, the results of RGHS, CBLA, and TEBCF show more color correction, although the results of RGHS and CBLA show red-shifts, with CBLA showing the most. While enhancing the visibility of objects in the water, TEBCF introduces noise. Subsequently, the deep learning-based comparison methods outperform the first four methods overall, and we observe that FUnIE-GAN and DICAM achieve superior color correction outcomes on the source domains. Nevertheless, DICAM cannot stabilize recovery on the unseen domain, where the results exhibit an orangish color bias. In addition, the recovery results are generally hazy; for example, coins and plates with more details are hard to recover clearly, even if FUnIE-GAN’s generalizability is a little greater than TOPAL’s. The UDAformer displays various color deviations in several domains: purple in the bluish domain, yellowish in the greenish domain, and red in the yellowish domain.

On the contrary, the proposed UPD-Net shows a powerful ability to recover the images on both the source and unseen domains. On the two source domains, the restored results almost completely remove the background light related to the environment, the color of the objects is well corrected, most closely resembling the GTs, and the contrast is also significantly improved. Our approach has a stable recovery ability even in highly turbid water. For instance, in line 2,6, we display two objects that are extremely challenging to identify in the turbid water. UPD-Net is able to precisely restore them, recovering the targets’ colors and details, to a state that is very close to the ground truths. Apart from its robust recovery ability on the training domain, our suggested approach can also reliably accomplish this recovery ability on an unseen domain. The final three rows of data demonstrate that UPD-Net can handle a variety of inputs, including vivid cards, richly detailed coins, and plates with vibrant colors. Its outputs also seem to be as close to the ground truth as the performance is on the trained domains. The model, which contains a water-type classifier, is insensitive to the type of water, which helps to enable its multi-domain applicability, resulting in excellent generalization. In conclusion, it is evident that the suggested approach possesses both a large generalization capacity versus unseen domains and a strong recovery capability against muddy water.

Fig. 6
figure 6

Recovery results of samples in the domains 1, 2, 3.

Full size image

To further verify the effectiveness of the proposed method in the real underwater environment, we also perform test experiments on images from a lake. The visual result is shown in Fig. 7, from which it can be seen that UPD-Net has significantly improved the quality of the degraded image and the Rubik’s Cube with both the colors and details being well recovered, for example, zooming in on the image we can see that the “1” and “8” in the blue blocks of the Rubik’s Cube are easier to see. Our model successfully achieves this by learning features independent of the water type and then generating clear versions based on these features. Since there are no publicly available images of the three polarization states in other real water domains, we cannot further validate our model. On the one hand, we look forward to polarization data from deep or shallow water, on the other hand, we will try to obtain these images and make them publicly available in the future.

Fig. 7
figure 7

Recovery result in the domain 4.

Full size image

Ablation study

Finally, we also perform ablation experiments to verify the necessity and effectiveness of our network structure and loss functions used. Experiments are performed on test data evenly from three domains. The results are presented in Table 3. Replacing the input multi-polarization images and multi-encoder combination with the input intensity image and the single-encoder combination resulted in a decline in performance, indicating that the polarimetric images do provide additional valuable information that enhances recovery performance. The removal of each of the three loss functions also degrades the performance. Of these, the domain adversarial loss in Eq. (7) plays a pivotal role. As can be observed in Table 3 and Fig. 8, the UPD-Net demonstrates superior performance compared to the network lacking the water-type classifier. The UPD-Net, equipped with \(\:{\text{L}}_{\text{d}}\), is capable of learning domain-agnostic features, thereby enabling it to handle multiple domains, including the source domain and those that are unseen, and to generate images of superior quality. The polarization loss ensures that the network retains the polarization information during encoding and thus is well utilized during decoding. Furthermore, the SSIM loss in Eq. (9) and the generative adversarial loss in Eq. (10) also contribute to the network. The SSIM loss facilitates the generator to produce images close to the ground truths in terms of structure, and the generative adversarial loss supervises the generated images that are generally consistent with the ground truths. In sum, the network structure and loss functions employed in our approach are effective, which ensures the model’s excellent recovery and domain generalizability.

Table 3 Quality values of the results for the cases with different settings in the domains 1, 2, 3.
Full size table
Fig. 8
figure 8

Recovery results for the cases with or without domain-adversarial learning loss.

Full size image

Conclusion

In conclusion, based on the collected rich underwater polarimetric image dataset containing three domains, multiple turbidity levels, and several scenes, we present a specially designed UPD-Net based on domain-adversarial learning and generative-adversarial learning to recover the underwater polarimetric images in varied environments. The combination of the water-type classifier and domain adversarial loss enables the network to generate domain-agnostic features and recover images independent of water types. Comparison experiments show that our method is state-of-the-art in terms of visual effect and value metrics and that it has a strong recovery ability in different domains, even in some waters with high turbidity. To verify the domain generalization ability of the method, we test it on images in unseen domains, the results show that the proposed network is effective for both indoor and outdoor environments. The network has great potential for underwater imaging, recognition, and vision applications in different environments. One of our future works is to obtain more images in real underwater environments for more comprehensive validation and improvement of the proposed model, and the second is to optimize the computational efficiency of the model for practical use.