Straightening trajectory of hooked fibers in the fiber transport channel of rotor spinning investigated by fluid solid coupled simulation

Abstract

The airflow in the transport channel contributes to the accelerated straightening of the hooked fibers, which greatly influences the structural properties of the yarn. To study the straightening process of hooked fiber in the fiber transport channel, Altair EDEM 2022 software was used to establish flexible fiber models, and combined with ANSYS Fluent 2022R1 simulation software, the fluid-solid coupling method was used to simulate the air velocity distribution in the fiber transport channel and the straightening process of the hooked fibers in the airflow field. The numerical simulated air flow is verified by Hagen-Poissuille pipe flow equation. The effects of different fiber transport channels on the straightening of various hooked fibers were discussed. The results show that the straightening effect of leading hooked fiber in the airflow field is better than that of trailing hooked fiber with significant straight. In the case of the fiber transport channel with a circular cross-section outlet, the straightening of trailing hooked fiber can be slightly enhanced. Considering the feeding position of fibers transferred from carding roller to inlet of fiber transport channel, the collision of hooked fibers with the wall influences straightening of hook part or even reduces the straightness. Through the comparision on straightness between simulated and the experimental fibers, it is verified the better straightening of leading hooked fiber in the fiber sliver in the channel. The straightening process of hooked fibers influenced by airflow field and input location of fiber transport channel are simulated, which provides a reference for optimizing fiber transport channel structure and spinning prameters.

Introduction

Straightening of hooked fiber is very important to improve yarn quality. It is well known that the hooked fibers will be straightened by roller drafting during ring staple spinning process, and the trailing hooked fibers are easier to be parallelized than leading hooked fibers. However, rotor spinning will straighten the carded fibers through the difference in airflow velocity at the inlet and outlet of the fiber transport channel. Generally, increasing the gradual shrinkage ratio in cross-section between inlet and outlet increases airflow difference. In addition, the single fibers separated by the wire needles of carding roller are transported to the fiber transport channel randomly. Some input fibers are very close to the wall of transport channel, leading to the collision with great possibilities. It is obviously seen that the geometry of fiber transport channel is crucial for parallelization of fibers. Lawrence and Chen^1,2 observed the straightening of fibers in different fiber transport channels by using high-speed cameras and found that a narrower cross-section of the channel was more conducive to fiber straightening, and then an optimal geometry of the fiber transport channel was designed based on the empirical equation. However, it is difficult to observe the straightening process of hooked fibers in a closed rotor spinning equipment with a high-speed camera. The fluid simulation on airflow field velocity, pressure, turbulent kinetic energy, etc^3,4,5,6. is an effective way to solve this difficulty and can predict the influence of airflow on fiber movement and the final yarn quality^7,8. By adding an air replenishment channel on input end of the fiber transport channel, the improved airflow field in the fiber transport channel was simulated to predict the effect of the airflow on fiber transfer and straightening^8,9. However, there are no detailed reports on the effect of airflow in the fiber transport channel on fiber straightening trajectories.

The straightening of hooked fibers in the airflow of a fiber transport channel could be considered as a fluid-solid two-phase flow problem. The investigation on straightening of hooked fibers can be carried out by accurate calculation through coupling flexible fibers with fluid¹⁰. One of the key is to build an appropriate model for describing flexible fibers with complex deformations such as stretching, bending, and twisting in the airflow¹¹. Bretherton¹² used a mathematical model to describe the motion of rigid fiber particles in a low Reynolds number shear flow, and Bangert¹³ established rigid cylindrical fibers and investigated the change in the direction of fiber movement by using translational rotation equations in low-velocity flow. Yang et al.¹⁴ simplified the single fiber as particles released from the entrance of the fiber transport channel and studied the moving trajectory of fibers during spinning. This investigation ignored the fiber quality, interactions among fibers, and between fibers and the wall surface. Jin et al.¹⁵ regarded fiber clusters as a large number of particles and investigated the distribution of fibers in fiber transport channel, spinning rotor walls, and the shape of fiber rings formed by particles. In the case of considering flexible fibers as rigid particles and cylindrical objects, the deformable characteristics of fibers could not be described. Therefore, the chain fiber model was developed to accurately represent the characteristics of flexible fibers in the airflow field. Schmid et al.¹⁶ established a rod-chain fiber model, treating fibers as a certain number of cylindrical rods, with adjacent rods connected by elastic and viscoelastic joints. Pei et al.¹⁰ established a bead-rod flexible fiber model by connecting rigid balls with massless elastic rods. This fiber model could be stretched, bent, and twisted in the flow field, and the accuracy of the fiber model was verified by numerical simulation. Bead-spring chain model contained multiple spheres of equal mass contacting with each other, transforming between rigid and flexible fibers by varying the stretching, bending, and twisting constants. Needle chain model and needle-spring chain model^11,17 were built by connecting rigid needle rods with joints or springs¹¹. The fiber deformation could be realized by translation and rotation among the needle rods. Lin et al.¹⁷ used round beads and massless cylindrical rods to model bead-rod fibers, and the morphological changes of straightened fibers at the inlet of fiber transport channel in the airflow was studied. The above-mentioned fiber models are basically straight fibers.

In practice, there are more hooked fibers needed to be parallelized in the fiber transport channel. As a whole, The complex hooked fibers are divided into leading hooked fiber, trailing hooked fiber, and both ends hooked fiber¹⁸. When the hooked fibers move in the fiber transport channel, the probability of collision between the hooked part and the wall is relatively high. The interaction between fiber and wall surface has a great impact on fiber moving trajectory. The collision, therefore, cannot be ignored. It is more meaningful to accurately simulate straightening of these hooked fibers for improving the properties of rotor spun yarns.

The airflow field data in the fiber transport channel was simulated by ANSYS Fluent 2022R1, which is a commercial computational fluid dynamics (CFD) software. The results were validated according to the Hagen-Poissuille tube flow equation. Altair EDEM 2022 discrete element modeling software was used to establish bead-spring chain model of four flexible hooked fibers. By coupling the fiber movement with the airflow field¹⁹, the straightening of hooked fibers was simulated by varying the geometries of fiber transport channel and delivery locations from carding roller. The morphology of hooked fiber bundles before and after parallelization was observed by SEM, and the fiber straightening coefficient was calculated by achieving corresponding data from experiments on a rotor spinning. The straightening effect of different hooked fibers in the airflow field was verified by comparison between simulation and verifications from spinning experiments and morphological observation.

Numerical simulation model

Geometric model of fiber transport channel

The geometric model of the fiber transport channel includes the channel inlet (inlet 1), air supplementing inlet (inlet 2), and channel outlet (outlet 1), as shown in Fig. 1. The gradual condensed fiber transport channel straightens hooked fiber by accelerated airflow. Different channel geometries influence the airflow field produced in fiber transport channel. Therefore, according to the channels equipped on SDL-Y015F fast-type rotor spinning machine, the models with square and circular sections denoted as fiber transport channel I and II, respectively, were built. Two fiber inlet locations were set at the entrance of the fiber transport channel. Position 1 is close to the center line of the fiber transport channel, and position 2 is far away from the center line of the fiber transport channel. The parameters are listed in Table 1.

Fig. 1

Fiber transport channel geometric model I (a) and II (b).

Table 1 Boundary conditions and geometric parameters of simulated fiber transport channel.

Fiber particle contact model

When the fibers, modeled as discrete bead-spring chains, are moving through the fiber transport channel, there are unavoidable collisions, frictions, and adhesions among fiber-to-fiber and fiber-to-geometry. To update a fiber motion, the collision behavior of fiber was simulated by contact model. Considering the fiber model as particles in continuous contact, the default Hertz-Mindlin (no slip) contact model for EDEM, combining the Hertz contact theory and Mindlin adhesion theory, was introduced to accurately describe the contact behavior of solid surfaces. The contact mechanics model was listed in Fig. 2.

Fig. 2

Hertz-Mindlin(no slip) contact mechanics models: 1- particle stiffness; 2- damper; 3- friction unit.

As shown in Fig. 2, for each contact point, the force-displacement behavior of particles are described by the normal contact force F_n and tangential contact force F_t of the two contact particles.

The equation for the normal contact force F_n and tangential contact force F_t between particle i and particle j is as follows:

$${F_n}=\frac{{{4}}}{{{3}}}{E^ * }\sqrt {{R^ * }} \delta _{n}^{{\frac{{{3}}}{{{2}}}}}$$

(1)

$${{{F}}_{{t}}}= - {{{S}}_{{t}}}{\delta _{{t}}}$$

(2)

Tangential contact force F_t is not only related to tangential stiffness and particle overlap function, but also related to friction force, and friction force is related to the coefficient of friction and normal contact force F_n. That is, tangential contact force F_t is limited by friction µF_n. Where the equivalent Young’s Modulus E^*, the equivalent radius R^*, and tangential stiffness S_t are expressed as follows:

$$\frac{{{1}}}{{{E^ * }}}=\frac{{{{1-}}{v_i}^{{{2}}}}}{{{E_i}}}{{+}}\frac{{{{1-}}{v_j}^{{{2}}}}}{{{E_j}}}$$

(3)

$$\frac{{{1}}}{{{R^ * }}}=\frac{{{1}}}{{{R_i}}}+\frac{{{1}}}{{{R_j}}}$$

(4)

$${{{S}}_t}=8{{{G}}^ * }\sqrt {{{{R}}^ * }{\delta _{{n}}}}$$

(5)

In Eq. (1) to (5), E_i, v_i, R_i and E_j, v_j, R_j are Young’s modulus, Poisson’s ratio, and radius of particle i and particle j, respectively; G^* is the equivalent shear modulus; δ_n and δ_t are the function of normal overlap and tangential overlap functions of the particles, respectively. The overlap function is the overlap of two particles in the direction of perpendicular contact surfaces or parallel contact surfaces. The normal overlap function is usually related to the shape and size of the particles, indicating how close the particles are to each other. Tangential overlap functions are usually related to interactions between particles.

The elastic deformation occurs after the collision between fiber and fiber, fiber and wall surface, and fibers may be decelerated by damping force. The equation for the normal damping force Fd n and tangential damping Fd t between two particles is as follows:

$$F_{n}^{d}= - 2\sqrt {\frac{5}{6}} \beta \sqrt {{S_n}{m^ * }} {\varvec{v}}_{n}^{{rel}}$$

(6)

$$F_{t}^{d}= - 2\sqrt {\frac{5}{6}} \beta \sqrt {{S_t}{m^ * }} {\varvec{v}}_{t}^{{rel}}$$

(7)

where m^* is the equivalent mass of the particles; β is the coefficient; S_n is the normal stiffness between the particles; vrel nand vrel t are the normal component and tangential component of the relative velocity between the particles. m^*, β, and S_n are expressed as follows:

$${m^ * }={\left( {\frac{1}{{{{{m}}_{{j}}}}}{{+}}\frac{1}{{{{{m}}_{{i}}}}}} \right)^{ - 1}}$$

(8)

$$\beta =\frac{{ - {{lne}}}}{{\sqrt {{{l}}{{{n}}^2}{{e+}}{\pi ^2}} }}$$

(9)

$${{{S}}_{{n}}}=2{{{E}}^ * }\sqrt {{{{R}}^ * }{\delta _{{n}}}}$$

(10)

Fiber particle bonding model

The movement of flexible fiber in the airflow field is complex, and the fibers will be stretched, bent, and twisted, and etc. To achieve the characteristics of flexible fibers, the Bonding V2 model is required to form particles into flexible fibers with large aspect ratios. The bond makes the fiber resist deformation and only breaks when the stress exceeds the maximum value. The critical normal and tangential stress values are as follows:

$${{{{\sigma}}}_{{{max}}}}<\frac{{ - {{{F}}_{{n}}}}}{{{A}}}+\frac{{{{2}}{{{M}}_t}}}{{{J}}}{{{R}}_{{B}}}$$

(11)

$${\tau _{{{max}}}}<\frac{{ - {{{F}}_t}}}{{{A}}}+\frac{{{{2}}{{{M}}_n}}}{{{J}}}{{{R}}_{{B}}}$$

(12)

Where the expressions for the bond radius R_B, normal torque M_n, tangential torque M_t, normal contact force F_n, and tangential contact force F_t are as follows:

$${{{\delta}}}{{{F}}_{{n}}}= - {{{v}}_{{n}}}{{{S}}_{{n}}}A{{{\delta}t}}$$

(13)

$${{{\delta}}}{{{F}}_t}= - {{{v}}_t}{{{S}}_t}A{{{\delta}t}}$$

(14)

$${{{\delta}}}{{{M}}_{{n}}}= - {\omega _{{n}}}{{{S}}_t}{{J{\delta}t}}$$

(15)

$${{{\delta}}}{{{M}}_t}= - {\omega _t}{{{S}}_n}\frac{{{J}}}{2}{{{\delta}t}}$$

(16)

where δ_t is the time step, 0.0002 s; ω_n and ω_t are the normal and tangential angular velocities, respectively; A is the bonding area between the particles, and J is the rotational inertia of the particles with the following expression:

$$A=\pi {R_B}^{2}$$

(17)

$$J=\frac{1}{2}\pi {R_B}^{4}$$

(18)

Modeling the fiber and computational coupling process

The bead-spring chain model composed of particles with the same diameter and physical properties through the Bonding V2 contact mode was shown in Fig. 3a. For convenient observation of fiber deformation, the fiber particle radius was set as 0.2 mm, the total fiber length was 20 mm, and the projection length was 16.44 mm.

To compare the straightness of leading hooked fiber and trailing hooked fiber in the fiber transport channel, four different fiber models including Fibers I and II as leading hooked fiber and Fiber III and IV as trailing hooked fiber were established as shown in Fig. 3b. However, since the proportion of both ends hooked fiber in the sliver is small in comparison with that of leading hooked and trailing hooked fibers, only the straightening of leading hooked fibers and trailing hooked fibers in airflow of the fiber transport channel was investigated in this research. Therefore, the results of both ends hooked fibers are not included here. The Fig. 3c shows the coupling calculation process of Fluent-EDEM, the total simulation time is 0.01 s, divided into 50 times steps of 0.0002 s, and each time step updates and saves the result once.

Fig. 3

Meta-Particle flexible fiber model and computational coupling process. (a) Bead-spring chain model. (b) hooked fibers. (c) computational coupling process.

Numerical simulation and verification of airflow field

Simulation of airflow field

The velocity distribution of airflow in fiber transport channels I and II was simulated by ANSYS Fluent 2022R1, velocity values were extracted along the center line of fiber transport channel in the Y-axis direction. The results were shown in Fig. 4. According to the velocity distribution, the airflow velocity in the L₁ section is below 20 m/s. With the convergence of airflow from inlet 1 of fiber transport channel and air supplementing inlet, the airflow speed of L₂ section is significantly increased. This is attributed to the influence of cross-sectional area of the pipe geometry and the airflow velocity on gas flow. Since the total gas flow in the fiber transport channel is constant, the velocity is constantly increasing along the gradual shrinkage of cross-sectional area. The maximum value of the airflow velocity at the outlet 1 is 130 m/s and 167 m/s respectively, which is more than 10 times velocity of inlet 1.

Fig. 4

Velocity cloud diagram and velocity curve of airflow field in fiber transport channel. (a) Velocity distribution of fiber transport channel I. (b) velocity along center line of fiber transport channel I. (c) velocity distribution of fiber transport channel II. (d) Velocity along center line of fiber transport channel II.

It is also seen that the airflow velocity near the centerline of the fiber transport channel is higher than that near the wall. This leads to the tendency all of the fibers moving to the centerline. The airflow velocity in L₂ section of fiber channel II is obviously higher than that in fiber channel I. Therefore, it is expected that the airflow in channel II will accelerate the fiber more obviously, and hooked fiber may be straightened in channel II in advance than in channel I. The acceleration in advance is more beneficial to the straightening of hooked fiber.

Validation of airflow field by Hagen-Poissuille pipe flow

The Hagen-Poiseuille tube flow describes the ideal case of fluid flow in a cylindrical tube, which results from the pressure difference between the inlet and outlet of the tube. The airflow in the stabilized fiber transport channel can be regarded as a fully developed pipe flow. Therefore, the Hagen-Poiseuille tube flow Eq. (19) simplified by the N-S equation was used to calculate the fluid flow, fluid velocity, and pressure loss in the fiber channel. To facilitate the study, the fluid flow in the fiber transport channel was assumed to be incompressible, and both momentum conservation and mass conservation were satisfied. The Reynolds number at a point within the fiber transport channel was calculated according to the Reynolds number Eq. (20). Taking fiber transport channel geometric model II as an example, the maximum value of the Reynolds number is 2293, less than the critical value of 2300 for the airflow velocity. Therefore, the airflow at each point of the fiber channel can be regarded as a stable laminar flow, and the ideal velocity values of each point in the tube were obtained according to the Hagen-Poiseuille tube flow Eq. (21). The calculated value was used to verify the simulated airflow velocity.

$${u_c}=\frac{{\Delta p{D^2}}}{{16{{k}}l}}$$

(19)

$$Re=\frac{{vL\rho }}{{{k}}}$$

(20)

$${u_r}={u_c}\left[ {1 - {{\left( {\frac{r}{R}} \right)}^2}} \right]$$

(21)

where Re is the Reynolds number; the characteristic length L is regarded as radius of fiber particle, 0.2 mm; ρ is the air density; u_c is the air velocity at the centerline of the fiber transport channel; D and R are the equivalent diameter and radius of the tube, respectively; r is radius of fiber particle; Δp is the pressure difference; k is the aerodynamic viscosity coefficient, 1.8 × 10^− 5 Pa·s; l is the channel length. The airflow velocity u_c at the centerline of the fiber transport channel is obtained through simulation. Then 12 points on the centerline are taken and the ideal airflow velocity u_r is calculated according to the Hagen-Poiseuille flow equation.

Fig. 5

Comparison of fiber transport channel centerline airflow velocities.

It is seen from Fig. 5 that the maximum difference between simulated velocity u_c and ideal velocity u_r is 3.63%. Therefore, the airflow velocity obtained by simulation are essentially the same as those obtained from the calculations, verifying the accuracy of the simulated airflow in fiber transport channel.

Fiber straightening trajectory

Fiber straightening at position 1 of fiber transport channel model I

No airflow in the fiber transport channel was firstly simulated as illustrated in Fig. 6a. It is obviously seen that the time for the fiber passing through channel from position 1 is 0.012 s with the original fiber velocity. There is not straighented of the hooked part at all. On the contrary, If the leading hooked fiber is accelerated by the airflow of fiber transport channel, the hooked part is gradually straightened before reaching outlet 1, and the time is less than 0.01s as shown in Fig. 6b. This indicates that the airflow indeed has effect on straightening and accelerating the fiber. Further, according to the simulated moving trajectory, the hooked fiber in the fiber transport channel experiences the following processes:

• i. The airflow velocity at the centerline of the fiber transport channel is higher than the velocity near the wall, so that fibers will gradually shift toward the center line during the process of fiber straightening.

• ii. The section bc of fiber is firstly straightened. This is due to the close contact with straight part of the hooked fiber. When the fiber moves to the high-speed airflow near the outlet of the fiber transport channel, the section bc tend to be parallel to the main part.

• iii. The head of the fiber reaches the outlet of the fiber transport channel regardless of fully straightened of the hooked fiber.

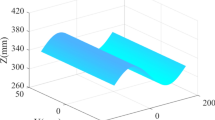
As shown in Fig. 4a, the airflow velocity in outlet of the fiber transport channel is high, while the hook and straight part of the leading hooked fiber are located in the airflow zone with high-velocity and low-velocity, respectively. Therefore, the hook part of the leading hooked fiber enters the high-speed airflow area of the fiber transport channel in advance. Figure 6b shows the straightening process of the leading hooked fibers in the fiber transport channel. Before 0.008 s, the hook part of the leading hooked fiber is unchanged. Till 0.009 s, the head of leading hooked fiber reaches the outlet, and the section bc of the fiber tends to be straightened.

Marking typical positions on the fiber as a, b,c and d, the velocities at the four points extracted from simulation were shown in Fig. 6c and d. At 0.008 s, the velocity difference between the head and tail end of fiber II is 1.61 m/s, and the resultant force (Fig. 6e) is stable and growing gradually. After 0.009 s, the velocity at point a is greater than the other three positions, and there is an obvious velocity difference between the head of the fiber and other positions. In the meanwhile, the resultant force difference between the head and tail end reaches a maximum value of 0.027 cN, and the leading hooked part of fiber II is basically straightened. Till 0.0095 s, the head part of fiber has passed through outlet 1, and the fiber remains straight. Therefore, the hook part will gradually be eliminated when the leading hooked fiber moves in the fiber transport channel. It is seen that the straightening effect of the leading hooked fiber in fiber transport channel I is obvious.

Fig. 6

Straightening process of leading hooked fibers in fiber transport channel I and velocity profiles of typical positional point. (a) Fiber movement without airflow. (b) straightening process of leading hooked fiber. (c) velocity of typical positions for fiber I. (d) velocity of typical positions for fiber II. (e) force at point a and d of fiber II.

Figure 7 shows the straightening process of trailing hooked fiber in the fiber transport channel I, the velocities at four typical positions, and the resultant force at the head and tail end of fiber IV. The straightening trajectory of trailing hooked fiber before 0.008 s is similar to leading hooked fiber, and the velocity difference between the head and tail end is 0.58 m/s. At 0.009 s, the head end of fiber is close to the outlet of the fiber transport channel, and the resultant force difference between the head and tail end reaches the maximum value of 0.0097 cN, but it is smaller than the leading hooked fiber. Therefore, the deformation of the fiber is not obvious. Furthermore, the resultant force at the head-end of the fiber fluctuates considerably. All of these might lead to weak straightenness of trailing hooked fiber. At 0.01 s, the straight head of the fiber has left from the fiber transport channel. The section bc which is close to straight part of fiber has been straightened, parallelling to the fiber body. This is the same as the straighting process of the leading hooked fibers. According to the velocity curves in Fig. 7b,c, the velocities at points a, b, and c slowly exceed point d after 0.008 s. In other words, the velocities of the main part of a fiber are gradually greater than hook part, which indicates that the straightening tendency of hook part of trailing hooked fiber occurs only near the outlet of the fiber transport channel. Overall, the straightening of the trailing hooked fiber in fiber transport channel I is less satisfactory.

Fig. 7

Straightening process of trailing hooked fibers in fiber transport channel I and velocity profiles of typical positional point. (a) Straightening process of trailing hooked fiber. (b) velocity of typical positions for fiber III. (c) fiber IV typical position velocity. (d) force at point ad of fiber IV.

Fiber straightening at position 2 of fiber transport channel model I

Position 2 of the fiber transport channel I was selected as the initial input point to simulate the influence of random distribution of carded single hooked fiber on straightening. The results were shown in Fig. 8. In comparison with position 1, the hooked fibers delivery from position 2 has great possibilities to collide with the channel wall. At 0.008 s, the fiber begins to hit the wall of the fiber transport channel till 0.0095 s when the fiber head reaches the outlet 1. From the straightening process of the four types of hooked fibers, the hook part of trailing hooked fiber has not been straightened due to the friction generated by the contact with the wall surface, and the head end of fiber I hits the wall to form a more complex hook, while the head end of fiber II hits the wall, the hook part is straightened under the combined effect of airflow and wall friction. Therefore, fiber II tends to be straightened easily in fiber transport channel when be in contact with the wall. For the other fibers deformed greatly after the fibers contact with the wall, the hook part still exists, and the fiber straightness has not been improved.

Fig. 8

Straightening process of hooked fibers at position 2. (a) Straightening process of leading hooked fiber. (b) Straightening process of trailing hooked fiber.

Straightening trajectory of fibers in fiber channel model II

The cross-section shape of outlet 1 of the fiber transport channel II is circular, and the contraction shape also gradually shifts from square to circular. The velocity distribution in Fig. 4 indicates that velocity of the L₂ section of fiber transport channel II is significantly higher than that of fiber transport channel I, which is more beneficial to fiber acceleration and straightening.

Figure 9 shows the straightening process of leading hooked fibers in fiber transport channel II and the velocity curves of typical position points. As shown in the velocity curve, the velocity of point a of the fiber is different from that of other points from 0.006 s, and the section bc of the fiber tends to be parallel to the section cd of the straight body. There is a large difference after 0.008 s, and the section bc has been completely parallel to the straight body of fiber. Till 0.009 s, the velocity difference between the head and tail end of the fiber reaches the maximum value, and the fiber is straightened. Fibers leave the fiber transport channel into the spinning rotor and gradually approach the slip surface after 0.0095 s.

Fig. 9

Straightening process of leading hooked fibers in fiber transport channel II and typical positional point velocity profiles. (a) Straightening process of leading hooked fiber; (b) velocity of typical positions for fiber I. (c) velocity of typical positions for fiber II.

Figure 10 shows the straightening trajectory of trailing hooked fibers in fiber transport channel II with velocity profiles at typical positions. Compared with the straightening process of fiber in the fiber transport channel I, the head end of fiber also reaches the outlet at 0.009 s, and the velocity difference between the point d and other points is obvious. At this time, the section bc of the hook part has been straightened and is parallel to the section ab, and the section cd is parallel to the section ab of the fiber body. At 0.0095 s, the head end of the fiber has left from the outlet of the fiber transport channel, and the hook part of fibers III and IV are almost parallel to the main body. It is concluded that the fiber straightening situation is better than the situation of the trailing hooked fibers in the fiber transport channel I.

Fig. 10

Straightening process of trailing hooked fibers in fiber transport channel II and typical positional point velocity profiles. (a) Trailing hooked fiber straightening process. (b) fiber III typical position velocity. (c) fiber IV typical position velocity.

Experimental and morphological verification of fiber straightening

The projected length of the hooked fiber model was measured by ImageJ image processing software, which has been extensively used to measure fiber diameter and length^20,21,22. By comparing it with the straightened fiber length l, the straightness of simulated fiber η is calculated. To verify the simulated straightening of hooked fibers in the fiber transport channel, the commercially available sliver was deliveried to a SDL-Y015F fast-type rotor spinning machine in both leading and trailing hooks. The fiber rings coagulated in the spinning rotor were removed. Keeping parameters of actual spinning consistent with the simulated ones, the input slivers and fiber rings were selected as the samples to measure straightness according to the schematic shown in Fig. 11. The average fiber length of the sliver was measured as 21.26 mm by using the Y111 fiber length analyzer. The sliver was held by the Y171 fiber cutter along the direction perpendicular to the fiber axis. By combing this sliver, some ungripped fibers are removed. Weighing the cut fibers on both sides of the gripped fibers and the middle gripped part as G_t, G_v, and G_h, respectively, the average straightness of the fiber was calculated by Eq. (22) according to the modified Lindsley method. The results were shown in Table 2.

Fig. 11

Calculation of fiber straightness.

$$\eta =\frac{{({G_t}+{G_v})H}}{{{G_h}L}}$$

(22)

Where η is the average fiber straightness; G_t is the weight after cutting off the head portion of fiber bundle, mg; G_v is the weight after cutting off the tail portion of fiber bundle, mg; G_h is the weight of the middle portion of the fiber bundle, mg; H is the length of the middle of the fiber bundle, 10 mm; L is the average length of the sliver bundle, mm.

Table 2 Projected length and straightness of fibers in fiber transport channel I.

In simulation, the initial straightness of modeled fiber is 82.20% with projected length of 16.44 mm and total length of 20 mm. It is seen from Table 2 that the simulated straightness of leading hooked fiber is increased by 7.90-12.00%, but trailing hooked fiber straightness is only increased by 2.25-2.70%. For the leading hooked fiber, the average straightness of the experiment is highly consistent with that of the simulated fiber, with an error of 0.16–4.20%. Meanwhile, the straightness results of the leading hooked fiber are compared with that of fiber ring in the spinning experiment, the fiber straightening effect of the leading hook is obvious with the improved straightness of 22.33%. This further verifies the simulation results of the leading hooked fiber straightening. For the trailing hooked fiber, the experimental straightness of fibers collected from fiber ring is 65.53%, which even deteriorated by 8.63% in comparison with the input sliver. On the one hand, this indicates the poor straightening of trailing hooked fibers during fiber transport channel, which is consistent with the simulated one. On the other hand, to straighten the hook part of the trailing hooked fiber, a backward force needs to be applied to the trailing hook, while the airflow in the transport channel always applies a forward force to trailing hook, which is not conducive to the straightening of the trailing hooked fiber. It is just because of the simulated results about straightening of trailing hooked fibers, when the unstraightened trailing hooked fibers enter the high-speed airflow area of spinning rotor, the airflow also exerts a forward force on trailing hook, which overlaps the main body of the fiber several times, resulting in a reduction in the straightness of the trailing hooked fibers²³. According to the simulation of fiber straightening and experimental verification, the airflow in the fiber transport channel can effectively improve the straightening of the leading hooked fiber, and the effect on the straightening of the trailing hooked fiber is less obvious.

The straightening of the fibers in the fiber ring and sliver was observed under the polarizing microscope (BK-POL, China), as shown in Fig. 12. The fiber specimen to be measured was picked up with a tweezer and placed on a slide with a coverslip on it. And then the prepared specimen was observed on the platform of the polarizing microscope until a clear image was obtained. Figure 12a,c show the straightness of the sliver and fibers in the fiber ring with leading hook feeding, and Fig. 12d,f show the straightness of the sliver and fibers in the fiber ring with trailing hook feeding. The hook of fibers was observed through a microscope, and the hook condition of some fibers in the fiber bundle was shown in Fig. 12b,e. There is a significant improvement in the fiber straightness within the fiber ring after the leading hooked fibers are drafted through the transport channel. The straightening of the fibers in the fiber bundle is observed through verification and also proved that the leading hooked fiber is easier to be straightened by the airflow of fiber transport channel. Therefore, the proportion of trailing hooked fiber should be reduced in the fiber preparation of rotor spinning.

Fig. 12

Straightness of fibers in sliver and fiber ring. (a) Sliver fed with leading hook(×4). (b) Leading hooked fiber(×10). (c) Leading hooked fiber ring(×4). (d) Sliver fed with trailing hook(×4). (e) Trailing hooked fiber(×10). (f) Trailing hooked fiber ring(×4).

Conclusion

In this paper, the fluid simulation software ANSYS Fluent 2022R1 and discrete element software Altair EDEM 2022 were combined to establish different models of fiber transport channels and flexible fibers. The fluid-solid two-phase flow coupling method was used to simulate the straightening trajectory of different hooked fibers in the flow field of two types of fiber transport channels.

The simulated airflow velocities in the fiber transport channel are verified based on the calculation results of the Hagen-Poiseuille tube flow equation. The velocity of the airflow field inside the fiber transport channel II is larger than that of the fiber transport channel I, especially the airflow velocity near the centerline is higher, increasing the velocity difference between the head and tail ends of the fiber, which is conducive to the straightening of the hooked fiber.

According to the straightening process of hooked fiber in the presence or absence of an airflow field, the interaction between fiber and airflow field in fluid-solid coupling is verified. By simulating the fiber straightening trajectory and comparing the difference in the combined force between head and tail end in the airflow, the leading hooked fiber is straightened, and the straightening effect is better than that of trailing hooked fiber. There is a slight improvement in the straightening effect of trailing hooked fiber within the fiber transport channel II, but the hook part is still not fully straightened. The spinning experiments and the observation on straightening condition of hooked fiber verify the theoretical simulation results.

The straightening of the hook part varies depending on the position of the fiber at the inlet to the transport channel. As the fiber moves closer to the centreline of the transport channel, the hook is eliminated or slightly straightened. However, when the fiber is close to the wall, the hook part collides with the wall of the fiber transport channel, the fiber II is more likely to straighten during contact with the wall, but other hooked fibers are easily deformed due to the collision, and the fiber straightness is not improved in the channel. Controlling the fibers input location will be one of effective way to straighten hooked fibers.