Introduction

The application of machine learning (ML) to predict future air pollution levels or occurrences of high pollution episodes has gained significant traction1,2,3,4. This growing use of ML in air pollution prediction can be attributed to various factors. Firstly, ML is adept at handling the intricate and often non-linear associations between numerous variables and air pollutant concentrations. ML algorithms are capable of processing large volumes of diverse and complex data, such as atmospheric and meteorological variables. They can uncover complex patterns and relationships that may have a bearing on air pollution levels, which enhances the depth and accuracy of their predictions5,6. Secondly, compared to traditional statistical methods, ML models can offer more precise predictions, especially when dealing with vast, high-dimensional datasets7. Thirdly, once trained, these models can deliver real-time or near-real-time predictions. Fourthly, ML can be automated and scaled, allowing extensive geographical coverage and continuous updates as new data emerges.

Utilizing ML, researchers can construct predictive models of exceptional accuracy that incorporate a multitude of elements including sources of emissions, meteorological conditions, and geographical attributes8,9,10. This leads to more accurate and dependable air quality predictions11. Furthermore, ML methodologies can evolve and learn from additionally collected data and new data sources once they become available, which allows for continual enhancement of their predictive precision over time. Methods for forecasting and predictions include traditional ML-based approaches such as Random Forests12,13 and statistical approaches such as autoregressive methods14, and deep learning methods15,16. In a forecasting task, the estimation of forthcoming pollutant levels is accomplished by making use of past data and usually environmental variables, essentially extending a time series into the future10,17. Alternatively, in a prediction framework, the aim is to predict pollutant levels based on measurements from other sources or locations, without taking into account trends of the target pollutant. This is analogous to estimating pollutant levels in areas where measurements are nonexistent or unachievable. Moreover, this approach offers valuable insights into the primary factors influencing specific pollutants.

Despite the advantages of ML techniques, building predictive models is data intensive and requires time and sometimes computationally intensive training. Additionally, those models are domain-dependent, which means, that they need to be trained on a specific problem, e.g. certain measurement stations and/or pollutants. To overcome those restrictions, transfer learning (TL) became popular among scientists10,18,19,20. The intuition behind transfer learning is to apply the knowledge gained in solving one known problem (source domain) to another, related problem (target domain). Although applied in many use cases in various domains such as transferring the knowledge gained from wind park sensors to newly installed ones to avoid training from scratch and to overcome data scarcity, it is hardly used in the field of atmospheric research18,21. Hence, it is of particular interest in this work to explore and showcase the utilization of TL in the application domain of predicting air quality.

Predicting the concentration of pollutants for the next day or week is important when, for example, planning outdoor activities. Ma et al.9,18 implemented a framework using Bidirectional Long Short-Term Memory (BLSTM) models to forecast PM2.5. In the paper from 2019, the authors transferred the knowledge acquired from models trained with small temporal resolution pollutants data to larger temporal resolution. As an outcome, the authors showed that TL can also improve pollution concentration forecasting accuracy in different temporal resolutions compared to directly training a model with data of higher temporal resolution. Dhole et al.22 used meteorological data and pollutants to predict PM2.5 concentrations. The authors proposed a multi-source knowledge transfer by creating 10 individual source models (one model per measurement station trained with their individual source data) and transferring the knowledge to the target station to predict PM2.5. Different ensemble architectures based on CNNs such as CNN-Long Short-Term Memory (CNN-LSTM) and CNN-Gated Recurrent Units (CNN-GRU) were used as source models. The authors showed, that a cumulative prediction with knowledge of each station performs better than using only using the knowledge from a single retrained station. By implementing various retraining strategies, an improvement of 35% compared to directly training the model with limited data of the target domain. In contrast to our study, Dhole et al.22 employed a more extensive dataset, comprising 10 source stations, each with 35,000 samples per station, while our dataset consists of 5 stations with 2885 samples per station. Furthermore, their methodology centred on generating hourly forecasts, diverging from our focus on long-term predictions. Additionally, they integrated past pollutant values into their model, whereas our study solely concentrates on predictive modelling, omitting the utilization of historical pollutant data due to its assumed unavailability or limited accessibility. Lastly, while the authors focused on transferring data solely within one city, our study extends this scope by examining the transferability of models between different cities. In the investigation conducted by Cheng et al.20, the focus was on knowledge transfer across ten measurement stations to evaluate its transferability. This transferred knowledge was subsequently employed to judiciously choose a suitable source station for training a ResNet-LSTM model. The key aim was to identify a source station exhibiting minimal errors in predicting PM2.5 concentrations in different domains.

To forecast air pollutants, conventional statistical techniques such as Auto-Regressive Integrated Moving Average (ARIMA) can be applied. In recent years, contemporary approaches like ML and particularly deep learning (DL) have exhibited superior performance in multiple scenarios compared to traditional methods17. Nonetheless, this improvement comes at the cost of increased complexity in model development and longer execution times23,24. Grivas and Chaloulakou25 utilized Multilayer Perceptrons (MLP) trained on meteorological and time-scale data to forecast hourly PM10 concentrations at four stations within the Greater Athens Area. Their developed models outperformed multiple linear regression models, emphasizing the intricate connection between meteorological factors and PM10 concentrations. Cai et al.26 employed neural networks to predict CO, NO2, PM10, and O3 concentrations along the roadside in Guangzhou, China. Besides showcasing superior accuracy over statistical models, the proposed models also displayed enhanced transferability, enabling predictions for nearby stations. Bekkar et al.8 assessed the performance of various deep learning architectures, including LSTM, Bi-LSTM, GRU, Bi-GRU, CNN, and a hybrid CNN-LSTM. Their study, using historical PM2.5 and meteorological features of diverse temporal resolutions, revealed that CNN-LSTM surpassed other models, primarily due to its internal architecture’s capability to extract both temporal and spatial features.

The aim of this study is to (1) understand the key features needed to make PM10 predictions, (2) to investigate whether the collective knowledge gained by creating a model out of multiple measurement stations leads to a better predictive PM10 accuracy compared to choosing a single station, (3) to explore the feasibility of TL, aiming to generalize models trained in one city to another, thus providing insights into potential applications of TL in similar scenarios, and (4) to estimate the number of labelled target samples needed by the transfer algorithm to yield a notable enhancement in performance compared to out-of-domain generalization.

Materials and methods

Air pollutant measurements in Graz and Zagreb

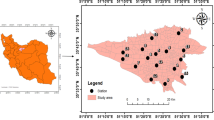
Graz is located in the south of Austria and is the second largest city in the country with 298,512 (2023) inhabitants27. Zagreb is the capital of Croatia and is located in the north with 768,054 (2021) inhabitants28. Graz hosts five governmental measurement stations, namely Don Bosco (D), North (N), East (E), South (S), and West (W), while Zagreb (Z) accommodates three governmental measurement stations, with one having long-term data and considered in this analysis2. The selection of stations as research subjects is grounded in the utilization of publicly accessible data29,30. A detailed description of the measurement stations in Graz can be viewed in Moser et al.31 and for Zagreb in Šimić et al.6. The stations in Graz recorded data in the period from 1.1.2014 to 25.11.2021 and the one selected station in Zagreb in the period from 1.1.2009 to 31.12.2020. The data from Zagreb can be accessed via Šimić et al.29 and Graz via Lovrić et al.30. All recorded measurements are daily averages (24 hours). This results in 2885 samples per Graz station (14,425 in total, without taking missing values into account), and in Zagreb: 4,382 samples. The annual mean PM10 evolution per station is shown in Fig. 1a. The geographical locations of each measurement station in Graz are depicted in Fig. 1b, and those in Zagreb are shown in Fig. 1c. Graz is located on the foothills of the Alps and Zagreb is on the slopes of the Medvednica Mountain. The cities exhibit a common characteristic, they occasionally exceed the EU regulation’s32 maximum number of days (35) on which a daily mean value for PM10 of 50 μg/m3 is exceeded. In both cities, the annual mean value for PM10 does not exceed the threshold of 40 μg/m3, as mandated by the second EU regulation on particulate matter.

Fig. 1
figure 1

Measurement station location. (a) Shows the evolution of the average annual PM10 value per station. (b) Shows the location of the measurement stations in Graz Don Bosco: \(47.055617^\circ\) N, \(15.416539^\circ\) E; North: \(47.09437^\circ\) N, \(15.415122^\circ\) E; East: \(47.059530^\circ\) N, \(15.466634^\circ\) E; South: \(47.041692^\circ\) N, \(15.433078^\circ\) E; West: \(47.069506^\circ\) N, \(15.403728^\circ\) E and (c) Zagreb with coordinates: \(45.811389^\circ\) N,\(15.989167^\circ\) E. Photos taken from Google maps ®.

Full size image

Feature engineering

Data pre-processing, specifically the exclusion of above-average PM10 values attributed to specific events like New Year’s fireworks or Sahara dust storms, is conducted following a methodology akin to that outlined in Lovrić et al.1.

Missing values

The presence of missing values poses a challenge in machine learning, as numerous algorithms are unable to accommodate them. Therefore, it is imperative to employ techniques for accurately detecting and managing missing values, such as by omitting them when necessary. A single sensor measurement comprises multiple features (e.g. temperature, wind speed, etc.). The number of missing values per feature is shown in Table 1. An extended version of this table including various other gaseous pollutants can be found in the supplementary material table Extended feature per station summary. The total number of missing meteorological values is 7771, while the total number of missing values for pollutants is 139. Station East has the most missing values. Some features are assumed to be the same in the other surrounding stations, such as humidity, air temperature, and air pressure. These missing features are imputed for station East with the values from the nearest station South. Features such as wind speed or wind peak are considered local and therefore cannot be imputed. These features are discarded. Additionally, the feature radiation of station North is also omitted, since it only occurs in this station and contains many missing values.

Table 1 This table summarizes the daily mean meteorological and the air quality feature PM10 available for each station.
Full size table

Encoding features

The features are coded in a way similar to the approach presented in Bekkar et al.8. All continuous wind degree values are expressed as one of multiple classes. 16 classes are used, resulting in \(22.5^\circ\) per class. For instance, the wind direction of \(8^\circ\) is labelled as class N (from \(348.75^\circ\) to \(11.25^\circ\)) and the wind direction of \(210^\circ\) is expressed as class SSW (from \(191.25^\circ\) to \(213.75^\circ\)). This transformation is done because it reduces variability in wind direction. For machine learning, each category is later changed into an ordinal feature, since most models can only handle numeric values.

Temporal features

Apart from the features present in the dataset from the measurement stations, additional temporal features may better explain the concentration of PM10, as previously observed in Lovrić et al.1. These features are considered global on a city level, as they affect each station in one city. Additional temporal features used in this work are: dayOfYear (adds information about the current day [from 1 to 365 or 366]; it is thought to explain much of the seasonal variation in PM10 concentration values), holiday (adds binary information about whether there is a holiday or not), dayBeforeHoliday and dayAfterHoliday (indicate one day before and after a holiday; it is assumed, that most polluting travel activities are carried out before and after a holiday), and weekend (denotes the binary weekend feature added on Saturdays and Sundays). It is important to note that while features like weekend and dayOfYear maintain consistent meanings across all stations in both cities, holiday, dayBeforeHoliday, and dayAfterHoliday may encode different semantics due to differences in holiday schedules between the cities.

Data analysis

When preparing data for ML models, it is crucial to investigate whether certain features, including both those inherent in the dataset and engineered ones like temporal features, contribute significantly to predicting PM10 concentrations. This analysis helps determine if these features can explain variations in PM10 values to a certain extent. A widely used method for assessing feature importance, particularly for non-linear data, involves calculating the mean decrease in impurity across all decision trees within a Random Forest (RF)33. Therefore, a RF is trained to predict PM10 concentration which is later used to outline the impact of temporal and meteorological features that explain PM10 concentrations. Expanding upon the previously discussed features, we introduce an additional temporal feature known as \(PM_{10}\)-lag into our analysis. Subsequently, we thoroughly examine its influence on the model’s predictive performance. Lag values are adept at capturing dependencies within time series data, making them particularly valuable in time series analysis6,34,35. In addition to RF, we applied the Shapley value method to further investigate feature importance. Rooted in game theory, this method has become a widely used approach for analyzing the contributions of individual features in various machine learning models36,37,38. The Shapley value method provides insights into how much each feature positively or negatively contributes to the model’s prediction- in our case, the PM10 concentration.

Model training and algorithms

For air pollution concentration modelling, several approaches were used: (1) a Random Forests regression (RF)12 based on our previous studies1,6; (2) Prophet (PRH)23 and (3) four deep learning architectures, namely a Multilayer Perceptron (MLP)39, (4) a Long Short-term Memory Network (LSTM)40 network with one LSTM and a 1-dimensional Convolutional Neural Network (CNN)41 and finally (5) Neural Basis Expansion Analysis for Time Series (N-BEATS) which have outperformed many models in various ML competitions42. The predicted variables (target or outcomes) in this study are the pollutant concentrations at a daily average frequency (PM10) at all the locations wherever measured, while the independent (input) features are the temporal and meteorological variables. The models operate under the assumption that the levels of PM10 and gaseous pollutants can be predicted using temporal and meteorological variables treated as separate and independent factors. Training data (source domain) consists of all available data from one measurement station (station-level) or from the concatenation of two or more measurement stations of Graz (city-level) and the test set (target domain) stems from all data of another station in the target domain which can either be station Zagreb or one station in Graz. Since the domain of the training data is different from that of the test data, this is considered an out-of-domain generalization (OODG). The intuition behind that is to test the predictive performance of a model tested on unseen data. The experiments are separated into station-level and city-level out-of-domain generalizations. Station-level OODG, uses the data from one station to train a model and tests it on the target domain Zagreb, whereas city-level OODG, uses the data from various stations to train the model. OODG in this work serves as a baseline to discern performance enhancements achieved through TL. An illustration of station and city-level OODG can be found in the supplementary materials (Fig. 1a,b).

Transfer learning

In classical machine learning, models are typically trained for specific tasks assuming that training and test data come from the same distribution. However, building individual models for each task can be resource-intensive in terms of computation, time, and expertise. Transfer learning (TL) addresses this by transferring knowledge from a source model to a target model, reducing computational costs and leveraging similarities between domains43,44. For example, predicting PM10 concentrations in Graz and Zagreb entails the same objective of predicting PM10 concentration but varies in the domain (i.e., the city). TL allows passing knowledge from a data-rich source model trained in one city to a target model in another city lacking training data, thus improving performance on the target task. Similarly to the experiments conducted in OODG, our experiments in TL are categorized into station and city-level. For further insights into the transfer learning algorithms, approaches utilized and an illustration of station and city-level transfer (Fig. 1c,d), please consult the supplementary materials, specifically the chapters on Transfer learning algorithms, Transfer learning approaches.

Sample injection

The TL technique used in this work, domain adaptation (DA), can be unsupervised, requiring no labelled data from the target domain, or supervised, requiring a few labelled target samples (PM10 values). Unsupervised DA can mimic supervised by adding labelled target samples to the source domain. In this context, providing the DA algorithm with data from the target domain or reusing data from the source domain as target data is referred to as injection. Different injection strategies, like station-level and city-level transfer, are explored, with data injected monthly (monthly injection) to preserve seasonality. Labelled target data can be gathered by assuming PM10 data is partially available in Zagreb (Scenario 1), or by artificially injecting PM10 data assuming numerical similarity between PM10 peaks and valleys in Graz and Zagreb (Scenario 2). Figure 2 depicts monthly city-level injection for Scenario 1, where labelled target data for January and July are transferred. In Scenario 2, labelled data from the source domain (station Graz South) replaces target data (station Zagreb), making it unsupervised.

Figure 2
figure 2

Supervised (1) and unsupervised (2) domain adaptation. Image adapted from Poelzl45.

Full size image

Evaluation

To measure prediction performance, we use the normalized root mean squared error (NRMSE) to address sensitivity to value ranges between different domains. NRMSE, as defined in Eq. 1, normalizes RMSE by the difference between the minimum min() and maximum \(max()\) y values of a test set, ensuring value range independence. Here, \(y_i\) and \(\hat{y_i}\) represent real and predicted PM10 values, respectively, with i iterating through the values and n denoting the total predictions.

$$\begin{aligned} {\text {NRMSE}} = \frac{\sqrt{\frac{\sum _{i=1}^n\left( y_i-\hat{y_i}\right) ^2}{n}}}{max(y_1,\ldots ,y_n) - min(y_1,\ldots ,y_n)} \times 100 \end{aligned}$$
(1)

Results

The results are presented across various subsections. Initially, in Section Results on feature importance, feature importance differences are explored, shedding light on their impact on predicting PM10 concentration. Subsequently, five models (RF, MLP, LSTM, CNN) are assessed for predicting PM10 values based on meteorological and temporal features. Among these models, the RF model emerges as the most promising, leading to exclusive focus on it for further investigation. Furthermore, a comparative analysis between station-level and city-level OODG approaches is conducted in Section Results on city-level and station-level out-of-domain generalization. Section Results on transfer learning applies diverse transfer algorithms to the identified optimal approach, with Section Results on injection methods further investigating the most effective transfer algorithm to enhance transferability.

Results on feature importance

The results from Fig. 3 show that in the city-level model combining features from Graz North, West, South, East, and Don Bosco stations, temperature is the most crucial feature (43%), followed by dayOfYear (22%) and relative humidity (15%). Other features like weekend, holiday, dayBeforeHoliday, and dayAfterHoliday are deemed unimportant. The station id holds a minor importance (5%). The station id encompasses a variety of station-specific properties, including geographical attributes (such as proximity to sources of pollution or surrounding urban infrastructure like tall buildings), which are not accounted for by other features. Adding lagged PM10 values to the city-level model elevates this feature to dominance (64%), followed by temperature (15%). Similar trends are observed in Zagreb station-level data, where temperature is the most important feature, followed by dayOfYear and windspeed. Feature windspeed is absent in the city-level model of Graz as it is not present in every station. When adding the lagged PM10 values, this becomes the dominant feature followed by temperature and windspeed. dayOfYear falls behind windspeed in this experiment. These findings underscore the importance of meteorological factors like temperature and temporal features like dayOfYear in PM10 concentration prediction, as well as the significance of lagged PM10 values in both city and station-level modelling.

To gain a deeper understanding of how features contribute to the model’s predictions, SHAP values are utilized, as shown in Fig. 4. The y-axis ranks the features by their importance, with the most influential at the top, while the x-axis displays the SHAP values, indicating the magnitude and direction of each feature’s impact on PM10 predictions. The color scale highlights the feature values, where red represents higher values and blue represents lower ones. In Fig. 4a, dayOfYear emerges as the most important feature, showing a seasonal trend: higher dayOfYear values, corresponding to summer, have negative SHAP values, likely due to reduced heating activities or increased use of alternative transportation like bicycles, while lower dayOfYear values (e.g., winter) exhibit both strongly positive and negative SHAP values, reflecting seasonal variability. One possible reason for the worsening air quality during winter in Graz is its geographical location. Graz is situated in a basin near the Alps, where temperature inversions frequently occur, trapping air pollution46. Temperature follows as the second most important feature, where higher temperatures (red points) tend to reduce PM10 concentrations, reflected by their negative SHAP values. Relative humidity shows that lower values (blue) correlate with lower PM10 predictions, indicating a distinct pattern. The feature id demonstrates variability across stations, as its SHAP values scatter on both the positive and negative sides, suggesting that PM10 levels differ notably between measurement stations. Binary features such as weekend, holiday, dayBeforeHoliday, and dayAfterHoliday have relatively weaker impacts; however, weekends tend to reduce PM10 predictions, likely due to reduced industrial and traffic activity. These results emphasize the significance of temporal and meteorological variability, with dayOfYear and temperature dominating the predictions while other features provide additional but weaker contributions. The same pattern can be observed for Zagreb as visualized in Fig. 4b. In this case, temperature emerges as more important than dayOfYear. The feature windspeed shows that higher windspeed values contributing negatively to PM10 predictions, suggesting that stronger winds help disperse pollutants, leading to lower PM10 concentrations. Pressure also displays a clear distinction: lower pressure values contribute negatively to PM10 predictions, while higher pressure values contribute positively. A similar pattern is observed for precipitation, where higher values tend to reduce PM10 concentrations. Overall, while the general trends are comparable to those seen in the Graz SHAP values, the relative importance and variability of the features differ slightly, with temperature taking precedence in Zagreb. Certain meteorological features, such as relative humidity, show distinct differences, with a long tail to the right in Zagreb, whereas in Graz the tail is to the left. These observations highlight subtle differences in feature behavior across the two locations.

Fig. 3
figure 3

Random forest feature importance. Each subfigure visually represents the significance of individual features, showing the percentage by which each feature explains the PM10 concentration. Features include temperature, day of the year, relative humidity (rh), station ID, weekend, holiday, day before and after holiday, wind speed (windsp), wind direction class (windDirClass), precipitation (precip), pressure, and lagged PM10 value. (a) Depicts the city-level model of Graz without the PM10-lag feature, while (b) includes this feature. (c,d) focus on a single station in Zagreb (station-level) using the same approaches. These figures highlight the significant influence of the lagged PM10 feature, indicating its explanatory power on the PM10 concentration of the subsequent day.

Full size image
Fig. 4
figure 4

SHAP values. Each subfigure visually represents the SHAP values of individual features, showing their contribution of the predicted pm10. Features include temperature, day of the year, relative humidity (rh), station ID, weekend, holiday, day before and after holiday, wind speed (windsp), wind direction class (windDirClass), precipitation (precip), and pressure. (a) Depicts SHAP values of the city-level model of Graz , while (b) the SHAP values of the single station in Zagreb (station-level).

Full size image

Results on city-level and station-level out-of-domain generalization

In this experiment, we investigated whether station-level or city-level OODG yields better predictive accuracy. Station-level models trained on single stations in Graz and tested on Zagreb showed significant variation in prediction performance. For example, training with data from Graz Don Bosco resulted in an NRMSE of 9.65, while Graz North yielded an NRMSE of 10.25, indicating inconsistent OODG performance. Conversely, city-level models trained on data from various Graz stations and tested on Zagreb produced predictions falling between the best and worst station-level results. Although city-level models entail longer training times, they leverage collective knowledge from multiple stations. Table 2 illustrates the outcome of this experiment, with Fig. 5 depicting OODG predictions between station and city-level models. The magnified segments in Fig. 5 emphasize prediction variability. Notably, data from station South enhances accuracy during specific periods, while station East slightly underperforms compared to the city-level approach. Crucially, city-level performance consistently falls between the most and least accurate station-level predictions, highlighting the importance of leveraging collective knowledge for improved OODG performance on station Zagreb.

Table 2 Station-level and city-level OODG.
Full size table
Fig. 5
figure 5

City-level and station-level Random Forest OODG predictions. Shows the difference between the best (station South) and worst station-level (station East) outcome compared to the city-level (all stations combined) approach.

Full size image

Results on transfer learning

Table 3 provides detailed results for various transfer learning algorithms. We explore unsupervised algortihms Nearest Neighbors Weighting (NNW) , Kullback-Leibler Importance Estimation Procedure (KLIEP), Correlation Alignment (CORAL), and supervised transfer AdaBoost for regression (TrAdaBoostR2), using RF as a regressor. NNW exhibits negative transfer effects, particularly when using data from single stations or a city-level model from Graz, while KLIEP does not yield notable improvements. CORAL displays mixed outcomes, including negative transfer and slight improvements, with a substantial 10% increase when transferring from Graz West to Zagreb. However, overall, it does not consistently enhance predictive accuracy for station Zagreb. In contrast, TrAdaBoostR2 shows significant performance gains of up to 22% when injecting target domain data (413 samples from station Zagreb: months January and July from 2014 to 2020), emerging as the most promising algorithm. Further investigation into its effectiveness at both city and station levels, along with determining the optimal number of target samples required from station Zagreb, is warranted to guide future analysis.

Table 3 Transfer Learning algorithms performance comparison.
Full size table

Results on injection methods

We explored the impact of injection quantity and timeframe on transferability from Graz to Zagreb. The experiments revealed that TrAdaBoostR2’s prediction performance for PM10 in Zagreb is highly contingent on injected samples (Table 4). Both the number of injections (from 59 to 821 samples from Zagreb into Graz) and the introduced seasonality pattern (monthly injections in January, February, June, and July) are crucial. This experiment investigates various injection quantities and their associated impact on transferability, distinguishing between the target (Scenario 1) and source injection (Scenario 2), both explained in Subsection Sample injection. While no substantial performance improvement was observed with source injection compared to OODG, our focus remains on target injection. Results of TrAdaBoostR2 with different numbers of injections are presented in Table 4.

Table 4 TrAdaBoostR2 results.
Full size table

Impact of dataset size

To further improve transfer learning, besides model-based improvements such as hyperparameter tuning or transfer learning-based settings (e.g., the number of injected values during transfer), the size of the training set might also influence the accuracy that can be achieved47. Therefore, additional data from 2009 to 2013 were retrieved, processed, and added to the original dataset, increasing its size by 60%. Initially, there were 2885 (total 14,425) samples per station; now, instead of 2885, there are 4668 samples (total 23,340). As a transfer learning algorithm, TrAdaBoostR2 was used, and data from January and July of each year were injected, resulting in 708 injected values, which account for approximately 16% of the total available PM10 data from the Zagreb station. The results in Table 5 highlight improvements in both scenarios, OODG and TL. The city-level model transferred to Zagreb showed an improvement from 8.5 to 7.86, representing a 9% increase. This demonstrates that, in this specific application, the number of training samples plays a significant role in enhancing transferability and achieving higher accuracy. However, this improvement in accuracy came at the cost of increased training time, which rose from 1 min and 48 s to 4 min and 17 s. This demonstrates that, in this specific application, the number of training samples plays a significant role in enhancing transferability and achieving higher accuracy, though with a higher computational burden.

Table 5 Extended dataset TrAdaBoostR2 results.
Full size table

Discussion

In this study, we combined data analysis and machine learning to obtain the most information in the field of air pollution investigation. In our feature importance analysis, we highlighted relevant features such as temperature and dayOfYear for making PM10 predictions. Additionally, we demonstrated the impact of lagged PM10 values (in this case, the PM10 concentration of the previous day) on PM10 predictions. The identified relevant features were further utilized to select a suitable ML model. Among the options explored, including Random Forests, LSTM, NBeats, CNN-LSTM, and MLPs, Random Forests exhibited the best performance in predicting PM10 concentrations, particularly in terms of OODG. The rationale behind Random Forests outperforming other architectures such as MLP, CNN-LSTM, or LSTM may be attributed to factors such as the limited availability of training data and the relatively lower complexity of the dataset. In Chae et al.48, among other methods, CNN and LSTM were utilized to predict PM10 and PM2.5 concentrations. In contrast to our investigation, their study employed a dataset exceeding 4 million samples for predictive modelling and increased data complexity by integrating additional air pollutants such as SO2, CO, O3, and NO2 alongside meteorological variables. It is worth noting that NBeats might not have achieved the performance of Random Forest since it is designed for univariate time-series forecasting. However, in our case, we perform multivariate time-series prediction, as we have multiple features to predict PM10 concentrations and do not consider past PM10 observations42.

We demonstrated that in an OODG scenario, the collective knowledge gained by training a model using data from multiple stations in Graz and testing on station Zagreb (average NRMSE 9.52) is, on average, better than training a model based on a single station in Graz and testing it on Zagreb (average NRMSE 10.12). One possible explanation might be the increased training data and higher flexibility of the model as it trains on a more diverse dataset. After establishing the baseline using OODG to make predictions on Zagreb based on a model trained with data from Graz, we successfully applied transfer learning by employing domain adaptation algorithms, both in a supervised (where the Zagreb target station requires to have PM10 values) and unsupervised (where the Zagreb target station does not require to have PM10 values) manner. The results clearly showed that the supervised domain adaptation algorithm TrAdaBoostR2 can significantly improve the PM10 prediction performance (up to 22%) compared to OODG. However, the other unsupervised algorithms used, such as CORAL, KLIEP, and NNW, showed a range of outcomes from minor improvements to slight deterioration compared to TrAdaBoostR2. CORAL showed both performance deterioration and improvements, as can be seen in Table 3. NNW and KLIEP did not demonstrate any noticeable improvement in our experimental results. Although showing performance improvements compared to unsupervised TL algorithms, supervised algorithm TrAdaBoostR2 has some downsides as it requires labelled target data injected during training. Estimating the number of injections is not straightforward; as depicted in Table 4, the number of injections and the years of the injected months influence the performance of the transferred model. There exists no clear pattern determining a “good” year from which data can be injected. It might be due to local weather conditions that differ between the cities, strongly influencing PM10 concentration. However, the empirical study revealed that injecting 177 samples (from at least January and July from 3 different years) assures an improvement compared to OODG.

In contrast to our work, transfer learning in the literature studied Deng et al.19, Dhole et al.22, Ma et al.9, Fong et al.10, Cheng et al.20 is mostly implemented using parameter-based approaches with underlying CNN-LSTM, CNN-GRU, or LSTM models, which typically require a larger number of data samples than our transfer approach. For example, Cheng et al.20 successfully implemented CNN-LSTM and demonstrated successful results in hourly predictions with parameter transfer. However, they utilized 10 source stations, each with 35,000 samples per station, giving a total of 350,000 training samples, compared to the 14,000 samples used in our case. Furthermore, the literature predominantly focuses on short-term prediction (hourly/daily/weekly), with the common scenario being data scarcity within a single city. Additionally, most authors concentrate on forecasting, which is a subcategory of prediction, considering past air pollutant concentration values to estimate future behaviour. For instance, in Fong et al.10, the approach involves forecasting, as data from the past 6 days are used to predict air pollution concentration for day 7. Our approach stands out as novel in the field of air pollution concentration prediction, demonstrating the effectiveness of training a model in one city and transferring it to another city, even with limited training samples, to make long-term predictions. This underscores how transfer learning can enhance cross-city predictions, even when little labelled air pollution concentration data is available, potentially enabling data-rich cities to improve prediction accuracy in data-poor cities over extended periods, despite differences in air pollution data between cities.

Conclusions

This study addresses the challenge of data sparsity when predicting air pollution concentration levels based on meteorological and temporal data in cities, impeding precise forecasts. To mitigate these data limitations, we conducted an in-depth exploration of transfer learning (TL) techniques and their feasibility in this application domain. This exploration facilitated the effective transfer of knowledge from the data-rich city of Graz to Zagreb allowing us to make more accurate predictions in Zagreb.

Our analysis employing Random Forests (RF) demonstrates the significant predictive roles of both temporal features specifically, the day of the year and meteorological features in predicting PM10 concentrations. Consequently, for the development of machine learning models such as LSTM, CNN, CNN-LSTM, RF, and MLP, only relevant features were selected based on our findings. RF demonstrated superior performance among the models assessed, likely due to its ability to effectively handle a limited amount of training data.

Based on our findings, RFs are further investigated for out-of-domain generalization (OODG). We evaluated the performance of RF models trained at the station level (using data from individual measurement stations in Graz) and at the city level (using data from multiple measurement stations in Graz) when predicting PM10 concentrations in Zagreb. Station-level models showed increased variability in their prediction performance across different stations in Graz, leading to inconsistent OODG. In contrast, city-level models demonstrated more consistent predictions, although they required longer training times due to their reliance on data from various stations. These findings suggest that, in this specific scenario, city-level models are preferred over station-level models in predicting values for stations in different domains.

To enhance OODG prediction performance further, we applied the same station and city-level approach with RFs to various unsupervised TL algorithms including Correlation Alignment (CORAL), Kullback-Leibler Importance Estimation Procedure (KLIEP), and Nearest Neighbors Weighting (NNW), which do not rely on labelled data in the target domain (such as PM10 values in Zagreb). Additionally, we explored the supervised TL algorithm AdaBoost for regression (TrAdaBoostR2), which requires a certain number of labelled target samples. However, the same consistent pattern as occurring in OODG emerged where city-level models exhibited more consistent performance, prompting their consideration for further analysis. The unsupervised algorithms did not yield significant or consistent performance improvements, the supervised algorithm TrAdaBoostR2 with the underlying city-level model achieved a notable reduction in normalized root mean squared error (NRMSE) to 7.3, representing a 22% improvement compared to OODG with an NRMSE of 9.445. This improvement was achieved by providing the supervised TL algorithm TrAdaBoostR2 with target labels (PM10 values from station Zagreb) from January, February, June, and July across all years, resulting in 821 values out of 4382 possible samples. Furthermore, selecting January and July of every second year (226 PM10 values) also resulted in a significant performance boost, with an NRMSE of 8.1, representing a 14% improvement compared to OODG with an NRMSE of 9.445.

Our study demonstrates the feasibility of transferring ML models between sites, even when only a portion of the pollutant data at the target site is available to the TL algorithm. This capability holds promise in broader contexts, enabling predictions in scenarios with limited data availability. Such applications are particularly relevant for filling in missing data in epidemiological studies. Nevertheless, it is imperative to acknowledge a limitation of TL in this study: while empirical results revealed that injecting 177 samples (from at least January and July from 3 different years) achieves a performance improvement compared to OODG, it remains a tedious task to select the most suitable months from certain years to achieve significant predictive results. This deviation in performance improvement highlights the complexity and potential unpredictability of supervised TL outcomes in this context. In addition to these limitations, the number of training samples also plays a crucial role in determining the transferability and accuracy of the model in the target domain. This adds another layer of complexity, as both data size and the selection of specific months or years need to be carefully considered to achieve significant predictive outcomes.

As next steps, the dataset could be enriched by incorporating data from multiple measurement stations across Europe using the data retrieval tool presented by He et al.49. This would expand the dataset and potentially improve prediction accuracy for Zagreb through TL. By including data from stations across Europe, the transferability of measurement stations between different domains-characterized by variations in environmental conditions, emissions, climate, traffic, or industrial activities-could be further explored. This investigation could provide insights into which domain differences are most relevant for transferring knowledge between cities to predict environmental pollution. These insights could also help identify optimal target samples to enhance supervised TL performance.