Introduction

Recent growth in digital information technology has led to the transmission of many sensitive and confidential images over public networks. The availability of such crucial information over public networks raises concerns for image security. Image security can be achieved using steganography, watermarking, and encryption. Image steganography hides the secret data under another image, video, or audio. In this technique, only the intended recipient and the sender are aware of the data. Watermarking is placing an invisible or visible mark inside an image or document. This technique is popular for proving the ownership of an image or document. Image encryption is the conversion of a raw image into a cipher image, which can be decrypted at the receiver end. It is a prominent technique to ensure data security, confidentiality, and integrity over the public network1,2,3.

Image encryption techniques are of two types. One is the classical encryption techniques like RSA, AES, and DES. Traditional encryption techniques have proven their significance on text data and have been widely used for web security and banking. However, due to the high computation time, such techniques are not suitable for digital images, which contain highly correlated data4,5. The other category of image encryption techniques includes the confusion and the diffusion step6. These techniques are popular for image encryption due to their low computation time and robustness against several attacks. Different authors have used various techniques in the confusion and diffusion steps. However, Chaos-based image encryption methods have gained attention due to chaos properties such as ergodicity, sensitivity to initial conditions and control parameters, random-like behavior, and unpredictability7,8. The performance of these methods depends upon the initial and the control parameters, which led to the need for optimal selection of these parameters for better performance of chaos-based encryption methods9,10.

Metaheuristic optimization techniques have been widely used for behavioral pattern guidance11, and optimal parameter selection. Metaheuristic techniques are of two major types, i.e., single objective and multi-objective metaheuristic techniques. Different single and multi-objective metaheuristic techniques like Particle Swarm Optimization (PSO)12, Bald Eagle Search (BES)13, multi-objective Brown Bear Optimization14, and multi-objective cheetah optimization15 algorithms have shown better performance in selecting the optimal parameters for different algorithms due to their high exploration and exploitation capabilities. This makes metaheuristic techniques suitable for selecting the initial and control parameters for the chaos-based image encryption methods. Various authors have used different metaheuristic techniques to select the initial and control parameters for chaos-based image encryption methods16.

Noshadian et al.17 have proposed an optimized image encryption technique based on Teacher Learning-Based Optimization (TLBO), Gravitational Search Algorithm (GSA), and logistic map. The authors have used a logistic map as an encryption key for diffusion and TLBO and GSA to optimize the map parameters. Farah et al.6 have proposed a new hybrid chaotic map for image encryption and generated a new substitution box using the Jaya algorithm. Saravanan and Sivabalakrishanan18 proposed an optimized hybrid chaotic map for image encryption. The authors have hybridized the 2DLCM and PWLCM map and performed parameter tuning using the improved whale optimization algorithm. The authors have analyzed the performance of their proposed algorithm on medical, natural, and satellite images. Kaur and Singh19 have used multiobjective evolutionary techniques to select the optimal parameters for the chaotic maps. The authors used the optimal parameters to generate a secret key, which is used to encrypt the image. They performed key, statistical, and differential analyses to analyze the performance of the encryption algorithm.

Luo et al.20 have used the hyperchaotic system and the updating process of particle swarm optimization for image encryption. They used the secure hash algorithm 256 to generate the initial keys for the hyperchaotic Lu system. The authors have analyzed the proposed algorithm using several attacks. Toktas and Erkan21 have designed a 2D fully chaotic map by utilizing the Artificial Bee Colony (ABC) for image encryption. The authors used ABC to minimize the quadruple objective function, which consists of the entropy, correlation coefficient, 0–1 test, and the Lyapunov exponent. Sameh et al.16 analyzed the impact of optimization of initial and control parameters for eight chaotic maps using nine metaheuristic optimization algorithms. Authors have computed the performance of encryption using sine, Tent, Circle, Gauss, singer, piecewise, and logistic maps without any optimization. Then, the authors used the Sine Cosine Algorithm (SCA), Moth Flame Optimization (MFO), Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), Genetic Algorithm (GA), Dragonfly Algorithm (DA), Ant Lion Optimizer (ALO), Whale Optimization Algorithm (WOA), and Multi-Verse Optimizer (MVO) to select the optimal value of the chaotic map parameters. The authors have compared the performance to analyze the impact of each optimization algorithm.

Sharma et al.22 utilized the Self Adaptive Bald Eagle Search (SABES) optimization algorithm to optimize the chaotic parameters of PWLCM, PWCM, and tent maps. The authors used the random permutation method in the confusion phase and optimized chaotic maps in the diffusion phase with the cyclic redundancy check and circular shift method to secure patient medical information, medical signals as well as medical images. Sharma and Sharma23 have used the Harris Hawk Optimization (HHO) algorithm to optimize the Duffing, Lorenz, and Henon maps parameters. The authors have used different chaotic maps at different stages, which led to larger key spaces and resulted in a highly robust method.

Novelty and contributions of the work

As mentioned earlier, different researchers have worked on image encryption using the chaotic map with optimized parameters using metaheuristic techniques. Still, to the best of our knowledge, a high-performance image encryption algorithm for different types of images consisting of hyperspectral images, grayscale, and RGB images is not available. This work designs a reliable image encryption algorithm based on a chaotic map optimized using the Iterative Cosine Operator (ICO) based Enhanced Hippopotamus Optimization (HO) algorithm. Overall, the main contributions of the paper are as follows:

  1. i.

    Designed ICO-HO, i.e., ICO-based HO, by integrating a new phase (phase 4) for position update of Hippopotamus Optimization (HO) by utilizing ICO and opposition-based learning to enhance the exploration and exploitation capabilities of the algorithm.

  2. ii.

    The proposed ICO-HO is used to design an adaptive image encryption method based on the chaotic maps, i.e., PWCM and PWLCM, with optimized parameters.

  3. iii.

    Analysis of the proposed encryption method on different types of images, including medical images, grayscale images, RGB images, and hyperspectral images.

The remaining paper has been divided into four more sections. The next section, section ii, elaborates on the Hippopotamus optimization algorithm. The proposed work, which consists of the ICO-HO algorithm and the image encryption architecture, is explained in section iii. The results are analyzed and discussed in section iv. Section v concludes the work and describes the future scope.

Understanding of Hippopotamus optimization

Hippopotamus optimization (HO)24 is inspired by the hippopotamus’s social behavior and defense process. Similar to the other population-based optimization algorithms, the Hippopotamus position is a candidate solution to the problem. The hippopotamus’s initial position is generated randomly, as given in Eq. (1).

$$\:{HO}_{ij}={L}_{j}+rand\times\:\left({U}_{j}-{L}_{j}\right)$$
(1)

Where \(\:{HO}_{ij}\) denotes the position of ith Hippopotamus in the jth dimension. \(\:{U}_{j},\:{L}_{j}\) denotes the upper and lower bounds for jth dimension, respectively. \(\:rand\) gives the random number between 0 and 1. Equation (2) gives the overall position matrix for M hippopotamus in the N dimension.

$$\:HO={\left[\begin{array}{ccc}{HO}_{\text{0,0}}&\:\begin{array}{cc}{HO}_{\text{0,1}}&\:\cdots\:\end{array}&\:{HO}_{0,N}\\\:\begin{array}{c}{HO}_{\text{1,0}}\\\:⋮\end{array}&\:\begin{array}{c}\begin{array}{cc}{HO}_{\text{1,1}}&\:\cdots\:\end{array}\\\:\begin{array}{cc}⋮&\:\cdots\:\end{array}\end{array}&\:\begin{array}{c}{HO}_{1,N}\\\:⋮\end{array}\\\:{HO}_{M,0}&\:\begin{array}{cc}{HO}_{M,1}&\:\cdots\:\end{array}&\:{HO}_{M,N}\end{array}\right]}_{M\times\:N}$$
(2)

The position update of the hippopotamus to explore the search space in the HO algorithm consists of three phases. The fitness value of each hippopotamus is computed using the fitness function \(\:fit\left(\right)\). Phase 1 exhibits the exploration using the social behavior of the hippopotamus. The hippopotamus group consists of females, calves, males, and the leader hippopotamus, as given by Eq. (3).

$$\:HO={HO}^{f}\cup\:{HO}^{c}\cup\:{HO}^{m}\cup\:{HO}^{L}$$
(3)

where \(\:{HO}^{f},\:{HO}^{c},{HO}^{m},{HO}^{L}\) represents the females, calves, males, and leader hippopotamus, respectively. Each hippopotamus is labeled to \(\:{HO}^{f}or\:{HO}^{c}or\:{HO}^{m}or\:{HO}^{L}\) based on its fitness value only. The position update for the male hippopotamus inside the water bodies is given by Eq. (4).

$$\:\left.{HO}_{ij}^{m}={HO}_{ij}+rand\times\:\left({HO}^{L}-{C}_{1}{HO}_{ij}\right)\:\right|\:i=\:\text{1,2},3,\dots\:,\left[\raisebox{1ex}{$M$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.\right]\:and\:j=\:\text{1,2},3,\dots\:.N\:$$
(4)

where \(\:{C}_{1}\) is the constant integer between 1 and 2. The position update for the female hippopotamus and calves i.e., \(\:{HO}^{fc}={H}^{f}\cup\:{H}^{c}\) is given by Eq. (5).

$$\:\left.{HO}_{ij}^{fc}=\:\begin{array}{c}{HO}_{ij}+{v}_{1}\times\:\left({HO}^{L}-{C}_{2}{RG}^{m}\right)\\\:\begin{array}{c}{HO}_{ij}+{v}_{2}\times\:\left({RG}^{m}-{HO}^{L}\right)\\\:{L}_{j}+rand\times\:\left({U}_{j}-{L}_{j}\right)\end{array}\end{array}\:\right|\:\begin{array}{c}T>0.6\\\:\begin{array}{c}else\:if\:rand>0.5\\\:else\end{array}\end{array}$$
(5)

where \(\:i=\:\text{1,2},3,\dots\:,\left[\raisebox{1ex}{$M$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.\right]\:and\:j=\:\text{1,2},3,\dots\:.N\). The \(\:{v}_{1},\:{v}_{2}\) are generated using Eq. (6) and \(\:T\) is generated using Eq. (7). \(\:{C}_{2}\)is the constant integer between 1 and 2. \(\:{RG}^{m}\) is the mean of the randomly selected hippopotamus from the available \(\:M\) hippopotamus.

$$\:v=\left\{\begin{array}{c}\begin{array}{c}{C}_{2}\times\:\overrightarrow{rand}+\left(\sim{\vartheta\:}_{1}\right)\\\:2\times\:\overrightarrow{rand}-1\end{array}\\\:\overrightarrow{rand}\\\:\begin{array}{c}{C}_{1}\times\:\overrightarrow{rand}+\left(\sim{\vartheta\:}_{2}\right)\\\:\overrightarrow{rand}\end{array}\end{array}\right.$$
(6)
$$\:T={e}^{-\raisebox{1ex}{$Cu{r}_{itr}$}\!\left/\:\!\raisebox{-1ex}{$Ma{x}_{itr}$}\right.}$$
(7)

where \(\:Cu{r}_{itr}\) and \(\:Ma{x}_{itr}\) is the current and maximum iteration, respectively. \(\:{\vartheta\:}_{1},\:{\vartheta\:}_{2}\:\) are the random integers between 0 and 1. The updated position of hippopotamus is accepted only if it is better than the previous fitness value given by Eqs. (8) and (9).

$$\:{HO}_{i}=\left\{\left.\begin{array}{c}{HO}_{i}^{m}\\\:{HO}_{i}\end{array}\right|\begin{array}{c}fit\left({HO}_{i}^{m}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}\right.$$
(8)
$$\:{HO}_{i}=\left\{\left.\begin{array}{c}{HO}_{i}^{fc}\\\:{HO}_{i}\end{array}\right|\begin{array}{c}fit\left({HO}_{i}^{fc}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}\right.$$
(9)

where \(\:fit\left(\right)\) is the fitness function. Phase 2 of the HO algorithms exhibits exploration and mimics the defense methodology of hippopotamus against predators. The position of the predator is given by the Eq. (10).

$$\:{P}_{j}={L}_{j}+rand\times\:\left({U}_{j}-{L}_{j}\right)\left|j=\:\text{1,2},3,\dots\:N\right.$$
(10)

The distance of a particular hippopotamus from the predator can be found using Eq. (11).

$$\:\overrightarrow{Dist}=\left|{P}_{j}-{HO}_{ij}\right|$$
(11)

The hippopotamus decides its defensive action based on the \(\:\overrightarrow{Dist}\) value i.e., distance from the predator. If the hippopotamus is in close vicinity of the predator i.e., \(\:fit\left({P}_{j}\right)<fit\left({HO}_{i}\right)\) then hippopotamus turns to face the predator otherwise it moves towards the predator as shown in Eq. (12).

$$\:{HO}_{ij}^{n}=\left.\begin{array}{c}{levy}^{r}\oplus\:{P}_{j}+\left(\frac{b}{\left(c-d*cos\left(2\pi\:g\right)\right)}\right)\cdot\:\left(\frac{1}{\overrightarrow{Dist}}\right)\\\:{levy}^{r}\oplus\:{P}_{j}+\left(\frac{b}{\left(c-d*cos\left(2\pi\:g\right)\right)}\right)\cdot\:\left(\frac{1}{2*\overrightarrow{Dist}+\overrightarrow{rand}}\right)\end{array}\right|\begin{array}{c}fit\left({P}_{j}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}$$
(12)

where \(\:i=\:\left[\raisebox{1ex}{$M$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.\right]+1,\left[\raisebox{1ex}{$M$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.\right]+2,\cdots\:M\:and\:j=\:\text{1,2},3,\dots\:.N\)

The updated position of the hippopotamus is accepted only if its fitness value is better than the existing fitness value as given by Eq. (13).

$$\:{HO}_{i}=\left\{\left.\begin{array}{c}{HO}_{i}^{n}\\\:{HO}_{i}\end{array}\right|\begin{array}{c}fit\left({HO}_{i}^{n}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}\right.$$
(13)

Phase 3 of the HO algorithm exhibits exploitation through the escaping behaviour of hippopotamus from the predator. Hippopotamus generally search for the nearest water bodies to escape from the predator. This phenomenon exhibits the exploitation search in the local region as hippopotamus explore the nearest water bodies. The local upper and lower bound for the current iteration can be found using the Eq. (14).

$$\:{U}_{j}^{local}=\raisebox{1ex}{${U}_{j}$}\!\left/\:\!\raisebox{-1ex}{$Cu{r}_{itr}$}\right.\:{L}_{j}^{local}=\raisebox{1ex}{${L}_{j}$}\!\left/\:\!\raisebox{-1ex}{$Cu{r}_{itr}$}\right.$$
(14)

The updated position of the hippopotamus is given by the Eq. (15).

$$\:{HO}_{ij}^{n}={HO}_{ij}+rand\left({L}_{j}^{local}+\alpha\:\left({U}_{j}^{local}-{L}_{j}^{local}\right)\right)$$
(15)

where \(\:\alpha\:\) is given by the Eq. (16).

$$\:\alpha\:=\left\{\begin{array}{c}2\times\:\overrightarrow{rand}-1\\\:\overrightarrow{rand}\\\:\overrightarrow{randn}\end{array}\right.$$
(16)

where \(\:\overrightarrow{randn}\) gives the random number with normal distribution. Hippopotamus will move to safer place only i.e., updated position is accepted only if its fitness value is better than the existing fitness value given by Eq. (17).

$$\:{HO}_{i}=\left\{\left.\begin{array}{c}{HO}_{i}^{n}\\\:{HO}_{i}\end{array}\right|\begin{array}{c}fit\left({HO}_{i}^{n}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}\right.$$
(17)

The whole process i.e., three phases of the HO algorithm repeats for each candidate solution, for the \(\:Ma{x}_{itr}\) iterations. HO algorithm is improved and utilized to optimize the parameters of the chaotic map discussed in the next section.

Proposed work

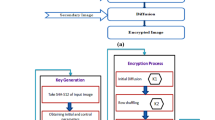
This work proposes the ICO-HO, i.e., Iterative Cosine Operator-based Hippopotamus Optimization algorithm that adds a new phase to the HO algorithm for position updates using the ICO operator and opposition-based learning. The proposed ICO-HO is further used to optimize the initial and control parameters of chaotic maps. This work also proposes a security framework that uses the optimized chaotic maps in confusion and diffusion steps. Overall work is explained in two phases. The first phase defines the proposed ICO-HO, i.e., Iterative Cosine Operator-based Hippopotamus Optimization. The second phase describes the security framework for the image encryption approach based on ICO-HO.

ICO-HO

ICO-HO improves the HO algorithm’s exploration and exploitation capabilities by using an Iterative Cosine Operator (ICO). ICO performs exploration at the initial iterations, which converts to the exploitation of search space as the iteration increases. Unlike the HO algorithm, which completes in three phases, ICO-HO completes its process in four phases. The first three phases of ICO-HO are the same as those of the HO algorithm, while the fourth phase updates the Hippopotamus position using Eq. (18).

$$\:{HO}_{i}^{n}=\left.\begin{array}{c}{HO}_{i}\times\:rand+{HO}^{L}\times\:cos\left(\raisebox{1ex}{$\left(\pi\:\times\:Cu{r}_{itr}\right)$}\!\left/\:\!\raisebox{-1ex}{$\left(2\times\:Ma{x}_{itr}\right)$}\right.\right)\\\:{HO}_{i}\times\:rand-{HO}^{L}\times\:cos\left(\raisebox{1ex}{$\left(\pi\:\times\:Cu{r}_{itr}\right)$}\!\left/\:\!\raisebox{-1ex}{$\left(2\times\:Ma{x}_{itr}\right)$}\right.\right)\end{array}\right|\begin{array}{c}rand<0.5\\\:else\end{array}$$
(18)

where, as presented in the previous section \(\:{HO}^{L}\) is the position of leader hippopotamus. \(\:Cu{r}_{itr}\:,\:Ma{x}_{Itr}\) are the current and maximum iterations, respectively. Equation (18) shows that the hippopotamus explores the search space toward the leader or opposite to the leader with a 50% probability of each case. This includes opposition-based leaning, as the optima may exist opposite the leader. This exploration at initial iteration converts to exploitation as the iteration increases due to the value of ICO i.e., \(\:cos\left(\raisebox{1ex}{$\left(\pi\:\times\:Cu{r}_{itr}\right)$}\!\left/\:\!\raisebox{-1ex}{$\left(2\times\:Ma{x}_{itr}\right)$}\right.\right)\) approaching towards zero. The updated position value of the hippopotamus is accepted only if it gives a better fitness value as compared to the existing fitness value, as represented by Eq. (19).

$$\:{HO}_{i}=\left\{\left.\begin{array}{c}{HO}_{i}^{n}\\\:{HO}_{i}\end{array}\right|\begin{array}{c}fit\left({HO}_{i}^{n}\right)<fit\left({HO}_{i}\right)\\\:else\end{array}\right.$$
(19)

The whole process is repeated for the \(\:Ma{x}_{Itr}\) times. The overall algorithm for ICO-HO is as follows.

figure a

A framework to secure the image is designed using the ICO-HO algorithm explained in the next subsection.

Proposed framework for image encryption approach

This framework proposed for image encryption is demonstrated in Fig. 1. This framework uses chaotic maps to encrypt images and ICO-HO to select optimum parameters for chaoctic maps. The chaotic maps are selected for the encryption due to their properties: fast processing, determinism, aperiodic behavior, pseudo-randomness, boundedness, and dynamical nature. Encryption methods based on chaotic maps are also more robust because control parameters and initial conditions highly influence these maps. The complete process is divided into two stages i.e., the parameter optimization stage and the encryption stage. A description of each stage is given in the following subsections.

Fig. 1
figure 1

Framework for the image encryption.

Full size image

Parameter optimization stage

In this stage, the proposed ICO-EHO has been used to solve the parameter optimization problem of the chaos-based encryption methods. The initial and the control parameters of chaotic maps are optimized using the ICO-EHO algorithm. In the proposed encryption method, two chaotic maps have been utilized: the Piecewise Linear Chaotic Map (PWLCM) and the Piecewise Chaotic Map (PWCM). The mathematical formulation for PWLCM and PWCM maps are presented in Eqs. (20) and (21) respectively.

$$\:{x}_{i}=F\left({x}_{i-1},{\eta\:}_{1}\right)=\left\{\begin{array}{c}\frac{{x}_{i-1}}{{\eta\:}_{1}},\:\:for\:\:0\le\:{x}_{i-1}<{\eta\:}_{1}\\\:\frac{{x}_{i-1}-{\eta\:}_{1}}{{0.5-\eta\:}_{1}},\:\:for\:\:{\eta\:}_{1}\le\:{x}_{i-1}<0.5\\\:0,\:\:\:\:\:\:\:\:\:\:\:for\:{x}_{i-1}=0.5\\\:F\left(1-{x}_{i-1},{\eta\:}_{1}\right),\:\:for\:0.5<{x}_{i-1}\le\:1\end{array}\right.$$
(20)

where the initial condition \(\:{x}_{i}\in\:\left[\text{0,1}\right]\) and the control parameter \(\:{\eta\:}_{1}\in\:\left[\text{0,0.5}\right]\) respectively

$$\:{y}_{i}\:=\left\{\begin{array}{c}\frac{\:\:{y}_{i-1}}{{\eta\:}_{2}}\:,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:for\:0\:<\:{y}_{i-1}\:<\:{\eta\:}_{2}\\\:\frac{\left({y}_{i-1}\:-\:{\eta\:}_{2}\right)}{\left(0.5\:-\:{\eta\:}_{2}\right)},\:\:for\:{\eta\:}_{2}\:\le\:\:{y}_{i-1}\:<\:0.5\\\:\frac{\left(1\:-\:{\eta\:}_{2}\:-\:{y}_{i-1}\right)}{\left(0.5-{\eta\:}_{2}\right)},\:for\:0.5<{y}_{i-1}<\left(1-{\eta\:}_{2}\right)\\\:\frac{\left(1\:-\:{y}_{i-1}\right)}{{\eta\:}_{2}},for\left(1-{\eta\:}_{2}\right)<{y}_{i-1}<1\end{array}\right.$$
(21)

where the PWCM map parameters \(\:{\eta\:}_{2}\) and \(\:{y}_{i}\) are defined as \(\:{\eta\:}_{2}\in\:\left[\text{0,0.5}\right]\) and \(\:{y}_{i}\in\:\left[\text{0,1}\right]\), respectively. The parameters of both chaotic maps i.e., \(\:{{{x}_{i}\:,y}_{i},\eta\:}_{1},\:{and\:\eta\:}_{2}\) are optimized using the ICO-EHO algorithm.

A bifurcation diagram of the chaotic maps shows the dynamic change in the behavior of the maps in terms of the control parameters. This diagram is used to analyze changes in the chaotic sequence in the whole definition of the control parameters. In Fig. 2, bifurcation diagrams of the PWLCM and PWCM maps are shown for the control parameter \(\:\eta\:ϵ[0,\:0.5]\) and initial parameter \(\:Xϵ\left[\text{0,1}\right]\).

Fig. 2
figure 2

Bifurcation diagram (a) PWLCM map (b) PWCM map.

Full size image

The bifurcation diagram shows that both maps exhibit chaotic behavior across the entire range of the control and initial parameters. In Fig. 2(a), PWLCM maps show the period-doubling cascade behavior, characterized by two bifurcation divisions. In contrast, the PWCM map presented in Fig. 2(b) shows a smoother and more continuous change in the behavior as control parameters vary, reflecting its abrupt and less predictable transitions.

Fig. 3
figure 3

Lyapunov exponent (a) PWLCM (b) PWCM.

Full size image

Lyapunov Exponent (LE) is used as a quantitative measure to analyze the perturbations in time series data. The positive value of the Lyapunov exponent reflects that neighboring trajectories are diverged with each other, showing instability within the time series. The negative values show that the neighboring trajectories converge to a single point, representing a stable trajectory. For the chaotic maps, the value of the Lyapunov exponent greater than 0 indicates that the map is reflecting the chaotic behavior. The change in the Lyapunov exponent values based on the control parameter is shown in Fig. 3.

Figure 3 indicates that the Lyapunov exponent of PWLCM maps is consistently greater than 0, indicating that the maps exhibit chaotic behavior in the entire range of control parameters. The LE values of the PWCM are higher than the PWLCM map values. Also, the PWCM map reaches its highest LE value at \(\:{\eta\:}_{2}=0.25\) after that, LE values decline but remain above 0.

Encryption stage

After optimizing the parameters of the chaotic maps, those parameters are utilized in the encryption process to enhance the security of the images. The encryption phase is divided into two phases: Confusion and diffusion phase. The confusion phase is responsible for breaking the correlation between the image pixel values by shuffling or scrambling the image pixel values. In the confusion phase, an optimized PWLCM map was used to shuffle the image pixel values. The map values have been generated with a size equal to the image size using the optimal parameters. Thereafter, the generated values of the map are sorted to give the scrambled indexes. The original image is rearranged using the scrambled index generated through sorted chaotic map values. The pseudocode of the confusion process is as follows:

figure b

After the confusion phase, the diffusion phase has been applied to the scramble image \(\:(scr\_img)\) pixels values. The optimized PWLCM and PWCM maps have been applied to modify the image pixel values in both row-wise and column-wise order. Firstly, the values of the chaotic map are generated using the optimized parameters, and then generated values are changed into discrete form using Eq. (22).

$$\:value=⌊\left({value}_{i}\times\:{10}^{14}\right)⌋\%\left(max\left(inputvalue\right)\right)$$
(22)

where \(\:max\left(inputvalue\right)\), is the maximum value of the input image. The pseudocode of the diffusion phase is as follows:

figure c

The analysis of the work has been done in the next section.

Results and analysis

The results and corresponding discussions have been explained in two subsections. Subsection 1, i.e., analysis of the ICO-HO algorithm, analyses the performance of the ICO-HO algorithm on CEC-2017 functions. The Friedman mean rank, analysis using qualitative metrics, and the convergence curve comparison are used for the performance analysis of ICO-HO. Subsection 2, i.e., analysis of the image encryption approach, comprises different attack analyses, key space analysis, and the comparison against different state-of-the-art techniques.

Analysis of ICO-HO algorithm

The performance of ICO-HO is compared with seven state-of-the-art algorithms namely HO24, WOA25, Arithmetic Optimization Algorithm (AOA)26, SCA27, MFO28, African Vultures Optimization Algorithm (AVOA)29, and RIME optimization algorithm (RIME)30 on CEC-2017 functions. The analysis has been done by comparing the best, average, and worst values and the Standard Deviation (SD), as shown in Table 1.

Table 1 Performance analysis of ICO-HO on CEC-2017 functions.
Full size table

Table 1 shows the performance comparison of ICO-HO with seven state-of-the-art techniques using average, best, worst, and standard deviation values. The rank for each function is assigned for every algorithm based on the average value. It can be easily analyzed that ICO-HO achieved the first rank for twelve functions, while ICO-HO gives a competitive solution for the remaining functions. Friedman mean rank analysis is applied to analyze the performance of each algorithm, which results in 1.93, 3.68, 6.17, 7.62, 5.89, 3.82, 4.34, and 2.51 values for ICO-HO, HO, WOA, AOA, SCA, MFO, AVOA, RIME algorithms respectively. The p-value for the Friedman mean rank analysis is 3.56E-24, which is less than 0.05, resulting in the rejection of the NULL hypothesis, i.e., there is a significant difference between the performance of algorithms. On the basis of the mean value obtained, ICO-HO has obtained the first position, indicating better performance than the other existing state-of-the-art algorithms. ICO_HO has shown better performance due to its high and balanced exploration and exploitation capabilities. RIME and HO algorithms have obtained the second and third positions, respectively.

Fig. 4
figure 4figure 4

Convergence comparison of ICO-HO with HO algorithm on (a) F5 (b) F6 (c) F8 (d) F16 (e) F20 (f) F26 functions.

Full size image

Convergence comparison of ICO-HO with HO algorithm

The comparison of the convergence curve for ICO-HO with the HO algorithm is shown on the randomly selected CEC-2017 functions, i.e., F5, F6, F8, F16, F20, and F26 in Fig. 4. The x-axis denotes the iterations, while the y-axis denotes the fitness value. A comparison was made with the 1000 iterations. The better convergence is exhibited by the ICO-HO as compared to the HO algorithm for all F5, F6, F8, F16, F20, and F26 functions. The better convergence is due to the newly added phase 4, which includes the position update based on ICO and opposition-based learning. The better exploration capabilities due to ICO at initial iterations in the ICO-HO show faster convergence by ICO-HO than the HO algorithm.

Analysis of proposed image encryption approach

The proposed encryption approach is tested on different types of medical images, including grayscale, RGB, and hyperspectral images. The medical images used for experimentation vary in size, file format, and bit depth, including both 8-bit and 16-bit images. The performance analysis has been done using visual analysis, statistical attack analysis (histogram, correlation analysis, variance analysis, chi-square analysis), differential attack analysis (NPCR and UACI), qualitative analysis (information entropy, MSE, and PSNR), key space and key sensitivity analysis. The visual analysis has been utilized to show the visual difference between the original, encrypted, and decrypted medical images31. Table 2 depicts the visual analysis of original, encrypted, and decrypted medical images.

Table 2 Visual depiction of original, encrypted, and decrypted images.
Full size table

The encrypted images in Table 2 clearly show that the visual information of the original images is completely hidden in the encrypted images generated using the propounded encryption method. This proves that the proposed encryption method effectively hides all the visual data of the images. Also, the visual appearance of the decrypted image is identical to the original image, indicating that the decrypted image maintains the same visual depiction as the original.

Statistical attack analysis

The presence of the relationship between the pixel values of the encrypted image, obtained using the encryption approach is analyzed through statistical methods. This analysis uses techniques such as histogram, variance, chi-square, and correlation coefficient measureo compute the pixel relationships in the encrypted images39. Histogram plots are used to visually analyze the uniformity of pixel values in the encrypted images. The uniformly distributed histogram of the encrypted images indicates that attackers cannot infer any information about the original image. Histogram plots of the original, encrypted, and decrypted images are depicted in Fig. 5 to analyze the uniformity of the encrypted images.

Fig. 5
figure 5figure 5

Histogram plots of (a,b) grayscale, (c,d) RGB, and (e,f) Hyperspectral images.

Full size image

From Fig. 5, it can be observed that the pixel values of the encrypted images are uniformly distributed, in contrast to the pixel distribution of the original images. Moreover, the histograms of the original and decrypted images are visually identical, indicating a similarity in the pixel distributions of the decrypted images. The variance and chi-square techniques are used to calculate the uniformity analysis of the encrypted images by analyzing the pixel distribution of the histogram40. The mathematical formulation of variance and chi-square is given by Eq. (23) and Eq. (24), respectively.

$$\:var\left(x\right)=\frac{1}{{k}^{2}}\:\sum\:_{i=1}^{k}\sum\:_{j=1}^{k}\frac{1}{2}{({x}_{i}-{x}_{j})}^{2}$$
(23)

where \(\:x\) be the vector of histogram values and \(\:x=\left\{{x}_{1},{x}_{2},\dots\:,{x}_{256}\right\}\), \(\:{x}_{i}\) and \(\:{x}_{j}\) represent the number of pixels with gray values equal to \(\:i\) and \(\:j\), respectively.

$$\:{\chi\:}_{test}^{2}=\sum\:_{i=1}^{M}\frac{({ob}_{i}-e{x}_{i})}{e{x}_{i}}$$
(24)

where \(\:e{x}_{i}\) is the expected frequency in a uniform distribution which is calculated as \(\:e{x}_{i}=\frac{width\times\:length}{256}\). The \(\:o{b}_{i}\) is the observed occurrence frequency of each gray level \(\:(0-255)\) in the histogram of the encrypted image and \(\:M\) represents the number of gray levels.

Table 3 shows the variance and chi-square values of the original as well as encrypted images. The variance of the encrypted images must remain below 5000, and the chi-square value should not exceed 29340.

Table 3 Analysis of variance and chi-square values for encrypted and original image.
Full size table

Table 3 indicates that the encrypted images’ variance and chi-square values meet the required thresholds of 5000 and 293, respectively. The correlation plot analysis is used to visualize the relationship among the encrypted images’ pixel values. In Fig. 6, the correlation plots of the encrypted and original images are shown to depict pixel relationships horizontally, vertically, and diagonally.

Fig. 6
figure 6

Correlation plots for original and encrypted images.

Full size image

The correlation plots of encrypted images are scattered and squared-shaped, showing no negative relationship, which ensures security from information leakage. The correlation coefficients of the original and encrypted images are listed in Table 4.

Table 4 Correlation coefficient for original and encrypted images.
Full size table

The correlation coefficient values of the encrypted images, which are close to zero or negative, indicate that the pixel values in the encrypted images have no relationship with neighboring pixels.

Differential attack analysis

A number of Pixel Change Rate (NPCR) and Unified Averaged Changed Intensity (UACI) methods are used to analyze the differential attack resistance of the encryption methods41. The NPCR and UACI values are calculated by generating two encrypted images, one from the original image and the other by changing a pixel value in the original image. The mathematical formulation of NPCR and UACI is presented by Eqs. (25) and (27) respectively.

$$\:N\left({enc}_{1},\:{enc}_{2}\right)=\sum\:_{i,j}\frac{D\left(i,j\right)}{T}\times\:100\:\%$$
(25)

where \(\:D\left(i,j\right)\) is given by Eq. (26)

$$\:D\left(i,j\right)=\left\{\begin{array}{c}0,\:if\:{enc}_{1}\left(i,j\right)={enc}_{2}(i,j)\\\:1,\:if\:{enc}_{1}\left(i,j\right)\ne\:{enc}_{2}(i,j)\:\end{array}\right.$$
(26)

\(\:{enc}_{1}\) and \(\:{enc}_{2}\) are two encrypted images, where \(\:{enc}_{1}\) is generated before and \(\:{enc}_{2\:}\)is generated after a one-pixel change in the original images. \(\:T\:\)denote the total number of pixels in each encrypted image.

$$\:\text{U}\left({\text{e}\text{n}\text{c}}_{1},\:{\text{e}\text{n}\text{c}}_{2}\right)=\sum\:_{\text{i},\text{j}}\frac{\left|{\text{e}\text{n}\text{c}}_{1}(\text{i},\text{j})-{\text{e}\text{n}\text{c}}_{2}(\text{i},\text{j})\right|}{\text{F}\times\:\text{T}}\times\:100\:\text{\%}\:$$
(27)

where \(\:T\) is the total number of pixels and \(\:F\) is the largest supported pixel value of an image of an encrypted image. \(\:{enc}_{1}\:\)and \(\:{enc}_{2}\) are the encrypted images generated before and after the one-pixel change in the original image. For NPCR and UACI to be considered acceptable, their values should exceed 99.60% and 33.40%, respectively42. The computed values of the UACI and NPCR for the encrypted images are given in Table 5.

Table 5 UACI and NPCR values of encrypted images.
Full size table

The UACI and NPCR values of the encrypted images show that values are within the desired range and successfully resist differential attacks.

Quantitative analysis

The information entropy, Peak Signal-to-Noise Ratio (PSNR), and Mean Square Error (MSE) metrics are used to quantify the encrypted images generated using the encryption methods43. The information entropy is used to measure the degree of unpredictability present in the information content of the encrypted images. For an encrypted image to exhibit pixel randomness, the entropy value should be close to 8 or 16. The MSE and PSNR are used to show discrepancies between the original and encrypted images to measure the image quality. An encryption algorithm having small PSNR values and high MSE values shows the presence of noise in the encrypted image. Table 6 shows the computed results of the metrics for the images.

Table 6 Analysis of information entropy, PSNR, and MSE.
Full size table

Table 6 reveals that the proposed encryption approach is extremely efficient due to the small PSNR values and large MSE values. This illustrates the robustness, safety, and efficacy of the propounded encryption approach.

Key space analysis

The key space analysis is used to check the resistance of the encryption approach against brute-force attacks. The key space of the encrypted approach should be greater than the required \(\:{2}^{128}\:\)bits44. The key space of the propounded approach is \(\:{10}^{16\times\:6}={10}^{96}\), as it uses six secret keys, each with a precision of \(\:{10}^{16}\). Therefore, the proposed encryption approach is secure from brute force attacks.

Comparison with other state-of-the-art techniques

The performance effectiveness of the ICO-HO algorithm utilized in the proposed encryption method has been evaluated through comparisons with other state-of-the-art optimization algorithms, i.e., PSO12, BES13, Cheetah Optimization (CO)45, Self-adaptive Bald Eagle Search (SABES) optimization22, Brown Bear Optimization (BBO)46, and Hippopotamus optimization (HO)24algorithms. In this evaluation process, only parameter selection of the chaotic maps was made using different optimization algorithms. Table 7 presents the achieved values of the performance metrics (correlation coefficient, entropy, NPCR, UACI) for the DICOM lung CT scan 16-bit images47.

Table 7 Performance comparison with the other metaheuristic optimization technique.
Full size table

Table 7 shows that the proposed encryption method based on ICO-HO achieved the highest entropy value, which ensures randomness in the pixel values of the encrypted image. Also, all correlation coefficient values, i.e., H, V, and D are lower compared to the other comparative methods, indicating a weak relationship among the pixel values of the encrypted image. The efficacy of the proposed encryption approach is analyzed by comparing the results with existing encryption methods for DICOM lung CT scan images. Entropy, UACI, NPCR, and correlation coefficient metrics are used for the comparison, given in Table 8.

Table 8 Comparison with state-of-the-art image encryption techniques.
Full size table

The proposed encryption method achieves competitive results across key performance metrics. It exhibits low correlation coefficients, ensuring weak pixel correlation among the encrypted pixel values. In the propounded approach, the entropy values are 7.9995 for 8-bit images and 15.8124 for 16-bit images, which are close to their respective ideals. Also, NPCR values were attained using the proposed encryption approach, which showed high sensitivity to pixel changes, while UACI values indicated strong encryption performance. The proposed technique maintains high entropy levels, ensuring that the encrypted images are nearly indistinguishable from random noise, thus providing robust protection against potential attacks and making it comparable to other state-of-the-art techniques.

Conclusions and future scopes

This paper proposes an adaptive encryption approach based on the optimized chaotic maps. The initial and control parameters of the chaotic maps are optimally selected utilizing the proposed Iterative Cosine Operator-based Hippopotamus Optimization (ICO-HO) algorithm. The efficacy of the ICO-HO algorithm is compared with seven state-of-the-art algorithms namely Hippopotamus Optimization (HO), Whale Optimization Algorithm (WOA), Arithmetic Optimization Algorithm (AOA), Moth Flame Optimization (MFO), Sine Cosine Algorithm (SCA), African Vultures Optimization Algorithm (AVOA), and RIME algorithm (RIME) on CEC-2017 functions. Friedman mean rank analysis gives 1.93, 3.68, 6.17, 7.62, 3.82, 5.89, 4.34, and 2.51 values for ICO-HO, HO, WOA, AOA, MFO, SCA, AVOA, RIME algorithms respectively with p-value 3.56E-24. This shows better performance of the ICO-HO algorithm than other comparative algorithms. The proposed encryption approach is applied to medical images of different modalities and sizes. The effectiveness of the proposed encryption approach is evaluated in RGB, grayscale, and hyperspectral medical images. The effectiveness of the adaptive encryption approach is analyzed using various performance metrics such as visual, histogram, chi-square, variance, NPCR, UACI, correlation coefficient, entropy, PSNR, and MSE. The histogram, chi-square, variance, and correlation coefficient analyses demonstrate the uniform distribution of the pixel values of encrypted images and show the security from the statistical attacks. The UACI and NPCR values for the encrypted images generated using the encryption approach are greater than 33.40% and 99.60%, respectively, which ensure security against differential attacks. The entropy values of 8-bit and 16-bit images are 7.9995 and 15.8124, respectively, which are closer to 8 and 16, which show the randomness of pixel values. Additionally, the propounded encryption approach is compared to the existing encrypted techniques, showing more randomness in the encrypted image than the other encrypted techniques. This work is being extended by designing new hybrid chaotic maps. The proposed ICO-HO algorithm can be applied to other optimization problems like band selection in hyperspectral images.