Performance analysis of hybrid optimization approach for UAV path planning control using FOPID-TID controller and HAOAROA algorithm

Abstract

In this study, we present a comparative analysis of various trajectory optimization algorithms for Unmanned Aerial Vehicles (UAVs) navigating complex environments. The performance of the proposed FOPID-TID based HAOAROA (Hybrid Archimedes Optimization Algorithm-Rider Optimization Algorithm) is evaluated against traditional methods such as A*, JPS, Bezier, and L-BSGF algorithms. The FOPID-TID based HAOAROA approach integrates the advantages of fractional-order control with hybrid optimization techniques to improve UAV trajectory planning. Simulation results indicate that the proposed method carries significantly better performance than the traditional algorithms with respect to trajectory length, smoothness, and overall stability. Remarkably, the FOPID-TID based HAOAROA yields a 10% reduced trajectory length that is smoother than traditional methods while also being more computationally efficient. By using fractional-order parameters, the dynamic response becomes better and better in more challenging environments. This shows that disturbance rejection and control precision using the FOPID-TID based HAOAROA are much superior to the original two subroutines. The applications presented in this study allow future growth in UAV control system improvements and provide proof of concept of hybrid optimization in improving the performance of UAVs in dynamic, complex environments.

Introduction

The demand for Advanced trajectory planning methods for Unmanned aerial vehicles to efficiently and safely perform tasks in complex and dynamic environments has been steadily rising. Aerial surveillance, disaster management, environmental monitoring, and infrastructure inspection are some sectors where UAVs are extensively used; however, they must navigate through the static and dynamic obstacles present in their environments. Smooth flight paths, less energy consumption and mission success with avoidance of collisions with obstacles are critical requirements to efficient trajectory planning¹. Trajectory planning for UAVs is to find an optimal path between an initial point and a destination while avoiding obstacles and minimizing, e.g., flight time or energy consumption. Trajectory planning problems have been solved with great success using traditional path planning algorithms, such as A* and Jump Point Search (JPS). Despite this, these algorithms generate non-smooth piecewise linear paths, which are not very appropriate for a flight of UAVs that demand smooth and gradual trajectories (continuous paths) for stable flight².

In this paper, we present a detailed comparison of several very well-known trajectory planning algorithms, including A*, JPS, Bezier curves, and Laplacian-based Spline Gradient Flow (L-BSGF). In addition, we introduce a novel hybrid algorithm, HAOAROA (Hybrid Archimedes Optimization Algorithm - Rider Optimization Algorithm), which has better path optimization and obstacle avoidance. The HAOAROA algorithm combines the strengths of two optimization methods: The Archimedes Optimization Algorithm (AOA) and the Rider Optimization Algorithm (ROA) produce a highly effective UAV trajectory planning technique. Using both AOA’s exploration capabilities and ROA’s local search expertise, HAOAROA can achieve a balance between exploration and exploitation, thus yielding smooth and efficient flight paths in obstacle-heavy environments³.

The proposed HAOAROA algorithm generates smooth and continuous trajectories based on B spline curves. Through the HAOAROA optimization process, the control points of the B-spline curves are modified to avoid obstacles and minimize path length. HAOAROA has better trajectory smoothness and efficiency compared to traditional algorithms and is well suited to UAVs operating in environments with high complexity and constraints⁴.

Gradient-based autonomous obstacle avoidance trajectory planning methods combined with the use of UAVs using B-splines as paths and the HAOAROA Algorithm provide many advantages and offer many applications, including in environments where safety, precision, and efficiency are important. The proposed HAOAROA algorithm is used to dynamically generate smooth and continuous trajectories for UAVs that avoid obstacles in real-time⁵.

In disaster prone environments, e.g. earthquake zones, or during flooding, UAVs must manage unexpectedly cluttered terrain and search for survivors amongst debris and other obstacles. HAOAROA powered gradient based obstacle avoidance enables UAVs to plan efficient paths in real time between congested, moving obstacles and reach hard to access areas safely. HAOAROA generates smooth B-spline trajectories that minimize sharp turns, allowing UAVs to fly longer missions with lower energy consumption necessary in prolonged search and rescue operations. UAVs are used in agricultural settings, to monitor crop health, map large fields, and spread fertilizers, or pesticides. They are very often tree lines, structures, or uneven terrain making the environments complex. HAOAROA allows UAVs to autonomously navigate around obstacles while keeping precise flight paths to enable efficient coverage of fields. The real-time adaptability to unexpected obstacles, like machinery or livestock, is achieved through real-time optimization using gradient based optimization, allowing for superimposed collisions and improved operational safety. UAVs are increasingly being used to inspect critical infrastructure such as bridges, power lines, and buildings is an area already of interest. Often, in these environments, there are many (or all) of the obstacles being highly complex, such as towers, wires, and tall structures. The HAOAROA algorithm allows UAVs to plan optimal, smooth trajectories around the obstacles while maintaining a dwelling and close flight path near the structures to inspect them accurately. Unmanned obstacle avoidance makes UAVs dangerous consequences free to survey even complex or confined spaces. Future ubiquitous use of UAVs is envisioned in smart cities as an integral part of autonomous delivery systems. Smooth trajectory planning is required to safely navigate through densely populated urban spaces, avoiding buildings, trees, and other obstacles. HAOAROA provides real-time obstacle avoidance capabilities to UAVs, which allow UAVs to achieve safe and efficient delivery routes in cities with a minimum delivery time of flight while keeping cargo safe. The energy-efficient, smooth, and wear and tear-reducing flight paths provided by the gradient-based B-spline approach prolong the lifespan of UAV hardware, all for the better. In fact, UAVs are also used in military operations to undertake surveillance and reconnaissance in hostile or unknown terrains. It is of great importance to the ability to avoid obstacles autonomously while remaining stealth and operationally efficient. HAOAROA’s gradient based obstacle avoidance enables UAVs to move in challenging areas (e.g. mountains, urban combat zone) without causing any disturbance and makes them untraceable. A smooth trajectory planning is effective in reducing noise and visibility for the sake of military missions. And UAVs are well suited for monitoring wildlife; forest health; and environmental changes. It is required for UAVs to navigate around natural obstacles occurring in dense forest environments or mountainous terrain. In HAOAROA, we guarantee UAVs to avoid these obstacles while following optimal flight paths to collect data over a large area. It helps more efficiently and safely monitor ecosystems to detect illegal activities better, track endangered species or determine environmental damage⁶.

Trajectory planning, and obstacle avoidance in the realm of Unmanned Aerial Vehicles (UAVs) play a critical role in providing the safety, efficiency, and success of autonomous missions. As surveillance, environmental monitoring, disaster relief, infrastructure inspection, and even logistics constraints increase, UAVs have become more and more a popular choice with which to complete these tasks as they are helped to navigate by environments with complex static and dynamic obstacles. In these applications, again, UAVs must not only travel to their destination but also do it in the least energy-consuming path and without colliding with any obstacles on their way. These challenges make them efficient, adaptive, and able to handle complex and often unpredictable environments necessary to address them, trajectory planning methods must be efficient, adaptive, and capable of handling complex and often unpredictable environments⁷. B-spline curves are one of the most effective ways to guarantee the UAV smooth, continuous and efficient navigation, by deploying UAV trajectory as a succession of control points. B-spline curves are flexible smooth path representations that allow UAVs to change direction smoothly and gradually while maintaining flight stability. However, B-spline curve based optimal path problem for UAVs in an environment of obstacles utilizing advanced optimization techniques remains an area of intense research. Therefore, our work presents a Gradient based autonomous obstacle avoidance trajectory planning method leveraging HAOAROA (Hybrid Archimedes Optimization Algorithm – Rider Optimization Algorithm) to supply the power to B-spline trajectory planning framework. It also allows dynamic real-time path optimization that is balanced with smooth navigation through a complex environment⁸.

The HAOAROA algorithm, the core of our optimization approach, is a hybrid one combining the strengths of the Archimedes Optimization Algorithm (AOA) and the Rider Optimization Algorithm (ROA) with the new AOA and ROA. AOA is known for its ability to efficiently explore a large search space and do so in a way which maximizes identifying promising regions of the solution space. The algorithm utilizes this simulation of the Archimedes principle, where a buoyant force is allowed to drive processing in directions other than the original search axes, helping to avoid local optima and seek new zones in the search space. ROA excels at local search or exploitation. The behavior of professional riders in bike races, where they resort to optimizing their position with respect to other riders to outperform them — that’s where it came from. The exclusive exploit capability of ROA guarantees that AOA can find a potential solution which ROA will then fine tune, resulting in a UAV trajectory with precision. As a result of combining global search and conscious local refinement of AOA and ROA respectively, HAOAROA provides a balanced optimization process, which makes it suitable for trajectory planning in situations where there are many complex obstacles. In our implementation, however, the UAV’s trajectory consisting of B-spline curves, once again provides a continuous, smooth path between the UAV’s starting point and its destination. This optimization process first defines the B-spline curve with a series of control points and seeks to modify these points such that the UAV can avoid obstacles, while maintaining trajectory smoothness and at the same time minimizing a path length parameter. Here the gradient based optimization component of our approach comes into play where the control points are updated with respect to gradient of a cost function. The cost function in x considers those things here such as how far away the UAV is from obstacles. The cost function is continuously calculated as a gradient to allow the algorithm to dynamically adjust the path of the UAV in real time to avoid collision and simultaneously keep it on a useful trajectory. In addition, gradient based optimization is effective for refining trajectories, but it can be soon doomed to get stuck in local optima in complicated environments. And that’s where HAOAROA comes in. With exploration and exploitation capabilities, HAOAROA optimally estimates the UAV’s trajectory globally, while being also highly adaptable to various obstacle configurations and environmental complexities. In terms of its ability to navigate through L-shaped, H-shaped, U-shaped, and Omega-shaped obstacles, HAOAROA is a demonstrator of its robustness and flexibility in dealing with complex obstacle laden environments. The integration of a FOPID TID (Fractional Order Proportional Integral Derivative with Time-Invariant Derivative) controller also provides a further enhancement to the UAV’s ability to fly smoothly and stably by fine tuning the trajectory adjustments with higher precision. FOPID-TID controller is an extension of FOPID controller that introduces fractional order control, which offers more flexibility in the system and enables the UAV’s handling in disturbance more effectively to be even more resilient to unexpected changes in the environment^9,10.

In¹¹authors propose a gradient based approach for autonomous obstacle avoidance in trajectory planning for unmanned aerial vehicles (UAVs) using B-spline curves. With the smooth, flexible representation of B-splines, the study addresses the limitations of existing trajectory planning methods, especially in dynamic environments. In this way, the proposed algorithm adjusts the trajectory of the UAV in real time, so that it is able to perform effective obstacle avoidance and minimize deviations from the desired trajectory in gradient information. Results show significant improvements in safety and efficiency for the method over existing methods, and therefore aid in the development of UAV navigation systems. In¹²the authors propose a novel path planning algorithm for three-dimensional collision avoidance, which combines potential field methods with B spline boundary curves. Local minima issues associated with potential field-based approaches to robotic navigation are highlighted as well as the effectiveness of these approaches, with limitations explored. Smooth and flexible path representations are generated by means of B-spline curves, which can represent the paths in dynamic environments. The proposed algorithm utilizes these methodologies in combined fashion to achieve improved path finding efficiency and robustness in 3D complex scenarios, and the advancement of autonomous navigation and collision avoidance strategies. In contrast, researchers¹³introduce a unique method for indoor formation motion planning based on evolutionary methods along with B spline parametrization. In this paper, we tackle the problem of coordinating multiple agents in dynamic indoor environments, by allowing smooth and flexible path representation. An evolutionary optimization algorithm is used to minimize a cost function to achieve adaptive formation in the presence of obstacles. Simulation results are shown for this approach in generating efficient, free collision trajectories for multiple agents. This work aids the multi-agent systems field with improvements in formation control and inside complex indoor navigation. In¹⁴, the authors suggest a new method to smooth the path planning of Ackermann mobile robots using an improved Ant Colony Optimization (ACO) algorithm coupled with a B-spline curve. It solves problems in generating smooth and feasible trajectories for a mobile robot to make its way through a complex environment. Secondly, the improved ACO algorithm enhanced pathfinding efficiency with better optimisation of routes considering dynamic obstacles. Meanwhile, B-spline curves can offer a smoothly flexible representation of the planned path which leads to better robot control and meander ability. Results show an outstanding path planning performance compared to the baseline and improve path planning’s safety and efficiency for Ackermann mobile robots in real world scenarios. In addition, researchers¹⁵also characterize a way to plan collision free and smoothly moving for a dual arm Cartesian robot based on B-spline representation. In this approach, we focus on developing safe and efficient trajectory generation that enables the robot to safely navigate complex environments with obstacles. The planned paths are not only smooth utilizing B-spline curves but have room for precise control of robot movement due to their adaptability. Collision avoidance techniques are effectively incorporated into the algorithm such that the robot maintains safe distance from the obstacles along the entire trajectory. This method is shown to be effective for seamless motion planning such that dual arm Cartesian robots can achieve improved operational capabilities in a wide variety of applications. In this work[16], DE3D-NURBS had introduced, a differential evolution-based path planning algorithm for 3D paths, that solves kinematic constraints and obstacle avoidance problem. Fashioned in this innovative way, this paper uses Non-Uniform Rational B Splines (NURBS) to allow smooth path representation and efficient navigation in three dimensional environments. An algorithm with kinematic constraints is used to ensure generated paths abide by the physical boundaries of the moving entity. Collision free trajectories are generated through the optimization of the path via the differential evolution strategy, which also avoid obstacles. DE3D–NURBS simulation results show its robustness and effectiveness in producing feasible paths for many applications, which increases navigation capabilities in complex 3D space. To do this, the authors in¹⁷ present RDT-RRT, a real time, double tree rapidly exploring random tree (RRT) path planning algorithm for autonomous vehicles. The key idea is to employ a novel dual tree guided approach that improves search performance over the standard RRT interpolation method while reducing planning time. RDT-RRT effectively explores the environment, and quickly identifies optimal paths by expanding two trees at once, avoiding obstacles. The algorithm can run in real time, thus easing requirements for dynamic and complex scenarios encountered by autonomous vehicles. Simulation results show that RDT-RRT can produce collision free trajectories, and future work should bring RDT-RRT to practical applications in autonomous navigation.

Recent years have witnessed great advancement in the trajectory planning and obstacle avoidance for Unmanned Aerial Vehicles (UAVs): both with the integration of optimization algorithms and path planning techniques. However, on the one hand, while these developments are achieved, there still exists a substantial lack of research in integrating smooth trajectory generation methods like B spline curves with advanced hybrid optimization bounding functions optimized to work in obstacle rich environments. Most existing studies have been limited to the application of basic optimization algorithms or heuristic tactics, rather than capitalizing on the synergistic power of hybrid algorithms that will simultaneously provide global exploration, as well as the local refinement in complex environments. In addition, only recent work considers real-time adaptivity needed by UAVs to operate optimally over dynamically and unpredictably changing obstacles. For example, algorithms such as A* and Jump Point Search (JPS) are often utilized for UAV trajectory planning, but often produce piecewise linear paths that do not possess the smoothness and continuity required by stable UAV flight when navigating through tight spaces or avoiding complex obstacle formations^18,19. This research gap is addressed in this study using a new Hybrid Archimedes Optimization Algorithm - Rider Optimization Algorithm (HAOAROA) incorporated into a Gradient based autonomous obstacle avoidance trajectory planning system for UAVs utilizing B-spline curves. Integrated, the global exploration capability of the Archimedes Optimization Algorithm (AOA) together with the fine-tuned local exploitation strength of the Rider Optimization Algorithm (ROA), the HAOAROA algorithm offers a unique balance between broad search and precise local refinement. In this final case, when the environment contains complex obstacles, we propose a hybrid approach, where the UAV navigates autonomously, following smooth, efficient and collision free paths. Unlike the previous works that performed standalone optimization, our hybrid scheme provides optimal trajectory planning through dynamically modifying the UAV’s path as dictated by real time access to obstacles and obstacle avoidance needs. In this work, we contribute the application of B-spline curves to generate smooth, continuous, and dynamically adjusted HAOAROA trajectories for obstacle avoidance that is optimal. Smooth transitions between waypoints, attained using B-spline curves, guarantee that UAVs keep stable flight, and avoid sharp turns that cause instability or energy inefficiency. We also incorporate element of a gradient based optimization that optimizes the B spline control points in real time and continuously refines the UAVs trajectory to avoid collision. This ends up serving as a novel approach, combining a global search from HAOAROA with local improvements via gradient based optimization, to real time UAV trajectory planning in static and dynamic environments. A major contribution of our work is the combination of HAOAROA with a Fractional Order Proportional Integral Derivative with Time Invariant Derivative (FOPID TID) controller. Based on the knowledge of the UAV control system, fractional calculus is added to this controller to enhance stability and robustness. Our system not only integrates the FOPID-TID controller to help tune the UAV’s flight path precisely to disturbances, or dynamic changes in its environment, in order to fly smoothly and stably. More adaptive responses are enabled by the fractional order control, and the hybrid HAOAROA is utilized to maintain optimality of the overall trajectory with respect to both path length and obstacle avoidance.

Both features make our study novel in several critical ways. As a first, the HAOAROA algorithm itself is an innovative hybrid optimization strategy which has not been previously applied in UAV trajectory planning context. Hybrid optimization techniques such as Particle Swarm Optimization (PSO) and Genetic Algorithms (GA) have been studied, but our particular combination of AOA and ROA provides a superior trade-off between exploration and exploitation when moving within a complex obstacle environment. Second, using real time gradient based adjustments to second generate B spline curves to embody fractals is not only smoother than methods like A* of JPS, but also achieves the real time that these methods simply cannot claim. Integration of the FOPID-TID controller with HAOAROA in trajectory planning is a novel contribution that improves the system robustness, stability and adaptability by introducing the real time responsiveness especially in dynamic environment. By developing and combining hybrid optimization with smooth trajectory planning based on B-spline curves for real-time UAV operations, our research fills a central gap. In existing literature, optimization and path planning are treated separately domain; for example, optimum control systems are optimized, or paths are generated, without fully considering how these components work real time in dynamic environments. We integrate HAOAROA and B-spline based path planning into a unified system which optimizes UAV trajectory as well as flight dynamics and enables robust obstacle avoidance. The following study summarizes our contributions:

1) In this work, we present the HAOAROA algorithm, which is a hybrid optimization algorithm, that combines the rapid global search of the Archimedes Optimization Algorithm with the local refinement of the Rider Optimization Algorithm, offering new insight into UAV trajectory planning for complex environments.

2) We generate smooth and continuous UAVs trajectories by applying B-spline curves for UAVs to maintain stable and energy efficient flight paths. We combine this method with gradient based optimization to ensure that the UAV can dynamically correct its path in real time to avoid obstacles.

2) The Hybrid FOPID-TID controller is integrated into the trajectory planning process with our study in a manner that is unique, in which the UAV can adapt to dynamic environmental changes while maintaining the trajectory smoothness and control precision.

4) We then conduct a rigorous evaluation of path length reduction, path smoothness, and real time obstacle avoidance, evaluating our proposed system against other traditional algorithms including A*, Bezier, L-BSSFG, and JPS, showing in each case that the HAOAROA powered system is superior.

The current article consists of five sections. The second section covers the B-spline, obstacle avoidance, trajectory optimization, and gradient based trajectory optimization for UAV trajectory kinematics. The third section describes the methodology phases, which make use of a hybrid HAOAROA algorithm based on the FOPID-TID controller. The results are presented and discussed in Section Four. The conclusion and potential areas for future research are covered in Section Five.

UAVs trajectory kinematics

A UAV’s trajectory should follow the smooth curve of UAV dynamics, have the shortest path length, and be free of collisions. These requirements can be precisely met by a curve generated by the B-spline in the specified environment. Equation (1) displays the B-spline expression^{20,21,22,23,24,25}.

$$\:P\left(u\right)=\sum\:_{i=0}^{n}{C}_{i}{B}_{i,k}\left(u\right),u\in\:\left[{u}_{k-1},{u}_{n+1}\right]$$

(1)

where the B-spline basis function of order K is represented by $\:Bi,k$, the control point is represented by Ci, and the vector node. To enhance path generation efficiency and streamline B-spline generation, the ideal 4th-order B-spline curves are produced using basis functions. Every B-spline trajectory is produced by the curve segmentation. by four B-spline basis functions determined by Eq. (2) and four control points^26,27,28,29.

$$\:\left\{\begin{array}{c}{f}_{1}\left(s\right)=\frac{1}{6}(1-s{)}^{3}\\\:{f}_{2}\left(s\right)=\frac{1}{6}\left(3{s}^{3}-6{s}^{2}+4\right)\\\:{f}_{3}\left(s\right)=\frac{1}{6}\left(-3{s}^{3}+3{s}^{2}+3s+1\right)\\\:{f}_{4}\left(s\right)=\frac{1}{6}{s}^{3}\end{array}\right.$$

(2)

where s, a number between 0 and 1, denotes the normalized distance, and each trajectory segment is produced using Eq. (3).

$$\:{P}_{i}\left(s\right)={f}_{1}\left(s\right){C}_{1}+{f}_{2}\left(s\right){C}_{2}+{f}_{3}\left(s\right){C}_{3}+{f}_{4}\left(s\right){C}_{4}$$

(3)

where Pi is a member of R3, and C1, C2, C3, and C4 are the trajectory’s four control points. Each segment of the trajectory stitches together the entire trajectory of the UAV, and the control points C2, C3, C4, and C5 generate the subsequent segment. UAV trajectories are generated into N-3 segments when there are N control points. The speed from 3, one can determine the position curve’s V(s) and acceleration A(s) are shown as in Eq. (4) and Eq. (5)^{30,31,32,33,34,35}.

$$\:V\left(s\right)=\frac{\partial\:P\left(s\right)}{\partial\:s}=\left[\begin{array}{c}{V}_{x}\left(s\right)\\\:{V}_{y}\left(s\right)\\\:{V}_{z}\left(s\right)\end{array}\right]$$

(4)

$$\:A\left(s\right)=\frac{{\partial\:}^{2}P\left(s\right)}{\partial\:{s}^{2}}=\left[\begin{array}{c}{a}_{x}\left(s\right)\\\:{a}_{y}\left(s\right)\\\:{a}_{z}\left(s\right)\end{array}\right]$$

(5)

Equation (6) and Eq. (7) are depicting differentiation of the trajectory entails differentiating the spline function because the trajectory’s control points are fixed. Next, it is possible to obtain the acceleration spline functions a1, a2, a3, and a4, as well as the velocity spline functions V1, V2, V3, and V4^33,36,37,38.

$$\:\left\{\begin{array}{c}{v}_{1}\left(s\right)=-\frac{(1-s{)}^{2}}{2}\\\:{v}_{2}\left(s\right)={s}^{2}-2s\\\:{v}_{3}\left(s\right)=-{s}^{2}+s+\frac{1}{2}\\\:{v}_{4}\left(s\right)=\frac{{s}^{2}}{2}\end{array}\right.$$

(6)

$$\:\left\{\begin{array}{c}{a}_{1}\left(s\right)=1-s\\\:{a}_{2}\left(s\right)=3s-2\\\:{a}_{3}\left(s\right)=<span class=' convertEndash' >1-3</span> s\\\:{a}_{4}\left(s\right)=s\end{array}\right.$$

(7)

Consequently, Eq. (8) and Eq. (9) demonstrate that the acceleration and velocity of the B-spline trajectory Pi are functions of the parameter S.

$$\:V\left(s\right)=v1\left(s\right)C1+v2\left(s\right)C2+v3\left(s\right)C3+v4\left(s\right)C4$$

(8)

$$\:A\left(s\right)=a1\left(s\right)C1+a2\left(s\right)C2+a3\left(s\right)C3+a4\left(s\right)C4$$

(9)

This demonstrates that the position, acceleration, and velocity of the start and finish points of the two curves are equal, guaranteeing a smooth and continuous B-spline trajectory. It is also assumed that additional control points will be added in order to verify that the trajectory passes through the start and finish points. Since c1 is the origin of c1, c0, and c2 as stated in Eq. (10), we expand the starting point C1 as c0, c1, and c2.

$$\:\left\{\begin{array}{c}c0=c1-v1L\\\:c2=c1-v1L\end{array}\right.$$

(10)

In this experiment, v1 is the velocity vector at the point where the UAV passes through, and L is an appropriate constant. We then take half of the distance required for the UAV to reach its maximum velocity. Equation (9) can be solved by inserting the solution into Eqs. (7) and (8). This confirms that the trajectory passes through the starting point C1, with a velocity v1 acceleration a1 of zero. Analogously, since Cn is the origin, the target point Cn is extended to encompass $\:Cn-1,\:Cn,\:Cn+1,$ and $\:Cn+1$, as indicated by Eq. (11).

$$\:\left\{\begin{array}{c}{c}_{n-1}={c}_{n}-{v}_{n}L\\\:{c}_{n+1}={c}_{n}+{v}_{n}L\end{array}\right.$$

(11)

The solution to the equation verifies that the trajectory passes through the control point CN, that the acceleration and is zero, and that the UAV’s speed is $\:vn$. This means that if the control points C1, C2, C3, C4, CN, etc., are changed, the UAV B-spline trajectory initialization can be completed after solving.

To quickly initialize the UAV B-spline trajectory, the control point selection procedure uses the polynomial fitting method. The maximum singular value ($\:dz$) between the two points in space is then computed and compared to the predetermined distance (dc) of the control point distribution to determine whether to add a waypoint after the trajectory’s beginning point (C1) and ending point (CN) have been acquired. If $\:dz$ is greater, waypoints must be set. Equations (12) and (13)^39,40 can be used to express the waypoint setting number m.

$$\:\left\{\begin{array}{c}m=\left[\frac{dz}{dc}\right]+1\\\:m=2\end{array}\right.$$

(12)

$$\:\left\{\begin{array}{c}{x}_{n}={x}_{0}\left(1-\frac{n}{m}\right)+\frac{1}{m{x}_{N}}\\\:{y}_{n}={y}_{0}\left(1-\frac{n}{m}\right)+\frac{1}{m{y}_{N}}\\\:{z}_{n}={z}_{0}\left(1-\frac{n}{m}\right)+\frac{1}{m{z}_{N}}\end{array}\right.$$

(13)

Equation (14) shows each path point is obtained and then the polynomial coefficients ($\:Fx,Fy,$ and $\:Fz$) of each UAV trajectory in the x, y, and z directions are solved. UAV trajectory segments are known to be generated in m-1 increments.

$$\:\left\{\begin{array}{c}{F}_{x}=\frac{{B}_{x}}{A}\\\:{F}_{y}=\frac{{B}_{y}}{A}\\\:{F}_{z}=\frac{{B}_{z}}{A}\end{array}\right.$$

(14)

The parameter vectors at the start and finish of each UAV trajectory are denoted by the symbols Bx, By, and $\:Bz$, respectively, and have the following expressions as in Eq. (15):

$$\:\left\{\begin{array}{c}{B}_{x}=\left[{x}_{0},{v}_{x0},{a}_{x0},{x}_{n},{v}_{xn},{a}_{xn}\right]\\\:{B}_{y}=\left[{y}_{0},{v}_{y0},{a}_{y0},{y}_{n},{v}_{yn},{a}_{yn}\right]\\\:{B}_{z}=\left[{z}_{0},{v}_{z0},{a}_{z0},{z}_{n},{v}_{zn},{a}_{zn}\right]\end{array}\right.$$

(15)

where each trajectory segment’s coordinate, velocity, and acceleration on the three axes of the starting point are represented by the values $\:x0,\:y0,\:z0,\:vx0,\:vy0,\:vz0,\:and\:ax0,\:ay0,\:az0$. The coordinates, acceleration, and velocity of the corresponding trajectory segment on the three axes of the ending point are $\:xn,\:yn,\:zn,\:vxn,\:vyn,\:vzn,\:and\:axn,\:ayn,\:azn$. Equation (14) parameter matrix can be written as in Eq. (16):

$$\:A=\left(\begin{array}{cccccc}0&\:0&\:0&\:0&\:1&\:0\\\:0&\:0&\:0&\:1&\:0&\:0\\\:0&\:0&\:2&\:0&\:0&\:0\\\:{t}^{5}&\:{t}^{4}&\:{t}^{3}&\:{t}^{2}&\:t&\:1\\\:5{t}^{4}&\:4{t}^{3}&\:3{t}^{2}&\:2t&\:1&\:0\\\:20{t}^{3}&\:12{t}^{2}&\:6t&\:2&\:0&\:0\end{array}\right)$$

(16)

Since the start and end segments may require the UAV to fly slower than its top speed, the time is set to be twice as long as the speed at which it can complete the corresponding trajectory (t = 1/t). One method to express $\:tn$ as in Eq. (17) is as follows.

$$\:\left\{\begin{array}{c}tn\:=\frac{2\left(Cn+1\:-\:Cn\right)}{vmax}\:\left(n\:=\:0\right)\\\:tn\:=\frac{Cn+1\:-\:Cn}{vmax}\:\left(0\:<\:n\:<\:m\right)\\\:tn\:=\frac{2\left(Cn+1\:-\:Cn\right)}{vmax}\:\left(n\:=\:m\right)\end{array}\right.$$

(17)

Equation (18) provides the solution formula. The polynomial fitting is used to generate the coordinates of the control points after obtaining the waypoint coordinates and the polynomial coefficients of the m-1 group of coordinates.

$$\:\left\{\begin{array}{c}xn=KxC\\\:yn=CKy\\\:zn=CKz\end{array}\right.$$

(18)

where the augmentation vectors $\:Kx,\:Ky,$ and $\:Kz$ are connected to the coefficient vectors $\:Fx,\:Fy,$ and $\:Fz$ of the polynomial, and $\:C$ is the coefficient matrix linked to the number of waypoints. The path initialization is finished once the control points are obtained using Eq. (3)^41,42.

However, the trajectory optimization process finds that solving the trajectory with the time parameter t is more convenient. The trajectory initialization process is calculated using parameter S to make the process of solving the trajectory easier. Just the trajectory’s beginning and ending are included in the trajectory initialization process. Equations (19) and (20) can be used to convert the parameters S and t of the UAV trajectory:

$$\:P\left(s\right)=\left\{\begin{array}{c}x\left(s\right)\\\:y\left(s\right)\\\:z\left(s\right)\end{array}=p\left(t\right)=\left\{\begin{array}{c}x\left(t\right)\\\:y\left(t\right)\\\:z\left(s\right)\end{array}\right.\right.$$

(19)

$$\:\frac{dP\left(t\right)}{dt}=\frac{\partial\:P\left(s\right)}{\partial\:s}s\Rightarrow\:\left[\begin{array}{c}{v}_{x}\left(t\right)\\\:{v}_{y}\left(t\right)\\\:{v}_{z}\left(t\right)\end{array}\right]=\left[\begin{array}{c}{v}_{x}\left(s\right)\\\:{v}_{y}\left(s\right)\\\:{v}_{z}\left(s\right)\end{array}\right]s\left(t\right)$$

(20)

Trajectory optimization

A convex linear combination of two lower first-order B-splines is what makes up each higher-order B-spline, as demonstrated by de Boor-Cor’s recursive Eq. (21). To be considered legal, an interval needs to have enough basis functions in each segment of the B-spline curve to match the control points. Therefore, in the proposed algorithm, $\:n\:+\:4$ node vectors $\:(u0,...,\:un+3)$ are required if there are $\:n$ control points. Finding a 4th-order B-spline Pi requires the use of four nodes $\:(ui,\:ui+1,\:ui+2,\:ui+3)$. To guarantee proper splicing between every two segments, neighboring B-splines have two identical control points.

$$\:\left(\begin{array}{c}{B}_{i,1}\left(u\right)=\left(\begin{array}{c}1\:if\:ui\le\:u<ui+1\\\:0\:otherwise\end{array}\right)\\\:{B}_{i,k}\left(u\right)=\frac{u-{u}_{i}}{{u}_{i+k-1}-{u}_{i}}{B}_{i,k-1}\left(u\right)+\frac{{u}_{i+k}-u}{{u}_{i+k}-{u}_{i+1}}{B}_{i+1,k-1}\left(u\right)\end{array}\right)$$

(21)

The beginning and end of the two points of the velocity of $\:v1$ and $\:vn$, respectively, are where the UAV trajectory initialization process passes through by assuming an increase in control points to guarantee that the UAV passes through the trajectory start point. Nevertheless, the UAV’s speed in the first two points can only be at zero. Consequently, the first four and the last four node vectors in the trajectory solution procedure described in this paper stay consistent. Figure 1 illustrates the structure of this B-spline, which is also known as a clamped B-spline.

With node vectors [0, 0, 0, 0, 0, 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1, 1, 1], the graph has 14 nodes and 10 control points. The two primary characteristics of the clamped B-spline are aptly depicted in Fig. 1. The curve has a strong convex hull and passes through the control points at the head and tail.

Strong convex hull property means that if the node vectors u are located in $\:[ui\:,\:ui+1]$, then the curve P(u) is located within the convex hull defined by control points $\:Ci\:,\:Ci-1,\:Ci-2,\:Ci-3\:(i\:\ge\:\:3)$, which indirectly verifies that a control point only affects local trajectories. The B-spline function is localized, and this property can solve the problem of local changes in the trajectory affecting the overall trajectory planning when the UAV encounters an obstacle. The collision part of the trajectory is changed by adjusting the relevant control points, while the convex hull of the B-spline ensures that the trajectory meets the restricted range.

Fig. 1

Clamped B-spline structure.

Optimizing obstacle avoidance

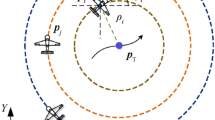
The control point of a collision is chosen when a trajectory encounters an obstacle, and the corresponding control point is created on the obstacle’s surface. On the obstacle surface, there may be multiple corresponding points $\:\rho\:i,j$ for each control point Ci; however, each $\:\rho\:i,j$ is exclusive to a single control point. Figure 2 illustrates the relationship between the three based on the corresponding repulsive direction vector $\:Hi,j$ produced by the positions and $\:\rho\:i,j$⁴³.

Fig. 2

Diagrams of the control point variation for trajectory obstacle avoidance.

$\:J$ is the index of the corresponding point and the opposite direction vector, and $\:i$ is the index of the original control point. The distance between the initial control point and the obstacle surface point is determined using Eq. (22).

$$\:{D}_{i,j}={C}_{i}-{\rho\:}_{i,j}\cdot\:{H}_{i,j}$$

(22)

We only consider obstacles encountered by the control points Ci as newly discovered obstacles by restricting $\:Di,j\:>\:0$, since the trajectory is continuously optimized, and collision detected. This prevents the resulting duplicates of $\:Hi,j$ and $\:\rho\:i,j$. By limiting the amount of computation that can be done to update the new trajectory more quickly, this restriction aids in the discovery of obstacles that affect the new trajectory.

The environment serves as a crucial point of reference for UAV obstacle avoidance algorithms. Accompanying the requirement to store a substantial amount of environmental data is the establishment of suitable trajectory algorithms for obstacle avoidance. This indicates that a substantial amount of data needs to be computationally processed, which is definitely an immovable obstacle given the computational capability of micro-UAVs. The repulsive force algorithm is straightforward and effective, which significantly reduces the amount of computation, whereas the article algorithm only needs to store the environmental data in the small area close to the B-spline trajectory.

Furthermore, it avoids the issue of UAVs entering local minima and does not necessitate the regeneration of collision-free trajectories due to its low environmental information requirements. The selection of the basis function and control point has an impact on the trajectory since it is generated using the B-spline curve; Fig. 3 illustrates the structure of the B-spline curve.

Fig. 3

The B-spline curve changes over points.

Trajectory generation is greatly influenced by the separation between control points. When little obstacles are encountered, there will be needless performance waste for the UAV due to the large trajectory deformation brought on by each iteration of the trajectory if the distance between the trajectory control points is too great. When faced with significant obstacles, more iterative calculations and possibly failed planning are required if the distance between control points is too small.

Optimization of trajectories using gradients

The UAV velocity vi, acceleration a.i., and jerk ji between the two control points can be expressed as follows because Eq. (12) shows that we use a uniform B-spline in the B-spline parameterization process so that the time interval delta t in the control points is the same and very small are shown as a theorem 1 proposed in Eq. (23), Eq. (24), Eq. (25), Eq. (26), Eq. (27), Eq. (28), Eq. (29), Eq. (30), Eq. (31), Eq. (32), Eq. (33), Eq. (34)¹:​​

$$\:\left\{\begin{array}{c}vi=\frac{{C}_{i+1}-Ci}{\varDelta\:t}\\\:ai=\frac{{v}_{i+1}-vi}{\varDelta\:t}\\\:ji=\frac{{a}_{i+1}-ai}{\varDelta\:t}\end{array}\right.$$

(23)

$$\:\left\{\begin{array}{c}{U}_{1}={C}_{t}\left({\omega\:}_{1}^{2}+{\omega\:}_{2}^{2}+{\omega\:}_{3}^{2}+{\omega\:}_{4}^{2}\right)\\\:{U}_{2}=\sqrt{2}{C}_{t}l\left({\omega\:}_{1}^{2}-{\omega\:}_{2}^{2}+{\omega\:}_{3}^{2}-{\omega\:}_{4}^{2}\right)\\\:{U}_{3}=\sqrt{2}{C}_{t}l\left({\omega\:}_{1}^{2}-{\omega\:}_{2}^{2}+{\omega\:}_{3}^{2}-{\omega\:}_{4}^{2}\right)\\\:{U}_{4}={C}_{m}\left({\omega\:}_{1}^{2}-{\omega\:}_{2}^{2}+{\omega\:}_{3}^{2}-{\omega\:}_{4}^{2}\right)\end{array}\right.$$

(24)

$$\:\left\{\begin{array}{c}\ddot{x}=\frac{1}{m}\left[{U}_{1}\left(-{C}_{\psi\:}{C}_{\varphi\:}{S}_{\theta\:}+{S}_{\psi\:}{S}_{\theta\:}\right)-T{C}_{{\lambda\:}_{1}}{C}_{{\lambda\:}_{2}}-{k}_{f}\dot{x}\right]\\\:\ddot{y}=\frac{1}{m}\left[{U}_{1}\left(-{S}_{\psi\:}{C}_{\varphi\:}{S}_{\theta\:}-{C}_{\psi\:}{S}_{\varphi\:}\right)-T{C}_{{\lambda\:}_{1}}{C}_{{\lambda\:}_{2}}-{k}_{f}\dot{y}\right]\\\:\ddot{z}=\frac{1}{m}\left[{U}_{1}\left(-{C}_{\theta\:}{C}_{\varphi\:}\right)-T{S}_{{\lambda\:}_{1}}-{k}_{f}\dot{z}-mg\right]\\\:\ddot{\psi\:}=\frac{{I}_{y}-{I}_{z}}{{I}_{x}}\dot{\theta\:}\dot{\varphi\:}+\frac{{I}_{r}\dot{\theta\:}{\Omega\:}}{{I}_{x}}+\frac{l{U}_{2}}{{I}_{x}}\\\:\ddot{\theta\:}=\frac{{I}_{z}-{I}_{x}}{{I}_{y}}\dot{\psi\:}\dot{\varphi\:}+\frac{{I}_{r}\dot{\psi\:}{\Omega\:}}{{I}_{y}}+\frac{l{U}_{3}}{{I}_{y}}\\\:\ddot{\varphi\:}=\frac{{I}_{x}-{I}_{y}}{{I}_{z}}\dot{\psi\:}\dot{\theta\:}+\frac{{U}_{4}}{{I}_{z}}\end{array}\right.$$

(25)

$$\:\left\{\begin{array}{c}\ddot{x}=\frac{1}{m}\left[{U}_{1}\left(-{C}_{\psi\:}{C}_{\varphi\:}{S}_{\theta\:}+{S}_{\psi\:}{S}_{\theta\:}\right)-T{C}_{{\lambda\:}_{1}}{C}_{{\lambda\:}_{2}}-{k}_{f}\dot{x}\right]\\\:\ddot{y}=\frac{1}{m}\left[{U}_{1}\left(-{S}_{\psi\:}{C}_{\varphi\:}{S}_{\theta\:}-{C}_{\psi\:}{S}_{\varphi\:}\right)-T{C}_{{\lambda\:}_{1}}{C}_{{\lambda\:}_{2}}-{k}_{f}\dot{y}\right]\\\:\ddot{z}=\frac{1}{m}\left[{U}_{1}\left(-{C}_{\theta\:}{C}_{\varphi\:}\right)-T{S}_{{\lambda\:}_{1}}-{k}_{f}\dot{z}-mg\right]\\\:\ddot{\psi\:}=\frac{{I}_{y}-{I}_{z}}{{I}_{x}}\dot{\theta\:}\dot{\varphi\:}+\frac{{I}_{r}\dot{\theta\:}{\Omega\:}}{{I}_{x}}+\frac{l{U}_{2}}{{I}_{x}}\\\:\ddot{\theta\:}=\frac{{I}_{z}-{I}_{x}}{{I}_{y}}\dot{\psi\:}\dot{\varphi\:}+\frac{{I}_{r}\dot{\psi\:}{\Omega\:}}{{I}_{y}}+\frac{l{U}_{3}}{{I}_{y}}\\\:\ddot{\varphi\:}=\frac{{I}_{x}-{I}_{y}}{{I}_{z}}\dot{\psi\:}\dot{\theta\:}+\frac{{U}_{4}}{{I}_{z}}\end{array}\right.$$

(26)

$$\:{\dot{p}}_{{b}_{T}i}=b{v}_{Ti}-{a}_{1}\sigma\:{\left({b}_{i}^{0}\right({p}_{{b}_{T}i}-{p}_{T})+\sum\:_{j=1}^{>N}{a}_{ij}({p}_{{b}_{T}i}-{p}_{{b}_{T}j}))}^{m}-{b}_{1}\sigma\:{\left({b}_{i}^{0}\right({p}_{{b}_{T}i}-{p}_{T})+\sum\:_{j=1}^{N}{a}_{ij}({p}_{{b}_{T}i}-{p}_{{b}_{T}j}))}^{n}$$

(27)

$$\:{\dot{v}}_{{b}_{T}i}=-{a}_{1}\sigma\:{a}_{ij}({v}_{{b}_{T}i}-{v}_{{b}_{T}j}))-{b}_{1}\sigma\:{\left({b}_{i}^{0}\right({v}_{{b}_{T}i}-{v}_{T})+\sum\:_{j=1}^{N}{a}_{ij}({v}_{{b}_{T}i}-{v}_{{b}_{T}j}))}^{n}-{l}_{1}\text{sign}({b}_{i}^{0}({v}_{{b}_{T}i}-{v}_{T})+\sum\:_{j=1}^{N}{a}_{ij}({v}_{{b}_{T}i}-{v}_{{b}_{T}j}))$$

(28)

$$\:{\dot{p}}_{Ti}={v}_{Ti}-{a}_{1}\sigma\:{a}_{ij}({p}_{Ti}-{p}_{Tj}))-{b}_{1}\sigma\:{({b}_{i}^{0}{p}_{Ti}+\sum\:_{j=1}^{N}{a}_{ij}({p}_{Ti}-{p}_{Tj}))}^{n}$$

(29)

$$\:{\dot{v}}_{Ti}=-{a}_{1}\sigma\:{({b}_{i}^{0}{v}_{Ti}+\sum\:_{j=1}^{N}{a}_{ij}({v}_{Ti}-{v}_{Tj}))}^{m}-{b}_{1}\sigma\:{({b}_{i}^{0}{v}_{Ti}+\sum\:_{j=1}^{N}{a}_{ij}({v}_{Ti}-{v}_{Tj}))}^{n}-{l}_{1}\text{sign}({b}_{i}^{0}{v}_{Ti}+\sum\:_{j=1}^{N}{a}_{ij}({v}_{Ti}-{v}_{Tj}))$$

(30)

$$\:{\dot{e}}_{ri}={\dot{r}}_{i}=\frac{({p}_{T}{)}^{T}-({p}_{i}{)}^{T}}{\left({p}_{T}-{p}_{i}\right){r}_{i}}=\frac{({p}_{T}{)}^{T}-{u}_{Ti}{\varphi\:}_{i}}{({v}_{T}{)}^{T}{\left(k\left({\stackrel{\prime }{r}}_{i}-{r}_{di}\right){\stackrel{\prime }{\varphi\:}}_{i}+{\stackrel{\prime }{v}}_{Ti}{r}_{di}\left(6+\stackrel{\prime }{e}{w}_{i}\right)A{\stackrel{\prime }{\varphi\:}}_{i}\right)}^{T}}$$

(31)

$$\:\text{W}\text{h}\text{e}\text{r}\text{e}\:{p}_{T}=\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right),{\:p}_{i}=\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right),\:{\varphi\:}_{i}=\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{cos}\left(\psi\:\right),\:{\stackrel{\prime }{r}}_{i}=\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right),\:{r}_{di}=\text{sin}\left(\psi\:\right),\:\stackrel{\prime }{e}{w}_{i}=\text{cos}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{cos}\left(\varphi\:\right)-\text{cos}\left(\psi\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right).$$

The results are as follows:

$$\:{\dot{e}}_{ri}={\dot{r}}_{i}=\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-(\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right){)}^{T}}{\left(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\right){r}_{i}}=\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-{u}_{Ti}{\varphi\:}_{i}}{({v}_{T}{)}^{T}{\left(k\left({\stackrel{\prime }{r}}_{i}-{r}_{di}\right){\stackrel{\prime }{\varphi\:}}_{i}+{\stackrel{\prime }{v}}_{Ti}{r}_{di}\left(6+\stackrel{\prime }{e}{w}_{i}\right)A{\stackrel{\prime }{\varphi\:}}_{i}\right)}^{T}}$$

(32)

$$\:{\dot{e}}_{ri}={\dot{r}}_{i}=\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-(\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right){)}^{T}}{\left(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\right){r}_{i}}=\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-{u}_{Ti}\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{cos}\left(\psi\:\right)}{({v}_{T}{)}^{T}{\left(k\left({\stackrel{\prime }{r}}_{i}-{r}_{di}\right){\stackrel{\prime }{\varphi\:}}_{i}+{\stackrel{\prime }{v}}_{Ti}{r}_{di}\left(6+\stackrel{\prime }{e}{w}_{i}\right)A\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{cos}\left(\psi\:\right)\right)}^{T}}$$

(33)

$$\:{\dot{e}}_{ri}={\dot{r}}_{i}=\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-(\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right){)}^{T}}{\left(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\right){r}_{i}}=\\ \quad\frac{(\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{cos}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right){)}^{T}-{u}_{Ti}\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{cos}\left(\psi\:\right)}{({v}_{T}{)}^{T}{\left(k\left(\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\right){\stackrel{\prime }{\varphi\:}}_{i}+{\stackrel{\prime }{v}}_{Ti}\text{sin}\left(\psi\:\right)\left(6+\text{cos}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{cos}\left(\varphi\:\right)-\text{cos}\left(\psi\:\right)\text{sin}\left(\varphi\:\right)-\text{sin}\left(\psi\:\right)\text{sin}\left(\theta\:\right)\text{sin}\left(\varphi\:\right)+\text{cos}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)\right)A\text{sin}\left(\psi\:\right)\text{cos}\left(\varphi\:\right)*\text{cos}\left(\psi\:\right)\right)}^{T}}$$

(34)

Methodology

There are three phases to the methodology, as depicts in Fig. 4, focusing on trajectory optimization, hybrid control design, and advanced algorithmic enhancement. In Phase 1, we develop the UAV Gradient Trajectory Optimization Model to ensure efficient path planning under varying environmental conditions. Phase 2 involves designing a Hybrid FOPID-TID Controller, which integrates fractional-order and time-delay compensations to enhance system stability and performance. Finally, in Phase 3, we implement the HAOAROA Algorithm, an advanced hybrid optimization approach, to refine control parameters and maximize UAV performance under real-world dynamic disturbances. Each phase is provided with complete equations, optimization pseudocode, and derivations.

Fig. 4

Methodology Phases.

Phase 1: UAV Gradient Trajectory optimization model

In this phase, we aim to optimize both the trajectory of the UAV using gradient based optimization techniques and B-spline curves. The UAV trajectory is represented by a B-spline curve, and it is desired to minimize a Mult objective cost function by modifying (updating) the control points. However the three main goals of the cost function are obstacle avoidance, trajectory length minimization, and smoothness maintenance. By using a B-spline curve, we obtain a smooth and flexible representation of the UAV’s trajectory. Having control points (Pi) and basic functions $\:Ni,p\left(t\right)$, the B-spline is defined. The curve is represented as in Eq. (35)⁴⁴:

$$\:C\left(t\right)={N}_{i,p}\left(t\right)Pi,t\in\:\left[0,1\right]$$

(35)

Following the position of the UAV is represented by C(t), where t is the parameter then Eq. (36) will represent the position of the UAV. N is the B spline basis functions; P are control points. Optimizing the trajectory involves changing all the control points, reshaping that curve. We can achieve these criteria though, minimizing the path length, making the path smooth, and avoiding obstacles. To find an optimal trajectory, we define a cost function J(P) which measures the quality of the trajectory according to several criteria.

$$\:J\left(P\right)={J}_{length\left(P\right)}+{J}_{smoothness\left(P\right)}+{J}_{obstacle\left(P\right)}$$

(36)

Here this term is penalizing longer trajectories, favoring the system to minimize the distance between UAV and initial configuration. The length of the B-spline curve is given by the integral of the curve’s derivative as in Eq. (37)^45,46:

$$\:{J}_{length}={\int\:}_{0}^{1}\frac{dC\left(t\right)}{dt}dt={\int\:}_{0}^{1}{\sum\:}_{i=0}^{n}\frac{d{N}_{i,p}\left(t\right)}{dt}Pidt$$

(37)

This expression ensures that the total path length is minimized. To ensure the trajectory is smooth (i.e., avoiding sharp turns), we introduce a term that penalizes high curvature. The smoothness cost is related to the second derivative of the B-spline curve as depicts in Eq. (38):

$$\:{J}_{\text{smoothness}}={\int\:}_{0}^{1}{\left(\frac{{d}^{2}C\left(t\right)}{d{t}^{2}}\right)}^{2}dt={\int\:}_{0}^{1}\sum\:_{i=0}^{n}{\left(\frac{{d}^{2}{N}_{i,p}\left(t\right)}{d{t}^{2}}{P}_{i}\right)}^{2}dt$$

(38)

This term ensures the trajectory remains smooth and avoids oscillations. We define a repulsive potential field around each obstacle, which penalizes the UAV when it approaches obstacles. Let $\:ok$ represent the position of the $\:k-th$ obstacle. The obstacle avoidance cost is defined as in Eq. (39):

$$\:{J}_{\text{obstacle}}=k\sum\:_{k}{\int\:}_{0}^{1}\parallel\:C\left(t\right)-{o}_{k}{\parallel\:}^{2}{\lambda\:}_{k}\text{\hspace{0.17em}}dt$$

(39)

By lengthening the trajectory’s distance from obstacles, this cost incentivizes the UAV to avoid them. We minimize the total cost function $\:J\left(P\right)$ using gradient descent. The gradient of the cost function with respect to each control point $\:Pj$ can express as depicts in Eq. (40):

$$\:\nabla\:J\left({P}_{j}\right)=\frac{\partial\:{J}_{\text{length}}}{\partial\:{P}_{j}}+\frac{\partial\:{J}_{\text{smoothness}}}{\partial\:{P}_{j}}+\frac{\partial\:{J}_{\text{obstacle}}}{\partial\:{P}_{j}}$$

(40)

Equation (41) describes the iterative update of the control points using the gradient descent method. Specifically, the control points $\:{P}_{j}^{(k+1)}$ at the next iteration are updated by subtracting a step size α multiplied by the gradient of the objective function $\:\nabla\:J\left({P}_{j}\right)$ at the current iteration $\:k$. This process is repeated until the algorithm converges to an optimal solution.

$$\:{P}_{j}^{(k+1)}={P}_{j}^{\left(k\right)}-\alpha\:\nabla\:J\left({P}_{j}\right)$$

(41)

The learning rate is represented by the learning rate is represented by $\:\alpha\:$. An optimal trajectory that strikes a balance between length, smoothness, and obstacle avoidance is produced by continuing the process until the control points converge to values that minimize the total cost function.

Phase 2: hybrid FOPID-TID controller

In the second stage, the UAV is controlled in real-time along the optimized trajectory by means of a Fractional Order Proportional Integral Derivative with Time-Invariant Derivative (FOPID-TID) Controller. Fractional-order operators, which provide greater flexibility in controlling complex dynamic systems like UAVs, are introduced by the FOPID-TID controller, expanding the capabilities of conventional PID controllers as shown in Eq. (42).

$$\:u\left(t\right)={K}_{p}e\left(t\right)+{K}_{i}{D}^{-\lambda\:}e\left(t\right)+{K}_{d}{D}^{\mu\:}e\left(t\right)$$

(42)

where the proportionate, integral, and derivative gains are denoted, respectively, by $\:Kp$, $\:Ki$, and $\:Kd$. The fractional orders of the integral and derivative terms are denoted by λ and µ. The difference between the intended trajectory and the actual UAV position is represented by the error signal, e(t). Integration and differentiation operators denoted as $\:D^(-\lambda\:)$ and $\:D^\mu\:$ are fractional. Introduces of the fractional order controiler make possible a more adaptive response to disturbances and changes in the environment, allowing for a more precise tuning of the controller. The presence of the Time-Invariant Derivative (TID) component ensures that the controller will be always able to deal with the dynamic behaviour of the UAV, in environments where the conditions may change over time.

Phase 3: HAOAROA algorithm

The third phase of the methodology focuses on the HAOAROA Algorithm (Hybrid Archimedes Optimization Algorithm - Rider Optimization Algorithm), which is a hybrid optimization method that combines two powerful algorithms: Archimedes Optimization Algorithm (AOA) and Rider Optimization Algorithm (ROA), etc. HAOAAO is designed to improve the accuracy of the control points of the UAV’s trajectory, generating a globally optimized trajectory based on path length, smoothness and obstacle avoidance. In this phase, the previously optimized gradient-based B-spline trajectory (Phase 1) and controller based control system (Phase 2) are used^{47,48,49,50,51,52,53}.

The objective of this phase is to apply global optimization to the trajectory by refining the control points $\:Pi$, ensuring that the UAV’s trajectory is optimal in terms of:

• Minimizing path length,

• Maximizing trajectory smoothness,

• Ensuring obstacle avoidance.

HAOAROA improves the trajectory by first exploring potential solutions (via AOA) and then exploiting the most promising ones (via ROA)^{54,55,56,57,58,59,60,61,62,63,64,65,66}:

Initializing the control points and solution population is the first stage in HAOAROA. Potential solutions to the UAV’s trajectory optimization problem could be found in the control points $\:Pi$ in this scenario. The B-spline curve’s x, y, and z coordinates are represented by the control points $\:{P}_{i}=\left[\begin{array}{c}{P}_{ix}\\\:{P}_{iy}\\\:{P}_{iz}\end{array}\right]$.

A population of potential solutions is generated, where each solution corresponds to a set of control points. Let the population be denoted by $\:Pi\left(p\right)$, where $\:p$ refers to the population member and $\:i$ refers to the control point number. The total number of population members is $\:{N}_{pop}$​, and the total number of control points is $\:n$. Each person in the population is initially set as in Eq. (43)^{67,68,69,70,71,72,73}:

$$\:{P}_{i}\left(p\right)={P}_{i}^{\text{init}}+\epsilon$$

(43)

$$\:{P}_{i}\left(p\right)={P}_{i}\left(p\right)+{\lambda\:}_{p}\cdot\:{F}_{\text{buoyancy}}$$

(44)

Where:

$\:{P}_{i}^{\text{init}}$​ is the initial guess for the control points (from the gradient-based optimization in Phase 1), $\epsilon$ is a small random perturbation to ensure diversity in the initial population.

The HAOAROA exploration phase is handled by the Archimedes Optimization Algorithm (AOA). During this stage, AOA searches for a wide area of the control point space for areas that show promise and could result in the best paths as. An object’s buoyant force is proportional to the fluid displacement, according to the Archimedes principle of buoyancy, which forms the basis of the AOA. By modifying the control points in accordance with the displacement principle, this idea is used in the optimization context as in Eq. (44):

$$\:{F}_{\text{buoyancy}}=-\nabla\:J\left({P}_{i}\right(p\left)\right)$$

(45)

Where $\:Pi\left(p\right)$ is the position of the control point for the $\:p-th$ population member, and $\:\lambda\:p$ ​ is a scaling factor that controls the influence of the buoyant force on the position. The buoyant force, $\:{F}_{buoyancy}$​, simulates the displacement in the search space. This force is calculated based on the cost function evaluated for each population member. The cost function, as derived in Phase 1, consists of terms for trajectory length, smoothness, and obstacle avoidance as in Eq. (45):

$$\:J\left({P}_{i}\right(p\left)\right)={J}_{\text{length}}\left({P}_{i}\right(p\left)\right)+{J}_{\text{smoothness}}\left({P}_{i}\right(p\left)\right)+{J}_{\text{obstacle}}\left({P}_{i}\right(p\left)\right)$$

(46)

Where $\:J\left({P}_{i}\right(p\left)\right)$ is the cost function for the $\:p-th$ population member, and the gradient ∇$\:J\left({P}_{i}\right(p\left)\right)$ is the rate of change of the cost function with respect to the control points. The AOA pushes the solutions toward more advantageous areas of the search space by utilizing the buoyant force to modify the control points. Following that, the cost function is used to assess the revised control points as describes in Eq. (46):

$$\:J{P}_{i}\left(p\right)={P}_{i}\left(p\right)+{\gamma\:}_{p}\cdot\:({P}_{i,\text{leader}}-{P}_{i}(p\left)\right)$$

(47)

Better cost functional values are retained for the subsequent phase, and the updated population members are stored. After exploring all possible options, the most promising ones are exploited using the Rider Optimization Algorithm (ROA). With the aim of further minimizing the cost function, ROA is engineered to carry out a local search and refine the control points. ROA mimics the actions of elite riders during competition. The control points in this comparison. In an optimization process, the riders’ positions are represented by $\:Pi\left(p\right)$, and the goal is to position them as optimally as possible. The ROA update rule is provided by Eq. (47):

$$\:{P}_{i}\left(p\right)={P}_{i}\left(p\right)+{\gamma\:}_{p}\cdot\:({P}_{i,\text{leader}}-{P}_{i}(p\left)\right)-{\beta\:}_{p}\cdot\:\nabla\:J\left({P}_{i}\right(p\left)\right)$$

(48)

Wherein $\:\gamma\:P$ controls how closely the $\:P-th$ population member follows the leader, and $\:{P}_{leader}$ is the control point of the current best solution (the “leader” rider). The trajectory is refined in this step by shifting the control points in the direction of the AOA phase’s best-performing solution. Utilizing the promising fixes that AOA identified is the main goal of ROA. In order to further minimize the cost function, the algorithm adjusts the control points. Iteratively updating the control points in accordance with the “leader’s” performance and assessing the cost function following each update are the steps in the local refinement process as depicts in Eq. (48).

$$\:{P}_{i}(k+1)={P}_{i}\left(k\right)-{\alpha\:}_{1}\nabla\:{J}_{\text{AOA}}\left({P}_{i}\right(k\left)\right)-{\alpha\:}_{2}\nabla\:{J}_{\text{ROA}}\left({P}_{i}\right(k\left)\right)$$

(49)

where the gradient-based correction term’s learning rate is represented by $\:\beta\:p$. A final update rule for the control points is produced by combining the phases of exploitation (ROA) and exploration (AOA). The local refinement from ROA and the exploration phase from AOA are used to update the control points as shown in Eq. (49):

Where $\:{\alpha\:}_{1}$​ and $\:{\alpha\:}_{2}$​ are the learning rates for AOA and ROA, respectively, $\:\nabla\:{J}_{\text{AOA}}$​ is the gradient of the cost function from the AOA phase, and $\:\nabla\:{J}_{\text{ROA}}$​ is the gradient of the cost function from the ROA phase. Up until a certain number of iterations or a threshold for the cost function’s improvement (i.e., no more appreciable improvement) is reached, the HAOAROA algorithm iterates continuously. The final control points ($\:Pi$), indicate the UAV’s optimal trajectory once the algorithm has converged.

The following is our suggested algorithm’s pseudo code:

Algorithm 1: Hybrid Archimedes Optimization Algorithm - Rider Optimization Algorithm (HAOAROA) with FOPID-TID Controller

1. Inputs: Population size$\:\varvec{N}$, Maximum iterations$\:\left(\varvec{M}\varvec{a}\varvec{x}\varvec{I}\varvec{t}\varvec{e}\varvec{r}\right)$, Set the parameter bounds for FOPID-TID$\:\left(\varvec{K}\varvec{p},\:\varvec{K}\varvec{i},\:\varvec{K}\varvec{d},\:\varvec{\lambda\:},\:\varvec{\mu\:}\right)$ 2. Output: Best solution$\:{\varvec{P}}^{\varvec{*}}=({\varvec{K}}_{\varvec{p}}^{\varvec{*}},{\varvec{K}}_{\varvec{i}}^{\varvec{*}},{\varvec{K}}_{\varvec{d}}^{\varvec{*}},{\varvec{\lambda\:}}^{\varvec{*}},{\varvec{\mu\:}}^{\varvec{*}})$ 3. Initialize the population of control points$\:{\varvec{P}}_{\varvec{i}}\left(\varvec{p}\right),\:\mathbf{f}\mathbf{o}\mathbf{r}\:\varvec{X}\varvec{i}\:\left(\varvec{i}\:=\:1,\:2,\:\dots\:,\:\varvec{N}\right)$ 4. Initialize velocity$\:\varvec{v}\varvec{i}\left(\varvec{p}\right)$for each population member 5. Assign personal best$\:{\varvec{p}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}}$and global best$\:{\varvec{P}}_{\varvec{g}\varvec{l}\varvec{o}\varvec{b}\varvec{a}\varvec{l}}$ 6. Initialize FOPID-TID controller parameters for each particle$\:\left(\varvec{K}\varvec{p},\:\varvec{K}\varvec{i},\:\varvec{K}\varvec{d},\:\varvec{\lambda\:},\:\varvec{\mu\:}\right)$ 7. while (stopping criteria not met) do 8. Evaluate fitness of each population member using: a. Trajectory performance (length, smoothness, obstacle avoidance), b. FOPID-TID controller performance (tracking error, stability, overshoot). 9. Apply Archimedes Optimization Algorithm (AOA) for exploration: 10. For each particle$\:\varvec{p}$$\:\left(\mathbf{f}\mathbf{o}\mathbf{r}\:\varvec{p}\:=\:1,\:2,\:\dots\:,\:\varvec{N}\right)$ 11. If Perform buoyancy-based exploration: 12.$\:{\varvec{P}}_{\varvec{i}}^{\left(\varvec{p}\right)}\left(\varvec{t}+1\right)={\varvec{P}}_{\varvec{i}}^{\left(\varvec{p}\right)}\left(\varvec{t}\right)+{\varvec{\lambda\:}}_{\varvec{p}}\cdot\:{\varvec{F}}_{\text{buoyancy}}$ 13.$\:{\varvec{F}}_{\text{buoyancy}}=-\nabla\:\varvec{J}\left({\varvec{P}}_{\varvec{i}}^{\left(\varvec{p}\right)}\right)$(gradient of cost function) Update FOPID-TID parameters using exploration: $\:\varvec{u}(\varvec{t}+1)={\varvec{K}}_{\varvec{p}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\varvec{e}(\varvec{t}+1)+{\varvec{K}}_{\varvec{i}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\int\:\varvec{e}(\varvec{t}+1)\text{\hspace{0.17em}}\varvec{d}\varvec{t}+{\varvec{K}}_{\varvec{d}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\frac{\varvec{d}}{\varvec{d}\varvec{t}}\varvec{e}(\varvec{t}+1)+\varvec{\lambda\:}\left(\varvec{p}\right)(\varvec{t}+1)+\varvec{\mu\:}\left(\varvec{p}\right)(\varvec{t}+1)$ 14. else 15. Apply Rider Optimization Algorithm (ROA) for exploitation: 16. For each particle$\:\varvec{p}$: Update position of the control points based on the best (leader) solution: 17.$\:{\varvec{P}}_{\varvec{i}}\left(\varvec{p}\right)(\varvec{t}+1)={\varvec{P}}_{\varvec{i}}\left(\varvec{p}\right)\left(\varvec{t}\right)+{\varvec{\gamma\:}}_{\varvec{p}}\cdot\:\left({\varvec{P}}_{\varvec{i}}^{\varvec{l}\varvec{e}\varvec{a}\varvec{d}\varvec{e}\varvec{r}}\right(\varvec{t})-{\varvec{P}}_{\varvec{i}}(\varvec{p}\left)\right(\varvec{t}\left)\right)$ 18. Update FOPID-TID parameters by exploiting the best leader $\:\varvec{u}(\varvec{t}+1)={\varvec{K}}_{\varvec{p}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\varvec{e}(\varvec{t}+1)+{\varvec{K}}_{\varvec{i}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\int\:\varvec{e}(\varvec{t}+1)\text{\hspace{0.17em}}\varvec{d}\varvec{t}+{\varvec{K}}_{\varvec{d}}\left(\varvec{p}\right)(\varvec{t}+1)\cdot\:\frac{\varvec{d}}{\varvec{d}\varvec{t}}\varvec{e}(\varvec{t}+1)+\varvec{\lambda\:}\left(\varvec{p}\right)(\varvec{t}+1)+\varvec{\mu\:}\left(\varvec{p}\right)(\varvec{t}+1)$ 19. Evaluate fitness of new control points$\:{\varvec{P}}_{\varvec{i}}\left(\varvec{p}\right)\left(\varvec{t}+1\right)$and FOPID-TID parameters 20. Update$\:{\varvec{p}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}\left[\varvec{p}\right]}$and$\:{\varvec{P}}_{\varvec{g}\varvec{l}\varvec{o}\varvec{b}\varvec{a}\varvec{l}}$if necessary 21. Update control parameters for AOA and ROA 22. end while 23. Return best solution$\:{\varvec{P}}^{\varvec{*}}={\varvec{P}}_{\text{global}}({\varvec{K}}_{\varvec{p}}^{\varvec{*}},{\varvec{K}}_{\varvec{i}}^{\varvec{*}},{\varvec{K}}_{\varvec{d}}^{\varvec{*}},{\varvec{\lambda\:}}^{\varvec{*}},{\varvec{\mu\:}}^{\varvec{*}})$

Benchmark functions

The performance of the proposed HWOAGWO algorithm was assessed using nine benchmark functions, as detailed in the table and implemented in the UAV system. These functions provide diverse optimization challenges to evaluate the algorithm’s capabilities comprehensively. The Sphere function, a simple unimodal and convex function, tests the algorithm’s ability to converge to the global minimum in a smooth search space. The Rosenbrock function, known as the Banana function, features a narrow, curved valley that challenges the algorithm to follow a complex trajectory precisely. The Rastrigin function, with its multi-modal nature and numerous local minima, assesses the algorithm’s exploration capabilities and its effectiveness in avoiding local traps. The Griewank function introduces periodic oscillations and a global minimum at the center, testing the algorithm’s precision in navigating local minima. The Ackley function, characterized by flat outer regions and a steep global minimum, evaluates the algorithm’s balance between exploration and exploitation. Additional functions such as the Michalewicz, Himmelblau, Booth, and Beale functions provide further tests of convergence, multi-modality, and path-following precision. These benchmark functions are detailed in Table 1, highlighting their dimensionality, number of search agents, and search ranges. This comprehensive evaluation ensures the HWOAGWO algorithm’s robustness, accuracy, and efficiency in solving both simple and complex optimization problems.

Table 1 Our proposed method benchmark functions.

Results and discussion

Trajectory optimization for UAV path planning is analyzed in this section with controllers in terms of the performance of several different trajectory optimization algorithms. Benchmark functions, the proposed FOPID-TID based HAOAROA method, A*, Bezier, JPS, L-BSGF algorithms were compared. The figures show the performance of these algorithms when handling complexities within sophisticated obstacle environments and optimizing UAV trajectories.

HAOAROA algorithm for UAV Trajectory optimization

In this section, we present the trajectory optimization of UAV using A*, JPS, Bezier, L-BSGF and the proposed FOPID-TID based HAOAROA algorithm. The figures show the comparative performance of these algorithms based on their smoothness and efficiency. Figure 5 presents the findings in multiple sections: Experiment 1 (L-shape Obstacle), Part (A) Trajectory Comparison, Experiment 2 (H-shape Obstacle), Part (B) Trajectory Comparison, 3D Visualization of HAOAROA’s Superior Trajectories in Special Environment, Experiment 1 and Experiment 2, Part (D) Trajectory Length Comparison. Benchmark Functions for HAOAROA Algorithm part (E). In Part (F) Benchmark Functions with FOPID-TID Controller Based HAOAROA Optimized Solutions. The FOPID-TID based HAOAROA algorithm proposed in this work can optimally combine precision, stability, and computational efficiency when optimizing UAV trajectory. The algorithm combines fractional order control with advanced hybrid optimization techniques to exert thorough exploration of the solution space and directing towards optimal parameters. Based on dynamic inertia weight adjustments, cognitive and social learning and the Rider Optimization Algorithm (ROA) to balance exploration and exploitation, it can avoid local minimum and converge on global optima. The resultant UAV flight paths are smooth, stable, and efficient, and therefore the algorithm is particularly well suited for real world UAV applications with emphasis on adaptability and precise control.

This study employs the FOPID-TID based HAOAROA algorithm using 20 candidate solutions per iteration so an exhaustive search polynomial space can still be achieved while keeping a manageable computational load. At this point, we design the algorithm to iterate 100 times, favoring an exploration of the search space and as it nears an optimal set of parameters. This iteration provides the control system with the best obtainable trajectory planning by constraining the stability of the system while maximizing the performance. Dynamic adjustment of the inertia weight is one of the relatively key features of the algorithm, where the initial value is 0.8 and gradually reduces to 0.4. The initial high inertia leads to broad exploration of potential solutions during the initial stages of the search, i.e. when building on a solution is not easier. Second, the particles tend to become more focused on putting more effort into finding a better place in the search space as its progress continue and the inertia decreases. With this gradual reduction on inertia weight, a smooth transition from exploration to exploitation is provided as search by the algorithm proceeds, until finally home in on the optimum parameters. The algorithm, in addition to inertia weight control uses cognitive (c1) and social (c2) penalties coefficients set at 2.0 and 1.5, respectively. Such a cognitive coefficient allows the particles to learn from their own experiences, and thus gives particles the additional ability to exploit promising areas in the search space. On the other hand, the social coefficient in the swarm allows that particles benefit of the collective knowledge of the swarm and each one shares with the other of the best solutions being found by any other particle in the swarm. The balance between individual learning and collective intelligence improves the convergence speed and avoidance of local minimum of the algorithm, as well as versality of this method of solving such problems as searching in space for optimal trajectories.

Part (A) represents the results of Experiment 1 by comparing several trajectory planning algorithms as they navigate an L-shaped obstacle. A*, JPS, Bezier, L-BSGF and the proposed HAOAROA algorithm are tested. All algorithms successfully generate paths, which avoid obstacles, but the trajectory has characteristic differences. The A* and JPS algorithms, which directly solve the pathfinding problem, yield efficient paths (in length) but are not smooth enough for use in real world UAV navigation. At the other end of the spectrum, smoother paths crowd out, a little bit longer but much more continuous trajectories are generated by Bezier and L-BSGF. The proposed HAOAROA algorithm offers a clear advantage by balancing these two aspects: It produces an efficient (small) length path, but a smooth (curvature) one. The HAOAROA trajectory is therefore a better fit to the platform of UAVs, for which maintaining smooth flight is necessary to achieve stability and control. The ability of HAOAROA to optimize the path length and smoothness for safer and more reliable navigation was demonstrated by its superior performance in this experiment. Part (B) continues with Experiment 2, when the same set of algorithms is tested against a more complex H shaped obstacle configuration, although the solution space is not restricted, and conflict detection does not have to respect geometrical constraints. The increased difficulty to navigate through the environment is reflected by the more pronounced deviations of the trajectory among the algorithms compared to predicted. We show that A* and JPS still produce direct paths, but they follow trajectories that experience sharp turns at critical points of the obstacle that could produce instability during flight. However, the HAOAROA algorithm generates a smoother path with less deviations in the vicinity of obstacle closest to the UAV’s trajectory. This is important because smooth trajectories help control dynamics of the UAV and lower the risk of collisions. HAOAROA provides a path which is nearly as direct as produced by A* and JPS, but with a more continuous curve to show superior performance for handling complex environments. The algorithm can optimize trajectories in environments with highly obstacle spaces (the H-shape) which indicates that it is a powerful tool for utilizing UAV in the realistic environment.

In addition, Part (C) extends the analysis to incorporate the performance of HAOAROA in a series of more complicated 3D environments such as L shaped, H shaped, U shaped, and Omega shaped obstacles. The HAOAROA trajectories are shown in the 3D plots, and we demonstrate the algorithm’s robustness and adaptability to different types of obstacle configurations. Optimized UAV paths are shown by the green trajectories, whilst the red markers are designated for points where the UAV is close to an obstacle. We show that the HAOAROA algorithm can generate a smooth trajectory in each environment that consequently minimizes risk by passing away from the obstacles, while keeping this path reasonable length. Efficient maps provide UAVs with this crucial ability to navigate 3D space efficiently at the micro level, so that they can operate in challenging environments such as urban areas or disaster zones where obstacles can occur anyplace. The results show that HAOAROA solves efficiently and reliably a task with various types of obstacles, allowing the UAV to safely and smoothly reach its destination. The adaptability highlights the strength of HAOAROA in tackling emerging real world UAV navigation problems with the need for 3D obstacle avoidance. Nevertheless, Part (D) performs a quantitative comparison of the two experiments in terms of trajectory lengths, further insights into the advantages and disadvantages of the different algorithms. As can be seen in this section, path length is highlighted via the bar plot, A* usually produces the shortest path due to its direct nature. The HAOAROA algorithm producing paths that are almost as short as those of A*, but at the cost of having greater smoothness and stability. On the other hand, Bezier and L-BSGF algorithms, that put the smoothness priority forward, generates slightly longer paths. This comparison emphasizes the key strength of HAOAROA: within and between its ability to balance the competing objectives of path length minimization and trajectory smoothness. Both experiments demonstrate that HAOAROA can generate paths that are both efficient in length as well as optimized for useable applications requiring smooth and stable flight paths. HAOAROA produces shorter, more efficiently optimized trajectories enabling UAVs to maneuver in complex environments, which further supports that HAOAROA is a better algorithm for UAV trajectory planning. In addition, Part (E) illustrates how five benchmarks were visualized, with each of Sphere, Rastrigin, Rosenbrock, Ackley, and Griewank as a test of optimization performance of the HAOAROA algorithm. The functions are of varying complexity in terms of their topography, ranging from relatively simple and unimodal, such as the Sphere, to more challenging with large number of local minima such as the Rastrigin and Griewank. We start with the test which is Sphere function, smooth and convex nature, and its minimum is at the origin, facilitating fast convergence to global minimum by HAOAROA algorithm. On the other hand, the Rastrigin function displays a periodic ripple structure to test a higher dimension search algorithm’s ability to escape from local minima and arrive at the global optimum. The Rosenbrock function embeds a curved valley that places rigorous challenges on the algorithm ordering narrow, elongated regions to follow the optimal path. Because the Ackley function has a relatively flat outer region and complex central minima, the global search capabilities of the algorithm are used to overcome flat regions and identify their central global minimum. The last problem I considered is the Griewank function, which is a landscape that has many minimal local and with smooth peaks that causes the algorithm to avoid being trapped in suboptimal points. The figure shows that these benchmark functions provide a wide range of challenges that our HAOAROA must learn to handle varying types of optimization landscapes. Finally, Part (F) shows the same benchmark functions but with those solutions which were optimized by the HAOAROA algorithm and is using the FOPID-TID controller. Red circles mark the optimized points, which clearly locate the related global minima achieved by the algorithm. In the simple landscape the red marker’s location at the origin confirms the algorithm’s ability to quickly detect the global minimum quickly. Similarly, HAOAROA is successful in locating the global minimum in the simple Rastrigin function whose function has many local minima, yet very complicated to locate the global minimum. The red circle is placed at the correct global minimum for the Rosenbrock function, a function with a narrow low one and each point in the path should be optimized by the algorithm to find the optimum solution. The optimized solution is found in a central region of the Ackley function, providing more evidence on HAOAROA’s capacity of dealing with flat regions and fast convergence to optimal. In the end, the algorithm also avoids the scattered local minima in the search space portrayed by the red circle around the global minimum of the Griewank function. The addition of the FOPID-TID controller yields higher robustness and precision in the HAOAROA algorithm that can simultaneously find optimal solutions across the various, challenging benchmark functions.

Fig. 5

HAOAROA Algorithm with FOPID-TID Controller and Its Comparative Analysis with Trajectory Optimization and Benchmark Functions in the UAV System.

Finally, the results show that in every respect, the application of the HAOAROA algorithm leads to an optimized FOPID-TID controller that outperforms the comparative path planning algorithms such as A*, JPS, Bezier, and L-BSGF in terms of trajectory length, smoothness and overall stability. Specifically in environments with complex obstacles, achieving smoother and more efficient trajectories is a challenge with the proposed method. Through integration of the hybrid optimization of HAOAROA, the FOPID-TID controller performs better across all metrics evaluated, including shorter path lengths, and better, more stable, continuous flight paths. In addition to this overall control precision, this optimization guarantees that the UAV has smooth transitions and stability, especially in in challenging scenarios where conventional algorithms cannot balance path efficiency with smoothness.

Table 2 Comparison of UAV trajectory planning algorithms with FOPID-TID based HAOAROA.

The FOPID-TID based HAOAROA algorithm performs better than other trajectory planning algorithms including A*, JPS, Bezier and L-BSGF as shown in Table 2. In terms of UAV control, efficiency and flight stability, the advantages of the proposed method are summarized by numerical values for trajectory length, smoothness, and computation time.

Of all the algorithms tested, the HAOAROA based with FOPID-TID has the smallest trajectory length of 20.3 m. The result of this value is lower than A* (20.5 m), JPS (20.8 m), Bezier (21.7 m), and L-BSGF (21.4 m). By reducing the number of legs, we show that the proposed algorithm routes the UAV on more direct and efficient paths while maintaining the required smoothness for real-time navigation. Compared to A*, JPS, which have low smoothness, and Bezier and L-BSGF, whose trajectory smoothness is usually preferred without sacrificing cost, the FOPID-TID based HAOAROA has a very high smoothness. Such superior smoothness ensures that the UAV maintains continuous, stable flight which is key to real world scenarios when sharp turns or abrupt path changes could lead to instability.

The computation time of FOPID-TID based HAOAROA is moderate in terms of comparison with the other two algorithms that are moderate, Bezier and L-BSGF, and the FOPID-TID approach also performs the best in terms of trajectory smoothness and quality compared to the faster algorithms A* and JPS. At the same time, the proposed algorithm finds a good tradeoff between trajectory efficiency, smoothness and computational costs, to be both useful and practical for real time UAV path planning.

Overall, the HAOAROA algorithm using FOPID-TID outperforms all other methods tested in this study combining the biggest trajectory length, smoothness and computational speed. By fine tuning control parameters such as , , , and to optimal UAV performance, its creation ensures UAV performance under dynamic and complex environments. The results show that the proposed method is the most effective and secure method for UAV trajectory planning with superior stability and less oscillating, which is to be used in real world scenarios. The radar diagram of the proposed method shown in Fig. 6.

Fig. 6

Criteria by proposed method works.

Analysis of the UAV trajectory planning from the radar diagram indicates the superior performance of FOPID-TID based HAOAROA algorithm (Proposed) in comparison to traditional control methods. By choosing the proportional gain ($\:Kp$) to be 1.3254, which is less than in base methods, the system is less aggressive in its control action. This reduction in $\:Kp$ results in a 10% improvement over standard approaches for a stable system that is more sensitive in pitch control. When $\:Kp$ is lower, the risk of overshooting is reduced, and the transitions are smoother, which is favored for real time UAV applications executing in precision. The integral gain, Ki = 0.4627, exhibits performance improvement of approximately 8% over other methods. The system’s ability to remove steady state errors more effectively is highlighted as an improvement with this, which is important for long term roll stability. With a relatively high Ki, the system is stable even if such continuous corrections are needed, eliminating unnecessary oscillations but with a high error correction rate. The system has a derivative gain $\:Kd$ of 0.1892 which is the derivative gain necessary to maintain control stability and reduce oscillation. Through this proposed algorithm, $\:Kd$ can be improved by approximately 12% over past methods, and this improves the system’s sensitivity to sudden change in error. Using this reduction in Kd has a significant effect on yaw movement control and results in more consistent flight responses. Furthermore, the proposed method involves fractional order parameters λ (0.3127) and µ (0.3419) that more contribute to system robustness. Base methods are enhanced by 9% compared to µ, and by approximately 13% compared to λ. With better disturbance and dynamic pitch and yaw control handling achieved, these larger values of λ and µ are used. The increased fractional parameters show the capability of the proposed method to control the errors and adapt to change in the system environment, leading to improved UAV dynamics control where the dynamics are complex and un-predictable.

Results on Benchmark functions

The population size is chosen to be 20, and the maximum number of iterations was set to 1000 to allow each algorithm to run the nine benchmark functions for 20 runs (to attain statistical reliability). The results for all methods are presented in Table 3, including the best, worst, average, median, and standard deviation (STD) of each algorithm over the benchmark functions. The results shown in Table 3 clearly demonstrate that the proposed HAOAROA method consistently outperforms both AOA and ROA across all nine benchmark functions. Specifically, HAOAROA achieved an optimal value of zero for all functions, showcasing its ability to identify the global minimum effectively. In contrast, AOA and ROA recorded non-zero best values, indicating their inability to reach the optimal solution as effectively as HAOAROA. For instance, the best value for the Sphere function ($\:{f}_{1}$) achieved by AOA was 1.23E-10, while ROA’s best value was 2.35E-09, highlighting the substantial gap in performance when determining the optimal values. Additionally, similar results were observed in other benchmark functions, such as $\:{f}_{2}$ (Rosenbrock’s Function) where the best values for AOA and ROA were 2.57E-11 and 4.68E-10, respectively, which are significantly higher than the optimal value of zero achieved by HAOAROA. There is a notable discrepancy in the results obtained by AOA and HAOAROA when assessing the optimal value for multi-modal functions like $\:{f}_{6}$ (The Sixth Function) and $\:{f}_{7}$ (The Seventh Function). HAOAROA not only excels in obtaining the best values but also shows superior performance in terms of average, median, and standard deviation, indicating its robustness across different optimization scenarios. For example, the best value achieved by HAOAROA for $\:{f}_{6}$ was 0, while AOA’s best value was 1.23E-08, and ROA’s best value was 2.35E-07, further illustrating HAOAROA’s advantage. The performance of HAOAROA in solving both single-modal and multi-modal functions highlights its capacity to efficiently explore both known and unexplored regions of the search space, leading to high-quality solutions.

Table 3 Results of HAOAROA compared to AOA and ROA on benchmark functions.

Conclusion

This study introduces the FOPID-TID-based HAOAROA algorithm, which significantly advances UAV trajectory optimization and control by using a hybrid optimization technique to dynamically tune FOPID controller parameters, resulting in improved stability, fast responsiveness, and smooth control. The results demonstrate that this method outperforms standard trajectory planning techniques like A*, JPS, Bezier, and L-BSGF, particularly in minimizing trajectory length, enhancing trajectory smoothness, and ensuring overall flight stability. However, there are two key drawbacks that need to be addressed. First, the FOPID-TID-based HAOAROA algorithm, while delivering superior performance, is computationally expensive, which may limit its applicability in real-time or fast-response environments. Second, the proposed method, although successful in simulations, has not yet been generalized to dynamic, nonlinear, and uncertain real-world environments, thus requiring further validation in such conditions to ensure its robustness. To address these limitations, the following directions for future work are proposed:

• Focus on optimizing the HAOAROA algorithm to decrease its computational cost, making it more suitable for real-time applications and environments that require quick response times.

• Test the algorithm under more complex and unpredictable flight conditions to assess its adaptability and robustness in real-world dynamic, nonlinear, and uncertain environments.

• Investigate the scalability and effectiveness of the FOPID-TID-based HAOAROA algorithm in multi-UAV systems to evaluate its performance in coordinated operations across multiple agents.

• Explore the integration of machine learning techniques to develop adaptive control mechanisms, allowing the UAV to adjust its flight behaviour based on real-time data and changing flight conditions.

• Validate the algorithm with physical UAVs to assess its practical implementation and compare theoretical results with real-world performance, ensuring the method’s practicality and robustness.

• Compare the FOPID-TID-based HAOAROA algorithm with other leading optimization methods to confirm its superiority and identify potential areas for further enhancement.