A method of coating life prediction based on high temperature thermal shock life test and three-dimensional heat transfer analysis

Abstract

In this study, a method for predicting the thermal shock life of coatings is proposed, and a model for predicting the thermal shock life of coatings based on high temperature thermal shock life test and three-dimensional heat transfer analysis is established. Firstly, the thermal shock life of coatings at different cooling and heating cycle temperatures is obtained through a designed thermal shock life testing device for silicide coatings at a wide-temperature range from 500℃ to 3000℃. Secondly, the actual thickness of the coating and the continuous oxidation in the thermal shock life test are taken into consideration. Based on the finite element analysis method, the three-dimensional heat transfer analysis for coatings with different oxidation thickness is carried out to obtain the average value of the maximum thermal stress range on the surface of the coating. Last, the least square method is used to process the data of the life prediction model. Then the parameters of the life prediction model are obtained based on the thermal shock life test of the coating and the average value of the maximum thermal stress range on the coating surface. It turns out that the predicted results of the thermal shock life prediction model established in this study are in good agreement with the tested results. Besides, the relative error is less than 6%. Therefore, the life prediction method proposed in this study can be used to predict the thermal shock life of silicide coatings. What’s more, the research work in this study can also provide a theoretical basis for the life prediction of coating materials.

Introduction

As coatings have been widely used in aerospace high temperature protection, life prediction remains a major topic in the research on coatings. The mathematical function relationship or life prediction model established by mathematical and physical methods and experimental means is of great significance to the process manufacturing and the design of structural material system of coatings. Previous studies have shown that the failure of coatings is the result of the combined action between oxidation and thermal cycling load at high temperature. Oxidation plays a key role in the failure of coatings which includes spalling and cracking.

The life prediction model based on interfacial oxidation was first proposed by Miller^1,2,3,4,5. Over the next decade, relevant institutions and scholars in various countries have made continuous revision and optimization of Miller’s model. Therefore, life prediction models based on various factors such as weight^6,7, thickness^8,9, creep and time¹⁰have been proposed in large quantities. However, these models are not in favor of actual production because they are complex to measure the process parameters. Nissley summarized these life prediction models in detail, which laid a foundation for the development of the coating life prediction model¹¹. The damage accumulation model based on specific parameters is established from the viewpoint of fracture mechanics and damage mechanics^12,13. During the service of the coating, when the value of damage parameter accumulates to a certain extent, the failure of the coating can be defined. The damage parameters can be defined as residual stress¹⁴, numbers of thermal cycling¹⁵, crack length¹⁶, damage area¹⁷and so on. In addition, life prediction models based on fluorescence^18,19, acoustic emission²⁰, fracture mechanics^{21,22,23,24,25}, energy release rate^16,26and effective thickness²⁷ of coatings have also been proposed by relevant scholars.

However, traditional methods for predicting material lifespan often involve complex operational procedures and require high measurement accuracy when assessing process parameters, making accurate lifespan prediction challenging. Additionally, lifespan prediction based on characterization methods often necessitates interrupting the test, introducing factors such as equipment aging and human errors that reduce reliability. Consequently, these challenges hinder precise lifespan predictions. In view of the limitations of existing lifespan prediction methods in the context of oxidation-resistant coatings, there is an urgent scientific need to develop a method suitable for predicting the lifespan of these coatings without interrupting the testing process or introducing operational complexities. In this study, firstly, the thermal shock life of coatings at different cooling and heating cycle temperatures is obtained through a designed thermal shock life testing device for silicide coatings at a wide-temperature range from 500℃ to 3000℃. Secondly, the actual thickness of the coating and the continuous oxidation in the thermal shock life test are taken into consideration. The three-dimensional heat transfer analysis for coatings with different oxidation thickness is carried out to obtain the average value of the maximum thermal stress range on the surface of the coating. Last, according to the results of thermal shock life test and three-dimensional heat transfer analysis, the prediction method of thermal shock life of coating materials is proposed. Then, the prediction model of coating life based on high temperature thermal shock life test and three-dimensional heat transfer analysis is established.

Modeling and theoretical analysis

Thermal shock life test device

Based on the heat transfer principle and ultra-high temperature fast direct electric heating method, the thermal shock life testing device for coatings is developed, which can realize the thermal shock life test of coatings at a wide-temperature range from 500℃ to 3000℃. The schematic diagram of the device is shown in Fig. 1. The device mainly consists of the test bench, the thermal shock life test system, the optical fiber pyrometer, the high-speed industrial CCD camera and the control system. The thermal shock life test system is placed on the test bench. The high-speed industrial CCD camera and optical fiber pyrometer are used to conduct real-time observation and temperature measurement on the specimen through the semi-transparent mirror (45° from the horizontal plane).

Fig. 1

Schematic Diagram of the Device.

The thermal shock life test system is placed horizontally on the test bench. In this system, the direct electric heating method is adopted. The specimen is used as a heating body through the utilization of its conductivity, and hollow brass electrodes are used on both ends of the specimen for clamping and conductive heating. The device adjusts the output of the power supply to make the specimen reach the target temperature within the set time. The device can also set the holding time and cooling time of the test. The brass electrodes are protected by water cooling system. Graphite felt is used as thermal insulation material to resist damage to the equipment and operators caused by high temperature thermal radiation of the specimen, and to reduce heat loss of the heating system at the same time. The thermal shock life test bench is shown in Fig. 2. The thermal shock life test procedure is shown in Fig. 3.

Fig. 2

Thermal shock life test bench.

Fig. 3

Thermal Shock Life Test Procedure.

Three-dimensional heat transfer modeling

In this study, the finite element model of the coating is established based on the direct electric heating method. The model is based on the following two assumptions. One is the good bonding between different materials. The other one is that the thermophysical and mechanical properties of the material are not dependent on temperature and the material is isotropic. Certainly, the above assumptions may lead to discrepancies between the predicted and actual behavior, which is also the reason for the error between the subsequent prediction results and the experimental data. We will conduct further research to address these issues in the future.

(1) Three-dimensions heat transfer modeling for resistance heating.

The three-dimensional heat conduction of resistance heating in the structure of anti-oxidation coating is studied by using the micro-element method. The surface area of any element inside the sample is $S_{{\text{d}}}$, the volume is $V_{1}$, and the total energy change in the volume $V_{1}$ is considered to be provided by the heat generated by the resistance heating:

$${\mathbf{J}}_{{1}} = \frac{{{\mathbf{E}}_{{\text{d}}} }}{{\rho_{{\text{e}}} }}$$

(1)

where ${\mathbf{J}}_{{\mathbf{1}}}$ is current density vector (A/m²), ${\mathbf{E}}_{{\mathbf{d}}}$ is the electric field intensity vector (V/m), and $\rho_{e}$ is resistivity (Ω·m).

The heat passing through the specimen is finally transformed into internal energy, and the heating power per unit volume $q_{{{\text{V}}_{{1}} }}$ produced by the energized electricity:

$$q_{{{\text{V}}_{{1}} }} = \rho_{{\text{e}}} {\mathbf{J}}_{{\text{d}}}^{{2}}$$

(2)

where ${\mathbf{J}}_{{\text{d}}}$ is resistance heating current density vector (Ω·m).

Resistance heating produces thermal power $Q_{1}$ in a volume:

$$Q_{1} = \int\limits_{{{\text{V}}_{1} }} {q_{{{\text{V}}_{1} }} dV}$$

(3)

The power $q_{{{\text{V}}_{{2}} }}$ of heat conduction per unit volume can be obtained from the following equation:

$$q_{{{\text{V}}_{{2}} }} = - \lambda \nabla T$$

(4)

where $\lambda$ is thermal conductivity (W/(m·K)), and $T$ is temperature field distribution function.

Therefore, the power $S_{{\text{d}}}$ of heat conduction through the closed surface $Q_{2}$ is given by the following equation:

$$Q_{2} = \oint_{{{\text{s}}_{{\text{d}}} }} { - \lambda \nabla Tds}$$

(5)

Since the temperature is unstable at all points inside the specimen, the change in internal energy per unit volume is $\frac{\partial }{\partial t}\left( {\rho cT} \right)$, and the change in internal energy per volume is:

$$Q_{3} = \int\limits_{{{\text{V}}_{1} }} {\frac{\partial }{\partial t}} \left( {\rho cT} \right)dV$$

(6)

where ρ is material (kg/m³), and c is specific heat of material (J/(kg·K)).

Based on the law of energy conservation and the divergence theorem, the governing differential equation for the three-dimensional heat conduction temperature field of resistive heating in the oxidation-resistant coating is:

$$\begin{gathered} \rho \left( {x,y,z} \right) \cdot c_{{\text{p}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial t} - \left\{ {\frac{\partial }{\partial x}\left[ {\lambda_{{\text{x}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial x}} \right] + } \right. \hfill \\ \frac{\partial }{\partial y}\left[ {\lambda_{{\text{y}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right] + \left. {\frac{\partial }{\partial z}\left[ {\lambda_{{\text{z}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial z}} \right]} \right\} \hfill \\ - q_{{{\text{v}}_{{1}} }} \left( {x,y,z,t} \right) = 0 \hfill \\ \end{gathered}$$

(7)

where $\rho (x,y,z)$ is density of the material (kg/m3), $c_{{\text{p}}} \left( {x,y,z} \right)$ is specific heat capacity of the material (J/(kg·K)), and $\lambda_{{\text{d}}} \left( {x,y,z} \right)$ is thermal conductivity of the material (W/(m·K)).

(2) Geometric model and mesh generation.

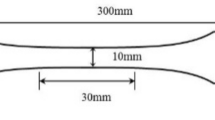
In this study, the silicide coating on the surface of the niobium hafnium alloy is taken as the research area. The physical model schematic diagram is shown in Fig. 4(a). Before oxidation, the coating is a double-layer structure. The matrix is the niobium hafnium alloy composite. After oxidation, SiO₂ is formed on the surface of the coating. The matrix is the niobium hafnium alloy composite, the middle layer is NbSi₂, and the outer layer is SiO₂. The brass electrodes are used to clamp the specimen on both ends. The dimensional parameters of the geometric model are shown in Table 1. The parameters for the coating, substrate, and oxidation layer were selected based on the typical dimensions and conditions observed in aerospace applications, ensuring the model’s relevance to real-world scenarios. The electrification voltage is set at 1.7 V and the grid divisions are set to refine.

Fig. 4

Three-dimensional Heat Transfer Physical Model of Coatings, (a) is physical Model, (b) is mesh structure and (c) is calculation results.

Table 1 The Dimensional Parameters of the Geometric Model.

The three-dimensional model is established directly in COMSOL finite element software. All the finite element meshes are refined four-node tetrahedral, and the Refine function in the software can be used to realize the dense transition of the meshes. The finite element mesh structure is shown in Fig. 4(b). There are 84,085 degrees of freedom in total, including 25, 428 internal degrees of freedom. The calculation results are shown in Fig. 4(c) and the material parameters are shown in Table 2.

Table 2 Material Parameter Table.

(3) Initial and boundary conditions.

Brass electrodes are used to clamp the specimen on both of its ends. At the initial time of 0 s, the initial temperature of the specimen is shown as follow:

$$\left. {T\left( {x,y,z,t} \right)} \right|_{{\text{t = 0}}} = T\left( {x,y,z,0} \right) = T_{{{\text{RT}}}}$$

(8)

where $T_{{{\text{RT}}}}$ is environmental temperature, here we took 20℃.

The diffuse reflection radiation heat transfer is set on the coating surface. The heat transfer mode is surface-to-surface radiation, and the air convection heat dissipation is set. The boundary conditions are presented as follows:

$$\begin{gathered} \left. { - \lambda_{{\text{x}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial x}} \right|_{x = 0} = q_{{{\text{V}}_{{1}} }} \left( {0,y,z,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {0,y,z,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{{4}} - T\left( {0,y,z,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(9a)

$$\begin{gathered} \left. { - \lambda_{{\text{x}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right|_{{\text{x = X}}} = q_{{{\text{V}}_{{1}} }} \left( {X,y,z,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {X,y,z,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{{4}} - T\left( {X,y,z,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(10b)

$$\begin{gathered} \left. { - \lambda_{{\text{y}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right|_{{\text{y = 0}}} = q_{{{\text{v}}_{{1}} }} \left( {x,0,z,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {x,0,z,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{4} - T\left( {x,0,z,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(11c)

$$\begin{gathered} \left. { - \lambda_{{\text{y}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right|_{{\text{y = Y}}} = q_{{{\text{v}}_{{1}} }} \left( {x,Y,z,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {x,Y,z,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{4} - T\left( {x,Y,z,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(12d)

$$\begin{gathered} \left. { - \lambda_{{\text{z}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right|_{{\text{z = 0}}} = q_{{{\text{v}}_{{1}} }} \left( {x,y,0,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {x,y,0,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{{4}} - T\left( {x,y,0,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(13e)

$$\begin{gathered} \left. { - \lambda_{{\text{z}}} \left( {x,y,z} \right)\frac{{\partial T\left( {x,y,z,t} \right)}}{\partial y}} \right|_{{\text{z = Z}}} = q_{{{\text{v}}_{{1}} }} \left( {x,y,Z,t} \right) + h_{{\text{f}}} \left[ {T_{{{\text{RT}}}} - T\left( {x,y,Z,t} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \sigma \left[ {T_{{{\text{RT}}}}^{4} - T\left( {x,y,Z,t} \right)^{4} } \right] \hfill \\ \end{gathered}$$

(14f)

where $h_{{\text{f}}}$ is convective heat transfer coefficient of the specimen surface, which is 10W/(m²·K), $\varepsilon$ is specimen surface emissivity, and $\sigma$ is Stefan-Boltzmann constant, which is 5.6694 × 10^–8(W/(m²·K⁴)).

(4) Thickness relationship of the coating before and after oxidation.

The coating material is NbSi₂. The oxidation product material is SiO₂. The surface area of the specimen is S. The thickness of the coating is $H_{{NbSi}_{2}}$ , density is $\rho_{{NbSi}_{2}}$ , and molar mass is $M_{{NbSi}_{2}}$ .The thickness of the oxidation product is $H_{{Sio}_{2}}$ , density is $\rho_{{Sio}_{2}}$ , and molar mass is $M_{{Sio}_{2}}$ . Therefore, the thickness conversion relationship of the oxide formed by the oxidation reaction of the coating is as follow:

$$d_{{{\text{zh}}}} { = }\frac{{H_{{{\text{SiO}}_{{2}} }} }}{{H_{{{\text{NbSi}}_{{2}} }} }}{ = }\frac{{2 \times \rho_{{{\text{NbSi}}_{{2}} }} }}{{M_{{{\text{NbSi}}_{{2}} }} }} \times \frac{{M_{{{\text{SiO}}_{2} }} }}{{\rho_{{{\text{SiO}}_{{2}} }} }}$$

(15)

The density of the coating is 5704 g/cm³ and the molar mass is 93 + 28 × 2 = 149 g/mol. The density of the oxidation product is 2200 g/cm³ and its molar mass is 28 + 16 × 2 = 60 g/mol. Therefore, according to formula (1), $d_{zh}\cong 2.1$.

(5) Flowchart of three-dimensional model simulation.

Based on the above content, the simulation flowchart shown in Fig. 5 can be obtained.

Fig. 5

The Simulation Flowchart.

Life prediction modeling

In this study, a method for predicting the life of coating materials under thermal shock condition is proposed. The method is based on the single parameter model¹⁵ for the prediction of thermal shock life of coatings, and the continuous oxidation of coatings in thermal shock life test is taken into consideration. The thermal shock life of the coating material is predicted by obtaining the number of the thermal shock when brittle fracture occurs. Thermal shock life test temperature is T₁∼T₂. The holding time is t₁. The cooling time is t₂. When the maximum temperature on the surface of the coating specimen rises to T₂, the holding time at the temperature of T₂ will be t₁. When the specimen is cooled by a natural cooling mode, the cooling time will be t₂. After cooling, the maximum temperature on the coating surface is T₁. If brittle fracture occurs to the specimen when the number of the thermal shock is n, and n can be regarded as the number of the thermal shock life of the coating.

In the three-dimensional heat transfer numerical analysis, the initial thickness of the silicide coating material is set to 0.5 mm. During the experiment, the coating undergoes continuous oxidation, generating oxidation products and gradually reducing the coating thickness. The applied voltage is adjusted to ensure that the maximum surface temperature of the coating at each oxidation thickness reaches 2300 °C (2573 K). The maximum thermal stress values on the surface of the coating are obtained for various oxidation thicknesses, including 0 mm, 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm, 0.5 mm. The average maximum thermal stress range on the surface of the coating under the oxygen thermal shock test conditions is calculated, which allows for the precise simulation of the temperature field at each stage of the oxidation process. The average value of the maximum thermal stress range on the coating surface under thermal shock condition can be obtained by calculation. Finally, the prediction model of thermal shock life based on the number of thermal shock life and the average value of the maximum thermal stress range on the coating surface is established.

(16)

where N_ts is the number of thermal shock life of the coating, $\Delta\overline{\sigma}$ is the average value of the maximum thermal stress range of the coating surface under thermal shock condition and its unit is kN/mm². A and b are the parameters obtained by the least square method. The model assumes that the specimen has no edge-angle effect and it is stress-free at room temperature.

(17)

In the equation, $l\leqslant i \leqslant h$ , $l\cdots i \cdots h$ represent the maximum temperature of the coating surface in the three-dimensional heat transfer numerical calculation and the unit is℃, $\overline{\sigma_{h}}$ is the average value of the maximum thermal stress on the coating surface at the temperature of h and the unit is kN/mm², $\overline{\sigma_{1}}$ is the average value of the maximum thermal stress on the coating surface at the temperature of l and the unit is kN/mm².

In the three-dimensional heat transfer numerical calculation, when the maximum temperature of the coating surface is i, $\overline{\sigma_{i}}$ can be obtained by taking the average of the maximum thermal stress values of the coating surface with different oxidation thickness. The equation is as follows.

(18)

In the equation, $\sigma_{i_0},\sigma_{i_1}, \sigma_{i_2}, \sigma_{i_3}, \sigma_{i_4}$ and $\sigma_{i_5}$ represent the maximum thermal stress values of the coating surface at the oxidation thickness of 0 mm, 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm and 0.5 mm respectively and the unit is kN/mm².

Results and discussion

Thermal shock life test

With the thermal shock life test device developed in this study, the thermal shock life tests of the silicide coating on the niobium hafnium alloy surface were carried out in different temperature ranges. In the thermal shock life test, since the specimen will undergo rapid brittle fracture once defects appear on the coating surface, the thermal shock life of the coating can be determined based on the number of brittle fractures of the specimen. The results are shown in Table 3.

Table 3 Thermal Shock Life Results.

Three-Dimensional heat transfer analysis

Based on the simulation model established in Sect. “Three-dimensional Heat Transfer Modeling”, the numerical calculation of the temperature field and thermal stress field of the silicide coating on the surface of the niobium hafnium alloy at 700℃, 1750℃, 1775℃, 1800℃, 1825℃, 1850℃, 1875℃, 1900℃, 1925℃, 1950℃, 1975℃, 2000℃ and 2025℃ were performed by using COMSOL simulation software. For different maximum temperatures of the coating surface, numerical calculations were performed to obtain the temperature field and thermal stress field under various oxidation thicknesses of the coating: 0 mm, 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm, and 0.5 mm. Based on these maximum surface temperatures, the maximum thermal stress values on the coating surface were determined. By Eq. (18), the average value of the maximum thermal stress on the coating surface can be obtained. The values of the maximum thermal stress on the coating surface (of different oxidation thickness) and the average values of the maximum thermal stress are shown in Table 4. The schematic diagram of the maximum thermal stress variation with temperature for different oxidation layer thicknesses is shown in Fig. 6.

Table 4 Maximum Thermal Stress Values (of different oxidation thickness) and Average Value of the Maximum Thermal Stress on the Coating Surface.

Fig. 6

The Maximum Thermal Stress Variation with Temperature for Different Oxidation Layer Thicknesses.

Coating life prediction

According to Eq. (17), simulation results in Table 3 and thermal shock life data in Table 2, the average values of the maximum thermal stress range on the coating surface are obtained. The coating thermal shock life test results and the average values of the maximum thermal stress range are shown in Table 5.

Table 5 Thermal Shock Life Test Results and Average Value of the Maximum Thermal Stress Range.

The least square method is used to deal with the data of the number of the thermal shock life and the average value of the maximum thermal stress range on the coating surface at the temperature ranges from 700℃ to 1800℃, 700℃ to 1825℃, 700℃ to 1850℃, 700℃ to 1875℃, 700℃ to 1900℃, 700℃ to 1925℃, 700℃ to 1950℃, 700℃ to 1975℃, 700℃ to 2000℃ and 700℃ to 2025℃. By this method, we can obtained that $A= 3.9508 \times 10^5$ , $b = -11.6441$. The relationship between the number of thermal shock life of the coating and the average value of the maximum thermal stress range on the surface is shown in Fig. 7.

Fig. 7

Fitting Diagram of the Number of the Thermal Shock Life and Average Value of the Maximum Thermal Stress Range.

Therefore, the thermal shock life prediction model of the silicide coating is as follow:

(19)

Relative error is used to evaluate the accuracy of the model.

(20)

where $f_{ts}$ is the number of the thermal shock life of the coating obtained by the test, while $N_{ts}$ is the predicted results by the life prediction model.

According to Eq. (19), the number of the thermal shock life is predicted under the testing temperature of 700℃ ~ 1750℃ and 1775℃. And aerobic thermal shock life tests were conducted in the same temperature range to obtain the thermal shock life of the sample parts. Then Eq. (20) is used to calculate the number of the thermal shock life and the predicted results by the model. The number of the thermal shock life obtained from the test, the predicted results by the model, and the relative error results are shown in Table 6.

Table 6 Tested Number, Predicted Number and Relative Error.

Discussion and future work

The experimental method and specimens presented in this study are specifically designed for the aerospace industry and are currently being employed in lifespan testing. The model for predicting the thermal shock life of coatings demonstrates strong agreement with experimental data, with a relative error of less than 8%. This level of accuracy is sufficient for aerospace. Compared to existing models, the proposed model method offers significant improvements in both predictive performance and computational complexity. The balance between predictive accuracy and computational efficiency also makes our approach particularly suitable for high-temperature engineering applications.

The current model has demonstrated good performance in predicting the lifespan of specific coatings. However, the distinct properties of materials, such as thermal conductivity, expansion coefficient, and melting point, may vary significantly across different coatings. As a result, the model may need adjustments to account for the specific properties of other coatings. In addition, the model simplifies the oxidation process and assumes that continuous oxidation is independent of temperature. In reality, oxidation kinetics can be more complex, and material properties may vary with temperature. To enhance the model’s generalizability, future work could focus on expanding its applicability to a wider range of materials and operating conditions. This may involve incorporating temperature-dependent material properties, simulating nonlinear oxidation behavior, and considering multiphysics interactions (e.g., mechanical loading and chemical corrosion) that influence the lifespan of coatings. Moving forward, the focus will be on further refining the experimental method and developing standardized protocols to enhance its applicability and reliability in industrial practices.

Conclusions

This study proposes a novel method for predicting the thermal shock life of coatings using high-temperature thermal shock tests and three-dimensional heat transfer analysis. A direct resistance heating system was employed, operating within a temperature range of 773 K to 2573 K. By analyzing the heat distribution and transfer mechanisms of MoSi₂ coatings before and after oxidation, it was found that heat distribution is uneven, with the highest temperatures concentrated in the center. The surface peak temperature ranges from 2073 to 2303 K when an electric voltage of 1.4–1.75 V is applied. With increasing oxidation thickness, the peak surface temperature increases linearly. Additionally, defects with diameters between 1 × 10⁻³ m and 3 × 10⁻³ m cause a rise in the surface temperature, which decreases with thicker coatings, both trends being roughly linear.

A model was established based on these findings, integrating thermal shock life testing and finite element analysis. The model considers oxidation thickness, with results showing good agreement with experimental data, with a relative error of less than 8%. This method provides a significant advancement in predicting the thermal shock life of coatings, offering both theoretical and practical contributions to the field, especially in high-temperature applications like aerospace. Future work will aim to refine this model by exploring additional factors influencing coating life and extend to other coating materials such as aluminum oxide or nickel-based coatings.