Introduction

Migration and redistribution of surface mass loading associated with atmospheric, hydrological, non-tidal ocean loading (AHNL) can induce crust deformation that shows seasonal variations, which can be observed by Global Navigation Satellite System (GNSS) stations. Over past several decades, the GNSS technology has made significant advancements in measurement precision and accuracy, such as ionospheric delays and other errors corresponding to satellite and receiver clocks1,2,3,4. GNSS time series accumulated over several decades have rich geophysical signals related to real tectonic deformation, non-linear deformation associated with seasonal variations (mainly annual and semi-annual). Seasonal deformation caused by AHNL can bias station velocity but also lead to a substantial decrease in the solution accuracy of GNSS time series5,6,7,8,9,10,11. Hence, investigating AHNL effect on seasonal oscillations derived from GNSS observations can provide useful data for geodetic and extreme climate change studies.

It is well known that atmospheric, hydrological and non-tidal ocean loading, the most recognized surface mass loading, can result in the seasonal deformation from GNSS time series. Many studies have focused on AHNL effect on seasonal oscillations of GNSS vertical time series. Li et al.12 adopt surface loading models to study the AHNL contributes of seasonal oscillations in GNSS for the Eurasian plate, the result shows that annual variations between GNSS vertical time series and AHNL deformation are physically related for most GNSS stations. Dong et al.8revealed that the maximum annual amplitudes at GNSS stations caused by atmospheric, hydrological, and non-tidal ocean loading can reach 4 mm, 7–8 mm, and 2–3 mm, respectively, accounting for about 40% of the GNSS vertical seasonal variations. It has confirmed that non-tidal ocean loading correction can effectively improve the accuracy of GNSS vertical displacements in coastal regions13. Jia et al.14investigated the seasonal variations of GNSS vertical time series at 468 stations in global region, the demonstrate shows 71% of all stations display scatter reduction after removing the deformation related to atmospheric loading from the GNSS vertical time series, atmospheric loading can lead to annual amplitude of up to 1.6 mm. It is found that GNSS vertical seasonal variations influenced by hydrological loading varied from millimeters to centimeters15,16,17,18,19. Extensive researches have proved that surface mass loading deformation derived from the GRACE model and GNSS vertical time series have strong correlation and consistency in regional scale, especially in the region of significant changes of land water storage7,20,21,22. Previous studies indicate that the impact of different surface mass loading (atmospheric, hydrological, non-tidal ocean loading) on GNSS vertical seasonal variations differ in different region.

Hong Kong, the low latitude coastal area with a size of 100 km×100 km, is situated in East Asia at the intersection of the South China Plate and the Eurasian Plate (Fig. 1). Numerous studies have investigated ocean tide loading (OTL) effect on GNSS time series in the Hong Kong region, the result shows OTL obviously contribute to seasonal variations in GNSS time series23,24. Zhou et al. reveals clear seasonal variations in the OTLD parameters of the six main tidal constituents in Hong Kong. Specifically, the amplitude variations of these constituents range from 4 to 25.1%, while the phase oscillations fluctuate between 8.8° and 20.4°25. However, the effects of hydrological, atmospheric, and non-tidal oceanic loading are often overlooked. Given that ANHL is a major contributor to seasonal oscillations in GNSS time series, it is necessary to investigate the ANHL impact on GNSS time series in Hong Kong. The AHNL deformation can be calculated by surface loading models and GRACE model, which was often used to analyze seasonal variations in GNSS vertical time series. Compared with GRACE model limited by spatial and temporal resolution, the surface loading models can obtain small-scale deformation. Here, we apply surface loading models to research the seasonal variations between GNSS vertical time series and ANHL deformation.

The rest of this paper is organized as follows. Section 2 describes the GNSS data, AHNL data and the methods of ICA and wavelet analysis; Sect. 3 carried out the period analysis for GNSS vertical time series and AHNL deformation using continuous wavelet transform (CWT) and cross wavelet transform (XWT). Moreover, ICA method was employed to extract the periodic signals from the GNSS vertical time series; Sect. 4 presents the conclusions.

Data and methods

GNSS data

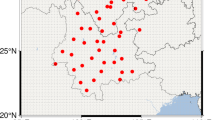
To avoid the influence of their positions such as rooftop, we adopt the position time series spanning from 2013.01.01 to 2022.03.29 of 9 GNSS stations located on bedrock in Hong Kong GNSS fiducial network (Fig. 1), which provided by the Nevada Geodetic Laboratory (NGL) (http://geodesy.unr.edu/, accessed on 30 November 2022; Blewitt et al.26). The GNSS data processing is conducted by Gipsy X software. NGL analysis center utilizes ionospheric free combination to remove ionospheric effects, Vienna Mapping Function (VMF1) model to correct tropospheric delays, FES2004 to correct tidal loading effects, and antenna phase center correction parameters refer to the absolute antenna phase calibration file provided by the International GNSS Service (IGS) center.

Fig. 1
figure 1

Spatial distribution of 9 GNSS stations in Hong Kong (generated by GMT627).

Full size image

Before analyzing the relationship between GNSS vertical displacement and AHNL deformation, we need preprocessing the GNSS vertical time series (such as outlier removal, offset correction, and interpolation of missing data) due to poor observation environment, earthquake or replacement of GNSS equipment. The primary preprocessing methods employed in this paper are as follows: 1) Outliers were detected and removed from GNSS vertical time series using 3 sigma Inter Quartile Range (3IQR)28;2) A least squares linear regression method was carried to correct offset in the GNSS vertical displacement; 3) Missing data in the GNSS vertical displacement records at 9 stations in Hong Kong were interpolated using the Regularized Expectation Maximization (RegEM) method29. This approach accounts for the correlation and physical context among the 9 stations at Hong Kong, requiring no prior information or reliance on external data models. Instead, it relies solely on the intrinsic characteristics of the data. The RegEM method has been widely adopted in GNSS time series interpolation28,30,31. Figure 2 displays the GNSS vertical time series of the HKMW stations after preprocessing, demonstrating that the interpolation results using the RegEM method align well with the overall movement trend.

Fig. 2
figure 2

Vertical Displacement of HKMW Stations After Preprocessing. (a) represent original GNSS vertical time series; (b) represent the result of offset corrections; (c) represent the result of outlier removal; (d) represent the result of interpolation.

Full size image

Surface loading models data

Compared with GNSS vertical time series, we utilized the surface loading models data with ATML, HYDL and NTOL, obtained from International Mass Loading Service (IMLS) in this research32, calculating by Green’s function approach.

The GEOSFPIT numerical weather model33, with a spatial resolution of 2’ and temporal resolution of 3 h, was employed to estimate deformation, which is believed to be driven by hydrological loading (HYDL) and atmospheric loading (ATML). Additionally, the Earth’s elastic response to ocean bottom pressure variations, known as non-tidal ocean loading deformation, was computed using MPIOM06 model34. To match the daily GNSS vertical time series, the atmospheric, hydrological, and non-tidal ocean loading deformations were averaged to daily solutions. Moreover, they were converted to millimeters to match the units of the GNSS time series for subsequent analysis in this study. The loading deformations of HKKT used in this paper is shown in Fig. 3. The HYDL, ATML, and NTOL deformation exhibit a significant seasonal variation, with fluctuation of −4 ~ 4 mm, −4 ~ 4 mm, −4 ~ 2 mm, respectively.

Fig. 3
figure 3

Loading deformations of (a) HYDL, (b) ATML, (c) NTOL and (d) AHNL at HKKT station, respectively.

Full size image

Independent component analysis

ICA decomposes a group time series into a set of modes, which each mode composed of temporal orthogonal eigenvectors and corresponding spatial response (SR). By selecting a number of independent components (ICs), ICA reduces the dimensionality of the time series, allowing it to capture the most informative internal patterns from the original data.

For a regional or global GNSS station network, linear trends, offsets, and seasonal components are estimated using the least squares fitting method. These components are then subtracted from the original GNSS time series, leaving a residual data matrix The covariance matrix B is defined as:

$$X\left( t \right)=AS\left( t \right)$$
(1)

Decomposed the symmetric matrix B as:

$$Y\left( t \right)=WX\left( t \right)$$
(2)

The matrix of eigenvectors, characterized by non-zero diagonal eigenvalues, can be applied in a linear transformation. Using an orthogonal function basis, the residual time series is then defined as follows35,36:

$$W={A^{ - 1}}$$
(3)

Where is the IC of the matrix, which represents a temporal signature of the mode, and can also be defined as:

$${D_{season}}=\sum {AS}$$
(4)

Cross wavelet transform

we first review the continuous wavelet transform (CWT) as outlined by Grinsted et al.37. The continuous wavelet transforms of a time series \(X{\text{n}}\), (n = 1,2,., N) is defined as:

$$W_n^X(s)=\sqrt{\delta t/s}\sum_{n=1}^{N}X_{n^{\prime}}\varphi_{0}[(n^{\prime}-n)\delta t/s]$$
(5)

where \(W_{n}^{X}\left( s \right)\) is the wavelet coefficient, δt is the time step, s is the wavelet scale, \({\varphi _0}\) is the mother function, \(n^{\prime}\)is reversed time, \(\sqrt {\delta t/s}\)the normalization factor37,38. Unlike traditional methods, such as Fourier analysis, which analyze periodicities in the frequency domain under the assumption of stationary processes over time, the continuous wavelet transform (CWT) extends time series into the time-frequency domain, allowing for the identification of localized and transient periodicities.

XWT combines wavelet analysis and cross spectrum, which often utilized to research.

the phase relationship between two time series in time-frequency space37. The XWT of two time series \({X_n}\) and \({Y_n}\) is defined as:

$${W^{XY}}={W^X}{W^{Y*}}$$
(6)

where \({Y^*}\) refers to the complex conjugation of \({W^Y}\). By applying the XWT, regions with significant common power in the time-frequency domain are identified, which also reveals the phase relationship between the two time series. In cases where the series are physically related, a stable or slowly varying phase lag is typically observed. To calculate the relative phase, we use the circular mean of the phase values outside the cone of influence (COI), along with the semblance derived from the XWT. The phase relationship between two time series can be measured using the circular mean of their phases. The cone of influence refers to the region where the wavelet power, influenced by a discontinuity at the boundary, has decreased to a fraction \({e^{ - 2}}\)of the value at the boundary. The circular mean of a set of angles (\({\alpha _i}\), i = 1, 2,. . ., N) is defined as:

$${a_m}=\arg \left( {X,Y} \right)=\arg \left[ {\frac{1}{n}\sum\limits_{{i=1}}^{n} {\cos \left( {{\alpha _i}} \right),\frac{1}{n}\sum\limits_{{i=1}}^{n} {\sin \left( {{\alpha _i}} \right)} } } \right]$$
(7)

The XWT-based semblance39 was then calculated:

$${\rho _i}=\cos \left( {{\alpha _m}} \right)$$
(8)

where the value of ρi varied from − 1 (inversely correlated) to 1(fully correlated).

Results and analysis

Deformations comparison between GNSS and AHNL

It is clear from Fig. 4 that an annual signal is visible in both GNSS vertical time series and AHNL deformations. For all stations, the amplitude of the vertical GNSS time series is relatively large, indicating that the AHNL deformations is not able to completely contribute to the seasonal oscillations of GNSS time series in Hong Kong. The deformation signals appear to be in phase with the vertical signal and exhibit a smaller amplitude, with the average amplitude of GNSS vertical displacements being 3.69 mm and the loading deformations showing an amplitude of 3.48 mm. The average phase of the GNSS vertical time series is 117.96°, while the loading deformations have an average phase of 139.29°. This suggests that loading may contribute to the non-linear fluctuations in GNSS time series to a certain extent.

Fig. 4
figure 4

GNSS vertical time series and corresponding AHNL deformations at 9 stations.

Full size image
Table 1 Correlation between AHNL deformations and GNSS, and RMS Variation of GNSS vertical time series after loading correction.
Full size table

To further investigate the relationship between the AHNL deformations and the GNSS vertical time series, we calculated the correlation coefficients between the deformation derived from GNSS and AHNL. As shown in Fig. 5(a) and Table 1, the results display a strong correlation between the AHNL deformations and the GNSS vertical time series, with most stations showing correlation coefficients greater than 0.5.

The result of the reduction in root mean square (RMS) after removing the AHNL deformations from GNSS vertical time series is showed in Fig. 5(b) and Table 1. A higher correlation between the GNSS vertical time series and the AHNL deformations corresponds to a greater reduction in RMS. For most stations, the RMS reduction by approximately 15%, while the reduction was around 20% at HKSL, HKST, and HKWS. Moreover, we found whether the value of RMS decreases depend on the relative phase between GNSS vertical time series and the AHNL deformations. Therefore, the CWT was adopted to perform the period analysis, and the morlet wavelet is chosen as the mother wavelet function.

Fig. 5
figure 5

The correlation coefficient between the GNSS vertical time series and the AHNL deformations (a), RMS percentage reduction between original and environmental loading correction GNSS vertical time series at all stations (b) (generated by GMT627).

Full size image

Figures 6 and 7 shows the CWT result of GNSS vertical time series and AHNL deformations, the yellow and blue correspond to the peak and trough values of energy density, respectively. The color transition from blue to yellow indicates an increasing trend in the wavelet energy spectrum. The area enclosed by the thick black solid line indicates regions that have passed the 95% confidence level significance test, while the region below the thin black solid line represents the cone of influence (COI). The main oscillation periods of the AHNL deformations are 256–512 days (0.7–1.4 cpy (1 cycle per year)), which have passed the significance test in the whole time domain (Fig. 6). In Fig. 7, the peak spectral energy is mainly concentrated on the period bands of 256–512 days and 512–1024 days. The high spectral energy in the period bands of 256–512 days and 512–1024 days exists in the whole time domain for the most stations, while the high spectral energy in the period band of 512–1024 days only exists in the time span of 2017–2022 at HKNP station. Furthermore, the high-frequency components are attributed to technical errors and noise in the GNSS measurements. Figures 6 and 7 indicates that both GNSS vertical time series and AHNL deformations at all stations exhibit significant annual cycles corresponding to a 256–512 days scale throughout the entire time domain. This result reveal that AHNL deformations are the primary cause of the annual fluctuations in GNSS vertical time series.

Fig. 6
figure 6

Wavelet power spectrum of AHNL deformations for 9 stations.

Full size image
Fig. 7
figure 7

Wavelet power spectrum of GNSS vertical time series for 9 stations.

Full size image

Seasonal deformations extracted by ICA

From Figs. 6 and 7, the annual signals of 256–512 days exits in the GNSS time series. Here, ICA method was applied to separate the seasonal signal from the GNSS time series based on blind source technology. We uses a trial and error method40 to determine five principal components for the ICA method to process the GNSS vertical coordinate time series. Figure 8 illustrates the time and spatial responses of IC1-IC5 and corresponding to power spectral density, where upward arrows denote positive spatial responses and downward arrows denote negative spatial responses. The result indicates that both IC2 and IC5 exhibit significant annual signals. However, the spatial response of IC2 is inconsistent, whereas IC5 demonstrates a uniform spatial response. Furthermore, the PSD result of IC2 and IC5 mainly have annual signal, while IC1, IC3, and IC4 have high frequency signal. Based on Fig. 8, IC5 can be identified as annual signal from the GNSS stations caused by AHNL.

Fig. 8
figure 8

Time and Spatial response and power spectral density of IC1-IC5.

Full size image

Figure 9 reveals that a comparison between the annual signals extracted using ICA and the AHNL deformations shows that all annual signals in the GNSS vertical time series display the same amplitude and phase as the loading signals. It further confirms that the AHNL deformations is the driving factor of the annual variations observed at GNSS stations. However, it is noteworthy that the annual signals extracted by ICA display a higher amplitude than the corresponding loading signals. This suggests that AHNL deformations can partly account for the amplitude of annual oscillations in GNSS vertical time series, while other factors (e.g., systematic error of GPS solution, thermal expansion effect), may also contribute to the annual variations observed at GNSS stations.

Fig. 9
figure 9

Comparison of ICA-derived seasonal signals with AHNL deformations.

Full size image

To quantify the relationship between AHNL deformation and seasonal deformation extracted by ICA, we calculated the Lin correlation coefficient between the two deformations. Compared with the traditional Pearson correlation coefficient, the Lin correlation coefficient takes into account the similarity of the amplitude and shape of the AHNL deformation and seasonal deformation41,42.The Lin correlation between ATML, HYDL, NTOL, AHNL deformations and IC5 is shown in Fig. 10. This result indicates that ATML, HYDL, and NTOL deformations are weakly correlated with IC5, with an average Lin correlation coefficient of approximately 0.26. In contrast, the AHNL deformations shows a stronger correlation with IC5, with an average Lin coefficient of 0.6. Its further evidence that in the Hong Kong region, ATML, HYDL, and NTOL collectively contribute to the annual oscillation observed in the GNSS vertical time series.

Fig. 10
figure 10

Lin Correlation coefficient between (a) ATML deformations, (b) HYDL deformations, (c) NTOL deformations, (d) AHNL deformations and ICA-derived seasonal signals (generated by GMT627).

Full size image

Cross wavelet transform analysis

In order to further analyze the relationship between the AHNL deformations and the GNSS vertical time series, the XWT method was used to research the relative phase relationship between the GNSS and AHNL deformations in time-frequency space. Figure 11 displays the cross wavelet spectrum of GNSS vertical time series and AHNL deformations at all stations. The thick, black contours designate the significance test at the 95% level, and the thin, black line indicates the COI that delimits the region not influenced by edge effects. The relative phase relationship between two time series is described by the arrow (with antiphase pointing left and in-phase pointing right; the downward-pointing arrow represents the vertical GNSS time series leading the environmental loading time series by 90°). The phase angle will vary little or be consistent37 between the GNSS vertical time series and AHNL deformations, which are physically related. Since the low frequency component (1 cycle per year (cpy)) is more significant than the other frequency components, we focus on the relative phasing at the frequency closest to 1cpy. From Fig. 11, the obvious common power was located in the period range of 256 ~ 512 days in the whole time span between the GNSS and AHNL deformations.

Moreover, as shown in Fig. 11, the relative phasing angle of the period less than 128 days fluctuated violently, sub-seasonal peaks of the GNSS vertical time series may be caused by some technique errors (e.g., unmodeled high-order ionospheric path delays error and tropospheric delay error)43. We therefore calculate the mean value of the XWT-based semblance to better reflect the phase relationship between GNSS vertical time series and loading deformations. The results in Fig. 12 indicate that for some sites (e.g., HKNP, HKOH, HKST and HKWS) the mean semblance value is close to 1, revealing that AHNL deformations is a representation of the driving force for the annual oscillations in GNSS vertical time series. However, for other stations (e.g., HKLT, HKMW and HKSS), the mean semblance value is not close to 1, demonstrating that AHNL deformations is not a complete representation of the driving force for the annual motions of GNSS stations.

Fig. 11
figure 11

Cross wavelet spectrum of GNSS vertical time series and AHNL deformations for 9 stations.

Full size image
Fig. 12
figure 12

The mean value of the XWT-based semblance that is outside the COI at the period closest to 1 yr.

Full size image

Conclusion

In this study, aiming to research the AHNL contributors of seasonal oscillations in GNSS observations at Hong Kong, the GNSS data and AHNL deformations of 9 stations over period from 2013.01.01 to 2022.03.29 was used in this study. We performed the wavelet analysis and ICA method to investigate the seasonal oscillations in GNSS vertical time series. From this research, the following conclusions can be drawn:

1) Our result shows that AHNL deformation and GNSS vertical time series exhibit similar annual amplitudes and phases, demonstrating a strong correlation with an average coefficient of 0.54. The average RMS reduction is 15% at all stations after AHNL correction, implying that AHNL is a primary factor contributing to the annual oscillations observed by GNSS stations in Hong Kong region.

2) ICA method can effectively separate the seasonal signals related to AHNL. GNSS vertical time series and AHNL deformations at all stations exhibit significant annual cycles corresponding to a 256–512 days scale throughout the entire time domain, indicating that AHNL deformations is the primary factor causing the annual oscillations in Hong Kong. However, the mean XWT-based semblance of some GNSS stations is not close to 1, demonstrating that the environment loading cannot completely explain the annual oscillation in GNSS observations. Other geophysical factors, systematic errors and environment loading modelling errors jointly result in the annual oscillations in GNSS observations of the Hong Kong region.