Prototype based contrastive graph clustering network for reducing false negatives

Abstract

Contrastive graph clustering methods significantly enhance the clustering performance of graph data by leveraging multi-view augmentation and contrastive loss. In particular, Self-Supervised Graph Contrastive Learning (SS-GCL) has gained attention due to its lower dependence on labeled data. However, SS-GCL approaches often rely on pseudo-labeling to categorize samples into positive and negative pairs, which can lead to false negatives and degrade clustering performance. To address this issue, a prototype-driven contrastive graph clustering network is proposed. This network uses prototypes as data-driven cluster centers to form high-confidence sample sets while discarding boundary samples and aggregating the remaining samples into augmented embeddings. Additionally, a cross-view decoupled contrastive learning mechanism is designed, utilizing a mean squared error contrastive loss function based solely on positive samples. This mechanism performs alignment calculations across views for the augmented positive sample embeddings, effectively preventing the generation of false negative samples. Experimental results demonstrate that the proposed method outperforms current state-of-the-art baseline methods regarding accuracy and clustering effectiveness across multiple datasets.

Introduction

With the widespread application and remarkable success of Graph Neural Networks (GNNs), leveraging GNNs for graph representation learning has become a popular research focus. However, most GNN models are primarily designed for (semi-)supervised learning scenarios, posing significant challenges in the face of scarce labeled data and high annotation costs. To address this issue, self-supervised learning (SSL) has gradually gained attention as a promising solution that eliminates the need for manual data labeling. The extension of SSL to graph-structured data has given rise to new research paradigms¹. Among these, Graph Contrastive Learning (GCL) has emerged as an effective strategy for utilizing unlabeled data, demonstrating significant advantages in various domains such as social network analysis^2,3, bioinformatics^4,5, and recommendation systemsrecommendation systems^6,7. This approach not only captures the complex structural information of graphs but also exhibits strong flexibility and scalability.

The core idea of GCL is to define positive pairs (different augmented views of the same node or graph) and negative pairs (representations of different nodes or graphs) and to maximize the similarity within positive pairs while minimizing the similarity between negative pairs. This design effectively improves the feature representation, robustness, and generalization capability of the model. Inspired by GCL, methods such as MVGRL⁸ treat different augmented views of the same node as positive pairs and generate negative pairs by randomly shuffling features. SCAGC⁹ and GDCL¹⁰ further enhance the quality of negative samples by randomly selecting samples from different clusters. CCGC¹¹ and CICL¹², on the other hand, construct reliable positive and negative pairs by mining trustworthy pseudo-labels. However, these methods may treat semantically similar but not identical nodes or graph instances (e.g., nodes from different classes with similar structures) as negative samples, potentially leading to semantic conflicts, also known as class collision.

To address this issue, prototype-based contrastive learning has been proposed. Its core idea is to group nodes, subgraphs, or graphs into prototypes (cluster centers of semantically similar instances) through clustering methods. Contrastive learning is then performed between instances and their prototypes, or across different prototypes. Prototype contrastive learning, leveraging a prototype contrastive loss, enables the model to learn embeddings with stronger semantic consistency while avoiding class collision issues. For example, PCL¹³ implicitly encodes the semantic structure of the data into the embedding space. By constructing a prototype contrastive loss (ProtoNCE), it treats the embedded samples and their prototypes with the same pseudo-labels as positive pairs, while treating other prototypes as negative pairs. Experiments have shown that, compared to traditional contrastive losses, prototypes influenced by clustering exhibit higher mutual information with ground-truth labels. Gao et al.¹⁴ introduced a new contrastive learning method based on category prototypes, called Contrastive Prototype Learning (CPL). CPL uses class prototypes as anchors, pulling query samples of the same class closer while pushing query samples of different classes farther apart. Although traditional GCL methods and prototype-based contrastive learning methods have achieved some success in graph clustering, traditional GCL methods require a large number of negative pairs. This reliance often leads to false negatives when inaccurate pseudo-labels cause positive node pairs to be incorrectly labeled as negative pairs. This issue results in a decline in embedding quality and ultimately degrades model performance. While prototype-based contrastive learning reduces the number of negative pairs, it still cannot entirely avoid the occurrence of false negatives.

To address the above challenges, a prototype-driven graph contrastive learning clustering network is proposed. The proposed network consists of two main modules: 1) a Multi-Scale Attribute Feature Aggregation (MSAFA) module and 2) a Multi-Scale Prototype-driven Data Augmentation (MSPDA) module. First, the MSAFA module extracts embeddings from raw graph data, capturing features from low to high levels. These embeddings are aggregated to create augmented representations, which are treated as positive pairs. A cross-view decoupling contrastive learning mechanism is introduced in this module, using a mean squared error contrastive loss function based solely on positive samples. This mechanism aligns embeddings across views, ensuring robust and consistent representation learning while avoiding false negatives.

The MSPDA module further integrates feature learning with clustering tasks. By performing clustering calculations, prototypes for each category are obtained, and the closest high-confidence samples are selected while discarding boundary samples. These prototypes are used as the foundation for constructing positive pairs, enabling the model to avoid the dependency on pseudo-labels and effectively preventing false negatives. The cross-view decoupling contrastive learning mechanism ensures that augmented representations remain aligned across views, enhancing the model’s ability to capture semantic consistency in clustering tasks.

Finally, feature learning and clustering are jointly optimized to improve overall performance. The contributions of this paper can be summarized as follows:

• A cross-view decoupling contrastive learning mechanism is proposed to avoid false negative samples by focusing exclusively on positive sample alignment through a mean squared error contrastive loss function.

• The MSAFA and MSPDA modules are designed to integrate feature learning with clustering tasks, achieving better clustering performance through prototype-driven high-confidence sample selection.

• Extensive experiments are conducted on six datasets, comparing the proposed approach against twelve state-of-the-art baselines. The results demonstrate that the proposed method outperforms advanced clustering methods in terms of accuracy and effectiveness.

Related work

Contrastive clustering methods

Deep graph clustering has recently attracted significant attention, particularly methods based on contrastive learning, which demonstrate superior performance and have gained popularity among researchers^{8,15,16,17,18}. Contrastive learning works by maximizing intra-class similarity and minimizing inter-class similarity through the design of positive and negative sample pairs. This approach adaptively learns discriminative feature representations, allowing models to distinguish between classes or graph structures in an unsupervised manner.

For instance, CCGC¹¹ filters and constructs positive samples from high-confidence clusters by mining pseudo-labels. Pseudo-labels from different clusters are treated as negative samples. Similarly, DCAGC¹⁹ introduces a neighbor contrastive module to enhance node representations based on KNN neighbors. Since neighbor nodes obtained through KNN should have similar representations, these neighbors are defined as positive samples. In contrast, other neighbors are defined as negative samples, making the learned node representations more suitable for clustering tasks. CONVERT²⁰ develops a reversible perturbation recovery network to generate enhanced views with reliable semantic consistency. The model is guided by clustering information and employs a label-matching mechanism to align high-confidence pseudo-labels with semantic labels. MVGRL⁸is a contrastive multi-view representation learning model designed for both node and graph levels. It uses graph diffusion to create an additional structural view, which, alongside the original graph, is fed into the network to obtain the graph’s embedding representation. A comparator contrasts node representations from one view with graph representations from another, evaluating their consistency. CICL²¹ is a Clothing-Invariant Contrastive Learning (CICL) framework. Two new strategies are introduced in CICL: Random Clothing Augmentation (RCA) and Semantic Fusion Clustering (SFC). Finally, they designed prototype contrastive loss, cross-view similarity contrastive loss, and semantic alignment contrastive loss to optimize the model.

Combining prototype learning with contrastive learning

Recently, many works have combined prototype learning with contrastive learning, achieving significant results across various fields. Yuan et al.²² infer the initial clustering distribution of anti-noise event prototypes based on the latent representations of events. They then construct four permutation-invariant self-supervised signals to guide the representation learning of event prototypes. Gao et al.¹⁴ propose a new contrastive learning approach centered on support set class prototypes, called Contrastive Prototype Learning (CPL). CPL uses class prototypes as anchors, bringing query samples of the same class closer while pushing apart query samples of different classes. Li et al.²³ introduce a prototype contrastive learning framework that bridges contrastive learning and clustering for unsupervised representation learning. In a related work, Li et al.²⁴ propose Contrastive Prototype Prompting (CPP), a simple yet novel continual learning framework that explores the embedding space as a whole. CPP utilizes task-specific prompts from contrastive learning to address the challenges of semantic drift and prototype interference. Additionally, a multi-prototype strategy enriches the representational capacity of prototypes, seamlessly integrating into the CPP framework. Chen et al.²⁵ present a Multi-Prototype Learning (MPL) framework that matches the most suitable prototype for each predicate. The MPL framework enhances the accuracy of predicate reasoning and improves model interpretability. Zhang et al.²⁶ propose an end-to-end clustering framework called Multi-Level Graph Contrastive Prototype Clustering (MLG-CPC). This method first extracts feature representations from raw data using an encoder and then generates high-level semantic prototypes and clusters sequentially through a projection head and a low-level predictor. Cheng et al.²⁷ introduce a novel method that incorporates graph structure into prototype learning, leveraging both local and global information to enhance clustering performance.

Although these clustering methods based on graph contrastive or prototype contrastive learning have achieved notable success, they still struggle to avoid the false negative problem inherent in contrastive learning.

False negative elimination

The accuracy and effectiveness of negative samples in contrastive learning remain significant challenges. False negative samples may cause models to incorrectly treat similar samples as dissimilar, disrupting semantic connections and weakening representation learning. Several researchers have proposed solutions to address this issue in recent years. Huynh et al.²⁸ argue that generating positive sample pairs is relatively straightforward, but accurately constructing negative pairs is much more difficult. They propose strategies for false negative elimination and attraction to identify and minimize the impact of potential false negatives. Lu et al.²⁹ highlight that most current methods define all samples within the neighborhood as positive and those outside as negative, leaving the false negative problem unresolved. They introduce the Decoupled contrastive multi-view clustering algorithm based on higher-order random walks (DIVIDE), which assesses the affinity between anchor points and higher-order neighbors using multi-step random walks, identifying intra-cluster samples outside the neighborhood. Chen et al.³⁰ propose a self-supervised contrastive learning framework to mitigate the effects of false negatives, incrementally detecting and removing them. Jin et al.³¹ emphasize that ensuring the accuracy and effectiveness of negative samples remains a significant challenge. They propose a Semi-supervised Instance-based graph Pseudo-Label Distribution Learning framework (SIP-LDL) to mitigate the impact of false negatives. Similarly, Liu et al.³² assert that false negative sample pairs compromise the performance of methods using InfoNCE contrastive loss. They propose a multi-view clustering framework, Deep Contrastive Multi-View Clustering under Semantic feature guidance (DCMCS), to reduce the impact of false negative pairs. Pang et al.³³ proposed an inter-channel pseudo-label refinement method (IPR). The authors constructed a clustering consistency matrix and set a threshold. Elements in the consistency matrix greater than the threshold retained the pseudo-labels corresponding to their respective clusters. In this way, IPR effectively eliminated noisy labels that exhibited inconsistent clustering results across different channels, while retaining more reliable pseudo-labels, thus mitigating the impact of false negatives.

While these methods alleviate the false negative problem and improve clustering performance, false negatives continue to introduce uncertainty in data representation and clustering. To address this, a cross-view decoupled contrastive learning mechanism is proposed. Unlike existing methods, this approach treats data-augmented samples as positive, without identifying negative ones. Consistency alignment is performed among positive samples from different views, reducing the impact of false negatives.

Fig. 1

Overview of the proposed network.

Methods

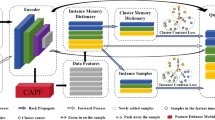
This section introduces the proposed prototype-driven contrastive graph clustering network, as shown in Fig. 1. The network consists of two primary components: the Multi-Scale Attribute Feature Aggregation Graph Contrastive Module (MSAFA) and the Multi-Scale Prototype-Driven Data Augmentation Graph Contrastive Module (MSPDA). In MSAFA, two dual-layer Multi-Layer Perceptron (MLP) graph encoders are constructed, each with unshared parameters, one of which incorporates randomly added noise. As a result, even with the same input, the two encoders produce different feature representations, generating dual-view outputs. In this module, aggregation calculations are performed to fuse low-level and high-level sample features, enhancing feature richness and distinguishability, and generating latent representations ${z^{{v_1}}}$ and ${z^{{v_2}}}$. A cross-view decoupled contrastive learning mechanism is introduced, using a mean squared error contrastive loss function that considers only positive samples to constrain the similarity between embeddings from different views. This enables the model to learn more robust and consistent representations across views. In MSPDA, the multi-scale views $h_1^{{v_1}}$, $h_2^{{v_1}}$ from Encoder 1 and those $h_1^{{v_2}}$, $h_2^{{v_2}}$ from Encoder 2 are processed through k-means clustering to generate prototypes (cluster centers) for each category. According to the clustering concept, samples clustered around prototypes are assumed to have high similarity. Thus, high-confidence sample sets are collected to generate augmented views. To mitigate the influence of false negative samples, a cross-view decoupled contrastive learning mechanism is used to align embeddings from different augmented views. This enables the model to learn features better suited for clustering tasks.

Detailed definitions of these modules are provided in the following sections.

Notations and problem definition

Given an undirected graph $G = \left\{ {X,E,A} \right\}$, $V = \left\{ {{v_1},{v_2},...,{v_N}} \right\}$ represents the set of N nodes in the graph G, E represents the set of edges in the graph G, and these nodes are partitioned into K categories. Here, $X \in {\mathbb {R}^{N \times D}}$ and $A = \left\{ {{a_{ij}}} \right\} \in {\mathbb {R}^{N \times N}}$ represents the attribute matrix and the adjacency matrix of the graph G respectively. The degree matrix is defined as $D = diag\left( {{d_1},{d_2},...,{d_N}} \right) \in {\mathbb {R}^{N \times N}}$, where ${d_i} = \sum \nolimits _{\mathrm{{i}} = {v_i},j = {v_j}} {{a_{ij}}}$, $\left( {{v_i},{v_j}} \right) \in E.$ Therefore, the Laplacian matrix is defined as $L = D - A$. $\hat{A} = A + I$ is the adjacency matrix of the graph G with self-loops added, and I is the $N \times N$ identity matrix. The corresponding symmetrically normalized graph Laplacian matrix is denoted as $\tilde{L} = I - {\hat{D}^{ - \frac{1}{2}}}\hat{A}{\hat{D}^{ - \frac{1}{2}}}$, and $\hat{D}$ is the degree matrix corresponding to $\hat{A}.$

Graph contrastive module with multi-scale attribute feature aggregation (MSAFA)

Graph contrastive learning methods typically learn node or graph representations by contrasting positive and negative sample pairs. For instance, CCGC¹¹ and CONVERT²⁰ use high-confidence pseudo-labels to guide the creation of positive and negative sample pairs, followed by designing contrastive loss functions to optimize the model. However, pairs created with inaccurate pseudo-labels are prone to the false negative problem. To address this issue, a decoupled contrastive learning mechanism is designed, treating all data-augmented samples as positive, eliminating the need for negative samples. Embedding representations from different data-augmented views are aligned, resulting in more robust and consistent embeddings. Based on this concept, it is essential to improve sample quality by eliminating noise and enhancing feature richness. Therefore, the MSAFA module incorporates noise processing, twin encoders for specific views, and a decoupled contrastive loss function.

Cui et al.³⁴ argue that the entanglement between filters and weight matrices does not improve performance in unsupervised graph representation learning and can harm training efficiency. They propose a carefully designed Laplacian smoothing filter to mitigate this issue and more effectively eliminate high-frequency noise in node features. Inspired by this approach, a Laplacian smoothing filter is also adopted to remove high-frequency noise and obtain the smoothed attribute matrix $\tilde{X}$, as shown in Eq. 1:

$$\begin{aligned} \tilde{X} = {\left( {I - \tilde{L}} \right) ^t}X, \end{aligned}$$

(1)

where $\tilde{L}$ represents the symmetric normalized graph Laplacian matrix, t is the number of layers of Laplacian filtering, I is the identity matrix, and X is the attribute matrix. The $\tilde{X}$ matrix is then fed into the MSAFA module for further computation.

The MSAFA module consists of two MLP encoders with identical structures but non-shared parameters, also known as twin encoders. Both encoders are configured with two layers, each containing the same number of neurons. The difference is that random noise $\varepsilon$ is added to the parameters of one encoder. After passing $\tilde{X}$ through the twin encoders, the sample-specific view embeddings are obtained, as shown in Eqs. 2 and 3 :

$$\begin{aligned} & h_1^{{v_1}},h_2^{{v_1}} = ML{P_1}\left( {\tilde{X},{\theta _1}} \right) , \end{aligned}$$

(2)

$$\begin{aligned} & h_1^{{v_2}},h_2^{{v_2}} = ML{P_2}\left( {\tilde{X},{\theta _2} + \varepsilon } \right) , \end{aligned}$$

(3)

where $h_1^{{v_1}}$ and $h_2^{{v_1}}$ refer to the low-level and high-level embedding views from Encoder 1, while $h_1^{{v_2}}$ and $h_2^{{v_2}}$ refer to the low-level and high-level embedding views from Encoder 2. ${\theta _1}$ and ${\theta _2}$ are the parameters of the encoders. Next, L2 normalization is applied to $h_1^{{v_1}}$, $h_2^{{v_1}}$, $h_1^{{v_2}}$, and $h_2^{{v_2}}$, as shown in Eqs. 4 and 5:

$$\begin{aligned} & h_1^{{v_1}} = \frac{{h_1^{{v_1}}}}{{\left\| {h_1^{{v_1}}} \right\| }}, h_2^{{v_1}} = \frac{{h_2^{{v_1}}}}{{\left\| {h_2^{{v_1}}} \right\| }}, \end{aligned}$$

(4)

$$\begin{aligned} & h_1^{{v_2}} = \frac{{h_1^{{v_2}}}}{{\left\| {h_1^{{v_2}}} \right\| }}, h_2^{{v_2}} = \frac{{h_2^{{v_2}}}}{{\left\| {h_2^{{v_2}}} \right\| }}. \end{aligned}$$

(5)

To enrich sample features and enhance their distinguishability, an aggregation function is used to fuse low-level and high-level features, resulting in the aggregated views ${z^{{v_1}}}$ and ${z^{{v_2}}}$, as shown below:

$$\begin{aligned} & {z^{{v_1}}} = {f_{agg}}\left( {h_1^{{v_1}},h_2^{{v_1}}} \right) , \end{aligned}$$

(6)

$$\begin{aligned} & {z^{{v_2}}} = {f_{agg}}\left( {h_1^{{v_2}},h_2^{{v_2}}} \right) . \end{aligned}$$

(7)

Where the ${f_{agg}}\left( \cdot \right)$ function represents the aggregation calculation, and in this paper, the aggregation function used is the concatenation operation.

In contrastive learning, representations of the same instance from different views should be more similar, while representations of different instances should be more distinct. Therefore, the similarity between cross-view representations ${z^{{v_1}}}$ and ${z^{{v_2}}}$ is calculated using Eq. 8, as shown below:

$$\begin{aligned} {Z_{ij}} = z_i^{{v_1}} \cdot { {z_j^{{v_2}}} ^\top }, \end{aligned}$$

(8)

where ${Z_{ij}}$ refers to the cosine similarity between node i in view ${z^{{v_1}}}$ and node j in view ${z^{{v_2}}}$ .

In summary, a decoupled contrastive learning mechanism is designed, treating all data-augmented samples as positive samples. Using the target loss function, cross-view positive samples with similar semantic content are consistently aligned, constraining the similarity between embeddings from different views. This enables the model to learn more robust and consistent representations across views. With this design, the following decoupled mean squared error contrastive loss function ${\pounds _{mcl}}$ is proposed, calculated using Eq. 9:

$$\begin{aligned} {\pounds _{mcl}} = \frac{1}{{{N^2}}}\sum \limits _{i = 1}^N {\sum \limits _{j = 1}^N {\left\| {{Z_{ij}} - {I_{ij}}} \right\| _2^2} }, \end{aligned}$$

(9)

when i equals j, ${I_{ij}}$ it equals 1; otherwise, ${I_{ij}}$ it is equal to 0.

Typically, existing contrastive learning methods rely on constructing positive and negative sample pairs, which, as noted in the introduction, can lead to false negative samples that hinder model optimization. The proposed decoupled contrastive learning mechanism effectively mitigates the impact of false negative samples.

Multi-scale prototype-driven data augmentation graph contrastive module (MSPDA)

Relying solely on the MSAFA module for feature learning may neglect the relationship between feature learning and clustering. Therefore, the clustering results from the MSPDA module are used to iteratively guide feature learning, gradually improving clustering performance. A multi-scale prototype-driven data augmentation method is designed based on the output of the MSAFA module. In the PCL method²³, prototypes are defined as “representative embeddings of a set of semantically similar instances.” The CPLAE method¹⁴ defines prototypes as the average of instance embeddings within each category. The ProPos and DPN methods^35,36 use cluster centers obtained via k-means as prototypes. Thus, samples clustered around a prototype are likely to belong to the same category. Inspired by this, the k-means algorithm is used to obtain the prototype $C_j^u$ for each category. The distance between samples and prototypes is calculated, and samples with distances below the threshold $\tau$ are collected, while boundary samples with greater distances are discarded. The remaining samples, referred to as high-confidence samples, form the high-confidence sample set $n < N$. The calculation formulas for $C_j^u$ and ${S^{{v_1}}},{S^{{v_2}}}$ are as follows:

$$\begin{aligned} & C_j^u = {f_{k - means}}(h), \end{aligned}$$

(10)

$$\begin{aligned} & s_i^u = \left\{ {\begin{array}{*{20}{c}} {h_{i,j}^u}& {d\left( {h_{i,j}^u,C_j^u} \right) < \tau }\\ 0& {else} \end{array}} \right. , \end{aligned}$$

(11)

where $u \in \left\{ {{v_1},{v_2}} \right\}$, $h \in \left\{ {h_1^u,h_2^u} \right\}$ and $j = \left[ {1,2, \ldots ,K} \right]$. $C_j^u$ represents the cluster center of the category j obtained by applying k-means on view u. The function $d\left( \cdot \right)$ represents the Euclidean distance calculation and $\tau$ is the threshold distance. $h_{i,j}^u$ represents the embedding of samples belonging to the category j in view u. Thus, the high-confidence sample set is defined as ${S^u} = \left\{ {s_1^u,s_2^u, \ldots ,s_n^u} \right\}$.

Inspired by ProPos³⁶, the k-means algorithm is used to obtain each cluster center as the prototype for each category. However, unlike ProPos, which uses prototypes as pseudo-labels to construct positive and negative sample pairs, this approach can lead to false negatives due to inaccurate pseudo-labels. To avoid generating false negatives, decoupled contrastive learning is adopted, considering all high-confidence samples as positive and aligning their embeddings across different views. This approach enables the model to learn more suitable features for clustering tasks. Thus, a decoupled mean squared error contrastive loss function is proposed for high-confidence sample sets, as shown below:

$$\begin{aligned} & {S_{ij}} = S_i^{{v_1}} \cdot { {S_j^{{v_2}}} ^\top }, \end{aligned}$$

(12)

$$\begin{aligned} & {\pounds _{hcl}} = \frac{1}{{{n^2}}}\left( {\sum \limits _{i = 1}^n {\sum \limits _{j = 1}^n {\left\| {S_{ij}^{\left( 1 \right) } - {I_{ij}}} \right\| _2^2 + \left\| {S_{ij}^{\left( 2 \right) } - {I_{ij}}} \right\| _2^2} } } \right) , \end{aligned}$$

(13)

where $S_{ij}^{\left( 1 \right) }$ and $S_{ij}^{\left( 2 \right) }$ represent the similarity matrices of high-confidence sample embeddings from the first and second layers of Encoder 1 and Encoder 2, respectively.

Therefore, the loss of the entire framework can be represented as:

$$\begin{aligned} \pounds = \alpha {\pounds _{mcl}} + \left( {1 - \alpha } \right) {\pounds _{hcl}}, \end{aligned}$$

(14)

where $\alpha$ is the balancing parameter.

The complete algorithm is summarized in Algorithm 1. Discriminative embeddings and excellent clustering results are obtained through the joint optimization of the MSAFA and MSPDA modules.

Algorithm 1

The training procedure of the proposed method

Experiments

Dataset description

Six widely adopted benchmark graph datasets¹⁶ were used, including CORA, CITESEER, BAT, EAT, UAT, and AMAP. Detailed descriptions of these datasets are presented in Table 1.

Table 1 Statistical information of the six benchmark graph datasets.

Table 2 Clustering performance comparison between the proposed method and 12 baseline methods across 6 datasets.

Table 3 Ablation study of the proposed method on 6 datasets.

Implementation details

Initialization settings for each module and dataset are configured to ensure fairness in the experiments. The Adam optimizer is used for encoder optimization, with learning rates adjusted according to each dataset. Specifically, the learning rate is set to 0.00005 for CORA, CITESEER and AMAP, 0.001 for BAT, 0.0005 for EAT, and 0.005 for UAT. An MLP is used as the encoder, with the number of neurons in each layer varying by dataset. For AMAP, the first layer has 500 neurons and the second 300. For CORA and CITESEER, the first layer has 800 neurons and the second 300. For BAT, the first layer has 50 neurons and the second 20. For EAT and UAT, the first layer has 200 neurons and the second 100. When using k-means to calculate cluster prototypes, the Euclidean method is used to compute distances between samples and cluster centers, with the average of each cluster serving as its prototype. To calculate the high-confidence sample set, samples are sorted by distance to the prototype in ascending order. Samples with distances below the threshold $\tau$ are selected to form the high-confidence sample set. Finally, the balancing parameter $\alpha$ for each dataset is adjusted when computing the overall target loss.

Evaluation metrics

Clustering performance is evaluated using four metrics: Accuracy (ACC), Normalized Mutual Information (NMI), Adjusted Rand Index (ARI), and F1-score (F1)³⁷. ACC represents the average correct classification rate of clustered samples. NMI measures the degree of information shared between clustering results and true labels. NMI quantifies the mutual dependence between two sets of labels, normalized between 0 and 1, where 0 indicates no shared information and 1 indicates identical clustering. ARI is a chance-corrected metric that measures the similarity between two clusterings. It adjusts the Rand Index (RI), which measures the consistency of whether two data points are classified into the same or different clusters. ARI corrects RI by considering the expected value of random classifications, with values ranging from − 1 to 1. A value of 1 indicates perfect clustering, 0 indicates random clustering, and negative values indicate performance worse than random. F1 is the harmonic mean of precision and recall, commonly used to evaluate classification performance. F1 can also be used to evaluate clustering performance for a specific category.

Fig. 2

2D Visualization Results of the CORA and CITESEER Datasets. The first row shows the visualization results of the CORA dataset, and the second row shows the visualization results of the CITESEER dataset.

Experimental results and analysis

The model is implemented on a computer running Windows 10 with an 11th Gen Intel(R) Core(TM) i5-11600KF @ 3.90 GHz CPU, 32 GB RAM, and a GeForce RTX 3060 Ti GPU. To reduce the effect of randomness, the proposed method is executed 10 times, and the mean and variance of the results are reported. The training epochs for all six datasets are set to 400.

Performance comparison

To verify the superiority of the proposed method, it is compared against 15 baseline methods. The baseline methods are divided into two categories: traditional graph clustering methods (MGAE³⁸, DAEGC³⁹, ARGA⁴⁰, SDCN⁴¹, DFCN⁴², AGE³⁴) and contrastive graph clustering methods (MVGRL⁸, AGC-DRR⁴³, ProGCL⁴⁴, CCGC¹¹, AutoSSL⁴⁵, CONVERT²⁰, GraphLearner⁴⁶, GLAC-GCN⁴⁷, GLAGC⁴⁸).

Table 2 presents the clustering performance comparison of the proposed method and the 12 baseline methods across 6 datasets. On the CORA dataset, the proposed method improves ACC by 0.45% to 39.76%, NMI by − 0.68% to 43.20%, ARI by 0.62% to 49.77%, and F1 by − 0.05% to 48.91% compared to the baseline methods. On the CITESEER dataset, the proposed method improves ACC by 1.8% to 10.57%, NMI by 0.96% to 10.89%, ARI by 1.24% to 13.37%, and F1 by -2.52% to 4.94%. On the AMAP dataset, ACC improves by 1.08% to 37.25%, NMI by 0.02% to 37.18%, ARI by − 0.94% to 32.98%, and F1 by − 1.74% to 40.32%. On the BAT dataset, ACC improves by − 0.08% to 40.38%, NMI by 0.12% to 35.82%, ARI by − 0.71% to 38.13%, and F1 by 0.17% to 48.30%. On the EAT dataset, ACC improves by 0.05% to 27.02%, NMI by 1.34% to 29.62%, ARI by 0.12% to 25.70%, and F1 by 0.41% to 37.01%. On the UAT dataset, ACC improves by 2.03% to 25. On the UAT dataset, ACC improves by 2.03% to 25.78%, NMI by 0.77% to 18.37%, ARI by − 0.68% to 17.78%, and F1 by 2.78% to 32.23%.

The proposed method shows improvements across all six datasets, particularly in the ACC and NMI metrics, where it achieved optimal results in most of the datasets. Moreover, contrastive graph clustering methods generally outperform traditional methods due to their enhanced feature representations, adaptability to graph complexity and heterogeneity, and robustness to noise-factors that collectively improve clustering effectiveness. Overall, the proposed method demonstrates superior clustering performance compared to the baseline methods.

Fig. 3

Sensitivity analysis of hyperparameter $\tau$ on six datasets.

Fig. 4

Sensitivity analysis of hyperparameter $\alpha$ on six datasets.

Ablation studies

This section further verifies the performance of the proposed method by analyzing the effectiveness of the MSAFA and MSPDA modules. In this experiment, “MSAFA” refers to the configuration where only the MSAFA module is used, “MSPDA” refers to the configuration with only the MSPDA module, and “Ours” refers to the combination of both MSAFA and MSPDA, representing the proposed prototype-driven data augmentation graph contrastive clustering network. As shown in Table 3, removing either module negatively impacts model performance, indicating that both multi-scale attribute feature aggregation and multi-scale prototype-driven data augmentation are crucial for effective graph clustering.

Visualization analysis

To demonstrate the superiority of the proposed method in clustering performance, the CORA and CITESEER datasets are selected for visualization using the t-SNE algorithm⁴⁹. The proposed method is compared with four baseline methods. As shown in Fig. 2, in the four baseline methods, samples of the same category are more dispersed, with many different category samples clustered together, resulting in relatively poor clustering within the same category. This may be due to the generation of false negative samples. In contrast, with the proposed method, samples of the same category are more tightly clustered, with fewer samples dispersed into other clusters, and the clustering between categories is more distinct. This demonstrates that the proposed method effectively addresses the problem of false negative samples.

Analysis of hyperparameter $\tau$

The impact of hyperparameters on the model is analyzed using six datasets. As shown in Fig. 3, $\tau$ values are selected from the range [0.1, 0.9] with a step size of 0.2, resulting in five total values. The results indicate that different $\tau$ values have a noticeable effect on the model’s performance. Overall, values in the range [0.5, 0.9] performed better.

Analysis of hyperparameter $\alpha$

Additionally, the parameter $\alpha$, which balances the contributions of the modules, is analyzed. The results are shown in Fig. 4. The experimental results show that different $\alpha$ values have little effect on the model’s performance. This demonstrates that the synergy between the two modules reduces the influence of hyperparameters, enhancing the model’s robustness.

Conclusion

This paper proposes a prototype-driven contrastive graph clustering network to address the issue of false negatives in contrastive clustering methods. The model enhances feature learning through the Multi-Scale Attribute Feature Aggregation (MSAFA) and Multi-Scale Prototype-Driven Data Augmentation (MSPDA) modules. A cross-view decoupled contrastive learning mechanism, utilizing a mean squared error contrastive loss function, focuses solely on positive samples, enabling the model to learn robust and consistent representations across views and improving clustering performance. Experiments on six datasets demonstrate the effectiveness and superiority of the proposed method over existing approaches. The results highlight its potential for tackling clustering challenges in high-dimensional and complex data, offering broad application prospects.

While the proposed method achieves promising results, there are still areas for further improvement. Inspired by CDC⁵⁰ and DGCN⁵¹, two key directions are identified:

• High-Quality Anchor Selection: As highlighted in CDC, the integration of a similarity-preserving regularizer to adaptively learn high-quality anchors has shown potential for improving clustering stability and scalability. Incorporating such mechanisms into our framework may enhance its capability to process large-scale and complex data efficiently.

• Heterophilic and Multimodal Data: Following the graph-agnostic clustering approach of DGCN, which simultaneously handles homophilic and heterophilic graphs, our future work will explore extending the proposed method to support heterogeneous datasets. This includes improving its robustness and generalization across diverse graph structures and multimodal information.

These enhancements aim to further improve the scalability, adaptability, and application scope of the proposed method, paving the way for its deployment in broader real-world scenarios.