Introduction

Roller bearings, which possess the advantage of high load carrying capacity and the ability to accommodate high rotational speeds, are widely used in rotating machinery. The stiffness characteristics of roller bearings are essential to reduce noise, heat, energy consumption, and wear. In practice, the stiffness of roller bearings can be influenced by many factors, such as rotational speed, clearance, and temperature. It is therefore necessary to ensure that the accurate stiffness of the roller bearing is estimated under various influencing factors to improve the reliability of the rotating machinery and determine the remaining life of the needle roller bearing.

Early studies on the stiffness of rolling element bearings, which were carried out by many researchers1,2,3, established different nonlinear relationships between the deformation and the external load for roller element bearings. For instance, Harris and Kotzalas3 proposed a power-law relationship between the deformation and the external load for a roller bearing. Recently, Demirhan and Kanber4 numerically investigated the stress and displacement distributions on a cylindrical roller bearing by using a two-dimensional finite element (FE) model with the consideration of steel shaft-bearing system.

Wei et al.5 carried out FE analyses on the pre-loaded hollow cylindrical roller bearing to investigate the effect of load, interference magnitude, and hollow ratio on the radial stiffness of the bearing. Guo and Parker6 developed a three-dimensional FE/contact mechanics model to determine the fully-populated stiffness matrix corresponding to two radial, one axial, and two angular coordinates of rolling element bearings. Chen and Wang7 proposed a method to study the radial stiffness of a cylindrical roller bearing with a corrected roller generator, which was derived by coupling this load-approach function into a complete mechanical model of the bearing. Hao et al.8 developed a finite element model for obtaining the displacement, raceway stress, and bearing stiffness characteristics of the inner and outer rings of the N1013M cylindrical roller bearing mounted in a bearing housing. Hao and his colleagues9 also experimentally investigated the time-varying stiffness of the cylindrical roller bearing due to thermal behavior, i.e. the warm-up process and different lubricant oil temperatures. Han et al.10 developed an analytical method for calculating the radial stiffness, load distribution, and displacement of the rotor center for the radially loaded ball and roller bearings, with consideration of two boundary positions of the inner ring supported on an even or odd number of rolling elements. Ri et al.11 investigated a numerical method for creating a comprehensive stiffness model of a cylindrical roller bearing, taking into account the radial clearance. The model was based on the Hertz contact and elastohydrodynamic lubrication theories. Hu et al.12 established a four-degree-of-freedom quasistatic model based on the basic analysis theory of rolling bearings. They analyzed the deformation, load distribution, stiffness, and fatigue life of an NU1014 cylindrical roller bearing with different roller profiles under various load and rotating speed conditions.

A failure analysis was carried out for a NA4848 needle roller bearing in a previous study13. In this study, experimental tests were carried out on a NA4848 needle roller bearing under different clearances, rotational speeds, and applied loads. The characteristics of the tested radial stiffness were analyzed. A finite element (FE) model of the NA4848 was established, and a mesh sensitivity study was performed to obtain mesh-independent FE results, such as relative displacements and contact stresses. The analytical and FE predictions were compared to the test results. The analytical predictions show good agreement with the test results for both relative displacements and stiffnesses. The finite element predicted values of relative displacements are 0.009–0.018 mm higher than analytically calculated and experimental results, and the finite element predicted values of stiffness are 36 × 106-164 × 106 N/mm higher than analytically calculated and experimental results. In addition, it is found that the predicted values of the finite element method for the contact stresses are about 400–600 MPa lower than the analytically calculated results. However, when taking the scatter into account, the FE analyses are likely to be used for predicting the remaining life of the NA4848 needle roller bearing in future studies.

Experimental

Test apparatus and procedure

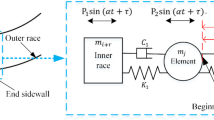
The test rig consisted primarily of a servo-electric motor, a universal joint coupling, a reducer, a fixture, the loading system, and a data acquisition system, as can be seen in Fig. 1. The needle roller bearing being tested was installed on the test rig using the fixture. The tested needle roller bearing was installed on the test rig by using the fixture. A radial load, in the range of 10-50kN, and a rotational speed, in the range of 0-15 rpm, were applied to the tested needle roller bearing. Two different assembly clearances, i.e. 0.05 mm and 0.1 mm, were tested for the tested needle roller bearing, respectively. Two Bojke BLG-30 N-485 laser displacement sensors were used to monitor the displacements of the inner and outer rings of the tested bearing, i.e., 1 and 2. All tests were carried out at room temperature, and lubricating oil was used for lubrication and cooling.

Test results

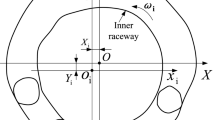
Hao et al.8 experimentally identified the nonlinear stiffness characteristics of the bearing. They used the function obtained from curve-fitting the data of radial load versus relative displacement of the inner ring. The relative displacement of the inner ring is r = 2 - 1. The stiffness can be calculated as the reciprocal of the differentiated curve-fitting function, as shown in Eq. 1.

$$\:{K}_{r}=\frac{1}{\frac{d{\delta\:}_{r}}{d{F}_{r}}}$$
(1)

where, Kr is the radial stiffness of the bearing, with a dimension of N/mm, and \(\:\frac{d{\delta\:}_{r}}{d{F}_{r}}\) is the reciprocal of the relative radial displacement of the bearing to the radial load, with a dimension of 1.

Fig. 1
figure 1

The test rig.

Full size image

Figure 2 shows the experimental relationship between the radial relative displacement, r, and the radial loading, Fr, at different rotational speeds and assembly clearances. It can be seen in Fig. 2 that the effects of the tested rotational speeds and clearances on the radial relative displacements are not significant. However, the radial relative displacements for the assembly clearance of 1.0 mm are slightly higher than those for the assembly clearance of 0.05 mm. Figure 3 shows the experimentally determined stiffnesses based on Eq. 1 versus radial loads at different rotational speeds and radial clearances. As shown in Fig. 3, the stiffness increases with the increase in radial load at different rotational speeds and assembly clearances.

Fig. 2
figure 2

Experimental relationship between the radial relative displacement, r, and the radial loading, Fr.

Full size image
Fig. 3
figure 3

Experimentally determined stiffnesses versus radial loads at different rotational speeds and radial clearances.

Full size image

FE analysis of dynamic stiffness of the needle roller bearing

Finite element modelling

A finite element model for the NA4848 was established using the commercial code ABAQUS 202214. The penalty function method was adopted for each contact pair, and the friction coefficient for each contact pair was taken as 0.1. Mesh sensitivity analyses were carried out using three types of mesh designs for the needle roller, as shown in Fig. 4. A general purpose linear brick element, with reduced integration (i.e. C3D8R element) was used to mesh the FE models15,16,17. The total number of C3D8R elements for the three designs were 80,640, 127,232, and 166,656, respectively. A radial load was applied to a central reference point on the inner ring, which was coupled to the inner surface of the ring. An encastre boundary condition was applied to the outer surface of the outer ring, constraining all degrees of freedom of the nodes on the bottom surface. A radial load of 50kN was applied to the FE model for the mesh sensitivity study. According to the test results, the rotational speed (in the range of 0-15 rpm) had no significant effect on displacement and stiffness. Therefore, a maximum experimental rotational speed of 15 rpm was used for all FE analyses. Figure 5 shows the contact pressure values corresponding to the number of elements. It can be seen in Fig. 5 that 127,232 C3D8R elements were found to be capable of giving sufficiently accurate results using relatively less calculation time.

Fig. 4
figure 4

Three types of mesh designs for the needle roller for total elements: (a) 80,640; (b)127,232; (c) 166,656.

Full size image
Fig. 5
figure 5

Contact pressure values corresponding to the number of elements.

Full size image

Finite element predictions

The FE-predicted von Mises stress distributions of each component of the NA4848 needle roller bearing with two radial clearances of 0.05 mm and 0.1 mm, a radial load of 50kN, and a rotational speed of 15 r/min are shown in Figs. 6 and 7, respectively. From Figs. 6 and 7, it can be seen that the von Mises stresses in the loaded needle roller are the highest with 428.5 MPa and 451.7 MPa for both clearances, followed by the outer ring with 194.2 MPa and 157.6 MPa for both clearances, the inner ring with 131.6 MPa and 155.4 MPa for both clearances, and the cage with the lowest stresses with 66.78 MPa and 53.69 MPa for both clearances, respectively. There is both rolling and sliding between the needle roller and the inner/outer rings, and the contact area is similar to an elongated ellipse.

Fig. 6
figure 6

The FE-predicted von Mises stress distributions of each component of the NA4848 needle roller bearing (clearances: 0.05 mm ): (a) needle roller; (b) outer ring; (c) inner ring; (d) cage.

Full size image
Fig. 7
figure 7

The FE-predicted von Mises stress distributions of each component of the NA4848 needle roller bearing (clearances: 0.1 mm): (a) needle roller; (b) outer ring; (c) inner ring; (d) cage.

Full size image

Figure 8 (a) and (b) show the von Mises stress versus rotational angle results with two assembly clearances for the nodes of each component of the NA4848 needle roller bearing that have the maximum von Mises stress. It can be seen in Fig. 8 that the levels of stress for the needle rollers are much higher than those for the other components of the NA4848 needle roller bearing for two radial clearances. The von Mises stress values of the rolling needle under two types of radial clearances are 530.453 MPa and 555.078 MPa, respectively. The von Mises stress values of the outer ring under two types of radial clearances are 198.687 MPa and 171.786 MPa, respectively. The von Mises stress values of the inner ring under two types of radial clearances are 138.316 MPa and 161.574 MPa, respectively. The von Mises stress values of the cage under two types of radial clearances are 71.4292 MPa and 70.8446 MPa, respectively.

Fig. 8
figure 8

Von Mises stress versus rotational angle results: (a) 0.05 mm radial clearance; (b) 0.1 mm radial clearance.

Full size image

The contact stress distributions of the needle roller with two radial clearances of 0.05 mm and 0.1 mm, a radial load of 50kN, and a rotational speed of 15 r/min are shown in Fig. 9. It can be seen that the contact stress of the needle roller with a radial clearance of 0.05 mm is 59.76 MPa, which is lower than the 65.69 MPa with a radial clearance of 0.1 mm.

Fig. 9
figure 9

The contact stress distributions of the needle roller with two radial clearances: (a) 0.05 mm and (b) 0.1 mm.

Full size image

Figure 10 show the von Mises stress and contact stress distributions along the needle roller total length under different radial clearances. It can be seen that the maximum stress occurs at the ends of the needle rollers at about 12 mm. The von Mises stress and contact stress profiles for the radial clearances of 0.05 mm are almost consistent with those for the radial clearances of 0.01 mm, except for the radial load is in a value of 30kN. Figure 11 shows the FE-predicted maximum von Mises/contact stresses versus radial loads under two radial clearances. As shown in Fig. 11, the relationship between the FE predicted maximum stress and radial load for the radial clearance of 0.1 mm is linear while that for radial clearance of 0.05 mm is nonlinear.

Fig. 10
figure 10

(a) von Mises stress and (b) contact stress distributions along the needle roller total length under different radial clearances.

Full size image
Fig. 11
figure 11

FE-predicted maximum von Mises/contact stresses versus radial loads under two radial clearances.

Full size image

Discussion

Harris and Kotzalas3 suggested a correlation between the applied radial load, Fr, and the maximum radial deflection, δmax, as shown in Eqs. 2and 3.

$$\:{F}_{r}=Z{K}_{n}{\delta\:}_{max}^{n}{J}_{r}\left(\epsilon\:\right)$$
(2)
$$\:{\delta\:}_{max}={\delta\:}_{r}-\frac{1}{2}{P}_{d}$$
(3)

Where Fr is the applied radial load on the needle roller bearing, Z is the number of the rollers in the needle roller bearing, Kn is the load-deflection factor, δr is the ring radial shift, Pd is the clearance of the bearing, Jr(ε) is the radial integral which is a function of load distribution factor, ε.

For the needle roller bearing with a given clearance and load, Eq. 2 can be solved by trial and error method, as demonstrated in Ref3. in detail. The value of parameter Kn in Eq. 2 is shown in Eqs. 4 and 5.

For steel roller-steel raceway contact,

$$\:{K}_{n}=0.46294{K}_{l}$$
(4)
$$\:{K}_{l}=7.86\times\:{10}^{4}{l}^{\frac{8}{9}}$$
(5)

where l is the effective length of the roller. The total roller lengths and logarithmic roller profiles for NA4848 were determined in our previous study13. Therefore, l can be taken as the straight portion of the crowned roller, with a value of 30 mm.

Figures 12 and 13 show the comparison between the tested and FE results of relative displacement and stiffness for different rotational speeds and radial clearances and those obtained from Harris and Kotzalas’s method, respectively. Multiply the finite element prediction of the maximum strain of the needle roller with the radius of the needle roller to obtain the finite element prediction of the relative displacement. It can be seen that the FE predicted the relative displacements are almost keep constant and larger than those obtained from test data and analytical results. The analytical calculated relative displacements show good agreement with test results for two different radial clearances. It can be seen that the predicted values of the FE method of stiffness are 36 × 106-164 × 106 N/mm higher than the analytical calculations and experimental results.

Fig. 12
figure 12

Comparison between the tested and FE results of relative displacement and stiffness for different rotational speeds and radial clearances and those obtained from Harris and Kotzalas’s method.

Full size image
Fig. 13
figure 13

Comparison between the tested and FE results of stiffness for different rotational speeds and radial clearances and those obtained from Harris and Kotzalas’s method.

Full size image

Based on Hertz’s contact theory18,19,20,21, the maximum contact stress between the needle roller and the bearing ring can be given by Eq. 6 and Eq. 7, respectively.

$$\:{\sigma\:}_{max}=\frac{2Q}{\pi\:lb}$$
(6)
$$\:b=3.35\times\:{10}^{-3}{\left(\frac{Q}{l\varSigma\:\rho\:}\right)}^{\frac{1}{2}}$$
(7)

where Q is the normal force between rolling body and raceway; b is the short half-axis of projection touching ellipse; Σρ is the sum of the curvatures, \(\:\varvec{\varSigma\:}\varvec{\rho\:}=\frac{1}{{\varvec{R}}_{\varvec{i}\varvec{n}\varvec{n}\varvec{e}\varvec{r}}}+\frac{1}{{\varvec{R}}_{\varvec{r}\varvec{o}\varvec{l}\varvec{l}\varvec{e}\varvec{r}}}\)

Figure 14 shows the comparison between the analytical and FE results of contact stress for different radial clearances. Contact stresses predicted by the FE method are 400–600 MPa lower than those calculated analytically.

Fig. 14
figure 14

Comparison between the analytical and FE results of contact stress for different radial clearances.

Full size image

Conclusion

This study proposed a numerical method for predicting the displacement and stiffness of a needle roller bearing under different conditions. Experimental and analytical validations were carried out to validate the numerical predictions. The concluding remarks are as follows:

(1) A testing system was established to obtain the displacement of the inner and outer rings of the tested bearing under different conditions. The experimental results show that the effect of the tested rotational speeds on the radial stiffness is not significant, and the minimum radial stiffness occurs when the radial loading is 20 kN.

(2) Finite element analyses were performed to predict the displacement and contact stress of the needle roller bearing under a load of 50kN and a rotational speed of 15 rpm. The FE results show that the maximum von Mises stress occurs on the needle rollers for both radial clearances. The von Mises stress and contact stress distributions along the total length of the needle roller show that the effect of radial clearance on the stress profile is insignificant, except for a radial load of 30kN. The relationships between the FE predicted maximum stress and radial load for radial clearances of 0.05 mm and 0.1 mm are linear and nonlinear, respectively.

(3) The FE and Harris and Kotzalas’s analytical predictions of the relative displacement and stiffness for different rotational speeds and radial clearances were compared with test results. Comparing with the test results, the FE results show significant overpredictions, while the analytical predictions show good agreement. The FE predicted contact stresses are lower than those obtained from analytical predictions.

(4) Due to the insufficient testing apparatus, the experimental tests were only carried out under relatively low rotational speeds, i.e., ≤ 15 rpm. Thus, we suggest considering an optimized testing method for high rotational speed conditions in future studies. The power loss and load distribution, which are essential for evaluating the remaining life of bearings, should also be investigated in the future.