Swin-transformer for weak feature matching

Abstract

Feature matching in computer vision is crucial but challenging in weakly textured scenes due to the lack of pattern repetition. We introduce the SwinMatcher feature matching method, aimed at addressing the issues of low matching quantity and poor matching precision in weakly textured scenes. Given the inherently significant local characteristics of image features, we employ a local self-attention mechanism to learn from weakly textured areas, maximally preserving the features of weak textures. To address the issue of incorrect matches in scenes with repetitive patterns, we use a cross-attention and positional encoding mechanism to learn the correct matches of repetitive patterns in two scenes, achieving higher matching precision. We also introduce a matching optimization algorithm that calculates the spatial expected coordinates of local two-dimensional heat maps of correspondences to obtain the final sub-pixel level matches. Experiments indicate that, under identical training conditions, the SwinMatcher outperforms other standard methods in pose estimation, homography estimation, and visual localization. It exhibits strong robustness and superior matching in weakly textured areas, offering a new research direction for feature matching in weakly textured images.

Introduction

Image feature matching plays a fundamental and crucial role in some computer vision tasks, for example, in functions like Simultaneous Localization and Mapping^1,2 and Structure-from-Motion^3,4, where it finds extensive applications. Feature detection, feature description, and feature matching are three essential steps in traditional image feature matching^5,6,7,8,9, and none of them can be omitted. Compared to traditional methods, deep learning technologies exhibit unique advantages in image feature matching. Deep learning can automatically learn features through extensive datasets, thus offering more vital generalization capabilities and eliminating the need for manual feature adjustments for different tasks. In image feature matching, deep learning methods could be broadly divided into two categories. One category uses deep learning to improve the traditional feature detection process, including replacing classic feature detectors^10,11, substituting traditional feature descriptors^12,13,14, or even replacing both feature detectors and descriptors simultaneously^15,16. These methods are typically implemented using Convolutional Neural Network (CNN) architectures. The other category completely abandons traditional feature detectors and descriptors, directly outputting the final matching results through end-to-end training^17,18,19. The design inspiration for this approach comes from the increasingly popular Transformer model in recent years, with its core focus on feature matching using the attention mechanism. For weakly textured scenes, traditional methods require projecting patterns into the scene for feature matching, necessitating additional equipment and operations^20,21.

In deep learning, the convolutional neural network (CNN) is the mainstream backbone for extracting high-dimensional features. Since the advent of AlexNet²², CNNs have almost monopolized various computer vision tasks. In recent years, influenced by Transformers²³, the application of Transformers in computer vision has been extensively studied, and some works^{24,25,26,27,28,29,30,31}, have achieved remarkable results. Among them, inspired by the Vision Transformer (ViT)³⁰, the proposed Swin Transformer²⁸ introduced a revolutionary backbone network to the field of computer vision. Swin-Transformer can replace CNNs as a new choice for feature extraction²⁸. In image feature matching, the SuperGlue¹⁹ method utilizes a graph neural network as its backbone, representing feature points as graph nodes, with the connections between nodes indicating potential matching relationships. The LoFTR¹⁷ method employs a ResNet network as its backbone for feature extraction, while MatchFormer¹⁸ combines convolutional networks and Transformers for image feature extraction. Although these methods are effective in extracting image features, they do not specifically enhance weakly textured regions. Moreover, they adopt a global self-attention mechanism, which tends to overlook weak texture information²⁶, resulting in a limited number of feature matches in weakly textured scenes. Therefore, we propose an innovative image feature matching method, SwinMatcher, which uses a Swin-Transformer integrated with cross-attention and positional encoding mechanisms instead of traditional CNNs to extract high-dimensional image features. This allows the local self-attention mechanism to enhance the learning of weak textures, maximally preserving the features of weak textures; for scenes with repetitive patterns, the cross-attention mechanism can learn the relationship between weak texture feature matches across two images. After constructing a confidence matrix through a feature pyramid network to obtain coarse-grained feature matches, our designed optimization module refines these coarse matches, yielding high-quality sub-pixel match results. SwinMatcher, compared to traditional feature-matching methods, involves more straightforward steps and achieves a more significant number of feature matches in weakly textured scenes compared to other methods based on the same principle. Figure 1 demonstrates the superiority of SwinMatcher. The heatmap shows that SwinMatcher captures more features more effectively in weak texture areas. Additionally, the matching results indicate that our method yields more correspondences.

Figure 1

SwinMatcher can detect more correspondences compared to LoFTR.

We summarize our innovation and contributions in three aspects:

• A new feature-matching method called SwinMatcher has been designed. This method combines local self-attention, global cross-attention, and positional encoding to accurately identify and match weak texture features, thereby achieving high-precision matching of weak textures.

• Propose a local self-attention mechanism to learn from weakly textured areas to preserve the features of weak textures maximally.

• A new optimization module of refining coarse-grained matches achieves precise matching at the sub-pixel level.

Related work

The traditional feature detection stage is omitted in feature matching without detectors. Instead, high-level features of images are extracted through CNNs, dense descriptors are directly generated, or dense feature matching is performed.^32,33 first adopted a learning-based approach, using contrastive loss to learn pixel-level feature descriptors. Like detector-based methods, the matching of dense descriptors is typically achieved through nearest neighbor search. NCNet³⁴ adopted a different strategy, directly learning dense correspondences through an end-to-end learning method. This approach constructs a 4D cost volume to enumerate all potential image matches and normalizes them through 4D convolution to ensure neighborhood consistency among matches. Sparse NCNet³⁵ improved upon NCNet by introducing sparse convolutions to enhance efficiency. DRC-Net³⁶ continued this line of research, utilizing CNN feature maps of two different resolutions to construct two 4D matching tensors and fusing them to achieve high-confidence feature matching while proposing a coarse-to-fine matching strategy to improve the accuracy of dense matching. However, despite the 4D cost volume considering all possible matches, the receptive field of 4D convolutions is still limited to the neighborhood area of each match. LoFTR¹⁷, while maintaining neighborhood consistency, also leverages the global receptive field from the Transformer to achieve international consistency among matches, which was not fully utilized in NCNet and its successors. MatchFormer¹⁸ improved upon the structure of the Transformer layers from LoFTR¹⁷, where LoFTR¹⁷ first uses a ResNet network to extract features and then processes them through Transformer layers, whereas MatchFormer¹⁷ combines CNN and Transformer layers.

In recent years, the Transformer model²³ has received widespread attention in computer vision. In processing visual tasks, such as image classification^30,37,38, object detection^39,40,41, and segmentation^42,43, Transformers explore different regions through global interactions, thereby learning about critical areas in images. Given its excellent performance, Transformers have also been applied to image feature matching^17,18,19. For instance, SuperGlue¹⁹, LoFTR¹⁷, and MatchFormer¹⁸ all utilize self-attention and cross-attention mechanisms to process features extracted from CNNs. However, In certain vision tasks that rely on local features, such as object detection, semantic segmentation, and feature-matching, the global attention mechanism of Transformers tends to focus excessively on the overall image information while being less effective at capturing details in local regions²⁶. Additionally, the SwinTransformer²⁸, which implements attention mechanisms within windows and thus preserves local features well, loses global information. To address the above issues, we propose the SwinMatcher method, which employs a local self-attention mechanism to learn about weak texture areas, thereby maximally preserving the features of weak textures. At the same time, we also use cross-attention and positional encoding mechanisms to understand the image features correctly matched between two scenes, achieving higher matching precision. Finally, to obtain sub-pixel level matches, we introduce a matching optimization algorithm that calculates the final feature matches by mutually computing the spatial expected coordinates of the local two-dimensional heat maps of correspondences to achieve efficient and robust weak texture feature matching.

Figure 2

The overall process of SwinMatcher.

Method

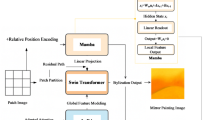
To achieve feature matching between two images, ${{I}^{A}}$ and ${{I}^{B}}$, we propose the SwinMatcher method, the overall process of which is illustrated in Fig. 2. SwinMatcher comprises three main modules: First, the SwinMatcher Backbone Module extracts coarse-grained feature maps ${{\tilde{F}}^{A}}$ and ${{\tilde{F}}^{B}}$, and fine-grained feature maps ${{\hat{F}}^{A}}$and ${{\hat{F}}^{B}}$ (Note: When performing cross-attention, the local self-attention results of Image ${{I}^{A}}$ are used as the Q values for cross-attention, while the local self-attention results of Image ${{I}^{B}}$ are used as the K and V values); next, the Matching Module uses the mutual nearest neighbor to match coarse-grained feature maps ${{\tilde{F}}^{A}}$ and ${{\tilde{F}}^{B}}$, generating a confidence matrix ${{P}_{c}}$ and producing coarse-grained match predictions ${{M}_{c}}$ based on a confidence threshold. Finally, for each selected coarse-grained match prediction $(\tilde{i},\tilde{j})\in {{M}_{c}}$, the Refine Module obtains the final sub-pixel match results ${{M}_{f}}$ by mutually calculating the spatial expected coordinates of local two-dimensional heat maps in the fine-grained feature maps ${{\hat{F}}^{A}}$and ${{\hat{F}}^{B}}$.

SwinMatcher backbone

Figure 3 presents a detailed overview of the SwinMatcher Backbone architecture. The first step of this architecture involves processing the input grayscale image through a convolutional partition module, dividing it into non-overlapping blocks, similar to the Vision Transformer(ViT)³⁰. In our implementation, images are segmented into multiple $5\times 5$ windows. These windows’ raw value features are then passed through a linear embedding layer, projecting the features into a high-dimensional space (denoted as ${{C}_{1}}$). The input images $I\in {{\mathbb {R}}^{2\times H\times W\times 1}}$ (2, H, W, 1, representing the number of images, height, width, and channels) are processed through the Patch Partition layer, resulting in output ${{I}_{1}}\in {{\mathbb {R}}^{2\times \frac{H}{2}\times \frac{W}{2}\times {{C}_{1}}}}$. We use ${{S}_{SM{{B}_{i}}}}(\cdot )$ to process each stage and apply the feature pyramid network $FPN(\cdot )$ to extract image features:

$$\begin{aligned} & {{I}_{i+1}}={{S}_{SM{{B}_{i}}}}({{I}_{i}}),\text i=1,2,3,4 \end{aligned}$$

(1)

$$\begin{aligned} & \quad \{({{\tilde{F}}^{A}},{{\tilde{F}}^{B}}),({{\hat{F}}^{A}},{{\hat{F}}^{B}})\}=FPN({{I}_{i}}),\text i=1,2,3,4 \end{aligned}$$

(2)

This results in feature maps of the original images at 1/8 and 1/4 of their sizes.

Figure 3

SwinMatcher backbone module.

SwinMatcher block

In the SwinMatcher Block, the attention mechanism is central, encompassing self-attention and cross-attention. The self-attention mechanism is designed concerning the Swin Transformer²⁸, an improvement on the standard multi-head self-attention of the original Transformer²³. The self-attention mechanism in Transformers calculates the correlation between all positions in a sequence on a global scale. Unlike CNNs, which are specifically designed to capture local patterns, Transformers lack an explicit local inductive bias. As a result, when processing fine-grained local features, it may neglect local feature information at distant positions relative to the current features. This leads to smaller weights for distant local features after multiple layers of self-attention, and even combining CNNs cannot guarantee amplification of these distant local features. To address this issue, we employ local self-attention, which restricts the distance between features, ensuring that distant feature weights are preserved. For an image input of size $H\times W\times C$, the Swin Transformer first reshapes it into a feature map of size $\frac{HW}{{{M}^{2}}}\times {{M}^{2}}\times C$, which is then divided into $M\times M$ non-overlapping local windows, with $\frac{HW}{{{M}^{2}}}$ representing the number of windows. Self-attention is then computed for each window. For local window features $X\in {{\mathbb {R}}^{{{M}^{2}}\times C}}$, matrices Q, K, V are explicitly calculated for local attention:

$$\begin{aligned} Q=X{{P}_{Q}}, K=X{{P}_{K}}, V=X{{P}_{V}} \end{aligned}$$

(3)

where ${{P}_{Q}},{{P}_{K}},{{P}_{V}}$ is a shared projection matrix across different windows. Typically, $Q,K,V\in {{\mathbb {R}}^{{{M}^{2}}\times d}}$. The attention matrix calculated within the local window through the self-attention mechanism is:

$$\begin{aligned} Attention(Q,K,V)=SoftMax(Q{{K}^{T}}/\sqrt{d}+B)V \end{aligned}$$

(4)

where B is a learnable relative position encoding, denoted as W-MSA for window-based multi-head attention. Next, a multi-layer perceptron (MLP), which consists of two fully connected layers connected by a GELU non-linearity for further feature transformation, is used. Layer normalization (LN) is added before W-MSA and the MLP, with residual connections. The entire process is represented as:

$$\begin{aligned} & X'=W\text {-}MSA(LN(X))+X \end{aligned}$$

(5)

$$X'\, = \,MLP(LN(X))\, + \,X$$

(6)

However, conducting self-attention only within windows leaves no interaction between different windows. Therefore, self-attention between windows is needed, which is achieved by the shifted window multi-head attention mechanism (SW-MSA)²⁸. The shifted window moves the previously divided windows by ($\left\lfloor M/2 \right\rfloor ,\left\lfloor M/2 \right\rfloor$) pixels. The process is similar to S-MSA, represented as:

$$\begin{aligned} & X'=SW\text {-}MSA(LN(X))+X \end{aligned}$$

(7)

$$X'\, = \,MLP(LN(X))\, + \,X$$

(8)

So, W-MSA and SW-MSA constitute a complete local self-attention mechanism, as shown in Fig. 4a.

Figure 4

SwinMatcher block.

To enhance the connection between the features of two images to be matched, we adopt a local self-attention mechanism and introduce a cross-attention mechanism. The primary function of cross-attention is to learn the similarity between pairs of images. Due to the potential inconsistency in feature positions between two images, we opt for a global cross-attention mechanism to address this challenge. The Q values for cross-attention are obtained by passing the local self-attention results of Image ${{I}^{A}}$ through a linear layer, while the K and V values are derived by passing the local self-attention results of Image ${{I}^{B}}$ through another linear layer, as shown in Fig. 4b. Additionally, both local self-attention and cross-attention mechanisms can be independently repeated N times as needed to strengthen the effectiveness of feature extraction and matching.

Matching and coarse to fine module

The most common method for feature matching is mutual nearest neighbor (mutual N.N.) matching, which requires that the matched features are each other’s nearest neighbors.

$$\begin{aligned} (f_{ab}^{A},f_{cd}^{B}) mutual N.N.\Leftrightarrow \left\{ \begin{matrix} (a,b)=argmi{{n}_{ij}}\left\| f_{ij}^{A}-f_{cd}^{B} \right\| \\ (c,d)=argmi{{n}_{kl}}\left\| f_{ab}^{A}-f_{kl}^{B} \right\| \\ \end{matrix} \right\} \end{aligned}$$

(9)

Here, $f_{A}^{ab}$ represents the feature points in image ${{I}_{A}}$, and $f_{B}^{ab}$ represents the feature points in image ${{I}_{B}}$. (i, j, k, l) denote the position indices in the matching score matrix, where (i, j) corresponds to the position index of a feature point in image ${{I}_{A}}$, and (k, l) corresponds to the position index of a feature point in image ${{I}_{B}}$. By applying the hard mutual nearest neighbor condition described in Eq. (9) to filter matches, the majority of candidate matches can be eliminated. However, this approach is not suitable for end-to-end trainable methods because such decisions are non-differentiable. Therefore, a softer mutual nearest neighbor filtering $M(\centerdot )$ is employed, which not only makes the decision process smoother but also enhances differentiability, enabling the calculation of feature matching scores.

$$\begin{aligned} \hat{c}=M(c), {{\hat{c}}_{ijkl}}=r_{ijkl}^{A}r_{ijkl}^{B}{{c}_{ijkl}} \end{aligned}$$

(10)

Here, $r_{A}^{ijkl}$ and $r_{B}^{ijkl}$ represent the ratios of the score for a specific match ${{c}_{ijkl}}$ to the best score for each dimension corresponding to images ${{I}_{A}}$ and ${{I}_{B}}$, respectively.

$$\begin{aligned} r_{ijkl}^{A}=\frac{{{c}_{ijkl}}}{ma{{x}_{ab}}{{c}_{abkl}}}, r_{ijkl}^{B}=\frac{{{c}_{ijkl}}}{ma{{x}_{cd}}{{c}_{ijcd}}} \end{aligned}$$

(11)

This soft mutual nearest neighbor filtering acts as a gating mechanism on the input by reducing the matching scores of pairs that are not mutual nearest neighbors.

We define two scores, obtained from the relevant feature map c by performing a sofmax operation along the dimensions corresponding to images ${{I}_{A}}$ and ${{I}_{B}}$.

$$\begin{aligned} s_{ijkl}^{A}=\frac{exp({{c}_{ijkl}})}{\sum \nolimits _{ab}{exp({{c}_{abkl}})}}, s_{ijkl}^{B}=\frac{exp({{c}_{ijkl}})}{\sum \nolimits _{cd}{exp({{c}_{ijcd}})}} \end{aligned}$$

(12)

Note that the score s here is positive and normalized using the softmax function, ensuring $\sum \nolimits _{ab}{s_{ijab}^{B}}=1$. Therefore, these scores can be interpreted as discrete conditional probability distributions, representing the probability that $f_{A}^{ij}$ and $f_{B}^{ij}$ are matched given the position (i, j) in image ${{I}_{A}}$ or the position (k, l) in image ${{I}_{B}}$. If we denote the discrete random variable representing the matching positions (unknown a priori) as (I, J, K, L), and (i, j, k, l) as a specific matching position, then:

$$\begin{aligned} \mathbb {P}(K=k,L=l|I=i,J=j)=s_{ijkl}^{B}, \mathbb {P}(I=i,J=j|K=k,L=l)=s_{ijkl}^{A} \end{aligned}$$

(13)

Then, a hard assignment in one direction can be performed by selecting the most probable match: $f_{kl}^{B}\text { assigned to a given }f_{ij}^{A}\Leftrightarrow (k,l)=argma{{x}_{cd}}\mathbb {P}(K=c,L=d|I=i,J=j)=argma{{x}_{cd}}s_{ijcd}^{B}$. Similarly, the matches of $f_{kl}^{B}$ to $f_{ij}^{A}$ can be obtained.

Through the SwinMatcher Backbone stage, we obtained feature maps of 1/8 and 1/4 sizes. For coarse-grained matching on the 1/8 size feature map, we used a differentiable matching layer and a dual softmax operation. Initially, a score matrix S is computed for transformed features via $S(i,j)=\frac{1}{\tau }\cdot \left\langle {{{\tilde{F}}}^{A}}(i),{{{\tilde{F}}}^{B}}(j) \right\rangle$, where $\tau$ is a temperature coefficient. Applying softmax on both dimensions of S (referred to as dual softmax), we obtain the probability of soft mutual nearest neighbor matching. With dual softmax, the matching probability ${{P}_{c}}$ is:

$$\begin{aligned} {{P}_{c}}(i,j)=soft\max {{(S(i,\cdot ))}_{j}}\cdot soft\max {{(S(\cdot ,j))}_{i}} \end{aligned}$$

(14)

Based on the confidence matrix ${{P}_{c}}$, we select matches with confidence above threshold ${{\theta }_{c}}$ and further use Mutual Nearest Neighbor (MNN) criteria to filter potential outlier coarse-grained matches. We represent the coarse-grained match prediction as:

$$\begin{aligned} {{M}_{c}}=\left\{ (\tilde{i},\tilde{j})|\forall (\tilde{i},\tilde{j})\in MNN({{P}_{c}}),{{P}_{c}}(\tilde{i},\tilde{j})\ge {{\theta }_{c}} \right\} \end{aligned}$$

(15)

After establishing coarse-grained matches, we use an association-based method to refine coarse matches to the resolution of the original image. For each coarse match $(\tilde{i},\tilde{j})$, we first locate its position $(\hat{i},\hat{j})$ on the 1/4 size fine-grained feature maps ${{\hat{F}}^{A}}$ and ${{\hat{F}}^{B}}$, then crop two sets of local windows of size $w\times w$. Generating two transformed local feature maps $\hat{F}_{tr}^{A}(\hat{i})$ and$hat{F}_{tr}^{B}(\hat{j})$ centered around $\hat{i}$ and $\hat{j}$, we associate the center vector of $\hat{F}_{tr}^{A}(\hat{i})$ with all vectors of $\hat{F}_{tr}^{B}(\hat{i})$, resulting in a probability heat map representing each pixel in $\hat{j}$’s neighborhood matched with $\hat{i}$. By computing the expectation over the probability distribution, we achieve the final position ${\hat{j}}'$ with sub-pixel precision on ${{I}^{B}}$. Similarly, we also calculate the sub-pixel accuracy matching positions ${\hat{i}}'$ on ${{I}^{A}}$. Then tally all correspondences of $\left\{ \left( {\hat{i}}',{\hat{j}}' \right) \right\}$ to obtain the last fine-grained matches ${{M}_{f}}$.

Loss function

The final loss includes coarse-grained loss and fine-grained loss: $L={{L}_{c}}+{{L}_{f1}+{{L}_{f2}}}$. We have tested different loss weights, such as $L={0.5{L}_{c}}+{{L}_{f1}}+{{L}_{f2}}$, $L={{L}_{c}}+{2{L}_{f1}} + {{L}_{f2}}$ and $L={{L}_{c}}+{{L}_{f1}} + {2{L}_{f2}}$. But the final training performance was slightly weaker than $L={{L}_{c}}+{{L}_{f1}+{{L}_{f2}}}$.

The coarse-grained loss function is the negative log-likelihood loss on the confidence matrix ${{P}_{c}}$, returned by the dual softmax operation. We use camera poses and depth maps to compute the real label values for the confidence matrix during training. We define the true coarse-grained matches $M_{c}^{gt}$ as mutual nearest neighbors between two sets of grids at 1/8 resolution. The distance between the two grids is measured by the reprojection distance of their center positions. We minimize the negative log-likelihood loss of the grids in $M_{c}^{gt}$:

$$\begin{aligned} {{L}_{c}}=-\frac{1}{\left| M_{c}^{gt} \right| }\sum \limits _{(\tilde{i},\tilde{j})\in M_{c}^{gt}}{\log {{P}_{c}}}(\tilde{i},\tilde{j}) \end{aligned}$$

(16)

We use L2 loss for fine-grained level refinement, similar to^13,44. For each point $\hat{i}$ to be matched, we also measure its uncertainty by calculating the total variance ${{\sigma }^{2}}(\hat{i})$ of the corresponding heatmap. The objective is to optimize the fine-grained positions with lower uncertainty, resulting in a weighted loss function:

$$\begin{aligned} {{L}_{f1}}=\frac{1}{\left| {{M}_{f}} \right| }\sum \limits _{(\hat{i},{\hat{j}}')\in {{M}_{f}}}{\frac{1}{{{\sigma }^{2}}(\hat{i})}{{\left\| {\hat{j}}'-{{{{\hat{j}}'}}_{gt}} \right\| }_{2}}} \end{aligned}$$

(17)

Here, ${{{\hat{j}}'}_{gt}}$ is calculated by converting each $\hat{i}$ from $\hat{F}_{tr}^{A}(\hat{i})$ to $\hat{F}_{tr}^{B}(\hat{j})$ using real camera poses and depth information. When calculating ${{L}_{f1}}$, if $\hat{i}$’s converted position falls outside of $\hat{F}_{tr}^{B}(\hat{j})$’s local window, we ignore the pair $(\hat{i},{\hat{j}}')$. The calculation process for matching point is the same:

$$\begin{aligned} {{L}_{f2}}=\frac{1}{\left| {{M}_{f}} \right| }\sum \limits _{({\hat{i}}',\hat{j})\in {{M}_{f}}}{\frac{1}{{{\sigma }^{2}}(\hat{i})}{{\left\| {\hat{i}}'-{{{{\hat{i}}'}}_{gt}} \right\| }_{2}}} \end{aligned}$$

(18)

During training, the gradient is not backpropagated through ${{\sigma }^{2}}(\hat{i})$ and ${{\sigma }^{2}}(\hat{j})$.

Experiments

We use ScanNet⁴⁴ for our indoor training dataset, and outdoor training, we use MegaDepth⁴⁵. We adopt methods from LoFTR¹⁷ and SuperGlue¹⁹ for sampling images for training, with the overlap scores of these image pairs ranging between 0.4 and 0.8. The SwinMatcher model uses the AdamW optimizer, with an initial learning rate of $3.5\times {{10}^{-4}}$ and a batch size 8. It was trained for 90 epochs on 8 RTX 2080 Ti GPUs until convergence. The entire model underwent end-to-end training with randomly initialized weights. The local self-attention mechanism was applied four times during training, and the cross-attention mechanism was used four times. Additionally, we set the parameter ${{\theta }_{c}}$ to 0.2, with both the local self-attention window size and the fine-grained matching window size set to $5\times 5$.

Pose estimation

Indoor image matching faces challenges due to lack of texture, high self-similarity, and complex three-dimensional geometric structures. To demonstrate the effectiveness of SwinMatcher in pose estimation for indoor scenes, we selected the ScanNet⁴⁴ dataset and our dataset of weakly textured indoor wall images for experimentation. Table 1 compiles the area under the curve (AUC) of pose error and precision for various methods, where SwinMatcher outperforms the previous best method, showing significant improvements in AUC@${5}^{\circ }$, AUC@${20}^{\circ }$, and precision, with a 1.71% increase in AUC@${20}^{\circ }$ in particular. Experiments were conducted for outdoor pose estimation using the MegaDepth⁴⁵ test dataset and our weakly textured outdoor wall images dataset. Table 2 similarly compiles the AUC of pose error and accuracy for various methods, with our method showing improvements in AUC@${10}^{\circ }$, AUC@${20}^{\circ }$, and precision, notably achieving a 2.16% increase in AUC@${20}^{\circ }$.

Table 1 Indoor pose estimation on ScanNet⁴⁴.

Table 2 Outdoor pose estimation on MegaDepth⁴⁵.

Homography estimation

We conducted unified homography estimation tests on the HPatches⁵⁵ dataset and our weakly textured indoor wall images dataset. In the tests, a reference image was paired with five other photos. Feature matching was performed for each image pair, and homography estimation was calculated using OpenCV, adopting the RANSAC method to enhance robustness. Table 3 compiles the area under the curve (AUC) of angular error, precision, and recall rate at different thresholds (3 pixels, 5 pixels, 10 pixels) for various methods. Our method outperformed others in AUC@3px, AUC@10px, precision, and recall rate, with the most remarkable improvement observed in AUC@10px, increasing by 2.22%.

Table 3 Homography estimation on the HPatches⁵⁵ and weakly textured indoor wall datasets.

Visual localization

Similar to previous work, we conducted experiments on visual localization. We evaluated our method on the Long-Term Visual Localization Benchmark⁵⁶, which focuses on benchmarking visual localization methods under different conditions, such as day-to-night changes, scene geometry changes, and indoor scenes with large areas of texture-less regions. The evaluation was performed using the HLoc⁵⁷ method. Table 4 compiles the localization accuracy at angles of ${10}^{\circ }$ and distances of 0.25m, 0.50m, and 1m under DUC1 and DUC2 conditions. Our method showed significant improvements, especially under DUC2, where the accuracy increased by 1.59%.

Table 4 Visual localization using the HLoc⁵⁷ method.

Robustness experiments

To evaluate the robustness of SwinMatcher under changes in illumination and viewpoint, we conducted feature-matching tests using the HPatches⁵⁵ and our weakly textured indoor wall dataset. We calculated the Mean Matching Accuracy (MMA) and the correspondences from a 1-pixel to 10-pixel threshold¹³. Tables 5 and 6 compile the number of correspondences for different methods on the HPatches⁵⁵ and our weakly textured indoor walls dataset, where the SwinMatcher method performed the best, having the highest number of correspondences, averaging an improvement of 14.09% over the best. Figure 5 compiles the average matching accuracy of other methods under various lighting conditions and viewpoint changes on the HPatches⁵⁵ and our weakly textured indoor walls dataset. Under changes in illumination, our method had the best matching accuracy from 1 pixel to 10 pixels. In the case of viewpoint changes, our method had higher matching accuracy than other end-to-end methods, slightly lower than the detector-based method SuperPoint+SuperGlue. Considering different lighting and viewpoint changes, below a 5-pixel threshold, our method exhibited the highest matching accuracy, and in the 6 to 10-pixel range, it was higher than other end-to-end methods and slightly lower than the detector method SuperPoint+SuperGlue. These experimental results fully demonstrate the high robustness of SwinMatcher.

Table 5 The number of correspondences on the HPatches⁵⁵ indoor dataset.

Table 6 The number of correspondences on the dataset of weakly textured indoor wall images.

Figure 5

The average matching accuracy under illumination and viewpoint changes, as well as overall, on the HPatches⁵⁵ and weakly textured indoor wall dataset.

Table 7 Pose estimation on the SIM2E⁵⁸ dataset.

Pose estimation on the SIM2E dataset

We conducted pose estimation experiments on the newly released 2022 SIM2E⁵⁸ dataset. We compared our method with detector-based methods, SIFT⁷ + SuperGlue¹⁹ and SuperPoint⁴⁷ + SuperGlue¹⁹, as well as detector-free methods, LoFTR¹⁷, MatchFormer¹⁸, and Aspanformer⁴⁹. As shown in Table 7, our method achieved the highest performance in AUC@${10}^{\circ }$, AUC@${15}^{\circ }$, and AUC@${20}^{\circ }$.

Visualization

To visually demonstrate the superiority of our method, we compared the feature-matching results with the benchmark method LoFTR. We compared the performance of the feature-matching in indoor and outdoor objects, walls, and walls under different lighting conditions, both indoor and outdoor. Figure 6 intuitively shows the feature-matching performance of our method compared to others in indoor and outdoor scenarios, with our method achieving a higher number of correspondences. Figure 7 intuitively shows the matching performance of our method compared to others on indoor and outdoor weakly textured walls, with our method achieving a higher number of correspondences and detecting more weak texture information, such as performing feature matching on trees outdoors. Figure 8 intuitively shows the matching performance of our method compared to others on indoor and outdoor weakly textured walls under different lighting conditions, with our method detecting a higher number of correspondences and more weak texture information.

Figure 6

The feature matching performance of indoor and outdoor objects, our method can detect more correspondences.

Figure 7

The feature matching performance on indoor and outdoor walls, our method can detect more weak texture information.

Figure 8

The feature matching performance on indoor and outdoor walls under different lighting conditions, our method can detect more weak texture information.

Weak texture region matching

We validated the effectiveness of SwinMatcher for matching weak texture regions on the ScanNet⁴⁴ weak texture dataset. First, we captured the local texture features of the image using the Gray-Level Co-occurrence Matrix (GLCM). Then, we distinguished between high and low-texture regions by analyzing contrast and homogeneity. The comparison results are shown in Fig. 9. In the contrast map, low-texture areas are represented in cool colors, while high-texture regions are shown in warm colors. Conversely, in the homogeneity map, low-texture areas are depicted in warm colors and high-texture regions in cool colors. Figure 9 demonstrates that most of the image consists of low-texture regions. Yet, our method effectively performs feature matching in these low-texture areas, with many matching feature points. Therefore, our method proves to be effective for matching between weak texture images.

Figure 9

Feature matching in high and low texture regions.

Running time

The original Transformer has a high computational cost, so even though our method uses a modified version of the Transformer to accelerate computation, it still requires slightly higher computational resources. We calculated the number of parameters and GFLOPs for LoFTR¹⁷, Aspanformer⁴⁹, Matchformer²⁸, MR-Matcher⁵¹, OAMatcher⁵⁰ and ours, as shown in Table 8. From this, we can see that we are not the best, but we are not the worst either. Overall, it is acceptable. We are also researching ways to reduce the computational load of the Transformer.

Table 8 Runtime comparison.

Ablation study

The experiments in this subsection were all tested on the Scannet⁵⁵ dataset. To verify the rationality of the model design, we conducted ablation experiments. We compared the impact of different local window sizes on the model, and the results are shown in Table 9. When the local window size increases, although the accuracy improves, the improvement is limited, and the number of matched feature points decreases sharply. Therefore, to obtain more matched feature points, we ultimately set the local window size to $5 \times 5$. Meanwhile, we also compared the impact of different modules on the model. The self-attention represents the use of the self-attention mechanism in the SwinMatcher Block, and the cross-attention represents the use of the cross-attention mechanism in the SwinMatcher Block. The numbers in parentheses indicate the number of times the attention mechanisms are used. As shown in Table 10, we tested the effects of different module combinations. Using only the self-attention mechanism without the cross-attention mechanism resulted in the poorest performance. The best performance was achieved by using both the self-attention and cross-attention mechanisms. We also compared the use of different numbers of attention mechanisms. Using only two attention mechanisms was not as effective as using four. However, beyond four times, merely increasing the number of attention mechanisms did not improve performance but instead increased unnecessary parameter amounts.

Table 9 The impact of different local window sizes on the model.

Table 10 The impact of different modules on the model.

Conclusion

This study proposes a SwinMatcher method, a feature-matching approach focusing more on weakly textured areas. By considering the inherently significant local characteristics of image features, we utilize a local self-attention mechanism to learn the features of weak textures and employ cross-attention and positional encoding mechanisms to identify the relationships between weak textures within the scene. After filtering for coarse matches using the mutual nearest neighbor, we obtain the final sub-pixel matches by mutually calculating the spatial expected coordinates of local two-dimensional heat maps. Under the same training conditions, our method achieved the best results, with an improvement of 1.17% in AUC@${20}^{\circ }$ for indoor pose estimation, 2.16% in AUC@${20}^{\circ }$ for outdoor pose estimation, 2.22% in AUC@10px for homography estimation, and a 1.59% increase in accuracy on DUC2 for visual localization. In matching weakly textured areas, our method had the highest number of correspondences, showing a 14.09% improvement. Under lighting conditions, our method demonstrated the best matching accuracy from 1 pixel to 10 pixels. Our method exhibited higher matching accuracy in viewpoint changes than similar end-to-end methods. Considering different lighting and viewpoint changes below a 5-pixel threshold, our method displayed the highest matching accuracy, with higher precision in the 6 to 10-pixel range compared to similar end-to-end methods. However, Our method has limited capabilities in training high-resolution images. Thus our future work will focus on reducing the computational complexity of training high-resolution images without compromising matching performance.