Introduction

In seismic exploration, the geological structure can be acquired by analyzing the reflection signals collected by the geophone arrays. However, these signals are inevitably contaminated by background noise, impacting the reliability of the following processing procedures. Consequently, obtaining clean seismic data through denoising techniques is a critical processing step. Compared to other regions, suppressing seismic noise in deserts is more challenging. First, desert areas experience strong and complex wind effects, resulting in higher random noise energy. “Multiple types of strong noise, weak effective signal” is a common feature of seismic data in these regions1. Second, the terrain in deserts is complex, with loose and variable surface conditions, causing desert random noise to have lower frequencies, mainly distributed between 0 and 20 Hz, while surface waves range from 0 to 15 Hz2. The effective signal’s dominant frequency is primarily distributed between 10 and 25 Hz. This leads to serious spectral aliasing among the three in the low-frequency band. These two factors bring challenges and significantly improve the degree of difficulty in denoising task. Therefore, developing efficient denoising techniques adapted to the desert environment can not only improve the quality of the data but also significantly enhance exploration efficiency, reduce costs, and play an essential part in accurately locating oil and gas reservoirs and imaging geological structures.

Currently, the widely used denoising algorithms can generally be classified into five types: low-rank methods3, sparse transform methods4, predictive filtering5, wave equation-based methods6, and deep learning (DL)7. In low-rank methods, the emergence of background noise will raise the rank of the seismic data, whereas clean seismic data can be thought of as a low-rank matrix. It means the background noise can be attenuated by reducing the rank of seismic data. Typical methods include singular value decomposition (SVD)8 and robust principal component analysis (RPCA)9. Moreover, sparse transform methods denoise seismic data by converting the signal into a sparse domain and applying thresholding. For example, wavelet transform (WT)10 and curvelet transform11 leverage the sparse properties in given domains to reconstruct the reflection signals. In contrast, predictive filtering techniques, like f-x deconvolution12 and adaptive filtering13, design filters based on the assumption that signals are predictable. Furthermore, wave equation-based denoising methods model the propagation characteristics of seismic waves to remove noise from seismic data. Different types of wave equations are derived for different types of media14,15.

Although the four traditional methods mentioned above have achieved good denoising results on field data, they require low-rank structures, sparsity, linear event assumptions, and velocity models as prerequisites. They also rely on parameter selection, which increases computational costs. To clarify, the wave equation denoising strategy involves a theoretical foundation for random noise modeling, derived from geological structures and data acquisition scenarios. The established models, however, are frequently overly idealized and challenging to modify for actual circumstances. Additionally, as exploration becomes more sophisticated, the amount of data increases quickly and processing costs rise, which restricts the use of these conventional techniques.

As deep learning techniques have demonstrated reliable and effective outcomes in tasks such as image processing16, target detection17, and natural language processing (NLP)18, they are being progressively incorporated into seismic exploration. In deep learning methods, neural networks are employed as function approximators to establish mapping relationships between different data distributions, thereby enabling effective seismic data denoising. Currently, deep-learning-based methods have been gradually applied to denoise the seismic data, and typical frameworks include recurrent neural networks19, feedforward neural networks20, generative adversarial networks (GAN)21, and convolutional neural networks (CNN). Among these, variants based on GAN and CNN have attracted increasing attentions and achieved extensively discussion.

In general, GAN consists of a generator and a discriminator. Zhang et al.22 combined the Swin Transformer (ST) with GAN and constructed a U-Net-based seismic data generator, which achieved better results in seismic data reconstruction and denoising. Li et al.23 proposed a Cycle-GAN-based denoising framework, demonstrating significant suppression of low-frequency seismic noise. Despite the promising performance of GAN-based frameworks, their denoising accuracy cannot be guaranteed. False events are consistently detected in the denoised data, which could lead to unforeseen issues with the final processing results24.

Compared with GAN, CNN-based denoising methods are more suitable for seismic data due to its rotation invariance and weight sharing strategy. For instance, Dong et al.25 employed an adaptive denoising convolutional neural network (DnCNN) model for desert seismic denoising, overcoming the challenge of processing low-frequency signals faced by previous methods. This model not only mitigated the impact of surface waves but also effectively improved the signal-to-noise ratio(SNR). Vineela et al.26 suggested a wavelet-integrated CNN that replaces pooling and up-sampling with discrete and inverse wavelet transforms. This method produced excellent denoising results by preserving detailed features while minimizing the loss of important information. Lin et al.27 introduced a branch-based denoising network, BCDNet, which includes a main denoising network and an additional branch network integrated into the pooling layers of the main network. Yao et al.28 designed a denoising network, DnResNeXt, for desert areas using skip connections and group convolution, which shows a better effect than DnCNN or ResNet.

From the aforementioned researches, we can infer that deep learning methods, particularly CNN frameworks, can be successfully applied to seismic data denoising and produce promising results. However, most CNNs lack sufficient feature interaction, and often reuse the same features at the same resolution, which may lead to insufficient noise suppression when dealing with complex seismic records. Although some models use multi-scale networks to extract features from various scales independently and aggregate them to create the final features, this method does not fully take advantage of the mutual cooperation between the features. Aiming to better capture features and recover detailed information, we propose a multi-scale feature interaction enhancement network (MFIEN). Specifically, MFIEN employs a multi-scale feature interaction module (MFIM) to extract and analyze data features at different scales. By utilizing scale transformation operations, the features can be more fully integrated. The concept of cross-scale feature interaction is similar to traditional multi-scale decomposition methods, but with the advantage that features at different scales are not used independently after extraction. By utilizing scale transformation operations, the features can be more fully integrated. The concept of cross-scale feature interaction is similar to traditional multi-scale decomposition methods, but with the advantage that features at different scales are not used independently after extraction. Instead of extracting features separately, the features collaborate and interact to form a richer feature representation, and this interaction enhances the network’s adaptability when dealing with complex seismic data. Furthermore, a fusion feature enhancement module (FFEM) with dilated convolution is introduced, which expands the receptive field without changing the feature map size, allowing the feature map to contain more detailed information about the original data. Both synthetic and field data denoising results demonstrate that MFIEN achieves excellent performance in removing seismic random noise while preserving weak reflection signals.

The following is a summary of the main contributions:

  1. 1.

    To suppress the background seismic noise in the strong desert area, a network with multi-scale feature interactive fusion strategy is designed, which can more fully integrate features.

  2. 2.

    We also designed a Fusion Feature Enhancement Module to further extract detailed information.

  3. 3.

    In addition, we also construct a complete data set containing synthetic data and field noise for network training to ensure the denoising effect. The MFIEN suggested in this paper performs well when handling complex random noise, according to experiments conducted on both synthetic and field data.

The network structure and denoising principle of MFIEN

Denoising principle

As we know, multi-scale analysis is an appropriate approach to effectively extract the informative features existed in seismic data. For instance, the large-scale features are help in reconstruct the reflection events, while the local features have significances in recovering the weak signals. Therefore, MFIEN, designed in multi-scale scheme, aims to suppress the intense random noise in desert-area seismic data. The basic principle for the denoising process can be concluded as follows: Generally, the collected seismic data X is always assumed to be contaminated by additive noise, denoted as follows:

$$X=s+n$$
(1)

where n represents random noise and s represents the effective signal. As we know, background noise shares a similar frequency range with effective signals, making the degeneration of conventional denoising methods. In MFIEN, we aim to establish a complicated mapping between noise n and the noisy data X, and then use it to reconstruct clean record and separate intense noise. In other words, we aim to reconstruct the predicted noise having extremely close properties with real noise data, and then recover the desired signals by removing the noise components. Therefore, the training process of MFIEN can be expressed by the following equation:

$$RES\left( {X;\theta } \right)=\hat {n} \approx n$$
(2)
$${\theta ^*}={\text{argmin}}\left| {\hat {n} - n} \right|=\arg \hbox{min} \left| {RES\left( {X;\theta } \right) - n} \right|$$
(3)

where RES represents residual learning, \(\theta\) represents the network hyperparameters, and \(\hat {n}\) represents the noise predicted from the noisy record. The optimization process, shown in Eq. (16), uses the L2 loss function to calculate the error in each iteration, and the network hyperparameters of MFIEN are updated through gradient backpropagation.

$$L(\theta )=\frac{1}{{2B}}\sum\limits_{{i=1}}^{B} {||RES\left( {{s^{(i)}}+{n^{(i)}};\theta } \right) - {n^{(i)}}||_{F}^{2}}$$
(4)

where B is the batch normalization size, while s(i) and n(i) represent the effective signal and noise patches, respectively, and \({\left\| . \right\|_F}\) represents the Frobenius norm. Finally, removing the predicted noise will yield the desired clean data:

$$\hat {s}=X - \hat {n}$$
(5)

Network structure

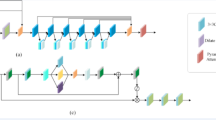
In this section, we give an in-depth explanation of the designing and network architecture of MFIEN. As shown in Fig. 1, MFIEN mainly consists of two components: MFIM, and FFEM. The original input seismic data is first processed by a 3 × 3 convolutional block, and the preliminary features are used as the input of MFIM and FFEM, respectively. Generally, the multi-scale feature extraction of desert-area seismic data is acquired from two aspects. For one thing, MFIM uses down\up-sampling operations to capture the potential feature in seismic data with different resolutions. For another, FFEM employs dilated convolutions to derive the multi-scale features. By utilizing these multi-scale features, the denoising performance can be enhanced, even confronted with intense desert-area noise.

Fig. 1
figure 1

Structure of MFIEN.

Full size image
  1. A.

    Multi-scale feature interaction module.

For MFIM, we use the operations of down-sampling to change the resolution of input feature maps. As shown in Fig. 1, MFIM has multi-scale architecture, using to extract the detailed and coarse features existed in seismic data. Unlike conventional single-scale network, such as DnCNN, MFIM has advantages in feature extraction ability because more multi-scale feature are taken into consideration. On this basis, abundant feature interactions in MFIM also enhance informative feature representation. For the detailed architecture, MFIM is composed of three branches, called L1, L2 and L3 from top to bottom. Generally, L1 branch (top branch) is used as the main branches, while L2 and L3 provide auxiliary features acquired from low-resolution seismic data to refine the effective features. The effect of L1 branch can be denoted as follows:

$$F_{{L1}}^{3}=Y_{{L1}}^{3}\left( {Y_{{L1}}^{2}\left( {Y_{{L1}}^{1}\left( {{F_{SF}}} \right)+{Y_{Deco}}\left( {F_{{L2}}^{1}} \right)} \right)+{Y_{Deco}}\left( {F_{{L2}}^{2}} \right)} \right)$$
(6)
$$F_{{L1}}^{5}=Y_{{L1}}^{5}\left( {Y_{{L1}}^{4}\left( {F_{{L1}}^{3}+{Y_{Deco}}\left( {F_{{L2}}^{3}} \right)} \right)+{Y_{Deco}}\left( {F_{{L2}}^{4}} \right)} \right)$$
(7)
$${F_{L1}}={Y_{L1}}\left( {{F_{SF}}} \right)=F_{{L1}}^{5}$$
(8)

where \(F_{{Li}}^{j}\left( {i=1,2;j=1,2,3,4,5} \right)\) denotes the output of convolutional block at L1 and L2 branches, and\(Y_{{L1}}^{n}\left( {n=1,2,3,4,5} \right)\)represents the effect of combined convolutional blocks (two Conv layers and a ReLU function). \({Y_{Deco}}\)denotes the transposed convolution (step 2). \({F_{SF}}\) denotes the preliminary features captured by the first 3 × 3 convolutional block, while \({F_{L1}}\) and \({Y_{L1}}\) represent the output and the corresponding operation of L1 branch, respectively.

L2 is used to capture the middle-scale feature, and down-sampling operation shrinks to half the size of input features. Then, multiple convolutional blocks are used to extract and fuse local features from the L3 branch. Different from the L1 branch, to make the network more lightweight, the convolutional blocks used in the L2 and L3 branches only include one ReLU function and one convolutional layer with a 3 × 3 kernel. Finally, the extracted features are up-sampled to its original size. The specific operations of the L2 branch are as follows:

$$F_{d}^{2}={Y_d}\left( {{F_{SF}}} \right)$$
(9)
$$F_{{L2}}^{2}=Y_{{L2}}^{2}\left( {Y_{{L2}}^{1}\left( {F_{d}^{2}+{Y_{Deco}}\left( {F_{{L3}}^{1}} \right)} \right)+{Y_{Deco}}\left( {F_{{L3}}^{2}} \right)} \right)$$
(10)
$$F_{{L2}}^{4}=Y_{{L2}}^{4}\left( {Y_{{L2}}^{3}\left( {F_{{L2}}^{2}+{Y_{Deco}}\left( {F_{{L3}}^{3}} \right)} \right)+{Y_{Deco}}\left( {F_{{L3}}^{4}} \right)} \right)$$
(11)
$${F_{L2}}={Y_{up}}\left( {{Y_{L2}}\left( {{F_d}} \right)} \right)={Y_{up}}\left( {F_{{L2}}^{4}} \right)$$
(12)

where \({Y_d}\) and \(F_{d}^{2}\) denote the effect and captured features of down-sampling operation. Moreover, \(F_{{L2}}^{i}\left( {i=1,2,3,4} \right)\) and \(F_{{L3}}^{j}\left( {j=1,2,3,4} \right)\) represent the output of every convolutional block at L2 and L3 branches. \(Y_{{L2}}^{n}\left( {n=1,2,3,4} \right)\) denotes the effect of convolutional blocks at L2 branch. Yup is an up-sampling function. Additionally, FL2 is the final output of L2 branch.

Furthermore, the L3 branch uses similar strategy to L2 branch that using down/up-sampling operations to extract the local features. However, the input of L3 branch is obtained through two down-sampling operations, and the large-scale features can be extracted. For the detailed architecture, L3 stacks the convolutional layers to extract the potential features, and they are fed back to L2 branch to refine the captured features. Specifically, the effects of L3 branch can be concluded as follows:

$$F_{{_{{L3}}}}^{2}=Y_{{L3}}^{2}\left( {Y_{{L3}}^{1}\left( {{Y_{d2}}\left( {{Y_{d1}}\left( {{F_{SF}}} \right)} \right)} \right)} \right)$$
(13)
$$F_{{_{{L3}}}}^{3}=Y_{{L3}}^{3}\left( {{Y_{up1}}\left( {F_{{L3}}^{2}} \right)} \right)$$
(14)
$${F_{L3}}={Y_{up2}}\left( {Y_{{L3}}^{4}\left( {F_{{L3}}^{3}} \right)} \right)$$
(15)

where \(Y_{{L3}}^{n}\left( {n=1,2,3,4} \right)\) and \(F_{{L3}}^{j}\left( {j=1,2,3,4} \right)\) denote the effect and output of convolutional blocks. Yd1, Yd2 are the down-sampling operations, while Yup1 and Yup2 are the up-sampling operations. FL3 represents the output of L3 branch.

Finally, we add the information extracted from these three layers together, and then the extracted information is transferred to the FFEM for further feature extraction. This process is specifically described as:

$${F_{DF}}={Y_{DF}}\left( {{F_{L1}}+{F_{L2}}+{F_{L3}}} \right)$$
(16)

In the equation, YDF represents feature extraction effect, and FDF is the output features.

  1. B.

    Fusion feature enhancement module.

To further improve the denoising performance, we designed a fusion feature enhancement module, called FFEM, and added at the end part of the denoising network. Compared with MFIN, FFEM also aims to utilize the multi-scale features in seismic data. However, the extraction process of FFEM is accomplished by using various convolutional blocks. It can provide auxiliary multi-scale information and fuse with those features acquired by MFIN to improve the representation ability of weak reflection signals. For the detailed architecture, convolution operations are performed on the feature maps using different convolutional kernels (1 × 1, 3 × 3, 5 × 5,) and dilated convolutions with different dilation rates (d = 2, d = 3) to capture potential features from different scales. Finally, by fusing all feature maps, the final comprehensive feature map is obtained, integrating multiple receptive fields and enabling simultaneous consideration of both global information and local details.

Network parameter selection and training process

Construction of the training set

As indicated by Eq. (4), the training set consists of signal patches s(i) and noise patches n(i). This set directly determines the optimization quality of the network hyperparameters, which in turn affects the denoising performance. For the generating scheme of training set, we use synthetic signals to compose the signal set, and used field noise to consist of noise set. The reason for using synthetic records to compose signal set is that the pure reflection signals cannot be collect from real seismic data owing to the existence of intense random noise. The real data processed by other denoising methods are also not suitable because the residual noise may bring unexpectable and negative impacts on the denoising performance of the trained models. Therefore, using synthetic records seems as the only appropriate approach. In this study, the frequency range of synthetic signals are determined by analyzing pre-acquired seismic data, and we use Ricker wavelet to simulate the reflection signals, as shown in Eq. (17).

$$f\left( x \right)=A\left[ {1 - 2 \times {{\left( {\pi {f_0}\left( {t - {t_0}} \right)} \right)}^2}} \right] \times {e^{ - {{\left( {\pi {f_0}\left( {t - {t_0}} \right)} \right)}^2}}}$$
(17)

Among them, A, \({t_0}\) and \({f_0}\) are the amplitude, starting time and fundamental frequency, respectively. Table 1 give the detailed modeling parameters, and totally 50 synthetic seismic records are generated, containing various types of seismic events, such as hyperbolic events, crossing events and dipping events. The size of each record was 1024 × 128 (sampling time × number of traces). Then, using a 64 × 64 sliding window to divide the synthetic seismic records, and 10,000 signal patches are generated.

Table 1 Modeling parameters.
Full size table

For the noise dataset, we use field seismic noise data recorded in Tarim Basin. Generally, these records are obtained by geophone arrays in the desert area without artificial source excitation, primarily containing random noise. Moreover, 2332 seismic traces are recorded and each trace has 30,000 samples, with a sampling frequency of 500 Hz. Similar to the signal dataset, the collected noise data were randomly divided into 12,685 noise patches, each with a size of 64 × 64. On this basis, signal patches are combined with noise patches with random weights to form noisy patches with different SNR ranging from [− 10, 0]dB. Notably, noise patches are used as labelled data, while our purpose is to reconstruct them from their paired noisy patches. During the training process, we can finally obtain the trained models. Since application of multi-scale strategy in MFIEN and appropriate training set, we can infer that the trained models can effectively extract the potential features in seismic data and ensuring the denoising capability.

Hyperparameter selection and training process

Besides the training set, the setting of network hyperparameters is also a crucial factor determining the denoising capability of the network. Based on the hardware conditions, the batch size was 32, and the patch size was 64 × 64. Moreover, the learning rate was [10− 4, 10− 5], and the number of epochs was 50. Meanwhile, Adam method was utilized to optimize the training process. After 50 epochs, the loss function stabilized, and the model which have the best denoising effect was selected as the trained models and used to process synthetic and field seismic records. Specific training hyperparameters are shown in Table 2. And the Table 3 shows the specific training process for MFIEN. Meanwhile, the training process was conducted on a PC equipped with an Intel Core i5-9300 H CPU and an NVIDIA GeForce GTX 1650 Ti GPU.

Table 2 Training hyperparameters.
Full size table
Table 3 Training process.
Full size table

Analysis of synthetic seismic record processing results

This study first processed the synthetic seismic record. The simulation record for the test is shown in Fig. 2a, which includes 8 different types of reflection events: horizontal event, hyperbolic reflection event, cross events, bending events, and fault events. These reflection events are obtained with Ricker wavelets having sampling frequency of 500 Hz and fundamental frequencies ranging from 20 to 25 Hz. Moreover, real desert-area random noise collected in the Tarim Basin, as shown in Fig. 2b, is combined with clean data to generating noisy data (− 6.86 dB). As depicted in Fig. 2c, the effective signal is submerged by strong background noise, affecting the continuity of the reflection events. After using MFIEN, Fig. 2d,e present the denoising results and the removed noise, which indicate that MFIEN can accurately reconstruct the weak events, thereby demonstrating its strong amplitude preservation ability.

Fig. 2
figure 2

Denoising results analysis: (a) Clean data; (b) Field noise record; (c) Noisy data (− 6.86 dB); (d) Denoising results; (e) Filtered noise by MFIEN.

Full size image

Comparing methods

To validate the effect of MFIEN in noise reduction, this section evaluates MFIEN alongside other comparison methods, including two traditional approaches: wavelet transform (WT) and band-pass filter (BPF), as well as two deep learning-based method: the feedforward denoising convolutional neural network (DnCNN) and the network called cycle-GAN, specifically designed for low-frequency seismic noise suppression23. Specifically, the BPF is set with a passband range of [18–40 Hz], and the WT uses a ten-layer db5 basis function with a soft thresholding method for noise suppression. Moreover, DnCNN has a 17-layer network structure, and cycle-GAN uses the same architecture as in Li’s23 study. To ensure the objectivity of the denoising results, the same training dataset and experimental setup as those used for MFIEN are employed, as described in “Network parameter selection and training process”.

Comparative analysis of denoising performance

Here, we use the comparing algorithms described above to process the noisy records shown in Fig. 2c. The corresponding results (top subfigures) and eliminated noise data (bottom subfigures) are presented in Fig. 3a–e. Corresponding analysis reveals that WT fails to effectively recover the useful signals, and the processing result suffers from remained low-frequency noise. Although the BPF demonstrates better signal preservation, it can only filter out noise outside the passband range observing Fig. 3b, it is evident that there is signal loss in the denoised result. It is worth noting that the deep learning-based method, performs better in noise reduction compared to the two traditional methods mentioned above. Nevertheless, residual signals are present in the denoised results, as shown by the red blocks in Fig. 3c,d. And the denoising results still suffered from remained noise, which suggests that DnCNN and cycle-GAN need further improvement to effectively handle the complex noise in desert regions. The results shown in Fig. 3e demonstrate that the proposed MFIEN achieves superior noise suppression, with clear alignment of reflection events, and the filtered noise characteristics closely resemble the actual noise. This indicates that MFIEN provides better denoising performance with promising results in attenuating random noise and reconstructing effective signals. Additionally, a quantitative comparison of SNR improvements further validates the efficiency of MFIEN, with an SNR increment of 16.91 dB, significantly surpassing the other methods.

Fig. 3
figure 3

Comparison results between different methods. (a–d) Denoising results (top subfigures) and removed noise (bottom subfigures) of WT (− 1.07 dB), BPF (3.99 dB), DnCNN (7.17 dB), cycle-GAN (7.89 dB) and MFIEN (10.05 dB), respectively.

Full size image

To conduct a more in-depth comparison, we analyzed the processing results of the 92th trace using CNN-based methods (DnCNN, cycle-GAN and MFIEN), as shown in Fig. 4. It is noteworthy that in terms of amplitude, MFIEN is closer to the clean record. Additionally, the DnCNN and cycle-GAN’s result exhibit some residual noise, while MFIEN significantly outperforms the comparative methods in terms of performance.

Fig. 4
figure 4

Single-trace comparison result (no.92th trace).

Full size image

Spectral analysis of denoising performance

To comprehensively compare the denoising results, we performed a frequency domain analysis of the outcomes from the five methods. The top and bottom subfigures of Fig. 5a represent the F-K spectra of clean signal and noise, respectively. Figure 5b–f display the F-K spectra, which correspond to the results shown in Fig. 3a–e. The results clearly indicate that the denoised output from the WT differs significantly from the clean signal. Not only is the noise suppression incomplete, but useful information is also noticeably suppressed, as observed in the red elliptical block in Fig. 5b, where significant residual signals remain. The BPF can only retain signals within a fixed passband range, resulting in limited performance to the noise within the same frequency band. In the records processed by DnCNN and cycle-GAN, the signal is more discernible, but the F-K spectrum reveals that some low-frequency noise remains (red blocks in Fig. 5d,e). In contrast, Fig. 5f shows that the denoised result and the filtered noise from MFIEN closely resemble the reflection signals and field noise in spectral properties. These results indicate that the proposed method has excellent noise suppression and amplitude preservation capabilities, further confirming that MFIEN provides the best denoising performance for data from desert regions.

Fig. 5
figure 5

Comparison results in F-K domain. (a) F-K spectrum of clean data (top subfigure) and field noise record (bottom subfigure). (b–f) F-K spectra of denoising results (top subfigures) and predicted noise (bottom figures) by using WT, BPF, DnCNN, cycle-GAN, and MFIEN.

Full size image

Multiple SNR robustness testing experiment

To validate the adaptability of the proposed MFIEN to seismic data with varying SNRs, synthetic seismic records with ranging SNRs from − 10 to 0 dB are used as analyzed dataset. As discussed above, we compared it with WT, BPF, DnCNN, and cycle-GAN. To quantitatively assess the denoising capability, we selected SNR and root mean square error (RMSE) as metrics, which are defined as follows:

$$SNR=10{\log _{10}}\left( {{{\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\hat {s}}^2}\left( {i,j} \right)} } } \mathord{\left/ {\vphantom {{\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\hat {s}}^2}\left( {i,j} \right)} } } {\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\left( {s\left( {i,j} \right) - \hat {s}\left( {i,j} \right)} \right)}^2}} } }}} \right. \kern-0pt} {\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\left( {s\left( {i,j} \right) - \hat {s}\left( {i,j} \right)} \right)}^2}} } }}} \right)$$
(18)
$$RMSE=\sqrt {{{\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\left( {s\left( {i,j} \right) - \hat {s}\left( {i,j} \right)} \right)}^2}} } } \mathord{\left/ {\vphantom {{\sum\limits_{{i=1}}^{N} {\sum\limits_{{j=1}}^{M} {{{\left( {s\left( {i,j} \right) - \hat {s}\left( {i,j} \right)} \right)}^2}} } } {MN}}} \right. \kern-0pt} {MN}}}$$
(19)

Among them, \(\hat {s}\left( {i,j} \right)\) and \(s\left( {i,j} \right)\) denote the recovered signal and the pure record. Moreover, M and N are the total number of samples and traces.

Generally, promising results have a large SNR and a small RMSE. As shown in Table 4, MFIEN has the best performance, indicating by the highest SNR increment and the lowest RMSE, proving its effectiveness and generalization when handling seismic data with different properties. For example, in the case of − 4 dB noisy data, MFIEN enhances the effective signal with an SNR increment exceeding 17 dB. Additionally, to visually observe the impact of changes in the original data’s SNR on denoising performance, we plotted the corresponding results in Fig. 6. From the results, MFIEN exhibits the best denoising capability.

Table 4 Comparison of SNR and RMSE. The highest values are represented by bold. The lowest values are represented by Underline.
Full size table
Fig. 6
figure 6

Comparison in SNR and RMSE: (a) Results in SNR; (b) Results in RMSE.

Full size image

Analysis of computational cost

Computational cost is a crucial factor that influences the practical application of deep learning-based methods. To objectively evaluate these methods, it is necessary to track key metrics such as training time, processing time, and the average improvement in SNR. Table 5 presents a comparative analysis of WT, BPF, DnCNN, cycle-GAN, and MFIEN in terms of these metrics. While deep learning frameworks require longer training times, the testing phase is relatively fast. For example, the testing time for MFIEN is only 0.381 s. More importantly, trained models are adaptively obtained and do not require additional fine-tuning during the testing phase. This suggests that deep learning-based techniques perform more consistently than conventional methods. Furthermore, deep learning frameworks exhibit superior performance in suppressing low-frequency background noise in desert seismic data. This is reflected in the significantly improved SNR compared to traditional methods. For instance, the average improved SNR of MFIEN reaches 16.68 dB, which is more than 10 dB higher than WT, achieving the best results among the denoising methods. Based on these findings, we conclude that MFIEN provides remarkable denoising capability with an acceptable computational cost. Additionally, advancements in high-performance computing devices are likely to further mitigate the computational burden of such methods in the future.

Table 5 Computational efficiency analysis of different denoising methods.
Full size table

Processing results of actual desert-area seismic data

The data used in this study are actual desert common-shot records obtained from the Tarim Basin in Northwestern China. A common-shot record with 216 traces was processed, with a sampling frequency of 500 Hz. The actual record is shown in Fig. 7a, where the reflection events are significantly affected by background noise, resulting in poor continuity. Specifically, within the red block, the effective signals are disturbed by random noise, making the reflection events discontinuous and difficult to identify. Within the blue blocks, the effective signals are disturbed not only by random noise but also by strong low-frequency surface waves, causing some of the events to be completely truncated. Similarly, the field desert-area record was processed using WT, BPF, DnCNN, Cycle-GAN, and MFIEN, and the corresponding results are depicted in Fig. 7b–f.

Comparative analysis of the above results shows: (1) WT and BPF Performance: As observed in Fig. 7b,c, WT and BPF can only eliminate some of the random noise and surface waves. Residual noise continues to interfere with the reflection event, making it difficult to identify. There are still noticeable events in the filtered noise. After processing with the BPF and WT, the amplitudes of reflection signals are also diminished along with the noise attenuation procedure. Furthermore, BPF fails to accurately select the frequency domain coefficients corresponding to the effective signal, leading to significant attenuation of the signal’s amplitude and continuity, which is even worse than the original record. (2) CNN-based Methods: As shown in the Fig. 7d–f, deep learning-based methods achieve more thorough noise attenuation and clearer recovery of effective signals. However, after DnCNN and Cycle-GAN processing, some of the recovered reflection events are unclear, with discontinuities in certain regions. In contrast, MFIEN provides a clearer and more continuous recovery of the effective signal, with better restoration of some shallow details, as shown in area 1 of Fig. 7f. Additionally, the bottom subplot of Fig. 7f demonstrates that the noise components after MFIEN denoising have almost no signal leakage energy.

Fig. 7
figure 7

Comparison results for the field seismic record. (a) Desert-area field data. (b–f) Processing results (top subfigures) and removed noise (bottom subfigures) by using WT, BPF, DnCNN, cycle-GAN, and MFIEN.

Full size image

To further compare the denoising performance, we have zoomed in the two areas highlighted by the yellow blocks in Fig. 7b–f, and these are displayed in Fig. 8. Figure 8e gives the results of our method: In area 1, most of the intense interferences are suppressed, and the smoothness of the shallow information is obviously improved. In area 2, MFIEN effectively suppresses the interference from strong low-frequency surface waves, and the weaker, deeper reflection events are also well restored. In contrast, Fig. 8a shows that after WT denoising, the reflection events remain difficult to identify. As shown in Fig. 8b, the denoising result of BPF still suffers from residual noise, and the continuity of the reflection event is poor. As shown in Fig. 8c,d, DnCNN and cycle-GAN are failed to restore some weak reflection events.

Fig. 8
figure 8

Local zoomed-in comparison of different denoising methods. (a–e) Processing results obtained using WT, BPF, DnCNN, cycle-GAN, and MFIEN, respectively (top for Area 1, bottom for Area 2).

Full size image

We applied the trained model to another seismic record obtained from the same survey area but received by different receiver lines in order to further confirm the generalization. Here, we mainly focus on comparing the corresponding results obtained by deep learning-based methods (DNCNN, cycle-GAN, MFIEN), as shown in Fig. 9b–d. It is worth noting that the attenuation performance of MFIEN is superior to the compared networks. For example, in the yellow blocks in the Fig. 9, there are some discontinuous regions in the results of DnCNN and cycle-GAN. In contrast, the results of MFIEN are more continuous. Therefore, the results indicate that MFIEN has better denoising effect and certain generalization ability.

Fig. 9
figure 9

Denoising results of another field record acquired in a similar environment. (a) Field record. (b–d) Processing results obtained using DnCNN, cycle-GAN, and MFIEN, respectively (top for Denoising results, bottom for filtered noise).

Full size image

Conclusion

To address the issues of attenuating the intense and aliasing background noise desert-area seismic records, this paper proposes a novel CNN framework, named MFIEN, which uses multi-scale strategy. Specifically, a three-scale network architecture is utilized to capture comprehensive features by considering both global and local information.

Meanwhile, effective information interaction and feature fusion strategies also involve to enhance the feature extraction ability. Additionally, the Fusion Feature Enhancement Module, which incorporates dilated and conventional blocks with various sizes, extracts a broader range of information without altering the feature map size, thus preserving the structure of the seismic records and enhancing information features. On this basis, a training set consisting of a variety of analog signals and actual noise data is also used. It is shown the trained models of MFIEN can effectively separates reflection signals from strong random noise. Comparing results show that MFIEN provides clearer and more continuous reflection events compared to methods such as BPF, WT, and DnCNN, while preserving effective signals during noise suppression. The SNR improvement exceeds 17 dB. Therefore, MFIEN holds significant potential for handling complex random noise. However, its attenuation capability may decline when facing extremely low SNRs and strong coherent noise. Further simplification of the network structure is recommended without compromising denoising performance.