Introduction

Metacognition – “thinking about thinking” – refers to the higher-order cognitive capability that enables us to internally evaluate our own cognitive processes associated with various tasks1,2,3,4,5. Metacognitive abilities allow people to form confidence in the quality of their choices, even in the absence of immediate feedback6,7,8. Decision confidence, elicited around the time of an individual choice, can be conceptualized as the subjective probability of success given the available evidence (i.e., Bayesian posterior probability of the chosen option being correct)9,10,11,12,13. Previous studies in psychology and neuroscience have focused on the formation of confidence in perceptual6,14,15,16,17 and knowledge-based decisions13. Participants in these experiments were asked to indicate their confidence of the correctness of their judgment after each choice. Results showed that self-reported confidence was well captured by the posterior probability of the choice being correct18,19,20. Abnormalities in decision confidence are known to be related to psychiatric disorders21,22.

More recent studies in metacognition have examined whether and how human participants aggregate decision confidence in individual choices to form a “global” self-performance estimate (SPE). SPE is an overall belief about one’s skills and capacities to solve a given task. University students, for example, might integrate their performance in different assignments and exams to form an estimate of their overall academic abilities. It plays a key role in shaping our behaviours23, selecting goals to achieve24, and allocating time and resources25. For instance, finding it hard to achieve some objective after multiple attempts, many people will be inclined to stop investing more time or effort in it and turn to pursue another, more achievable goal.

Rouault and colleagues assessed how SPEs in perceptual decisions are constructed across multiple decisions18,19. They found that the feedback about the correctness of decisions affected SPEs significantly in a simple, perceptual decision-making task. Participants underestimated their performance (i.e., had lower SPEs) in the absence of feedback compared to the case with feedback, even though their objective performance in those decisions was not affected by the presence of feedback; that is, absence of feedback is associated with lower SPEs18. Computational modelling further suggests that participants formed the global SPEs by integrating decision confidence of each choice over multiple trials in a Bayesian manner18.

Unlike simple perceptual decisions, many decisions we make are computationally hard. Suppose you have to choose the set of items in a supermarket that maximise your satisfaction while sticking to your budget constraint. In a supermarket stocking just 100 items, assuming that you would only pick an item at most, you need to consider 2100 combinations of items to choose the optimal set from them, a computationally intractable task. Another example is constructing investment portfolios by picking stocks listed on the market given a budget or risk constraint26,27. There are currently more than 41,000 stocks listed on stock exchanges around the world28, which makes building portfolios another intractable task. While this kind of decision is ubiquitous in life, which is reflected in modern choice theories (e.g., utility maximization29 and satisficing30), it requires individuals to solve intractable, that is, computationally complex, problems31.

The mathematical framework of computational complexity allows the quantification of computational hardness – or computational resource requirements – of tasks such as decisions32. Behavioral studies to date have shown that the level of computational complexity is negatively related to human performance in decisions – the higher the level of computational complexity, that is, the more computational resources are required to compute the optimal course of action, the lower the performance in those decisions, that is, the less likely people are to choose the optimal course of action33. Importantly, the computational complexity of tasks, including decisions, can be quantified without reference to any particular algorithm – it is an objective attribute of a task. Furthermore, computational complexity can be quantified in a domain-general way. That is, the measures of computational complexity are not task-specific. It has been shown that such objective, task-independent measures of computational complexity predict both the extent of cognitive effort exerted on a decision as well as performance34. However, at this point, little is known about ‘metacognition’ in complex decisions. That is, whether and how humans internally evaluate their own performance in computationally complex decisions remains elusive.

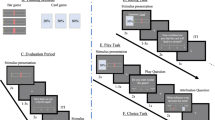
In the present study, we investigated the formation of SPEs in computationally complex economic decisions with reference to that in simple perceptual decisions. In line with previous studies on perceptual decision-making18,19, we examined the effects of decision difficulty and the presence/absence of feedback on SPEs. To this end, we conducted a behavioral experiment in which participants solved both a simple, perceptual decision-making task (sample task; Fig. 1a)18,35 as well as complex, economic decision-making task (knapsack task; Fig. 1b)34,36. The latter is based on the 0-1 knapsack problem, a canonical (NP-complete) constrained optimization computational problem34,37, in which task difficulty is manipulated by a theoretical measure of computational hardness (i.e., “instance complexity”34,36). The knapsack task is closely related conceptually to many daily decisions (e.g., attention allocation, budgeting, task management). The experiment consisted of four different types of blocks (Fig. 1e): two difficulty levels (easy vs. hard) and two feedback conditions (presence vs. absence of feedback). In each block, participants performed 10 trials of a task (Fig. 1f). Crucially, at the end of each block, participants submitted a bid in a Becker–DeGroot–Marschak (BDM) auction38 to purchase the right to complete additional 5 trials (Fig. 1c, f). Note that, in the additional 5 trials, no feedback was provided, and the difficulty level was the same as in the first 10 trials within the block. The auction procedure allowed us to measure a participant’s SPEs in an incentive-compatible manner (see Methods for details). If a participant thought that they could perform well in the additional trials, they should have bid high to secure the chance of attempting the additional trials. Participants were also asked to report their performance estimation on a Likert scale at the end of each block (Fig. 1d, f).

Fig. 1
figure 1

Experimental design. (a) Sampling task (simple perceptual decision-making). In each trial, participants indicated which stimulus, left or right, contained the larger number of dots. Task difficulty was manipulated by the difference in number of dots between the two stimuli. (b) Knapsack task (complex economic decision-making). In each trial, participants solved an instance of the 0-1 knapsack decision problem with six items, each of which had two attributes (weight (kg) and value ($)). Participants had to indicate whether there exists a subset of items for which (i) the sum of weights is less than or equal to the weight constraint (the kilogram amount shown in the centre circle) and (ii) the sum of values is at least as high as the target profit (the dollar amount at the centre). Task difficulty was manipulated by a theoretical measure of computational hardness, instance complexity. (c) BDM auction. At the end of each block, participants bid for the right to play an additional five bonus trials. (d) Self-reported performance rating. At the end of each block, participants were asked to estimate their task performance in the additional five bonus trials if attempted. (e) Block types. For each task, we employed a block-wise two-by-two design with two difficulty levels (easy vs. hard) and two feedback conditions (feedback vs. no-feedback). (f) Schedule of a block. Schematic examples of an easy block with feedback (top) and a hard block without feedback (bottom) are shown. In each block, participants performed 10 trials of a decision-making task (sampling or knapsack task) and then bid in the BDM auction to purchase the right to complete additional five bonus trials. Note that, in the additional trials, no feedback was provided, and the difficulty level was the same as the first 10 trials within the block.

Full size image

Results

Pilot experiment

We first conducted a pilot experiment (N = 17) to determine the sample size of the main experiment. In the sampling task, difficulty affected both objective performance (i.e., the proportion of correct choices; effect of difficulty: b =  − 0.435 \(\pm\) 0.066, Pcorr < 0.001; see Fig. 2a and Table S1) and SPEs (i.e., bid value in the BDM auction; effect of difficulty: b =  − 0.071 \(\pm\) 0.013, Pcorr < 0.001; see Fig. 2b and Table S2). As expected, they were lower in hard trials than in easy trials. Moreover, SPEs were lower in the no-feedback condition compared to the feedback condition (effect of feedback: b = 0.050 \(\pm\) 0.013, Pcorr < 0.001; see Fig. 2b and Table S2), although objective performance remained unchanged (effect of feedback: b = 0.070 \(\pm\) 0.065, P = 0.284; see Fig. 2a and Table S1). We observed a similar pattern of SPEs when considering self-reported performance ratings instead of BDM auction bids (effect of difficulty: b =  − 0.331 \(\pm\) 0.065, Pcorr < 0.001; effect of feedback: b = 0.360 \(\pm\) 0.065, Pcorr < 0.001; see Fig. 2c and Table S3). Overall, participant behavior in the sampling task was consistent with a previous study based on a similar task18.

Fig. 2
figure 2

Results of the pilot experiment. (a) Objective performance in the sampling task. Proportions of correct choices are plotted by block type. Bars indicate means \(\pm\) SEM across participants. Each grey dot denotes one participant. FB, feedback; NoFB, no-feedback. (b) Self-performance estimate (bid value) in the sampling task. Bid values in the BDM auction are plotted by block type. (c) Self-performance estimate (self-reported rating) in the sampling task. Self-reported performance ratings are plotted by block type. (d) Objective performance in the knapsack task. The format is the same as in panel (a). (e) Self-performance estimate (bid value) in the knapsack task. The format is the same as in panel (b). (f) Self-performance estimate (self-reported rating) in the knapsack task. The format is the same as in panel (c).

Full size image

In the knapsack task, objective performance was lower in hard trials compared to easy trials, but performance was not affected by the presence/absence of feedback (effect of difficulty: b =  − 0.799 \(\pm\) 0.074, Pcorr < 0.001; effect of feedback: b =  − 0.026 \(\pm\) 0.074, Pcorr = 0.724; see Fig. 2d and Table S4). SPEs (bid values) were lower in hard trials compared to easy trials (effect of difficulty: b =  − 0.090 \(\pm\) 0.013, Pcorr < 0.001; see Fig. 2e and Table S5). They were also lower in the absence of feedback (compared to the presence of feedback) but only in easy trials (effect of feedback: b = 0.036 \(\pm\) 0.013, Pcorr = 0.024; interaction effect: b =  − 0.036 \(\pm\) 0.013, Pcorr = 0.024; see Fig. 2e and Table S5), which is different to the pattern observed in the sampling task (Fig. 2b). The same pattern is present in self-reported performance ratings (effect of difficulty: b =  − 0.463 \(\pm\) 0.071, Pcorr < 0.001; effect of feedback: b = 0.257 \(\pm\) 0.071, Pcorr < 0.001; interaction effect: b =  − 0.199 \(\pm\) 0.071, Pcorr = 0.018; see Fig. 2f and Table S6).

We then determined the sample size in the main experiment to ensure a statistical power of at least 0.8 for the effects of interest (N = 36) (see Sect “Methods” for details).

Main experiment: objective performance

We first examined how objective performance in decisions was affected by difficulty and feedback about correctness of a decision. In both the sampling and the knapsack task, objective performance was lower in hard trials compared to easy trials (Fig. 3; effect of difficulty in the sampling task: b =  − 0.582 \(\pm\) 0.048, Pcorr < 0.001; knapsack task: b =  − 0.861 \(\pm\) 0.055, Pcorr < 0.001; see Table S7 and Table S8 for details). There was no significant difference in performance in the absence of feedback compared to presence of feedback (Fig. 3; effect of feedback in the sampling task: b =  − 0.005 \(\pm\) 0.048, P = 0.919; knapsack task: b =  − 0.014 \(\pm\) 0.055, P = 0.801; Table S7 and Table S8).

Fig. 3
figure 3

Objective performance in the main experiment. (a) Objective performance in the sampling task (proportion of correct choices by block type). Bars indicate mean \(\pm\) SEM across participants. Each grey dot denotes one participant. FB feedback, NoFB no feedback. (b) Effects of difficulty, feedback, and their interaction on objective performance in the sampling task. Effects were estimated with a generalized linear mixed-effect model (see Table S7). ***P < 0.001, **P < 0.01 (all p-values are Bonferroni corrected). (c) Objective performance in the knapsack task. The format is the same as in panel (a). (d) Effects of the difficulty, feedback, and their interaction on objective performance in the knapsack task (see Table S8). The format is the same as in panel (b).

Full size image

We confirmed participants were actively engaged in solving hard trials, rather than making random choices. In both the sampling and the knapsack task, participants’ objective performance in hard trials was significantly higher than the chance level (i.e., 0.5) (intercept: b = 0.715 \(\pm\) 0.073, Pcorr < 0.001 in the sampling task, and b = 0.646 \(\pm\) 0.067, Pcorr < 0.001 in the knapsack task).

Main experiment: self-performance estimates

In the sampling task, SPEs (bid values in the BDM auction at the end of each block) were significantly lower in hard trials compared to easy trials (effect of difficulty: b =  − 0.044 \(\pm\) 0.008, Pcorr < 0.001; Fig. 4a, b; Table S9) and in the absence of feedback compared to the presence of feedback (effect of feedback: b = 0.060 \(\pm\) 0.008, Pcorr < 0.001; Fig. 4a, b; Table S9). There was no significant interaction between difficulty and feedback conditions (interaction effect: b =  − 0.018 \(\pm\) 0.008, Pcorr = 0.085; Fig. 4a, b; Table S9). These findings replicate the results of previous studies18,35.

Fig. 4
figure 4

Self-performance estimates (bid values) in the main experiment. (a) Self-performance estimates in the sampling task. Bars indicate mean \(\pm\) SEM across participants. The bid value in the BDM auction is plotted by block type. The format is the same as in Fig. 2b. (b) Effects of difficulty, feedback, and their interaction on self-performance estimates in the sampling task. Coefficients were estimated with generalized linear mixed-effect models (see Table S9). ***P < 0.001, **P < 0.01 (all p-values are Bonferroni corrected). (c) Self-performance estimates in the knapsack task. Bars indicate mean \(\pm\) SEM across participants. The format is the same as in Fig. 2e. (d) Effects of difficulty, feedback, and their interaction on self-performance estimates in the knapsack task (see Table S10). The format is the same as in the panel (b).

Full size image

In the knapsack task, SPEs were lower in hard compared to easy trials (effect of difficulty: b =  − 0.077 \(\pm\) 0.009, Pcorr < 0.001; Fig. 4c, d; Table S10). SPEs were also lower in the absence of feedback compared to the presence of feedback but only in easy trials (Fig. 4c), indicated by the significant interaction between difficulty and feedback (b =  − 0.030 \(\pm\) 0.009, Pcorr = 0.005; Fig. 4d; Table S10).

We then directly tested the differential effects of feedback on SPEs in hard trials between the sampling and knapsack tasks (i.e., SPEs were lower in the absence of feedback compared to the presence of feedback only in the sampling task). The additional analysis revealed that, in hard trials, the effects of feedback differ between the two tasks, indicated by the significant interaction of task type and feedback (b =  − 0.027 \(\pm\) 0.009, Pcorr = 0.007; Table S11). We also confirmed that the interaction effect remained significant after controlling for potential effects of the participants’ objective performance (Tables S12–S14).

As a robustness check, we confirmed that our findings in relation to SPEs are robust with regards to the measurement of self-performance. The patterns of SPEs were similar when considering self-reported performance ratings instead of BDM auction bids (Fig. 5). In both tasks, self-performance ratings were lower in hard compared to easy trials (effects of difficulty: b =  − 0.267 \(\pm\) 0.044, Pcorr < 0.001 in the sampling task, and b =  − 0.400 \(\pm\) 0.044, Pcorr < 0.001 in the knapsack task; see Tables S15 and S16). In the sampling task, self-performance ratings were lower in the absence of feedback compared to the presence of feedback (effect of feedback is b = 0.288 \(\pm\) 0.044, Pcorr < 0.001; Table S15). In the knapsack task, the self-performance ratings were also lower in the absence of feedback compared to the presence of feedback but only in easy trials (Fig. 5c), as indicated by the significant interaction effect between difficulty and feedback (b =  − 0.163 \(\pm\) 0.044, Pcorr < 0.001; Table S16). In hard trials, the effects of feedback on self-performance ratings differ between the two tasks, as indicated by the significant interaction effect between task type and feedback (b =  − 0.139 \(\pm\) 0.045, Pcorr = 0.007; see Table S17). This interaction effect also remained significant after controlling for participants’ objective performance (Tables S18–S20).

Fig. 5
figure 5

Self-performance estimates (self-reported ratings) in the main experiment. (a) Self-performance estimates in the sampling task. Bars indicate mean \(\pm\) SEM across participants. The self-performance rating is plotted by block type. The format is the same as in Fig. 2c. (b) Effects of difficulty, feedback, and their interaction on self-performance estimates in the sampling task. Coefficients were estimated with generalized linear mixed-effect models (see Table S15). ***P < 0.001, *P < 0.05 (all p-values are Bonferroni corrected). (c) Self-performance estimates in the knapsack task. Bars indicate mean \(\pm\) SEM across participants. The format is the same as in Fig. 2f. (d) Effects of difficulty, feedback, and their interaction on self-performance estimates in the knapsack task (see Table S16). The format is the same as in the panel (b).

Full size image

Moreover, we examined potential effects of learning or experience. To this end, we included a factor variable representing the order of the blocks (i.e., 1 for the 1st block, 2 for the 2nd block and so on) into our GLMMs. The additional analysis revealed that the main results above were not affected by block order (Tables S21–S24). These results suggest that our findings are robust with regards to the choice of measurement of SPEs and block order.

Discussion

This study investigated metacognition in computationally complex decision-making. Specifically, we examined the effects of task difficulty and the presence of feedback about the correctness of a decision on the formation of global SPEs when people are making cognitively simple, perceptual and complex, economic decisions (i.e., the sampling and the knapsack tasks, respectively).

We replicate previous findings about the effects of task difficulty and the presence of feedback in perceptual decision-making18,35. In the sampling task, objective performance was lower in harder trials but was not modulated by the presence of feedback (Fig. 3a, b). Furthermore, SPEs were found to be modulated by both task difficulty and the presence of feedback (Fig. 4a, b): they were lower in harder trials and in the absence of feedback (compared to trials with feedback: i.e., a reduction of SPEs in the absence of feedback). Most studies of metacognition in perceptual decision-making to date have examined local confidence in individual decisions17,22,39. Only a small number of studies has investigated global SPEs18,19,35,40. Our findings thus contribute to the growing literature on the formation of SPEs in perceptual decision-making18,19,35.

In the knapsack task, a complex economic decision-making task, we found that objective performance was modulated by task difficulty, defined based on a theoretical measure of computational hardness (instance complexity) (Fig. 3c, d). This finding is consistent with findings about the effects of instance complexity on performance demonstrated by previous studies34,36. The present study thus contributes to the growing literature highlighting the importance of formal measures of computational complexity as a predictor of human performance in complex decisions34,36.

Similar effects of the theoretical measure of computational hardness were found on SPEs in the knapsack task. Specifically, we demonstrated that SPEs were lower in harder trials, that is, trials with lower instance complexity (instance complexity is inversely correlated with computational hardness34,36) (Fig. 4c, d). This result indicates that participants were able to sense task difficulty while evaluating the quality of their complex decisions, even though the difficulty level was not explicitly indicated to them in the experiment. To the best of our knowledge, this is the first demonstration that people are capable of internally evaluating their own performance in computationally complex decisions, similar to perceptual decisions18,19, knowledge-based judgment13, motor control41,42, and memory retrieval43.

Moreover, we show that in the knapsack task, feedback modulates SPEs differently in easy and hard trials (Fig. 4c, d). In easy trials, participants displayed lower SPEs in the absence of feedback compared to the presence of feedback. This pattern of SPEs in easy trials is consistent with the genuine reduction of SPEs in the absence of feedback observed in the sampling task18, despite the substantial differences between cognitive burden required for solving the sampling (i.e., counting dots and computing the difference) and knapsack (i.e., combinatorial optimisation) tasks. Strikingly, one previous study of perceptual decision-making18 suggests such a pattern of SPE may result from a metacognitive process in which people integrate information about feedback (that is, in the presence of feedback) and decision confidence (in the absence of feedback) over multiple trials in a Bayesian manner.

In hard trials of the knapsack task, on the other hand, we did not observe any modulation of SPEs by feedback (Fig. 4c). Both in the presence and absence of feedback, participants displayed low SPEs around the chance level even though objective performance was above chance level (Fig. 3c). This pattern cannot be explained by the same kind of Bayesian integration18 that can account for pattern of SPEs observed in easy trials (Fig. 4c) and in the sampling task (Fig. 4a). The pattern of SPEs observed in hard trials can potentially be explained by metacognitive control of cognitive resources. When participants are making hard decisions, a larger proportion of their (limited) cognitive resources is allocated to the decision-making process, leaving little or no resources to other metacognitive and other cognitive processes. In this case, not enough resources are allocated to paying attention to or memorizing feedback (in the presence of feedback) and decision confidence (in the absence of feedback), leading to the failure of incorporating such information into estimates of global self-performance. As a result, participants exhibited low SPEs, around chance level, in hard trials regardless of the presence or absence of feedback. Following this speculation, participants should exhibit more accurate SPEs (i.e., higher discriminability about the objective performance) in easy as compared to hard trials in complex decision-making. The discriminability of SPE (correlation between SPE and performance) was found to be slightly greater in easy trials than in hard trials (easy trials: r = 0.266 \(\pm\) 0.106, mean \(\pm\) SEM across participants; hard trials: r = 0.216 \(\pm\) 0.111), which is at least to some degree consistent with our speculation, although the difference was not statistically significant (P = 0.752, two-tailed paired t-test). Those findings suggest that distinct cognitive mechanisms may be involved in the estimation of global self-performance in easy and hard problems in computationally complex decision-making. Future work is needed to examine this conjecture in more details.

In both the sampling and knapsack tasks, SPEs were approximately at the chance level (i.e., 0.5) in hard trials without feedback, while the objective performances exceeded the chance level (Fig. 4a, c). This phenomenon could be related to previous reports suggesting that metacognitive insights often lag behind above-chance objective performance when no feedback is provided44,45.

Our study has several limitations. First, we only collected a limited number of SPEs (i.e., two data points per condition and task), due to the relatively long duration of a trial in the knapsack task (approximately 30 s). This makes it difficult to implement advanced data analyses (e.g., computational model fitting) to further elucidate the possible mechanisms underlying the formation of SPEs. Second, the current study used the knapsack decision problem as a representative of computationally intractable problems. However, it remains an open question whether the results we found here are generalizable to other computationally intractable problems. To explore this question, future studies should test the generalizability of the patters of SPEs found in the knapsack decision task to other NP-complete problems such as Boolean satisfiability problem (K-SAT)46,47,48 and the traveling salesperson problem (TSP)49. Lastly, the attribution of differences between SPEs of two types of decision-making in the current study needs further investigation. The difference between the two types of tasks may not simply be limited to computational difficulty, but also to perceptual uncertainty, as the stimuli in the perceptual task were only flashed on the screen briefly, while in the knapsack task, they were much longer. Also, it could be attributed to the difference in objective performance between the two tasks, as participants had slightly higher accuracy in the knapsack task compared to the sampling task (Fig. 3a, c). Another possibility could be the difference in participants’ familiarity with the two types of tasks. While we did not recruit individuals with prior experience in the knapsack or sampling task for our past experiments, we cannot strictly rule out this possibility.

In conclusion, this study provides insights into metacognition in complex decision-making by examining the effects of task difficulty and feedback on global SPEs in a computationally hard task. In contrast to perceptual decisions, our findings suggest that people estimate their global performance in complex decisions through distinct metacognitive mechanisms for easy and hard instances. We believe that the current study is the first step towards a comprehensive understanding of how humans learn about their own performance when making complex decisions.

Methods

The study protocol was approved by the University of Melbourne Human Research Ethics Committee (Ethics ID 1954681.1), and all analyses were conducted in accordance with relevant guidelines and regulations.

Participants

We recruited 17 and 36 participants from the University of Melbourne for the pilot and main experiment, respectively (five males, age range = 19–38 and the mean \(\pm\) SD = 23.71 \(\pm\) 3.26 years in the pilot experiment; and 15 males, age range = 18–32 and the mean \(\pm\) SD = 22.31 \(\pm\) 5.19 years in the main experiment). The sample size of the main experiment was determined based on a power analysis based on pilot data (see the section of Data analysis below). All participants gave their informed consent.

Experimental task

Overview

Participants performed two decision-making tasks in the experiment (in-person for the pilot experiment and online for the main experiment): the sampling task (Fig. 1a) and the knapsack task (Fig. 1b). Details of both tasks are provided below.

The experiment consisted of 16 blocks (eight blocks for each of the two tasks). The blocks differed with regards to two factors: difficulty (easy or hard) and the presence of feedback about the correctness of a decision (presence or absence of feedback). The factorial design resulted in four types of blocks (Fig. 1e): easy-feedback, easy-no feedback, hard-feedback, hard-no feedback. Each combination of the four block types and the two decision-making tasks was presented twice in the 16 blocks of the experiment in a random order.

In each block, participants solved 10 trials of the same level of difficulty (Fig. 1f). After that, they were instructed to indicate their willingness to pay to earn the chance of attempting an additional five trials of the same level of difficulty as the preceding 10 trials in the same block using a Becker-DeGroot-Marschke (BDM) auction50 (Fig. 1c). The auction procedure enabled us to measure a participant’s self-performance estimates in an incentive-compatible manner38. Note that no feedback was provided in the additional bonus problems.

Participants were instructed at the beginning of the experiment that it would take approximately 1.5 h and that they could not leave if they finished it earlier.

Sampling task

In each trial, participants saw two boxes on the screen that contained a number of dots. Participants were asked to decide which of two boxes contained the larger number of dots18,19,22,35 (Fig. 1a). The difficulty of the decision was modulated by the adjusting the difference in number of dots in the two boxes (the differences were 46 and 18 dots in easy and hard trials, respectively). Each trial started with a fixation cross displayed at the centre of the screen (1.2 s). On the subsequent screen, two black boxes containing a different number of white dots were briefly flashed (300 ms). Participants had 3 s to indicate which of the two boxes they thought contained the larger number of dots.

Knapsack task

Participants solved 80 trials of the 0–1 knapsack decision problem34,36 (Fig. 1b). Each trial started with a screen displaying a fixation cross at the centre (1.2 s). On the next screen, six items were presented at random locations. Each item has two attributes: a value and a weight. Item values (in dollars) were indicated with dollar bills, and item weights (in kilograms) were indicated with a black weight symbol. The size of both the dollar bills and the weight symbols were proportional to the value and weight, respectively, they indicated. The weight limit (capacity) of the knapsack in kilograms and the target profit in dollars were displayed inside a green circle at the centre of the screen, and the green circle indicated the time remaining in the trial (maximum of 25 s). Participants were asked to indicate whether there exists a subset of items whose total weight does not exceed the capacity, while the total of value is at least as high as the target profit. Once participants had solved the instance, the indicated their response (“YES” or “NO”) by pressing a corresponding button on the keyboard (maximum of 3 s).

Following previous studies34, we defined the difficulty of each trial in terms of ‘instance complexity’ (IC): the distance between the target profit and the maximum profit attainable in the corresponding instance of the optimization variant of the 0-1 knapsack problem. Note that IC is inversely correlated with computational hardness, which means a lower value of IC corresponds to a higher level of computational hardness. Specifically,

$$IC= \left|\frac{p-{p}^{*}}{\sum {v}_{i}}\right|$$

where \(p\) is the target profit of the problem, \({p}^{*}\) is the maximum profit achievable in the corresponding optimization instance (i.e. the highest total value of a knapsack achievable with the given set of items and the given weight constraints), and \({v}_{i}\) denotes the values of i-th item. Note that IC relies on the weight information, although it does not appear in the above formula (see Text S1). The values of IC were 0.16 and 0.01 in easy and hard trials, respectively.

Self-performance estimates (SPE)

At the end of each block, participants were asked to indicate their SPEs in two ways: a bid in a BDM auction, and a self-reported rating on a Likert scale. After finishing 10 trials in a block, a participant was endowed with A$1 and made a bid for the chance of attempting an additional 5 trials. These additional five trials were of the same difficulty level as the first 10 trials within the preceding block. A participant was rewarded with A$0.2 for each correct decision. In each BDM auction, a counter-bid was drawn randomly from the range A$0-A$1. If the participant’s bidding value was equal or greater than the counter-bid, the participant paid the counter-bid and could attempt an additional five trials. Otherwise, the participants kept the initial endowment of A$1 and left the block. This auction mechanism is incentive-compatible in the sense that the optimal strategy for a participant is to always bid the number closest to their true belief about the proportion of additional trials they thought they could solve correctly (i.e., SPE; See Text S2). Participants were explicitly instructed in the optimal strategy, and using a questionnaire, we confirmed that they correctly understood it. Participants were also asked to report their self-performance directly. Specifically, a participant was asked to indicate on a 6-point Likert scale (0 = none of them, 5 = all of them) of how many additional trials they thought they could solve correctly. Note that self-reported performance ratings were found to be highly correlated with the bid values (sampling task: \(r=\) 0.752 \(\pm\) 0.050, mean \(\pm\) SEM across participants; knapsack task: \(r=\) 0.760 \(\pm\) 0.043), suggesting that these two represent consistent but not the exact same constructs. The order of the BDM auction and the Likert rating was randomized across blocks and participants.

Reward payment

Participants received a show-up fee of A$10 and were a payment of A$0.2 for each correct answer for both the first 10 and the 5 bonus trials in each block.

Data analysis

Pilot experiment

We examined the effects of difficulty and feedback on trial-by-trial objective performance and block-by-block SPEs (i.e., BDM bid value) using generalized linear mixed effect models (GLMMs). We modelled objective performance as follows: logit P(correct) ~ 1 + D + F + D x F + (1 | participants) (see Tables S1 and S4). Here, P(correct) was coded as 1 if the participant chose the correct option and 0 otherwise. D denotes the difficulty (coded as −1 for easy and 1 for hard problems), F denotes the feedback (coded as −1 for problems without feedback and 1 for problems with feedback), and D × F indicates the interaction. We added participant random effects on the intercept. We modelled global SPEs as follows (see Tables S2-S3 and Tables S5-S6): BDM value ~ 1 + D + F + D x F + (1 | participants) with participant random effects on the intercept.

Determination of the sample size

We determined the sample size of the main experiment based on the estimations of the GLMMs described above by using glmer and powerCurve function in R, aiming for a statistical power of at least 0.8 given a significance level a = (0.05/3) for the effects of interest: i.e., effects of difficulty and feedback and the interaction on SPEs in the knapsack task. The required sample size is N = 36.

Main experiment

We examined the effects of difficulty and feedback on trial-by-trial objective performance and block-by-block global SPEs using the same models we used for the analysis of the pilot data (see above).

We also compared participants’ global SPEs in hard blocks across two types of tasks by performing additional GLMM analyses. First, we modelled global SPEs as follows: BDM value ~ 1 + T + F + T x F + (1 | participants). Here, T denotes the task type (coded as −1 for the sampling task and 1 for the knapsack task), F denotes the feedback (coded as −1 for problems without feedback and 1 for problems with feedback), and T × F indicates the interaction. We added participant random effects on the intercept. Second, to exclude the possibility that the differential effects of feedback on SPEs in hard trials between two tasks can be attributed to the difference in participants’ objective performance across tasks, we modelled SPEs as BDM value ~ 1 + T + F + T x F + P + (1 | participants), where P indicates participants’ objective performance (i.e., the proportion of correct choices) in each of the hard blocks. Furthermore, we tested whether the differential effects of feedback on SPEs in hard trials between two tasks can be attributed to the difference in participants’ objective performance in the first and the second half of each hard block by modelling SPEs as follows: BDM value ~ 1 + T + F + T x F + P1 + (1 | participants), where P1 indicates participants’ objective performance in the first half of each of the hard blocks and BDM value/self-performance rating ~ 1 + T + F + T x F + P2 + (1 | participants), where P2 indicates participants’ objective performance in the second half of each of the hard blocks.

We also compared participants’ objective performance in hard trials to chance level (i.e., 0.5) by performing a GLMM analysis. We modelled participants’ performance in hard trials as follows: logit P(correct) ~ 1 + F + (1 | participants), where P(correct) was coded as 1 if participant chose the correct option and 0 otherwise. If participants’ performance accuracy is greater than chance, then the intercept term should be greater than 0.

To examine robustness of our results related to our main study, we added block order as an explanatory variable of no interest to the models of both trial-by-trial objective performance and block-by-block SPEs (see Tables S21-S24).

The power analysis was conducted in R (version 4.2.1) using the glmer (version 1.1.30) and powerCurve (version 1.0.6) functions. The GLMMs were estimated in MATLAB (version R2022_a) using the fitglme function.