Research on maximum power point tracking of photovoltaic power generation based on improved hybrid optimization algorithm

Abstract

Due to environmental factors’ influence, the power–voltage (P–V) curve of a photovoltaic array typically presents multiple peaks. The traditional gravitational search algorithm is inclined to fall into local optimal solutions and demonstrates poor performance in maximum power point tracking. Consequently, this paper proposes applying the PSO algorithm for optimizing the GSA parameters. Meanwhile, introducing the gravitational constant into the GSA algorithm accomplishes the dynamic adjustment of the three key parameters in PSO. Furthermore, the Levy flight step is incorporated to enhance the global search capability. The improved algorithm can improve the search speed and accuracy by adding memory and group interaction to the particle update formula to alleviate oscillation. Simulink modeling and simulation analysis reveals that, compared with traditional algorithms, the improved algorithm can identify the maximum power point of the photovoltaic array more rapidly and stably under static and dynamic shading conditions.

Introduction

With the acceleration of economic development, the excessive utilization of traditional fossil fuel resources has resulted in significant environmental pollution and resource depletion. Consequently, there is a growing concern regarding developing and utilizing renewable energy sources. Among these, solar energy stands out as an inexhaustible resource. Due to the continuous reduction in production costs and improvements in conversion efficiency, photovoltaic power generation has become one of the mainstream power generation methods today. As a result, it has been widely adopted in many countries and regions¹. Being vast and rich in resources, China provides a significant opportunity for the rational layout of the photovoltaic industry and the enhancement of energy efficiency. The domestic photovoltaic industry emerged in the 1970s. In the mid to late 1990s, the photovoltaic power generation industry entered a stable development stage. According to relevant data, the average annual growth rate of China’s photovoltaic power generation industry from 2003 to 2009 reached 110%, making it the country with the most significant output of photovoltaic cells worldwide in 2007. In 2010, it even reached 117.04%. By 2013, the production capacity and output reached 42 GM and 25.1 GW, respectively. As of 2023, the global cumulative installed capacity of photovoltaics has reached 1546 GW, with the new installed capacity of photovoltaics in 2023 being 390 GW. It is expected that the global cumulative installed capacity of photovoltaics will reach 18,200 GW by 2050.

In recent years, both domestic and international scholars have conducted extensive research on photovoltaic maximum power point tracking (MPPT) under varying illumination conditions. The control algorithms can be broadly classified into traditional algorithms, intelligent algorithms, and their combinations. The discovery of the photovoltaic phenomenon in liquids by French physicist E. Becquerel in the early nineteenth century marked the beginning of interest in photovoltaic power generation². Since then, photovoltaic technology has gained increasing attention from experts and industry professionals, resulting in the development of numerous new technologies. After nearly two centuries of progress, the photovoltaic power generation industry has reached a relatively mature stage.

Traditional algorithms, such as the perturbation and observation method and the conductance increment method, have been widely used and continuously refined. For example, a seminal study³ combines the conductance increment method, the perturbation and observation method, and the constant voltage method, thereby reducing the time required to track the maximum power point and minimizing oscillations upon reaching the maximum power. Building on the essential characteristics of the variable acceleration perturbation method, literature⁴ introduces and utilizes this method for accelerated search, achieving high precision with reduced search time by incorporating a genetic algorithm. In a research proposal⁵, a cutting-edge performance optimization technology based on the conductance increment approach was put forward, maximizing the efficiency of the off-grid solar photovoltaic system. An innovative control methodology suggested in the literature⁶ involves an Adaptive Superposition of Stepless Voltage Perturbation based on the Conductance Increment method, ensuring rapid and efficient maximum power point control. Some intelligent algorithms have also been investigated, such as the AI-based algorithm discussed in Literature⁷, the modified tracking mechanism for PV system MPPT technology proposed in Literature⁸ based on the horse optimization method (HOM), and the discussion of MPPT technology based on machine learning in Literature⁹. These three algorithms can effectively achieve global MPPT; however, their efficiency is contingent upon a substantial amount of training data and time. Meanwhile, the MPPT algorithm is not merely a theory. Literature¹⁰ proposed applying the MPPT algorithm to spacecraft applications, undoubtedly a breakthrough for future technological advancement. These two algorithms can effectively achieve global MPPT, but their efficiency depends on a large amount of training data and time. References^11,12 proposed optimized algorithms based on the enhanced version of COOT and an MPPT approach based on ant colony optimization and fuzzy control, notably enhancing the tracking speed and accuracy. Comparative simulations conducted in literature¹³ between the Bacterial Foraging method and the traditional Perturbation and Observation method affirm the former’s superior global search ability under local shading conditions. Furthermore, papers^14,15 put forward an algorithm based on dung beetle optimization and a comparative method of PV MPPT under local shading conditions based on Meta-inspired heuristics. The results indicated that both methods could track the maximum power point more rapidly and precisely. Reference¹⁶ presented an innovative grey wolf optimization algorithm that employs the Nelder-Mead search method and can converge rapidly under partial shading conditions. Document¹⁷ sets forth a novel group-based maximum power point tracking (MPPT) method to address the issue of local shading in solar photovoltaic technology. Concurrently, Document¹⁸ proposes an enhanced global MPPT approach to mitigate overheating in photovoltaic systems under partial shading circumstances, thereby enhancing tracking accuracy and ameliorating hot spot effects. Paper¹⁹ presents a novel meta-heuristic algorithm called the hippopotamus algorithm, similar to the hierarchical wolf algorithm. The algorithm updates the population using different behavior patterns to avoid being trapped in local optimal solutions.Papers^20,21 propose a novel MPPT mechanism based on a multi-universe optimization algorithm and an MPPT study based on the advanced Great Wall Construction algorithm, respectively. The results show that the maximum power point can be tracked faster and more accurately, whether in normal lighting conditions or under partial shading. A study²² emphasizes the dependence of the Particle Swarm algorithm on parameter selection for effective search, as there is a risk of getting stuck in local optimal solutions. In contrast, literature²³ advocates for a Particle Swarm Optimization (PSO)-based photovoltaic MPPT approach that focuses on global search abilities through adaptive mutation to expand the search range. However, this approach faces challenges such as prolonged convergence times and power fluctuations during tracking. To address these limitations, researchers²⁴ propose an Adaptive Inertia Weight Particle Swarm algorithm that adjusts the non-linear inertia weight of velocity updates to improve global search speed and accuracy. However, this algorithm does not dynamically adjust the velocities of the cognitive and social factors during the iteration process, leaving room for further optimization. Paper²⁵ introduces a particle swarm optimization algorithm with an adaptive gain factor strategy, which enables real-time MPPT control. Traditional MPPT methods are advantageous due to their operational simplicity. However, under partial shading conditions, these methods struggle to quickly locate the maximum power point of the photovoltaic panel, resulting in a relatively low overall utilization rate of production capacity. On the other hand, intelligent algorithms excel in global search capabilities, allowing them to identify the maximum power point even in complex environmental conditions with multi-peak characteristics. Nevertheless, these algorithms also have areas that need improvement, such as unstable tracking times, significant PowerPoint fluctuations, and low accuracy. Therefore, it is necessary to optimize these algorithms further to enhance the overall utilization rate of photovoltaic cells.

To address the challenges mentioned above, this paper proposes an MPPT algorithm based on a hybrid optimization of the gravitational search algorithm (GSA) and PSO, tailored to the output characteristics of photovoltaic arrays. By dynamically adjusting the inertia weight, cognitive factor, and social factor in the PSO algorithm and the gravitational constant in the GSA and incorporating the Lévy flight step size to enhance global search capability, the algorithm improves convergence speed and accuracy. Additionally, to mitigate fluctuations in the maximum power value during the tracking process, relevant factors such as memory and population information exchange are integrated into the particle update formula, enabling accurate and rapid tracking of the maximum power point under varying lighting conditions.

This paper is structured into several key sections, and the superiority of the proposed algorithm is manifested through the simulation of maximum power point tracking (MPPT) with MATLAB/Simulink. The first section presents the output characteristics of the photovoltaic array and the solar cell model. The second section introduces traditional intelligent algorithms such as PSO and GSA and proposes an improved algorithm designated as PLGSA, where P represents PSO and L represents Levy flight. The third section analyses and contrasts the tracking speed and accuracy of each algorithm under stable lighting conditions and scenarios involving sudden changes in lighting. The final section summarises the optimization algorithms.

Output characteristics of photovoltaic arrays and models of solar panels

Analysis of output characteristics of photovoltaic cells

Theoretically, the output characteristic curve of photovoltaic cells is nonlinear. To study the influence of light intensity and temperature on these output characteristics, a controlled variable approach is required. This involves varying the light intensity while maintaining a constant temperature or varying the temperature while keeping the light intensity constant and then recording the resulting changes in output characteristics. In this paper, we focus on conditions where the temperature is constant, setting it to the standard temperature of 25 °C. The light intensities are varied at levels of 1000, 800, 600, 400, and 200 W/m², respectively. The resulting output characteristic curves are shown below:

From the P–V and I–V characteristic curves of the photovoltaic array under different light intensities, as shown in Figs. 1 and 2, it is evident that the short-circuit current, open-circuit voltage, and output power are significantly influenced by light intensity. These three parameters are positively correlated with light intensity, meaning that as light intensity increases, the sum of the photovoltaic cells $I_{sc}$, $U_{oc}$ and the output power of the system also increase.

Fig. 1

P–V curves under different light intensities.

Fig. 2

I–V curves under different light intensities.

Solar cell panel model

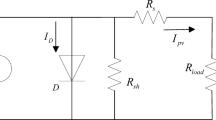
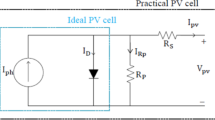
Based on the fundamental principles of solar cell electrical energy output, the equivalent circuit diagram of the solar cell, as shown in Fig. 3, can be derived.

Fig. 3

Equivalent circuit of photovoltaic cell.

The model consists of an ideal current source $I_{ph}$ and a parallel diode ($d_{1}$), with parallel and series resistors $R_{sh}$ and $R_{s}$, respectively. The current source generates photocurrent, the magnitude of which is proportional to the solar irradiance (G) and temperature (T). The diode model represents the semiconductor effect of the photovoltaic panel, while the resistors $R_{sh}$ and $R_{s}$ simulate the ohmic losses in the semiconductor material. Applying Kirchhoff’s current law, the output current $I_{p}$ can be expressed as:

$$ I_{p} = I_{ph} - I_{d1} - I_{sh} $$

where $I_{ph}$ is the photocurrent of the current source, $I_{d1}$ is the current passing through the diode $d_{1}$, and $I_{sh}$ is the current of the parallel resistor $R_{sh}$. Using the diode current expression and applying Ohm’s law, $R_{sh}$ is rewritten as:

$$ I_{p} = I_{ph} - I_{s} \left( {e^{{\frac{qE}{{AKT}}}} - 1} \right) - \frac{{V_{d1} }}{{R_{sh} }} $$

where $V_{d1}$ is the voltage at both ends of the diode $d_{1}$, $I_{d1} = I_{s} \left( {e^{{\frac{qE}{{AKT}}}} - 1} \right)$ is the diode $d_{1}$ current flowing through, $I_{s}$ is the PN junction reverse saturation current of the equivalent diode inside the photovoltaic cell, generally taken as 8 to 10 $\mu A$; A is the ideal coefficient of the diode; K is the Boltzmann constant, approximately 1.38 * 10^–23 J/K; T is the temperature in the current state.

According to Kirchhoff’s current law, its output current $I_{p}$ can be expressed as the following formula:

$$ I_{p} = I_{ph} - I_{s} \left( {e^{{\frac{{q(V_{p} + I_{p} R_{s} )}}{AKT}}} - 1} \right) - \frac{{V_{p} + I_{p} R_{s} }}{{R_{sh} }} $$

Among them, $I_{ph}$ is the photocurrent generated inside the photovoltaic cell, $V_{p}$ is the output voltage, and $R_{s}$ is the series resistance. In the ideal form, as the intrinsic free internal resistance of the solar cell itself, the shunt resistance $R_{sh}$ is very large, and the series resistance $R_{s}$ is particularly small. To simplify the mathematical model of the solar cell, they can be ignored. Thus, the following equation is obtained:

$$ I_{p} = I_{ph} - I_{s} \left( {e^{{\frac{{qV_{p} }}{AKT}}} - 1} \right) $$

Through the above formula, bring it back inversely to find $V_{p}$:

$$ V_{p} = \frac{AKT}{q}{\text{1n}}\left( {\frac{{I_{ph} - I_{p} }}{{I_{s} }} - 1} \right) $$

From the above two equations, it is clear that the voltage and current output of a solar cell are closely related to temperature and light intensity. However, in practical research, it is not feasible to calculate the photovoltaic cell’s output directly using these equations. By considering the short-circuit current $I_{sc}$ and open-circuit voltage of the photovoltaic cell $V_{oc}$ and after simplifying the expression, the method of undetermined coefficients $I_{p} = I_{ph} - I_{s} \left( {e^{{\frac{{qV_{p} }}{AKT}}} - 1} \right)$ can be used to obtain:

$$ I = I_{sc} \left( {1 - C_{1} e^{{\frac{V}{{C_{2} V_{oc} }} - 1}} } \right) $$

Under general standard conditions (25 °C, 1000 W/m²), when the photovoltaic system operates at the maximum power point ($I_{mpp}$, $V_{mpp}$), the following expression is obtained when substituted into the equations:

$$ I_{mpp} = I_{sc} \left( {1 - C_{1} e^{{\frac{{V_{mpp} }}{{C_{2} V_{oc} }} - 1}} } \right) $$

At room temperature, $e^{{\frac{{V_{mpp} }}{{C_{2} V_{oc} }}}}$ is much greater than 1, allowing us to neglect the 1 in the expression. This simplifies to:

$$ C_{1} = \left( {1 - \frac{{I_{mpp} }}{{I_{sc} }}} \right)e^{{\frac{{ - V_{mpp} }}{{C_{2} V_{oc} }}}} $$

In the open-circuit state, the main circuit is disconnected, so the output current $I_{p}$ is 0, and the output voltage $V_{p}$ is equal to $V_{oc}$. By substituting the current voltage in the open-circuit state into $I_{mpp} = I_{sc} \left( {1 - C_{1} e^{{\frac{{V_{mpp} }}{{C_{2} V_{oc} }} - 1}} } \right)$, and substituting $C_{1}$ into $C_{1} = \left( {1 - \frac{{I_{mpp} }}{{I_{sc} }}} \right)e^{{\frac{{ - V_{mpp} }}{{C_{2} V_{oc} }}}}$, we obtain:

$$ I_{sc} \left[ 1 \right. - (1 - \frac{{I_{mpp} }}{{I_{sc} }})e^{{\frac{{ - V_{mpp} }}{{C_{2} V_{oc} }}}} \left. {\left( {e^{{\frac{1}{{C_{2} }}}} - 1} \right)} \right] = 0 $$

The value of $C_{2}$ is solved from the above equation as follows:

$$ C_{2} = \left( {\frac{{V_{mpp} }}{{V_{oc} }} - 1} \right)\left[ {1{\text{n}}\left( {1 - \frac{{I_{mpp} }}{{I_{sc} }}} \right)} \right]^{ - 1} $$

After establishing the equations for solving the parameters $C_{1}$ and $C_{2}$, the values of $I_{sc}$,$V_{oc}$, $I_{mpp}$ and $V_{mpp}$ for the photovoltaic current under standard conditions (25 °C, 1000 W/m²) can be substituted into the equations $C_{1} = \left( {1 - \frac{{I_{mpp} }}{{I_{sc} }}} \right)e^{{\frac{{ - V_{mpp} }}{{C_{2} V_{oc} }}}}$ and $C_{2} = \left( {\frac{{V_{mpp} }}{{V_{oc} }} - 1} \right)\left[ {1{\text{n}}\left( {1 - \frac{{I_{mpp} }}{{I_{sc} }}} \right)} \right]^{ - 1}$ to solve for the specific values of $C_{1}$ and $C_{2}$. By substituting $C_{1}$ and $C_{2}$ into $I = I_{sc} \left( {1 - C_{1} e^{{\frac{V}{{C_{2} V_{oc} }} - 1}} } \right)$, the functional relationship between the output voltage and current of the solar cell under standard conditions can be determined. This relationship allows for the determination of the characteristic curve, enabling the study of the solar cell’s output characteristics.

The simulation presents the inherent characteristics of the engineering model of the solar panel, as detailed in Table 1.

Table 1 Intrinsic characteristics of the model of solar panels engineering

MPPT algorithm strategies

PSO algorithm

The PSO algorithm is a swarm intelligence algorithm inspired by the flight and foraging behavior of bird flocks. In PSO, the particle swarm is modeled as a group of birds flying in search of food²⁶. The speed of each particle’s movement is influenced by two parameters: the particle’s current best position and the best position found by the particle throughout its history. The updated formulas for the particle’s velocity and position can be determined using the following equations:

$$ v_{i}^{{d + {1}}} = wv_{i}^{d} + c_{1} r_{1} (p_{beesti} - x_{i}^{d} ) + c_{2} r_{2} (G_{best} - x_{i}^{d} ) $$

$$ x_{i}^{d + 1} = x_{i}^{d} + v_{i}^{d + 1} $$

In these equations, the inertia weight is denoted by $\omega$, the individual learning factor is represented by ${\text{c}}_{1}$, and the social learning factor of the entire particle population is represented by ${\text{c}}_{2}$. The random numbers generated between 0 and 1 are represented by ${\text{r}}_{{1}}$ and ${\text{r}}_{2}$, and ${\text{P}}_{{{\text{besti}}}}$ and ${\text{G}}_{{{\text{best}}}}$ represent the best solution of the i-th particle and the global best solution of the group, respectively. The search mechanism of the PSO algorithm is illustrated in Fig. 4.

Fig. 4

Schematic diagram of the search principle of the PSO algorithm.

GSA

GSA is a novel meta-heuristic artificial intelligence optimization algorithm based on Newton’s Law of Universal Gravitation, proposed by Esmat et al. This algorithm is known for its strong global optimization capability and fast convergence speed²⁷. Liu Xiaogang and Ouyang Zigen utilized the enhanced global gravitational search algorithm in function optimization, demonstrating its feasibility in practical scenarios²⁸. Rather Sajad Ahmad et al. Integrated chaotic mapping and the gravitational search algorithm to address variable minimization issues in engineering design frameworks, such as in gearbox design and multi-disc clutch brake design²⁹. Gonggui Chen et al. Employed GSA to enhance the parameters of a simulated controller and optimize the power control system³⁰. Moeini et al. introduced an improved GSA algorithm that can identify infeasible particles before updating particle velocity and position, thereby optimizing the operation of large systems. Although the convergence speed was improved by removing infeasible particles, this reduction in particle number sometimes led to fluctuations in the optimal value³¹.

The basic principle of the GSA is as follows: The optimization problem is viewed as a group of particles freely moving in space. The closer a particle is to the optimal value, the greater its mass. According to the law of universal gravitation, an attractive force exists between particles, with the gravitational force being more vital for particles with greater mass. Consequently, all particles tend to move toward the position of the particle with the highest mass, which represents the best position, ultimately leading to the optimal solution to the problem. The position and velocity updates of particle p are governed by the following equations:

$$ x_{p}^{d} (t + 1) = x_{p}^{d} (t) + v_{p}^{d} (t + 1) $$

$$ v_{p}^{d} (t + 1) = rand_{p} \times v_{p}^{d} (t) + a_{p}^{d} (t) $$

Among them, $x_{p}^{d}$ represents the position of particle p in the d-th dimension; $v_{p}^{d}$ is the velocity of particle p in the dth dimension; $a_{p}^{d}$ is the acceleration of particle p in the d-th dimension. According to Newton’s second law, $a_{p}^{d}$ is defined as follows:

$$ a_{p}^{d} = \frac{{F_{p}^{d} (t)}}{{M_{p} (t)}} $$

Among them, $F_{p}^{d}$ is the sum of the gravitational forces that particle p receives from other particles in the dth dimension, and $M_{p}$ is the mass of particle p, which is related to the fitness.

In the GSA, the initial positions of all particles are randomly generated. The gravitational force between particle p and particle q can be expressed as:

$$ F_{pq}^{d} (t) = G_{(t)} \times \frac{{M_{p(t)} \times M_{q(t)} }}{{R_{pq(t)} + \varepsilon }} \times \left( {x_{q}^{d} (t) - x_{p}^{d} (t)} \right) $$

In this formula, d is the dimension of the optimization problem, $G_{{\left( {\text{t}} \right)}}$ signifies the gravitational constant at time t, $M_{p(t)}$ and $M_{q(t)}$ represent the masses of particles p and q respectively, $R_{pq(t)}$ is the Euclidean distance between particles p and q, $x_{p}^{d} (t)$ and $x_{q}^{d} (t)$ are the positions of particles p and q respectively, and $\varepsilon$ is a small constant to ensure that the denominator is not zero.

Among them, the gravitational constant is expressed as:

$$ G_{(t)} = G_{0} e^{{ - \frac{\alpha t}{T}}} $$

Among them, $G_{0}$ represents the gravitational constant at the initial moment, $T$ is the maximum number of iterations, and $\alpha$ is the attenuation factor. The gravitational constant $G_{{\left( {\text{t}} \right)}}$ decreases exponentially as the number of iterations increases. Figure 5 illustrates the search principle of the GSA.

Fig. 5

Schematic diagram of the search principle of the GSA.

In summary, the primary challenges of the GSA algorithm and its variants include convergence speed, optimal accuracy, and stability of the optimal value. To address these issues, this study proposes dynamic adjustments to the GSA algorithm’s gravitational constant and velocity update formula. Additionally, the study combines the PSO algorithm with GSA and incorporates Lévy flight to adjust the step size, thereby enhancing optimization accuracy dynamically. Finally, various simulations are conducted to test the performance of the proposed PLGSA-MPPT under these conditions. The simulation results are then compared with PSO-MPPT, GSA-MPPT, and HO-MPPT.

Based on the improved GSA

In the traditional PSO algorithm, the parameters of inertia weight $\omega$, cognitive factor $c_{1}$, and social factor $c_{2}$ are typically adjusted either linearly or set as fixed values. These methods can lead to longer tracking times for the maximum power point and reduce the efficiency of the photovoltaic system. In the PSO algorithm, the inertia weight $\omega$ is crucial for balancing global and local search abilities, while the cognitive factor $c_{1}$ and the social factor $c_{2}$ guide the particle towards its individual best position and the global best position, respectively.

In the early stages of PSO algorithms applied to MPPT in photovoltaic systems, selecting a larger inertia weight $\omega$ and cognitive factor $c_{1}$ increases the influence of the particle’s velocity and its individual best value on its current velocity. This enhances the particle’s autonomy, disperses the search range in the solution space, and strengthens the algorithm’s global search ability and accuracy. Simultaneously, choosing a smaller social factor $c_{2}$ slows down the convergence of particles toward the current global best position, reducing the influence of group experience on individual particles. This helps maintain particle diversity and prevents premature convergence of the particle swarm. As the iteration process progresses, gradually reducing the inertia weight $\omega$ and cognitive factor $c_{1}$ while increasing the social factor $c_{2}$ reduces particle autonomy and enhances the influence of the global best position on particles, thereby accelerating convergence.

In order to address these issues, the gravitational constant is introduced to dynamically adjust these three parameters. Additionally, to tackle fluctuations in the maximum power value during MPPT, factors related to memory and population information exchange are incorporated into the particle update formula. Simultaneously, Levy Flight is included to prevent being trapped in local optima. The flowchart of the PLGSA algorithm is depicted in Fig. 6.

Fig. 6

Flowchart of PLGSA.

There are several improvements to the algorithm:

Dynamic adjustment of inertial weight, cognitive factor, and social factor

First of all, As the number of iterations increases, the gravitational constant $G_{(t)}$ will decrease exponentially. Based on the previously discussed adjustment directions for the inertia weight $\omega$, cognitive factor $c_{1}$ and social factor $c_{2}$, and by integrating these with the gravitational constant $\omega$, cognitive factor $c_{1}$, and social factor $c_{2}$ can be expressed as:

$$ \omega (t) = \omega_{\max } G(t) $$

$$ c_{1} (t) = c_{1\max } G(t) $$

$$ c_{2} = \frac{{c_{2\max } }}{G(t)} $$

During the iteration process, the overall trend of all cognitive factors gradually decreases according to the exponential law governing the gravitational constant $G_{(t)}$. Within the same generation, the cognitive factors of different particles will vary depending on the quality of their individual historical best positions and the gravitational forces they experience. A smaller fitness value at the self-best position indicates that the particle is in a less optimal position, leading to a smaller mass and, consequently, a smaller gravitational force. As a result, the cognitive factor $c_{1}$ for that particle will also be smaller.

Meanwhile, During the iterative process, the trend of social factors gradually increases according to the exponential law governing the gravitational constant $G_{(t)}$. Within the same generation, the social factors of different particles will vary depending on the gravitational interaction between the particle’s position and the global optimal position. The greater the deviation of a particle’s fitness from the fitness value of the global optimal position, the smaller the particle’s mass. Conversely, the mass of the corresponding global optimal position is larger, resulting in a stronger gravitational pull and a larger social factor $c_{2}$.

The original GSA speed update formula has been rewritten

As mentioned earlier, to address the issue of fluctuations in the maximum power value, the original velocity update formula of the GSA has been rewritten:

$$ v_{p}^{d} (t + 1) = \omega (t) \times rand_{{p1}} \times v_{p}^{d} (t) + c_{1} \times rand_{{p2}} \times \left[ {best_{p} - x_{p}^{d} (t)} \right] + c_{2} \times rand_{{p3}} \times \left[ {best - x_{p}^{d} (t)} \right] + a_{p}^{d} (t) $$

$$ x_{p}^{d} (t + 1) = x_{p}^{d} (t) + v_{p}^{d} (t + 1) $$

Random adjustment of gravitational constant

Additionally, the gravitational constant $G_{(t)}$ has been modified. Previously, the gravitational constant decayed exponentially based solely on the attenuation factor, the number of iterations, and the maximum number of iterations. In the improved approach, the gravitational constant $G_{(t)}$ is combined with velocity to introduce greater randomness.

The current gravitational constant:

$$ G_{(t)} = G_{0} e^{{ - \frac{\alpha t}{T}}} + v $$

Levy flight joins

Building on this, Lévy flight is incorporated into the position update process. With its unique step length distribution, Lévy flight allows for extensive exploration of the search space, helping the optimization algorithm to escape local optima and increasing the likelihood of finding the global optimal solution. Additionally, the inherent randomness of Lévy flight enhances the algorithm’s robustness when dealing with complex and multimodal functions, making it better suited to a wide range of optimization problems.

Among them, Figs. 7, 8, 9 show some of the main updated code.

Fig. 7

Code for updating the gravitational constant.

Fig. 8

Code for updating speed and position.

Fig. 9

Levy flight code.

Simulation analysis

MATLAB/Simulink simulation model

This study focuses on the tracking speed and accuracy of the maximum power point. Our primary objective is to optimize the algorithm to achieve the fastest possible convergence speed and the highest possible accuracy. Figure 10 illustrates the simulation model developed in MATLAB/Simulink.

Fig. 10

MATLAB/Simulink simulation model.

The entire system includes the photovoltaic array, an anti-reverse current diode, a subsystem, a PWM generator, and a BOOST circuit, which comprises resistors, inductors, capacitors, and IGBT modules. During the operation of the photovoltaic system, real-time voltage and current are processed by the subsystem algorithm, and the duty cycle is output. This duty cycle is sent to the PWM generator, which generates the PWM waveform. Finally, the BOOST circuit is controlled to maintain the voltage at the reference voltage level.

The parameter settings for each component are as follows: Inductance: 20 mH, Capacitor 1:2 mH, Capacitor 2:5 μF, Resistance: 40 Ω. The MATLAB software version used is MATLAB R2022b. The computer used for the simulation is equipped with an Intel Core i7 8750H CPU and 16 GB of memory.

Initial condition setting

To verify the effectiveness of PLGSA in MPPT, simulations were conducted under both no-shading and variable-shading conditions using the simulation model shown in Fig. 1. The simulation experiments were carried out using the PSO, GSA, and PLGSA algorithms, with their results compared. For ease of comparison among the three methods, the MPPT controller employed a direct control approach with the duty cycle as the output. The number of particles $N = 10$, the maximum number of iterations $counter\_\max = 10$, and, for PSO and PLGSA, the inertia weight $\omega$ = 0.4, cognitive factor $c_{1}$ = 1.2, and social factor $c_{2}$ = 1.4 were kept consistent across all methods. The conditions tested are as follows:

Condition 1: As shown in Fig. 1, the irradiance of the three solar panels is 1000 ${\text{W}}/{\text{m}}^{2}$ each, and the temperature is 25 $^\circ {\text{C}}$. Under these conditions, the theoretical maximum power point of the photovoltaic system is 639.4500 W, and the corresponding theoretical voltage is 87.0000 V.

Condition 2: The irradiances of the three solar panels are 1000 ${\text{W}}/{\text{m}}^{2}$, 800 ${\text{W}}/{\text{m}}^{2}$, and 1000 ${\text{W}}/{\text{m}}^{2}$, respectively, with all temperatures set to 25 $^\circ {\text{C}}$. In this case, the theoretical maximum power point is 469.1363 W, and the corresponding theoretical voltage is 86.4000 V.

Condition 3: The irradiances of the three solar panels are 1000 ${\text{W}}/{\text{m}}^{2}$, 800 ${\text{W}}/{\text{m}}^{2}$, and 500 ${\text{W}}/{\text{m}}^{2}$, respectively, with all temperatures set to 25 $^\circ {\text{C}}$. Under these conditions, the theoretical maximum power point is 332.6700 W, and the corresponding theoretical voltage is 60.0000 V.

Figure 11 depicts the P–V output characteristics of solar energy under both normal lighting conditions and partial shading circumstances.

Fig. 11

Solar P–V output characteristic curves under normal lighting conditions and partial shading conditions.

Simulation verification in the case of no occlusion

The overall waveform of power tracking in the case of no occlusion is shown in Fig. 12. From Fig. 12, it is evident that the time required to track the maximum power differs among the three methods under Condition 1.

Fig. 12

Power tracking waveform in the case of no occlusion.

As depicted in Fig. 13, the tracking time needed by PSO-MPPT and HO-MPPT to reach the maximum power point is approximately 0.14 s and 0.11 s, respectively, and the maximum power they attained are 526.09 watts and 526.63 watts. Nevertheless, GSA-MPPT fluctuated after stabilizing for a period of time and ultimately settled at 503.72 watts. Compared with PLGSA-MPPT, the tracking time is approximately 0.09 s, and the maximum power tracked is 638.72 watts, which is relatively close to the theoretical maximum power of 639.45 watts. By contrast, PSO-MPPT, GSA-MPPT, and HO-MPPT increased the power by 112.63 watts, 135 watts, and 112.09 watts, respectively. The corresponding maximum power growth rates ($\lambda_{PSO}$, $\lambda_{GSA}$,$\lambda_{HO}$) are 17.61%, 21.11%, and 17.53%, respectively. The calculation methods for the maximum power increase rates $\lambda_{PSO}$, $\lambda_{GSA}$, and $\lambda_{HO}$ are as follows:

$$ \lambda_{PSO} = \frac{{P_{PLGSA} - P_{PSO} }}{{P_{MAX} }} \times 100\% $$

$$ \lambda_{GSA} = \frac{{P_{PLGSA} - P_{GSA} }}{{P_{MAX} }} \times 100\% $$

$$ \lambda_{HO} = \frac{{P_{PLGSA} - P_{HO} }}{{P_{MAX} }} \times 100\% $$

Fig. 13

Partial enlarged images in the case of no occlusion.

Among them, $P_{PLGSA}$, $P_{PSO}$, $P_{GSA}$ and $P_{HO}$ are the maximum power values of PLGSA-MPPT, PSO-MPPT, GSA-MPPT and HO-MPPT, respectively, and $P_{MAX}$ is the theoretical maximum power value.

The second and third cases are depicted in the following illustration.

Figures 14 and 15 represent respectively the overall waveform diagram and the locally enlarged diagram from 0.25 s to 0.5 s.

Fig. 14

Power tracking waveform under partial occlusion conditions (0.25–0.5 s).

Fig. 15

Power tracking waveform enlarged image under partial occlusion conditions (0.25–0.5 s).

According to Figs. 14 and 15, the maximum power point tracking time of GSA-MPPT is approximately 0.2 s. In comparison, the tracking time of PSO-MPPT and HO-MPPT is about 0.18 s, and their maximum powers are 419.99 W, 409.97 W, and 411.65 W, respectively. In contrast, the maximum power of PLGSA-MPPT can reach 467.05 W, which is relatively close to the theoretical actual maximum power of 469.14. By contrast, compared with PSO-MPPT, GSA-MPPT, and HO-MPPT, the power increase is 57.08 watts, 47.06 watts, and 55.4 watts, respectively. Furthermore, the growth rates of the maximum power point were 12.17%, 10.03%, and 11.81% respectively.

Figures 16 and 17 represent respectively the overall waveform diagram and the locally enlarged diagram from 0.5 to 0.75 s.

Fig. 16

Power tracking waveform under partial occlusion conditions (0.5–0.75 s).

Fig. 17

Power tracking waveform enlarged image under partial occlusion conditions (0.5–0.75 s).

It is evident that the theoretical maximum power amounts to 332.6700 watts. The PLGSA-MPPT achieved a power output of 329.80 watts, while the PSO-MPPT, GSA-MPPT, and HO-MPPT achieved power outputs of 317.21 watts, 282.30 watts, and 323.13 watts, respectively. The PLGSA-MPPT had power outputs that were 12.59 watts, 47.5 watts, and 6.67 watts higher than the PSO-MPPT, GSA-MPPT, and HO-MPPT, respectively. Furthermore, the tracking time was also improved, and the corresponding growth rates of the maximum power point were 3.78%, 14.28%, and 2.00%, respectively.

Simulation verification under abrupt changes in illumination

The initial illumination condition of the photovoltaic array corresponds to Condition 1. At 0.25 s, the illumination undergoes an abrupt change, transitioning to Condition 2. At 0.5 s, another abrupt change occurs, shifting the illumination condition to Condition 3. Figures 18 and 19 present the comparison images and summary comparison images of the three algorithms, respectively.

Fig. 18

Comparison of P–V images of the three algorithms under sudden changes in illumination.

Fig. 19

Summary of P–V images of the three algorithms under sudden changes in illumination.

Figures 20 and 21 are enlarged images of the scene when the lighting changes from 0.25 to 0.5 s and when it changes from 0.5 to 0.75 s, respectively.

Fig. 20

Enlarged image under the condition of sudden change of illumination from 0.25 to 0.5 s.

Fig. 21

Enlarged image under the condition of sudden change of illumination within 0.5–0.75 s.

The illumination condition was unobstructed during the time range of [0 s, 0.25 s].

Within the time interval of [0.25 s, 0.5 s], the PSO-MPPT, GSA-MPPT, and HO-MPPT algorithms achieved stable maximum power values of 390.38 W, 409.40 W, and 418.23 W, respectively. The tracking durations for these algorithms were 0.15 s, 0.24 s, and 0.14 s, respectively. In comparison to PSO-MPPT, GSA-MPPT, and HO-MPPT, the PLGSA-MPPT algorithm required a reduced tracking time of 0.02 s, 0.11 s, and 0.01 s, respectively, resulting in a tracking time of only 0.13 s. The maximum power obtained by the PLGSA-MPPT algorithm was 467.05 W, which was higher than the maximum power achieved by the other three methods by 76.67 W, 57.65 W, and 48.82 W, respectively. The corresponding maximum power increase rates were 16.34%, 12.29%, and 10.41% compared to PSO-MPPT and GSA-MPPT, respectively.

Within the time interval of [0.5 s, 0.75 s], the stable maximum power values obtained by PSO-MPPT, GSA-MPPT, and HO-MPPT were 290.58 W, 260.18 W, and 319.23 W, respectively, with tracking durations of 0.1 s, 0.25 s, and 0.07 s. In contrast to PSO-MPPT, GSA-MPPT, and HO-MPPT, the tracking time required by PLGSA-MPPT was reduced by 0.06 s, 0.21 s, and 0.03 s, respectively, reaching only 0.04 s. The maximum power achieved by PLGSA-MPPT was 329.80 W, which was 39.22 W, 69.62 W, and 10.57 W higher than the other three methods, respectively. Compared with PSO-MPPT and GSA-MPPT, the corresponding maximum power increase rates were 11.79%, 20.93%, and 3.18%, respectively.

Table 2 summarizes the tracking time and maximum power for each time period.

Table 2 Correlation indicators of three tracking effects under the condition of sudden changes in illumination.

In light of the aforementioned results, in all three instances, the average tracking time of PLGSA-MPPT was reduced by 0.0433 s, 0.1600 s, and 0.0200 s, respectively, compared to PSO-MPPT, GSA-MPPT, and HO-MPPT. Additionally, the average maximum power growth rate was increased by 15.2467%, 18.1100%, and 10.3733%, respectively. The simulation results indicate that the improved GSA not only significantly enhanced the dynamic response velocity of the system but also increased the stability and output efficiency of the photovoltaic power generation system.

Conclusion

To address the challenge of multi-peak P–V curves emerging under complex lighting conditions, this paper presents an enhanced PLGSA approach based on the original GSA. This method dynamically regulates the parameters of the PSO algorithm during the iteration process to enhance the convergence speed, incorporates the Levy flight to augment the global search capability for escaping local optima, and modifies the gravitational constant to increase randomness. The Simulink simulation outcomes demonstrate that, in contrast to the traditional PSO, GSA, and HO algorithms, the refined PLGSA algorithm can identify the maximum power point among multiple local peaks more effectively. On average, the search time of the three algorithms can be reduced by approximately 0.0744 s, representing an improvement of 14.5767%. When external conditions change, the enhanced algorithm can identify the new maximum power point more rapidly and stably, thereby minimizing power loss. The algorithm proposed in this paper also optimizes the structure of the photovoltaic power generation system, effectively enhancing the energy conversion efficiency of the photovoltaic array.

Looking ahead

In the future, efforts might persist in seeking new hybrid algorithms for maximum PowerPoint tracking to enhance photovoltaic conversion efficiency. If circumstances permit, research on the hardware design and study of photovoltaic systems related to maximum PowerPoint tracking methods can be carried out. Hence, future research could encompass improvements to photovoltaic system hardware and continuous exploration of integrating multiple intelligent algorithms without increasing complexity.