Introduction

The prediction and control of counter jet behavior in supersonic free streams represent a significant challenge in aerospace engineering, with implications for propulsion systems, aerodynamic design, and vehicle performance. Traditional computational methods often struggle to capture the complex, unsteady flow phenomena associated with supersonic jets interacting with external flows. However, the advent of machine learning techniques offers a promising avenue to address this challenge by providing accurate predictive capabilities and insights into the underlying flow physics1,2, and3.

Among various machine learning approaches, Long Short-Term Memory (LSTM) networks have gained prominence for their ability to effectively model and predict time-series data, making them well-suited for analyzing transient flow phenomena. Additionally, Proper Orthogonal Decomposition (POD) techniques offer dimensionality reduction capabilities, allowing for the extraction of dominant flow features and simplification of complex flow fields. The flow around supersonic vehicles are complex with several shocks4,5, and6.

In this context, the integration of machine learning techniques, specifically LSTM networks coupled with POD analysis, presents several advantages for predicting counter jet behavior in supersonic free streams. By leveraging historical flow data and incorporating physical insights derived from POD modes, LSTM networks can learn complex flow dynamics and accurately forecast the evolution of counter jet phenomena. The flow feature of the compressible flow is complex due to formation of the multiple shocks7,8, and9.

This paper aims to explore the advantageous applications of machine learning techniques, particularly LSTM networks combined with POD analysis, for the prediction of counter jet behavior in supersonic free streams. Through a comprehensive review of relevant literature and numerical experiments, we demonstrate the capabilities of this hybrid approach in capturing the intricate flow features associated with counter jet interactions. Furthermore, we discuss the potential implications of these predictive capabilities for improving the design and performance of supersonic propulsion systems, enhancing aerodynamic efficiency, and advancing aerospace engineering research10,11, and12.

By harnessing the predictive power of machine learning techniques, aerospace engineers can gain deeper insights into the complex flow physics governing counter jet behavior at supersonic speeds. This research represents a significant step towards developing more robust and efficient predictive tools for optimizing supersonic propulsion systems and advancing our understanding of high-speed flow phenomena13,14, and15.

Machine learning techniques have revolutionized various fields by enabling accurate predictions and improved understanding of complex phenomena. In the realm of fluid dynamics, the application of machine learning algorithms, such as Long Short-Term Memory (LSTM) models and Proper Orthogonal Decomposition (POD), has shown great promise in predicting counter jets at supersonic free streams. The combination of LSTM and POD techniques offers a powerful approach to capture and analyze the intricate dynamics associated with these flows, providing valuable insights and enhancing predictive capabilities15,16.

Counter jets refer to the phenomenon where two opposing jets of fluid interact with each other in a supersonic free stream. Understanding and predicting the behavior of counter jets is crucial in various engineering applications, including aerospace propulsion systems and high-speed flow control. However, the complex nature of these flows, characterized by shock waves, compression waves, and flow separation, poses significant challenges for traditional modeling and analysis approaches17.

Machine learning techniques, particularly LSTM models, have been successfully employed to capture the temporal dependencies and dynamic behavior of complex fluid flows. LSTM models are a type of recurrent neural network that can effectively model and predict time series data. By training LSTM models on high-fidelity simulation data or experimental measurements, it is possible to learn the underlying patterns and dynamics of counter jets at supersonic free streams18,19.

Furthermore, the combination of LSTM models with Proper Orthogonal Decomposition (POD) techniques enhances the predictive capabilities and provides a reduced-order representation of the flow field. POD is a dimensionality reduction technique that extracts the dominant spatial modes of a flow field, capturing the most significant features and eliminating redundant information. By integrating LSTM models with POD analysis, it is possible to reduce the computational complexity while preserving the essential characteristics of the counter jet dynamics20.

The advantages of utilizing machine learning techniques, specifically LSTM models and POD analysis, for the prediction of counter jets at supersonic free streams are manifold. Firstly, these techniques enable accurate predictions of complex flow phenomena, including shock waves, flow separation, and vortical structures21. Secondly, the reduced-order representation obtained through POD analysis allows for efficient and faster computation, making it feasible for real-time or near-real-time applications. Additionally, the insights gained from LSTM and POD analysis aid in understanding the underlying physics and mechanisms governing counter jet dynamics, facilitating the development of more effective flow control strategies22.

In conclusion, the application of machine learning techniques, such as LSTM models and POD analysis, offers substantial advantages for the prediction of counter jets at supersonic free streams. These techniques enable accurate predictions, reduced computational complexity, and enhanced understanding of the complex flow dynamics. By harnessing the power of machine learning, engineers and researchers can advance the design and optimization of aerospace propulsion systems and high-speed flow control, leading to improved efficiency, performance, and safety in supersonic flow applications.

The main outline of the present work is to predict and estimate the flow of the coolant jet released from the nose cone in the transient phase. The present work applied the Predictive Surrogate Model (POS) for the estimation of the flow jet feature of the coolant jet injected from the nose cone subjected to supersonic flow. In the applied methodology, the flow variables (i.e. velocity and mass concentrations of fuel jet) are estimated via a combination of the proper orthogonal Decomposition (POD) and Long Short-term Memory (LSTM) approaches. The results of the estimated flow variables are also compared with data from the Full order model (FOM) to evaluate the efficiency of the applied methodology in the prediction of the jet flow.

Computational technique

Full order model

The modeling of the transient coolant injection released from the nose cone is conventionally done via the computational fluid dynamic method23,24. ANSYS software is applied to perform computational modeling via solving Unsteady Reynolds Average Navier-Stokes (URANS) Eqs25,26, and27. In the modeling of the supersonic air stream over the nose cone, the energy equation is also considered. The turbulence characteristics of the flow are modeled via SST methodology for the calculation of the viscosity of the flow28,29, and30. The coolant is helium gas and the simulation of the secondary gas is performed via a species transport Eqs31,32. The flow of the supersonic air stream is assumed compressible and ideal gas law is considered for the relation of the pressure with density and temperature. Meanwhile, the second-order scheme is used for the discretization of the temporal and spatial terms in the momentum and continuity equations. Moreover, the pressure-velocity coupling is addressed via the Roe algorithm. The applied boundary condition for the simulation of the axisymmetric model of the nose cone is also demonstrated in Fig. 1.

Fig. 1
figure 1

schematic of selected model.

Full size image

The grid production for the selected model is demonstrated in Fig. 2. The size of the grid is adjusted based on the importance of the region and flow changes inside the domain. Ensure that the grid resolves geometric curvature and flow gradients adequately, especially near the nose tip. A general guideline is to use a non-dimensional grid spacing of Δ/≈10−4–10−3. In our model, the size of minimum grid is 3 × 10−8 near the nose cone. In the selected grid, the Y+ range near the nose is kept below 3.5.

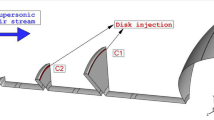
The applied boundary conditions for the nose cone with a coolant injector at the tip are also presented in the figure. The model is axis-symmetry and the jet nozzle diameter is 2 mm while the diameter of the nose is 70 mm. The height and length of the domain is more than 7 times of nose diameter. Free stream Mach velocity is 5 and the static pressure and temperature at inlet are 850 Pa and 210 K, respectively. Coolant jet is released with 10% total pressure of free stream at Mach = 1.

Fig. 2
figure 2

Grid generation.

Full size image

The grid study is also done to ensure the results of the selected grid is acceptable for the simulation of the jet injection from the tip of the nose cone at hypersonic flow. Figure 3displays the results of the heat flux along the selected model from experimental data presented by Muylaert33. The results of three different grids with 68,000, 90,000 and 110,000 cells are compared to validate the achieved data and evaluate the grid over the surface of the nose cone at test conditions. The results of the different grid also confirm that the model with 110,000 cells with minimum grid size of 3 × 10−8 near the nose cone is acceptable for the present work.

Fig. 3
figure 3

Validations.

Full size image

Predictive surrogate model

For the prediction of the flow variables, the reduced order model should be applied to minimize the data. In the present article, Proper Orthogonal Decomposition is used to reduce spatial dimensions to some latent features. This approach is widely used to decrease data and extract an optimal set of orthonormal bases. In fact, during the full model solution, the main functions are built via gathering temporal snapshots for each variable of interest. In this technique, the governing equations are operated to attain sets of equations for the coefficients of the expansions that can be solved to expect the actions of field variables in time and space. The POD is extraordinary in that the collection of basic functions is not just proper. The details of the POD technique have been fully presented in the previously published papers34.

Long Short-Term Memory (LSTM) is the efficient technique for the extraction of the feature from the reduced models. Hochreiter and Schmidhuber35 introduced LSTM as a progression of the Recurrent Neural Networks (RNNs) and it is predominantly devoted to apprehending temporal relationships within time series data. Because of their excellent recital in maintaining links across sequential data, LSTM models have found extensive application in various domains such as language modeling, engineering, and aerospace applications. The primary strength of LSTM lies in its combination of gating apparatuses, allowing the directive of data current. These gating mechanisms originally excerpt pertinent info from serial data to offer precise calculations.

Figure 4 demonstrates the schematic of applied POD and LSTM techniques for the selected model. As demonstrated in the figure, the variable snapshot is used for the extraction of the dominant POD Modes. The evaluation of the full order model and the Reduced order model (ROM) offer the acceptable POD mode for the data extraction. Then, input and output data are created. Also, data is split into train and test segments. The data of the reduced order model is trained via the LSTM technique and consequently, the predicted results are compared with test data to ensure the precision of the selected method for the estimation of the results. After validation, the field prediction is evaluated for different parameters.

Fig. 4
figure 4

structure of the POD + LSTM model for the prediction of the flow.

Full size image

Results and discussion

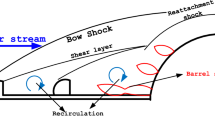
Periodic oscillation phenomena in counterflow jets arise from the complex interplay between the high-speed jet and the opposing flow. These oscillations, often referred to as shear-layer oscillations or flowfield instabilities, are characterized by periodic variations in velocity, pressure, and temperature in the region where the counterflow jet interacts with the surrounding fluid. When the counterflow jet meets the opposing flow, a shear layer forms at the interface (Fig. 5). This shear layer is susceptible to Kelvin-Helmholtz instabilities, which lead to periodic oscillations. These instabilities amplify and propagate downstream, manifesting as coherent vortical structures that oscillate at specific frequencies.

Fig. 5
figure 5

shear layer in (a) Mach contour (b) streamline.

Full size image

As mentioned before, ROM is initially evaluated via mode number to ensure the precision of the ROM. Figure 6 demonstrates the ROM mode for five main factors Axial velocity, Radial velocity, pressure, and temperature. If the borderline for the corrected results is near 90% energy of the real data, the mode number of these factors is not identical. In fact, the mode number of pressure data is 1 while axial velocity has a mode number of 3 when 90% of total energy is borderline.

Fig. 6
figure 6

Accumulated energy for POD modes of (a) axial, radial, and pressure (b) helium mass concentration and temperature variables.

Full size image

The reconstructed errors for these variables are demonstrated in Fig. 7. The change on-the-reconstructed errors is inherently related to the physic of the jet in contact with free stream. The comparison of the reconstructed errors related to the velocity and the pressure is evaluated via POD modes. The selected mode for the pressure is 1 while 3rd mode is chosen for the axial and radial velocity. Hence, the errors are almost in the same range for these factors as displayed in Fig. 7a. The reconstructed errors for the mass concentration and temperature factors are plotted in Fig. 5b. The POD mode of the mass contour is 4 while the selected mode number of the temperature is 2. The calculated errors of these factors show that the errors of these two factors are less than 20%.

Fig. 7
figure 7

Reconstructed Errors of (a) axial, radial, and pressure (b) helium mass concentration and temperature variables.

Full size image

Although the selected POD modes have a great influence on the efficiency of the predictor, there are other significant factors (i.e. degree of dependency on other variables and non-linearity) which also have a great influence on the errors, especially in counterflow jet released from the blunt body at supersonic flow. Therefore, it is challenging to provide a complete explanation for the predicted variables by the surrogate model proved. The evaluation of actual data and predicted data of the helium jet in front of the nose cone is demonstrated in Fig. 8. The figure demonstrates the contour of FOM at different time steps on the left side of the image while the contour of the predicted contour with different training sections of (60%, 70%, 80%, and 90%) are presented on right side of the figure. Since the flow complexity encountered to the free stream is high, the performance of the predictor with less training data is reduced. As noticed for the 40% prediction-(equivalent to 60% training data), the -difference between the coolant concentration of FOM and predicted data increases although the flow becomes stable and steady at the end of the period. The performance of the predictor for the estimation of the coolant concentration near the nose cone is acceptable when 80% of the data is chosen for the training and 20% of the data is for the test of the predictor.

Fig. 8
figure 8

Comparison of the coolant concentration contour of the predicted model and full order model for different training and test segmentations.

Full size image

The contour of the axial velocity for different segmentations of the test and training data is displayed in Fig. 9. This contour also shows that the performance of the predictor for the estimation of the velocity of the jet is improved when the training part is increased. As mentioned in the last paragraph, the estimation of the velocity is more complicated since the interaction of the jet is reduced by the stabilization of the coolant jet flow as demonstrated in Fig. 9.

Fig. 9
figure 9

Comparison of the coolant x-velocity contour of predicted model and full order model for different training and test segmentations.

Full size image

Quantitative evaluation of the prediction errors for four selected flow parameters of pressure, axial velocity, temperature and coolant mass fraction for the 80% training and 20% test is demonstrated in Fig. 10. The prediction errors of the selected factors indicate that the axial velocity and coolant mass fraction errors in the prediction section is higher than pressure and temperature. In fact, the main source of discrepancy of these factors is inherently related to the vortex produced in the recirculation region. The training data used for the machine learning model was derived from high-fidelity simulations that inherently capture the oscillatory behavior of the counterflow jet. We have ensured that the oscillation patterns, including their temporal and spatial dynamics, are represented in the dataset.

Fig. 10
figure 10

Prediction errors.

Full size image

Conclusion

The present article has investigated the usage of a predictive surrogate model for the estimation of a counter-flow jet released from the nose cone. Both the reduced-order model of POD and the machine learning method of LSTM are used and coupled for the prediction of the main flow parameters of the velocity, coolant mass fraction, and pressure near the nose cone with coolant injection from the tip of the nose. This work has tried to compare the performance of the POD + LSTM technique for the evaluation of the coolant jet progress in the transient phase of the jet released at the supersonic free stream. Evaluation of results for different test and training segmentations have been performed to evaluate the performance of this hybrid technique. The source of deviation of the prediction is mainly related to the formation of the vortex which is an inherently unstable and unpredicted factor.