Introduction

Based on the AO/OTA classification guidelines, reverse obliquity intertrochanteric fractures (ROIFs) are classified as the type of AO/OTA 31-A31. The main fracture line of ROIFs usually passes from the proximal-medial to the distal-lateral1. This is different from that of AO/OTA 31-A1 and A2. The proportion of AO/OTA 31-A3 fractures has reached to 5.3-23.5% of all femoral intertrochanteric fractures2,3. Nowadays, to reduce long-term immobilization and the associated complications, surgical treatment is recommended for most of ROIFs. Yet, the fixation failure rate of ROIFs remains high4,5. Therefore, how to improve the treatment effects of ROIFs has been a hot issue faced by orthopedic scholars.

Several extramedullary implants were used in fixing ROIFs initially, comprising the dynamic hip screw (DHS), the sliding hip screw, the proximal femoral anatomic plate, etc1,6,7,8. However, patients using the above fixation devices suffered lots of complications6,7,8. Moreover, the surgical trauma is relatively large when using extramedullary implants to fix ROIFs, such as the long incision and excessive blood loss. In view of this, scholars have tended to use intramedullary nails to treat such fractures and have achieved good clinical effects9,10. Intramedullary fixation has some advantages, including the short level arm, the central and minimally invasive fixation, and early weight-bearing. The common intramedullary implants for fixing ROIFs contain PFNA, Gamma3 nail and InterTAN. Notably, the neck screws of these intramedullary nails are approximately parallel to the main fracture line of ROIFs. This anatomical characteristic of ROIFs makes it significantly different from other types of intertrochanteric fractures. It also generates different biomechanical mechanisms. The proximal fracture fragment of ROIFs is prone to sliding downward and outward. The distal fragment has the trend for medial migration while the neck screw is prone to cutting out. The region between the implant junction and the main fracture line forms a stress concentration area. The fixation failure resulting from these factors is not uncommon in ROIF patients11. Other scholars used cables to resist this sliding tendency in ROIFs12,13. Yet, the insertion of cables brings additional soft tissue damage and prolongs operation time. Hence, there is no specially designed intramedullary implants for the treatment of ROIFs currently.

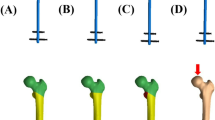
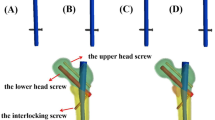
Based on these factors, our team proposed the modified proximal femoral nail (MPFN, Fig. 1A) to treat patients with ROIFs. Two screws are interlocked at the proximal part of the MPFN, including the neck screw and the subtrochanteric screw. The subtrochanteric screw passes through the tail of the neck screw and then the main nail, and is fixed below the lesser trochanter. The interlocking design aims to resist the sliding of the fracture fragment and disperse the local stress. Our team made biomechanical comparisons among the three fixation models (PFNA, InterTAN, and MPFN) for fixing ROIFs via finite element modelling. Finite element analysis (FEA) is a virtual technique which combines computer simulation and digitization. The mechanical properties of new implants could be evaluated via setting boundary conditions and loading loads14. Compared with clinical trials and cadaveric experiments, finite element technique possesses several advantages, including low cost, allowing repeated tests, etc. In this research, an AO/OTA 31-A3.1 ROIF model was established via finite element modelling. Three fixation models were evaluated in axial, bending, and torsion load cases. Our team assumed that the MPFN had the best biomechanical properties among the three fixation models in simulating loads.

Fig. 1
figure 1

Schematic diagrams of the three fixation models and three boundary conditions. (A) Schematic diagrams of the PFNA, InterTAN, and MPFN. (B) Boundary conditions for axial, bending, and torsion loads. PFNA denotes the Proximal Femoral Nail Antirotation. MPFN denotes the modified proximal femoral nail.

Full size image

Materials and methods

Construction of the AO/OTA 31-A3.1 ROIF model

Written informed consents were achieved from the volunteers, and all methods were conducted in accordance with relevant guidelines and regulations. The experimental protocols have been approved by the ethics committee of Xi’an Honghui Hospital. Twenty sets of intact femoral CT scans were gotten via a blinded and randomized trial. The mean values of CT data were obtained. Then, an intact three-dimensional (3D) femur model was established according to the above data via Mimics software (Materialize Company, Leuven, Belgium). These data were imported into the Studio software (3D system Inc., Rock Hill, SC, USA). The surface of the femur model was smoothed and polished. Based on the values of Hounsfield Unit (HU), cortex and cancellous bones were identified14. The boundary value was assumed to be 70015. On the basis of the AO/OTA classification, an osteotomy plane was performed which was set as 60 degrees relative to the sagittal plane above the lesser trochanter. Thus, an AO/OTA 31-A3.1 ROIF model was established15,16.

Construction of three implant models

The computer-aided design (CAD) software was used to depict 3D models of three implants (PFNA, InterTAN, and MPFN). Then, these implant models were assembled on the ROIF models. The anteroposterior (AP) and lateral images of the MPFN device are displayed graphically in Fig. 1A. The dimensions of the MPFN are illustrated as follows. The length of the main nail is 240 mm. The diameters for the proximal and distal parts of the main nail are designed as 17 mm and 10 mm, respectively. The diameters of the neck screw, the subtrochanteric screw, and two distal locking screws are designed as 10 mm, 5 mm, and 5 mm. The neck screw is located at the center of the femoral neck and head. The subtrochanteric screw is located below the lesser trochanter which interlocks with the main nail and the neck screw. The included angle between the subtrochanteric screw and the neck screw is at a right angle while between the main nail and the neck screw is 130 degrees, respectively.

Mesh convergence test and model validation

The tetrahedral element mesh was used during finite element setting. A convergence test was conducted to evaluate the reliability of these models referring to similar studies17. The maximum von Mises stress on bones was used for analyzing mesh convergence. The maximum stress on femur models were compared to five mesh sizes, including 3 mm, 2.5 mm, 2 mm, 1.5 mm, and 1 mm. The results indicated that the values of maximum stress on bones at the 1.5 mm mesh was approximate to those of the 1 mm and 2 mm meshes, and the difference was within 5%. Therefore, the mesh size of this study was defined as 1.5 mm. With maximum Degree of Freedom, field variables, including displacement and strain energy, were also in the range of 5% for both types of elements and there was no maximum stress point. The values of mesh convergence were within 5%, demonstrating the reliability of these models.

To perform model validation, our finite element model of the intact femur was compared to previous experimental data18. The vertical loads of 2,100 N were loaded onto the femoral head to evaluate axial stiffness. The values of axial stiffness from our finite element computation were 0.52 kN/mm which were within the interval (0.76 ± 0.26 kN/mm) of cadaveric experiments18. The results demonstrated that our finite element models were well validated.

Finite element settings of boundary conditions and loads

Material properties of bones and implants were set as homogeneous, isotropic, and linear elastic referring to previous literature14. Elements and nodes were 534,775 and 840,042 for the PFNA fixation model, 552,155 and 872,985 for the InterTAN while 537,984 and 847,212 for the MPFN, respectively. Titanium alloy was endowed with the three implants. The Young’s modulus was assumed to be 16,800 MPa, 840 MPa, and 110,000 MPa for cortex, cancellous bones, and Titanium alloy14. Poisson’s ratio was supposed to be 0.3 for cortex and Titanium alloy while 0.2 for cancellous bones, respectively19.

Frictional contacts were defined between different sections of these fixation models and the frictional coefficient was assumed to be 0.415. Boundary settings for axial, bending, and torsion loads are shown graphically in Fig. 1B. With regard to axial loads, the femoral condyle was properly fixed to inhibit extra movement of the whole configuration. In order to simulate axial compression, axial loads of 2,100 N were applied vertically to the femoral head. Under bending boundary conditions, the mid and distal femur was fixed at the same time. 175 N-loads acted laterally onto the femoral head to simulate bending force14. As to torsion load case, a torque force of 15 Nm loaded along the femoral neck axis to simulate rotation14.

Evaluation parameters and percent difference (PD)

Maximum stress on implants and bones, maximum displacement of models and fracture surface were tested via FEA under axial, bending, and torsion loads. Since the PFNA device has become one of the most widely applied implants in fixing intertrochanteric fractures, and has obtained relatively good therapeutic effects, it was defined as the control group during data analyzing. The percent difference was calculated through the following formula: PD =(P1 − Pa)/ P1 × 100%. Pa denotes the values of the InterTAN or MPFN models while P1 denotes the value of the PFNA model.

Results

Maximum stress on implants under three simulating loads

The nephograms of maximum stress on implants under axial, bending, and torsion loads are presented in Fig. 2. The von Mises stress concentration area was the junction between the neck screw and the main nail for the PFNA and InterTAN models. It was concentrated on the junction between the subtrochanteric screw, the neck screw and the main nail for the MPFN model. Under axial loads of 2,100 N, the maximum stress on implants was 241.34 MPa, 259.13 MPa, and 214.55 MPa for the PFNA, InterTAN, and MPFN models, respectively. This value was 64.83 MPa, 58.49 MPa, and 53.98 MPa for these models under bending loads. Besides, it was 53.53 MPa, 59.30 MPa, and 48.04 MPa under torsion loads of 15 Nm for the three fixation models, respectively. The values of maximum stress on implants for the MPFN models were less than those of the PFNA and InterTAN models in three simulating loads. Compared to the PFNA, the reduction of PD for the MPFN was 11.1%, 16.7%, and 10.2% in axial, bending, and torsion load cases, respectively.

Fig. 2
figure 2

Maximum stress on implants for the PFNA, InterTAN, and MPFN models under axial, bending, and torsion loads. PFNA denotes the Proximal Femoral Nail Antirotation. MPFN denotes the modified proximal femoral nail.

Full size image

Maximum stress on bones under three simulating loads

The nephograms of maximum stress on femurs under axial, bending, and torsion loads are exhibited in Fig. 3. The maximum stress on femurs was 174.92 MPa, 125.72 MPa, and 123.94 MPa for the PFNA, InterTAN, and MPFN models in axial load case, respectively. It was 60.20 MPa, 56.35 MPa, and 51.04 MPa for the three fixation models in bending load case. In addition, this index was 61.19 MPa, 27.64 MPa, and 34.46 MPa in torsion load case, respectively. The values of maximum stress on femurs for the MPFN models was less than those of the PFNA and InterTAN models in axial and bending tests. It was also lower for the MPFN model than that of the PFNA model in torsion test. Notably, compared to the PFNA, the PD reduction of this index for the MPFN was 29.1%, 15.2%, and 43.7% under axial, bending, and torsion load conditions, respectively.

Fig. 3
figure 3

Maximum stress on bones for the PFNA, InterTAN, and MPFN models under axial, bending, and torsion loads. PFNA denotes the Proximal Femoral Nail Antirotation. MPFN denotes the modified proximal femoral nail.

Full size image

Maximum displacement under three simulating loads

The nephograms of maximum displacement under three simulating loads are presented in Fig. 4. In axial load experiments, the maximum displacement was 19.35 mm, 18.58 mm, and 16.91 mm for the PFNA, InterTAN, and MPFN models, respectively. This parameter was 0.49 mm, 0.50 mm, and 0.43 mm in bending load experiments while 3.12 mm, 3.37 mm, and 2.55 mm in torsion load conditions. The values of maximum displacement for the MPFN models were smaller than those of the PFNA and InterTAN models in three load cases. The PD reduction of maximum displacement for the MPFN model was 12.6% in axial load case, 10.9% in bending load case, and 18.1% in torsion load case, compared to the PFNA model.

Fig. 4
figure 4

Maximum displacement for the PFNA, InterTAN, and MPFN models under axial, bending, and torsion loads. PFNA denotes the Proximal Femoral Nail Antirotation. MPFN denotes the modified proximal femoral nail.

Full size image

Maximum displacement of fracture surface (MDFS) under three simulating loads

The nephograms of MDFS in axial, bending and torsion loads are exhibited in Fig. 5. The MDFS was 13.51 mm, 13.82 mm, and 12.25 mm for the PFNA, InterTAN, and MPFN models in axial load case, respectively. It was 0.10 mm, 0.07 mm, and 0.07 mm in bending load case for the three fixation models. In addition, this index was 2.15 mm, 2.32 mm, and 1.78 mm in torsion load case, respectively. The values of MDFS for the MPFN models were smaller than those of the PFNA and InterTAN models in three load tests. Specially, compared to the PFNA, the PD reduction of this index for the MPFN was 9.3%, 33.4%, and 17.0% under axial, bending, and torsion load conditions, respectively.

Fig. 5
figure 5

Maximum displacement of fracture surface for the PFNA, InterTAN, and MPFN models under axial, bending, and torsion loads. PFNA denotes the Proximal Femoral Nail Antirotation. MPFN denotes the modified proximal femoral nail.

Full size image

Discussion

From an overall trend perspective, findings showed that maximum stress of the MPFN models was lower than those of the PFNA and InterTAN models, and maximum displacement was smaller for the MPFN models than those of the PFNA and InterTAN models under axial, bending, and torsion loads. Our results indicated that the MPFN had biomechanical advantages compared to PFNA and InterTAN for the management of ROIFs. The MPFN might be a good strategy for the treatment of ROIF patients.

Intramedullary fixation is recommended by most scholars for the treatment of unstable femoral trochanteric fractures20,21. This central fixation method typically allows patients with ROIFs to perform partial or complete weight-bearing early on, thereby reducing the incidence of bed-rest related complications22. Previous literature have demonstrated that stress applying to the femoral head surface could be as high as two to three times of one’s weight in walking23. Hence, the axial loads of 2,100 N were simulated via finite element method in this study. The unique design of the MPFN may be the reason for its superior axial stiffness compared to PFNA and InterTAN. The interlocking between the neck screw and the subtrochanteric screw restricts the sliding of the proximal fracture fragment in ROIFs. Simultaneously, the subtrochanteric screw disperses the stress at the junction between the main nail and the neck screw. These factors make the MPFN less prone to implant failure compared to PFNA and InterTAN.

Currently, there is few literature focusing on the antirotation of implants in patients with ROIFs. Based on our data, compared to the PFNA and InterTAN models, the MPFN model showed better antirotation performance in fixing ROIFs. The improvement of the MPFN’s antirotation may be due to its subtle structure. A small triangular and rigid structure is formed between the main nail, the neck screw, and the subtrochanteric screw. In addition, a big triangular stable structure is shaped between the neck screw, the subtrochanteric screw, and the medial wall of the proximal femur. This conforms to the principle of triangular stable structure proposed by Zhang et al.24. Proximal Femur Bionic Nail (PFBN) is a new type of implant designed based on triangular stability theory for fixing intertrochanteric fractures. Biomechanical studies have shown that compared to PFNA and InterTAN, the PFBN had better mechanical properties in fixing AO/OTA 31-A1.3 and 31-A3 fractures25,26. The two neck screws of PFBN are located at the proximal fragment above the main fracture line of ROIFs, so this design may not provide good antirotation for ROIFs. The neck screw and the subtrochanteric screw of the MPFN device are located on both sides of the fracture line of ROIFs. These two screws are locked in a right angle, ensuring good resistance to rotation. As shown in our results, this interlocking structure of the MPFN also provided better anti-compression and anti-bending properties, compared to the PFNA and InterTAN devices.

Several scholars emphasized the importance of medial support for intertrochanteric fractures27,28,29. Chen et al.’s study indicated that the reduction loss incidence after surgery due to comminuted medial wall was approximately 20% in patients with trochanteric fractures27. Song et al.’s study demonstrated that the comminuted medial wall was a relatively reliable parameter to predict implant failure after intramedullary fixation for femoral intertrochanteric fractures29. Nie et al. conducted biomechanical experiments and demonstrated that the medial wall of proximal femur was more important than the lateral wall for patients with trochanteric fractures28. A medial support nail-II (MSN-II) with the triangular stability structure was developed for the treatment of ROIFs16. Nie et al.’s research showed that compared with PFNA-II, the MSN-II exhibited better mechanical stability for fixing ROIFs under increasing axial loads via finite element analysis16. Although the MSN-II consists of two neck screws, the two screws are almost parallel to the fracture line of ROIFs. This limits its overall antisliding capacity. The design of the MPFN enables it to provide good medial support through the subtrochanteric screw and effectively resist sliding via the right angle locking structure.

This study has some limitations. Ligaments, muscles, and tendons were not considered during finite element modelling. This is a common phenomenon in similar studies on the biomechanical properties of new orthopedic implants17,30. Notably, the interaction between new implants and bones was the focus of this study. Therefore, ignoring the influence of soft tissues was reasonable to some extent. What’s more, the force applying to the femoral head is complex in reality, but we simplified it into axial compression, bending, and torsion loads. In further study, we will try to simulate the loads during walking and motion. Besides, we assigned the femur model as a homogeneous material property. The femur of patients is actually a heterogeneous structure. Yet, the current digital simulation technique is still unable to fully simulate heterogeneous materials via finite element modelling. Finally, cadaveric experiments and clinical studies will be conducted to further validate our current conclusions.

Conclusion

The modified proximal femoral nail presented the best biomechanical performance, followed by the InterTAN nail, and the PFNA for fixing reverse obliquity intertrochanteric fractures. The MPFN has the potential to be a promising device for patients with ROIFs.