Introduction

As a natural geological material, rock is widely distributed in nature. The rock mass has undergone a long geological tectonic activity, and various defects such as cracks, joints, and holes have been developed, which has a great influence on the rock’s mechanical properties and the safety construction of geotechnical engineering1,2,3,4. Currently, it is found that stress is concentrated around the hole-shaped defects in both theoretical and practical research. These defects belong to weak structural planes of rock mass, which have some characteristics of discontinuity and heterogeneity and can result in the instability and failure of the engineering structure5,6. Designers are required to accurately understand the mechanical properties of rock mass and the failure mechanism of micro-damage to macro-process since complex rock mechanics problems are often encountered in engineering construction, such as mining, tunnel, and roadway excavation4,7. To accurately study this failure mechanism, it is necessary to reveal the strength and deformation of rock mass and the macroscopic failure law of crack initiation and development during the loading process of rock with hole defects. Therefore, it is of great significance for engineering construction to study the macroscopic failure and mechanical properties of defected-rock.

At present, there are two main approaches for studying the mechanical properties of rocks with defects, including laboratory tests and numerical simulations. Laboratory tests mainly include tensile and shear tests and uniaxial, biaxial, and triaxial compression tests. Scholars studied the mechanical characteristics and failure mechanism of rock using Tomography (CT), scanning electron microscope (SEM), digital image correlation technology (DICT), infrared thermal imaging (ITI), and acoustic emission (AE)4,8,9,10,11,12. Meanwhile, some scholars combine numerical simulation with laboratory tests to analyze the reliability of numerical results and provide a theoretical basis for practical engineering3,13,14.

In laboratory tests, Wu et al.15 carried out uniaxial tests on sandstone with five different shapes of holes and obtained the analytical solution of stress by using the complex variable function theory. Results indicated that the degree of strength deterioration of holes from low to high is: circular, inverted U, trapezoidal, and square. Peng et al.16 combined the experiments and infrared detection to study the deformation and strength of marble with elliptical holes under uniaxial compression and revealed that the peak strength decreases first and then increases with the increase of the longitudinal axis and minimum value exists when the transverse axis is equal to the longitudinal axis. Huang et al.17 conducted uniaxial compression tests on granite samples containing three non-coplanar holes to determine the failure mode and revealed the crack evolution mechanism around the prefabricated hole in the granite samples by analyzing the displacement field. He et al.11 conducted cyclic loading-unloading tests on red sandstone with 8 different hole numbers and arrangement modes. The test results indicated that the compressive strength decreases with the increase of the number of holes, but decreases first and then increases as the angle between the hole arrangement and the loading direction increases. Wu et al.8 studied the influence of the horizontal distance between the center of holes and cracks on the mechanical properties of pre-defective rock-like materials. The results showed that the peak strength, peak strain, and elastic modulus decrease monotonously and nonlinearly with the increase of spacing. Zhao et al.10 revealed the mechanical properties of double-hole rock with different arrangements by laboratory test. Results indicated that the stress-strain curve has obvious fluctuation, and there are three failure modes: only shear failure, main shear and auxiliary tensile failure, and main tensile and auxiliary shear failure. The deformation and failure process of rock with hole defects includes two stages: rock bridge penetration and overall instability. Yang et al. obtained the strength deformation and crack expansion process of inclined rock and rock-like material with intermittent joints with 3D-DIC and acoustic emission based on uniaxial compression tests9,18. Li et al.5 carried out dynamic splitting tests on rocks with different hole sizes and found that the peak stress is inversely proportional to the hole size. The specimen was split into two fragments along the loading direction when the ratio of inner and outer ring diameters was less than 0.3, which was consistent with the failure mode under static load. However, the specimen generated secondary cracks perpendicular to the loading direction and was splitted into four blocks as the ratio of inner to outer diameter increases. Besides, some scholars studied the spall behavior and wave propagation of granitic rock with microdefects by high-speed digital image correlation (HDIC) and a short-bar combined-wave method19,20,21,22, which are helpful for understanding the mechanical properties of granite with microdefects.

Although the laboratory test approach can visually observe the failure mode of the defected-rocks under external load, it cannot accurately capture the initiation and propagation of cracks. Besides, laboratory test has the disadvantages of high cost and long time. As a result, some scholars adopt numerical methods to explore the mechanical properties and fracture process of rock with defects to improve the research efficiency.

As a mature commercial software, the Particle Flow Code (PFC) is favored by most scholars and employed to study the rock cracking process23,24,25,26,27,28,29. For example, Tan et al.24 simulated the fracture morphology of rocks with different shapes of holes under uniaxial compression with PFC and found that the shape of the hole has a great influence on the stress distribution, and the stress is more likely to concentrate at the corner. Cai et al.23 also adopted PFC to study the influence of hole shape on rock mechanical properties and cracking mechanisms and applied the research results to the excavation calculation of underground caverns. Zeng et al.4 performed a numerical investigation of brittle sandstone samples with different shapes of holes under uniaxial compression using PFC and the correctness of the simulation results is verified by experiments. Rong et al.25 explored the effect of defect location on AE events and rock fracturing based on PFC modeling and demonstrated that the position of defect holes affects the AE characteristics. Based on the discrete element method, Gui et al.12 investigated the mechanical properties and failure modes of disc and cylindrical rock samples with different arrangements of circular holes under Brazilian splitting and uniaxial compression. Besides, some other numerical methods are also used to study rock cracking, such as the Discontinuous Deformation Analysis (DDA), Numerical Manifold Method (NMM), and Rock Failure Process Analysis (RFPA), etc. For instance, Li et al.14 carried out a series of DDA simulations of crack propagation in brittle materials under dynamic loading and applied it to rock blasting. Zheng et al.30 developed a collaborating approach for hole detection based on the NMM framework and successfully captured the deformation and mechanical behavior of a square plate with a circular hole. Zhao et al.31 captured the fracture characteristic of rock-like materials with a hole under uniaxial compression using RFPA, the crack propagation and failure process was well captured.

However, although PFC can truly simulate the cracking problem of rock, its parameter calibration is very complicated due to its large number of microscopic parameters and the crack. Meanwhile, RFPA simulates crack propagation by deleting damaged elements, so that the crack morphology is not intuitive. Besides, the energy evolution and acoustic emission events of rocks containing hole defects are rarely reflected in the above work. Therefore, some existing numerical simulation work is not comprehensive enough to understand the deformation and fracturing mechanism of defected-rocks.

As a coupling method, the finite-discrete element method (FDEM) fully combines the advantages of both finite and discrete elements, which has been widely applied in rock mechanics and geotechnical engineering in recent years. FDEM was originally conceived by Munjiza in 198932. Later, some scholars also made contributions to the contact calculation, joint element constitutive, and triangular element constitutive of FDEM, which improved the computational performance of FDEM33,34,35,36,37. Meanwhile, some other scholars developed many coupling models on the mechanical framework of FDEM, making FDEM simulate multi-field coupling problems. For example, Rougier et al.35 developed and validated a 3D FDEM through laboratory tests of the Hopkinson test. Lei et al.38 proposed a smooth contact algorithm for FDEM and verified its rightness via several numerical examples. Lisjak et al.33 simulated the crack development and AE events of intact rock samples under compression via FDEM. Zheng et al.39 proposed a constitutive model for joint elements, which can simulate the nonlinear mechanical behavior of rock before compression, overcoming the shortcomings of the original constitutive model that cannot simulate the real deformation of rock. Deng et al.40 carried out an FDEM modeling of the tunnel failure during excavation. Ma et al.13 combined FDEM with CT technology to study the fragmentation of rock grains. Du et al.41 employed the 3D FDEM to investigate the anisotropic behavior of layered surrounding rock. Yan et al. developed the software of MultiFracS based on the framework of FDEM42,43,44, which have also been widely used in geotechnical engineering45,46,47,48,49,50,51,52. However, FDEM has not been used to study the mechanical properties of defected-rock under uniaxial compression, especially the energy evolution characteristics were not revealed in previous studies. Therefore, we focus on revealing the mechanical behavior and energy evolution of rocks containing different defect characteristics utilizing the advantages of FDEM in simulating solid cracking in this paper.

The structure of this paper is organized as follows. In section “Model and method”, the fundamentals of FDEM and the failure criteria of joint elements are briefly introduced. In section “Parameter calibration and numerical model”, the microparameters are calibrated and then the rock numerical models with different defect characteristics are established. We try to reveal the influence mechanism of defect content, size, shape, and orientation on the mechanical properties, failure mode, energy dissipation, and acoustic emission of rock in section “Results and discussion”. The conclusions of this paper are drawn in section “Conclusions”. The findings in this paper have a theoretical value for understanding the mechanical behavior and energy evolution of defected-rocks, which have great significance for studying the stability of rock mass with defects. All the simulations in this paper are performed in MultiFracS.

Model and method

Principles of the finite-discrete element method (FDEM)

Figure 1 presents the principles of FDEM, in which the continuum is separated into solid triangles and the initial zero-thickness joint element is inserted in these solid triangles53. The generation of cracks is represented by the broken joint elements. Some latest work about FDEM can be referred to the special issue of FDEM54.

Fig. 1
figure 1

Fundamentals of FDEM.

Full size image

Fracture constitutive models of the joint element

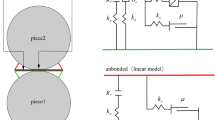
Figure 2 shows the schematic diagram of the fracture constitutive model of the joint element. As plotted in Fig. 2, there are three fracture constitutive models of the joint element: (1) Model I for tensile failure, (2) Model II for shear failure, and (3) Mixed Model I-II for tensile-shear failure. More introduction to this fracture constitutive model can be found in some other works32,55,56,57,58,59,60,61,62,63.

Fig. 2
figure 2

Constitutive model of the joint element.

Full size image

Considering the heterogeneity of materials

Rock is a complex and heterogeneous natural geotechnical engineering material. Its mineral composition is diverse and its properties are quite different. In geotechnical engineering, the Weibull distribution function is widely used to consider the heterogeneity characteristics of rock and soil64,65,66. To characterize the rock heterogeneity, the material properties are assumed to obey the following probability density function:

$$f(a)=\frac{m}{a}{\left( {\frac{a}{{{a_0}}}} \right)^{m - 1}}\exp \left[ {{{\left( {\frac{a}{{{a_0}}}} \right)}^m}} \right]$$
(1)

where: a represents the material parameters that meet the distribution of the function; a0 is approximately equal to the average value of material properties for all elements; m denotes the geometric shape of the Weibull distribution function, here m is defined as the homogeneity index.

Figure 3 illustrates the Weibull distribution function with different m values. The distribution of a tends to be more concentrated when the value of m changes from small to large, and the shape of the Weibull distribution changes from short to high as well as from wide to narrow, indicating that the material is more homogeneous. When \(m \to \infty\), a = a0, indicating that the material is completely homogeneous.

Fig. 3
figure 3

Weibull distribution with different m index.

Full size image

Parameter calibration and numerical model

Parameter calibration

In the numerical simulation, parameter calibration is very important to ensure the reliability of parameter selection. In this paper, mudstone is taken as the research object, and the microscopic parameters input in MultiFracS software are calibrated by uniaxial and triaxial compression experiments on complete mudstone samples. As Yan and Tong36 reported, the mechanical parameters input in FDEM can directly use that obtained in the laboratory test when the penalty parameter of the joint element is taken as 100 times the elastic modulus, and only two parameters named fracture energies (GfI and GfII) need to be calibrated. Thus, we select the mechanical parameters of mudstone obtained by Liu et al.67 as the input in MultiFracS directly. Then, only two microscopic parameters, mode I fracture energy (GfI) and mode II fracture energy (GfII) need to be calibrated.

In the experiments, the mudstone samples were first dried to reduce their water content to 0% and then the dried samples were weighed in the experiment. After that, water was added gradually to the top of the samples until reached the preset water content. When the water-bearing samples were prepared, they were wrapped with plastic film to prevent water loss. Subsequently, the samples were placed in a dry environment for 15 days to ensure uniform water distribution. Finally, uniaxial compression and triaxial compression tests were carried out on samples with different water contents. For the triaxial compression test, four groups of experimental tests with confining pressures of 1 MPa, 2 MPa, 3 MPa, and 4 MPa are performed. The obtained experimental uniaxial compression strength is 23.5 MPa, and the triaxial compression strength under four confining pressures is 27.5 MPa, 31 MPa, 31.05 MPa, and 33.68 MPa, respectively.

The parameter calibration results are shown in Fig. 4. Figure 4a is the comparison between the experimental and simulation results of the uniaxial stress-strain curve of the intact sample. The uniaxial stress-strain curve simulated in this paper matches well with the experimental curve if GfI = 2 J/m2 and GfII = 10 J/m2. Meanwhile, the peak strength obtained by the experiment is 23.5 MPa, while that obtained in this paper is 23.60 MPa, and the relative error is only 0.43%. Figure 4b shows the comparison between the experimental and simulation results of the triaxial stress-strain curve of the intact sample. Similarly, we find that only when GfI = 2 J/m2 and GfII = 10 J/m2, the triaxial compression stress-strain curve simulated in this paper can match well with the experimental curve. In particular, the peak strength is close to the experimental results, and the error is less than 7%. The peak strain determined by numerical simulation is different from that determined by experimental tests in Fig. 4 because the established numerical model has no pores, but the real rock sample has pores and there is a pre-compression stage under uniaxial compression. Besides, the current FDEM cannot model the pre-compression process of rock under uniaxial compression.

Based on the above analysis, the mode I fracture energy (GfI) and mode II fracture energy (GfII) calibrated by uniaxial and triaxial compression experiments are 2 and 10 J/m2, respectively. The remaining mechanical parameters extracted from Liu et al.67 are listed in Table 1.

Fig. 4
figure 4

Parameter calibration (a) stress-strain curves of uniaxial and (b) triaxial compression experiments.

Full size image
Table 1 Mechanical parameters of the modeled rock.
Full size table

Numerical model

In this paper, the effects of defect characteristics on the mechanical behavior, failure mode, energy dissipation and acoustic emission of rock are studied by uniaxial compression numerical experiments. The main characteristics of rock defects include defect content, defect size, defect shape and defect orientation. Consequently, four groups of numerical models are established (Fig. 5). Figure 5a presents the numerical models containing different defect contents. The defects are assumed as hole shape, and the defect content (Cd) is set to 0%, 2%, 4%, 6%, 8% and 10%, respectively. Figure 5b shows the numerical models with different defect sizes (L). When the defect content is 10%, the diameters of the circular defects are set to 5, 6, 7, 8, 9 and 10 mm, respectively. Figure 5c presents the numerical model with different defect shapes. All the defect content is 6% and we select four different defect shapes, including triangle, square, hexagon, and circle. It should be mentioned that the natural defect shapes in rock mass can be diverse and difficult to characterize by the numerical model. Although some scholars built any random defect shape by using advanced modeling techniques, it is still difficult to correspond with the natural defect shape. Therefore, here we adopt a simplified method to study the influence of defect shape on rock mechanical properties by setting the defect shape as several simple geometric shapes. Figure 5d shows the schematic diagram of the numerical model with different defect orientations. Here, the elliptical defect is considered, and the angle between the long axis direction and the horizontal direction of the ellipse is defined as the defect orientation (α), which is set to 0°, 15°, 30°, 45°, 60°, 75° and 90°, respectively.

Fig. 5
figure 5

Numerical model of rocks with different defect characteristics (a) defect content, (b) defect size, (c) defect shape and (d) defect orientation.

Full size image

Results and discussion

Effect of defect content on the mechanical behavior and energy dissipation

Figure 6 shows the effect of defect content on the stress-strain curves and failure modes. In Fig. 6a, we find that the uniaxial compressive strength of the complete rock sample is very high. However, once defects exist, such as the defect content rises to 2%, the peak strength drops sharply. As defect content increases, the peak strength gradually decreases. In Fig. 6b, many shear failures and few tensile failures occur in the intact rock sample under uniaxial compression. When the rock contains defects, the crack initiates and expands from the defect, and tensile failure mainly occurs. Especially, with the increase of the defect content, the tensile failure gradually dominates.

Fig. 6
figure 6

Effect of defect content on the (a) stress-strain curves and (b) failure modes (yellow-tensile crack, red-shear crack).

Full size image

Figure 7 shows the evolution of peak strength and elastic modulus with defect content. When the defect content increases from 0 to 2%, the peak strength decreases from 23.60 MPa to 7.43 MPa, and the reduction is 68.52%. However, the defect content decreases from 7.43 MPa to 3.12 MPa with a reduction of 58% if the defect content continues to increase from 2 to 10%. It indicates that the initial increase of defect content can seriously reduce the strength of the rock, and the further increase of defect content has little effect on the peak strength. On the other hand, the elastic modulus decreases gradually with the increase in defect content, indicating that the defect content also has a great influence on the elastic modulus.

Fig. 7
figure 7

Evolution of peak strength and elastic modulus with defect content.

Full size image

Figure 8 illustrates the energy dissipation, crack number and AE characteristics with different defect contents. Generally, with the increase of calculation steps, the strain energy inside the sample is gradually accumulating. When the specimen is not broken, the system maintains quasi-static conditions due to the small loading rate, the kinetic energy is always 0. Once the specimen is broken, the strain energy decreases sharply and the kinetic energy increases suddenly accompanied by a large number of acoustic emission events, resulting in an increase of cracks. The difference is that the strain energy suddenly decreases and the kinetic energy increases when it is destroyed for the complete sample, which shows a brittle failure. For the rock samples with defects, since the stress is concentrated at the defects under uniaxial compression, the crack initiates at the defects when the concentration stress reaches the tensile strength of the rock. Therefore, the acoustic emission event occurs with a small loading step, as shown in Fig. 8b–f.

It should be noted that the acoustic emission in each step is calculated by subtracting the accumulated number of fractured joint elements at the current time step from that at the last time step. According to the fracture constitutive model of joint elements, FDEM can automatically count the number of tensile and shear cracks when cracking occurs. The acoustic emission of tensile failure in the current time step is obtained by subtracting the cumulative number of tensile cracks at the current time step from the cumulative number of tensile cracks at the last time step. Similarly, the acoustic emission of shear failure in the current time step is obtained by subtracting the cumulative number of shear cracks at the current time step from that at the last time step.

In addition, the peak strain energy for the complete pattern reaches 920 J. When the defect content is 2%, 4%, 6%, 8% and 10%, the peak strain energy is 95, 83, 54, 34.5 and 28 J, respectively, indicating that the peak strain energy gradually decreases with the increase of defect content. At the same time, the occurrence of acoustic emission events is also closely related to the defect content. The acoustic emission events of shear failure become less, while that of tensile failure increase with the increase of defect content, indicating that the rock samples with high defect content are more prone to tensile failure, which corresponds to the failure mode in Fig. 6b.

The spectrum characteristics of AE in Fig. 8 can be concluded as follows. In the initial loading stage, the AE spectrum height is relatively small because of no damage or small damage generated in the rock sample, indicating that only a small amount of AE occurs. As the loading progresses, the AE spectrum becomes higher and denser, indicating that the accumulation of internal damage in the rock gradually increases. When the kinetic energy reaches its peak, the sample is completely damaged and the AE spectrum is the highest. This is the spectral characteristic of rock samples during whole loading, which is applicable to all samples with different defect contents.

Fig. 8
figure 8

Energy dissipation, crack number, and AE characteristics with different defect contents.

Full size image

Effect of defect size on the mechanical behavior and energy dissipation

Figure 9 shows the uniaxial compression stress-strain curves and failure modes under different defect sizes. In Fig. 9a, we find that there is no obvious relationship between the uniaxial compressive strength and defect content, and the peak strength is between 2.8 MPa and 3.55 MPa for different defect sizes. This indicates that the defect size has little effect on the peak strength with a certain defect content. Figure 9b presents the uniaxial compression failure mode with different defect sizes. The cracks propagate through the defects, and a smaller defect size leads to a denser e crack distribution and more crack number. Overall, the rock sample mainly takes tensile failure due to the existence of defects.

Fig. 9
figure 9

Effect of defect size on the (a) stress-strain curves and (b) failure modes.

Full size image

Figure 10 illustrates the evolution of peak strength and elastic modulus with defect size. As we can see, the defect size has little effect on the peak strength and elastic modulus. The overall peak strength fluctuates between 2.8 MPa and 3.55 MPa, while the elastic modulus fluctuates in a smaller range, between 1.07 GPa and 1.13 GPa. It is proved that when the defect content is constant, the mechanical behavior of the rock sample is less affected by the defect size. However, the peak strength curve changes significantly when the defect size is 6 mm. This is because although the defect content is constant, the defect distribution is generated randomly, which may have little effect on the modeling results. As we can see in Fig. 10, the peak strength corresponding to different defect sizes fluctuates only within a very small range of 2.8 MPa to 3.55 MPa. Therefore, it can be considered that the evolution of peak strength is less affected by the defect size.

Fig. 10
figure 10

Evolution of peak strength and elastic modulus with defect size.

Full size image

Figure 11 illustrates the energy dissipation, crack number and AE characteristics with different defect sizes. The strain energy gradually accumulates with the increase of loading steps. Similarly, when the rock is not broken, the kinetic energy is always 0. However, when the crack initiates, the kinetic energy gradually increases with many acoustic emission events. Subsequently, as the rock is further compressed, more and more cracks are generated, and more and more acoustic emission events occur. Finally, when the rock sample is completely broken, the strain energy suddenly decreases after reaching the peak. In general, for different defect sizes, the peak strain energy is between 21 J and 35 J, and the kinetic energy is between 15 J and 22 J, indicating that the defect size has little effect on the evolution of strain energy and kinetic energy. On the other hand, the number of tensile cracks in the sample with defects is much larger than that of shear cracks, indicating that the existence of defects makes the rock more prone to tensile failure under uniaxial compression. The above crack characteristics correspond to the failure mode in Fig. 9b.

The spectrum characteristics of AE in Fig. 11 can be concluded as follows. The AE spectrum height is relatively small at the beginning due to small damage generated in the rock sample, indicating that only a small amount of AE occurs. With continuous loading, the AE spectrum is higher and denser, indicating that the accumulation of internal damage in the rock gradually increases. When the kinetic energy reaches its peak, the sample is completely damaged and the AE spectrum is the highest. After the peak kinetic energy, the AE spectrum height decreases and only a small amount of damage occurs. This is the spectral characteristic of rock samples during whole loading, which is applicable to all samples with different defect sizes.

In summary, we consider that the uniaxial compressive strength, elastic modulus and energy dissipation are less affected by the defect size with the same defect content. However, it has a certain influence on the failure mode and the number of cracks. A larger defect size can make the rock more prone to tensile failure with a smaller total number of cracks.

Fig. 11
figure 11

Energy dissipation, crack number and AE characteristics with different defect sizes.

Full size image

Effect of defect shape on the mechanical behavior and energy dissipation

Figure 12 presents the stress-strain curves and failure modes with different defect shapes. It is worth noting that for the four different shapes of defects, their areas are the same, that is, the defect content is consistent, which is a prerequisite. Figure 12a indicates that the rock samples with circular defects have the largest peak strength of 4.78 MPa, and followed by the rock samples with square defects, which is 4.15 MPa. However, the uniaxial compressive strength of rocks with triangular and hexagonal defects is both about 3.2 MPa. This phenomenon demonstrates that the rock mass with circular and square defects has higher peak strength and better stability than that with triangular and hexagonal defects.

Figure 12b shows the uniaxial compression failure mode corresponding to different defect shapes. We find that cracks always initiate and propagate at the top corner of the defect in rock samples containing triangular and hexagonal defects because stress concentration is more likely to occur at the top corner. For the samples with square defects, cracks initiate and propagate in the middle of the upper and lower sides of the square, which has a greater ability to withstand external loads. Generally, the rock is still dominated by tensile failure regardless of the shape of the defect. Furthermore, the rock samples containing triangular defects have the greatest number of macro cracks, while it is the opposite for the rock samples containing hexagonal defects. The above results agree with some previous studies23,24.

Fig. 12
figure 12

Effect of defect shape on the (a) stress-strain curves and (b) failure modes.

Full size image

Figure 13 shows the peak strength and elastic modulus corresponding to different defect shapes. As we can see, the peak strength and elastic modulus of the sample with circular defects are the largest. Overall, the defect shape greatly affects the uniaxial compressive strength of the rock sample, but it has little effect on the elastic modulus. Specifically, the uniaxial compressive strength of the samples with four different shape defects is between 3.2 MPa and 4.78 MPa, while the elastic modulus is just between 1.1 GPa and 1.26 GPa.

The influence mechanism of defect shape on the peak strength of rock can be explained as follows. Since the apex angles and loading directions of triangular and hexagonal defects are consistent, stress is easier to concentrate at these apex angles under uniaxial compression. With further loading, cracks first initiate and propagate in these areas, leading to rock failure, with a lower peak strength. For rock samples containing circular defects, the stress is evenly distributed around the defects, which is difficult to crack and therefore has the highest peak strength. The rock sample with square defects has a higher strength than the sample with triangular and regular hexagonal shapes because the vertex angle is not completely consistent with the loading direction. However, due to the concentration of vertex stress, its strength is lower than that of the sample with a circular shape.

Fig. 13
figure 13

Peak strength and elastic modulus corresponding to different defect shapes.

Full size image

Figure 14 presents the energy dissipation, crack number, and AE characteristics with different defect shapes. Overall, the energy dissipation characteristics and acoustic emission events of rock samples with different defect shapes under uniaxial compression are similar. However, the peak strain energy of the samples with triangular and hexagonal defects is small, which is 30 J and 26 J, respectively, while that with square and circular defects is 46 J and 52 J, respectively. This indicates that the rocks with square and circular defects have a stronger ability to store strain energy under external load. Meanwhile, the kinetic energy also shows similar characteristics. The kinetic energy of the sample with hexagonal defects is the smallest, which is 14 J, and the sample with square defects has the largest kinetic energy of 35 J. For acoustic emission events, the rock samples with four different shapes of defects are still dominated by tensile failure, especially the samples with hexagonal defects only have very few acoustic emission events of shear failure, and the total number of cracks is also the least. On the contrary, the rock samples with circular defects have the largest crack numbers. The spectrum characteristics of AE in Fig. 14 are similar to those in Fig. 11, which is applicable to all samples with different defect shapes.

Based on the above analysis, we conclude that rock samples with circular and square defects have higher strength, strain energy, and rock mass stability. Since the rock samples containing triangular and hexagonal defects are more likely to produce concentrated stress at the defect corner resulting in lower peak strength and smaller peak strain energy. Consequently, the rock mass with such shaped defects has a low stability.

Fig. 14
figure 14

Energy dissipation, crack number, and AE characteristics with different defect shapes.

Full size image

Effect of defect orientation on mechanical behavior and energy dissipation

Figure 15 shows the effect of defect orientation on the stress-strain curves and failure modes. We can see from Fig. 15a that the uniaxial compressive strength increases gradually with the increase of the defect orientation. For example, the uniaxial compressive strength is only about 3.1 MPa when the defect orientation is 0° and 15°, while that reaches 6.5 MPa with a defect orientation of 90°. Figure 15b presents the failure mode corresponding to different defect orientations. Regardless of the defect orientation, a lot of splitting tensile failures and few shear failures occur in the rock samples. The cracks initiate and propagate at the long axis of the ellipse due to stress concentration.

Fig. 15
figure 15

Effect of defect orientation on the (a) stress-strain curves and (b) failure modes.

Full size image

Figure 16 illustrates the evolution of peak strength and elastic modulus with defect orientation. As the defect orientation increases from 0° to 15°, the peak strength and elastic modulus are basically equal. However, the peak strength and elastic modulus show a linear increase trend with a further increase in defect orientation, which is consistent with the experimental results of Yang et al.1. When the loading direction is consistent with the direction of the long axis of the ellipse, the strength and elastic modulus of the rock sample are the highest.

In other words, the rock along defect orientation can be considered as a weakened bedding surface. Hu et al.68 indicated that as the angle between the weakened bedding surface and loading direction increase from 0° to 90°, both the rock strength and elastic modulus increase. In this paper, we also find that the peak strength and elastic modulus increase with the increase of defect orientation, as presented in Fig. 17. Thus, we can correspond the results obtained in this paper with that phenomenon revealed by the previous study68.

Fig. 16
figure 16

Evolution of peak strength and Elastic modulus with defect orientation.

Full size image

Figure 17 shows the energy dissipation, crack number, and AE characteristics with different defect orientations. The strain energy at different defect orientations shows similar characteristics with calculation steps, that is, it increases first and then suddenly decreases after reaching the peak since crack initiation releases the strain energy. Whereas, the peak strain energy increases as the defect orientation increases. For example, when the defect orientation is 0° and 15°, the peak strain energy is only about 25 J; but it reaches 68 J and 86 J when the defect orientation is 75° and 90°, respectively. The above indicates that the rock sample with a larger defect orientation has a stronger ability to withstand deformation. The kinetic energy also shows a similar characteristic. Once cracks are generated in rock, the kinetic energy increases and finally keeps stable. The acoustic emission events indicate that the rock samples with different defect orientations mainly undergo tensile failure under uniaxial compression, and only a small number of shear failure acoustic emission events occur, which matches the failure mode presented in Fig. 15b. The spectrum characteristics of AE in Fig. 17 are similar to those in Fig. 11, which is applicable to all rock samples with different defect orientations. Besides, the larger the defect orientation is, the later the crack initiates. The number of cracks is also significantly different with different defect orientations. Specifically, when the defect orientation is between 0° and 60°, the number of cracks is basically between 800 and 1200, while it is about 1400 and 1500 with defect orientation of 75 ° and 90 °.

In summary, we consider that the defect orientation has a great influence on the uniaxial compressive strength, elastic modulus, and energy dissipation of the rock, but has little effect on the failure mode and the number of cracks. A greater defect orientation can lead to a higher uniaxial compressive strength, elastic modulus, and peak strain energy.

Fig. 17
figure 17

Energy dissipation, crack number and AE characteristics with different defect orientations.

Full size image

Conclusions

In this paper, FDEM is used to study the mechanical properties of rock samples with hole defects. Firstly, the input microscopic parameters in FDEM are calibrated by uniaxial and triaxial compression tests on intact rock samples. Then, a series of uniaxial compression numerical experiments are performed on rock samples with defects to reveal the influence mechanism of defect characteristics (content, size, shape and orientation) on the mechanical behavior, failure mode, energy dissipation and acoustic emission. Based on the numerical results, the following conclusions can be drawn:

  1. (1)

    FDEM can be well employed to capture the mechanical behavior, failure mode and energy dissipation and acoustic emission of rock samples with defects, which provides a powerful tool for studying the mechanical properties of defected-rocks.

  2. (2)

    The defect content seriously affects the mechanical properties of rock. With the increase in defect content, the peak strength, elastic modulus and peak strain energy of rock samples all decrease. The failure mode is dominated by tensile, and AE events of shear failure decrease.

  3. (3)

    Under the same defect content, the uniaxial compressive strength, elastic modulus and energy dissipation of the rock are less affected by the defect size, but the failure mode and crack numbers are greatly affected. A larger defect size results in more tensile failure and fewer cracks.

  4. (4)

    The strength and peak strain energy of rocks with circular and square defects are larger than those with triangular and hexagonal defects because the rocks containing triangular and hexagonal defects are more likely to produce concentrated stress at the defect vertex angle.

  5. (5)

    As the defect orientation increases, the rock strength, elastic modulus and peak strain energy all show a gradual increase trend. However, the failure mode is not greatly affected by the defect orientation, and the overall failure mode is dominated by tensile failure. When the defect orientation is between 0° and 60°, the number of cracks is about 1000, while it increases to 1500 with defect orientations of 75° and 90°.

Although the FDEM model used in this paper can effectively simulate the mechanical behavior and energy evolution of defected-rocks under uniaxial compression, the potential-based contact algorithm used here still has the limitations of low computational efficiency and high computational time when calculating models with a large number of meshes. In the future, the contact algorithm of FDEM should be optimized to enable complex models to be computed with large-scale and more meshes, reducing computational costs.