Finite element analysis for pullout resistance and progressive failure of strip anchors in strain softening marine soils

Abstract

Given the limited research on regularization mechanisms in finite element analysis of the ultimate pullout resistance of plate anchors, particularly considering soil strain softening, this paper employs a Cosserat continuum regularization mechanism combined with a Mohr–Coulomb matched Drucker–Prager constitutive model (MC-matched DP model) to address this issue. Implementing the User-Defined Element function in ABAQUS, the numerical solution was developed and validated against existing literature to verify the accuracy of the MC-matched DP model for analyzing plate anchor pullout resistance. This study demonstrates that the Cosserat continuum model effectively resolves common issues such as numerical convergence difficulties and mesh dependency encountered in finite element calculations for softening soils. Subsequently, the model was applied to conduct a detailed analysis of the ultimate pullout resistance of plate anchors and the progressive failure process of the soil. Parametric analyses were performed to explore the combined effects of plate anchor inclination, burial depth, and degree of strain softening on ultimate resistance and failure mechanisms. Based on these analyses, an expression for the ultimate resistance coefficient N_c, incorporating the influences of plate anchor inclination, burial depth, and strain softening, was formulated, providing a valuable reference for geotechnical engineers in practical applications.

Introduction

With the continuous increase in human demand for energy, marine energy development has become one of the focuses of the industry. At present, a large number of offshore structures have been built around the world to provide necessary conditions for energy development. These structures mainly include offshore drilling platforms, wind power equipment, and photovoltaic equipment that has emerged in recent years. At the same time, offshore resource exploitation has a trend of continuous development towards deep sea, which inevitably puts higher requirements on the bearing capacity and stability of marine equipment foundations.

As a common marine anchoring foundation, plate anchors have been widely used because of their convenient installation, low cost and ability to be used in deep sea conditions^1,2,3,4. The pull-out resistance of plate anchors has always been a hot topic in marine geotechnical engineering research. Many scholars have discussed the pull-out resistance of plate anchors from multiple aspects such as theoretical analysis, experimental research and numerical simulation. Vesić⁵ proposed an analytical solution for the pullout resistance of plate anchors based on the cavity expansion theory of rigid-plastic materials. Das⁶ proposed a general method to estimate the pullout resistance of shallow and deep horizontal plate anchors, and gave an empirical expression of the resistance through model tests. Rowe and Davis⁷ conducted experimental and numerical studies on the anchoring capacity of horizontal and vertical plate anchors in clay, and utilized finite element analysis to predict the ultimate pullout resistance coefficients with various plate anchor configurations and different soil types. Merifield et al.¹ used the upper and lower limit analysis method to conduct an in-depth analysis of the ultimate pullout capacity of plate anchors. Their work not only established a theoretical framework to evaluate the ultimate resistance, but also verified the validity of this theoretical framework by comparing with laboratory test results. In addition, Das⁸ studied the resistance of inclined shallow buried square plate anchors through laboratory model tests, and Merifield et al.⁹ used limit analysis to evaluate the stability of inclined strip plate anchors. Yu et al.¹⁰ studied the coupling effect of plate anchor inclination, clay heterogeneity and gravity on the ultimate pullout resistance of strip plate anchors. In addition, Yu et al.¹¹ investigated the influence of strain softening behavior of clay under cyclic loading on the ultimate pullout capacity of plate anchors.

It should be noted that previous studies have focused on the ultimate pullout resistance of plate anchors in non-softening marine soils. However, many studies have shown that strain softening is very common in marine soils, especially in marine overconsolidated clays, sensitive soils and frozen soils^{12,13,14,15,16,17}. Therefore, it is necessary to reasonably consider the strain softening characteristics of the soil in the calculation of the pullout resistance of the plate anchor and the analysis of its progressive instability process. However, there are still limited studies that consider the influence of strain softening in the finite element numerical analysis of plate anchors. Zhou and Randolph¹⁸ used the modified Tresca model considering strain softening to conduct large deformation finite element analysis of plate anchor pullout. Charlton et al.¹⁹ used the kinematic hardening constitutive model which can consider the structural degradation of clay to evaluate the ultimate pullout resistance of inclined plate anchors in structural clay. Shin et al.²⁰ considered the strain softening and strain rate dependence of the soil and conducted a finite element large deformation analysis of the plate anchor pullout process. Chen et al.²¹ considered strain softening and used a multi-scale approach to uncover the effects of inclined loading on the bearing capacity of horizontal plate anchors in sand. Ghorai et al.²² adopted a large deformation finite element method combined with a strain softening constitutive model to investigate the effects of soil sensitivity, initial embedment depth, loading eccentricity, and other factors on the uplift resistance.

It should be noted that the above limited studies on the resistance analysis of plate anchors in strain softening soils are all based on classical finite elements. However, many studies^23,24,25,26 have shown that if the strain softening of soil strength are considered in elasto-plastic finite element analysis, the control equations cannot remain stable, which often leads to pathological dependence of the calculation results on the finite element mesh size. Although the influence of strain rate in the study by Shin et al.¹⁹ can alleviate the mesh dependence problem to some extent, as noted by Singh et al.²⁷, the effectiveness of incorporating viscosity (or rate) effects into the constitutive equations to reduce mesh dependence diminishes as the strain rate decreases. This implies that as the strain rate decreases, merely increasing the viscosity effect to enhance simulation accuracy may be insufficient to address the problem, and the applicability of this method is therefore limited. At present, an effective way to overcome the mesh-dependence problem is to introduce a reasonable regularization mechanism into the finite element governing equations. The commonly used methods include integral nonlocal theory^28,29,30, gradient plasticity theory^31,32 and Cosserat continuum theory (also known as micropolar theory)^26,33,34,35. Among them, the Cosserat continuum theory considers the rotational degrees of freedom of material points, which has better physical consistency with clay. Therefore, this study will be conducted within the Cosserat continuum framework.

The Cosserat continuum theory, introduced by E. and F. Cosserat in 1909³⁶, initially attracted little attention due to the absence of material constitutive relationships. It gained recognition only after Günther³⁷ and further advancements in elasticity by researchers like Mindlin³⁸ and Eringen³⁹. In the early 1990s, de Borst²⁴ extended the theory by incorporating the von Mises yield criterion into an elastoplastic model, deriving a constitutive integration algorithm, and implementing it numerically. This breakthrough enabled finite element simulations of strain localization caused by strain softening in geomechanics. Since then, further developments^26,40,41 have established the Cosserat finite element method as a powerful tool for tackling strain localization problems in geomechanics. However, to the best of the author’s knowledge, there is no research on the introduction of the Cosserat continuum theory into the finite element analysis of the pull-out resistance and progressive instability process of plate anchors in marine softening soils.

In order to more effectively analyze the ultimate pull-out resistance and progressive instability process of plate anchors in marine softening soil, this paper combines the strain softening effect into the Drucker–Prager constitutive model matching Mohr–Coulomb under the Cosserat continuum, and uses the UEL subroutine interface of the finite element software ABAQUS to complete the numerical implementation. This method is further used to conduct a detailed analysis of the ultimate pull-out resistance and progressive instability process of plate anchors.

Theory and numerical implementation

Introduction of the two-dimensional plane strain Cosserat continuum theory

According to the research by Li and Tang²⁶, in the two-dimensional Cosserat continuum theory, each material point has three degrees of freedom, as

$${\varvec{u}} = [\begin{array}{*{20}c} {u_{\text{x}} } & {u_{\text{y}} } & {w_{\text{z}} } \\ \end{array} ]^{{\text{T}}}$$

(1)

where $u_{\text{x}}$,$u_{\text{y}}$ represent the translational degrees of freedom; $w_{\text{z}}$ represents the rotational degree of freedom introduced by the Cosserat theory. The stress and strain vectors are defined as

$${\varvec{\sigma}} = \left[ {\begin{array}{*{20}c} {\sigma_{{\text{xx}}} } & {\sigma_{{\text{yy}}} } & {\sigma_{{\text{zz}}} } & {\sigma_{{\text{xy}}} } & {\sigma_{{\text{yx}}} } & {\frac{{m_{{\text{zx}}} }}{{l_{{\text{c}}} }}} & {\frac{{m_{{\text{zy}}} }}{{l_{{\text{c}}} }}} \\ \end{array} } \right]^{\text{T}}$$

(2)

$${\varvec{\varepsilon}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{{\text{xx}}} } & {\varepsilon_{{\text{yy}}} } & {\varepsilon_{{\text{zz}}} } & {\varepsilon_{{\text{xy}}} } & {\varepsilon_{yx} } & {k_{{\text{zx}}} l_{{\text{c}}} } & {k_{{\text{zy}}} l_{{\text{c}}} } \\ \end{array} } \right]^{\text{T}}$$

(3)

where $k_{{\text{zx}}}$,$k_{{\text{zy}}}$ represent the micropolar curvatures; $m_{{\text{zx}}}$,$m_{{\text{zy}}}$ are the corresponding couple stresses (see Fig. 1); $l_{{\text{c}}}$ is the internal length parameter.

Fig. 1

Distribution diagram of stress components of two dimensional Cosserat continuum.

Define the elastic prediction value of the load incremental stress in terms of the elastic strain:

$${\varvec{\sigma}}^{E} = D_{e} \varepsilon$$

(4)

$$D_{e} = \left[ {\begin{array}{*{20}c} {\lambda + 2G} & \lambda & \lambda & 0 & 0 & 0 & 0 \\ \lambda & {\lambda + 2G} & \lambda & 0 & 0 & 0 & 0 \\ \lambda & \lambda & {\lambda + 2G} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {G + G_{c} } & {G - G_{c} } & 0 & 0 \\ 0 & 0 & 0 & {G - G_{c} } & {G + G_{c} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {2G} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {2G} \\ \end{array} } \right]$$

(5)

where G_c is the Cosserat shear modulus, the Lame constant is $\lambda = 2G\nu /\left( {1 - 2\nu } \right)$, and G and λ are the shear modulus and Poisson’s ratio, respectively, in the classical sense.

The static equilibrium equation for the plane strain Cosserat continuum can be written as

$${\varvec{L}}^{{\text{T}}} {\varvec{\sigma}} + {\varvec{f}} = 0$$

(6)

where ${\varvec{f}}$ is body force, and the differential operator matrix ${\varvec{L}}$ is defined as

$${\varvec{L}} = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}} & 0 & 0 & 0 & {\frac{\partial }{\partial y}} & 0 & 0 \\ 0 & {\frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial x}} & 0 & 0 & 0 \\ 0 & 0 & 0 & { - 1} & 1 & {l_{{\text{c}}} \frac{\partial }{\partial x}} & {l_{{\text{c}}} \frac{\partial }{\partial y}} \\ \end{array} } \right]^{{\text{T}}}$$

(7)

The geometric equation is defined as

$${\varvec{\varepsilon}} = {\varvec{Lu}}$$

(8)

Strain softening Cosserat continuum MC-matched DP yield criterion

The Drucker–Prager (DP) model has been widely adopted in geotechnical engineering due to its good convergence in numerical computations^42,43. Additionally, the DP model has been effectively extended to the Cosserat continuum framework by Li and Tang²⁶. According to Wei et al.⁴⁴, the coefficients in the Cosserat continuum DP yield criterion proposed by Li and Tang²⁶ can be reasonably adjusted, resulting in a Cosserat continuum MC-matched DP yield criterion that demonstrates high consistency with the Mohr–Coulomb (MC) yield criterion when computing the strength of geomaterials. The relative positions of this yield criterion, along with the MC and classic DP criteria, in the principal stress space Π plane are illustrated in Fig. 2. This criterion has been effectively applied in slope stability analysis and studies of shallow foundation bearing capacity^{44,45,46,47,48}. Therefore, this study will also adopt this criterion for subsequent analyses.

Fig. 2

Illustration of the relative position of MC-matched DP criterion and MC criterion on the Π plane in the principal stress space.

Under two-dimensional plane strain conditions, the Cosserat continuum MC-matched DP yield surface equation is represented as

$$F = q + A_{{{\upvarphi }}} \sigma_{{\text{h}}} + B_{{{\upvarphi }}} = 0$$

(9)

$${\text{where}}\quad q = (\frac{1}{2}{\varvec{\sigma}}^{{\text{T}}} \user2{P\sigma })^{\frac{1}{2}}$$

(10)

$$\sigma_{{\text{h}}} = \frac{1}{\sqrt 3 }(\sigma_{{{\text{xx}}}} + \sigma_{{{\text{yy}}}} + \sigma_{{{\text{zz}}}} )$$

(11)

$$A_{{{\upvarphi }}} = - \sin \varphi$$

(12)

$$B_{{{\upvarphi }}} = - \sqrt 3 C \cdot \cos \varphi$$

(13)

$${\varvec{P}} = \left[ {\begin{array}{*{20}c} 2 &\quad { - 1} &\quad { - 1} &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ { - 1} &\quad 2 &\quad { - 1} &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ { - 1} &\quad { - 1} &\quad 2 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad \frac{3}{2} &\quad \frac{3}{2} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad \frac{3}{2} &\quad \frac{3}{2} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 3 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 3 \\ \end{array} } \right]$$

(14)

Considering the strain-softening behavior where cohesion C decreases gradually with increasing equivalent plastic strain $\overline{\varepsilon }^{{\text{p}}}$, the cohesion can be expressed as

$$C = C_{{{\text{u0}}}} - h_{\text{p}} \overline{\varepsilon }^{{\text{p}}}$$

(15)

where $h_{\text{p}}$ represents the softening modulus, which can be determined through common tests of soil such as triaxial compression and plane strain tests. Specific determination methods are detailed in Tang et al.⁴⁵.

According to Li and Tang²⁶, the equivalent plastic strain can be defined as

$$\overline{\varepsilon }^{{\text{p}}} = \Delta \lambda \left[ {1 + sign(\sigma_{\text{h}} )\frac{{A_{\uppsi } }}{\sqrt 3 }} \right]$$

(16)

$${\text{where}}\quad A_{{\uppsi }} = - \sin \psi$$

(17)

$\Delta \lambda$ is the plastic multiplier; $\psi$ represents the plastic potential angle (dilation angle).

The plastic potential function is expressed as

$$G = q + A_{{\uppsi }} \sigma_{{\text{h}}} + B_{{\uppsi }}$$

(18)

$$B_{{\uppsi }} = - \sqrt 3 C \cdot \cos \psi$$

(19)

With the yield surface equation and the plastic potential function defined, the standard derivation of the constitutive integration algorithm can be conducted. Figure 3 presents a flowchart outlining the constitutive integration algorithm at a Gauss point, providing a clear depiction of the execution logic for the model’s constitutive integration algorithm. For more detailed derivation of the algorithm, refer to Li and Tang²⁶.

Fig. 3

Flowchart of the constitutive integration algorithm for the model.

For enhanced computational efficiency, this study employs numerical implementation via User Element subroutine (UEL) within the finite element software ABAQUS. The used element type is the reduced integration quadrilateral 8-node element, as illustrated in Fig. 4. As the finite element numerical implementation of the Cosserat continuum model has been thoroughly detailed in the authors’ previously published papers. Due to space limitations, this content will not be redundantly expanded upon in this paper. For further details, please refer to Li and Tang²⁶ and Wei et al.⁴⁴.

Fig. 4

Schematic of the reduced integration quadrilateral 8-Node isoparametric element.

Method validation

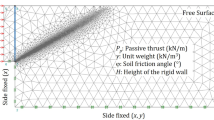
To verify the reliability of the MC-matched DP model used in this paper for calculating the pull-out resistance of plate anchors, this section will compare the model’s results with those from existing literature^1,10,49. In order to ensure that the basic conditions are as consistent as the literature, we degenerate the Cosserat model in this paper into a classical continuum model by taking l_c as 0, and also calculate the common non-softening and non-gravity soil. The calculation uses an 8-node plane strain quadrilateral element. To avoid the influence of boundary effects, the size of the soil domain is set to 28B × 14B according to Cheng et al.⁵⁰. In this numerical simulation, the width B of the strip plate anchor is 3 m and the thickness is 0.3 m. Horizontal constraints are applied to the vertical boundary of the soil domain, fixed constraints are applied to the degrees of freedom fixed in both directions. In order to improve the calculation accuracy, the mesh within a certain range near the anchor plate is refined. The size, mesh division and boundary conditions of the finite element model of plate-anchor with a buried depth of H and an inclination angle of $\beta$ are shown in Fig. 5. The pulling direction of the plate-anchor is perpendicular to the plate-anchor, as shown in Fig. 5. The calculation uses displacement control, applying nodal displacements to the plate-anchor to simulate the uplift resistance.

Fig. 5

Schematic diagram of model size, mesh division and boundary conditions.

Consistent with the literature^1,10,49, for the undrained condition of saturated clay, the Poisson’s ratio $\upsilon =0.49$, friction angle and dilatation angle $\varphi =\phi =0$. The cohesion C is directly taken as the soil undrained shear strength ${{C}_{\text{u}}=S}_{\text{u}}=20\text{kPa}$, and the elastic modulus E is taken as $500{S}_{\text{u}}$. It is assumed that the plate anchor is rigid, i.e., it is assumed that it does not deform during the pull-out process.

The pull-out resistance of a plate anchor is influenced by the strength of the anchor-soil interface. When a plate anchor is subjected to a pull-out force, suction may develop behind it. According to Rowe and Davis⁷, there are two extreme cases: the “vented” condition, where there is no suction or adhesion, and the “attached” condition, where separation is not allowed. These two scenarios represent the lower and upper bounds of the actual pull-out resistance, respectively.

To determine the ultimate pull-out resistance of a plate anchor in non-softening soils, this paper follows the method of Yu et al.¹⁰, selecting the extreme value from the load–displacement curve. This approach ensures the full development of the soil’s failure mechanism.

The ultimate resistance coefficient (N_c) of plate anchor has been widely used, and its expression is shown as

$${N}_{\text{c}}=\frac{{F}_{\text{u}}}{A{S}_{\text{u}}}=\frac{{P}_{\text{u}}}{{S}_{\text{u}}}$$

(20)

where, ${N}_{\text{c}}$ is the pull-out resistance coefficient; ${F}_{\text{u}}$ is the ultimate pull-out force; $A$ is the plate anchor area, and for strip plate anchors, is its width B; ${S}_{\text{u}}$ is the undrained shear strength of clay.

Das and Puri⁸ also proposed a simple empirical relationship to estimate the ultimate pull-out resistance coefficient (${N}_{{\text{c}}\upbeta}$) of inclined plate anchors, as shown in formula (21).

$${N}_{{\text{c}}\upbeta}={N}_{\text{c}(\upbeta ={0}^{\circ })}+\left[{N}_{\text{c}(\upbeta =9{0}^{\circ })}-{N}_{\text{c}(\upbeta ={0}^{\circ })}\right]{\left(\frac{\beta }{9{0}^{\circ }}\right)}^{2}$$

(21)

where ${N}_{\text{c}(\upbeta ={0}^{\circ })}$ is the ultimate resistance coefficient when $\beta = 0^{ \circ }$, and ${N}_{\text{c}(\upbeta =9{0}^{\circ })}$ is the ultimate resistance coefficient when $\beta = 90^{ \circ }$.

Figure 6 shows the comparison between the calculation results of this paper and the relevant literature under the conditions of H/B = 2 (shallow burial) and H/B = 8 (deep burial). For the case of attached, under the deep burial condition, it hardly changes with the change of the inclination angle, while under the shallow burial condition, it decreases with the increase of the inclination angle. For the vented case, both deep burial and shallow burial increase with the increase of the inclination angle. The results of this paper are in good agreement with the results of previous studies. To analyze more intuitively, Fig. 7 illustrates the deviations between the calculation results of this study and those reported in the literature. It is evident that, apart from an 11.2% deviation for H/B = 2 (vented) and β = 90^∘ compared to the results of Merifield et al.¹, all other deviations are within 10%. This confirms the effectiveness of the MC-matched DP model used in this paper for calculating the ultimate pull-out resistance of plate anchors.

Fig. 6

Curves of ultimate pull-out resistance coefficient with inclination.

Fig. 7

Deviation between the N_c calculated in this paper and the literature.

Finite element analysis of plate anchor pull-out resistance in strain-softening clay

In this section, we will use the Cosserat continuum model presented in this paper to conduct a detailed study on the pull-out resistance of plate anchors in strain-softening clay. The computational model dimensions, boundary conditions, and loading protocols are consistent with those in Fig. 5. Additionally, referring to Wei et al.⁴⁴ on the bearing capacity of shallow foundations in marine-sensitive soils, the initial cohesion $C_{{\text{u}}}$ (undrained shear strength) of the soil is set to 12.0 kPa. The remaining material parameters, including E, $\upsilon$, $\varphi$ and $\phi$, are identical to those used in the validation section.

The determination of the Cosserat shear modulus ($G_{{\text{c}}}$), the internal length parameter ($l_{{\text{c}}}$), and the mesh discretization strategy will be detailed subsequent to the specific analysis presented later in the text. The parametric analysis will primarily encompass the anchor plate’s inclination angle ($\beta$), the embedment ratio (H/B), and the strain softening modulus ($h_{{\text{p}}}$). For the ensuing calculations, $\beta$(°) is slated to assume values of 0°, 30°, 45°, 60°, and 90°; H/B will consider values of 2, 4, 6, 8, and 10; and $h_{{\text{p}}}$ will range from 0 to 2.0 $C_{{\text{u}}}$ in increments of 0.5 $C_{{\text{u}}}$. In some previous experimental studies on strain-softening clays, the h_p​ parameter also falls within this range^27,29,45,51. In the subsequent calculations of this paper, the interaction between the plate anchor and the soil will be modeled entirely under the “attached” condition, assuming that there is no separation between the plate anchor and the soil. As demonstrated by Cheng et al.⁵⁰, when an “attached” connection is used between the anchor plate and the soil, the inclusion of soil weight has minimal impact on the calculation of the plate anchor’s pull-out resistance. Therefore, the effect of soil weight will not be considered in this study, and the analysis will assume weightless soil.

Mesh sensitivity analysis and determination of Cosserat continuum parameters

Due to the instability in the governing equations when analyzing strength strain-softening conditions using classical continuum elastoplastic finite element methods, there is a pathological dependency on the mesh size, leading to ill-posed computational results. Therefore, it is necessary to employ methods with a regularization mechanism to address this issue, such as the Cosserat continuum finite element model utilized in this paper. When analyzing plane strain problems, the Cosserat continuum finite element model introduces two additional parameters compared to the classical continuum model, namely the Cosserat shear modulus ($G_{{\text{c}}}$) and the internal length parameter ($l_{{\text{c}}}$).

Li and Tang²⁶ and Tang et al.⁵² have demonstrated that as long as the Cosserat shear modulus $G_{{\text{c}}}$ is taken to be not less than half of $G$, the regularization effectiveness can be ensured in calculations. Moreover, variations in the value of $G_{{\text{c}}}$ within the allowable range have a minimal impact on the computational results. Therefore, in this paper, $G_{{\text{c}}}$ is directly taken as half of $G$. However, the value of $l_{{\text{c}}}$ does have a certain impact on the calculation results. $l_{{\text{c}}}$ is a parameter positively correlated with soil particle size. Generally, a larger $l_{{\text{c}}}$ leads to higher bearing capacity predicted by the finite element model and results in a greater shear band thickness. However, for clay, relevant studies^{53,54,55,56,57} indicate that the actual shear band thickness typically ranges from 1 to 10 mm. To calibrate lc based on the actual shear band thickness, $l_{{\text{c}}}$ usually needs to be taken as 1/5 to 1/3 of the shear band thickness^24,54,58. Additionally, to ensure that finite element simulations incorporating strain softening can fully overcome mesh dependency, the element size should not exceed $l_{{\text{c}}}$. Although in many cases it is unnecessary to completely eliminate mesh dependency, the element size should at least be on the same order of magnitude as $l_{{\text{c}}}$. This typically requires the element size to be in the millimeter range, which is feasible for simulating small soil specimens, such as the plane strain compression tests. However, for the large-scale plate anchor uplift scenarios considered in this study, employing such a fine mesh is evidently impractical.

Given that this study primarily focuses on the ultimate pullout resistance of the plate anchor, we conducted simulations with various combinations of $l_{{\text{c}}}$ and mesh sizes within an acceptable range of mesh resolutions. The final $l_{{\text{c}}}$ value and mesh discretization strategy were determined based on the criteria of sufficiently mitigating mesh dependency and avoiding overestimation of the ultimate pullout resistance compared to classical continuum models^44,46.

Referring to the trial calculation strategy proposed by Wei et al.⁴⁴, the value of l_c is initially set within the range of 0.01 to 0.1 times the key dimensions of the geometric model based on empirical experience. Subsequently, in the Cosserat ideal elastoplastic model without considering strain softening, $l_{{\text{c}}}$ is taken as six different cases of 0.01B, 0.02B, 0.03B, 0.04B, 0.06B, and 0.10B, and the calculation results are compared with those of the classical continuum elastoplastic model (where $l_{{\text{c}}}$ is taken as 0). The aim is to identify several values of $l_{{\text{c}}}$ where the deviation of the ultimate bearing capacity does not exceed the allowable precision range which can be set according to actual conditions (in this paper, it is simply set at 5%). Then, for the several values of $l_{{\text{c}}}$ that meet the bearing capacity error requirements, the calculation domain is divided into meshes of different refinements to conduct regularization analysis considering strain softening. Through comparison, the final value of $l_{{\text{c}}}$ is ultimately determined.

Figure 8 presents the $P/C_{{\text{u}}}$-displacement curves calculated under no strain softening conditions for different values of $l_{{\text{c}}}$. It can be observed that compared to the results of the classical continuum model ($l_{{\text{c}}}$ = 0), the cases where $l_{{\text{c}}}$ takes the values of 0.01B, 0.02B, 0.03B, 0.04B, 0.06B, and 0.10B exhibit ultimate resistance that are 4.2%, 4.2%, 5.0%, 10.9%, 10.9%, and 17.1% higher, respectively. Therefore, the three scenarios where $l_{{\text{c}}}$ is taken as 0.01B, 0.02B, and 0.03B all meet the requirement set in this paper that the deviation does not exceed 5%.

Fig. 8

Curves of $P/C_{{\text{u}}}$- displacement.

Next, a regularization analysis is conducted for the three scenarios where $l_{{\text{c}}}$ takes the values of 0.01B, 0.02B, and 0.03B, considering the strain-softening condition. For comparative purposes, the classical continuum case ($l_{{\text{c}}}$ = 0) is also included in the regularization analysis. To ensure that the regularization analysis is more representative, the soil softening modulus $h_{{\text{p}}}$ is set to 2.0 $C_{{\text{u}}}$, which is the most severe softening condition in the subsequent parametric analysis of this paper. It is believed that if regularization can be guaranteed under this condition, it can certainly be ensured under other less severe softening conditions. The mesh size, denoted as 'a', in the area near the plate anchor is refined into three cases: a = 0.1B, a = 0.05B, and a = 0.04B. The meshes in other regions are re-divided using the same size ratio as shown in Fig. 5. The $P/C_{{\text{u}}}$-displacement curves obtained for the three $l_{{\text{c}}}$ values under the three different mesh sizes are shown in Fig. 9.

Fig. 9

Curves of $P/C_{{\text{u}}}$—displacement for various mesh size (a) ((a) $l_{{\text{c}}}$ = 0.00B (classical continuum); (b) $l_{{\text{c}}}$ = 0.01B; (c) $l_{{\text{c}}}$ = 0.02B; (d) $l_{{\text{c}}}$ = 0.03B).

As shown in Fig. 9, the classical continuum model ($l_{{\text{c}}}$ = 0.00B) exhibits significant mesh dependency when strain softening is considered. The computational results fail to converge as the mesh size decreases. When the mesh size (a) is reduced to 0.04B, calculations are even forced to terminate prematurely near the peak of the load capacity curve, preventing the analysis of the post-peak failure process in plate anchor extraction. In contrast, the three scenarios employing the Cosserat continuum model (with $l_{{\text{c}}}$ values of 0.01B, 0.02B, and 0.03B) all demonstrate superior mesh convergence. Notably, the case with $l_{{\text{c}}}$ set at 0.03B shows the optimal regularization effect, leading to the selection of 0.03B as the definitive value for $l_{{\text{c}}}$. Considering both convergence and computational efficiency, the mesh for the calculation domain is chosen with a mesh size (a) of 0.05B (as illustrated in the mesh division of the aforementioned Fig. 5) for subsequent calculations.

As depicted in Fig. 10, the contour of the equivalent plastic strain is presented for the given parameter configuration. More precisely, with the mesh density set to a = 0.05B = 150 mm and the characteristic length set to l_c = 0.03B = 90 mm, as selected for this study, the simulation results indicate a shear band thickness of about 700 mm. This value is significantly larger than the typical shear band thickness observed in actual clay materials, which ranges from 1 to 10 mm. As previously mentioned, to predict the shear band width more accurately, it is necessary to use a smaller l_c and finer mesh size. However, due to limitations in computational resources and technical feasibility, implementing such improvements in large-scale engineering simulations poses significant challenges. This limitation underscores the need for advancements in computational power and further optimization of finite element algorithms, which could address these shortcomings in future research and applications.

Fig. 10

Contour of equivalent plastic strain ($l_{{\text{c}}}$ = 0.03B and a = 0.05B).

Analysis of the influence of embedment depth and inclination angle on N_c

Figure 11 presents the curves of the ultimate pull-out resistance coefficient $N_{{\text{c}}}$ varied with the embedment ratio H/B for different angles $\beta$ under various $h_{{\text{p}}}$. It can be observed that under different $\beta$ values, the trend of $N_{{\text{c}}}$ changing with H/B is essentially the same. In shallow embedment conditions (H/B < 4), the $N_{{\text{c}}}$ is relatively small and gradually increases with the increase of H/B. In deep embedment conditions (H/B ≥ 4), the variation of H/B has a minor impact on the $N_{{\text{c}}}$. When H/B ≥ 4, and the soil is in a non-softened state ($h_{{\text{p}}}$ = 0), $N_{{\text{c}}}$ remains essentially constant and does not change with embedment depth. However, when soil softening is considered ($h_{{\text{p}}}$ > 0), $N_{{\text{c}}}$ tends to increase with the increase of H/B, and the rate of increase gradually slows down as H/B increases.

Fig. 11

Variation curves of $N_{{\text{c}}}$ with H/B under different conditions ((a) $h_{{\text{p}}}$ = 0.0 $C_{{\text{u}}}$; (b) $h_{{\text{p}}}$ = 0.5 $C_{{\text{u}}}$; (c) $h_{{\text{p}}}$ = 1.0 $C_{{\text{u}}}$; (d) $h_{{\text{p}}}$ = 1.5 $C_{{\text{u}}}$; (e) $h_{{\text{p}}}$ = 2.0 $C_{{\text{u}}}$).

Figure 12 presents the variation curves of the $N_{{\text{c}}}$ with the inclination angle $\beta$ under different embedment ratios H/B and various softening modulus $h_{{\text{p}}}$. Under different softening modulus h_p conditions (0.0C_u, 0.5C_u, 1.0C_u, 1.5C_u, 2.0C_u), it can be observed that as the $\beta$ increases, $N_{{\text{c}}}$ exhibits a gradual decreasing trend. Moreover, the rate at which $N_{{\text{c}}}$ decreases with the increase of $\beta$ is faster for smaller H/B ratios. When H/B is 2 and 10, respectively, $N_{{\text{c}}}$ decreases by 14.2% and 1.8% as $\beta$ increases from 0° to 90°.

Fig. 12

Curves of the $N_{{\text{c}}}$ with inclination angle $\beta$ under different conditions ((a) $h_{{\text{p}}}$ = 0.0 $C_{{\text{u}}}$; (b) $h_{{\text{p}}}$ = 0.5 $C_{{\text{u}}}$; (c) $h_{{\text{p}}}$ = 1.0 $C_{{\text{u}}}$; (d) $h_{{\text{p}}}$ = 1.5 $C_{{\text{u}}}$; (e) $h_{{\text{p}}}$ = 2.0 $C_{{\text{u}}}$).

Analysis of the Influence of Strain Softening on N_c

Figure 13 presents the variation curves of the $N_{{\text{c}}}$ with the softening modulus $h_{{\text{p}}}$ for different embedment ratios H/B and various inclination angles $\beta$. It can be observed that for different inclination angles $\beta$, the trend of $N_{{\text{c}}}$ changing with the softening modulus $h_{{\text{p}}}$ is similar. That is, as the softening modulus $h_{{\text{p}}}$ increases, $N_{{\text{c}}}$ gradually decreases.

Fig. 13

Curves of $N_{{\text{c}}}$ versus $h_{{\text{p}}} /C_{{\text{u}}}$ under different conditions ((a) $\beta$ = 0°, (b) $\beta$ = 30°, (c) $\beta$ = 45°, (d) $\beta$ = 60°, (e) $\beta$ = 90°).

Figure 13 shows the distribution of equivalent plastic strain at foundation instability for $\beta$ = 0° and H/B = 8, with $h_{{\text{p}}}$ values of 0.5 $C_{{\text{u}}}$, 1.0 $C_{{\text{u}}}$, 1.5 $C_{{\text{u}}}$, and 2.0 $C_{{\text{u}}}$. From the preceding analysis, it is evident that the soil softening characteristics progressively intensify from cases (a) to (d). Figure 14 demonstrates that the degree of soil strain softening has no significant impact on the failure mechanism of the foundation soil. However, the more pronounced the softening characteristic, the higher the value of the equivalent plastic strain and the greater the degree of strain localization.

Fig. 14

Distribution of equivalent plastic strain at foundation instability under different conditions ((a) $h_{{\text{p}}}$ = 0.5 $C_{{\text{u}}}$, (b) $h_{{\text{p}}}$ = 1.0 $C_{{\text{u}}}$, (c) $h_{{\text{p}}}$ = 1.5 $C_{{\text{u}}}$, (d) $h_{{\text{p}}}$ = 2.0 $C_{{\text{u}}}$).

Progressive failure analysis of strain-softening soil for plate anchor pull-out

One advantage of the Cosserat continuum finite element model in this paper is its ability to represent the progressive instability process to some extent, when considering strain softening. Figure 15, taking the case of $\beta$ = 45°, H/B = 8, and $h_{{\text{p}}}$ = 1.5 $C_{{\text{u}}}$ as an example, presents the dimensionless resistance ($P/C_{{\text{u}}}$)—displacement variation curve calculated using the finite element model of this paper. It can be observed that the resistance first increases linearly with the increase of displacement, then reaches a peak point after a curvilinear growth phase, and gradually decreases as displacement increases after reaching the peak point. To more clearly reveal the intrinsic causes of this phenomenon, six points on the curve are selected: Point A is located in the linear increase phase, Points B and C are in the curvilinear increase phase, Point D is at the peak point, and Points E and F are in the descending phase. The equivalent plastic shear strain distribution and cohesion distribution corresponding to these six points are given, as shown in Figs. 15 respectively.

Fig. 15

Distribution of equivalent plastic strain at different loading stages.

As Figs. 16 shown, at Point A, where the plastic strain is zero, the cohesion has not softened, and the entire model is in the elastic phase. Hence, the $P/C_{{\text{u}}}$- displacement curve shows a linear increase. At Point B, the soil at both ends of the plate anchor has developed a certain range of plastic strain. Due to strain softening, the cohesion at the corresponding locations has decreased, causing the $P/C_{{\text{u}}}$- displacement curve to deviate from the linear relationship observed in the purely elastic phase. At Point C, the area of the plastic zone has further expanded, and the cohesion within the plastic zone has also further decreased. However, the extent of the plastic zone and the value of plastic strain are still small at this stage, the degree of strength softening of the soil at the corresponding location is not significant, and most of the soil at key positions is still in the elastic phase, resulting in the $P/C_{{\text{u}}}$- displacement curve showing a gradually decelerating increase. At the peak Point D, it can be observed that both the range of the plastic zone and the value of plastic strain at the ends of the plate anchor have significantly increased compared to previous stages, and the softening of the cohesion at the corresponding location is more pronounced. However, It should be noted that the plastic zone does not form a complete failure mechanism at the peak piont, which is a characteristic of progressive failure in strain-softening soil. At Point E, the plastic zone has become significantly larger, and the cohesion in the plastic zone shows a more dramatic gradient change, indicating that the soil strength in this area is rapidly decreasing, thus the $P/C_{{\text{u}}}$- displacement curve shows a clear downward trend. At Point F, the plastic zone has penetrated, forming a complete failure mechanism, and the accumulated value of plastic strain is also higher than in the previous stages, with the cohesion at the corresponding location further reduced, so the $P/C_{{\text{u}}}$- displacement curve remains in a continuous downward state.

Fig. 16

Cohesion distribution at different loading stages.

It can be observed that the numerical method established in this paper is capable of simulating and analyzing the progressive failure process of the plate anchor, from keying to ultimate instability, to a certain extent. However, it is important to emphasize a limitation: the softening mechanism employed in this study assumes a linear reduction in the undrained shear strength of the soil with increasing equivalent plastic strain, without imposing a residual strength limit. This assumption becomes inapplicable when analyzing the post-failure behavior during plate anchor pullout involving large plastic deformations. Therefore, the Cosserat finite element model developed in this study requires enhancement by incorporating a nonlinear strain-softening mechanism that imposes a residual strength limit, along with the adoption of large deformation techniques. Such advancements would enable a more comprehensive and thorough analysis of the entire progressive instability process during plate anchor pullout. This represents one of the key areas of ongoing research by the authors.

Ultimate pull-out resistance coefficient formula for inclined anchors considering strain softening of soil

In practical geotechnical engineering, engineers are more accustomed to determining relevant indicators using formulas or by consulting tables. Therefore, it is meaningful to propose effective expressions based on advanced numerical computation methods through parametric analysis. Here, we first establish the expression for the ultimate pull-out resistance coefficient of plate anchors without considering strain softening ($h_{{\text{p}}}$ = 0).

Das and Puri (1989) proposed a simple empirical relationship based on laboratory research findings to estimate the resistance of inclined anchors. This relationship is formulated as Eqs. (19).

In the formula, $N_{{{{\text{c}}\upbeta}}}$ represents the pullout coefficient for an anchor plate at any inclination angle between 0° and 90°; $N_{{\text{c}}(\upbeta = 0^{\circ})}$ and $N_{{\text{c}}(\upbeta = 90^{\circ})}$ are the pullout force coefficients for the horizontal and vertical plate anchors, respectively. Merifield et al.⁹ have verified the applicability of this relationship in homogeneous clay without the influence of gravity.

The predicted results are consistent with the overall trend of the calculated results in this study; however, the relationship appears to underestimate the ultimate pullout resistance coefficient. Therefore, we have further refined this expression to obtain the following ultimate pullout resistance coefficient ($N_{{{{\text{c}}\upbeta}}}$) as a function of the plate anchor inclination angle β (in degrees), expressed as

$${N}_{{\text{c}}\upbeta}={N}_{\text{c}(\upbeta ={0}^{\circ })}+({N}_{\text{c}(\upbeta =9{0}^{\circ })}-{N}_{\text{c}(\upbeta ={0}^{\circ })})\frac{2.5{\beta }^{2}}{6000+2{\beta }^{2}}$$

(22)

Subsequently, considering the case without softening, the ultimate pull-out resistance coefficient $N_{{{\text{cH}}}}$ is examined for different depths of embedment. Since there is a significant change in resistance between shallow and deep embedment conditions, this will be presented in two cases.

In the case of shallow embedment (H/B < 4), the ultimate pull-out bearing capacity coefficient is given as

$$\left\{ {\begin{array}{*{20}c} {N_{{{\text{cH}}\left( {{\upbeta } = 0^\circ } \right)}} = - 0.26(\frac{H}{B})^{2} + 2.35\frac{H}{B} + 7.835} \\ {N_{{{\text{cH}}\left( {{\upbeta } = 90^\circ } \right)}} = - 0.18(\frac{H}{B})^{2} + 2.35\frac{H}{B} + 6.425} \\ \end{array} } \right.,\quad ({2} \le H/B < {4})$$

(23)

In the case of deep embedment (H/B ≥ 4), the uplift resistance coefficient is provided as

$$\left\{ {\begin{array}{*{20}c} {N_{{{\text{cH}}\left( {{\upbeta } = 0^\circ } \right)}} = 0.0045\frac{H}{B} + 13.05655} \\ {N_{{{\text{cH}}\left( {{\upbeta } = 90^\circ } \right)}} = 0.01\frac{H}{B} + 12.905} \\ \end{array} } \right.,\quad (H/B \ge {4})$$

(24)

Based on Eqs. (22), (23), and (24), the expression for the anchor plate resistance coefficient $N_{{{\text{c (}}h_{\text{p}} { = 0)}}}$, which couples embedment depth and inclination angle without strain softening, can be derived as

$$N_{{{\text{c(}}h_{{\text{p}}} = 0)}} = \left( { - 0.26\left( {\frac{H}{B}} \right)^{2} + 2.35\frac{H}{B} + 7.835} \right) + \left( {0.12\left( {\frac{H}{B}} \right)^{2} - 1.85} \right)\frac{{2.5\beta ^{2} }}{{6000 + 2\beta ^{2} }},\quad (2 \le H/B < 4)$$

(25)

$$N_{{{\text{c(}}h_{{\text{p}}} = 0)}} = 0.0045\frac{H}{B} + 13.05655 + \left( {0.055\frac{H}{B} - 0.15155} \right)\frac{{2.5\beta ^{2} }}{{6000 + 2\beta ^{2} }},\quad (H/B \ge {\text{4}})$$

(26)

To verify the effectiveness of the formula, Fig. 17 presents a comparison between the results calculated using the formula and the numerical calculation results from the previous text. It can be seen that the proposed formula fits the numerical calculation results very well, with errors not exceeding 3.6%.

Fig. 17

Comparison curves of formula and numerical results considering embedment depth and inclination angle.

Due to the limited research on the impact of strain softening on the ultimate pull-out resistance of anchor plates, this section focuses on determining the expression for the ultimate resistance coefficient of strip anchors considering strain softening. The previous text has provided the calculation formula for the coefficient that couples embedment depth and inclination angle. Therefore, this section will directly construct the expression for the ultimate pull-out resistance coefficient of anchor plates, incorporating embedment depth, inclination angle, and strain softening. Through dividing the $N_{{\text{c}}}$ values obtained under 150 different conditions in this paper by the corresponding $N_{{\text{c(hp = 0)}}}$, it is observed that the effect of strain softening gradually decreases with the increase of the embedment ratio H/B. Therefore, the same approach is taken here to divide into two cases based on embedment depth, and the resulting formula is as

$$N_{{\text{c}}} /N_{{c\left( {h_{{\text{p}}} = 0} \right)}} = 0.0328(\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }})^{2} - 0.1613\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }} + 0.9978,\quad ({2} \le H/B < {4})$$

(27)

$$N_{{\text{c}}} /N_{{c\left( {h_{{\text{p}}} = 0} \right)}} = 0.004(\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }})^{2} - 0.0595\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }} + 0.9784,\quad (H/B \ge {4})$$

(28)

In the formula, $N_{{\text{c(hp = 0)}}}$ represents the resistance coefficient without strain softening. To validate the effectiveness of the formula, Fig. 18 presents the comparison between the results calculated using the formula and the numerical calculation results from the previous text. It can be seen that the proposed formula fits the numerical calculation results very well, with errors not exceeding 5%.

Fig. 18

Comparison curves of formula and numerical results considering embedment depth, inclination angle, and strain softening ((a) Shallow embedment (H/B < 4) (b) Deep embedment (H/B ≥ 4)).

Based on Eqs. (23), (24), (25) and (26), the expression of the plate anchor ultimate resistance coefficient $N_{{\text{c}}}$, coupling depth, inclination angle, and strain softening, can be derived as

$$N_{{\text{c}}} = \left[ {( - 0.26\left( {\frac{H}{B})^{2} + 2.35\frac{H}{B} + 7.835} \right)(0.12\left( {\frac{H}{B})^{2} - 1.85} \right)\frac{{2.5\beta^{2} }}{{6000 + 2\beta^{2} }}} \right]\left[ {0.0328(\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }})^{2} - 0.1613\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }} + 0.9978} \right],\quad ({2} \le H/B < {4})$$

(29)

$$N_{{\text{c}}} = \left[ {\left( {0.0045\frac{H}{B} + 13.05655} \right)\left( {0.055\frac{H}{B} - 0.15155} \right)\frac{{2.5\beta^{2} }}{{6000 + 2\beta^{2} }}} \right]\left[ {0.004(\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }})^{2} - 0.0595\frac{{h_{{\text{p}}} }}{{C_{{{\text{u}}0}} }} + 0.9784} \right],\quad (H/B \ge {4})$$

(30)

To verify the validity of the formula, Fig. 19 presents the deviations between the formula and the numerical calculation results for a total of 150 cases discussed earlier. It can be observed that the proposed formula fits the numerical calculation results quite well, with the maximum deviation not exceeding 7%.

Fig. 19

Deviation between formula and numerical results for coupling depth, angle, and strain softening.

Conclusions

This study employed the UEL function of ABAQUS to investigate the pull-out resistance and progressive instability of plate anchors in strain-softening soils using the Cosserat continuum MC-matched DP model. Initially, we validated the accuracy of the MC-matched DP model by comparing the pull-out resistance results with those reported in the literature. In addition, through a mesh sensitivity analysis, we developed a method for determining the internal length parameter (l_c) and mesh refinement for plate anchor scenarios. This demonstrated that our model effectively addresses common numerical convergence issues and mesh dependency problems encountered in classical finite element analyses of strain-softening problems. Furthermore, through parametric analysis, we investigated the combined effects of plate anchor inclination, burial depth, and strain softening on the pull-out resistance and failure mechanisms, leading to the following conclusions as

(i) Parametric analysis revealed that in shallow burial conditions (H/B < 4), the pull-out resistance of the anchor plate is relatively low and increases gradually with increasing H/B. When H/B ≥ 4 and $h_{{\text{p}}}$ = 0 (no softening), $N_{{\text{c}}}$ remains approximately constant and does not change with burial depth. However, when H/B ≥ 4 and $h_{{\text{p}}}$ > 0 (softening), $N_{{\text{c}}}$ increases with increasing H/B, but the rate of increase decreases as H/B increases.

(ii) For different inclinations $\beta$, the trend of $N_{{\text{c}}}$ changing with the softening modulus $h_{{\text{p}}}$ is generally consistent, i.e., $N_{{\text{c}}}$ decreases as $h_{{\text{p}}}$ increases. The degree of strain softening in the soil has no significant effect on the failure mechanism, but higher softening levels result in higher values of equivalent plastic strain and greater strain localization.

(iii) Through comprehensive analysis of the entire process from the initial pullout to instability of the plate anchor, it was found that when the load–displacement curve reaches its peak, the plastic zone has not yet fully penetrated, indicating that a complete failure mechanism has not yet formed. A complete failure mechanism corresponds to a point in the post-peak softening segment of the curve. Detailed analysis of the distribution of equivalent plastic strain and cohesion at different loading stages elucidates the underlying reasons for the shape of the load–displacement curve at each stage. This indicates that the Cosserat finite element model employed in this study is capable of simulating, to a certain extent, the progressive failure process of soil induced by the uplift of plate anchors.

(iv) To make the research outcomes more applicable in practice, based on the results of parametric analysis, an expression for $N_{{\text{c}}}$ was derived, which simultaneously accounts for the effects of plate anchor inclination, burial depth, and strain softening. This may provide important reference information for geotechnical engineers in practical applications.