Introduction

Molecules from medicinal plants are increasingly used in many areas. These are very often used in the manufacture of drugs intended to treat numerous diseases1 such as malaria, cancer or even viral hepatitis2,3. Lipinski’s “rule of 5s”4 is the most widely used for the identification of “drug-like” compounds. According to this rule, compounds that do not meet at least two of the criteria have a very high chance of having absorption or permeability problems5. Nowadays, molecules isolated from plant have also seen their applications increase in the field of nanotechnologies due to their particular structures consisting of benzene rings6, multiple bonds and hydrogen bond acceptors7,8,9,10,11. Those molecules can be used as semiconductor or insulator for the manufacture of electronic devices. They can also be used in nonlinear optics and optoelectronics devices due to their structures7. Many of those molecules with particular structures are isolated from plant. This is the case of limonoids of the Meliaceae family, whose structures very often give interesting physico-chemical properties8,12.

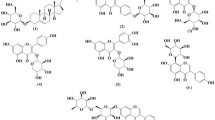
The three limonoids namely: 17-epi-methyl-6-hydroxylangolensate (compound A: C27H34O8), 7-desacetoxy-7-oxogedunin (compound B: C26H30O6) and 7-deacetoxy-7R-hydroxygedunin (compound C: C26H32O6) were isolated from the active fraction of the Khaya grandifoliola13 plant by Kouam et al.14 and were found to be able to protect the normal human hepatocyte cell line L-02 against paracetamol-induced hepatotoxicity. This plant of the Meliaceae family is used in traditional medicine for the treatment of liver-related diseases14. Molecular compounds A, B and C, with respective molecular masses 486.2254 g/mol, 438.2042 g/mol and 440.2199 g/mol, belong to the same family and have their molecular structures composed of furan, cyclohexanone, cyclohex-2-enone, δ-valerolactone and benzene groups.

In 1970, Ollis and his co-workers15 made the vibrational analysis of compound B. It appears from this analysis that the stretching vibrations of the C = O bond of the cyclohex-2-enone, cyclohexanone and δ-valerolactone groups are respectively 1685 cm− 1, 1720 cm− 1 and 1745 cm− 115. The melting point of this compound B is between 260 °C and 264 °C. Most of the studies carried out to date on these three molecular compounds concern the identification and isolation of these different structures from plants.

Considering the importance of these molecular compounds for human health, their specific molecular structures similar to those of Rubescin D and E molecules8,16, molecular compounds A, B and C can be considered as promising candidates for medical, electronic and nonlinear optical applications. In this work, we used ab initio HF and DFT numerical simulation methods (B3LYP, B3PW91 and ωB97XD) to make a comparative study of the structural, electronic, spectral and thermodynamic properties. We made a comparative study of the local and global reactivities and deduce the antioxidant properties of each of the molecular compounds A, B and C. The details of the calculations are given in Sect. 2. The results are discussed in Sect. 3 and the summary in Sect. 4.

Methodology

To determine the properties of the studied molecular compounds A, B and C, we first optimized those compounds using DFT-B3LYP/6-311G(d, p) method. B3LYP (Becke, three.

parameter, Lee-Yang-Parr) correlation functional1,17 was choose because it is the most used functional for this purpose and have proved base on our previous research and in the literature to provide the most stable molecular structure18. After optimization, the optimized structure were used for the calculation of HOMO-LUMO energy gap. The following equation were used:

$$\:{E}_{gap}={E}_{LUMO}-{E}_{HOMO}$$
(1)

The fundamental gap (\(\:{E}_{f}\)) were calculated as19:

$$\:{E}_{f}=IP-EA$$
(2)

Ionization potential (\(\:IP\)) and electron affinity (\(\:EA\)) were calculated using the finite difference method12,19,20. Some global reactivity descriptors such us chemical potential

$$\:{\mu\:}_{CP}=-\chi\:=\frac{{E}_{LUMO}+{E}_{HOMO}}{2}$$
(3)

and electrophilicity index

$$\:\omega\:=\frac{{({E}_{LUMO}+{E}_{HOMO})}^{2}}{4({E}_{LUMO}+{E}_{HOMO})}$$
(4)

were calculated. IP and EA were used to determine electro-donating power (\(\:{\omega\:}^{-}\))

$$\:{\omega\:}^{-}=\frac{{(3IP+EA)}^{2}}{16(IP-EA)}$$
(5)

and electro-accepting power (\(\:{\omega\:}^{+}\))

$$\:{\omega\:}^{+}=\frac{{(IP+3EA)}^{2}}{16(IP-EA)}$$
(6)

The lower values of \(\:{\omega\:}^{-}\) imply a greater capacity for donating charge and the higher values of \(\:{\omega\:}^{+}\) imply a greater capacity for accepting charge21. Electro-donating index (\(\:{R}_{d}\))

$$\:{R}_{d}=\frac{{\omega\:}^{-}}{{w}_{Na}^{-}}$$
(7)

and electro-accepting index (\(\:{R}_{a}\))

$$\:{R}_{a}=\frac{{\omega\:}^{+}}{{w}_{F}^{+}}$$
(8)

were also calculated. When \(\:{R}_{d}=1,\:<1\:or>1\), the molecular compound is considered as an effective electron donor, a more effective electron donor or a less effective electron donor than Na respectively. For \(\:{R}_{a}=1,\:<1\:or>1\), the molecular compound is represent respectively as effective electron acceptor, a less effective electron acceptor or a more effective electron acceptor than F. \(\:{w}_{Na}^{-}\) and \(\:{w}_{F}^{+}\)was calculated using the same formula as \(\:{\omega\:}^{-}\) and \(\:{\omega\:}^{+}\). The IP and EA respectively used for this purpose were for Na (5.1391; 0.547926) eV and for F (17.42282; 3.4011898) eV22. The vibrational frequency analysis were done for all the studied compounds using HF and DFT (B3LYP, B3PW91 and \(\:\omega\:\)B97XD) methods with the 6-311G(d, p) basis set implemented in Gaussian 09 program package23. In order to understand the electronic transitions of the studied compounds, calculations were done on the optimized form of compounds A, B and C in vacuum and in solvent media (water and chloroform) using TD-DFT-B3LYP/6-311G(d, p) method6. We also determine in this work some nonlinear optical parameter such as: polarizability (\(\:\alpha\:\)), hyperpolarizability (\(\:\beta\:\)), anisotropy of polarizability (\(\:\varDelta\:\alpha\:\)) and molar refraction (\(\:MR\))8. Some thermodynamic parameter such as standard enthalpy (\(\:H\)), standard Gibbs free energy (\(\:G\)), heat capacity at constant volume (\(\:{C}_{v}\)), standard entropy (\(\:S\)) and heat capacity at constant pressure (\(\:{C}_{P}\)) were plotted and describe.

Results

Optimized structures and structural analysis

Optimized structures

The optimized molecular structures obtained using DFT-B3LYP/6-311G(d, p) methods of the studied molecular compounds A, B and C are presented in Fig. 1.

The total energies obtained for those molecular compounds A, B and C in kcal/mol are respectively − 1036325.912, -916439.169 and − 917198.548. The vibrational frequencies analysis were then performed on the optimized form and no negative frequencies were observed for all the studied compounds mining that the molecular compounds A, B and C are all stable at this level.

Fig. 1
figure 1

Optimized molecular structures of compounds A, B and C obtained using the DFT/B3LYP/6-311G(d, p) methods. Red atoms stand for oxygen, dark grey for carbon and white for hydrogen.

Full size image

Structural properties

In terms of structure, it was observed that molecular compounds B and C are similar and differ only in the presence of the C = O double bond in compound B which is replaced in compound C by C – OH bond. The latter differ from compound A but keep the same skeleton.

Table 1 Some interatomic distances (Å) and valence angles (°) of our molecular structures obtained at the B3LYP level using 6-311G(d, p) basis set.
Full size table

Table 1 presents some structural parameters (bond lengths (in Å) and valence angles (in °)) found in the three studied molecular compounds A, B and C. The values presented were obtained using DFT/B3LYP/6-311G(d, p) methods. These values were compared to the values of the identical groups found in the Rubescin D molecule obtained using the DFT/B3LYP/6-311 + + G(d, p) method8.

Regarding the values of bond lengths, we observe that these are similar for the three compounds A, B and C. The ranges of variations between A and B, A and C, B and C are between 0 and 6.314%, 0 and 1.796% and between 0 and 5.487%, respectively. Comparing our values to the theoretical values available in the literature for the Rubescin D molecule, it appears that the greatest difference is obtained by the C-C bond of the cyclohex-2-enone group for compounds B and C, and for cyclohexanone group for compound A8.

Also in Table 1, some valence angles (C-C-C and C-O-C) of the three molecular compounds are presented. It emerges from this that, the values vary slightly when we move from one molecular system to another. It is noted that, the values obtained are close to the theoretical values available in the literature8. The differences observed here may be due to the systems to which these groups are attached or to the basis set of calculations used. The bond lengths as well as the valence angles presented in Table 1 are mainly those of the specific groups (furan, cyclohexanone, cyclohex-2-enone and δ-valerolactone) found in the three molecular compounds.

Vibrational frequencies analysis

The vibrational frequency analysis of a molecular system is a very useful characterization method which provides information on the molecular stability as well as on the movement of an atom or a group of atoms, for a given system and frequency. Figure 2 gives a representation of the IR vibrational frequency of molecular compounds A, B and C obtained using B3LYP/6-311G(d, p). According to Fig. 2, it come out that the IR vibrational frequencies of compounds A and C are similar and different from the vibrational frequencies of compound B due to the absence O – H bond. For all those compounds, we found that the stretching vibration of aromatic C – H bonds are found in the range of 2950 cm-1 to 3200 cm-1. This is closer to the observation generally made for this vibration in the literature24.

Fig. 2
figure 2

IR intensity of compounds A, B and C obtained using B3LYP/ 6-311G(d, p) basis set.

Full size image
Fig. 3
figure 3

IR intensity of compounds A, B and C obtained at the B3LYP, B3PW91, ωB97XD and HF levels using 6-311G(d, p) basis set.

Full size image

In Fig. 3, a comparison of vibrational frequencies using HF and DFT(B3LYP, B3PW91 and ωB97XD) methods is done along with 6-311G(d, p) basis set.

Table 2 presents some values of the vibrational frequencies as well as the corresponding values of the IR intensities, followed by the different interpretations of the vibrations of the atoms or groups of atoms belonging to at least two of the three molecular systems. The values of the vibrational frequencies presented in this Table 2 were obtained from Gaussian 09 program package23 using DFT (B3LYP, B3PW91, \(\:\omega\:\)B97XD) and HF methods. It is observed from Table 2 that the values of the vibrational frequencies increase from B3LYP level to the HF level passing respectively through the B3PW91 and \(\:\omega\:\)B97XD levels. The O-H unscaled stretching vibration values are found at approximately 3817.65 cm− 1, 3849.04 cm− 1, 3910.84 cm− 1 and 4163.69 cm− 1 for molecular compound A at the B3LYP, B3PW91, \(\:\omega\:\)B97XD and HF levels, respectively. For molecular compound C, these values are respectively at 3830.43 cm− 1, 3860.63 cm− 1, 3916.47 cm− 1 and 4174.54 cm− 1. Using the scaling factors 0.8454, 0.9346, 0.94218 and 0.9069 respectively at the HF, B3PW91, B3LYP and \(\:\omega\:\)B97XD levels, we obtain values for the stretching vibrations of the O – H bond between 3300 cm− 1 and 3600 cm− 1 as predicted in the literature25,26. Using those scaling factors, we found that the C – H bond stretching vibrations are between 2747.91 cm− 1 and 2902.34 cm− 1 for molecular compound A, between 2939.78 cm− 1 and 3126.45 cm− 1 for compound B and between 2940.28 cm− 1 and 3126.34 cm− 1 for compound C respectively at the HF and B3LYP levels. The values of the stretching vibrations of the C = O bond of the molecular compounds A, B and C are all between 1634.44 cm− 1 and 1720.29 cm− 1 whatever the method used and taking into account the scaled factor. For molecular compound B, the values of the vibrational frequencies of the C = O double bond obtained by taking into account the scaling factors given above, are close to the experimental values obtained by Ollis and his collaborators in 197015. For compound B, the unscaled vibrational frequencies of the C = O bond of the cyclohex-2-enone, cyclohexanone and δ-valerolactone groups varies from 3.52 to 4.43%, from 4.62 to 5.48%, from 6.62 to 7.36% and from 15.28 to 16.45% respectively at the B3LYP, B3PW91, \(\:\omega\:\)B97XD and HF. From the obtained values, it is clear that the B3LYP functional provides more accurate results than all other DFT functionals. The results obtained by the ab initio HF method are not accurate because : \(\:\frac{{\text{F}}_{\text{i}}-{\text{F}}_{\text{e}\text{x}\text{p}}}{{\text{F}}_{\text{e}\text{x}\text{p}}}>10\text{\%}\). This can be explained by the fact that in the HF method, the electron-electron interaction is not specifically taken into account. The difference with the experimental values of the scaled vibrational frequencies of the C = O double bond of the cyclohex-2-enone, cyclohexanone and delta-valerolactone groups vary respectively between 1.553% and 2.716%, 2.194% and 3.307% and between 1.416% and 2.633% whatever the method.Generally, the stretching vibration values of the C = O bonds are between 1650 cm−1 and 1800 cm− 127. We can therefore, in view of all the above, conclude that the values of the stretching vibrations of the O-H, C-H and C = O bonds are in agreement with the results found in the literature.

Table 2 Some calculated and unscaled vibrational frequencies (cm-1) and IR intensity (M-1 cm-1) of our molecular structures (A, B and C) obtained at the B3LYP, B3PW91, \(\:\omega\:\)B97XD and HF levels using the 6-311G(d, p) basis set.
Full size table

UV-vis spectrum

In order to investigate the properties of electronic absorption, TD-DFT(B3LYP) along with 6-311G(d, p) basis set were used in gas phase and in solvent (water and chloroform) media. TD-DFT(B3LYP) have proved to be the most reasonable method used to determine UV-vis28 due to the generally observed strong correlation between theoretical and experimental data18. Theoretical wavelength, excitation energy, oscillator strength along with major contributions obtained using TD-DFT/B3LYP/6-311G(d, p) method is presented in Table 3. According to this Table 3, it come out that the wavelength and excitation energy follow inverse relationship. For compound A, the major contribution corresponds to the maximum intensity regardless of the solvent used, on the other hand, for compounds B and C, the contribution varies during the passage from the gas phase to the solvated phase.

Table 3 Theoretical electronic absorption spectra of molecular compounds a, B and C (absorption wavelength (nm), excitation energy E (eV), oscillator strength (f) and major contribution obtained using TD-B3LYP/6-311G(d, p) method.
Full size table

s

UV-vis absorption spectra of compounds A, B and C is presented in Fig. 4. We observed from Fig. 4; Table 3 that, the maximum picks are found in the UV region between 230 nm and 356 nm.

Fig. 4
figure 4

UV-vis absorption spectra of compounds A, B and C obtained using TD-B3LYP in gas phase and in solvent media employing 6-311G(d, p) basis set.

Full size image

Electronic properties, global and local reactivity descriptors

Frontier molecular orbitals analysis

Frontier molecular orbital (FMO) analysis describes the excitation of an electron from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO)1,29. The energetic behavior of the studied compounds was analyze using HF and DFT(B3LYP, B3PW91 and \(\:\omega\:\)B97XD) methods along with 6-311G(d, p) basis set. Figures 5, 6 and 7 give the representation of the 3D HOMO – LUMO energy of the studied compounds A, B and C respectively. Red and green colors represent respectively the positive and negative phase30. The HOMO–LUMO energy gap is an important parameter which give information on the activity of a giving molecular system.

Fig. 5
figure 5

3D HOMO-LUMO energy of compound A: 17-epi-methyl-6-hydroxylangolensate obtained using the 6-311G(d, p) basis set.

Full size image
Fig. 6
figure 6

3D HOMO-LUMO energy of compound B: 7-deacetoxy-7-oxogedunin obtained using the 6-311G(d, p) basis set.

Full size image
Fig. 7
figure 7

3D HOMO-LUMO energy of compound C: 7-deacetoxy-7R-hydroxygedenium obtained using the 6-311G(d, p) basis set.

Full size image

From this Figs. 5, 6 and 7, it emerge that compound B (Fig. 6) is the most reactive compound follow by compounds C (Fig. 7) and A (Fig. 5) respectively since it has the smallest value of energy gap. We also observed that, the HOMO level is mainly located on the furan group of each compound, whereas the LUMO level is mainly located on the cyclohex-2-enone group for compounds B and C, and cyclohexanone for compound A. This result give information about the charge transfer on a giving molecular system. In Figs. 6 and 7, the positive and negative phase of the compound B change respectively into negative and positive phase in compound C. This result is due to the fact that the C = O double bond in compound B was replace by C-OH bond in the compound C.

The fundamental gap (\(\:{E}_{f}\)) calculated as the difference between Ionization potential (IP) and electron affinity (EA) is well suitable to describe the reactivity of a compound31. As shown in Table 4, \(\:{E}_{f}\) is related to the hardness (\(\:\eta\:\)) by the relation \(\:{E}_{f}=2\eta\:\).

Table 4 Electronic and global reactivity descriptors of compounds a, B and C obtained at the B3LYP, B3PW91, \(\:\omega\:\)B97XD and HF levels using 6-311G(d, p) basis set.
Full size table

In Fig. 7, a relationship between \(\:{E}_{gap}\) and \(\:{E}_{f}\) is presented. From this Fig. 8 and Table 4, it come out that, similar values of \(\:{E}_{f}\) are obtain for compounds B and C respectively at the B3LYP, B3PW91 \(\:\omega\:\)B97XD and HF levels. For all the studied compounds, the short correlated DFT functional (B3LYP and B3PW91) values of \(\:{E}_{gap}\) respectively \(\:{E}_{f}\) are very close and different from the values obtained for the long correlated DFT functional (\(\:\omega\:\)B97XD) and non-correlated HF method. From Fig. 8, we observed that, for compound A, B and C, when we move from short, long and non-correlated methods, the correlation equations are giving respectively by : \(\:Y=0.281X+7.010\) (eV), \(\:Y=-0.038{X}^{2}+0.676X+5.450\) (eV) and \(\:Y=-0.034{X}^{2}+0.621X+5730\) (eV).

Fig. 8
figure 8

correlation graphs of fundamental gap in respect of the energy gap of compounds A, B and C obtained using short and long correlated DFT functionals and non-correlated HF method.

Full size image

Donor – acceptor parameter

DFT-B3LYP/6-311G(d, p) methods were used to determine some donor – acceptor parameter such as: Ionization potential (IP), Electron affinity (EA), electro-donating power (\(\:{\omega\:}^{-}\)), electro-accepting power (\(\:{\omega\:}^{+}\)), electro-donating index (\(\:{R}_{d}\)) and electro-accepting index (\(\:{R}_{a}\)) and also chemical potential (\(\:{\mu\:}_{CP}\)) and electrophilicity index (\(\:w\)). According to Table 5, compound C is consider as the most easily oxidized substances and therefore the most efficient antiradicals, since it has the lowest value of IP. Regarding EA values of the studied compounds, it come out that compound B have both large and positive value mining that it have a great capacity for accepting charge than compounds C and A and therefore represent the most efficient antiradicals expressed in terms of electron accepting capacity.

Taking into account electro-donating and electro-accepting power, we observed from Table 5 that compound A have the greatest capacity of donating charge while compound B have the greatest capacity of accepting charge. Comparing our results \(\:{\omega\:}^{-}\) to those of known structure in the literature, it emerge that compounds A, B and C are better antioxidant than \(\:\beta\:-\)carotene, psittacofulvins and astaxanthin21. From Table 5, it also come out that compounds A, B and C are better antireductant than vitamin A, C and E, \(\:\beta\:-\)carotene, psittacofulvins and astaxanthin21.

Table 5 Vertical Ionization energies (IP), vertical electron affinities (EA), electron donation and acceptance powers (\(\:{\omega\:}^{-};\:{\omega\:}^{+}\)), electro donating and accepting index (\(\:{R}_{d};\:{R}_{a}\)), chemical potential (\(\:{\mu\:}_{CP}=-\chi\:\)) and electrophilicity index (\(\:w\)) of molecular compounds a, B and C obtained using DFT-B3LYP/6-311G(d, p) method.
Full size table

Analysis of \(\:Ra\) and \(\:Rd\) indexes lead us to the conclusion that, compounds A, B and C are less effective electron acceptor than F and a more effective electron donor than Na atom. According to Xavier and his coworkers32 and base to the results presented in Table 5, we conclude that compounds A and B can be consider as good nucleophile respectively good electrophile since the values of chemical potential and electrophilicity index are low respectively higher for compounds A and B.

Local reactivity descriptors

In order to determine the atoms that are most likely to react during a chemical reaction, we studied the local reactivity of the molecular compounds A, B and C. This study is based on the use of Fukui functions f(r) determined using natural atomic charges provided by NPA when performing NBOs calculation33,34. The Fukui function f(r) is a local reactivity descriptor that indicates the best way to change the number of electrons in a molecule35. It measures the response of the electron density to the addition of electrons (electrophile) \(\:{f}_{k}^{+}\left(r\right)\) or to the donation of electrons (nucleophile) \(\:{f}_{k}^{-}(r\)), when detecting a mechanism of reaction36. This electrophilic or nucleophilic character of each atom can also be determined by the parameter \(\:\varDelta\:f\left(r\right)={f}_{k}^{+}\left(r\right)-\:{f}_{k}^{-}\)(r). Thus the atom will be electrophilic if ∆f < 0 and nucleophilic if ∆f > 012,36. According to the curves presented in Fig. 9, were the x axis represent the atoms number giving in Fig. 1, we can conclude that atoms C4, C9 and C11 of compound A, atoms C1, C8 and C15 of compound B, atoms C1, C15 and H63 of compound C have an electrophilic character because, for each molecule, these atoms have the lowest ∆f value. Atoms O12, O16 and C51 of compound A, atoms O19, C50 and C54 of compound B, atoms C49, C57 and O62 of compound C have a nucleophilic character. These atoms are therefore the most likely to react during a chemical reaction and indicate the propensity of the electronic density to deform at a given position to accept or donate electrons.

Fig. 9
figure 9

Electrophilicity/nucléophylicity of compounds A, B and C obtained at the HF, B3LYP, B3PW91 and ωB97XD levels using 6-311G(d, p) basis set in gas phase.

Full size image

Nonlinear optical properties

Table 6 presents some nonlinear optical parameters values of the molecular compounds A, B and C. These parameters were obtained by means of formulas present in the literature37,38. It emerges from this Table 6 that, compound A gives higher values ​​of µ, ⍺ and β. The difference is found to be approximately of the order of 1.22%, 5.65% and 14.60% between the molecular compounds A and B; 42.83%, 4.79% and 22.81% between molecules A and C; then 42.13%, 0.91% and 8.89% between compounds B and C respectively for µ, ⍺ and β. By comparing our first-order molecular hyperpolarizability values ​​with the molecule taken as reference (urea molecule β = 372.8 × 10− 33 esu)37, we notice that our values ​​are larger and differ approximately on the order of 759.75%, 623.67% and 565.27% for the molecular compounds A, B and C, respectively. In addition to this, it is observed from the values of energy gap that, β follow inverse relationship with Egap for all our molecules. These results allow us to conclude that molecular compounds A, B and C have very good stability and are potential candidates for nonlinear optical applications.

Table 6 Dipole moment (µ), average polarizability (⍺), anisotropy of polarizability (∆⍺), molar refractivity (MR), first order hyperpolarizability (β), the vector component of hyperpolarizability (βvec) and the angle (Ɵ) of compounds a, B and C respectively obtained using the 6-311G(d, p) basis set.
Full size table

The values ​​of βx, βy and βz of molecule A are similar whatever the method used. This suggests that, during the polarization process of this molecule, charges should be transferred in x, y or z directions. For molecules B and C, we observe that, the values ​​of βx and βy are very high compared to the values ​​of βz, with βx greater than βy. This suggests that, during the polarization process of these two molecules, the charges is expected to be transfer between the x and y directions and be closer to x than to y. The values ​​of the angles between βvec and β are also given in Table 6.

Thermochemical properties of compounds a, B and C

The values of Enthalpy (H), standard Gibbs free energy (G), standard entropy (S), heat capacity at constant pressure (Cp) and heat capacity at constant volume (Cv) of compounds A, B and C are giving in Table 7. These values were obtained using short correlated (B3LYP), long correlated (ωB97XD) DFT functional and non-correlated HF method. The results presented in Table 7 were obtained using the standard temperature (T = 298.15°K) and pressure (P = 1atm). From this Table 7, it can be seen that, compound A has the lowest values of G and H respectively the highest values of S, Cp and Cv whatever the method used. According to Table 4, we found that, the values of the studied thermodynamic parameters decrease when we move from short correlated to long correlate DFT functional and from non-correlated HF method.

Table 7 Standard enthalpy H (kJ/mol), standard Gibbs free energy G (kJ/mol), standard entropy S (J/mol.K), heat capacity at constant pressure cp and volume cv (J/mol.K) of compounds a, B and C obtained using the 6-311G(d, p) basis set.
Full size table

Temperature is a very important thermodynamic parameter for therapeutic molecules. It is generally used for production and storage purpose39. It also provides information about the balance of energetic forces driving binding interactions and is essential for understanding and optimizing molecular interactions40. Due to its importance, the effect of temperature on G, H, S and Cp was examined. Figure 10 show the variation curves of some thermodynamics parameters obtained using B3LYP/6-311G(d, p) method. From this Fig. 10 and according to the obtained values, it come out that for all the studied compounds, the values of H, S and Cp increase, while the values of G decrease with the increase of temperature. The temperature values ​​considered for the variation of the thermodynamic parameters were chosen because they are not far from the minimum and maximum temperature of the globe. When the temperature move from 200 K to 330 K, the values of H move from − 4334430.54 to -4334365.66 kJ/mol, from − 3832990.06 to -3832932.44 kJ/mol and from − 3836104.73 to -3836045.98 kJ/mol respectively for compounds A, B and C. For standard free energy (G) the values vary from − 4334563.51 to -4334666.01 kJ/mol, from − 3833110.94 to -3833203.74 kJ/mol and from − 3836226.14 to -3836319.55 kJ/mol respectively for compounds A, B and C. The high and negative values of Gibbs free energy (G) obtained for the studied molecular compounds shows that they can easily be bind to biomolecular complex.

Fig. 10
figure 10

Plots of H (left lower), G (left upper), S (right lower) and Cp (right upper) with temperature of cmpounds A, B and C obtained using B3LYP/6-311G(d, p).

Full size image

Conclusion

Three molecules from the Khaya Grandifolia plant, namely compounds A, B and C, were studied in this manuscript using DFT (B3LYP, B3PW91 and \(\:\omega\:\)B97XD) and HF methods as well as the 6-311G(d, p) basis set. Similar values ​​were found when analyzing their structural parameters. The study of their vibrational frequency leads us to the conclusion that these molecular compounds are all stable. It appears from all the compounds studied that the stretching vibrations of aromatic C-H bonds are between 2950 and 3200 cm− 1. UV-vis analysis of compounds A, B, and C shows that the maximum peaks are in the UV region between 230 and 356 nm. We also noted from this previous result that for compound A, the maximum peak corresponds to the maximum intensity while for compounds B and C, it corresponds respectively to the transition from the HOMO-2 form to LUMO + 1 and from HOMO-2 to LUMO. From the HOMO-LUMO energy gap, it appears that compound B is the most reactive compound, followed respectively by compounds C and A. From the 3D HOMO-LUMO curves, it appears that the positive and negative phases of the compound B change to its opposite in compound C. Certain donor-acceptor parameters namely \(\:,\:EA,\:Rd,\:Ra,\)\(\:{\mu\:}_{CP}\), \(\:\omega\:\), \(\:{\omega\:}^{-}\) and \(\:{\omega\:}^{+}\) calculated in this manuscript lead us to the conclusion that compound A has the highest capacity to give charges while compound B has the highest capacity to accept charges than compounds C and A. We can also conclude that, compound C is the most easily oxidizable compound and therefore the most efficient antiradical. By comparing the results obtained for the molecular compounds studied, we found that compounds A, B and C are better antioxidants than β-carotene, psittacofulvens and astaxanthin, better antireductants than vitamins A, C and E, β-carotene, psittacofulvens and astaxanthin. Compounds A, B, and C are less efficient electron acceptors than fluorine and more efficient electron donors than Na. compounds A and B can be considered as good nucleophiles respectively good electrophiles due to their \(\:{\mu\:}_{CP}\) and \(\:\omega\:\) values. From the nonlinear optical parameters of these compounds, we can conclude that they can be used as nonlinear optical materials. During the polarization process, charges can be transferred in the X, Y or Z direction for compound A while for compounds B and C, charges can be transferred between the X and Y directions. Some thermodynamic properties such as standard Gibbs free energy (G), enthalpy (H), standard entropy (S), heat capacity at constant volume (Cv) and Heat capacity at constant pressure (Cp) were calculated. It appears from the results obtained that the molecular compounds studied can easily bind to biomolecular complexes.